Experimental Research of Inter-Satellite Beaconless Laser Communication Tracking System Based on Direct Fiber Control

Abstract

We propose a compact, beaconless inter-satellite laser communication tracking system based on direct fiber control to address the complexity and resource demands of conventional pointing, acquisition, and tracking (PAT) architectures. Unlike traditional sensor-based or beacon-assisted schemes, the proposed method employs a piezoelectric ceramic tube (PCT) to generate high-frequency, small-amplitude nutation of the single-mode fiber (SMF) tip, enabling real-time alignment correction using only the coupled optical power of the communication signal. This fully closed-loop tracking approach operates without position sensors and eliminates the need for beam splitting, external beacon sources, or auxiliary position detectors. A theoretical model is developed to analyze the influence of algorithm parameters and optical spot jitter on dynamic tracking performance. Experimental results show that the closed-loop system reliably converges to the optical spot center, achieving a fine-tracking accuracy of 4.6 $\mathsf{\mu }$rad and a disturbance suppression bandwidth of 200 Hz. By significantly simplifying the terminal architecture, the proposed approach provides an efficient and SWaP-optimized solution for inter-satellite and satellite-to-ground optical communication links.

1. Introduction

Free-space optical communication (FSOC) requires high-precision pointing, acquisition, and tracking (PAT) to maintain stable laser beam alignment [1,2,3]. Spatial light coupling is particularly vulnerable to platform vibrations, alignment errors, and environmental disturbances, all of which can significantly degrade coupling efficiency in practical inter-satellite scenarios [4,5,6,7]. Consequently, fine tracking systems (FTSs) are essential to compensate for coarse tracking residuals (CTRs) via high-bandwidth control, ensuring link stability and continuity [8,9,10,11].

Current fine tracking strategies generally fall into two categories: sensor-based and nutation-based methods. Sensor-based systems utilize quadrant detectors (QDs) or CMOS imagers to drive fast-steering mirrors (FSMs). For example, Wang et al. optimized a CCD–FSM architecture to enhance tracking bandwidth [10]. Legacy missions such as SILEX [12] and recent demonstrations like OSIRIS4CubeSat [13] have successfully validated this sensor-based architecture on-orbit. However, these methods inherently require beam splitting—reducing the optical power available for communication—and are susceptible to non-common-path errors induced by thermal drift or structural deformation. Alternatively, nutation-based schemes infer pointing errors from the modulation of coupled optical power. Swanson et al. demonstrated high-bandwidth tracking using an electro-optic nutator [14]; however, such systems typically suffer from higher complexity and insertion loss compared to mechanical solutions. Gao et al. subsequently validated mechanical nutation for fiber coupling [15].

Direct fiber control utilizing piezoelectric actuation has also been implemented in spaceflight, most notably in NASA’s Lunar Laser Communication Demonstration (LLCD) [16,17]. While the LLCD terminal achieved high-accuracy fine tracking using mechanically nutated fiber tips [16], its architecture relied on a dedicated uplink beacon, auxiliary coarse-tracking sensors, and a complex inertial stabilization platform [17]. Such beacon-assisted schemes entail significant optical complexity and impose stringent boresight alignment requirements.

Despite these advancements, the experimental demonstration of a fully beaconless, fiber-only closed-loop PAT system within a compact terminal architecture remains underexplored. This gap is particularly critical for small-satellite platforms, where strict size, weight, and power (SWaP) constraints often preclude the use of conventional, sensor-intensive tracking hardware.

To address this need, we propose an inter-satellite beaconless PAT system based on direct fiber control. By eliminating beacon sources, beam splitters, and external position sensors, the system utilizes a piezoelectric ceramic tube (PCT) to induce high-frequency fiber nutation and performs closed-loop correction solely from the received communication signal power. By integrating a piezoelectric ceramic tube with a single-mode fiber, a compact actuation–reception mechanism is realized, in which communication signal reception, power-modulation-based directional tracking correction without position sensors, and fine pointing execution are jointly enabled within a single structure. Despite its simplified architecture, the proposed system achieves microradian-level tracking accuracy and demonstrates a disturbance rejection bandwidth of 200 Hz in experiments, indicating strong potential for resource-constrained intersatellite and satellite-to-ground optical communication applications.

The paper is organized to reflect the development from system design to experimental verification. Section 2 introduces the system architecture and operating principle. Section 3 focuses on the theoretical analysis of the proposed fiber-nutation-based tracking method. Section 4 presents the experimental setup and discusses the closed-loop tracking performance. Conclusions and future work are provided in Section 5.

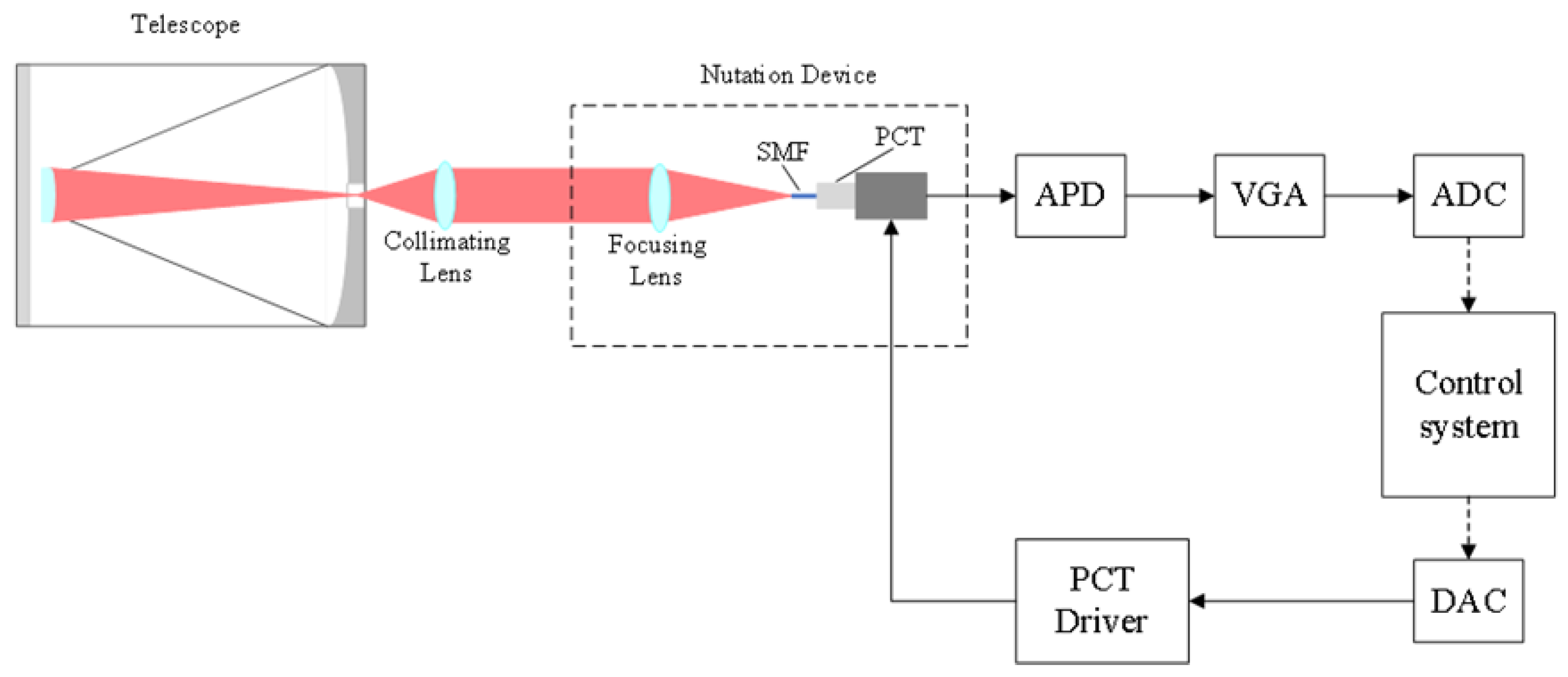
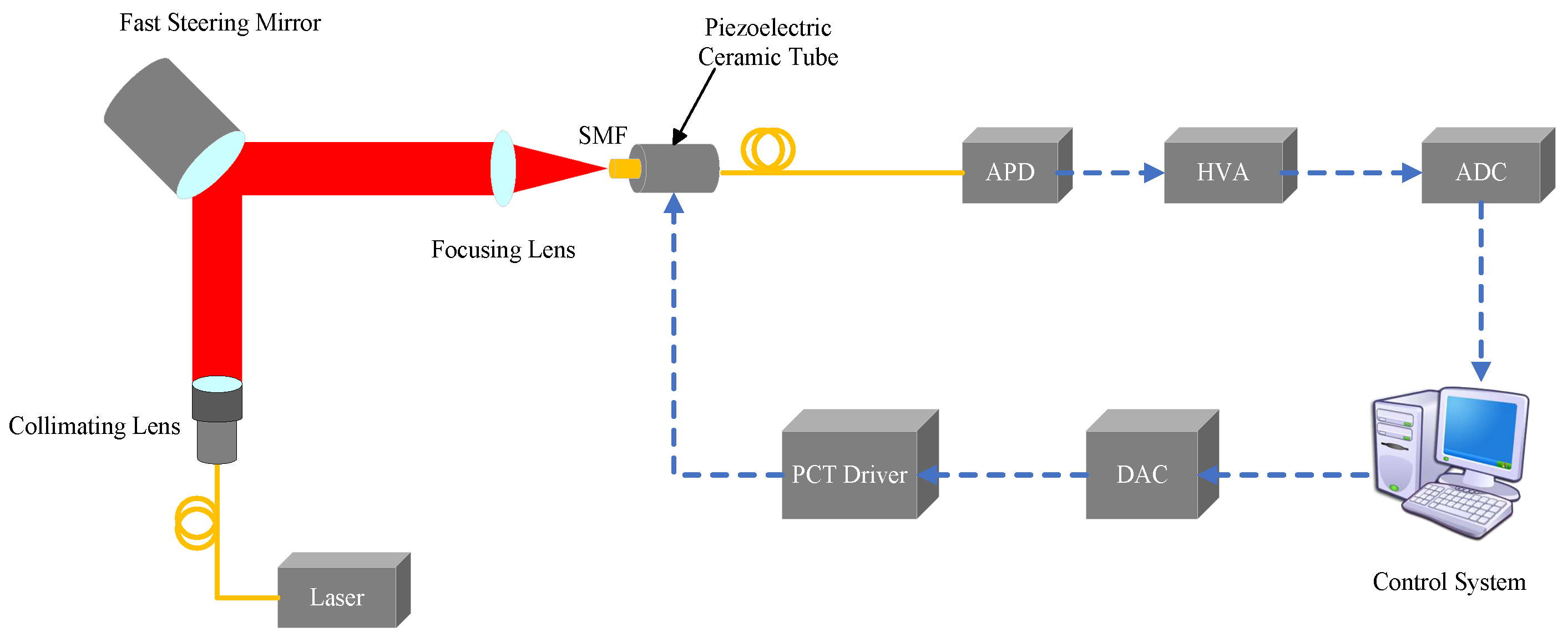
2. System Architecture

The architecture of the fiber nutation tracking system based on direct fiber control is illustrated in Figure 1. The incident light entering the telescope is focused onto the focal plane by a coupling lens. A piezoelectric ceramic tube (PCT) directly drives the fiber end face, which is fixed at its center, to perform high-frequency, small-amplitude two-dimensional nutation within the focal plane.

The control system estimates in real time the displacement direction of the incident spot relative to the fiber end face based on variations in the feedback voltage collected by the photodetector, and computes the required displacement compensation through a control algorithm. The control signal is then delivered to the PCT driver via digital-to-analog conversion, actuating the miniature PCT actuator to move the fiber end face toward the spot center. In this manner, the fiber end face continuously follows the spot center, ultimately achieving closed-loop reception and tracking of the incident optical beam.

In the proposed system architecture, the piezoelectric ceramic tube and the single-mode fiber are integrated to form a compact actuation reception mechanism. The PCT drives the fiber tip to perform high-frequency, small-amplitude nutation in the focal plane, which induces periodic modulation of the coupled optical power. The resulting power variation provides directional information for tracking correction, enabling the control algorithm to update the nutation center and realize closed-loop tracking without the use of position sensors. Through this integration, communication signal reception, tracking control based on optical power modulation, and fine pointing execution are realized within a single unified structure.

These results demonstrate that the system achieves tracking accuracy on the order of a few microradians, and the spot position remains highly stable after convergence.

3. Fiber Nutation Principle Based on Direct Fiber Control

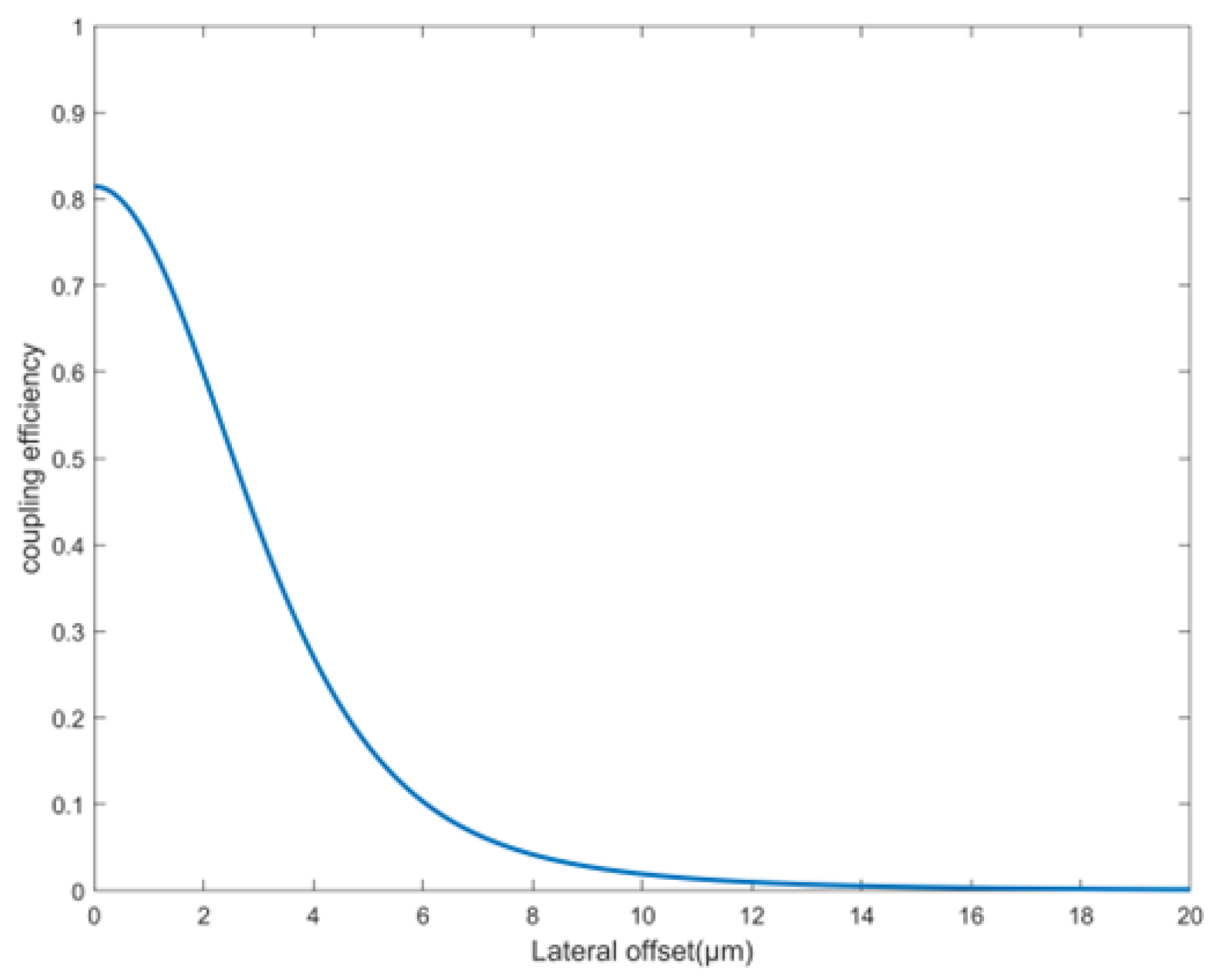
3.1. Principle of SMF Coupling

In space laser communication systems, when a signal beam is transmitted from a space platform over a sufficiently long propagation distance, it can be approximated as a plane wave upon reaching the receiving aperture. After passing through a lens, the beam is focused onto the focal plane, forming an Airy disk that couples into the fiber. The mode field intensity distribution of the Airy pattern at the fiber end face is given by [16,17]:

$$U\left(r\right)=exp\left[jk\left(f+{\displaystyle \frac{r^2}{2f}}\right)\right]{\displaystyle \frac{\pi D^2}{4\lambda f}}\left[2{\displaystyle \frac{J_1(kDr/2f)}{kDr/2f}}\right]$$

(1)

where $\lambda$ is the wavelength of the laser emitted by the space platform, k is the wavenumber, $J_1$ represents the first-order Bessel function, and r denotes the radial distance from the optical axis. Considering that only the amplitude affects the coupling efficiency, Equation (1) can be simplified as:

$$A\left(r\right)={\displaystyle \frac{\pi D^2}{4\lambda f}}\left[2{\displaystyle \frac{J_1(3.83r/\omega )}{3.83r/\omega }}\right]$$

(2)

where $\omega =1.22\lambda f/D$. Since only the fundamental mode exists in SMF, it can be approximated as a Gaussian distribution, and its amplitude can be expressed as:

$$M\left(r\right)=\sqrt{{\displaystyle \frac{2}{\pi {\omega }_0^2}}}exp\left(-{\displaystyle \frac{r^2}{{\omega }_0^2}}\right)$$

(3)

where ${\omega }_0$ is the mode field radius of the single-mode fiber (SMF). The coupling efficiency from free-space light into the SMF is defined as the ratio of the power coupled into the SMF $P_c$ to the total optical power incident on the fiber end-face $P_a$. In practical applications, due to platform vibrations and assembly misalignments, the laser beam cannot be perfectly projected onto the center of the SMF core after passing through the optical reception system. This results in a deviation between the focused spot and the SMF core at the receiver end, primarily due to lateral displacement. When a lateral offset $\rho$ exists in the optical link, the coupling efficiency expression for the SMF is given by:

$$\eta ={\left|{\int }_0^{\infty }{\int }_0^{2\pi }A\left(r\right)M(r-\rho )rdrd\theta \right|}^2\approx {\eta }_{max}exp\left(-{\displaystyle \frac{{\rho }^2}{{\omega }_0^2}}\right)$$

(4)

Typically, the radius of a single-mode fiber (SMF) is between 4∼5 $\mathsf{\mu }$m. Figure 2 shows the relationship between lateral offset and coupling efficiency for an SMF radius of 5 $\mathsf{\mu }$m.

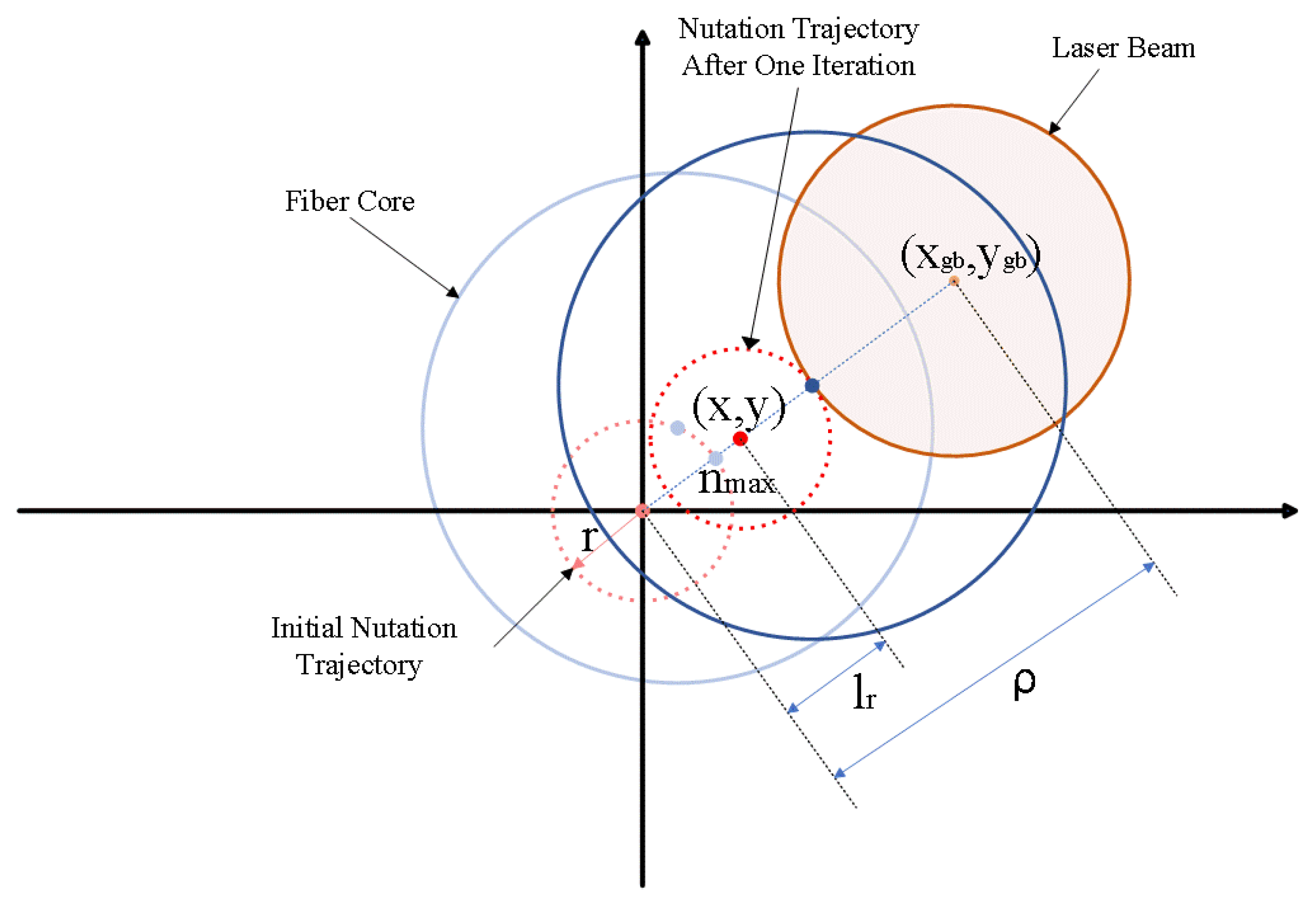
3.2. Algorithm for Fiber Coupling

Based on the field-matching principle, when the focal spot of the incident light is not perfectly aligned with the fiber core, the coupling efficiency decreases. During the process of fiber nutation, the coupling efficiency changes periodically. If no variation is observed, it indicates that the incident beam center coincides with the fiber core, achieving precise alignment. The spatial light is directly coupled into the SMF through the optical system, and the coupled light is converted into an electrical signal by a detector and sent to the controller, forming a closed-loop control system. The fiber is positioned at the center of the PCT. A Cartesian coordinate system is established with the initial fiber end-face position as the origin. Two independent sinusoidal voltages with a 90° phase difference are applied to drive the azimuth and elevation axes of the PCT, enabling the SMF end face to scan in a circular trajectory. The initial nutation center is (0,0), the nutation radius is r, the step size per iteration is $l_r$, and the number of sampling points per cycle is N. The coordinates of the nth sampling point ($n=0,1,2,\dots ,N$) on the circular trajectory is expressed as:

$$\left\{\begin{array}{c}x=rsin\left(2\pi {\displaystyle \frac{n}{N}}\right)\hfill \\ y=rcos\left(2\pi {\displaystyle \frac{n}{N}}\right)\hfill \end{array}\right.$$

(5)

During one nutation cycle, the optical power received by the SMF at each sampling point is compared. The point with the maximum power is marked as $P_{max}$, and the nutation center is shifted toward that direction by a convergence step. The coordinates of any point on the new circular trajectory after the offset are expressed: ($n=0,1,2,\dots ,N$) on the circular trajectory are expressed as:

$$\left\{\begin{array}{c}x=rsin\left(2\pi {\displaystyle \frac{n}{N}}\right)+l_{r}sin\left(2\pi {\displaystyle \frac{n_{max}}{N}}\right)\hfill \\ y=rcos\left(2\pi {\displaystyle \frac{n}{N}}\right)+l_{r}cos\left(2\pi {\displaystyle \frac{n_{max}}{N}}\right)\hfill \end{array}\right.$$

(6)

After m iterations, the focal spot of the incident light converges to the spot center. At this time, the coordinates $(x_m,y_m)$ of any point on the circular trajectory are expressed as:

$$\left\{\begin{array}{c}{x}_m=rsin\left(2\pi {\displaystyle \frac{n}{N}}\right)+\sum _{j=1}^m{l}_{r}sin\left(2\pi {\displaystyle \frac{n_{jmax}}{N}}\right)\hfill \\ y_m=rcos\left(2\pi {\displaystyle \frac{n}{N}}\right)+\sum _{j=1}^m{l}_{r}cos\left(2\pi {\displaystyle \frac{n_{jmax}}{N}}\right)\hfill \end{array}\right.$$

(7)

The fiber nutation tracking process in the focal plane is illustrated in Figure 3.

Assuming the spot center is $s={[x_{gb},y_{gb}]}^T$, the center of the fiber nutation at the kth iteration is $c_k={[x_k,y_k]}^T$. The lateral offset vector between the current position and the spot center is given by:

$$e_k=s-c_{k-1}$$

(8)

At this point, the lateral offset is ${\rho }_k=\left|\right|e_k\left|\right|$. In practical free-space optical communication systems, due to platform disturbances, atmospheric fluctuations, or vibrations, the geometric center of the incident optical spot at the receiver typically exhibits periodic variations. When disturbances are present, assuming a sine disturbance along the x-axis, the position of the spot center at the kth iteration is given by:

$$s_k=\left[\begin{array}{c}{x}_0+asin(k\Delta \varphi )\\ y_0\end{array}\right],\Delta \varphi =2\pi {\displaystyle \frac{f_2}{f_1}}$$

(9)

where $f_1$ is the nutation frequency, $f_2$ is the disturbance frequency, and a is the disturbance amplitude. The maximum drift of the spot center within one nutation cycle is $D=2a|sin(\Delta \varphi /2\left)\right|$. Assuming the system sampling frequency is $f_m=n{f}_1$ (corresponding to a phase sampling interval of $2\pi /n$), if the drift angle of the spot center is smaller than $2\pi /n$, this angle drift no longer affects the algorithm’s judgment results and offset calculation, meaning that the spot center is effectively stationary during one nutation cycle. Under this condition, the updated nutation center at the kth iteration is:

$$c_k=c_{k-1}+l_r{u}_k,u_k={\displaystyle \frac{e_k}{{\rho }_k}}$$

(10)

When the frequency ratio between nutation and disturbance is fixed, each nutation cycle results in a fixed drift $d_k$ due to the disturbance, which can be expressed as:

$$d_k=s_{k+1}-s_k$$

(11)

Accordingly, the error vector at the $k+1$th iteration is:

$$e_{k+1}=e_k-l_r{u}_k+d_k$$

(12)

Using the triangle inequality to estimate the upper bound, we obtain:

$$\left|\right|e_{k+1}\left|\right|\le \left|\right|e_k\left|\right|-l_r+\left|\right|d_k\left|\right|$$

(13)

For the system to converge (i.e., the error magnitude must decrease), the following condition must be satisfied: $\left|\right|e_{k+1}\left|\right|<\left|\right|e_k\left|\right|$. The following can be derived:

$$l_r>\left|\right|d_k\left|\right|$$

(14)

The convergence step size $l_r$ must be greater than the current optical spot disturbance’s fluctuation amplitude to ensure overall error convergence. During convergence, the actual offset is given by:

$${\rho }_{k+1}^2=\left|\right|e_{k+1}{\left|\right|}^2=\left|\right|e_k-l_r{u}_k+d_k{\left|\right|}^2$$

(15)

Since $u_k$ is the unit vector of the nutation center update direction, which is in the same direction as $e_k$, we have $e_k={\rho }_k{u}_k$, and thus:

$$\left|\right|e_k-l_r{u}_k\left|\right|=|{\rho }_k-l_r|$$

(16)

Substituting Equation (16) into Equation (15), we obtain:

$${\rho }_{k+1}^2={({\rho }_k-l_r)}^2+2({\rho }_k-l_r)u_k·d_k+\left|\right|d_k{\left|\right|}^2$$

(17)

Using the Cauchy–Schwarz inequality and triangle inequality, the upper and lower bounds for the nutation center’s relative drift are derived as:

$${\rho }_{k+1}\in \left[\right|{\rho }_k-l_r|-D,|{\rho }_k-l_r|+D]$$

(18)

Under ideal conditions, when no external disturbance is present, the fiber end face continuously approaches the spot center via circular scanning. However, since the convergence step size $l_r$ is fixed, it is difficult to stop exactly at the target point during system operation. This results in a ‘overshoot-backlash’ phenomenon, causing the optical power measured in one nutation cycle to vary. After sufficient iterations, the final error ${\rho }_k$ is constrained to a range. When periodic external disturbances are present, the spot center will exhibit periodic oscillations. Each nutation iteration causes a shift $d_k$ in the spot center, and its modulus is less than D, so the equivalent error will be amplified by an upper bound, with the total error mapped within a range of:

$$0\le {\rho }_k\le l_r+D$$

(19)

We define the system’s steady-state error as the average relative center drift after k iterations of convergence:

$$\overline{\rho }=\sum _{n=0}^k{\rho }_k$$

(20)

When the fiber end face performs circular scanning with a nutation radius r, the relative static deviation from the target is ${\rho }_0$, representing the distance between the nutation center and the spot center. Under ideal conditions, assuming the spot center is stationary, the instantaneous position relative to the target point is $\sqrt{{\rho }_0^2+r^2-2{\rho }_{0}rcos\varphi }$. The average coupling efficiency over one nutation cycle can be expressed as:

$$\overline{\eta }({\rho }_0,r)={\eta }_{max}exp\left[-{\displaystyle \frac{({\rho }_0^2+r^2)}{{\omega }_0^2}}\right]I_0\left({\displaystyle \frac{2{\rho }_{0}r}{{\omega }_0^2}}\right)$$

(21)

As shown in Figure 4, when the spot center coincides with the fiber core center, the average coupling efficiency decreases as the nutation radius increases. This is because a larger nutation radius results in a larger average lateral offset of the fiber end-face during one scanning cycle, causing the energy to be distributed over a wider area and thus reducing the overall coupling efficiency. Typically, the mode field radius of a single-mode fiber is around 5 $\mathsf{\mu }$m, and when $r<$ 1.1557 $\mathsf{\mu }$m, the average coupling efficiency loss is less than 5%, with low sensitivity to changes in the nutation radius. Under ideal conditions, where no disturbances are present, the steady-state error after kth iterations converges to a two-point limit cycle. The nutation center oscillates between two points near the spot center. When disturbances exist, the steady-state error falls within a specific range $[0,l_r+D]$, and its value is given by:

$$\overline{\rho }={\displaystyle \frac{l_r+D}{2}}$$

(22)

As indicated earlier, the frequency ratio $r_f$ is inversely proportional to D. As the frequency ratio increases, the steady-state error approaches $l_r/2$. The average coupling efficiency after kth iterations of convergence is then:

$$\overline{\eta }(\rho ,r)={\eta }_{max}exp\left[-{\displaystyle \frac{({(l_r/2)}^2+r^2)}{{\omega }_0^2}}\right]I_0\left({\displaystyle \frac{l_{r}r}{{\omega }_0^2}}\right)$$

(23)

Figure 5 illustrates the change in average coupling efficiency with convergence step size when the nutation radius ranges from 0.25 to 1.5 $\mathsf{\mu }$m. The disturbance amplitude is $3 \mathrm{\mu }$m, and as shown in Figure 5, the average coupling efficiency decreases monotonically as the convergence step size $l_r$ increases. As $l_r$ increases, the discretization error and overcorrection effect introduced by excessively large step sizes lead to a significant reduction in steady-state coupling efficiency. Additionally, the nutation radius has a significant impact on the coupling efficiency curve: under the same convergence step size, a larger nutation radius corresponds to lower average coupling efficiencies. The range of nutation radius is determined based on previous analysis of the coupling efficiency decay characteristics when the spot center and fiber core are perfectly aligned. To maintain high coupling performance ($\eta \ge 0.95$), the allowed convergence step size decreases significantly as the nutation radius increases. This indicates that there is a significant coupling constraint between convergence step size and nutation radius: under large nutation radius, smaller step sizes are required to maintain stable high-efficiency coupling, whereas in small nutation radius conditions, larger step sizes are permitted, thus achieving faster convergence without compromising efficiency. Using the Cauchy–Schwarz inequality, the standard deviation of coupling efficiency after convergence can be expressed as:

$$Var\left[\eta \right]=E_{\rho }\left[Va{r}_{\varphi }\left(\eta \right|\rho )\right]+Va{r}_{\rho }\left(E_{\varphi }\left[\eta \right|\rho ]\right)$$

(24)

This decomposition corresponds to two physical effects: one is the rapid fluctuation caused by changes in nutation phase under fixed offset conditions, and the other is the slow drift fluctuation caused by lateral offset changes with convergence step size and disturbance amplitude. Using the Cauchy–Schwarz inequality, we can combine these two uncertainties into a closed-form expression. Considering the coupling between a single-mode fiber and a Gaussian beam, when only the lateral offset exists, the instantaneous distance between the spot center and the target point is $\sqrt{{\rho }^2+r^2-2\rho rcos\varphi }$. The instantaneous relative coupling efficiency is a function of the offset $\rho$ and nutation phase $\varphi$, and the average coupling efficiency $\overline{\eta }$ for one nutation cycle is given by:

$$E_{\varphi }\left[\eta \right|\rho ]=\overline{\eta }(\rho ,r)={\eta }_{max}exp\left[-{\displaystyle \frac{({\rho }^2+r^2)}{{\omega }_0^2}}\right]I_0\left({\displaystyle \frac{2\rho r}{{\omega }_0^2}}\right)$$

(25)

Similarly, the second moment can be derived as:

$$E_{\varphi }\left[{\eta }^2\right|\rho ]=exp\left[-{\displaystyle \frac{2({\rho }^2+r^2)}{{\omega }_0^2}}\right]I_0\left({\displaystyle \frac{4\rho r}{{\omega }_0^2}}\right)$$

(26)

The conditional variance is then given by:

$$Va{r}_{\varphi }\left[\eta \right|\rho ]=exp\left[-{\displaystyle \frac{2({\rho }^2+r^2)}{{\omega }_0^2}}\right]\left[I_0\left({\displaystyle \frac{4\rho r}{{\omega }_0^2}}\right)-I_0^2\left({\displaystyle \frac{2\rho r}{{\omega }_0^2}}\right)\right]$$

(27)

The center drift between the nutation center and the spot center is no longer monotonically decreasing after convergence, but is constrained within a steady-state range. The standard deviation of center drift is given by:

$${\sigma }_{\rho }=\sqrt{Var\left(\rho \right)}={\displaystyle \frac{\Delta }{\sqrt{12}}}={\displaystyle \frac{l_r+D}{\sqrt{12}}}$$

(28)

where $\Delta \triangleq {\rho }_{max}-{\rho }_{min}=l_r+D$. When the distribution of the random variable $\rho$ around a central value $\overline{\rho }$ is sufficiently concentrated, the first-order Taylor expansion can be used for approximation.

$$Va{r}_{\rho }\left(\overline{\eta }\left(\rho \right)\right)\approx {\left[{\overline{\eta }}^{\prime }\left(\overline{\rho }\right)\right]}^2{\sigma }_{\rho }^2\approx {\left[\overline{\eta }\left(\overline{\rho }\right){\displaystyle \frac{2}{{\omega }_0^2}}\left(-\overline{\rho }+r{\displaystyle \frac{I_1\left(z_0\right)}{I_0\left(z_0\right)}}\right)\right]}^2{\sigma }_{\rho }^2$$

(29)

Finally, the approximate formula for the standard deviation of coupling efficiency can be derived as:

$${\sigma }_{\eta }\approx {\left\{exp\left[-{\displaystyle \frac{2({\overline{\rho }}^2+r^2)}{{\omega }_0^2}}\right]\left[I_0\left({\displaystyle \frac{4\overline{\rho }r}{{\omega }_0^2}}\right)-I_0^2\left({\displaystyle \frac{2\overline{\rho }r}{{\omega }_0^2}}\right)\right]+{\left[\overline{\eta }\left(\overline{\rho }\right){\displaystyle \frac{2}{{\omega }_0^2}}\left(-\overline{\rho }+r{\displaystyle \frac{I_1\left(z_0\right)}{I_0\left(z_0\right)}}\right)\right]}^2{\displaystyle \frac{{\Delta }^2}{12}}\right\}}^{1/2}$$

(30)

In Figure 6, we present the variation of the relative standard deviation of center drift ${\sigma }_{\eta }$ with the frequency ratio $f_1/f_2$ for different convergence step sizes $l_r$. As observed, with an increase in the convergence step size $l_r$, the system’s drift standard deviation gradually increases, indicating that the system stability deteriorates. On the other hand, as the frequency ratio $f_1/f_2$ increases, the standard deviation for all curves significantly decreases and stabilizes, indicating that at higher frequency ratios, the system’s stability improves and the drift stabilizes. This result suggests that at lower frequency ratios, the convergence step size has a more pronounced impact on system stability, whereas at higher frequency ratios, the system’s stability increases.

Although nutation scanning introduces instantaneous lateral offsets during each cycle, the theoretical analysis results demonstrate that, with appropriate selection of the nutation radius and convergence step size, the efficiency loss and steady-state tracking error remain bounded and do not compromise the overall accuracy or stability of the system.

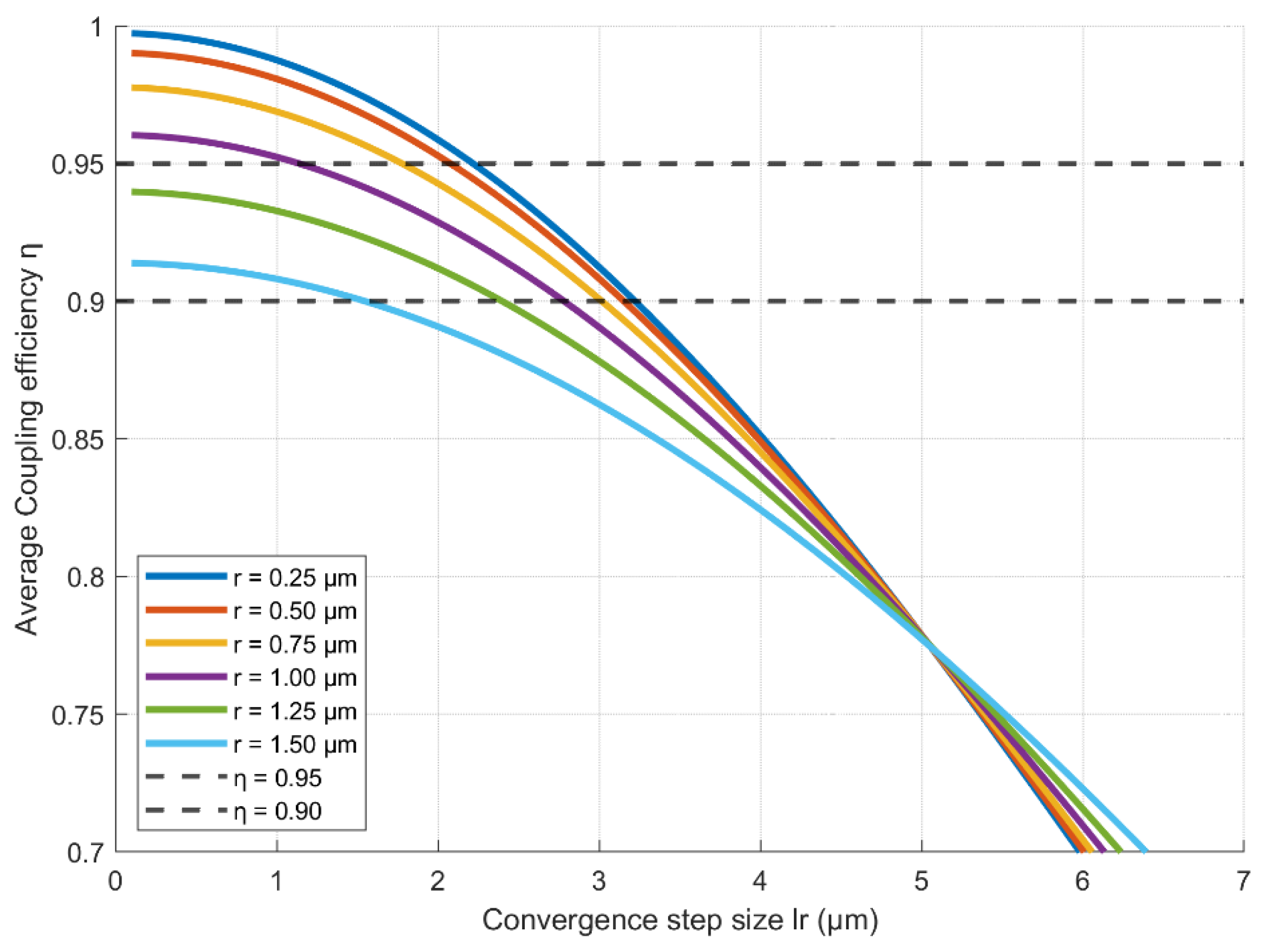
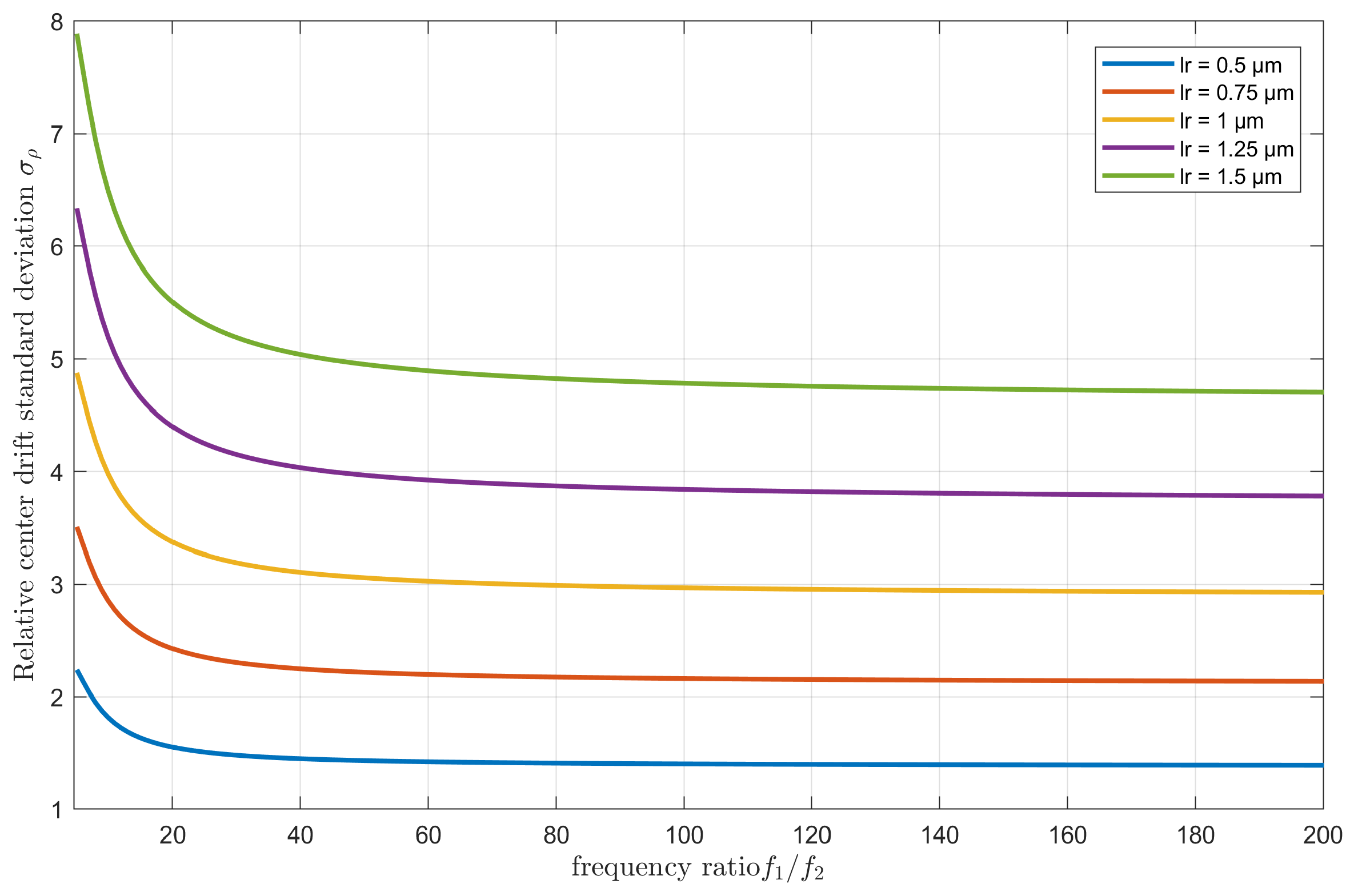
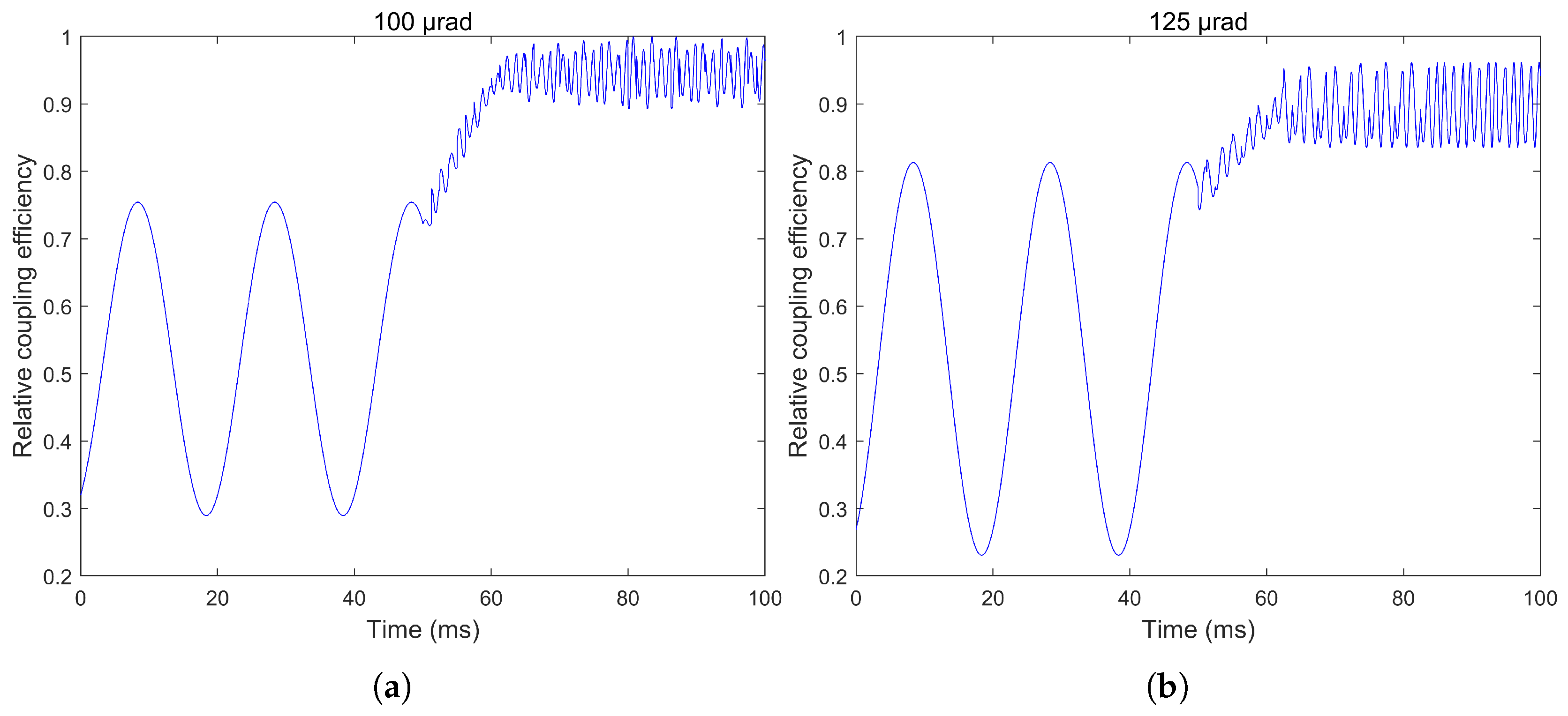
3.3. Tracking Performance Evaluation

This system does not employ imaging detectors and cannot directly measure traditional tracking residuals. Considering that lateral offsets significantly impact the coupling efficiency of the single-mode fiber (SMF), this paper uses relative coupling efficiency, lateral offset, and the standard deviation of relative coupling efficiency as parameters to characterize tracking performance. Relative coupling efficiency is defined as the ratio of the current coupling efficiency to the maximum coupling efficiency. Thus, the relative coupling efficiency can be expressed as Ref. [18]:

$${\eta }_{rel}\left(t\right)={\displaystyle \frac{\eta \left(t\right)}{{\eta }_{max}}}={\displaystyle \frac{P\left(t\right)/P_{in}}{P_{max}/P_{in}}}={\displaystyle \frac{P\left(t\right)}{P_{max}}}$$

(31)

where $P\left(t\right)$ and $\eta \left(t\right)$ represent the coupled power and coupling efficiency into the SMF, $P_{max}$ and ${\eta }_{max}$ denote the maximum coupled power and maximum coupling efficiency, while $P_{in}$ is the incident optical power. Assuming the spot position and optical power at the SMF focal plane remain constant within the same cycle, the coupling efficiency at the maximum and minimum points within the kth convergence cycle is expressed as:

$$\left\{\begin{array}{c}{\eta }_{cqmax}={\displaystyle \frac{P_{cmax}}{P_a}}={\eta }_{max}exp\left(-{\displaystyle \frac{{\rho }_{max}^2}{{\omega }_0^2}}\right)\hfill \\ {\eta }_{cqmin}={\displaystyle \frac{P_{cmin}}{P_a}}={\eta }_{max}exp\left(-{\displaystyle \frac{{\rho }_{min}^2}{{\omega }_0^2}}\right)\hfill \end{array}\right.$$

(32)

where $P_{cmax}$ and $P_{cmin}$ represent the maximum and the minimum coupled optical power within the cycle, and $\rho$ is the lateral offset, which is the distance between the nutation center and the spot center at that moment. The lateral offset is then given by:

$$\rho =\left|{\displaystyle \frac{{\omega }_0^2}{4r}}ln{\displaystyle \frac{P_{cmax}}{P_{cmin}}}\right|$$

(33)

Typically, control bandwidth is evaluated as the frequency at which the system gain drops by 3 dB. However, since this system lacks an imaging detector, amplitude cannot be directly measured. Therefore, a new method for evaluating control bandwidth is defined: the disturbance frequency at which the optical power amplitude received by the detector in the closed-loop state drops to 70.7% of that in the open-loop state is regarded as the system’s control bandwidth.

4. Experiment

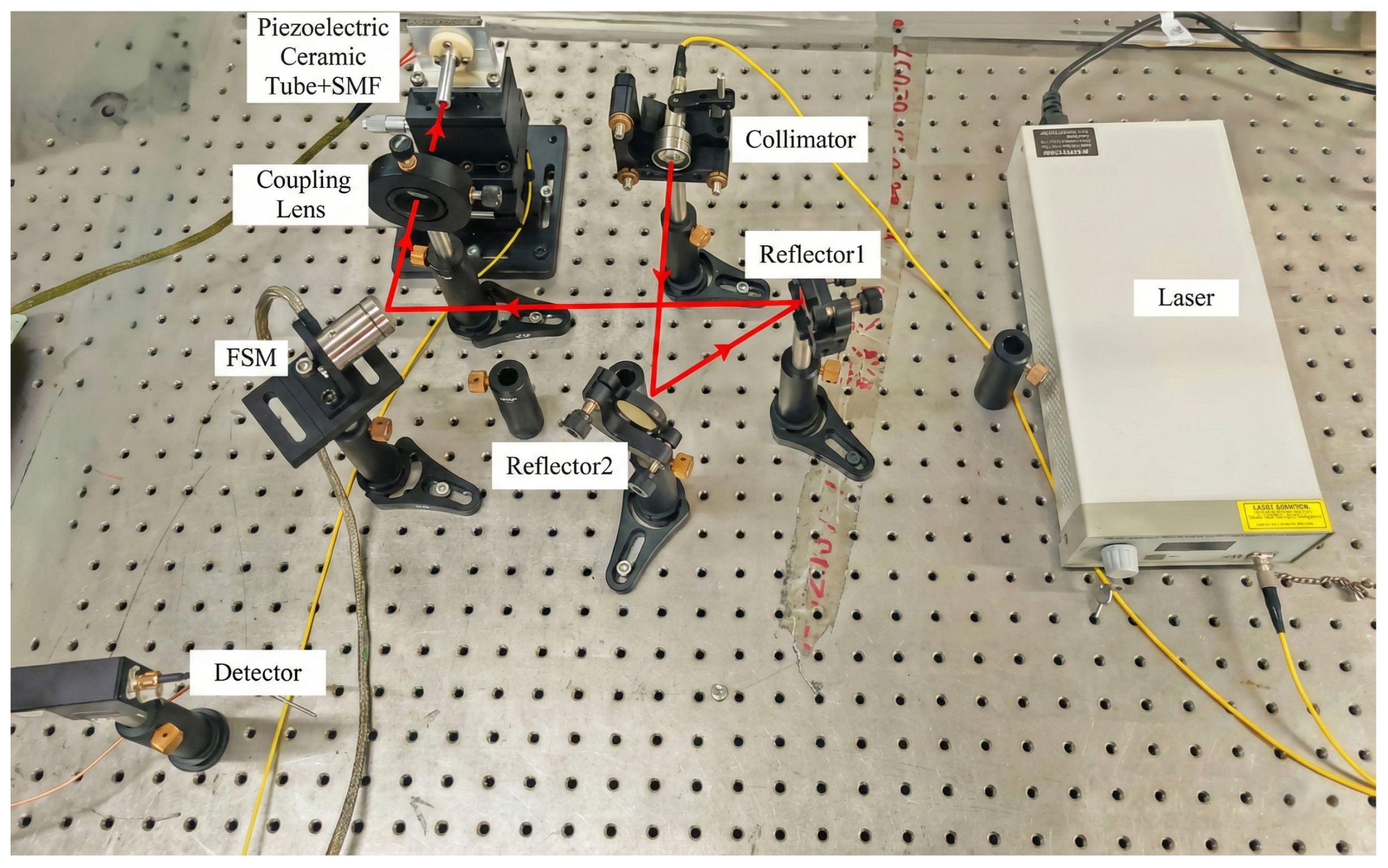
4.1. Set Up

To verify the performance of the proposed nutation tracking system based on direct fiber control, a desktop experimental platform was constructed. The system block diagram is shown in Figure 7. The platform consists of four modules: the optical signal generation module, free-space transmission module, fiber nutation tracking module, and nutation control module.

The optical signal generation module consists of a laser source and a collimator. The laser emits a 1550 nm wavelength beam with a power of 0.1 mW, which is collimated by the collimator to simulate the laser entering the fine tracking system after passing through the coarse tracking mechanism. Figure 8 shows the corresponding desktop experimental setup.

The free-space transmission module consists of a fast steering mirror (FSM), which generates disturbance signals to simulate real satellite platform vibrations. The typical vibration spectra of satellite platforms are predominantly distributed below 50 Hz, with vibration amplitudes reaching tens to hundreds of microradians [19]. The fiber nutation tracking module primarily includes the fiber nutation device, coupling lens, photodetector, and amplifier. The nutation frequency of the fiber nutation device is 1000 Hz, with the lens parameters being $R=24.5$ mm and $f=60$ mm. As the core of the experimental system, the fiber nutation control module calculates the offset between the optical spot and the fiber based on the electrical signal from the photodetector. It determines the direction of nutation center adjustment and converts this information into a control voltage, which is fed back to the PCT, driving the fiber nutation device to complete iterative tracking correction. Prior to closed-loop operation, the experimental system was carefully aligned to establish a well-defined initial operating point. Specifically, the optical axes of the laser source, coupling optics, fast steering mirror, and single-mode fiber were adjusted under static conditions to maximize the coupled optical power. This maximum-coupling condition was used as the reference alignment for subsequent experiments.

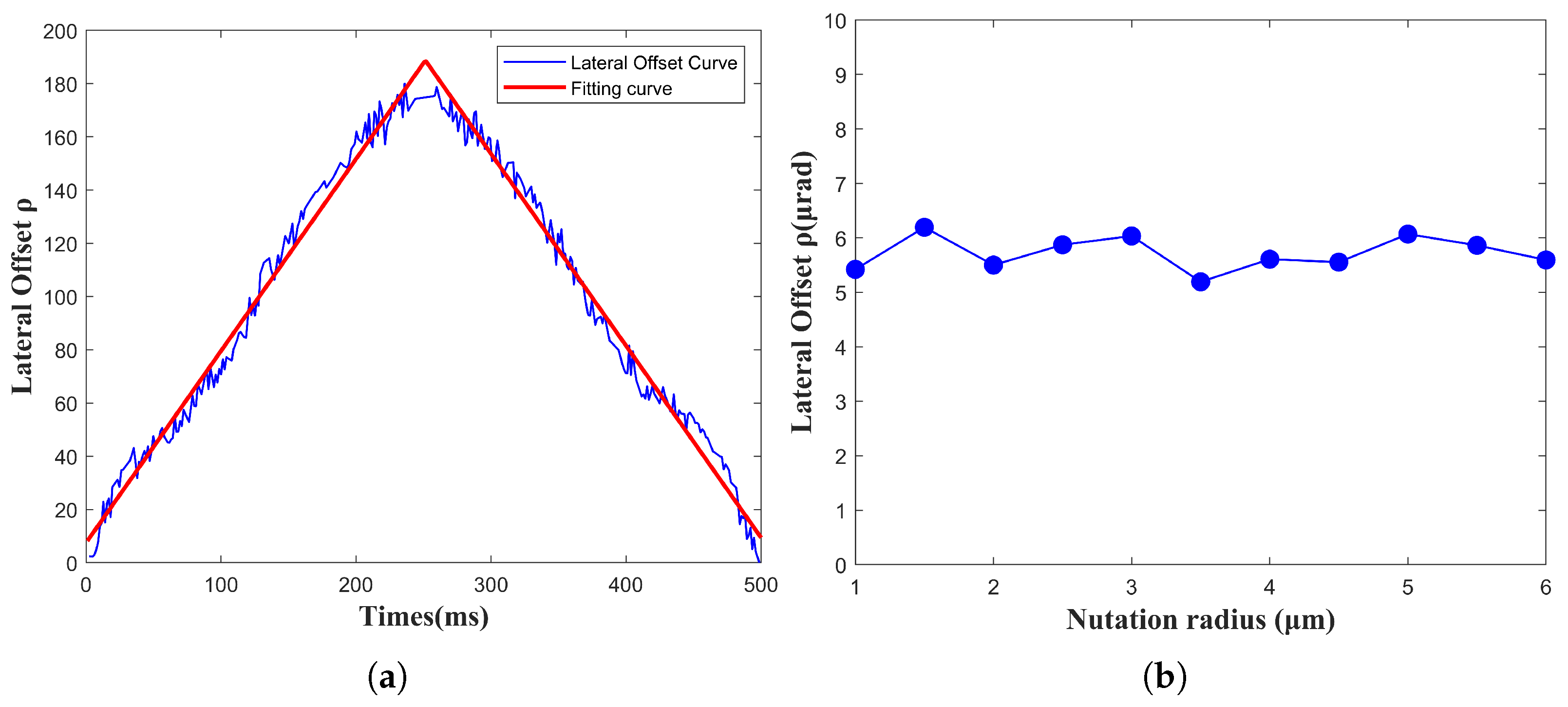
4.2. The Performance of the Closed-Loop System

The field of view (FOV) of the fiber nutation device is defined as the angular range corresponding to a drop in coupling efficiency to $1/e$ of its maximum value [19]. The FOV of this system can be calculated using the formula $FOV=2\omega /f$, yielding an FOV of approximately 183.3 $\mathsf{\mu }$rad. First, to validate the accuracy of lateral offset calculation, a linear scanning motion with a ±180 $\mathsf{\mu }$rad angular amplitude and 1 Hz frequency was applied to the fiber end face using the FSM, simulating uniform lateral offset of the spot on the SMF end face. Simultaneously, the lateral offset was calculated using the theoretically derived Equation (12), and a linear fit of the computed offset was performed. The results are shown in Figure 9. Figure 9a shows the real-time lateral offset measured during FSM scanning of the fiber end face, while Figure 9b presents the average calculation error of lateral offset under different nutation radius.

Within the field of view of the fiber nutation device, the lateral offset at each moment can be accurately computed. Moreover, the average calculation error of the lateral offset across different nutation radius is around 5.5 $\mathsf{\mu }$rad, approximately 3% of the maximum coupling offset, indicating that the system maintains stability and consistency under different nutation settings. This error is mainly due to random disturbances in the experimental environment and circuit noise, consistent with the expected deviations of the theoretical model under non-ideal conditions.

Next, we introduced different initial lateral offsets using the FSM to test the system’s closed-loop correction ability under static conditions. By applying different deflection voltages to the FSM, we generated initial position deviations of approximately 100 $\mathsf{\mu }$rad, 200 $\mathsf{\mu }$rad, and 300 $\mathsf{\mu }$rad in the incident beam, with a nutation radius of $r=1\mathsf{\mu }$m, and recorded changes in coupling efficiency and fiber displacement before and after closing the loop. These values are selected to represent typical residual pointing errors after coarse tracking in practical free-space optical communication systems, spanning moderate to relatively large initial misalignment conditions while remaining within the effective field of view of the proposed system.

As shown in Figure 10a, under open-loop conditions, the relative coupling efficiencies corresponding to the initial offsets were approximately 80.64%, 43.61%, and 19.35%, respectively. After activating closed-loop tracking, the relative coupling efficiency in all cases increased rapidly and stabilized around 97%. Under closed-loop conditions, the coupling efficiency increased significantly with minimal fluctuation, indicating that the system can effectively improve coupling efficiency to near-optimal levels under varying initial alignment errors while maintaining good stability. The measured coupling efficiency deviates from the theoretical value, which is primarily due to Fresnel reflection, absorption loss, and optical path errors at the fiber end face during the experiment. In addition, practical electromechanical limitations, including finite actuator resolution, minor nonlinearity of the piezoelectric ceramic tube under high-frequency excitation, and electronic noise in the detection circuitry, further constrain the achievable coupling efficiency.

Figure 10b shows the time evolution of lateral offset during closed-loop tracking under different initial offset conditions. As observed from the figure, the system rapidly reduces the lateral offset between the optical spot and the fiber within a short time and stabilizes it at a very low level, indicating that the system can quickly correct initial alignment errors and keep the optical spot precisely and stably positioned on the fiber end face. To evaluate the system’s tracking accuracy and stability, we use the average lateral offset after convergence and its standard deviation.

Table 1. Comparison of closed-loop states under different initial conditions.

Initial Offset ($\mathsf{\mu }$rad)	Average Lateral Offset After Convergence ($\mathsf{\mu }$rad)	Coupling Efficiency Standard Deviation (%)
50	6.8844	1.56
100	5.6032	1.34
150	4.6207	1.99
200	6.7450	1.11
250	6.0191	1.66
300	7.7056	1.32

summarizes the steady-state performance under different initial offset conditions.

For different initial offsets, the average lateral offset after closed-loop convergence is approximately 5 $\mathsf{\mu }$rad, with the corresponding lateral offset standard deviation around 1.5%. These results demonstrate that the system achieves tracking accuracy on the order of a few microradians, and the spot position remains highly stable after convergence. And, within the system field of view, the closed loop convergence behavior is largely independent of the initial alignment error.

In conclusion, under various initial offset conditions, this system can effectively and rapidly align the SMF to the optical spot, significantly improving coupling efficiency while maintaining high stability. We then evaluated the system’s performance under dynamic disturbances. Sinusoidal voltage signals with varying frequencies and amplitudes were applied to simulate satellite platform vibrations. Previous experimental and analytical studies have shown that low-frequency platform vibrations, typically below 100 Hz, can induce angular jitter and significantly degrade the coupling efficiency and stability of free-space optical links [20]. Based on this, the frequency range most affecting the tracking system is below 100 Hz, with vibration amplitudes within 100 $\mathsf{\mu }$rad. Therefore, periodic disturbances with a frequency of 50 Hz were introduced to the fiber end face using the FSM, with vibration amplitudes set to 100 $\mathsf{\mu }$rad and 125 $\mathsf{\mu }$rad to simulate microvibrations of varying intensities. Figure 11 shows the change in relative coupling efficiency from open-loop to closed-loop states under a 50 Hz vibration frequency for two different vibration amplitudes. As shown, under open-loop conditions, the detected optical power fluctuates sinusoidally with large amplitude, reaching approximately 28.08% and 34.96% for 100 $\mathsf{\mu }$rad and 125 $\mathsf{\mu }$rad disturbances, respectively. In the closed-loop state, the average power output from the photodetector increases significantly, while the fluctuation decreases markedly: in Figure 11a, the power variation is reduced to 5.22%, and the relative coupling efficiency reaches approximately 93.60%. In Figure 11b, the power variation is 7.1%, corresponding to a relative coupling efficiency of approximately 89.36%. This shows that although coupling performance in the closed-loop system slightly declines with increasing disturbance amplitude, it still reduces power fluctuations caused by large-amplitude vibrations by more than half, maintaining a high average coupling efficiency overall.

Finally, we fixed the vibration amplitude at 25 $\mathsf{\mu }$rad and varied the frequency of the sinusoidal disturbance signal applied to the FSM in the range of 25 Hz to 225 Hz to evaluate the system performance. Figure 12a shows the variation in average relative coupling efficiency under open-loop and closed-loop states at different disturbance frequencies. Figure 12b displays the amplitude of the coupling efficiency as a function of vibration frequency.

As shown in Figure 12, the closed-loop relative coupling efficiency decreases as the disturbance frequency increases. When the frequency reaches 200 Hz, the efficiency drops to 80.86%, and its fluctuation exceeds 70.7% of the open-loop value. This indicates that the system’s ability to maintain coupling efficiency significantly declines beyond 200 Hz, along with a loss of stability. The control bandwidth of the system is approximately 200 Hz, as shown in Figure 12. Within the typical vibration frequency range of 0–150 Hz (with amplitudes up to 25 $\mathsf{\mu }$rad), the system effectively suppresses disturbances. However, once the disturbance frequency exceeds 175 Hz, the tracking performance starts to degrade noticeably.

5. Conclusions

This paper presents an inter-satellite beaconless laser communication tracking system based on direct fiber control, which eliminates the need for additional beacon sources or imaging detectors, significantly simplifying system architecture and reducing resource requirements. Experimental results show that the system maintains high coupling efficiency and stability under both varying initial alignment errors and external disturbances, such as satellite platform vibrations. The system achieves a control bandwidth of 200 Hz, making it suitable for both inter-satellite and satellite-to-ground laser communication scenarios. The successful validation of this system provides a new solution for the development of free-space optical communication technologies, with broad application potential. Future research may focus on optimizing the system’s dynamic tracking performance to better adapt to more complex and harsh space environments.