High-Precision Construction of Off-Axis Multi-Reflective Systems for a Single Field of View Based on a Stable Initialization Seed Curve Extension Algorithm
Abstract
1. Introduction
2. Construction Method of a Single-Field Off-Axis Multi-Reflective Freeform System Based on SI-SCE
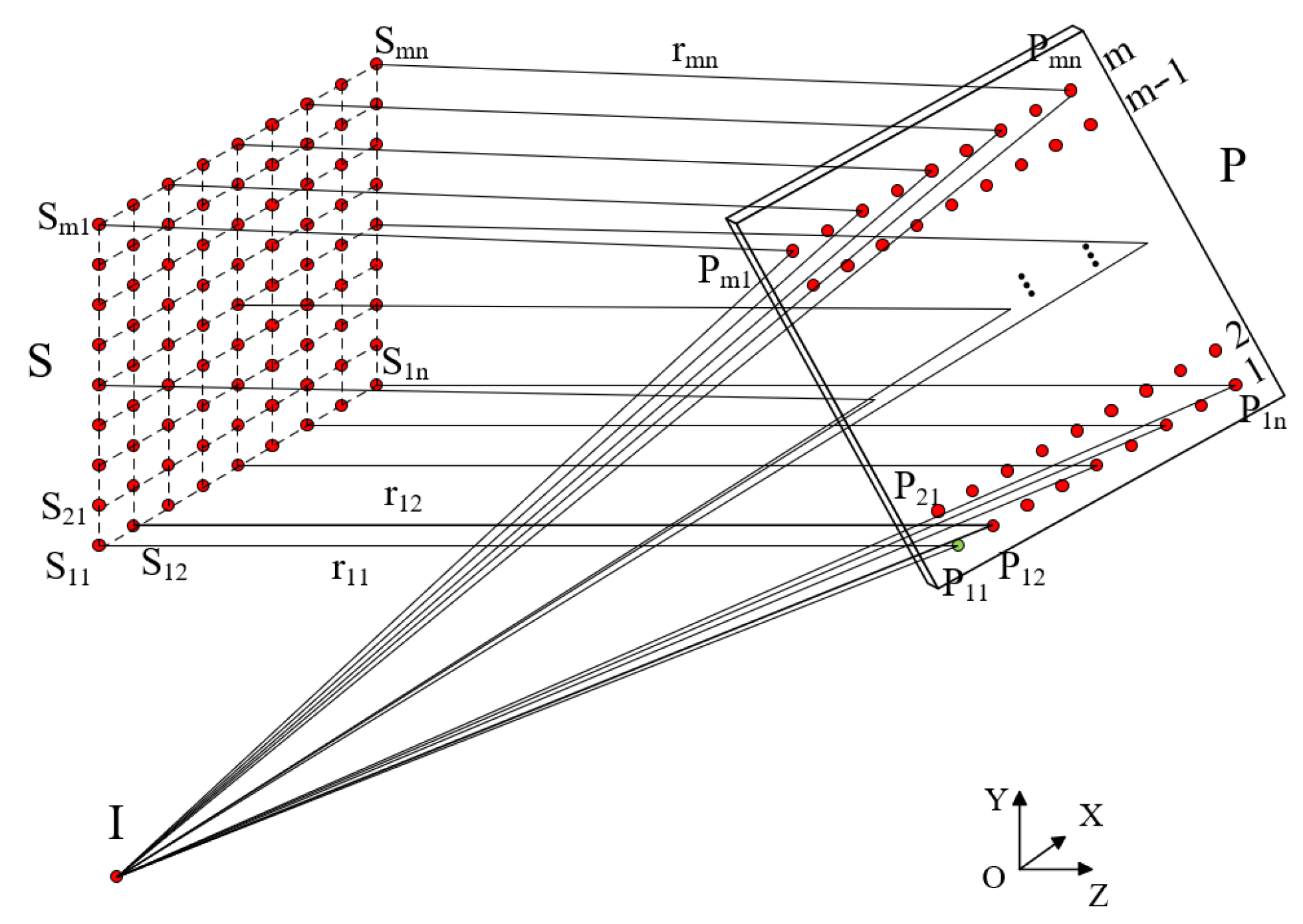
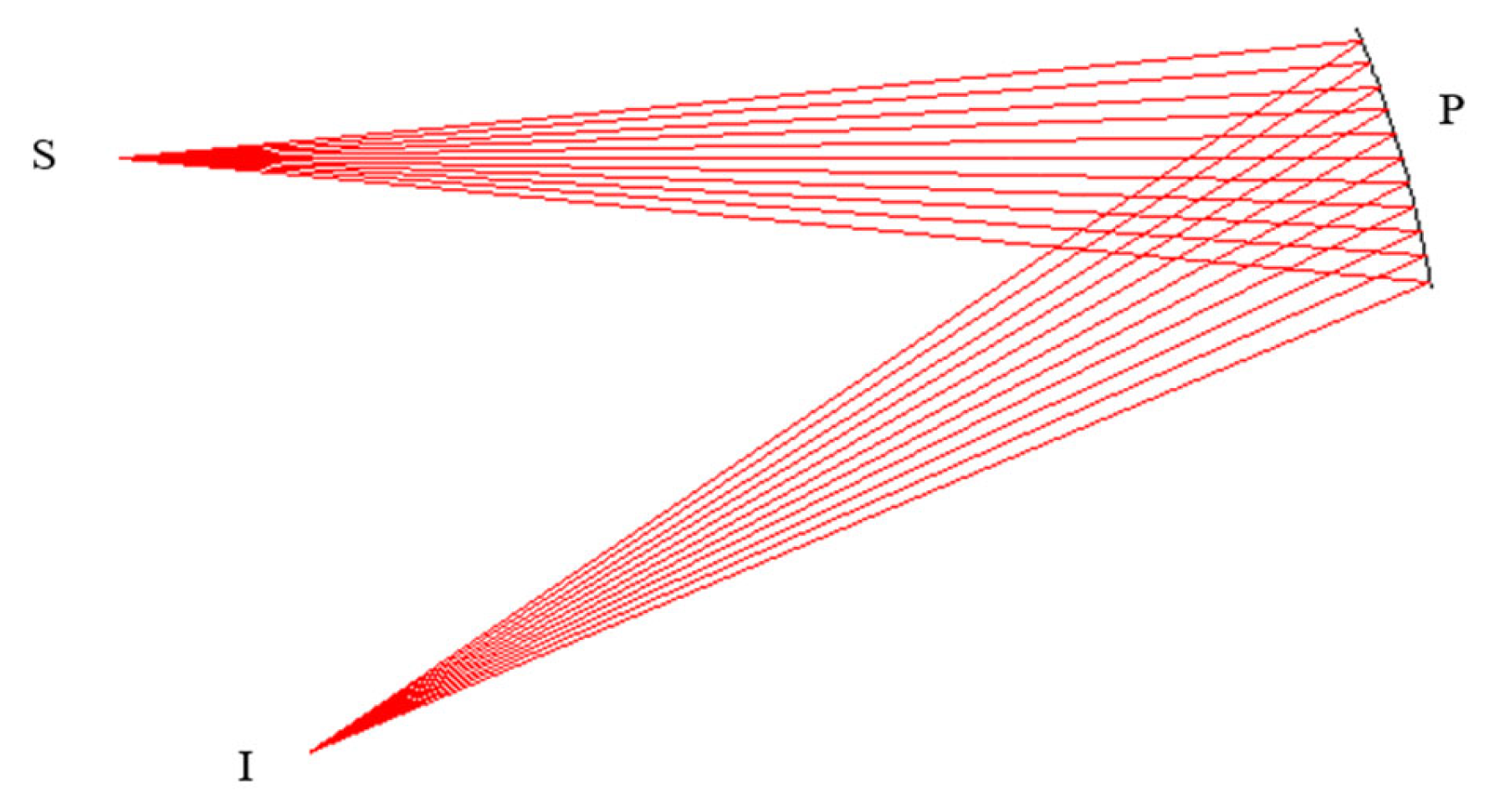
2.1. The Fundamental Construction Principle of the SCE Algorithm
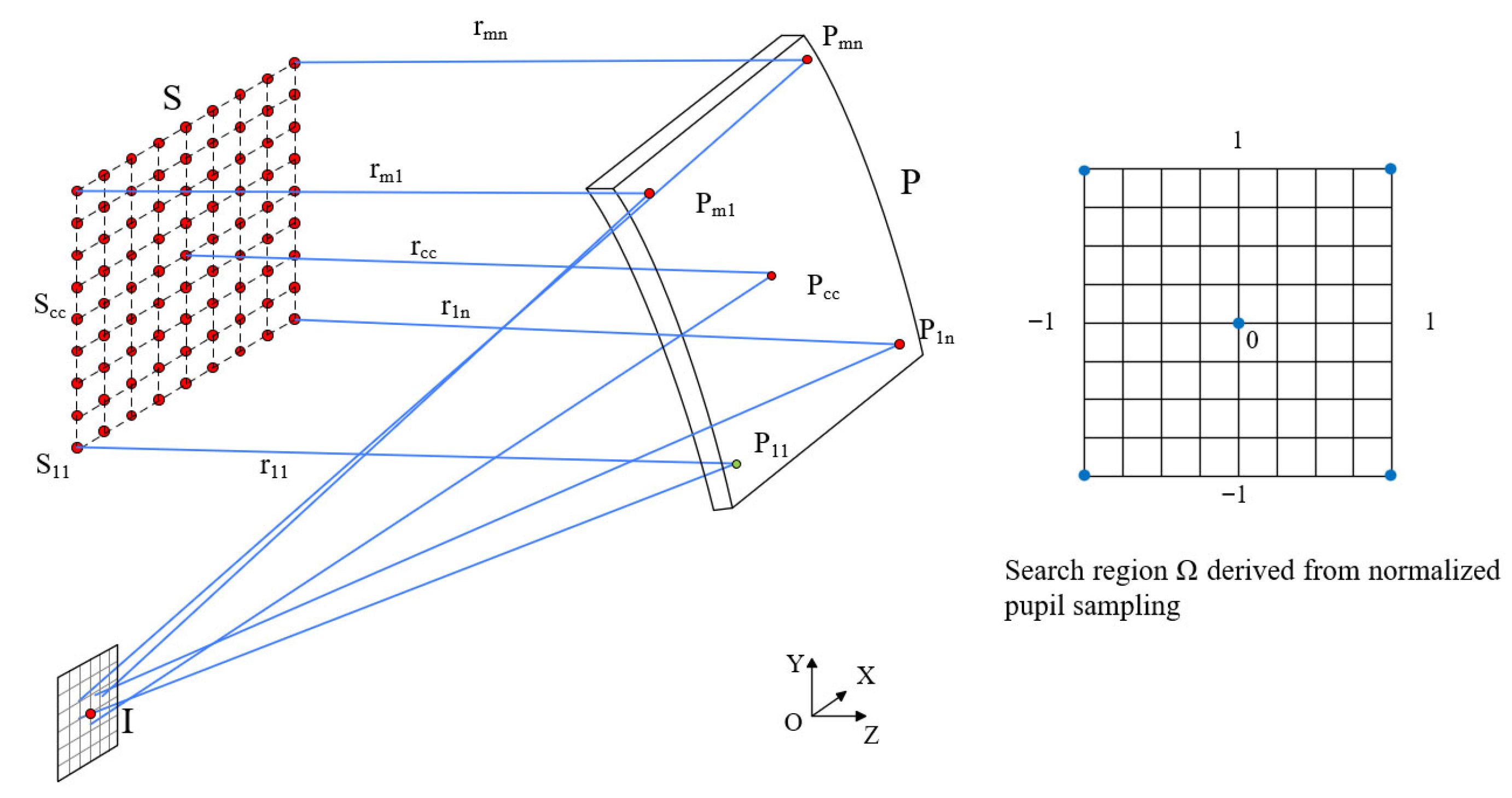
2.2. Single-Field Off-Axis Single-Reflective Freeform Construction Using the SI-SCE Algorithm Based on Ray Tracing and Fermat’s Principle
2.2.1. Single-Field Off-Axis Single-Reflective Freeform Construction with Infinite Object Distance
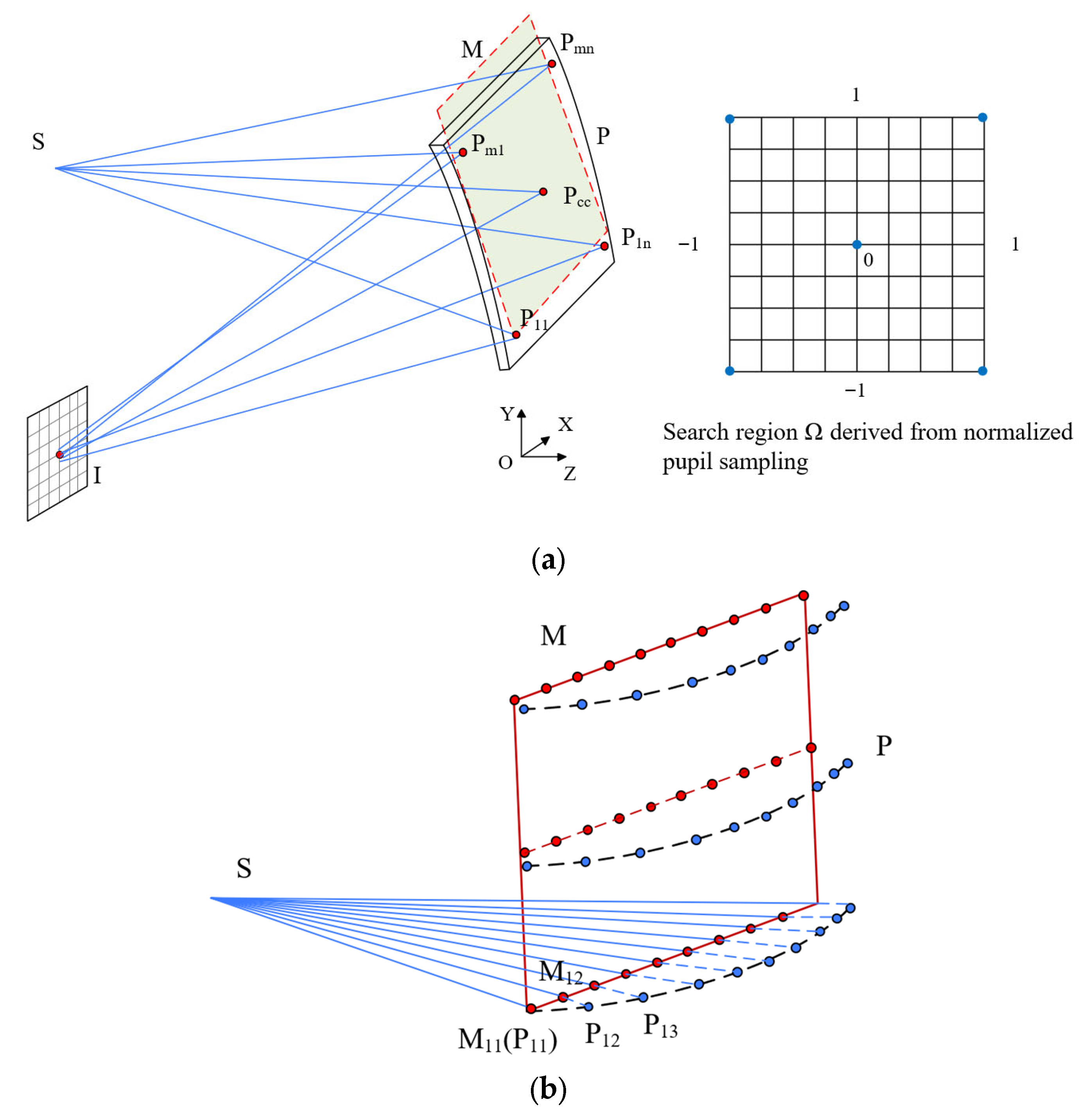
2.2.2. Single-Field Off-Axis Single-Reflective Freeform Construction with Finite Object Distance
2.2.3. Single-Field Off-Axis Single-Reflective Freeform Surface Construction
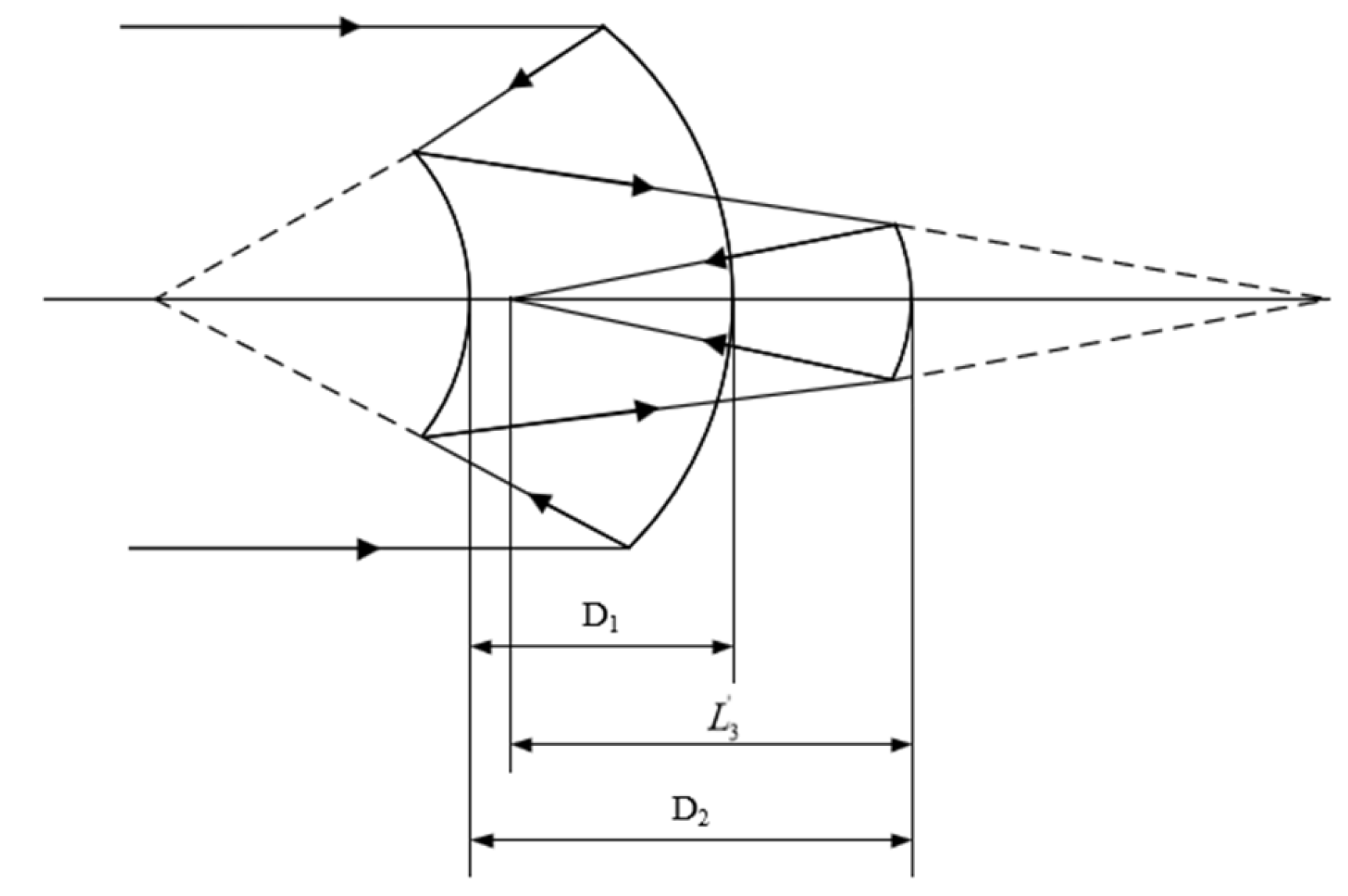
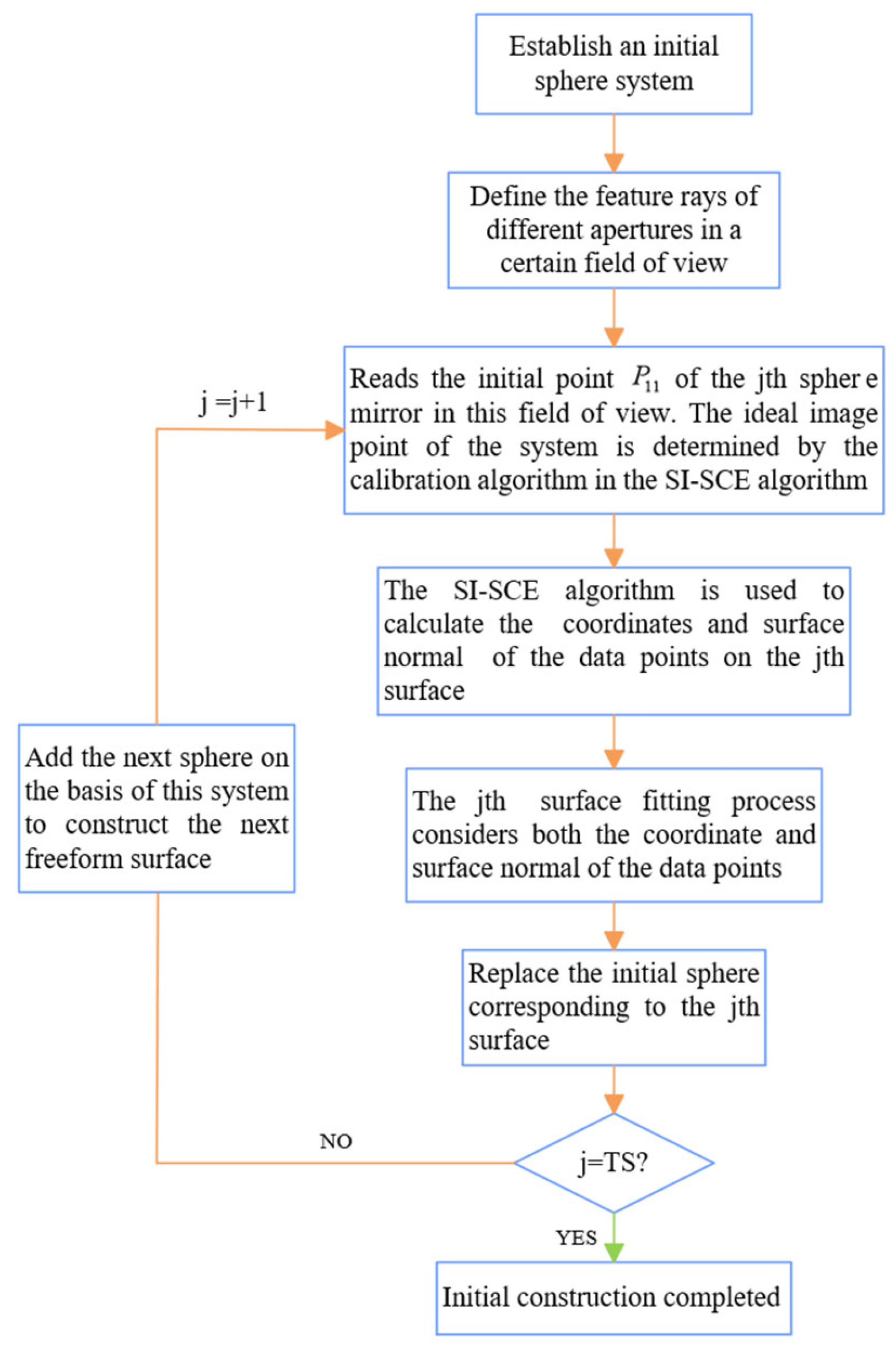
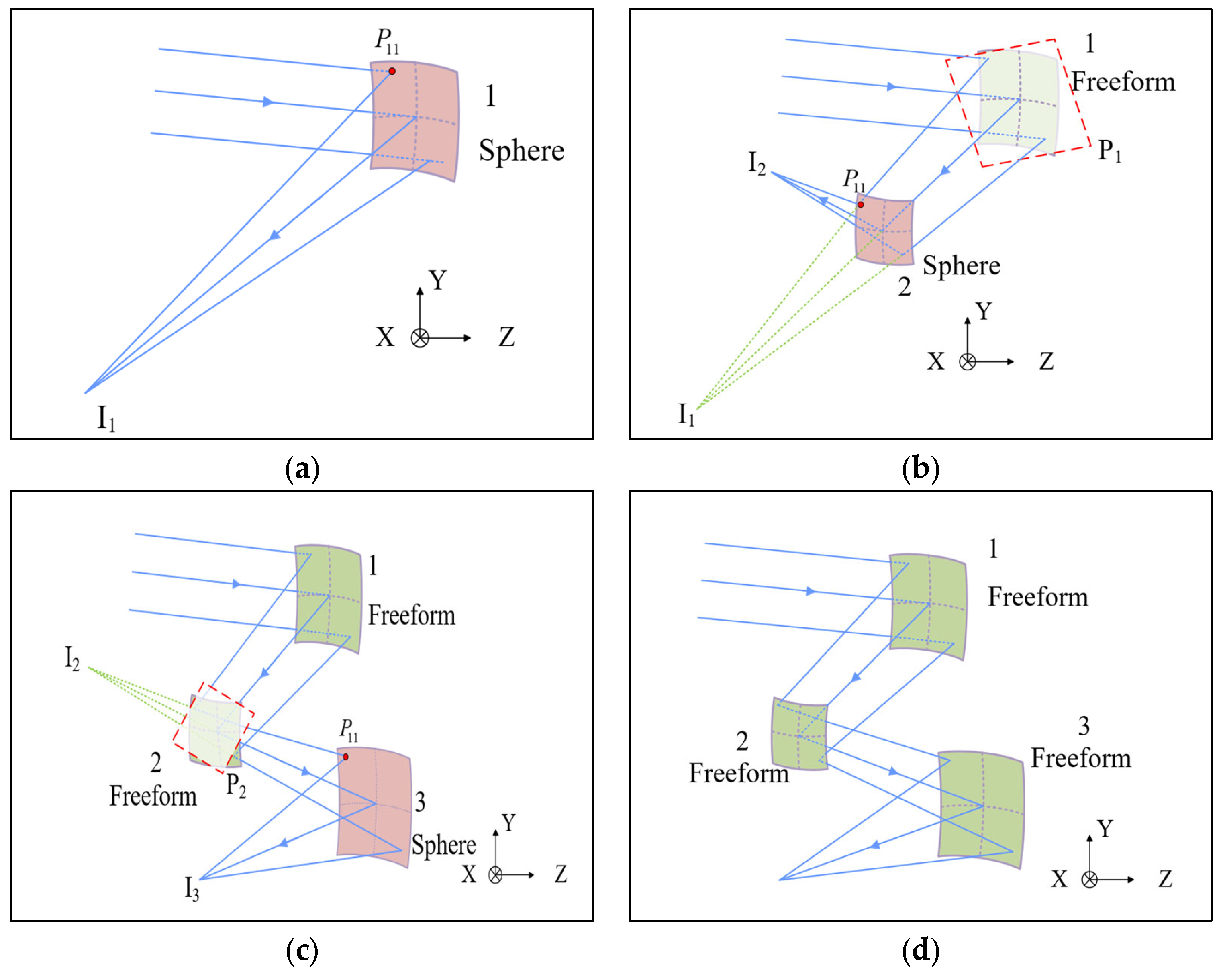
2.3. Construction of Single-Field Off-Axis Multi-Reflective Freeform Surface Systems Under Application-Oriented and System Parameter Constraints
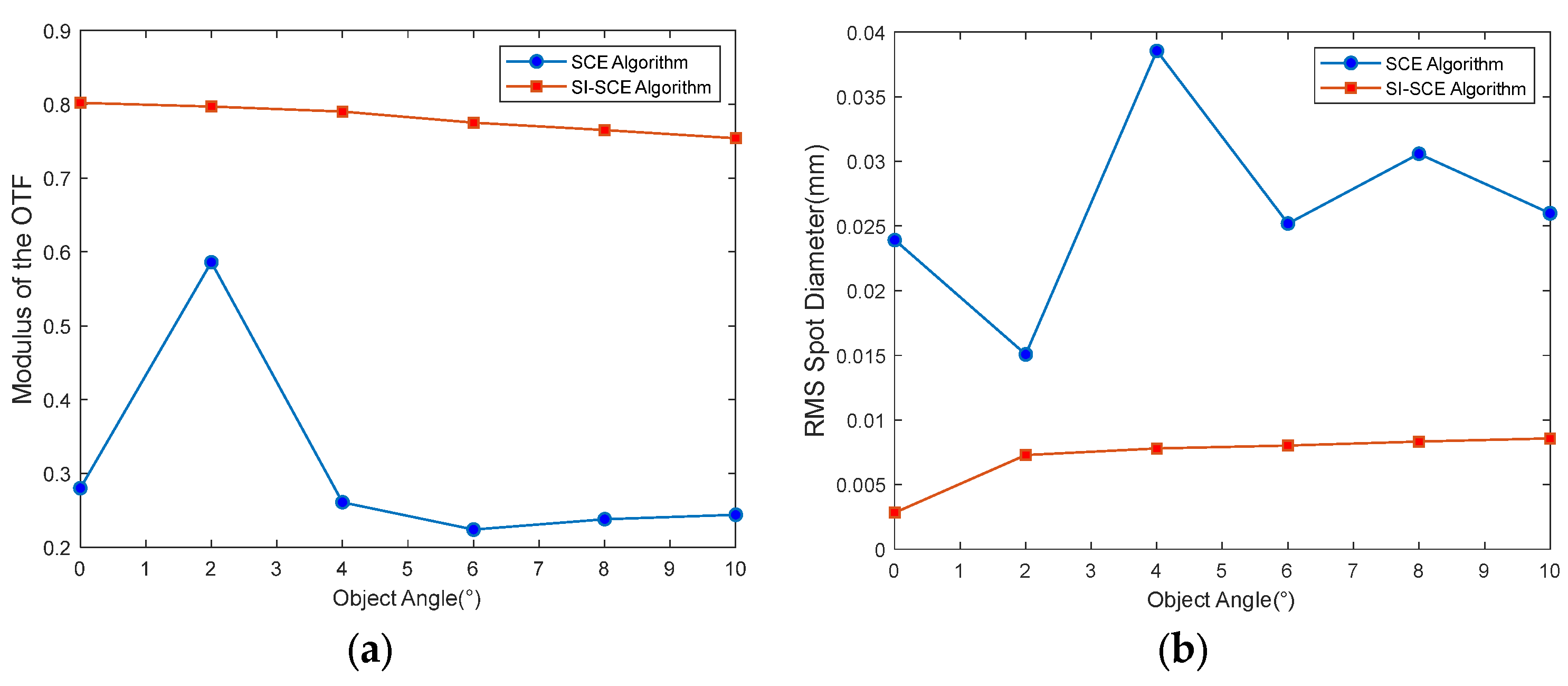
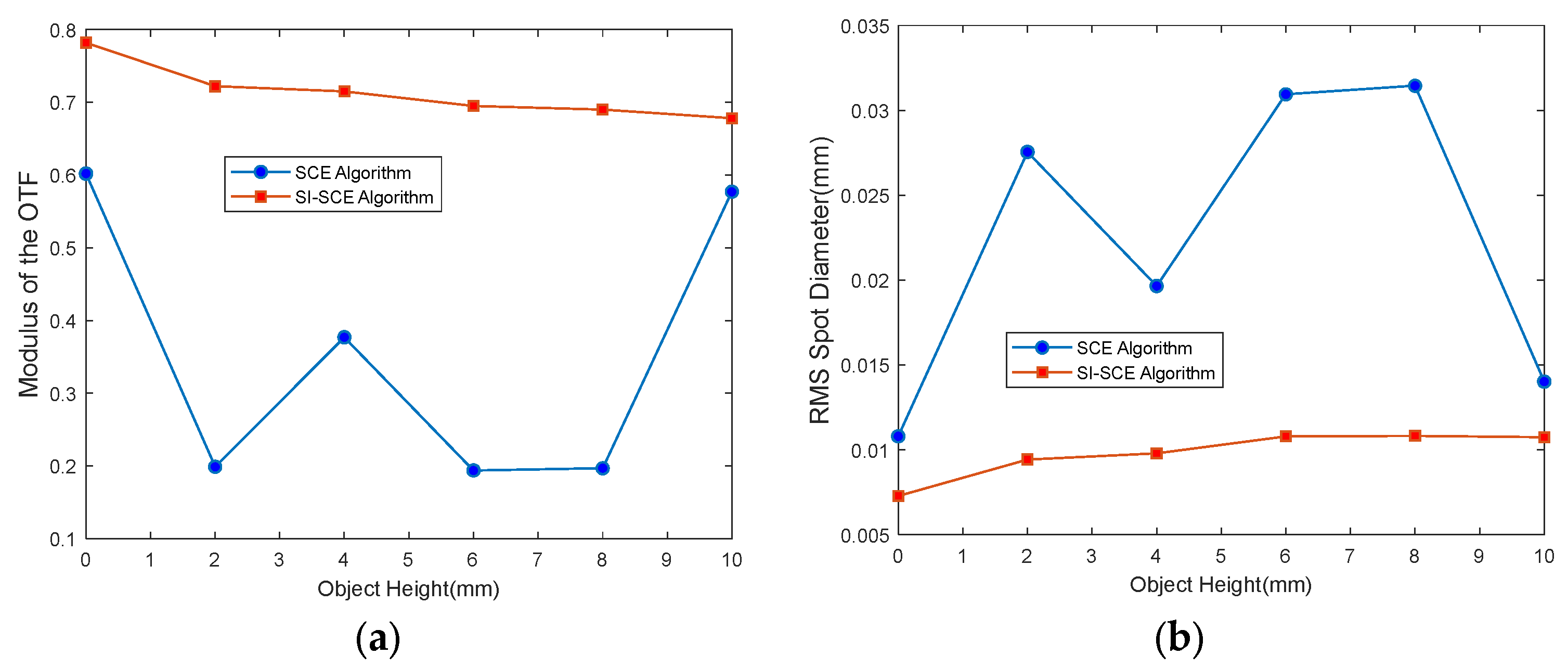
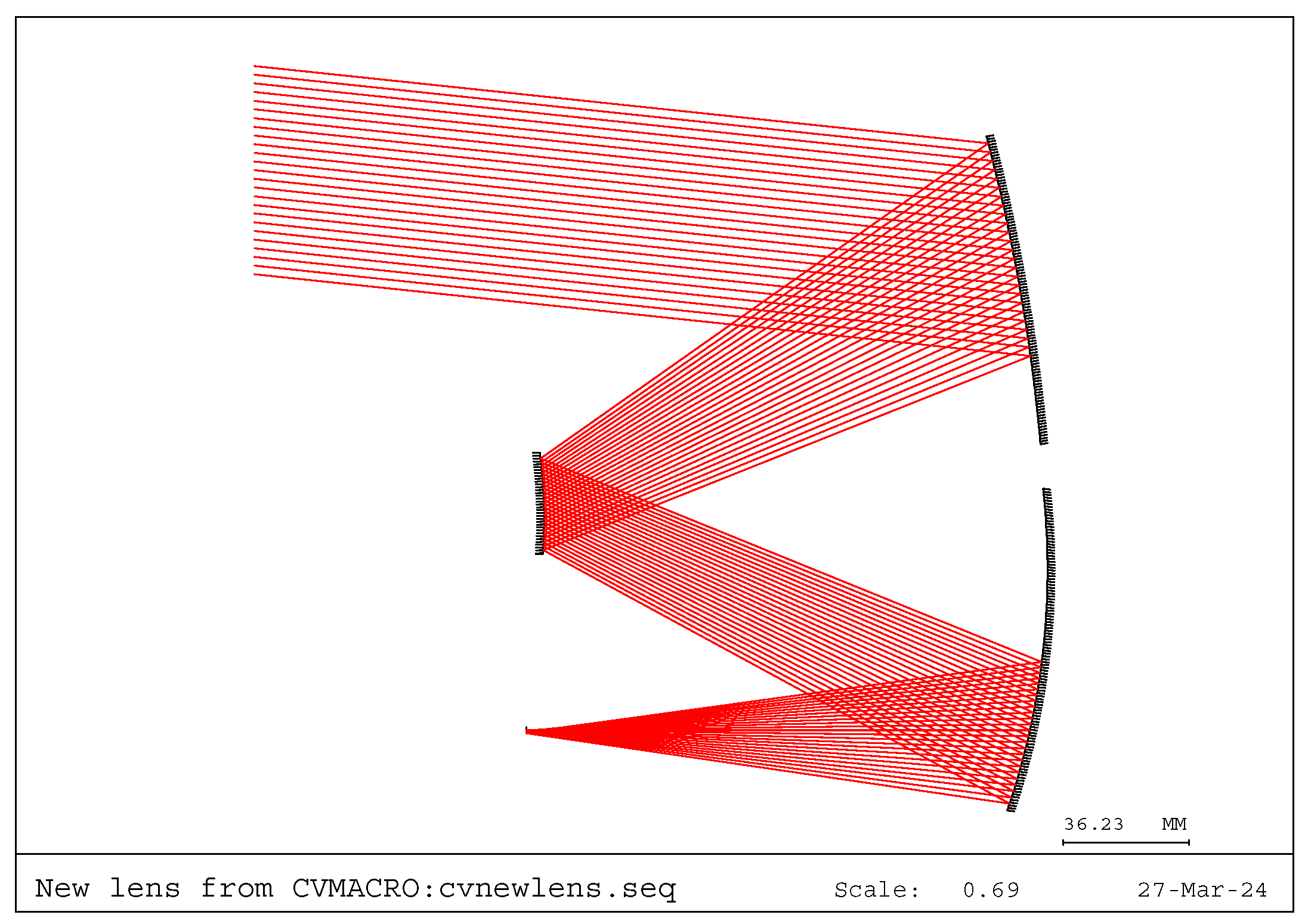
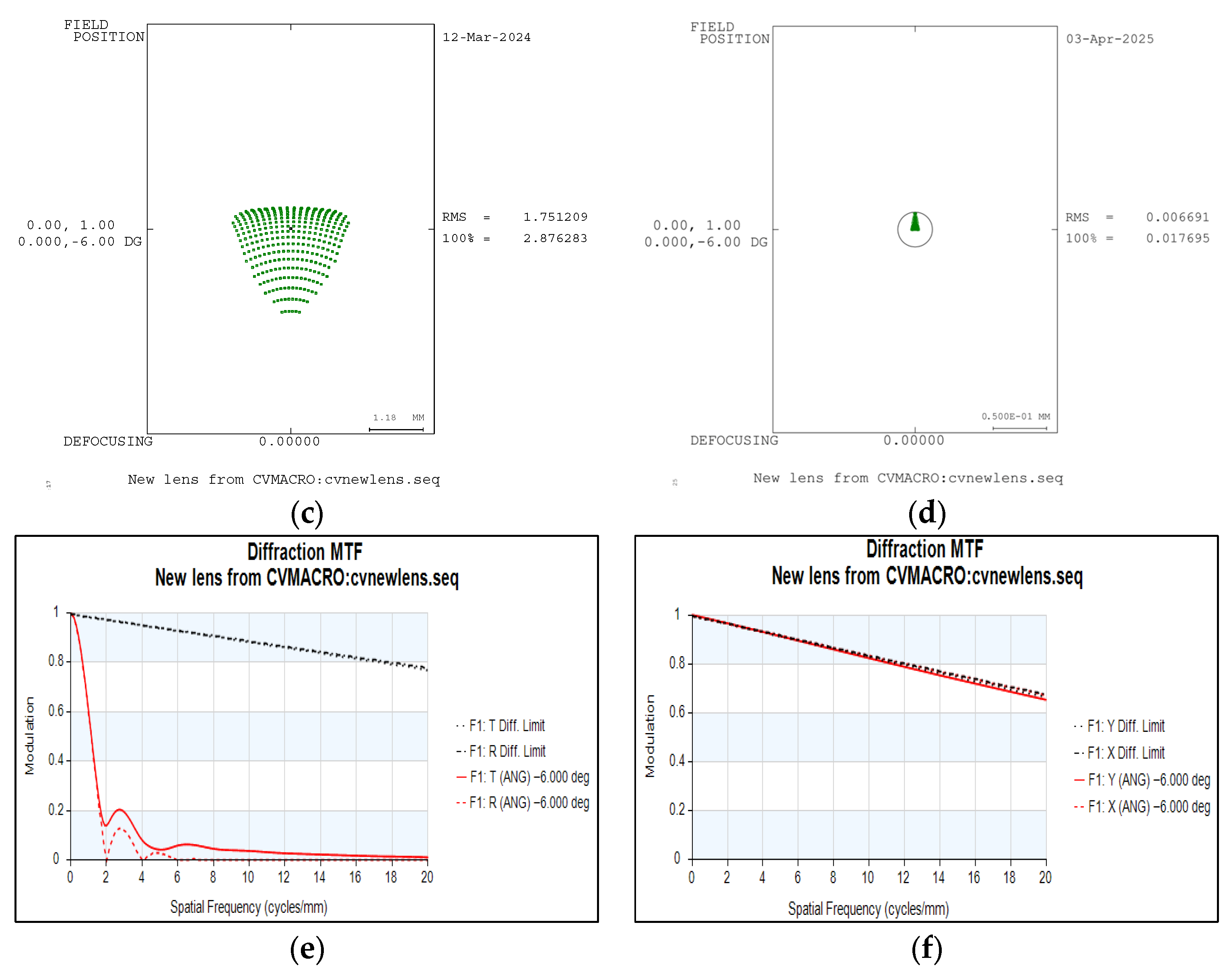
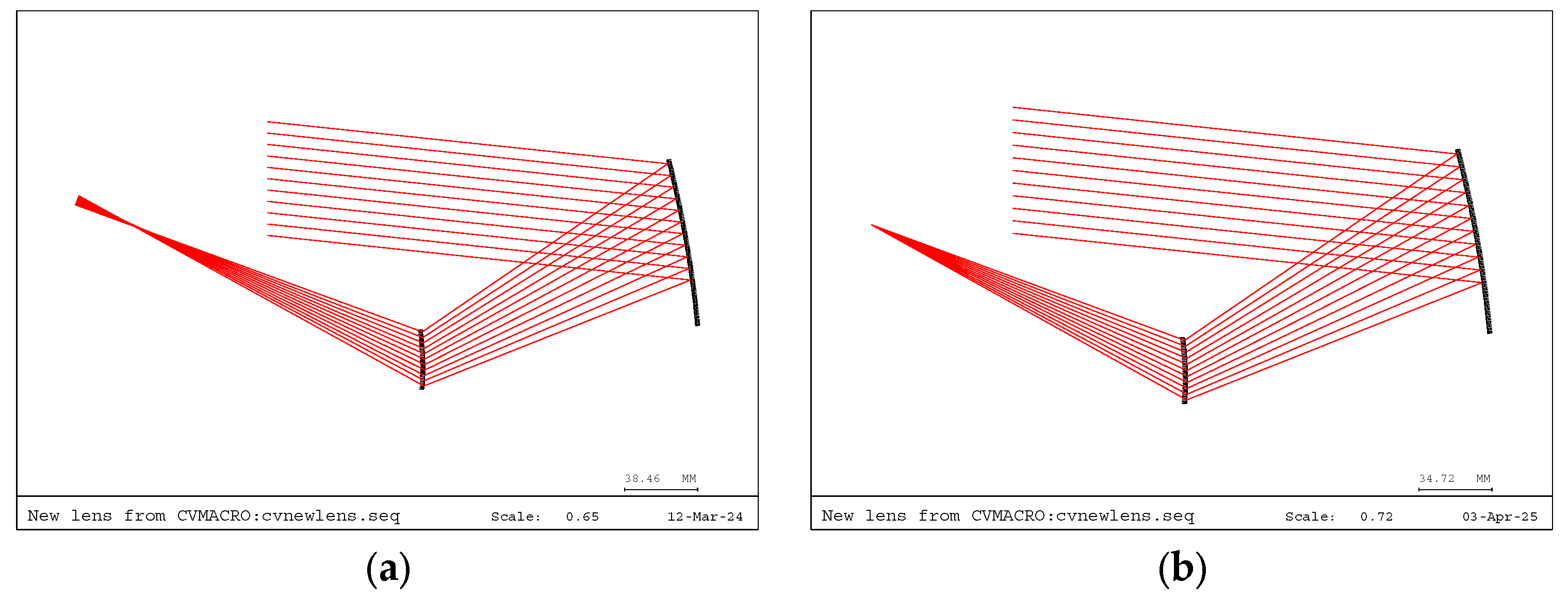
3. Design of an Off-Axis Three-Mirror Freeform System Using the SI-SCE Algorithm
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1: Single-field off-axis multi-mirror freeform surface construction algorithm |
|
References
- Jia, X.; Jia, H. Off-axis freeform optical design for large curved field of view imaging. Appl. Opt. 2024, 63, 8152–8163. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, T.; Lyu, X.; Cheng, D.; Wang, Y. Ultra-simplified and low-cost head-up display system enabled by freeform holographic element. Opt. Laser Technol. 2024, 178, 111253. [Google Scholar] [CrossRef]
- Chen, X.; Hu, L.; Liu, J.; Wang, C.; Bai, C.; Zheng, Y.; Qin, Y.; Yang, H.; Jiang, P. Design of a compact off-axis two-mirror freeform optical antenna for shaping and transmitting an elliptical beam emitted by laser diode. Appl. Opt. 2023, 63, 239–248. [Google Scholar] [CrossRef]
- Zhao, G.; Zhu, J. Design of off-axis reflective dual-channel zoom freeform optical systems. Opt. Commun. 2025, 574, 131079. [Google Scholar] [CrossRef]
- Kumar, S.; Zhong, W.; Williamson, J.; Kumar, P.; Furness, T.; Lou, S.; Zeng, W.; Jiang, X. Design, fabrication, and testing of freeform mirror-based head-up display system. Opt. Laser Technol. 2025, 186, 112653. [Google Scholar] [CrossRef]
- Zhao, G.; Zhu, J. Off-axis zoom optical systems based on mirror rotation and their design method. Opt. Laser Technol. 2024, 177, 111031. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, J.; Wu, X.; Jin, G. Direct design of freeform surfaces and freeform imaging systems with a point-by-point three-dimensional construction-iteration method. Opt. Express 2015, 23, 10233–10246. [Google Scholar] [CrossRef]
- Yu, B.; Tian, Z.; Su, D.; Sui, Y.; Yang, H. Design and engineering verification of an ultrashort throw ratio projection system with a freeform mirror. Appl. Opt. 2019, 58, 3575–3581. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, J. Design method of freeform off-axis multi-mirror optical systems. Photonics 2022, 9, 534. [Google Scholar] [CrossRef]
- Volatier, J.-B.; Druart, G. Differential method for freeform optics applied to two-mirror off-axis telescope design. Opt. Lett. 2019, 44, 1174–1177. [Google Scholar] [CrossRef]
- Duerr, F.; Benítez, P.; Miñano, J.C.; Meuret, Y.; Thienpont, H. Analytic design method for optimal imaging: Coupling three ray sets using two free-form lens profiles. Opt. Express 2012, 20, 5576–5585. [Google Scholar] [CrossRef]
- Duerr, F.; Benítez, P.; Miñano, J.C.; Meuret, Y.; Thienpont, H. Analytic free-form lens design in 3D: Coupling three ray sets using two lens surfaces. Opt. Express 2012, 20, 10839–10846. [Google Scholar] [CrossRef] [PubMed]
- Nie, Y.; Thienpont, H.; Duerr, F. Multi-fields direct design approach in 3D: Calculating a two-surface freeform lens with an entrance pupil for line imaging systems. Opt. Express 2015, 23, 34042–34054. [Google Scholar] [CrossRef] [PubMed]
- Nie, Y.; Mohedano, R.; Benítez, P.; Chaves, J.; Miñano, J.C.; Thienpont, H.; Duerr, F. Multifield direct design method for ultrashort throw ratio projection optics with two tailored mirrors. Appl. Opt. 2016, 55, 3794–3800. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Wang, Y.; Hua, H. Free form optical system design with differential equations. In Optical Design and Testing IV (SPIE2010); Photonics Asia: Beijing, China, 2010; pp. 190–197. [Google Scholar]
- Hicks, R.A. Controlling a ray bundle with a free-form reflector. Opt. Lett. 2008, 33, 1672–1674. [Google Scholar] [CrossRef]
- Hicks, R.A.; Croke, C. Designing coupled free-form surfaces. J. Opt. Soc. Am. A 2010, 27, 2132–2137. [Google Scholar] [CrossRef]
- Pan, H.; Su, Z.; Zhang, Y.; Wu, T. Construct freeform surface directly in an initial layout of an off-axis reflective image system by seed curve extension and simulated annealing algorithm. J. Eur. Opt. Soc.-Rapid Publ. 2020, 16, 9. [Google Scholar] [CrossRef]
- Mao, B.; Yang, T.; Xu, H.; Chen, W.; Cheng, D.; Wang, Y. FreeformNet: Fast and automatic generation of multiple-solution freeform imaging systems enabled by deep learning. Photonics Res. 2023, 11, 1408–1422. [Google Scholar] [CrossRef]
- Nie, Y.; Zhang, J.; Su, R.; Ottevaere, H. Freeform optical system design with differentiable three-dimensional ray tracing and unsupervised learning. Opt. Express 2023, 31, 7450–7465. [Google Scholar] [CrossRef]
- Sun, Y.; Wei, Y.; Zhang, Y.; Zhao, J. Automated generation of easy-assembly off-axis three-mirror imaging systems based on few-shot machine learning. Appl. Opt. 2025, 64, 1068–1077. [Google Scholar] [CrossRef]
- Wang, L.; Qian, K.; Luo, Y. Discontinuous free-form lens design for prescribed irradiance. Appl. Opt. 2007, 46, 3716–3723. [Google Scholar] [CrossRef]
- Wang, K.; Liu, S.; Chen, F.; Qin, Z.; Liu, Z.; Luo, X. Freeform LED lens for rectangularly prescribed illumination. J. Opt. A Pure Appl. Opt. 2009, 11, 105501. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Su, Z.; Pan, H.; Chen, X.; Zhang, W. Freeform optical surface design in an off-axis reflective imaging system by a double seed curve extension algorithm. Appl. Opt. 2021, 60, 942–948. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Su, Z.; Zhang, Y.; Hu, L. Design of Freeform Off-Axis Reflective Afocal Systems by Orthogonal Seed Curve Extension Algorithm. Acta Opt. Sin. 2022, 42, 0108001. [Google Scholar]
- Zhang, Y.; Su, Z.; Pan, H. Optical design and tolerance analysis freeform automotive head-up display. Acta Photonica Sin. 2020, 49, 922002. [Google Scholar] [CrossRef]
- Zhang, Y. Design of Off-Axis Freeform Reflective System by Double Seed Curve Extension Algorithm. Master’s Thesis, Jiangnan University, Wuxi, China, 17 June 2021. [Google Scholar]
- Yang, T.; Zhu, J.; Hou, W.; Jin, G. Design method of freeform off-axis reflective imaging systems with a direct construction process. Opt. Express 2014, 22, 9193–9205. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Zhu, J.; Wu, X.; Yang, T.; Jin, G. Generating optical freeform surfaces considering both coordinates and normals of discrete data points. JOSA A 2014, 31, 2401–2408. [Google Scholar] [CrossRef]
- Pan, J. Design, Processing, and Inspection of Optical Aspherical Surfaces; Suzhou University Press: Suzhou, China, 2004. [Google Scholar]


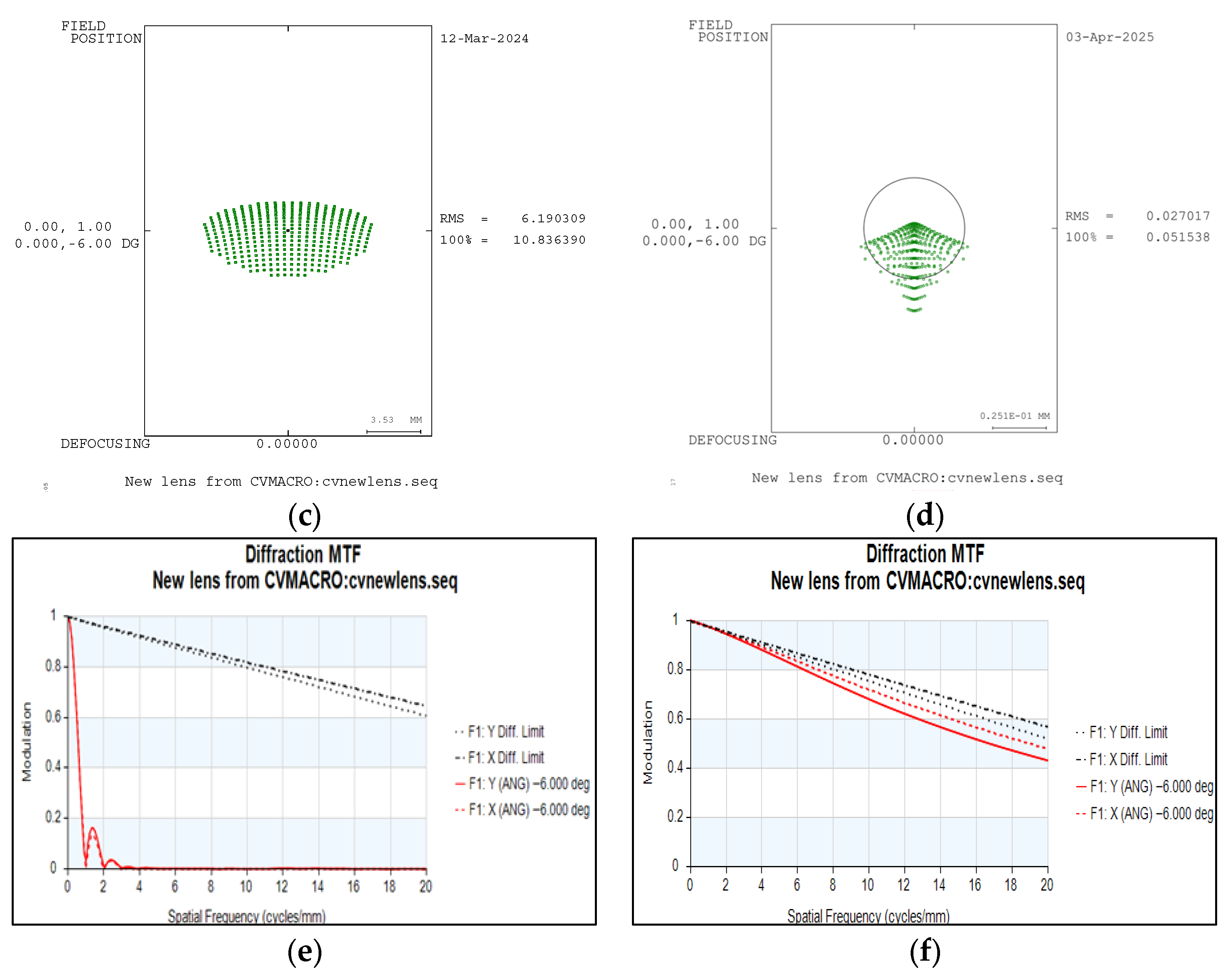


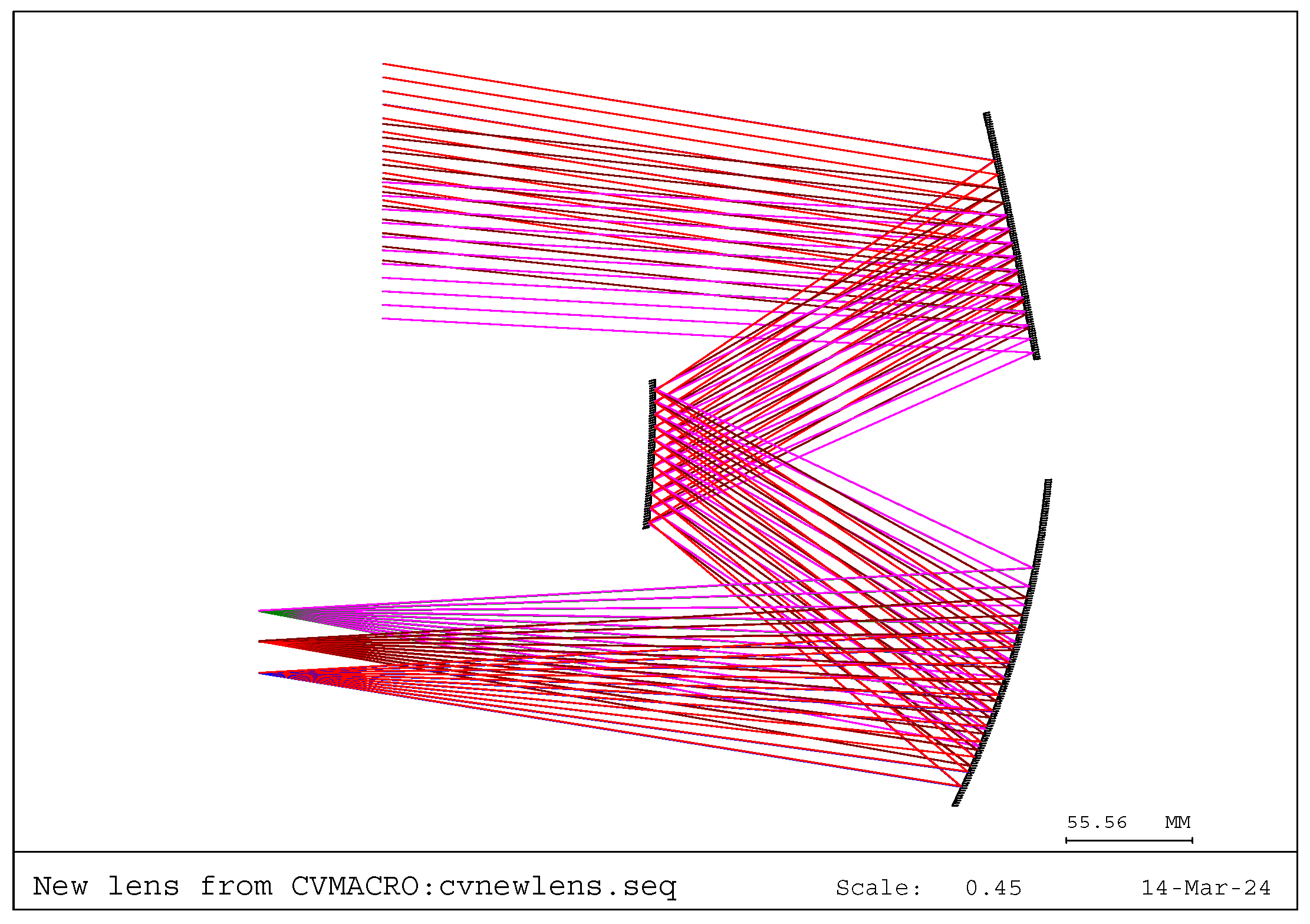
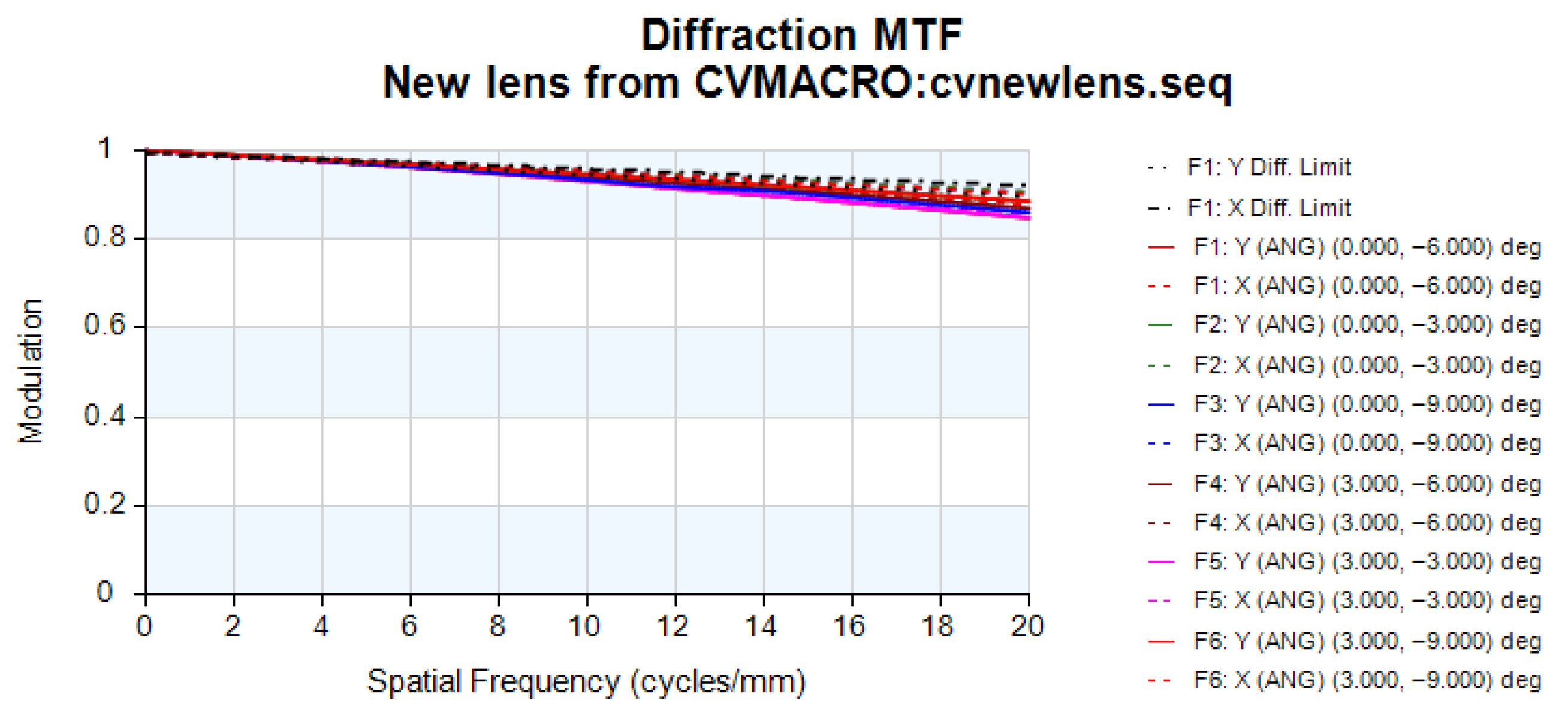
| Parameter | Specification |
|---|---|
| Field of view (FOV) | |
| F-number | 3.4 |
| Entrance pupil diameter | 60 mm |
| Effective focal length | 204 mm |
| Detector pixel size | |
| Wavelength | |
| Configuration | Off-axis three-mirror |
| Freeform Surface | Initial Point | Ideal Image Point |
|---|---|---|
| Freeform 1 | (−30, 30.757, 192.793) | (0, −115.852, −37.885) |
| Freeform 2 | (−13.043, −47.323, 61.137) | (0, 7.059, −86.031) |
| Freeform 3 | (−25.798, −100.861, 205.389) | (0, −126.529, 43.521) |
| Coefficient | Primary Mirror | Secondary Mirror | Tertiary Mirror |
|---|---|---|---|
| Radius | −590.7090 | 1185.3700 | 415.2863 |
| Conic | 0.2268 | −20 | −0.9900 |
| −4.4069 × 10−5 | 0.3560 | 0.3897 | |
| 0.0007 | −0.0020 | −0.0027 | |
| 0.0006 | −0.0014 | −0.0027 | |
| 5.8921 × 10−7 | 2.1873 × 10−6 | 2.0143 × 10−6 | |
| −1.1693 × 10−6 | −4.6285 × 10−6 | 7.9194 × 10−7 | |
| 2.2569 × 10−9 | −5.0074 × 10−9 | −4.2920 × 10−9 | |
| 3.9277 × 10−9 | −6.770 × 10−9 | −1.0571 × 10−8 | |
| 2.5782 × 10−9 | −2.7457 × 10−9 | −2.2173 × 10−9 | |
| 2.7460 × 10−12 | 2.8341 × 10−11 | 2.1429 × 10−11 | |
| −5.2078 × 10−12 | −6.4195 × 10−11 | 2.9839 × 10−11 | |
| −3.8565 × 10−12 | −1.6673 × 10−11 | −5.4016 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Huo, J. High-Precision Construction of Off-Axis Multi-Reflective Systems for a Single Field of View Based on a Stable Initialization Seed Curve Extension Algorithm. Photonics 2025, 12, 1141. https://doi.org/10.3390/photonics12111141
Hu Y, Huo J. High-Precision Construction of Off-Axis Multi-Reflective Systems for a Single Field of View Based on a Stable Initialization Seed Curve Extension Algorithm. Photonics. 2025; 12(11):1141. https://doi.org/10.3390/photonics12111141
Chicago/Turabian StyleHu, Yuan, and Jiaqi Huo. 2025. "High-Precision Construction of Off-Axis Multi-Reflective Systems for a Single Field of View Based on a Stable Initialization Seed Curve Extension Algorithm" Photonics 12, no. 11: 1141. https://doi.org/10.3390/photonics12111141
APA StyleHu, Y., & Huo, J. (2025). High-Precision Construction of Off-Axis Multi-Reflective Systems for a Single Field of View Based on a Stable Initialization Seed Curve Extension Algorithm. Photonics, 12(11), 1141. https://doi.org/10.3390/photonics12111141





