The Diffusion of Triplet Excitons in Perylenediimide Derivative Crystals
Abstract
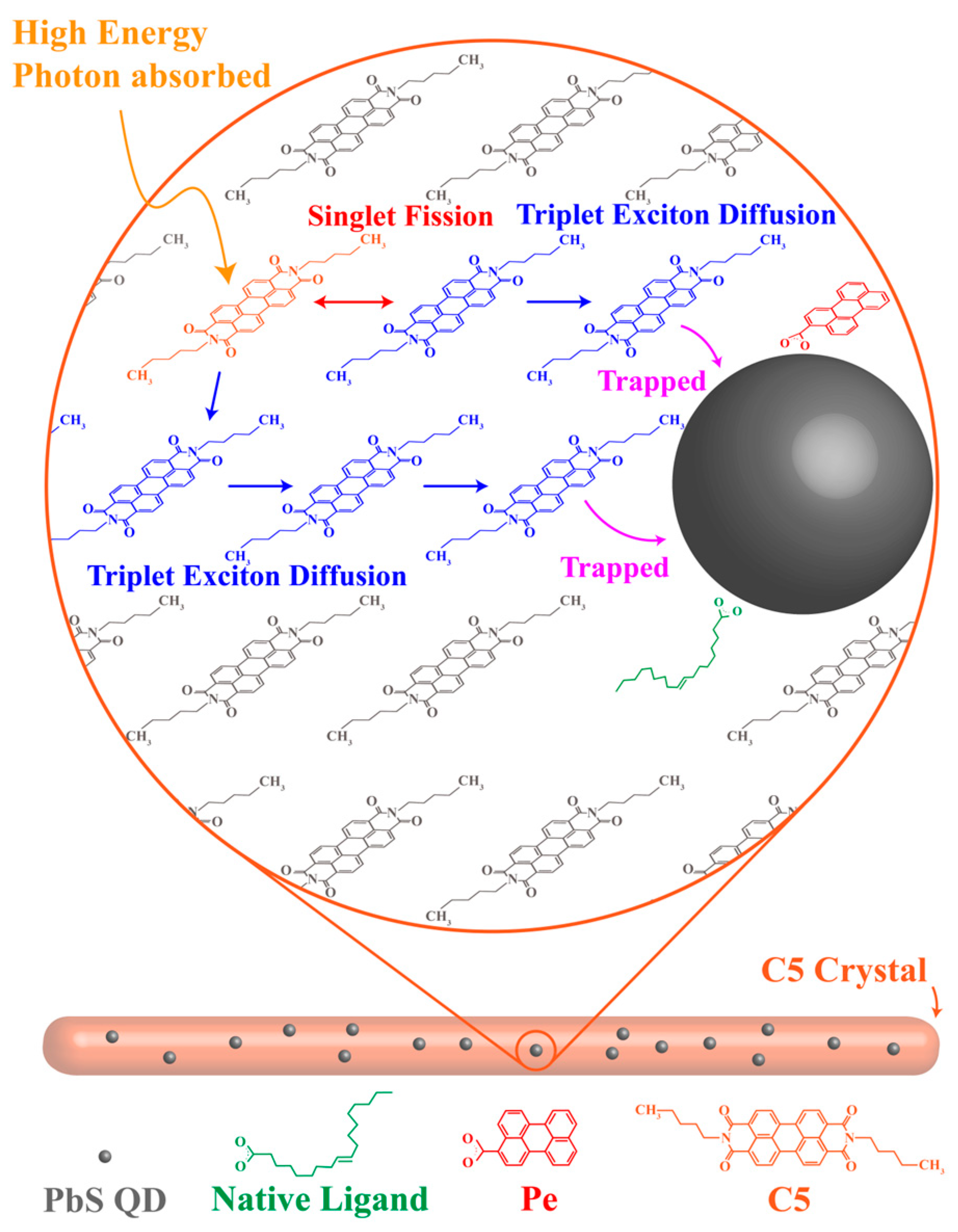
1. Introduction
2. Materials and Methods
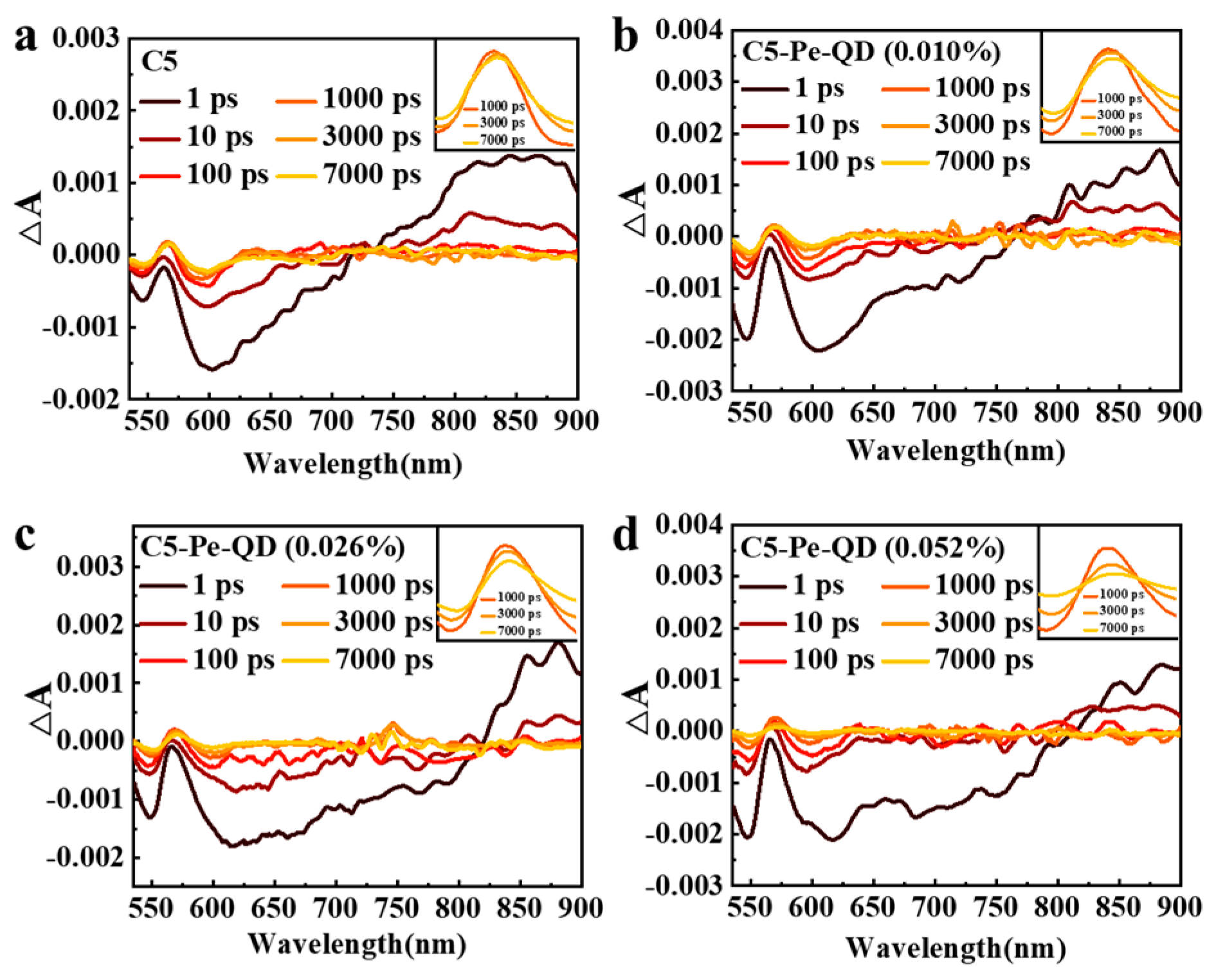
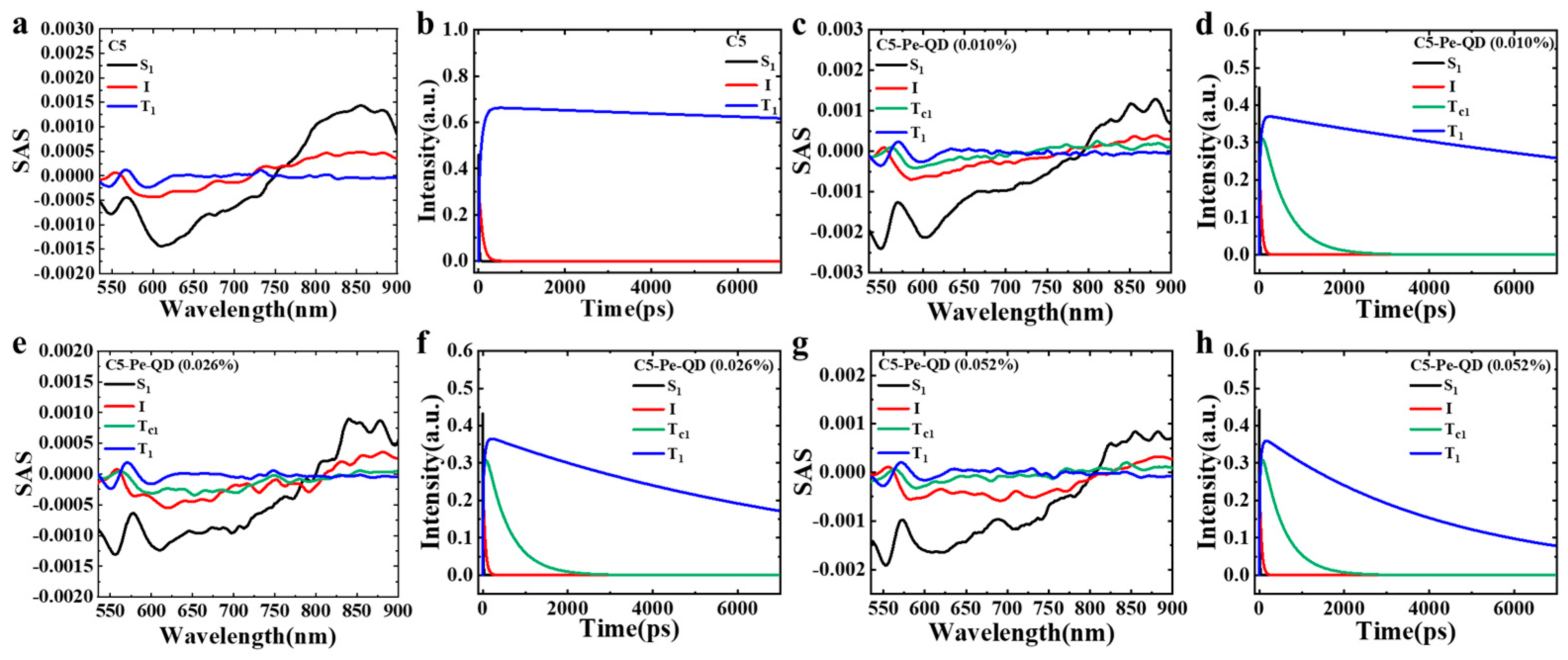
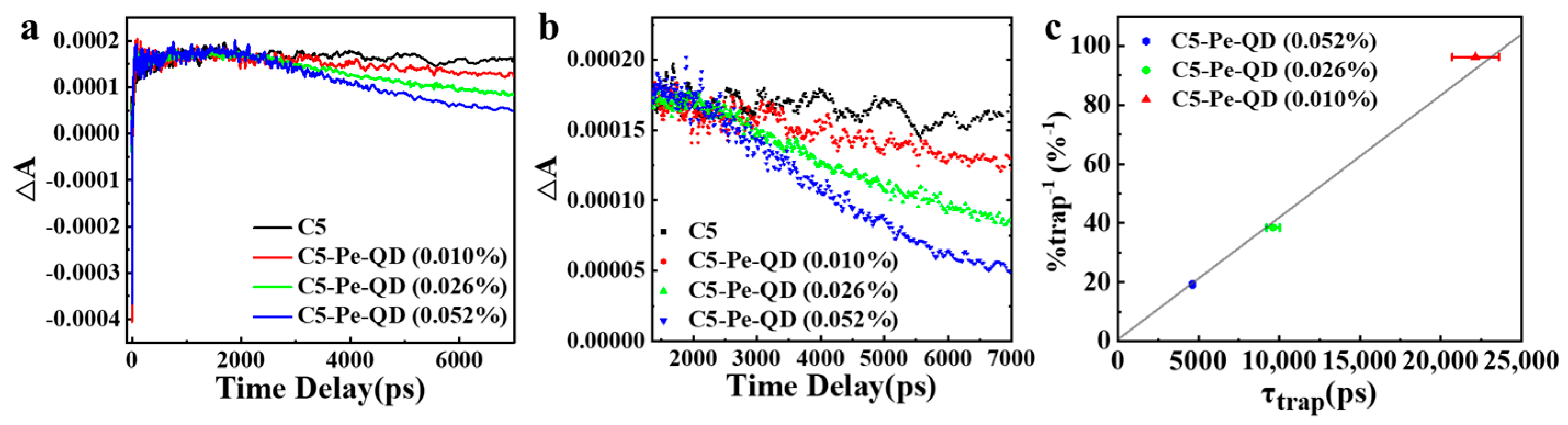
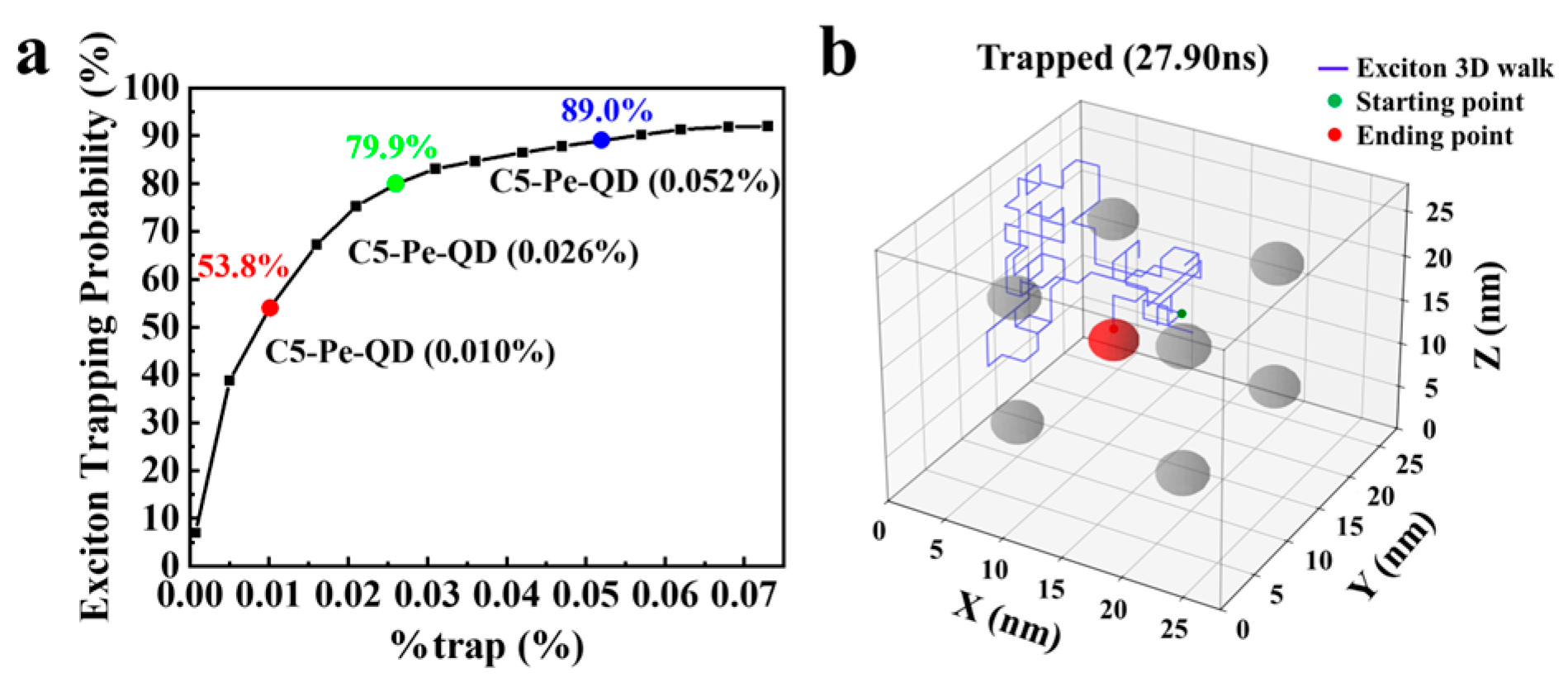
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miyata, K.; Conrad-Burton, F.S.; Geyer, F.L.; Zhu, X.-Y. Triplet Pair States in Singlet Fission. Chem. Rev. 2019, 119, 4261–4292. [Google Scholar] [CrossRef]
- Einzinger, M.; Wu, T.; Kompalla, J.F.; Smith, H.L.; Perkinson, C.F.; Nienhaus, L.; Wieghold, S.; Congreve, D.N.; Kahn, A.; Bawendi, M.G.; et al. Sensitization of silicon by singlet exciton fission in tetracene. Nature 2019, 571, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Greißel, P.M.; Wollny, A.-S.; Bo, Y.; Thiel, D.; Weiß, R.; Guldi, D.M. Molecular Acenes for Light Capture, Conversion, and Storage. Acc. Mater. Res. 2025, 6, 172–182. [Google Scholar] [CrossRef]
- Casanova, D. Theoretical Modeling of Singlet Fission. Chem. Rev. 2018, 118, 7164–7207. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; He, Z.; Wang, H.; Yang, K.; Zhang, Y.; Zhang, Y.; Geng, Z.; Duan, M.; Tang, B.; Xin, J.; et al. Unraveling Cross-Scale Fluorination Mechanisms in Non-Fullerene Acceptors for High-Efficiency Organic Photovoltaics. Adv. Funct. Mater. 2025, 35, e17542. [Google Scholar] [CrossRef]
- Baikie, T.K.; Allardice, J.; Dowland, S.A.; Ghosh, P.; Li, A.; Xiao, J.; Delport, G.; Sharma, A.; Greenham, N.C.; Rao, A. Singlet Fission Luminescent Solar Concentrators. Nano Lett. 2025, in press. [CrossRef]
- Wang, T.; Liu, H.; Wang, X.; Tang, L.; Zhou, J.; Song, X.; Lv, L.; Chen, W.; Chen, Y.; Li, X. Intramolecular singlet fission and triplet exciton harvesting in tetracene oligomers for solar energy conversion. J. Mater. Chem. A 2023, 11, 8515–8539. [Google Scholar] [CrossRef]
- Casillas, R.; Papadopoulos, I.; Ullrich, T.; Thiel, D.; Kunzmann, A.; Guldi, D.M. Molecular insights and concepts to engineer singlet fission energy conversion devices. Energy Environ. Sci. 2020, 13, 2741–2804. [Google Scholar] [CrossRef]
- Shi, X.; Geng, Y.; Wang, Z.; Zhou, E.; Fu, H.; Wang, L. Conjugated Polymer Singlet Fission Material with High Triplet Energy and Long Multiexciton Lifetime via Donor-π-Acceptor Strategy. Adv. Funct. Mater. 2025, 35, 2420771. [Google Scholar] [CrossRef]
- Pace, N.A.; Korovina, N.V.; Clikeman, T.T.; Holliday, S.; Granger, D.B.; Carroll, G.M.; Nanayakkara, S.U.; Anthony, J.E.; McCulloch, I.; Strauss, S.H.; et al. Slow charge transfer from pentacene triplet states at the Marcus optimum. Nat. Chem. 2020, 12, 63–70. [Google Scholar] [CrossRef]
- Rao, A.; Friend, R.H. Harnessing Singlet Exciton Fission to Break the Shockley–Queisser Limit. Nat. Rev. Mater. 2017, 2, 17063. [Google Scholar] [CrossRef]
- Hou, S.; Geng, Z.; Yang, J.; Li, Y.; Zhuo, S.; Chen, S.; Wu, Y.; Li, C.; Lin, H. Ligand Triplet Energy Transfer from Perylene Diimide Derivatives to PbS Quantum Dots in Solution. J. Phys. Chem. C 2025, 129, 518–525. [Google Scholar] [CrossRef]
- Gao, C.; Shi, H.; Qu, J.; Gao, B.; Hou, C. Efficient Triplet Energy Transfer from Singlet Fission Crystals to Ligand-Functionalized Quantum Dots in Composites. J. Phys. Chem. C 2025, accepted. [Google Scholar]
- Futscher, M.H.; Rao, A.; Ehrler, B. The Potential of Singlet Fission Photon Multipliers as an Alternative to Silicon-Based Tandem Solar Cells. ACS Energy Lett. 2018, 3, 2587–2592. [Google Scholar] [CrossRef]
- Akselrod, G.M.; Deotare, P.B.; Thompson, N.J.; Lee, J.; Tisdale, W.A.; Baldo, M.A.; Menon, V.M.; Bulovic, V. Visualization of exciton transport in ordered and disordered molecular solids. Nat. Commun. 2014, 5, 3646. [Google Scholar] [CrossRef]
- Gray, V.; Toolan, D.T.W.; Dowland, S.; Allardice, J.R.; Weir, M.P.; Zhang, Z.; Xiao, J.; Klimash, A.; Winkel, J.F.; Holland, E.K.; et al. Ligand-Directed Self-Assembly of Organic-Semiconductor/Quantum-Dot Blend Films Enables Efficient Triplet Exciton-Photon Conversion. J. Am. Chem. Soc. 2024, 146, 7763–7770. [Google Scholar] [CrossRef] [PubMed]
- Irkhin, P.; Biaggio, I. Direct Imaging of Anisotropic Exciton Diffusion and Triplet Diffusion Length in Rubrene Single Crystals. Phys. Rev. Lett. 2011, 107, 017402. [Google Scholar] [CrossRef]
- Wünsche, J.; Reineke, S.; Lüssem, B.; Leo, K. Measurement of triplet exciton diffusion in organic light-emitting diodes. Phys. Rev. B 2010, 81, 245201. [Google Scholar] [CrossRef]
- Tabachnyk, M.; Ehrler, B.; Bayliss, S.; Friend, R.H.; Greenham, N.C. Triplet diffusion in singlet exciton fission sensitized pentacene solar cells. Appl. Phys. Lett. 2013, 103, 153302. [Google Scholar] [CrossRef]
- Kroeze, J.E.; Koehorst, R.B.M.; Savenije, T.J. Singlet and Triplet Exciton Diffusion in a Self-Organizing Porphyrin Antenna Layer. Adv. Funct. Mater. 2004, 14, 992–998. [Google Scholar] [CrossRef]
- Giebink, N.C.; Sun, Y.; Forrest, S.R. Transient analysis of triplet exciton dynamics in amorphous organic semiconductor thin films. Org. Electron. 2006, 7, 375–386. [Google Scholar] [CrossRef]
- Lunt, R.R.; Giebink, N.C.; Belak, A.A.; Benziger, J.B.; Forrest, S.R. Exciton diffusion lengths of organic semiconductor thin films measured by spectrally resolved photoluminescence quenching. J. Appl. Phys. 2009, 105, 053711. [Google Scholar] [CrossRef]
- Hetzer, C.; Basel, B.S.; Kopp, S.M.; Hampel, F.; White, F.J.; Clark, T.; Guldi, D.M.; Tykwinski, R.R. Chromophore Multiplication To Enable Exciton Delocalization and Triplet Diffusion Following Singlet Fission in Tetrameric Pentacene. Angew. Chem. Int. Ed. 2019, 58, 15263–15267. [Google Scholar] [CrossRef]
- Grieco, C.; Doucette, G.S.; Pensack, R.D.; Payne, M.M.; Rimshaw, A.; Scholes, G.D.; Anthony, J.E.; Asbury, J.B. Dynamic Exchange During Triplet Transport in Nanocrystalline TIPS-Pentacene Films. J. Am. Chem. Soc. 2016, 138, 16069–16080. [Google Scholar] [CrossRef]
- Utzat, H.; Andernach, R.; Dimitrov, S.D.; McCulloch, I.; Heeney, M.; Durrant, J.R.; Bronstein, H. Synthesis and Exciton Dynamics of Triplet Sensitized Conjugated Polymers. J. Am. Chem. Soc. 2015, 137, 10383–10390. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Liu, X.; Geng, Z.; Wang, H.; Xu, Z.; Miao, Z.; Liang, Q.; Liu, J. Controlling the Third Component Distribution Toward High-Efficient Ternary Organic Solar Cells. Adv. Energy Mater. 2025, 15, 2406136. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Fu, S.; Wan, L.; Wang, H.; Zhang, Y.; Liu, Z.; Peng, J.; Li, J.; Song, C.; et al. In-Depth Investigation of Morphology Evolution in Highly Efficient Pseudo-Planar Heterojunction All-Polymer Organic Photovoltaics. Adv. Funct. Mater. 2025, 35, 2500975. [Google Scholar] [CrossRef]
- Wan, Y.; Wiederrecht, G.P.; Schaller, R.D.; Johnson, J.C.; Huang, L. Transport of Spin-Entangled Triplet Excitons Generated by Singlet Fission. J. Phys. Chem. Lett. 2018, 9, 6731–6738. [Google Scholar] [CrossRef]
- Volek, T.S.; Verkamp, M.A.; Ruiz, G.N.; Staat, A.J.; Li, B.C.; Rose, M.J.; Eaves, J.D.; Roberts, S.T. Slowed Singlet Exciton Fission Enhances Triplet Exciton Transport in Select Perylenediimide Crystals. J. Am. Chem. Soc. 2024, 146, 29575–29587. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Guo, Z.; Zhu, T.; Yan, S.; Johnson, J.; Huang, L. Cooperative Singlet and Triplet Exciton Transport in Tetracene Crystals Visualized by Ultrafast Microscopy. Nat. Chem. 2015, 7, 785–792. [Google Scholar] [CrossRef]
- Gutiérrez Álvarez, S.; Lin, W.; Abdellah, M.; Meng, J.; Židek, K.; Pullerits, T.; Zheng, K. Charge Carrier Diffusion Dynamics in Multisized Quaternary Alkylammonium-Capped CsPbBr3 Perovskite Nanocrystal Solids. ACS Appl. Mater. Interfaces 2021, 13, 44742–44750. [Google Scholar] [CrossRef]
- Proppe, A.H.; Xu, J.; Sabatini, R.P.; Fan, J.Z.; Sun, B.; Hoogland, S.; Kelley, S.O.; Voznyy, O.; Sargent, E.H. Picosecond Charge Transfer and Long Carrier Diffusion Lengths in Colloidal Quantum Dot Solids. Nano Lett. 2018, 18, 7052–7059. [Google Scholar] [CrossRef]
- Zhitomirsky, D.; Voznyy, O.; Hoogland, S.; Sargent, E.H. Measuring Charge Carrier Diffusion in Coupled Colloidal Quantum Dot Solids. ACS Nano 2013, 7, 5282–5290. [Google Scholar] [CrossRef]
- Zhitomirsky, D.; Voznyy, O.; Levina, L.; Hoogland, S.; Kemp, K.W.; Ip, A.H.; Thon, S.M.; Sargent, E.H. Engineering Colloidal Quantum Dot Solids within and beyond the Mobility-Invariant Regime. Nat. Commun. 2014, 5, 3803. [Google Scholar] [CrossRef] [PubMed]
- Tenney, S.M.; Tan, L.A.; Tan, X.; Sonnleitner, M.L.; Coffey, B.; Williams, J.A.; Ronquillo, R.; Atallah, T.L.; Ahmed, T.; Caram, J.R. Efficient 2D to 0D Energy Transfer in HgTe Nanoplatelet–Quantum Dot Heterostructures through High-Speed Exciton Diffusion. J. Phys. Chem. Lett. 2023, 14, 9456–9463. [Google Scholar] [CrossRef]
- Cadena, D.M.; Sowa, J.K.; Cotton, D.E.; Wight, C.D.; Hoffman, C.L.; Wagner, H.R.; Boette, J.T.; Raulerson, E.K.; Iverson, B.L.; Rossky, P.J.; et al. Aggregation of Charge Acceptors on Nanocrystal Surfaces Alters Rates of Photoinduced Electron Transfer. J. Am. Chem. Soc. 2022, 144, 22676–22688. [Google Scholar] [CrossRef]
- Savage, R.C.; Orgiu, E.; Mativetsky, J.M.; Pisula, W.; Schnitzler, T.; Eversloh, C.L.; Li, C.; Müllen, K.; Samorì, P. Charge Transport in Fibre-Based Perylene-Diimide Transistors: Effect of the Alkyl Substitution and Processing Technique. Nanoscale 2012, 4, 2387–2393. [Google Scholar] [CrossRef]
- Williams, M.L.; Schlesinger, I.; Jacobberger, R.M.; Wasielewski, M.R. Mechanism of Ultrafast Triplet Exciton Formation in Single Cocrystals of π-Stacked Electron Donors and Acceptors. J. Am. Chem. Soc. 2022, 144, 18607–18618. [Google Scholar] [CrossRef]
- Williams, M.L.; Palmer, J.R.; Tyndall, S.B.; Chen, Y.; Young, R.M.; Garzon-Ramirez, A.J.; Tempelaar, R.; Wasielewski, M.R. Molecular Engineering Charge Transfer and Triplet Exciton Formation in Donor–Acceptor Cocrystals. J. Chem. Phys. 2025, 163, 084505. [Google Scholar] [CrossRef]
- Wang, H.; He, Z.; Liu, X.; Xin, J.; Geng, Z.; Yang, K.; Zhang, Y.; Duan, M.; Qin, B.; Liang, Q.; et al. Temporally Stepwise Crystallization via Dual-Additive Orchestration: Resolving the Crystallinity–Domain Size Paradox for High-Efficiency Organic Photovoltaics. J. Energy Chem. 2026, 112, 370–383. [Google Scholar] [CrossRef]
- Wu, Y.; Lu, L.; Yu, B.; Zhang, S.; Luo, P.; Chen, M.; He, J.; Li, Y.; Zhang, C.; Zhu, J.; et al. Dynamic Evolving Exothermicity Steers Ultrafast Formation of a Correlated Triplet Pair State. J. Phys. Chem. Lett. 2023, 14, 4233–4240. [Google Scholar] [CrossRef]
- Le, A.K.; Bender, J.A.; Arias, D.H.; Cotton, D.E.; Johnson, J.C.; Roberts, S.T. Singlet Fission Involves an Interplay between Energetic Driving Force and Electronic Coupling in Perylenediimide Films. J. Am. Chem. Soc. 2018, 140, 814–826. [Google Scholar] [CrossRef] [PubMed]
- Snellenburg, J.J.; Laptenok, S.P.; Seger, R.; Mullen, K.M.; van Stokkum, I.H.M. Glotaran: A Java-Based Graphical User Interface for the R Package TIMP. J. Stat. Soft. 2012, 49, 1–24. [Google Scholar] [CrossRef]
- Guyot-Sionnest, P. Electrical Transport in Colloidal Quantum Dot Films. J. Phys. Chem. Lett. 2012, 3, 1169–1175. [Google Scholar] [CrossRef]
- Ompong, D.; Singh, J. Diffusion Length and Langevin Recombination of Singlet and Triplet Excitons in Organic Heterojunction Solar Cells. ChemPhysChem 2015, 16, 1281–1285. [Google Scholar] [CrossRef] [PubMed]
- Perez Garcia, S.E.; Cervantes Vergara, B.A.; Estrada, J.C.; Holland, S.; Maltez, D.P.R.; Tiffenberg, J. Studying Single-Electron Traps in Newly Fabricated Skipper-CCDs for the Oscura Experiment Using the Pocket-Pumping Technique. J. Appl. Phys. 2024, 136, 204502. [Google Scholar] [CrossRef]
- McClintock, L.; Song, Z.; Travaglini, H.C.; Senger, R.T.; Chandrasekaran, V.; Htoon, H.; Yarotski, D.; Yu, D. Highly Mobile Excitons in Single-Crystal Methylammonium Lead Tribromide Perovskite Microribbons. J. Phys. Chem. Lett. 2022, 13, 3698–3705. [Google Scholar] [CrossRef]
- Gilmore, R.H.; Lee, E.M.Y.; Weidman, M.C.; Willard, A.P.; Tisdale, W.A. Charge Carrier Hopping Dynamics in Homogeneously Broadened PbS Quantum Dot Solids. Nano Lett. 2017, 17, 883–901. [Google Scholar] [CrossRef]
- Mikhnenko, O.V.; Blom, P.W.M.; Nguyen, T.Q. Exciton diffusion in organic semiconductors. Energy Environ. Sci. 2015, 8, 1867–1888. [Google Scholar] [CrossRef]
- Gao, C.; Shi, H.; Liu, W.; Yang, Q.; Zhang, S.; Gao, B.; Wang, J.; Zhu, X.; Jia, P.; Zhu, H.; et al. Efficient Singlet Fission in Perylenediimide Derivative Nanocrystals. J. Phys. Chem. C 2022, 126, 18767–18777. [Google Scholar] [CrossRef]
- Deng, S.; Shi, E.; Yuan, L.; Jin, L.; Dou, L.; Huang, L. Long-range exciton transport and slow annihilation in two-dimensional hybrid perovskites. Nat. Commun. 2020, 11, 664. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira Neto, P.H.; da Silva Filho, D.A.; da Cunha, W.F.; Acioli, P.H.; e Silva, G.M. Limit of Exciton Diffusion in Highly Ordered π-Conjugated Systems. J. Phys. Chem. C 2015, 119, 19654–19659. [Google Scholar] [CrossRef]
- Talebi, S.; Gharehbash, K.; Jalali, H.R. Study on Random Walk and Its Application to Solution of Heat Conduction Equation by Monte Carlo Method. Prog. Nucl. Energy 2017, 96, 18–35. [Google Scholar] [CrossRef]
- Roberts, D.T.; Sadeghi, S.M. Excitation-Dependent Exciton Diffusion in Semiconductor Quantum Dot Thin Films with Spatially Patterned Lifetimes. ACS Photonics 2024, 11, 2578–2586. [Google Scholar] [CrossRef]
- Zhang, H.; Su, Q.; Chen, S. Suppressing Förster Resonance Energy Transfer in Close-Packed Quantum-Dot Thin Film: Toward Efficient Quantum-Dot Light-Emitting Diodes with External Quantum Efficiency over 21.6%. Adv. Optical Mater. 2020, 8, 1902092. [Google Scholar] [CrossRef]
- Kodaimati, M.S.; Wang, C.; Chapman, C.; Schatz, G.C.; Weiss, E.A. Distance-Dependence of Interparticle Energy Transfer in the Near-Infrared within Electrostatic Assemblies of PbS Quantum Dots. ACS Nano 2017, 11, 5041–5050. [Google Scholar] [CrossRef]
- Jia, Z.; Shao, H.; Xu, J.; Dai, Y.; Qiao, J. Crown ether-assisted room-temperature halide passivation for high-efficiency PbS quantum dots enabling large-area and long-lifetime near-infrared QD-OLEDs. Nano Res. 2023, 16, 7537–7544. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Shi, H.; Qu, J.; Gao, B.; Hou, C. The Diffusion of Triplet Excitons in Perylenediimide Derivative Crystals. Photonics 2025, 12, 1132. https://doi.org/10.3390/photonics12111132
Gao C, Shi H, Qu J, Gao B, Hou C. The Diffusion of Triplet Excitons in Perylenediimide Derivative Crystals. Photonics. 2025; 12(11):1132. https://doi.org/10.3390/photonics12111132
Chicago/Turabian StyleGao, Changyu, Hongyan Shi, Jiafan Qu, Bo Gao, and Chunfeng Hou. 2025. "The Diffusion of Triplet Excitons in Perylenediimide Derivative Crystals" Photonics 12, no. 11: 1132. https://doi.org/10.3390/photonics12111132
APA StyleGao, C., Shi, H., Qu, J., Gao, B., & Hou, C. (2025). The Diffusion of Triplet Excitons in Perylenediimide Derivative Crystals. Photonics, 12(11), 1132. https://doi.org/10.3390/photonics12111132




