Multi-Peak Narrowband Perfect Absorber Based on the Strong Coupling Between Fabry–Perot Mode and SPP Waveguide Mode
Abstract
1. Introduction
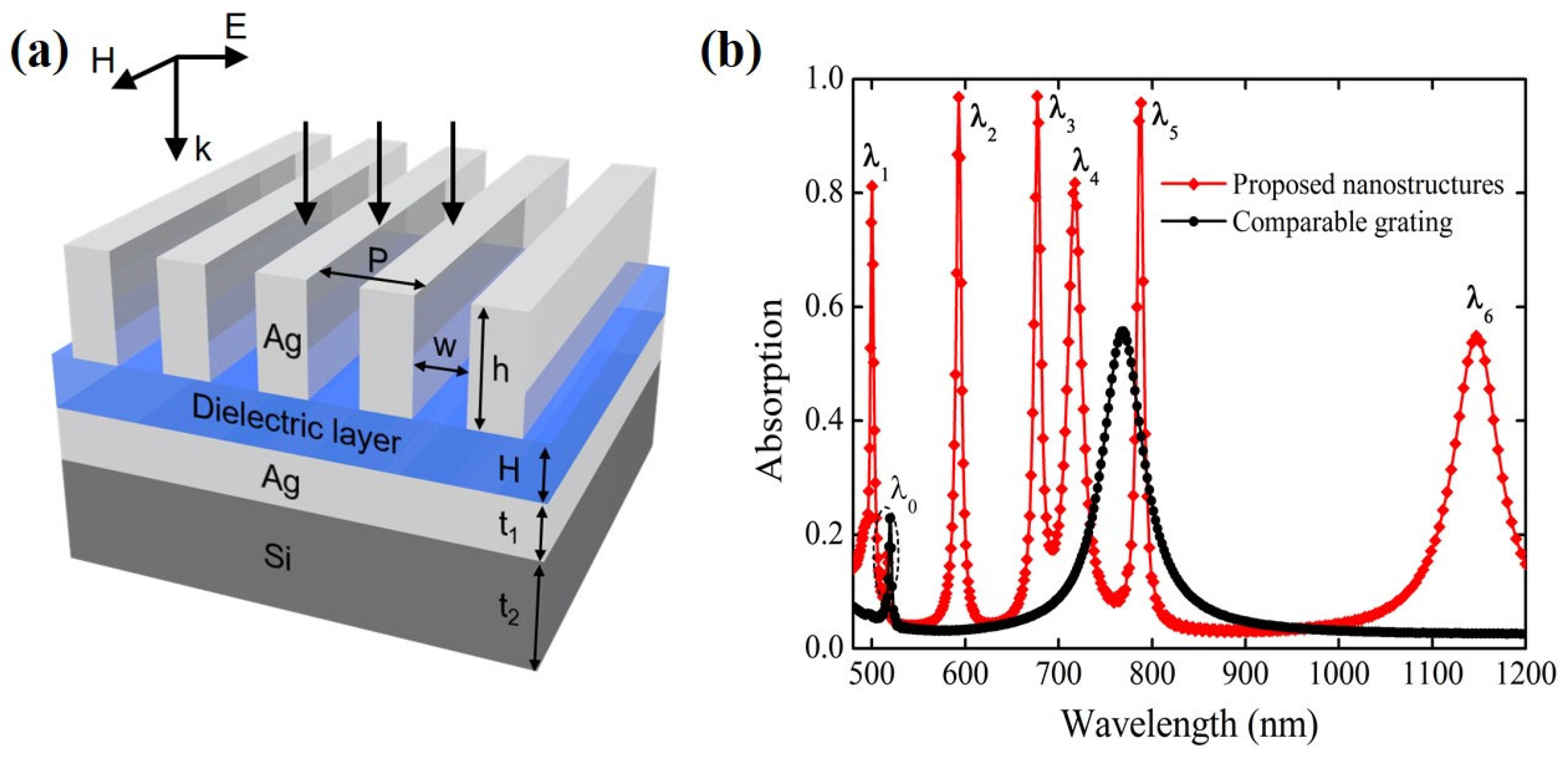
2. Modeling and Simulation
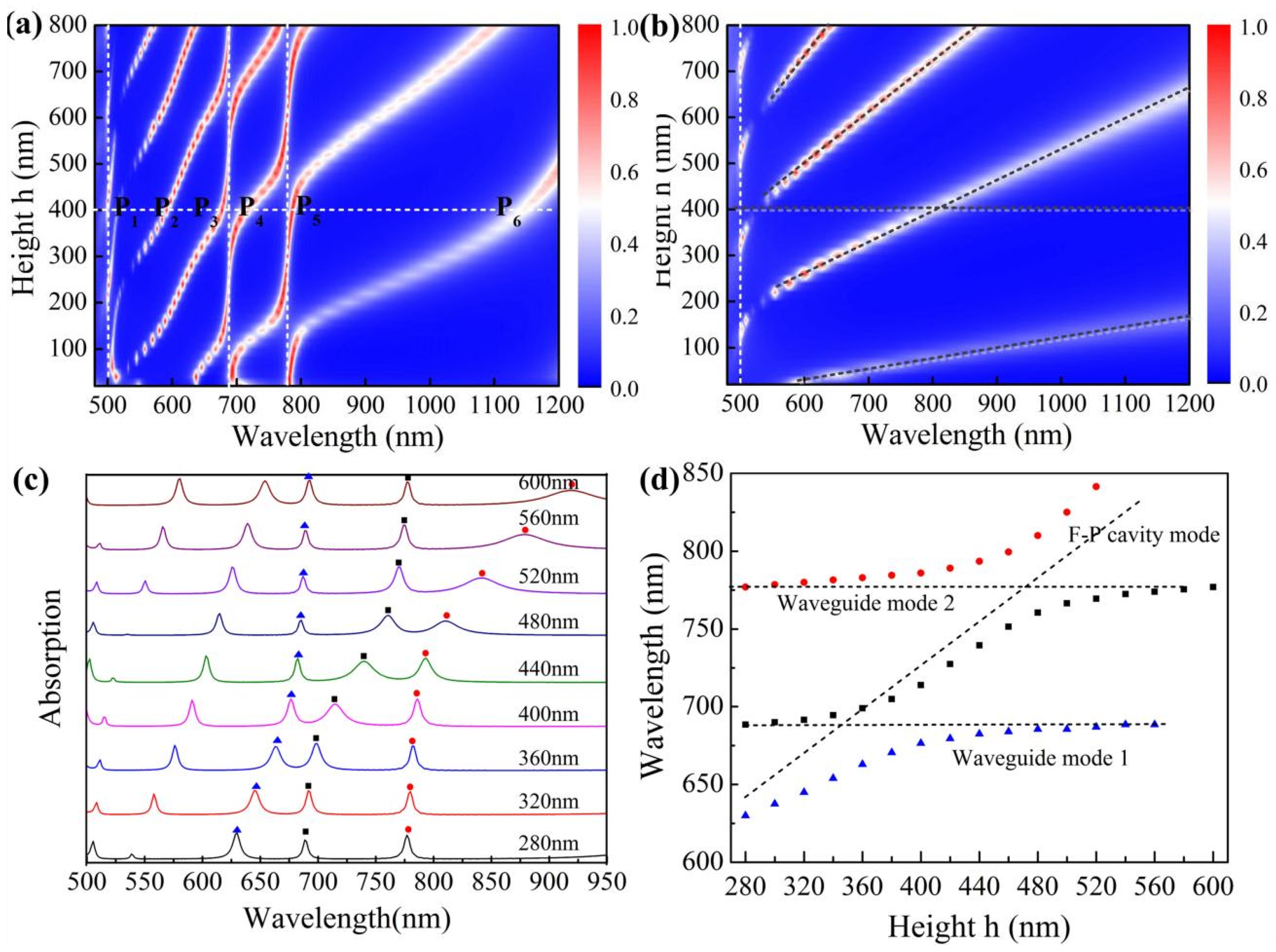
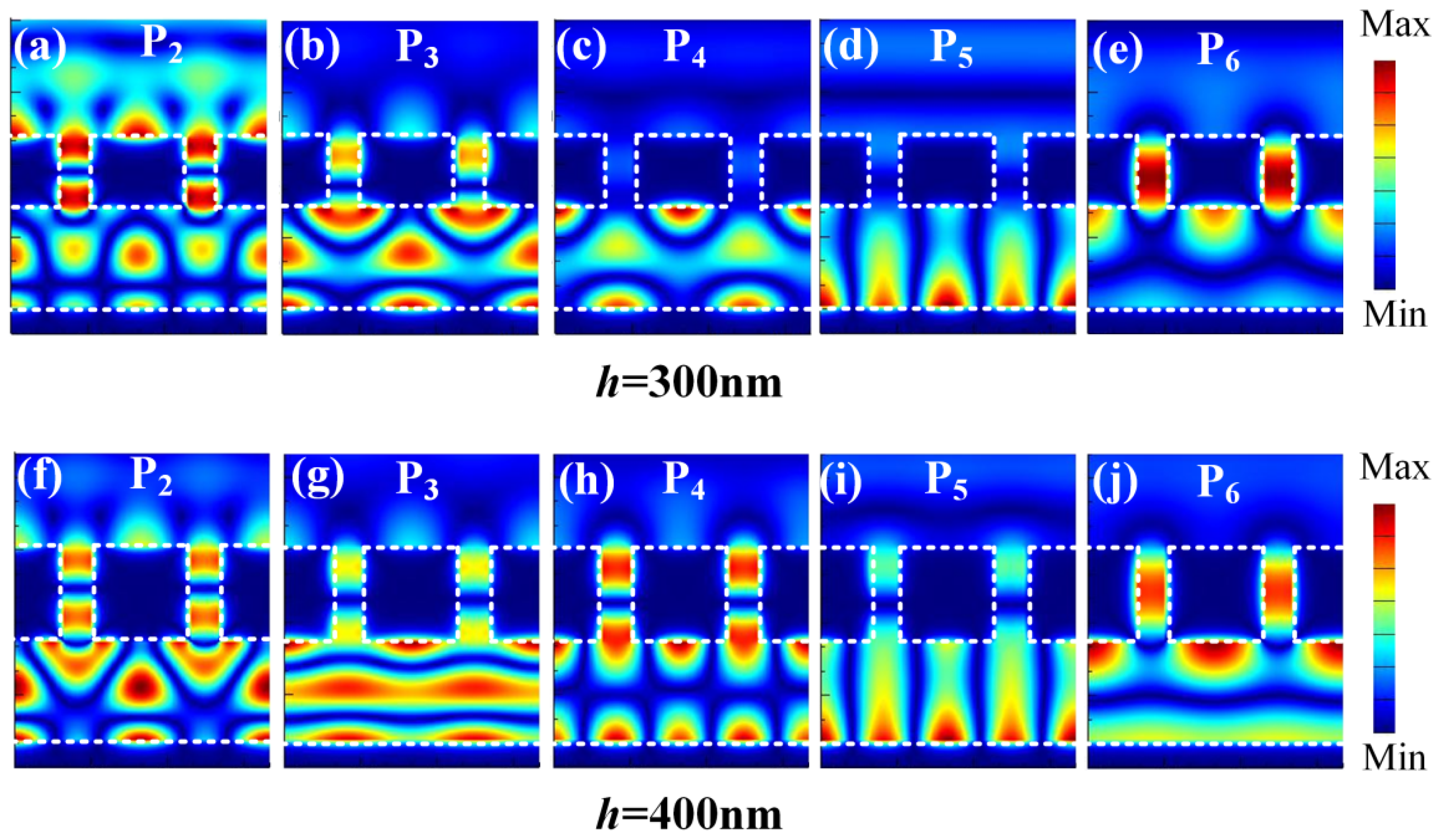
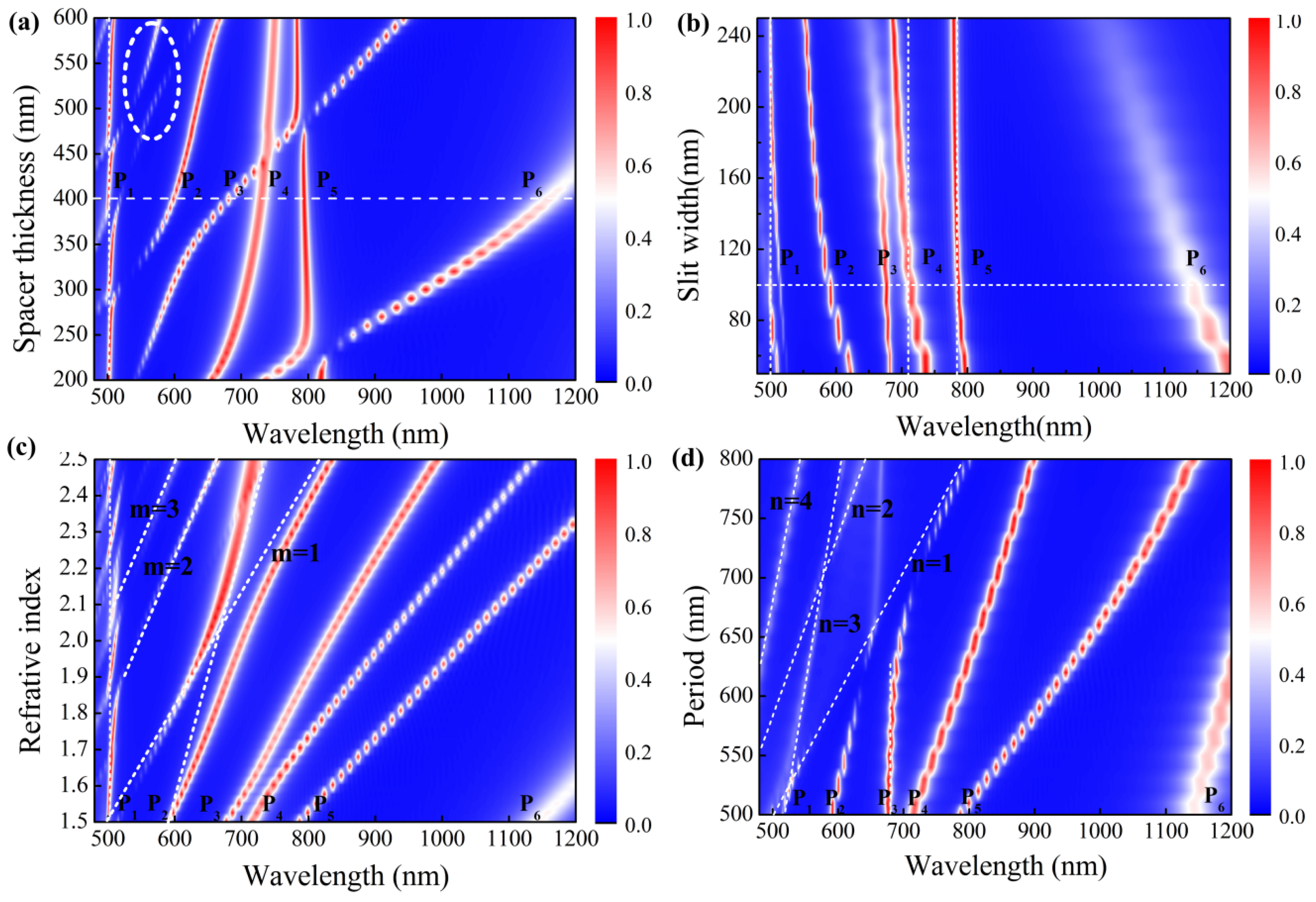
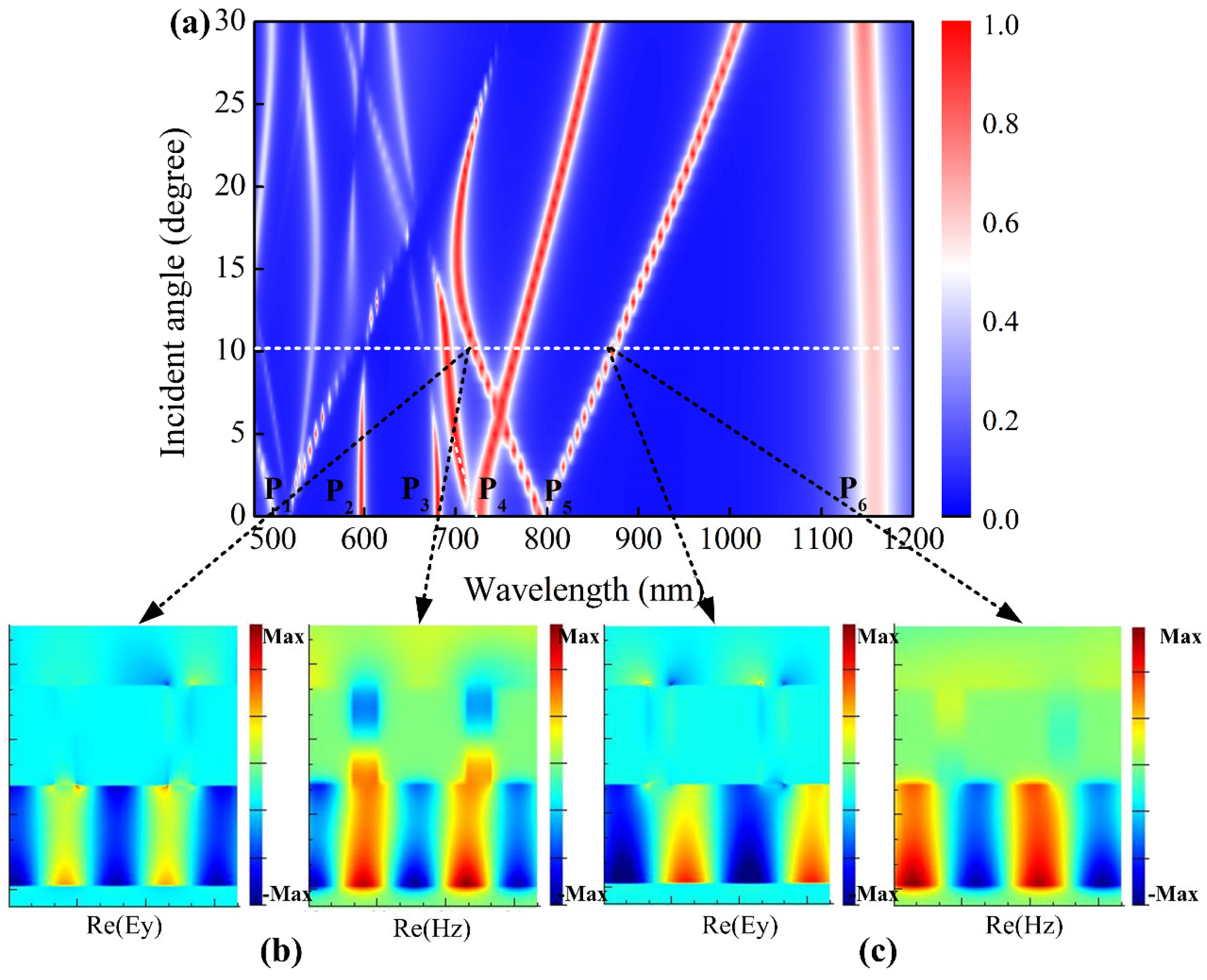
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lameirinhas, R.A.M.; Torres, J.P.N.; Baptista, A.; Martins, M.J.M. A New Method to Analyse the Role of Surface Plasmon Polaritons on Dielectric-Metal Interfaces. IEEE Photonics J. 2022, 14, 2236409. [Google Scholar] [CrossRef]
- Maleki, M.J.; Soroosh, M.; Akbarizadeh, G. A compact low-loss 2-to-4 plasmonic decoder based on suspended graphene for surface plasmon polariton transmission. Diam. Relat. Mater. 2024, 144, 110983. [Google Scholar] [CrossRef]
- Liu, X.; Tyler, T.; Starr, T.; Starr, A.F.; Jokerst, N.M.; Padilla, W.J. Taming the blackbody with infrared metamaterials as selective thermal emitters. Phys. Rev. Lett. 2011, 107, 045901. [Google Scholar] [CrossRef]
- Stipe, B.C.; Strand, T.C.; Poon, C.C.; Balamane, H.; Boone, T.D.; Katine, J.A.; Li, J.-L.; Rawat, V.; Nemoto, H.; Hirotsune, A. Magnetic recording at 1.5 Pb m−2 using an integrated plasmonic antenna. Nat. Photonics 2010, 4, 484–488. [Google Scholar] [CrossRef]
- Zhou, L.; Tan, Y.; Ji, D.; Zhu, B.; Zhang, P.; Xu, J.; Gan, Q.; Yu, Z.; Zhu, J. Self-assembly of highly efficient, broadband plasmonic absorbers for solar steam generation. Sci. Adv. 2016, 2, e1501227. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Valentine, J. Metamaterial perfect absorber based hot electron photodetection. Nano Lett. 2014, 14, 3510–3514. [Google Scholar] [CrossRef] [PubMed]
- Nan, X.; Lai, W.; Peng, J.; Wang, H.; Chen, B.; He, H.; Mo, Z.; Xia, Z.; Tan, N.; Liu, Z.; et al. In situ photoelectric biosensing based on ultranarrowband near-infrared plasmonic hot electron photodetection. Adv. Photonics 2024, 6, 026007. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.; Smith, D.; Padilla, W. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Liu, X.; Padilla, W.J.; Zhou, L.; Qiu, M. High performance optical absorber based on a plasmonic metamaterial. Appl. Phys. Lett. 2010, 96, 251104. [Google Scholar] [CrossRef]
- Liu, G.; Liu, Y.; Tang, L.; Liu, X.; Fu, G.; Liu, Z. Semiconductor-enhanced Raman scattering sensors via quasi-three-dimensional Au/Si/Au structures. Nanophotonics 2019, 8, 1095–1107. [Google Scholar] [CrossRef]
- Chen, Y.; You, K.; Lin, J.; Zhao, J.; Ma, W.; Meng, D.; Cheng, Y.; Liu, J. Design of a Broadband Perfect Solar Absorber Based on a Four-Layer Structure with a Cross-Shaped Resonator and Triangular Array. Photonics 2022, 9, 565. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, G.; Liu, X.; Huang, S.; Wang, Y.; Pan, P.; Liu, M. Achieving an ultra-narrow multiband light absorption meta-surface via coupling with an optical cavity. Nanotechnology 2015, 26, 235702. [Google Scholar] [CrossRef]
- Zhang, M.; Fang, J.; Zhang, F.; Chen, J.; Yu, H. Ultra-narrow band perfect absorbers based on Fano resonance in MIM metamaterials. Opt. Commun. 2017, 405, 216–221. [Google Scholar] [CrossRef]
- Li, Z.; Butun, S.; Aydin, K. Ultranarrow band absorbers based on surface lattice resonances in nanostructured metal surfaces. ACS Nano 2014, 8, 8242–8248. [Google Scholar] [CrossRef]
- Liu, Z.; Ye, J. Highly controllable double Fano resonances in plasmonic metasurfaces. Nanoscale 2016, 8, 17665–17674. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Li, G.; Lei, D.; Cheah, K.W. Efficient energy exchange between plasmon and cavity modes via Rabi-analogue splitting in a hybrid plasmonic nanocavity. Nanoscale 2013, 5, 9129–9133. [Google Scholar] [CrossRef]
- He, X.; Jie, J.; Yang, J.; Han, Y.; Zhang, S. Asymmetric dielectric grating on metallic film enabled dual- and narrow-band absorbers. Opt. Express 2020, 28, 4594. [Google Scholar] [CrossRef]
- Qin, L.; Liu, F.; Yuan, F.; Zhang, A.; Zhang, K. An angle-tuned polarization-independent multi-narrowband perfect absorber. J. Opt. 2022, 24, 095002. [Google Scholar] [CrossRef]
- Yang, C.; Shen, W.; Zhang, Y.; Zhao, D.; Liu, X. Multi-narrowband absorber based on subwavelength grating structure. Opt. Commun. 2014, 331, 310–315. [Google Scholar] [CrossRef]
- Wen, X.; Deng, S. Plasmonic Nanostructure Lattices for High-Performance Sensing. Adv. Opt. Mater. 2023, 11, 2300401. [Google Scholar] [CrossRef]
- Borui, L.; Yao, Z.; Tsai, D.P.; Shumin, X. Meta-device: Advanced manufacturing. Light Adv. Manuf. 2024, 5, 117–132. [Google Scholar]
- Liu, Y.; Ma, W.-Z.; Wu, Y.-C.; Meng, D.; Cheng, Y.-Y.; Chen, Y.-S.; Liu, J.; Gu, Y. Multi-peak narrow-band metamaterial absorber for visible to near-infrared wavelengths. Results Phys. 2023, 47, 106374. [Google Scholar] [CrossRef]
- Zhai, Y.; Chen, G.; Xu, J.; Qi, Z.; Li, X.; Wang, Q. Multiple-band perfect absorbers based on the combination of Fabry-Perot resonance and the gap plasmon resonance. Opt. Commun. 2017, 399, 28–33. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3. [Google Scholar]
- Ai, Z.; Liu, H.; Cheng, S.; Zhang, H.; Yi, Z.; Zeng, Q.; Wu, P.; Zhang, J.; Tang, C.; Hao, Z. Four peak and high angle tilted insensitive surface plasmon resonance graphene absorber based on circular etching square window. J. Phys. D Appl. Phys. 2025, 58, 185305. [Google Scholar] [CrossRef]
- Cheng, R.; Zhou, Y.; Liu, J.; Hu, S.; Liu, H.; Pan, J.; Huang, W.; He, X.; Liang, B.; Zhang, L. Independently tunable multi-band terahertz absorber based on graphene sheet and nanoribbons. Opt. Express 2022, 30, 3893–3902. [Google Scholar] [CrossRef]
- Zhong, Q.; Wang, T.; Jiang, X.; Cheng, L.; Yan, R.; Huang, X. Near-infrared multi-narrowband absorber based on plasmonic nanopillar metamaterial. Opt. Commun. 2020, 458, 124637. [Google Scholar] [CrossRef]
- Zhou, W.; Wu, Y.; Yu, M.; Hao, P.; Liu, G.; Li, K. Extraordinary optical absorption based on guided-mode resonance. Opt. Lett. 2013, 38, 5393–5396. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Yan, X.; Li, P.; Mou, Y.; Wang, W.; Guan, Z.; Xu, H. Mechanism of resonant perfect optical absorption in dielectric film supporting metallic grating structures. Opt. Express 2016, 24, 19435–19447. [Google Scholar] [CrossRef]
- Liang, Y.; Peng, W. Theoretical study of transmission characteristics of sub-wavelength nano-structured metallic grating. Appl. Spectrosc. 2013, 67, 49–53. [Google Scholar] [CrossRef]
- Liang, Y.; Peng, W.; Hu, R.; Xie, L. Extraordinary optical properties in the subwavelength metallodielectric free-standing grating. Opt. Express 2014, 22, 19484–19494. [Google Scholar] [CrossRef]
- Kaplan, A.F.; Xu, T.; Guo, L.J. High efficiency resonance-based spectrum filters with tunable transmission bandwidth fabricated using nanoimprint lithography. Appl. Phys. Lett. 2011, 99, 143111. [Google Scholar] [CrossRef]
- Ho, Y.L.; Huang, L.C.; Delaunay, J.J. Spectrally Selective Photocapacitance Modulation in Plasmonic Nanochannels for Infrared Imaging. Nano Lett. 2016, 16, 3094–3100. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Liu, M.; Cheng, S.; Wang, J.; Yi, Y.; Li, B.; Tang, C.; Gao, F. Bilayer graphene metasurface with dynamically reconfigurable terahertz perfect absorption. Curr. Appl. Phys. 2025, 80, 282–290. [Google Scholar] [CrossRef]
| Reference | Number of Peaks | Maximum Peak Absorption | FWHM (Full-Width at Half-Maximum) | Wavelength |
|---|---|---|---|---|
| [27] | 4 | 98.5% | ~5 nm | 2200–2400 nm |
| [28] | 5 | 85.7% | / | 5–100 um |
| [29] | 5 | 99.3% | 15 nm | 800–2000 nm |
| [23] | 5 | 99.9% | 5 nm | 750–3000 nm |
| Proposed | 6 | 98.5% | 8 nm | 450–1200 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, Y.; He, W.; Chen, Q. Multi-Peak Narrowband Perfect Absorber Based on the Strong Coupling Between Fabry–Perot Mode and SPP Waveguide Mode. Photonics 2025, 12, 1131. https://doi.org/10.3390/photonics12111131
Zhai Y, He W, Chen Q. Multi-Peak Narrowband Perfect Absorber Based on the Strong Coupling Between Fabry–Perot Mode and SPP Waveguide Mode. Photonics. 2025; 12(11):1131. https://doi.org/10.3390/photonics12111131
Chicago/Turabian StyleZhai, Yusheng, Weiji He, and Qian Chen. 2025. "Multi-Peak Narrowband Perfect Absorber Based on the Strong Coupling Between Fabry–Perot Mode and SPP Waveguide Mode" Photonics 12, no. 11: 1131. https://doi.org/10.3390/photonics12111131
APA StyleZhai, Y., He, W., & Chen, Q. (2025). Multi-Peak Narrowband Perfect Absorber Based on the Strong Coupling Between Fabry–Perot Mode and SPP Waveguide Mode. Photonics, 12(11), 1131. https://doi.org/10.3390/photonics12111131





