Generation of Computer-Generated Holograms as Anti-Counterfeiting Tags via Hybrid Fabrication Using Additive Manufacturing and Nanoimprint Lithography

Abstract

This paper presents a hybrid fabrication method for producing anti-counterfeit optical elements on plastic products and surfaces targeting multidiscipline applications such as food, pharmaceuticals, luxury goods, and electronics industry. Our proposition combines the design flexibility and rapid prototyping capabilities of stereolithography three-dimensional (SLA 3D) printing with nanoimprint lithography (NIL) to create unique optical security tags onto plastic surfaces. The proposed approach is cost-effective, scalable, and tailored for mass production, addressing the increasing demand for secure and reliable authentication solutions. NIL is substrate agnostic, offering material selection versatility and realization of security tags onto polymer surfaces, which are widely used across various sectors such as packaging industry, medical devices, and flexible electronics. This enables integration into a wide range of materials, further enhancing applicability on flat and 3D shape surfaces. An evaluation method based on digital reconstruction has been used to ensure robust performance and verification of the produced optical security features. The results demonstrate that this hybrid approach provides a reproducible and technically feasible path for the development of optical anti-counterfeiting tags suitable for large-scale implementation, particularly within fast-moving consumer goods (FMCG).

1. Introduction

Counterfeiting is a growing global concern, threatening brand integrity, consumer trust, and regulatory compliance across multiple industries [1,2]. As counterfeiters employ increasingly sophisticated replication methods, conventional anti-counterfeiting measures, such as holographic stickers, watermarks, and serial numbers, are becoming easier to replicate [3,4]. Thus, there is a pressing need for innovative, scalable, and cost-efficient solutions that provide robust protection against counterfeiting [5].

One effective hardware-based solution to this challenge is to embed a unique, observable characteristic within the device or object of interest. This characteristic serves as a distinctive identifier, functioning as a form of fingerprinting that ensures authenticity and enables easy detection of counterfeit products.

Conventional optical identifiers, such as barcodes or QR codes, provide traceability but can be easily copied or visually reproduced, offering limited protection against high-quality counterfeits. Moreover, they rely on visible digital patterns that may interfere with the product’s design or branding. In contrast, holographic identifiers combine aesthetic integration, high design complexity, and resistance to replication, offering an additional layer of security without altering the product’s appearance.

One promising avenue is the use of computer-generated holograms (CGHs), as they are complex optical patterns that are difficult to replicate, due to design complexity, phase control requirements and the need for the original digital blueprint, which makes accurate reproduction challenging [5,6,7,8]. CGH fabrication techniques, such as laser engraving, suffer from high costs and long processing times. An additional limitation is the restricted versatility in material processing. Different material categories need the use of different laser sources or systems; for instance, metal engraving requires a laser with different specifications (e.g., wavelength) compared to those used for engraving plastic. In the context of engraving anti-counterfeiting tags on products, the process typically involves marking the product’s surface [9,10,11].

Additive Manufacturing (AM) is the layer-by-layer fabrication of parts directly from a digital model, commonly known as 3D printing [12]. Direct manufacturing through 3D printing is recognized as a transformative process, enabling companies to bypass traditional production methods and move directly to manufacturing of products [13]. This innovation allows for the full integration of customization and co-creation, where consumers can actively participate in the design and creation of the product, thereby increasing its value [14]. Unlike traditional manufacturing, which is often tied to specific factories, direct manufacturing through 3D printing offers the advantage of flexibility, allowing products to be made on-demand with lower upfront costs. Furthermore, it reduces the need for extensive storage and transportation. Since products are made on-demand, companies can avoid the costs associated with warehousing and shipping finished goods, resulting in lower overall operational expenses and a more sustainable production process [15].

In this paper, we present a novel approach to anti-counterfeiting that integrates CGHs directly into the computer-aided design (CAD) design of the object’s surface before 3D printing. By defining the anti-counterfeit tag in the initial design, the holographic features are fabricated on the surface of the printed object in a single step, eliminating the need for post-processing.

This integration provides greater flexibility, allowing the tag to be placed anywhere within the object, whether on its surface or, in the case of non-flat geometries, within its internal areas. By embedding the security tag into the product’s geometry during 3D printing, it also becomes possible to conceal and protect the tag from wear and scratches. Such security tags can be integrated into internal or hidden surfaces, enhancing its durability and security.

SLA 3D printing has emerged as a promising approach for rapid prototyping within injection molding applications [16], enabling the fabrication of high-precision molds with reduced costs. Unlike traditional metallic inserts, SLA allows the prototyping of multiple geometries without the significant expenses associated with metal tooling, making it an efficient solution for iterative design and small-scale production [17]. This further strengthens the potential of 3D printed security tags, as they could serve as molds for large-scale production, similar to the injection molding process, thus expanding their applicability and scalability.

We further explored the combination of SLA 3D printed security tags with nanoimprint lithography (NIL). Specifically, we replicated the 3D-printed security tags using NIL to assess the potential for mass replication via a high-throughput process. Therefore, we investigated the feasibility of transferring the 3D printed optical structures onto flexible substrates which are widely used in the packaging industry. Preliminary results indicate that this combined approach successfully enhances the scalability and competence for direct manufacturing of security elements on polymer surfaces.

Furthermore, we introduce a digital reconstruction-based evaluation method, which provides a robust and industrially applicable verification technique for ensuring the authenticity of the fabricated holographic elements. Our results highlight the commercial feasibility of this approach, positioning it as a practical solution for industries requiring secure and scalable anti-counterfeiting measures.

The novelty of this work lies in the integration of established optical and fabrication methods into a unified workflow. By combining 3D printing of holographic masters with UV-NIL replication on flexible substrates and validating the outcome through digital reconstruction, this study demonstrates a scalable and quantitative route for the fabrication and assessment of optical anti-counterfeiting tags.

2. Materials and Methods

2.1. CGH Tag Design

The computer-generated holograms (CGHs) were designed by computing a binary phase mask using the Gerchberg–Saxton iterative phase retrieval algorithm. A beam splitter design was employed for phase mapping, ensuring optimal diffraction efficiency. The 2D phase mask (Figure 1b) was then converted into a 3D structure (Figure 1c) through an extrusion process along the z-axis. The imprinted features were designed with 1 mm height to ensure sufficient optical contrast for the digital reconstruction. While such feature thickness may affect substrate flexibility, this can be mitigated through appropriate selection of imprint resists with tailored mechanical properties, such as optimized Young’s modulus and elasticity. Formlabs PreForm v3.32.0 slicing software was used to generate support structures for the object (Figure 2a). Holograms of various sizes were designed and tested for printing. A dimension of 1.5 cm × 1.5 cm was selected for nanoimprint lithography (NIL) replication, as the structural features at this size were more clearly distinguishable and better suited for the intended application.

2.2. Materials & Methods

To fabricate the CGH structures, a Form 3 SLA 3D printer (Formlabs, Somerville, MA, USA) with a UV-curable Clear resin was used, selecting a 25 µm layer thickness to ensure precise pattern formation. The in-plane resolution, defined by the laser spot size (≈80 µm), enables high-detail reproduction of the CGH features. These printing characteristics were sufficient to produce CGH tags with well-defined structures suitable for optical analysis. The printing and post processing parameters were optimized to achieve sharp feature definition and reduced surface roughness, which is crucial for effective optical performance [18,19].

The printed CGH elements (Figure 3a) were used as master molds for soft lithography [20]. A silicone elastomer mixture of SILASTIC™ RTV-3481 (Dow Silicones Corporation, Midland, MI, USA) (1:20 ratio of curing agent to base material) was cast onto the 3D-printed structure to create a flexible working mold, which was allowed to cure for 6 h at room temperature. Once cured, the silicone mold was peeled off and used for ultraviolet light assisted nanoimprint lithography (UV-NIL) [21]. Throughout our experiments we used polyethylene terephthalate (PET) film as our substrate material [22]. An in-house UV curable acrylate resin was drop-cast onto the PET substrates, while the UV-NIL imprinting process was carried out using a desktop NIL tool from NIL Technology ApS. under controlled pressure and UV exposure conditions.

During the UV-NIL process the elastomeric stamp was brought into physical contact under 1 bar pressure for 2 min while UV light exposure was followed for 30 s. The imprinting resulted in pattern transfer, preserving the characteristic features of the CGH structures (Figure 4a). The replicated features retained the dimensions and aspect ratio of the 3D printed master (≈2.4:1), confirming accurate pattern transfer after imprinting.

2.3. Optical Characterization and Digital Reconstruction

The fabricated CGH tag structures were characterized using a handheld digital microscope. Image processing and digital reconstruction were performed using MATLAB R2025a, employing Fourier optics principles [5,22]. The grayscale image of the CGH was convoluted with the system’s impulse response function, assuming illumination by a 633 nm laser and free-space propagation over a 200 mm distance. Following this process, the far-field reconstructed images were retrieved, verifying the optical performance of the imprinted holograms.

The design of the holographic mask represents a classical phase optimization problem [23,24]. The primary objective of the optimization process was to identify the optimal phase mask that enables the best possible optical reconstruction of a desired response—in this case, the letter ‘H’ and letter ‘M’—using a conventional laser source. To achieve this, we developed an in-house code based on the Gerchberg–Saxton algorithm [25], which is used to design phase-only holograms. The Gerchberg–Saxton algorithm employs Fourier transforms to iteratively propagate between the input (hologram) and output (reconstruction) planes, updating the input light field according to a cost function. The cost function ensures that the optimization converges to the best solution. In our case, we used the Root Mean Square Error (RMSE) function to quantify the difference between the reconstructed light field and the target response, defined as:

$$RMSE=\left({\displaystyle \frac{1}{sqrt\left(n\right)}}\right)\times sqrt\left(sum\left(i,j\right)\left({\left(A_{out\left(i,j\right)}-A_{targ\left(i,j\right)}\right)}^2\right)\right)$$

where n is the total number of pixels in the light field, A_out is the amplitude in the reconstruction plane, A_targ is the amplitude of the desired output response, and i and j are the indices of the light field matrix. The optimization proceeds over a specified number of iterations, as determined by the user.

The output of the optimization process is a complex matrix containing the optimal amplitude and phase values for the holographic mask corresponding to the desired response. However, to imprint the holographic mask, we discard the amplitude values and retain only the phase information. The resulting phase-only holographic mask contains continuous values ranging from 0 to 2π. To simplify the fabrication process, we applied a global thresholding method [26] to quantize the phase values into binary shifts of 0 and π. The final binary holographic mask, intended for 3D printing and replicating via NIL, is shown in Figure 1b, where white pixels represent a phase shift of π radians and black pixels represent a shift of 0 radians.

The next step involved the digital reconstruction of the imprinted holographic mask. An RGB image of the imprinted hologram was captured using a conventional microscope, as shown in Figure 3a and Figure 4a. The black-and-white CGH period was repeated in a 4 × 4 array to generate the complete holographic structure. This stitching process creates the final hologram (Figure 3b and Figure 4b), which is digitally reconstructed to retrieve the encoded target image information. The polarity of the binary masks in Figure 3b and Figure 4b appears inverted with respect to each other, which originates from differences in illumination during image acquisition and automatic contrast handling during grayscale conversion. This inversion does not affect the optical behavior of the hologram, since the encoded information depends solely on the relative phase shift (0 or π). A global inversion only adds a constant phase offset, leaving the reconstructed intensity unchanged. The digital reconstruction of the hologram is based on Fourier optics, as outlined in [27]. A Gaussian beam was used to simulate the laser source illuminating the holographic mask, described by the following expression:

$$E\left(r,z\right)=E_0\times \left(w_0/w\left(z\right)\right)\times e^{\left(-r^2/w^2\left(z\right)\right)}\times e^{\left(-ikz\right)}\times e^{\left(-ik{r}^2/\left(2R\left(z\right)\right)\right)}\times e^{\left(i\psi \left(z\right)\right)}$$

where r is the radial distance from the center axis of the beam, z is the axial distance from the beam’s focus (or “waist”), i is the imaginary unit, k = (2π/λ) is the wave number (in radians per meter) for a free-space wavelength λ, and n is the refractive index of the medium. E₀ = E(0, 0) is the electric field amplitude (and phase) at the origin, w(z) is the beam radius at which the field amplitudes fall to 1/e of their axial values, w₀ = w(0) is the waist radius, R(z) is the radius of curvature of the beam’s wavefronts at z, and ψ(z) is the Gouy phase at z, representing the additional phase shift beyond the phase velocity of light.

The laser illumination of the imprinted hologram was simulated by multiplying the Gaussian beam with the hologram image captured by the microscope. The result of this multiplication will hereafter be referred to as U.

The light propagation from the hologram to the reconstruction plane over a given distance z was simulated as the convolution of the light field U with the impulse response h of the optical system:

$$U_{2\left(x,y\right)}=F^{-1}\left\{F\left\{U_{1\left(x,y\right)}\right\}\times F\left\{h\left(x,y\right)\right\}\right\}$$

where U₂ is the light field in the reconstruction plane, F denotes the Fourier transform, and F⁻¹ represents the inverse Fourier transform.

The impulse response h(x, y) for free-space propagation is given by:

$$h\left(x,y\right)=\left(e^{\left(ikz\right)}\right)/\left(j\lambda z\right)\times e^{\left(ik/2z\ast \left(x^2+y^2\right)\right)}$$

where k is the wavenumber, λ is the wavelength, and z is the propagation distance.

3. Results

3.1. Fabrication

The successful integration of computer-generated holograms into 3D-printed objects for anti-counterfeiting tags was achieved through a direct 3D printing method, without the need for additional steps like laser engraving. This approach enabled the seamless embedding of the CGHs directly into the 3D-printed structures, ensuring efficient and precise manufacturing. By incorporating the CGHs into the 3D printing process, the need for post-production steps was eliminated, simplifying the workflow and offering a high-throughput solution. This method also ensured that the features were integrated within the object, making them more resistant to tampering and enhancing their durability.

Because the CGH layout is non-periodic, a single pitch is not defined. We therefore report the minimum resolved feature width and inter-feature gap. In this study, the lateral (x–y) resolution is limited primarily by the laser spot diameter of the SLA 3D-printing system and lateral cure spread in the photopolymer (effective spot ≈80 μm). Across the 1.5 cm × 1.5 cm area, the smallest feature width that printed with intact edges was ≈420 μm, and the smallest inter-feature gap that remained open was ≈380 μm. In exploratory prints, clearances <≈120 μm exhibited bridging. Downscaled variants (0.5 cm × 0.5 cm; Figure 2) were also fabricated. At this scale the narrowest gaps approached the process limit, so we used the 1.5 cm × 1.5 cm layout in all experiments, which provided sufficient edge contrast for reliable digital-microscope imaging and downstream analysis. Intermediate clearances (≈150–300 μm) were achievable locally in exploratory prints, but they did not resolve uniformly across the full 1.5 cm × 1.5 cm field due to spot overlap and lateral cure spread, with increased edge rounding after post-cure and cleaning.

To further extend the applicability of this method, UV-NIL was employed to enable the replication of the 3D-printed security tags onto flexible substrates. This not only introduces substrate versatility but also allows integration with scalable manufacturing methods such as injection moulding and roll-to-roll NIL [28], enhancing the potential for industrial adoption. Given the printed feature height of 1 mm and the minimum resolved lateral feature width of approximately 420 µm, the aspect ratio was ≈2.4:1. This geometry was preserved after replication, indicating effective pattern transfer fidelity in the NIL process.

The mould shown in Figure 2 corresponds to the same 1.5 cm × 1.5 cm CGH structure presented in Figure 3a, which served as the master for the NIL replication process.

Although the present structures fall within the microscale rather than the nanoscale, the same UV-NIL principles apply. This process is often referred to as microimprinting in similar contexts, yet the underlying mechanism (UV-assisted curing of a resist under conformal contact) remains identical to conventional NIL. The results confirm that UV-NIL can accurately replicate high-relief microstructures under mild conditions, highlighting its versatility beyond the nanoscale. In comparison to hot embossing, the UV-based process avoids thermal stress and enables replication on flexible polymer substrates, making it well suited for scalable production of optical tag structures.

3.2. Characterization

The 3D printed and replicated via NIL CGHs were optically characterized using a handheld digital microscope. The recorded RGB images were converted into grayscale for Fourier-based digital reconstruction. Figure 3a shows the 3D printed CGHs samples which have undergone the digital reconstruction process. Digital reconstruction using Fourier optics successfully retrieved the encoded letter ‘H’ and ‘M’ (Figure 3c), confirming that the CGHs function as intended. The reconstructed hologram showed a high contrast ratio between the encoded pattern and the background. UV-NIL maintains the optical performance of the holographic structures. The same protocol was used for the evaluation of the NIL replicated CGHs (Figure 4), where reconstructed holograms were also visible.

The fabricated CGHs were evaluated using optical microscopy and digital reconstruction techniques. The digital reconstruction process successfully retrieved the encoded holographic information, demonstrating machine-based authentication feasibility. The holographic patterns produced a distinct diffraction signature, making them difficult to replicate without access to the original fabrication process flow, as the latter involves multiple steps, parameters and techniques.

As can be seen in Figure 3 and Figure 4, the imaging conditions, i.e., the contrast between the edges of the CGH and the substrate background, play a decisive role in the quality of the reconstruction images. In particular, it is obvious that the contrast between the CGH structure and the background influences the image processing during black and white conversion, as the edges of the CGH structure determine the overall structure of the hologram perceived during this process. The absence of visible background texture or scattering in the bright and dark regions of the images confirmed that the surface roughness was adequate for the intended optical reconstruction.

To quantitatively evaluate the reconstruction quality of the NIL-replicated tags and compare them with the 3D printed tags, the digitally reconstructed intensity maps of both were analysed using an in-house Python-based image comparison framework (Python v3.13).

Each reconstruction was normalized identically to enable direct pixel wise comparison, and an absolute difference map was calculated to visualize local intensity variations. Edge-based similarity was quantified using the intersection-over-union (IoU) metric for multiple central regions of interest (ROIs) ranging from 0.2 to 1.0 of the image area. Multiple ROIs were selected to verify whether the level of agreement between the two reconstructions remains consistent across both the central and peripheral regions of the diffraction pattern.

For the global quantitative metrics (e.g., the normalized cross-correlation (NCC) [29], structural similarity index (SSIM) [30], optical efficiency ratio, average symmetric surface distance (ASSD), and 95th-percentile Hausdorff distance (HD95) [31]), the full image (ROI = 1) was analysed to include both the main diffraction pattern and the surrounding background. This approach ensures that the comparison accounts for the complete reconstructed optical field rather than only its high intensity region.

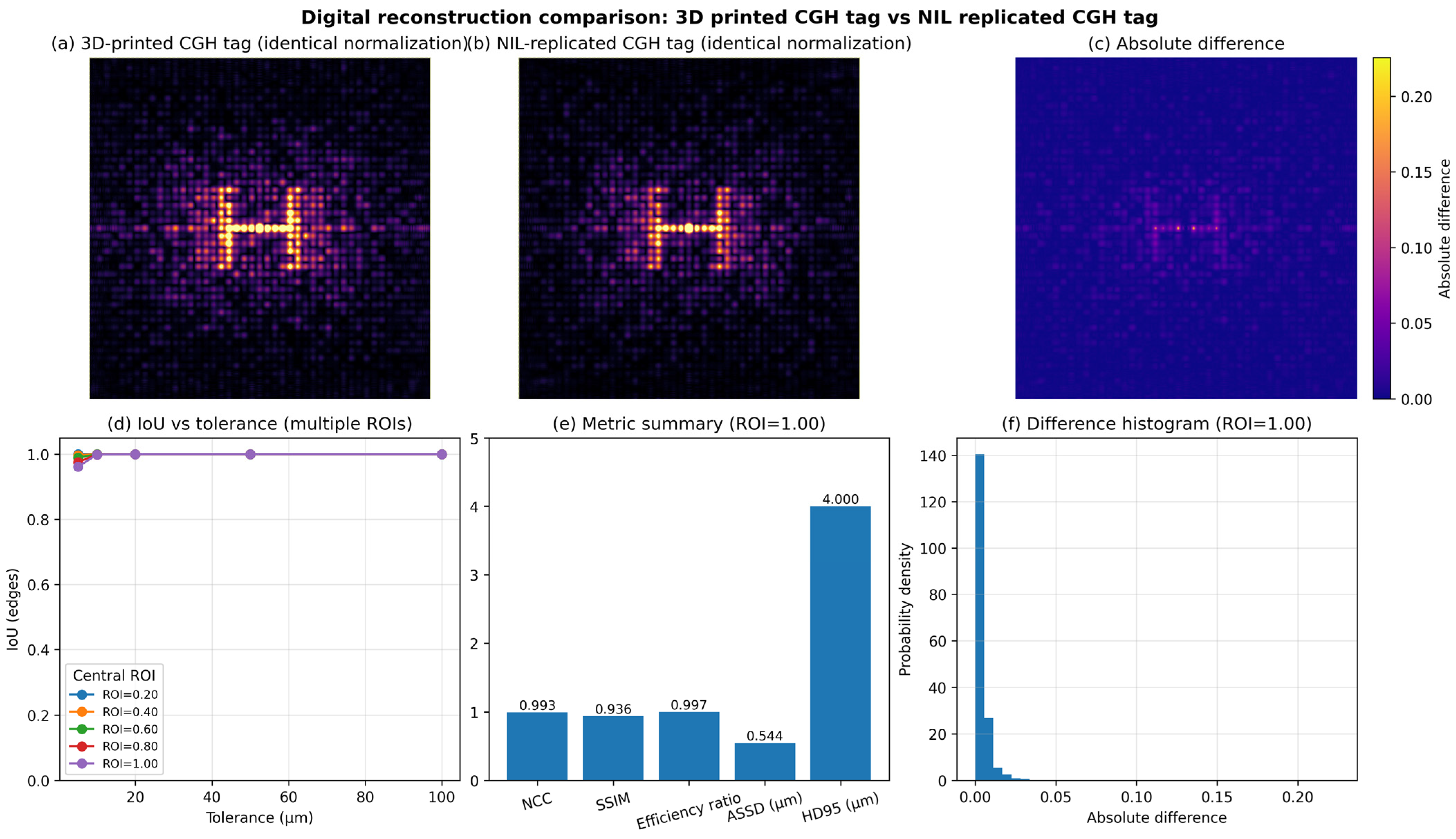
Figure 5 shows the quantitative comparison between the digital reconstructions of the 3D-printed and NIL-replicated “H” tag. Figure 5a,b present the normalized reconstructions of the 3D printed and NIL replicated tags, respectively, while Figure 5c displays their absolute difference map. Figure 5d shows the IoU as a function of positional tolerance for different ROIs, and Figure 5e summarizes the calculated quantitative metrics. The corresponding histogram of pixel-wise absolute differences is shown in Figure 5f. The IoU values above 0.96 across all ROIs demonstrate that the reconstructed optical fields of both tags are highly consistent throughout the reconstruction area. For the “H” tag, the high NCC (0.993) and SSIM (0.936) confirm strong global and local agreement, while the efficiency ratio (0.997) indicates that the replicated tag preserves almost the same optical response as the original. The ASSD (0.54 µm) and HD95 (4.0 µm) values show sub-micrometer average deviations and minimal local differences, confirming that the optical reconstruction of the NIL replicated tag closely matches that of the 3D-printed master.

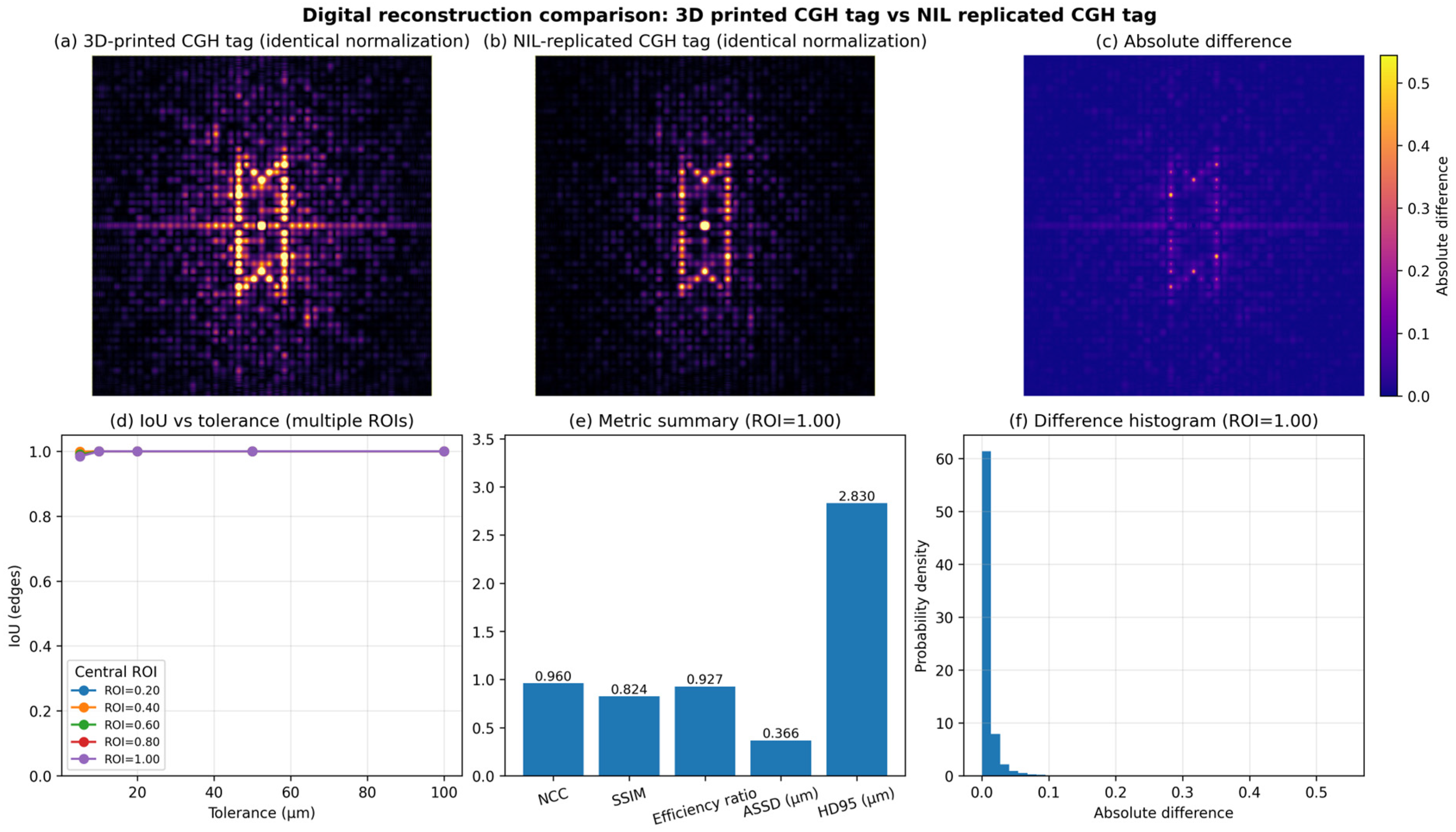
A similar analysis was performed for the “M” tag, as shown in Figure 6. The results show comparable behaviour. The NCC (0.96) and SSIM (0.824) demonstrate good global and local correspondence, and the efficiency ratio (0.93) indicates a small reduction in reconstructed intensity compared with the master. The ASSD (0.37 µm) and HD95 (2.8 µm) again confirm very limited spatial deviation. Because the reconstruction is performed digitally, illumination nonuniformity cannot contribute to these differences. The intensity variations observed are therefore attributed to small replication defects introduced during the NIL process.

Table 1. Quantitative comparison of digital reconstructions for 3D-printed and NIL-replicated CGH tags.

Tag	NCC	SSIM	Efficiency Ratio (Replica to Master)	ASSD (μm)	HD95 (μm)
H	0.993	0.936	0.997	0.544	4.00
Μ	0.960	0.824	0.927	0.366	2.83

All metrics were computed for ROI = 1 using identically normalized reconstructions. IoU values exceeded 0.96 across all evaluated ROIs (0.2–1.0) and positional tolerances (5–100 µm).

summarizes the quantitative comparison of the digital reconstructions obtained from the printed and NIL-replicated CGH tags.

These observations confirm that the NIL process successfully replicated the CGH patterns and that the replicated tags produce clear and accurate reconstructions. The optical performance of the replicas is very close to that of the 3D printed masters, supporting their use as functional optical tags.

3.3. Scalability

The scalability of the proposed method is supported by the quantitative correspondence between the 3D printed and NIL-replicated CGHs. The high similarity metrics (NCC > 0.96, SSIM > 0.82, IoU > 0.96 across all regions) confirm reliable pattern transfer and reproducible optical performance, indicating that the process can be extended to high-throughput production.

NIL offers a rapid, large-area replication process that is compatible with scalable manufacturing methods such as roll-to-roll and injection molding [32,33]. This combination of additive manufacturing and UV-NIL enables cost-efficient, flexible, and reproducible fabrication of optical security tags.

Furthermore, the integration of additional unique identifiers, such as physical unclonable functions (PUFs) [34], could further enhance the security and anti-counterfeiting potential of the proposed approach in industrial scale implementations.

4. Discussion

The proposed method represents a scalable and cost-effective fabrication route for optical tags. It focuses on the rapid and flexible production of holographic structures that yield clear optical reconstructions. Combining 3D printing with UV-NIL provides a practical route for the fabrication of tags, making it ideally suited for applications within the FMCG, pharmaceutical, and financial sectors, where secure and cost-efficient product marking is essential.

The optical characterization of the imprinted CGHs confirms their functional integrity and reconstruction accuracy. Quantitative comparison between the 3D printed and NIL replicated tags showed strong global and local correspondence, with NCC and SSIM values above 0.96 and 0.82, respectively, and intersection-over-union (IoU) values exceeding 0.96 across all evaluated regions. The sub-micrometer average deviations (ASSD < 0.6 µm) and low maximum deviations (HD95 < 4 µm) indicate that the NIL process preserved the encoded optical information with minimal distortion. The reconstructed intensity distributions of the replicated tags closely matched those of their 3D printed masters, confirming that replication defects had only a minor influence on the optical output.

The high degree of optical consistency between master and replica reconstructions demonstrates that the hybrid fabrication route effectively transfers the designed holographic features while maintaining their optical functionality. This confirms the robustness of the process for accurate, repeatable production of functional optical elements.

Overall, this study highlights the technical feasibility, economic viability, and security potential of CGHs produced by combining additive manufacturing with nanoimprint lithography. The proposed workflow supports large scale replication of 3D printed optical masters while maintaining high reconstruction quality, representing a significant step toward next generation, low-cost optical security features that are both robust and commercially scalable.

5. Conclusions

This study presents a novel hybrid approach for the design, fabrication, and evaluation of anti-counterfeiting tags using computer-generated holograms integrated onto the surface of 3D printed components and replicated by nanoimprint lithography. The method combines the design flexibility and rapid prototyping capabilities of 3D printing with the high-throughput replication efficiency of UV-NIL to produce unique optical security features. This combination enables scalable, cost-effective, and adaptable integration of CGH-based tags into plastic components across multiple industries.

Direct integration of CGHs onto the surface of 3D printed components eliminates the need for post-processing and allows seamless incorporation of optical security features during fabrication. This embedded configuration improves durability and protects the tags from physical wear and surface damage. By leveraging both additive manufacturing and NIL, the approach enhances the scalability and manufacturability of functional holographic elements, enabling large-scale production of secure and reproducible optical tags.

Quantitative analysis of the digital reconstructions confirmed that the NIL replicated CGH tags closely reproduce the optical response of their 3D printed masters. The high similarity of metrics and submicrometer spatial deviations demonstrate that replication defects introduced during NIL have negligible impact on the reconstructed optical patterns. The proposed digital reconstruction-based evaluation framework thus provides a robust tool for verifying optical performance and product authenticity. Overall, this hybrid process offers a commercially viable and scalable route toward next generation optical security features for anti-counterfeiting applications.