Hybrid Physical-Data Modeling Approach for Surface Scattering Characteristics of Low-Gloss Black Paint
Abstract
1. Introduction
2. Materials and Methods
2.1. BRDF Modeling for Optical Black Paints
2.1.1. Gradient Descent-Optimized Parameter Fitting for a Five-Parameter Model
2.1.2. Data-Driven MLP Model
2.2. BRDF Experimental Testing
3. Results
3.1. Model Fitting Results for SB-3A
3.1.1. Analysis of Scattering Characteristics
3.1.2. Gradient-Descent Optimized Five-Parameter Model Fitting Results
3.2. Hybrid Model Fitting Results
3.2.1. Residual Results Analysis
3.2.2. Hybrid Model Fitting Results
3.2.3. Ablation Experiment Results
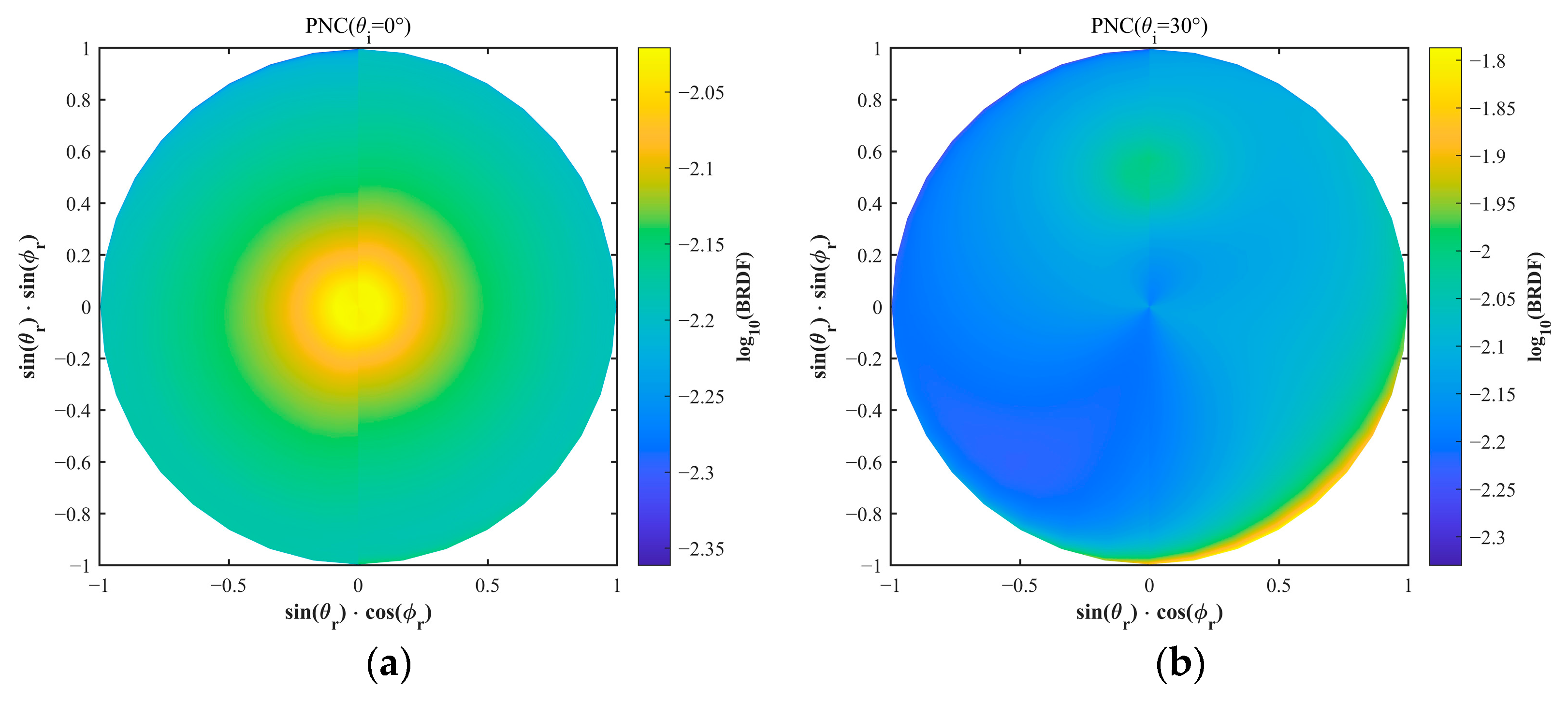
3.3. Validation of Model Predictive Capability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SB-3A | SB-3A Black Paint |
| Z306 | Z306 Black Paint |
| PNC | Polymer Nanocomposite Black Coating |
| BRDF | Bidirectional Reflectance Distribution Function |
| GD | Gradient Descent |
| MLP | Multilayer Perceptron |
| FDTD | Finite-Difference Time-Domain method |
| OLS | Ordinary Least Squares |
| SAA | Simulated Annealing Algorithm |
| PSO | Particle Swarm Optimization |
| IOF | The Fraunhofer Institute for Applied Optics and Precision Engineering |
| RMSE | Root Mean Squared Error |
| ASI | Azimuthal Sensitivity Index |
| FNN | Feedforward Neural Network |
| LiDAR | Light Detection and Ranging |
References
- Li, Z.; Zhou, Z.; Wang, Q.; Lu, S. Optimal of Black Anti-Static AZO/Al2O3-SiO2-VxOy Coatings for Spacecraft Stray Light on High Silicon Aluminum Alloys. Curr. Appl. Phys. 2023, 55, 44–52. [Google Scholar] [CrossRef]
- Truong, T.; Yuk, G.; Kim, J.; Youn, H.; Rho, J. Super Black Coating on the Commercial Black Anodized Al(6061) by Direct and Scalable CVD–Growth of Carbon Nanofibers. Adv. Mater. Interfaces 2024, 11, 2400032. [Google Scholar] [CrossRef]
- Kinast, J.; Telle, A.; Schröder, S.; Trost, M.; Risse, S. Stray light reduction of silicon particle reinforced aluminum for optical systems. SPIE 2019, 11180, 924–931. [Google Scholar] [CrossRef]
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7, 041308. [Google Scholar] [CrossRef]
- Bowman, R.; Padgett, M. Optical trapping and binding. Rep. Prog. Phys. 2013, 76, 026401. [Google Scholar] [CrossRef]
- Sforza, D.; Pellacini, F. Numerical approximations for energy preserving microfacet models. Comput. Graph 2023, 114, 36–44. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, Y.; Shi, B.; Subpa-Asa, A.; Sato, I. A Microfacet-Based Model for Photometric Stereo with General Isotropic Reflectance. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 48–61. [Google Scholar] [CrossRef] [PubMed]
- Bagher, M.; Snyder, J.; Nowrouzezahrai, D. A Non-Parametric Factor Microfacet Model for Isotropic BRDFs. ACM Trans. Graph. 2016, 35, 1–16. [Google Scholar] [CrossRef]
- Wang, K.; Zuo, S.; Wu, Q.; Lin, Z.; Zhang, Y.; Zhao, X. A Novel Compact Conformal 2-D FDFD Method for Modeling Waveports in 3-D FDTD. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 2091–2095. [Google Scholar] [CrossRef]
- Meyberg, R.; De Barros, M.; Mahseredjian, J. Efficient Corona Modeling for FDTD Simulations. IEEE Trans. Power Deliv. 2024, 39, 874–881. [Google Scholar] [CrossRef]
- Zhang, X.; Bekmambetova, F.; Triverio, P. A Stable FDTD Method with Embedded Reduced-Order Models. IEEE Trans. Antennas Propag. 2016, 66, 827–837. [Google Scholar] [CrossRef]
- Tekbaş, K.; Bérenger, J. FDTD Algorithm for Numerical Anatomical Models with Cells Containing Several Debye Media. IEEE Trans. Electromagn. Compat. 2021, 63, 947–950. [Google Scholar] [CrossRef]
- Kogon, A.; Sarris, C. Modeling of Finite Beams in Periodic FDTD Methods. IEEE Trans. Microw. Theory Tech. 2023, 71, 4307–4317. [Google Scholar] [CrossRef]
- Ahdab, Z.; Akleman, F. An Efficient 3-D FDTD-PE Hybrid Model for Radio Wave Propagation with Near-Source Obstacles. IEEE Trans. Antennas Propag. 2019, 67, 346–355. [Google Scholar] [CrossRef]
- D’Eon, E. An analytic BRDF for materials with spherical Lambertian scatterers. Comput. Graph. Forum 2021, 40, 153–161. [Google Scholar] [CrossRef]
- Saito, H.; Omata, K.; Ozawa, S. Recovery of shape and surface reflectance of specular object from relative rotation of light source. Image Vis. Comput. 2003, 21, 777–787. [Google Scholar] [CrossRef]
- Cheng, J.; Wen, J.; Xiao, Q.; Hao, D.; Lin, X.; Liu, Q. Exploring the Applicability of the Semi-Empirical BRDF Models at Different Scales Using Airborne Multi-Angular Observations. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2502905. [Google Scholar] [CrossRef]
- Han, Z.; Gu, X.; Zuo, X.; Bi, K.; Shi, S. Semi-Empirical Models for the Bidirectional Water-Leaving Radiance: An Analysis of a Turbid Inland Lake. Front. Environ. Sci. 2022, 9, 818557. [Google Scholar] [CrossRef]
- Zhu, W.; You, D.; Wen, J.; Tang, Y.; Gong, B.; Han, Y. Evaluation of Linear Kernel-Driven BRDF Models over Snow-Free Rugged Terrain. Remote Sens. 2023, 15, 786. [Google Scholar] [CrossRef]
- Bai, L.; Wu, Z.; Zou, X.; Cao, Y. Seven-parameter statistical model for BRDF in the UV band. Opt. Express 2012, 20, 12085–12094. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Gao, Y.; Gu, X. A seven-parameter BRDF model for retro-reflection. In Proceedings of the Third International Computing Imaging Conference (CITA 2023), Sydney, Australia, 1–3 June 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12921, pp. 1451–1456. [Google Scholar] [CrossRef]
- Zou, X.; Bai, L.; Wu, Z. Comparisons of multi-parameter Bidirectional Reflectance Distributional Function. In Proceedings of the 2012 International Symposium on Antennas and Propagation (ISAP2012), Xi’an, China, 22–26 October 2012; IEEE: New York, NY, USA, 2012; pp. 787–790. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Z.; Cai, W.; Lu, G. Analysis and Improvement on Integral Geometrical Attenuation Factor of Bidirectional Reflection Distribution Function. Acta Opt. Sin. 2022, 42, 1029001. [Google Scholar] [CrossRef]
- Wang, A.; Wu, Z. Parameter inversion of shadowing function in light scattering model. Infrared Laser Eng. 2014, 43, 332–337. [Google Scholar] [CrossRef]
- Liu, C.; Zhan, J.; Zhang, S.; Wang, C.; Fu, Q.; Li, Y.; Duan, J.; Jiang, H. Visible polarized reflection of target material surface based on improved Blinn masking function. Chin. Opt. 2024, 17, 1162–1174. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, J.; Wang, K. Modification of geometrical attenuation factor of bidirectional reflection distribution function based on random surface microfacet theory. Acta Opt. Sin. 2015, 64, 184213. [Google Scholar] [CrossRef]
- Ojaghi, S.; Bouroubi, Y.; Foucher, S.; Bergeron, M.; Seynat, C. Deep Learning-Based Emulation of Radiative Transfer Models for Top-of-Atmosphere BRDF Modelling Using Sentinel-3 OLCI. Remote Sens. 2023, 15, 835. [Google Scholar] [CrossRef]
- Sztrajman, A.; Rainer, G.; Ritschel, T.; Weyrich, T. Neural BRDF Representation and Importance Sampling. Comput. Graph. Forum 2021, 40, 332–346. [Google Scholar] [CrossRef]
- Hinderhofer, A.; Greco, A.; Starostin, V.; Munteanu, V.; Pithan, L.; Gerlach, A.; Schreiber, F. Machine learning for scattering data: Strategies, perspectives and applications to surface scattering. Appl. Crystallogr. 2023, 56, 3–11. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhao, J.; Xu, L.; Liu, F.; Li, Z. BRDF measurement of matte coating and its application. Opt. Precis. Eng. 2016, 24, 2627–2635. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, J.; Xu, L.; Liu, F.; Guo, Y.; Liu, K.; Zhao, Q. Analysis and calibration of precision for point source transmittance system. Acta Phys. Sin. 2016, 65, 114206. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, X.; Zhang, H.; Feng, J. Experiment Measurement and Optimization Modeling of Scattering Characteristic of Coated Surface. Laser Infrared 2008, 38, 519–530. Available online: https://magazine.laser-infrared.com/jgyhw/article/abstract/m380603 (accessed on 29 September 2025).
- Yuying, L.; Jingjing, D.; Zhao, S.; Zhang, J.; Shang, W.; Li, T.; Zheng, Y.; Lan, T.; Wang, Z. Optimization of five-parameter BRDF model based on hybrid GA-PSO algorithm. Optik 2020, 219, 164978. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, L.; Huang, Q.; Yang, F. Model and analysis of six-parameter polarized BRDF for cement board based on genetic algorithm method. In Proceedings of the Third International Computing Imaging Conference (CITA 2023), Sydney, Australia, 1–3 June 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12921, p. 10. [Google Scholar] [CrossRef]
- Li, Y.; Yang, P.; Bai, L.; Zhang, Z. BRDF modeling and optimization of a target surface based on the gradient descent algorithm. Appl. Opt. 2023, 62, 9486–9492. [Google Scholar] [CrossRef]
- Chen, S.; Xie, E.; Ge, C.; Chen, R.; Liang, D.; Luo, P. CycleMLP: A MLP-Like Architecture for Dense Visual Predictions. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 14284–14300. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Lv, T.; Cai, R.; Xu, J.; Wang, L. Bibliometric Analysis of Multi-Level Perspective on Sustainability Transition Research. Sustainability 2022, 14, 4145. [Google Scholar] [CrossRef]




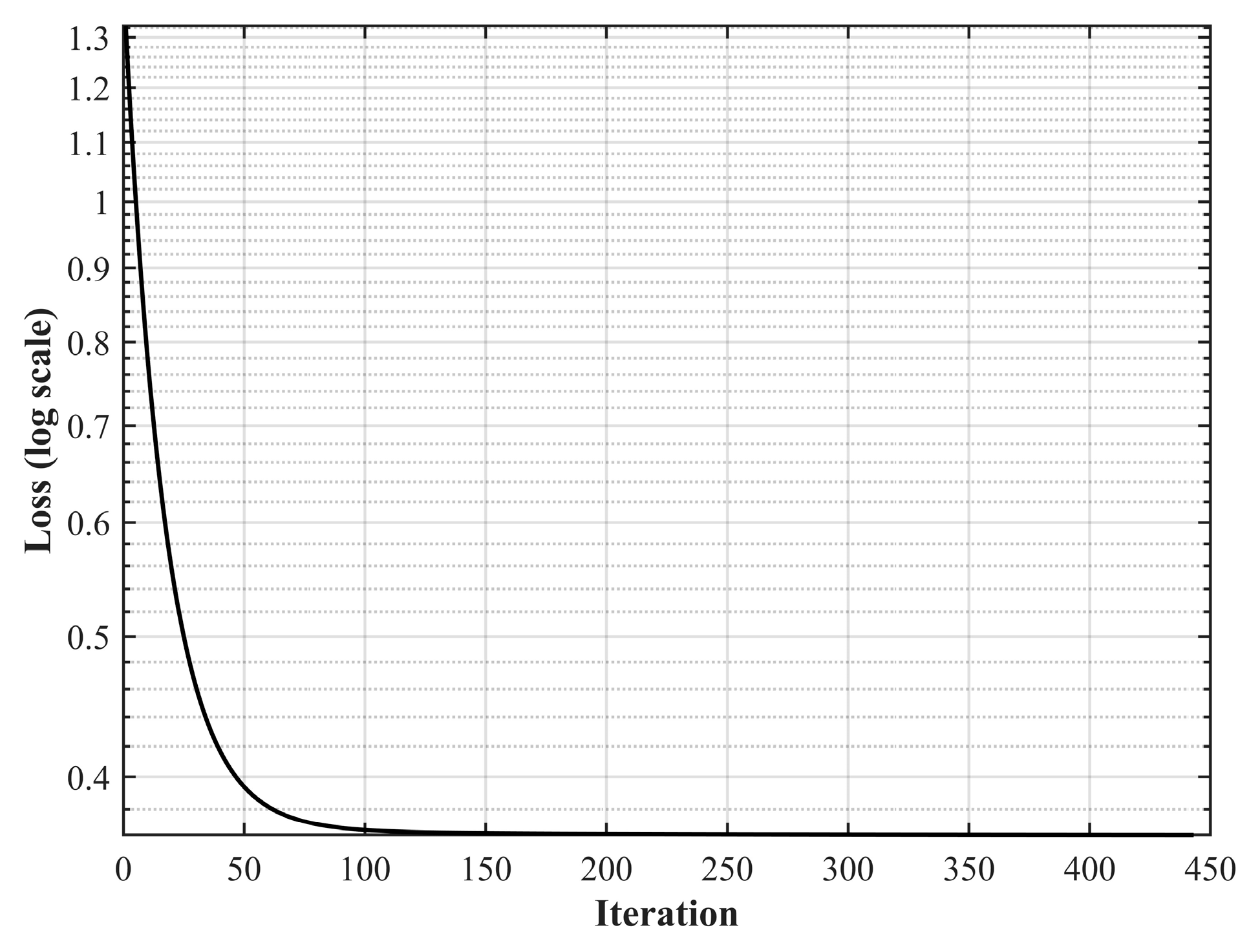





| Key Parameters | Value |
|---|---|
| Loss Function | MSE |
| Initial Parameters | (0.5, 0.5, 0.5, 0.5, 0.5) |
| Learning Rate | 0.01 |
| Max Iterations | 500 |
| Tolerance | 1 × 10−6 |
| Key Training Parameters | Value |
|---|---|
| Optimizer | Trainlm (Levenberg–Marquardt) |
| Loss Function | logarithmic residuals |
| Early stopping | max_fail = 20 |
| Epochs | 1000 |
| Data Split | 70% training, 15% validation, 15% test |
| Geometric Parameters | Physical Quantities | ||||
|---|---|---|---|---|---|
| Symbol | Definition | Unit | Symbol | Definition | Unit |
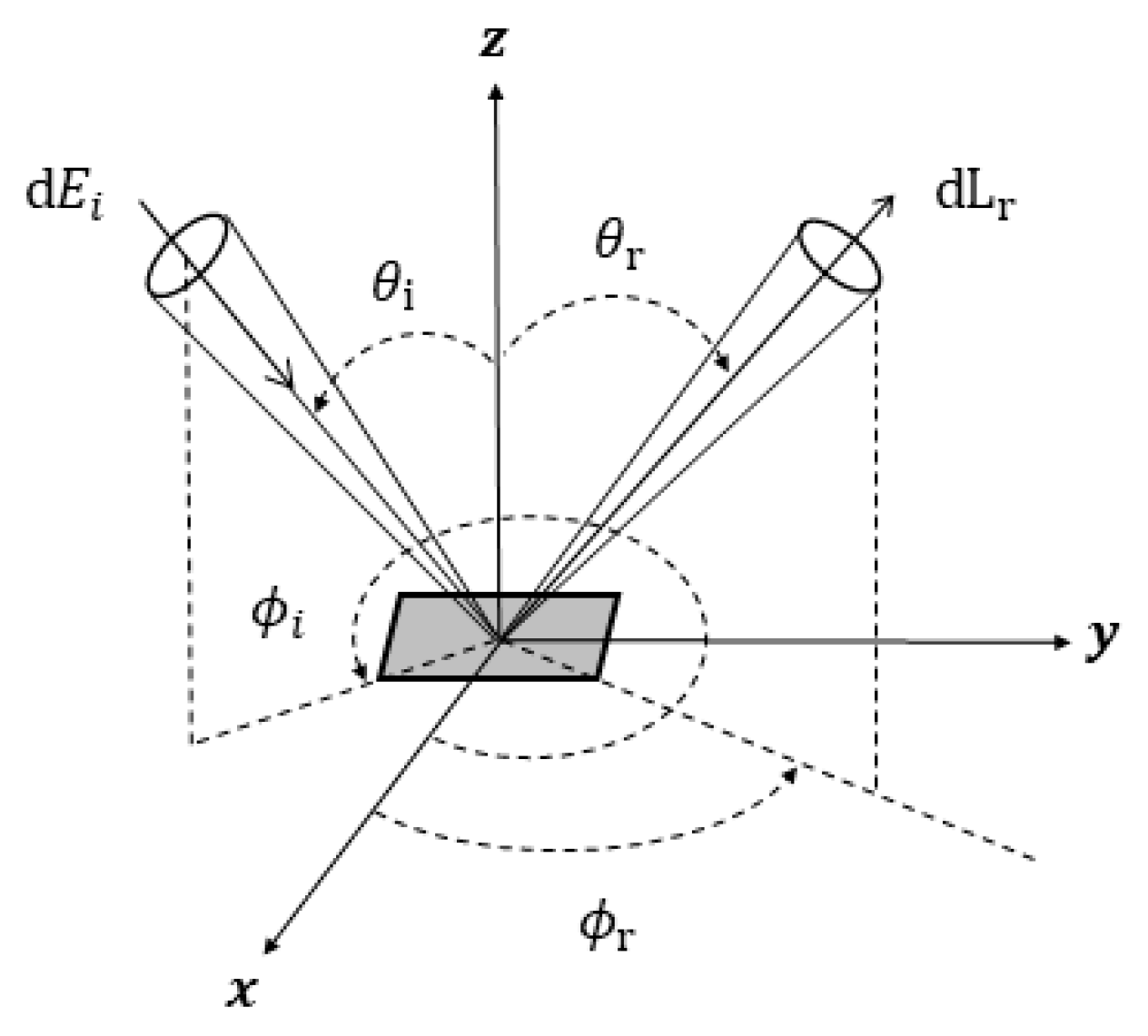
| the angle between z direction and the surface normal n | - | ASI | Azimuthal Sensitivity Index (Equation (13)) | - | |
| G | Shadowing function | - | dEi | Differential incident irradiance | W/m2 |
| the angle between the incident light ray and the surface normal | ° | dLr | Differential reflected radiance | W/m2/Ω | |
| the spherical projections of | ° | Mathematical description of BRDF | sr−1 | ||
| Incident zenith angle | ° | Five-Parameter model BRDF | sr−1 | ||
| Reflected zenith angle | ° | Final model BRDF | sr−1 | ||
| the spherical projections of | ° | Model-predicted BRDF value | sr−1 | ||
| the spherical projections of | ° | MLP model BRDF residual term | sr−1 | ||
| Incident azimuth angle | ° | BRDF of the sample surface | sr−1 | ||
| Reflected azimuth angle | ° | VS | Response voltage of the sample | V | |
| Surface Distribution Function | - | VR | Response voltage of the reference panel | V | |
| Model Parameters | the hemispherical reflectance of the reference panel | - | |||
| a | Exponential parameter of the distribution correction | - | Measurement wavelength | nm | |
| b | Scaling factor of the distribution correction | - | |||
| Fixed engineering parameter | - | ||||
| Fixed engineering parameter | - | ||||
| Fixed engineering parameter | - | ||||
| Fixed engineering parameter | - | ||||
| Specular reflection scaling coefficient | - | ||||
| Diffuse reflection coefficient | - | ||||
| Specular lobe shape parameter | - | ||||
| kb | kd | kr | a | b | RMSE | |
|---|---|---|---|---|---|---|
| −0.0239 | 0.0398 | 0.2782 | 0.5327 | 0.4429 | 0 | 0.0173 |
| 30 | 0.0197 | |||||
| 60 | 0.0288 | |||||
| 80 | 1.2066 | |||||
| Incident Angle θi (°) | Residual (sr−1) |
|---|---|
| 0 | 0.0075 |
| 30 | 0.0079 |
| 60 | 0.25 |
| 80 | 26.42 |
| Incident Angle θi (°) | RMSE | Residuals (sr−1) |
|---|---|---|
| 0° | 2.576 × 10−4 | 0.0461 |
| 30° | 2.993 × 10−4 | 0.0049 |
| 60° | 1.19 × 10−3 | 0.0020 |
| 80° | 1.178 × 10−2 | 0.0019 |
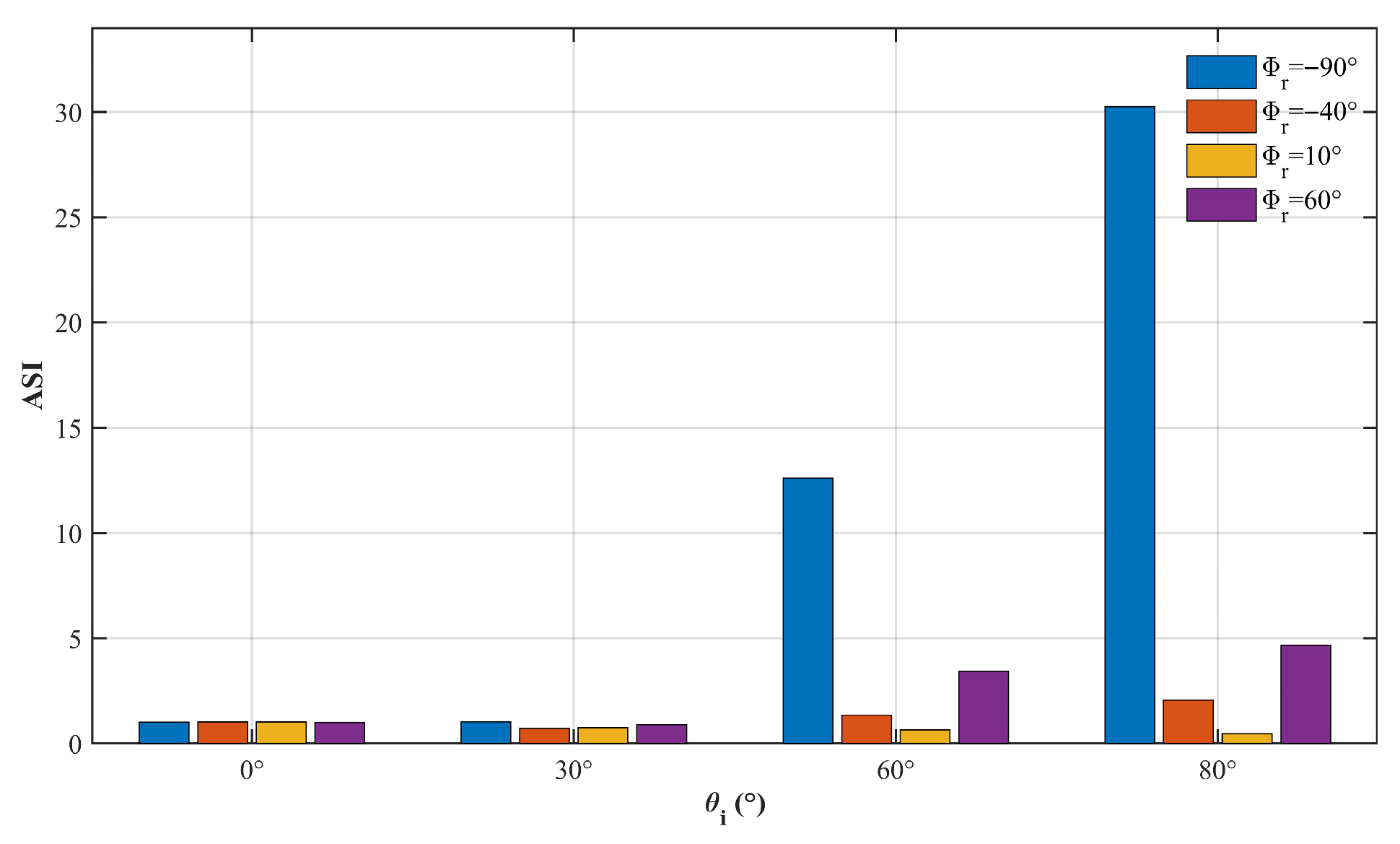
| Black Paints | Incident Angle θi (°) | Five-Parameter Model | RMSE (Hybrid Model) | ASI | |
|---|---|---|---|---|---|
| Fitting Parameters | RMSE | ||||
| Z306 | 0 | kb = −0.0349 | 0.0210 | 4.152 × 10−3 | 2.3901 |
| 30 | kd = 0.0506 | 0.0250 | 4.782 × 10−3 | 2.4053 | |
| 60 | kr = 0.2796 | 0.0382 | 1.384 × 10−2 | 8.5256 | |
| 80 | a = 0.5326, b = 0.4428 | 1.2831 | 1.867 × 10−2 | 24.9666 | |
| PNC | 0 | kb = 0.0114 | 0.0061 | 2.459 × 10−2 | 0.6070 |
| 30 | kd = 0.0046 | 0.0068 | 5.240 × 10−3 | 0.8935 | |
| 60 | kr = 0.2761 | 0.0159 | 7.656 × 10−3 | 5.9640 | |
| 80 | a = 0.5327, b = 0.4426 | 0.2484 | 1.230 × 10−2 | 32.0912 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Z.; Li, Z.; Liu, W.; Yin, Y.; Gao, L.; Zhao, J. Hybrid Physical-Data Modeling Approach for Surface Scattering Characteristics of Low-Gloss Black Paint. Photonics 2025, 12, 1077. https://doi.org/10.3390/photonics12111077
Mao Z, Li Z, Liu W, Yin Y, Gao L, Zhao J. Hybrid Physical-Data Modeling Approach for Surface Scattering Characteristics of Low-Gloss Black Paint. Photonics. 2025; 12(11):1077. https://doi.org/10.3390/photonics12111077
Chicago/Turabian StyleMao, Zhen, Zhaohui Li, Wei Liu, Yunfei Yin, Limin Gao, and Jianke Zhao. 2025. "Hybrid Physical-Data Modeling Approach for Surface Scattering Characteristics of Low-Gloss Black Paint" Photonics 12, no. 11: 1077. https://doi.org/10.3390/photonics12111077
APA StyleMao, Z., Li, Z., Liu, W., Yin, Y., Gao, L., & Zhao, J. (2025). Hybrid Physical-Data Modeling Approach for Surface Scattering Characteristics of Low-Gloss Black Paint. Photonics, 12(11), 1077. https://doi.org/10.3390/photonics12111077




