Tunable-Charge Optical Vortices Through Edge Diffraction of a High-Order Hermit-Gaussian Mode Laser
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Simulations
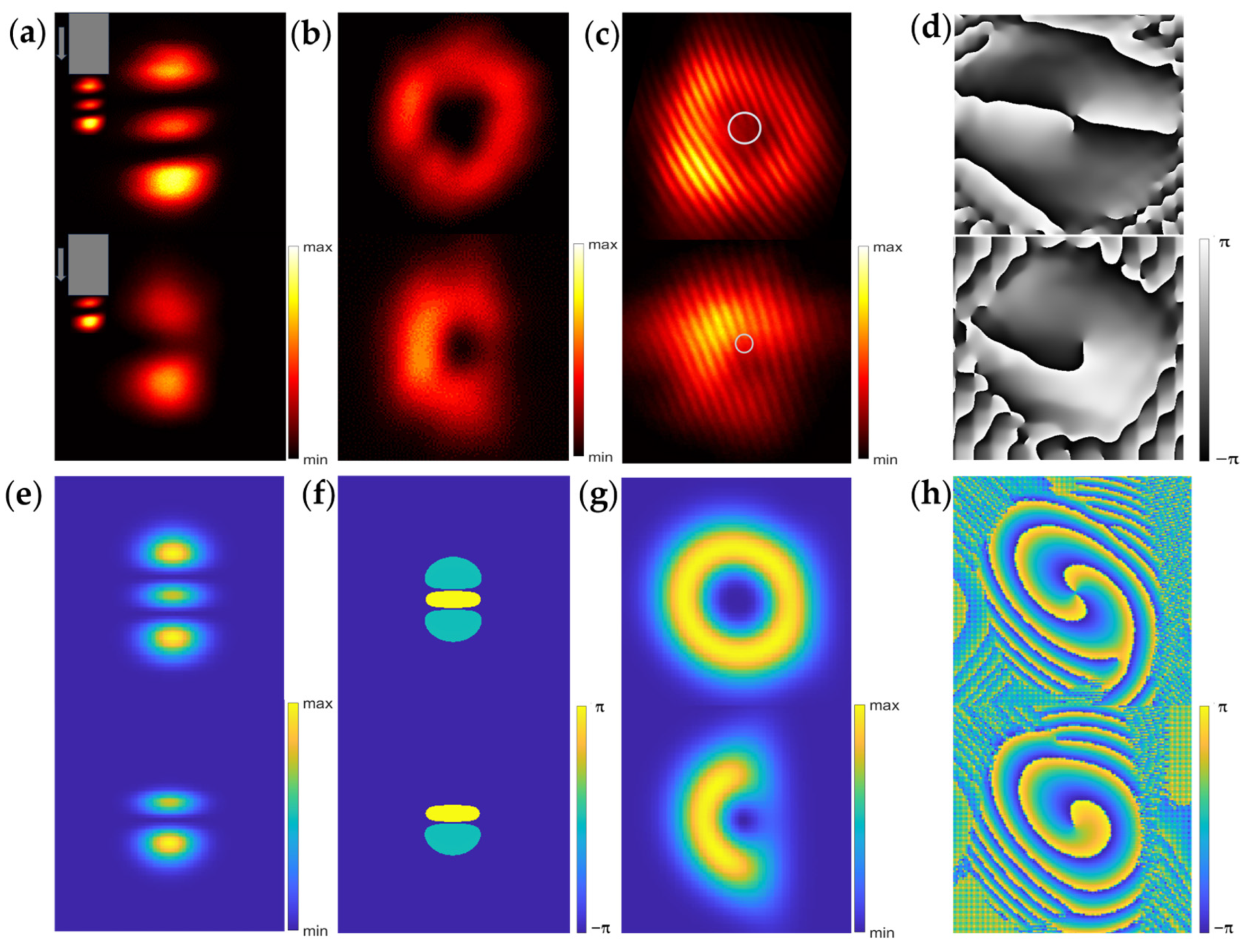
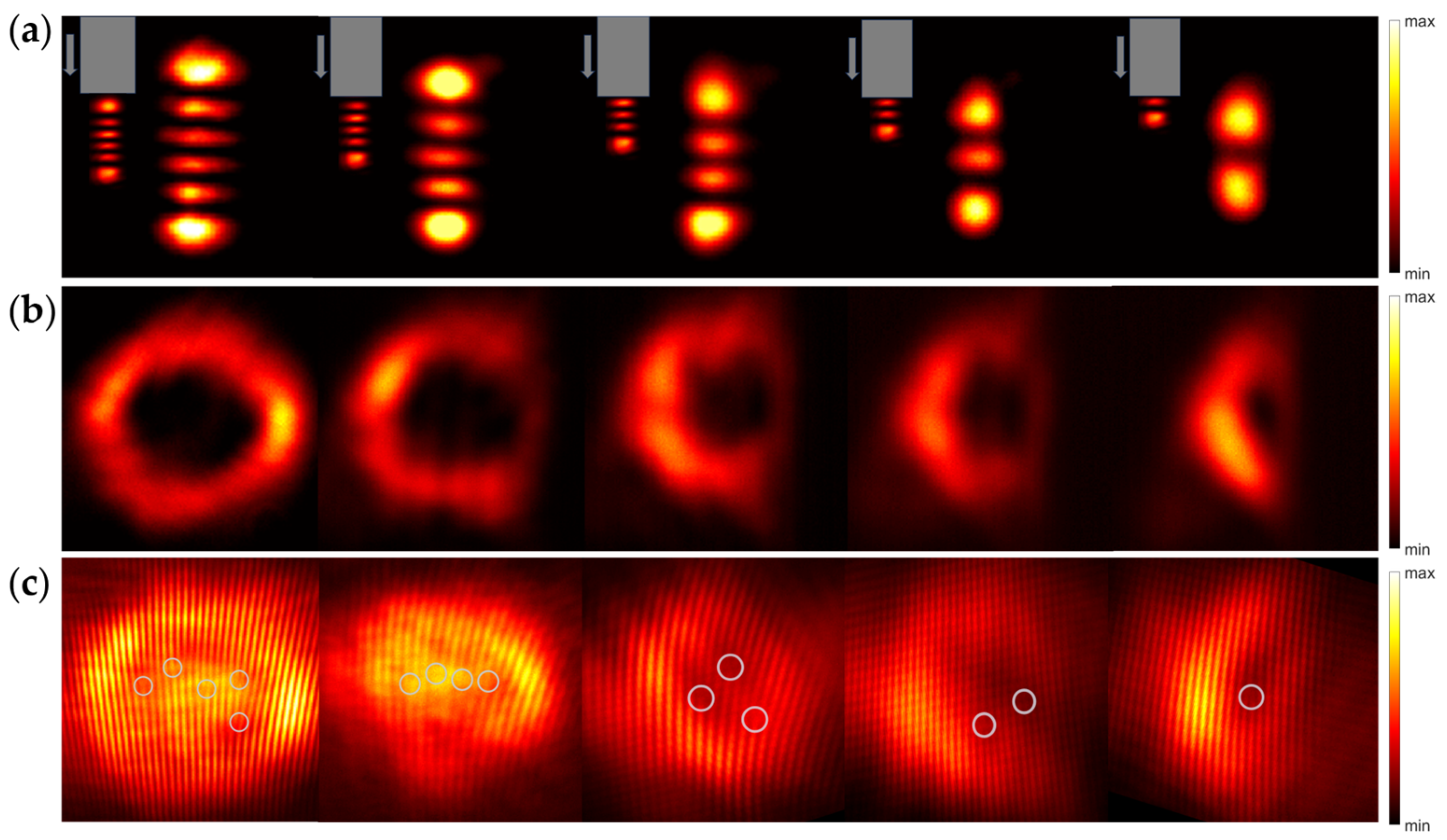
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HG | Hermit-Gaussian |
| OAM | orbital angular momentum |
| OC | output coupler |
| CL | cylindrical lens |
| LD | laser diode |
| SLM | spatial light modulator |
| DMD | digital micromirror device |
| SPP | spiral phase plate |
| CCD | charge-coupled device |
| TEM | transverse electromagnetic mode |
References
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Qiao, Z.; Kong, L.; Xie, G.; Qin, Z.; Yuan, P.; Qian, L.; Xu, X.; Xu, J.; Fan, D. Ultraclean femtosecond vortices from a tunable high-order transverse-mode femtosecond laser. Opt. Lett. 2017, 42, 2547–2550. [Google Scholar] [CrossRef] [PubMed]
- Willner, A.E.; Pang, K.; Song, H.; Zou, K.; Zhou, H. Orbital angular momentum of light for communications. Appl. Phys. Rev. 2021, 8, 041312. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- MacDonald, M.P.; Volke-Sepulveda, K.; Paterson, L.; Arlt, J.; Sibbett, W.; Dholakia, K. Revolving interference patterns for the rotation of optically trapped particles. Opt. Commun. 2002, 201, 21–28. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Optical trapping and moving of microparticles by using asymmetrical Laguerre–Gaussian beams. Opt. Lett. 2016, 41, 2426–2429. [Google Scholar] [CrossRef]
- Jack, B.; Leach, J.; Romero, J.; Franke-Arnold, S.; Ritsch-Marte, M.; Barnett, S.M.; Padgett, M.J. Holographic Ghost Imaging and the Violation of a Bell Inequality. Phys. Rev. Lett. 2009, 103, 083602. [Google Scholar] [CrossRef]
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef]
- Li, L.; Li, F. Beating the Rayleigh limit: Orbital-angular-momentum-based super-resolution diffraction tomography. Phys. Rev. E 2013, 88, 033205. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Liu, S.; Zhang, Y.-S.; Li, C.-F.; Guo, G.-C. Synthesis and observation of optical skyrmionic structure in free space. Phys. Rev. A 2024, 110, 043522. [Google Scholar] [CrossRef]
- Emile, O.; Emile, J. Naked eye picometer resolution in a Michelson interferometer using conjugated twisted beams. Opt. Lett. 2017, 42, 354–357. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.C.; Huang, Y.J.; Lin, Y.C.; Lu, T.H.; Chen, Y.F.; Huang, K.F. Picosecond optical vortex converted from multigigahertz self-mode-locked high-order Hermite-Gaussian Nd:GdVO4 lasers. Opt. Lett. 2009, 34, 3842–3844. [Google Scholar] [CrossRef]
- Soskin, M.S.; Gorshkov, V.N.; Vasnetsov, M.V.; Malos, J.T.; Heckenberg, N.R. Topological charge and angular momentum of light beams carrying optical vortices. Phys. Rev. A 1997, 56, 4064–4075. [Google Scholar] [CrossRef]
- Mao, L.; Yang, Z.; Zhou, L.; Liu, J.; Su, R.; Zheng, L.; Qiao, Z.; Zhuang, S.; Zhang, D. Manipulating Elliptical Photonic Orbits in Microlasers for High-Dimensional Encryption. Laser Photonics Rev. 2025, 19, 2500238. [Google Scholar] [CrossRef]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef]
- Fisher, A.D. A Review of Spatial Light Modulators. In Proceedings of the Topical Meeting on Optical Computing, Incline Village, NV, USA, 18 March 1985; p. TuC1. [Google Scholar]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
- Chen, Y.F.; Huang, T.M.; Kao, C.F.; Wang, C.L.; Wang, S.C. Generation of Hermite-Gaussian modes in fiber-coupled laser-diode end-pumped lasers. IEEE J. Quantum Electron. 1997, 33, 1025–1031. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chang, C.C.; Cho, C.Y.; Tuan, P.H.; Chen, Y.F. Generation of Higher Order Vortex Beams from a YVO4/Nd:YVO4 Self-Raman Laser via Off-Axis Pumping with Mode Converter. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 318–322. [Google Scholar] [CrossRef]
- Qiao, Z.; Xie, G.; Wu, Y.; Yuan, P.; Ma, J.; Qian, L.; Fan, D. Generating High-Charge Optical Vortices Directly from Laser Up to 288th Order. Laser Photonics Rev. 2018, 12, 1800019. [Google Scholar] [CrossRef]
- Pezzé, L.; Smerzi, A. Phase sensitivity of a Mach-Zehnder interferometer. Phys. Rev. A 2006, 73, 011801. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Z.; Gao, Y.; Wang, X.; Jie, Y.; Zhao, C. Self-healing and transformation characteristics of obstructed Hermite-Gaussian modes composed structured beams. arXiv 2021, arXiv:2112.03524. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, J.; Lu, X.; Wang, Z.; Zhao, C.; Cai, Y. Review on fractional vortex beam. Nanophotonics 2022, 11, 241–273. [Google Scholar] [CrossRef]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259. [Google Scholar] [CrossRef]
- Alexeyev, C.N.; Egorov, Y.A.; Volyar, A.V. Mutual transformations of fractional-order and integer-order optical vortices. Phys. Rev. A 2017, 96, 063807. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, S.; Liu, H.; Chen, X. Superhigh-Resolution Recognition of Optical Vortex Modes Assisted by a Deep-Learning Method. Phys. Rev. Lett. 2019, 123, 183902. [Google Scholar] [CrossRef]
- Vaity, P.; Banerji, J.; Singh, R.P. Measuring the topological charge of an optical vortex by using a tilted convex lens. Phys. Lett. A 2013, 377, 1154–1156. [Google Scholar] [CrossRef]
- Dwivedi, R.; Sharma, P.; Jaiswal, V.K.; Mehrotra, R. Elliptically squeezed axicon phase for detecting topological charge of vortex beam. Opt. Commun. 2021, 485, 126710. [Google Scholar] [CrossRef]
- Tao, S.H.; Yuan, X.C.; Lin, J.; Peng, X.; Niu, H.B. Fractional optical vortex beam induced rotation of particles. Opt. Express 2005, 13, 7726–7731. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhang, Y.; Li, Y.; Mao, L.; Zhao, P.; Qiao, Z. Tunable-Charge Optical Vortices Through Edge Diffraction of a High-Order Hermit-Gaussian Mode Laser. Photonics 2025, 12, 1076. https://doi.org/10.3390/photonics12111076
Li S, Zhang Y, Li Y, Mao L, Zhao P, Qiao Z. Tunable-Charge Optical Vortices Through Edge Diffraction of a High-Order Hermit-Gaussian Mode Laser. Photonics. 2025; 12(11):1076. https://doi.org/10.3390/photonics12111076
Chicago/Turabian StyleLi, Shuaichen, Yiyang Zhang, Ying Li, Linge Mao, Pengfan Zhao, and Zhen Qiao. 2025. "Tunable-Charge Optical Vortices Through Edge Diffraction of a High-Order Hermit-Gaussian Mode Laser" Photonics 12, no. 11: 1076. https://doi.org/10.3390/photonics12111076
APA StyleLi, S., Zhang, Y., Li, Y., Mao, L., Zhao, P., & Qiao, Z. (2025). Tunable-Charge Optical Vortices Through Edge Diffraction of a High-Order Hermit-Gaussian Mode Laser. Photonics, 12(11), 1076. https://doi.org/10.3390/photonics12111076




