Accuracy Analysis of Measuring Cylindrical Surfaces with Complex Parameters Using Two-Dimensional Pseudo Lateral Shearing Interferometry
Abstract
1. Introduction
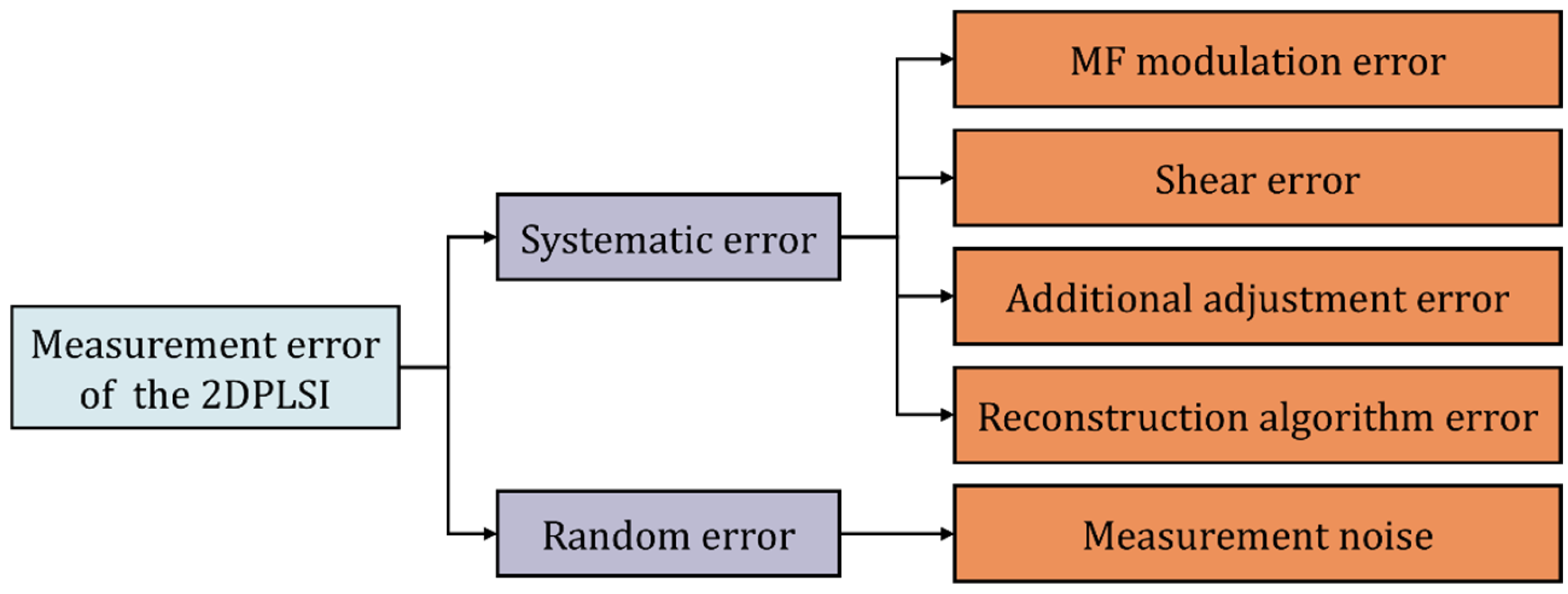
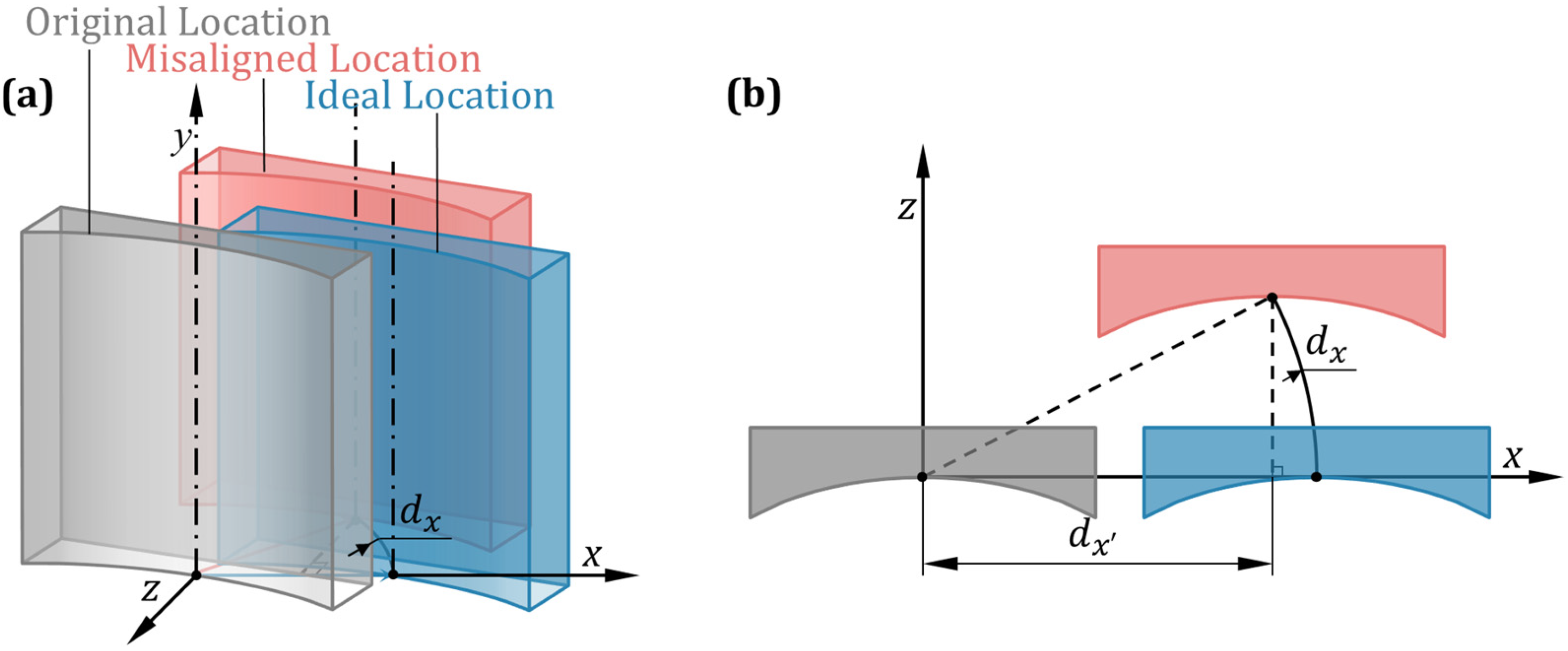
2. Analysis of 2DPLSI Measurement Error
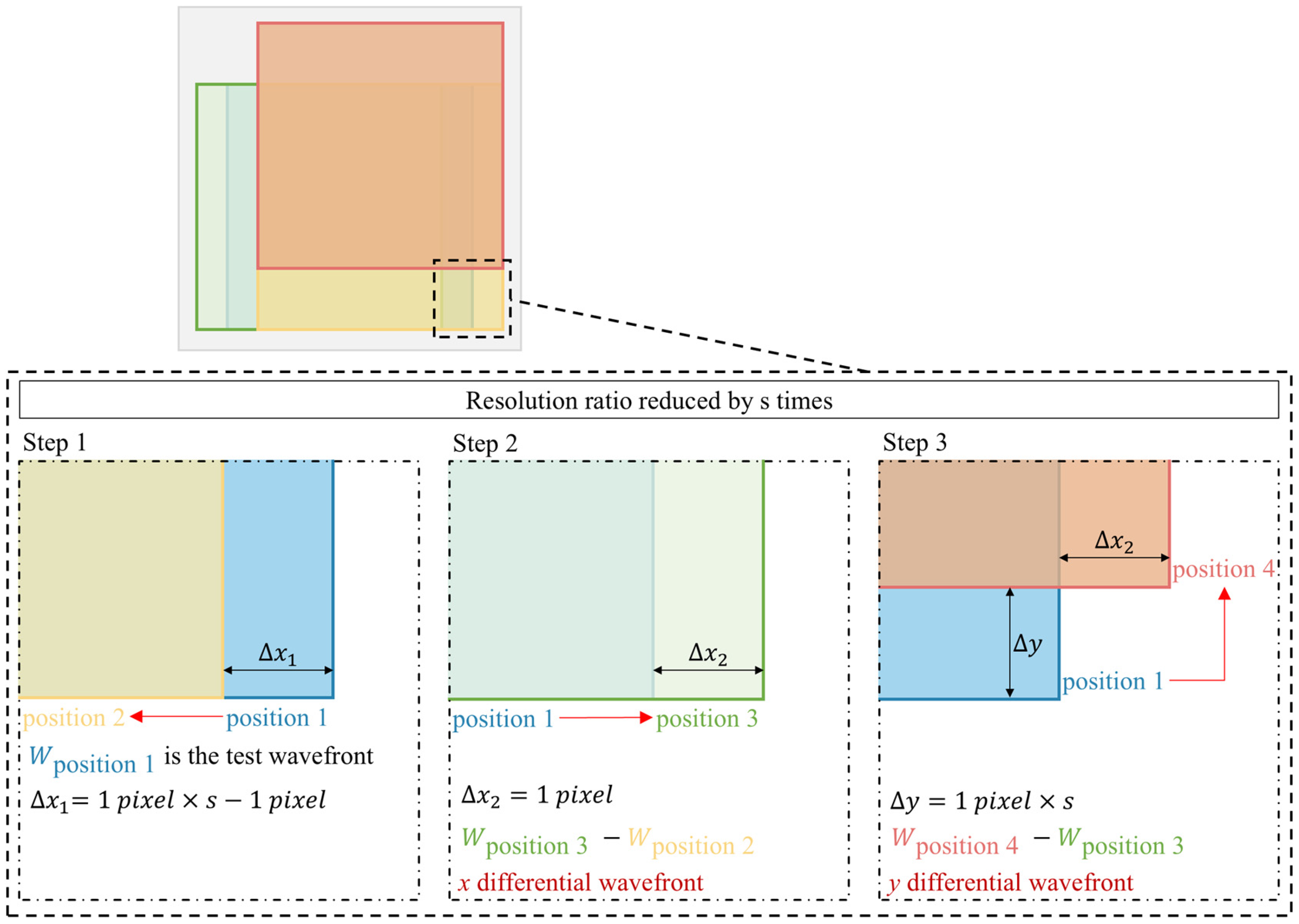
3. Error Simulation Method
3.1. Wavefront Construction Method
3.2. Principles
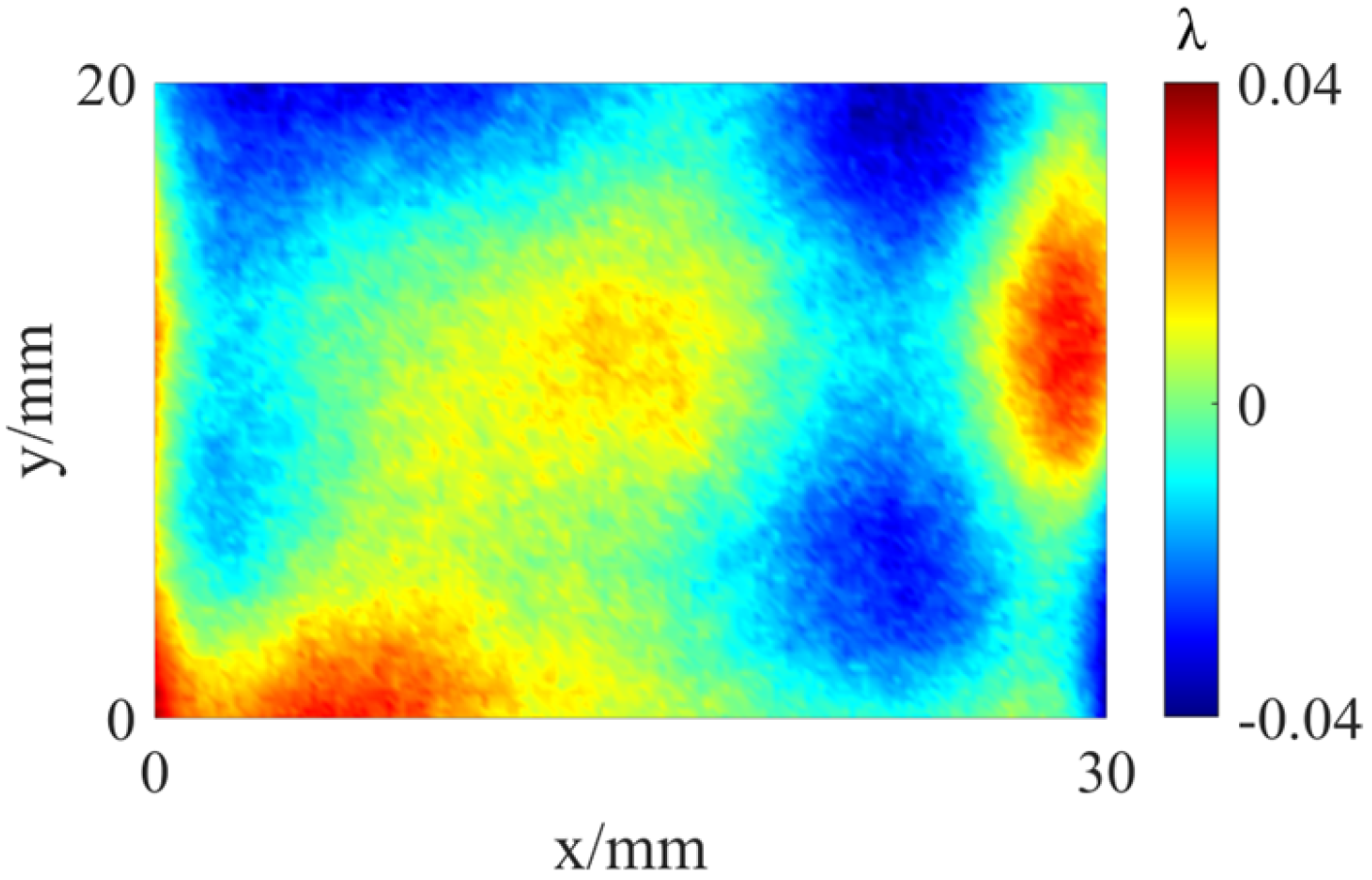
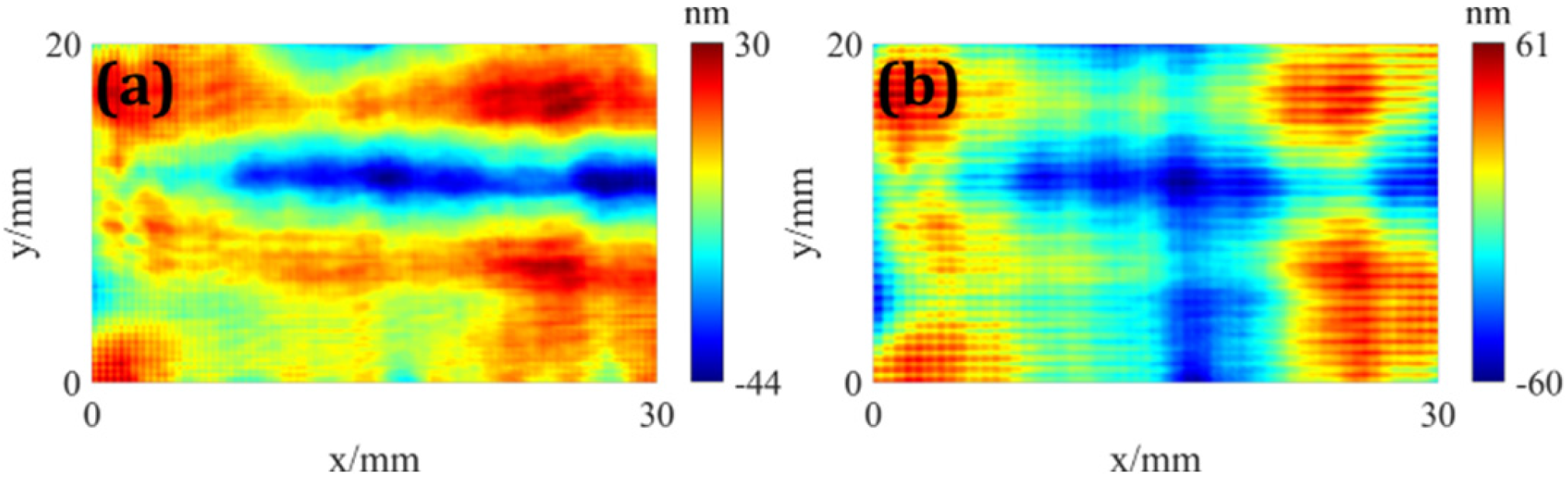
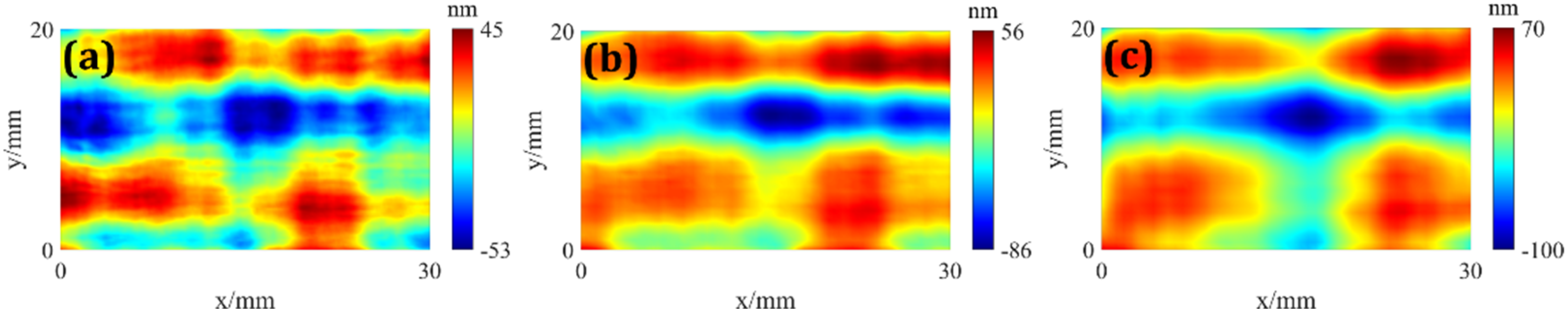
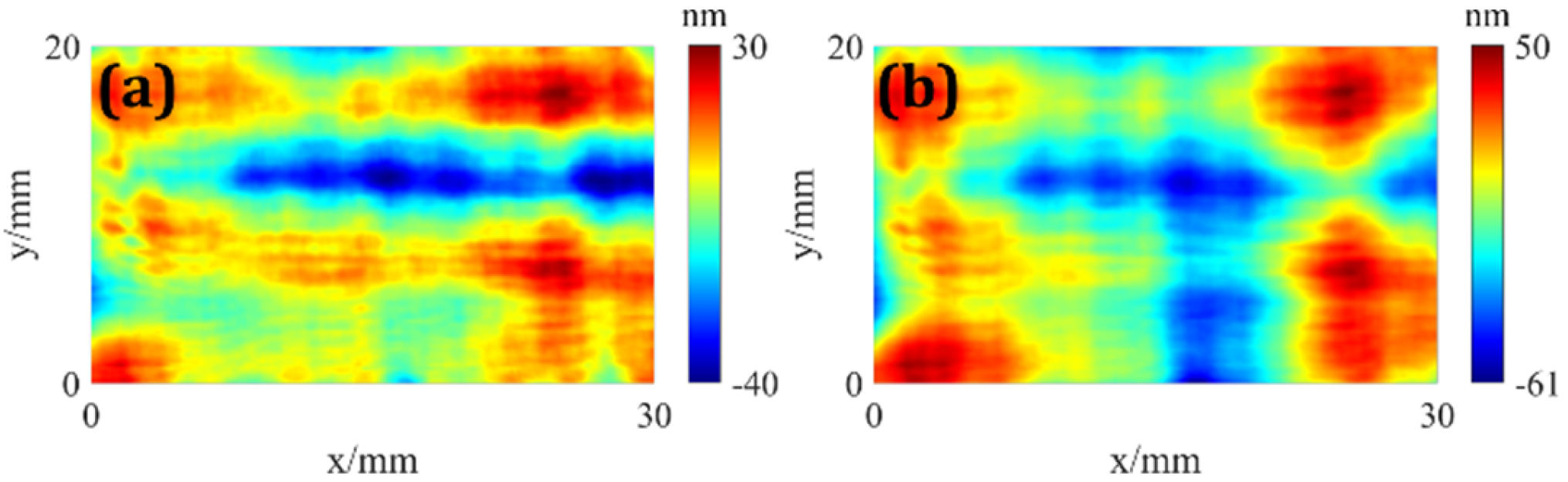
4. Error Simulation Results
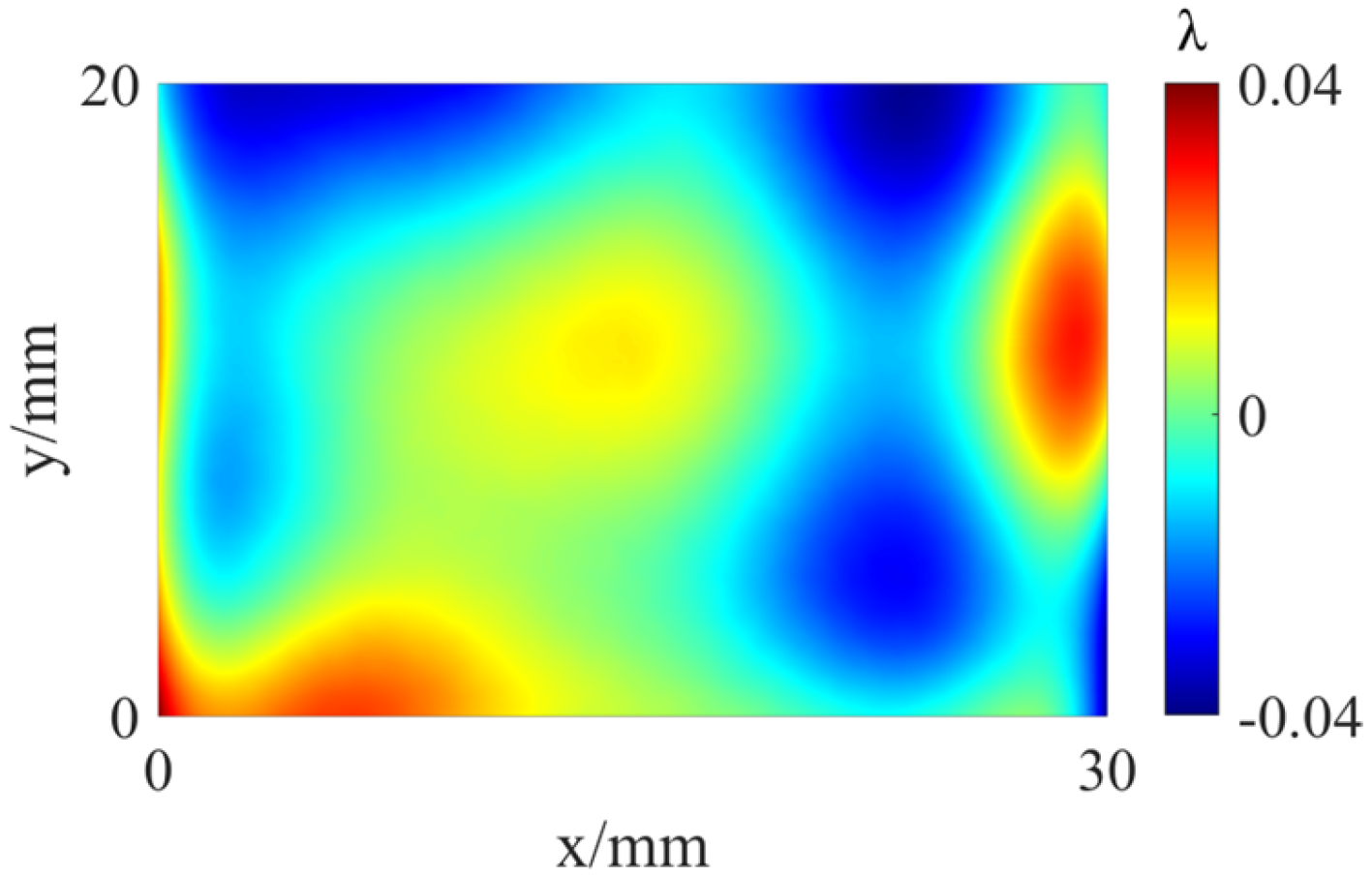
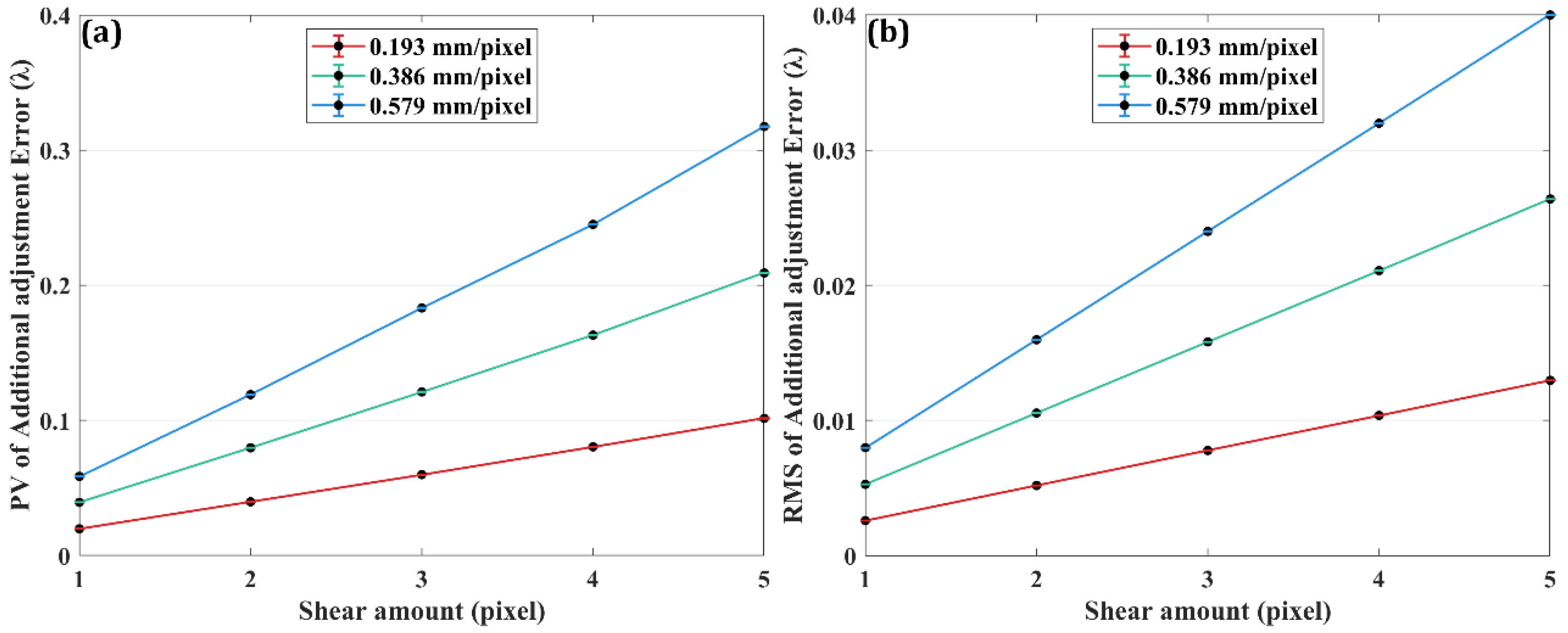
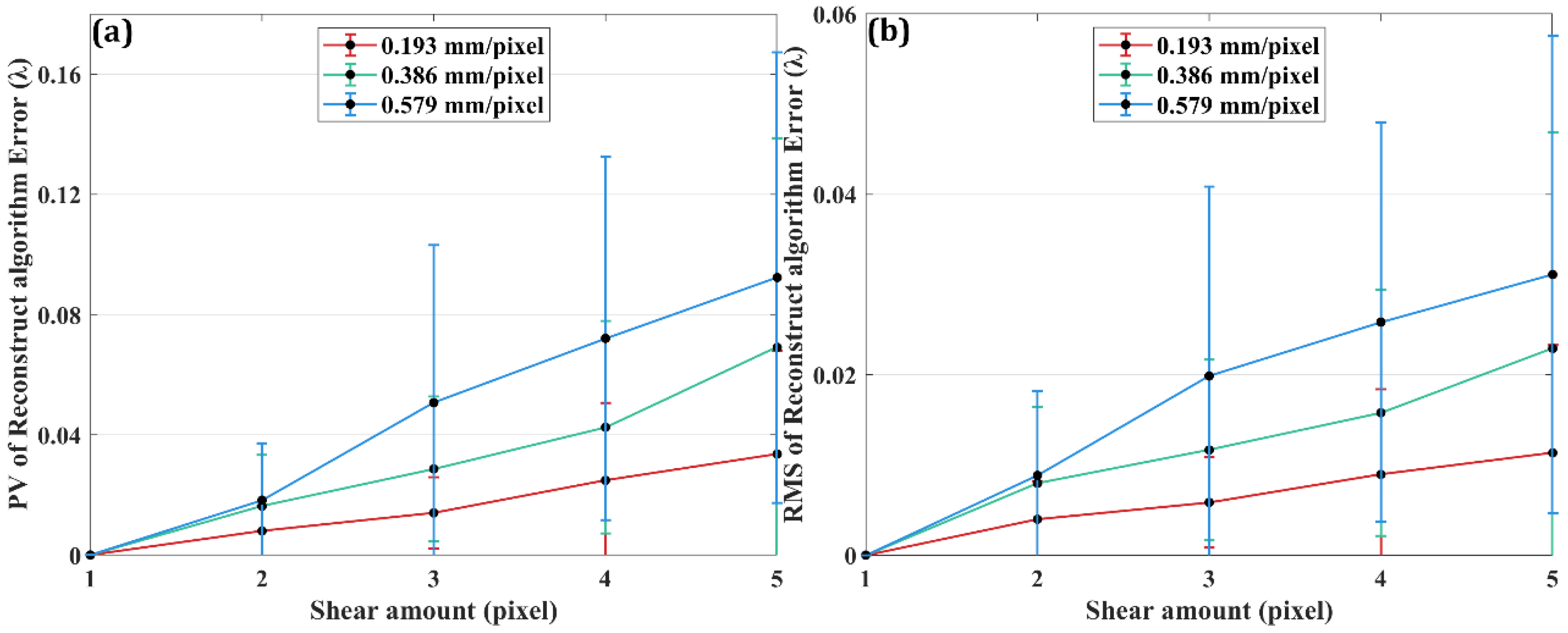
4.1. System Error
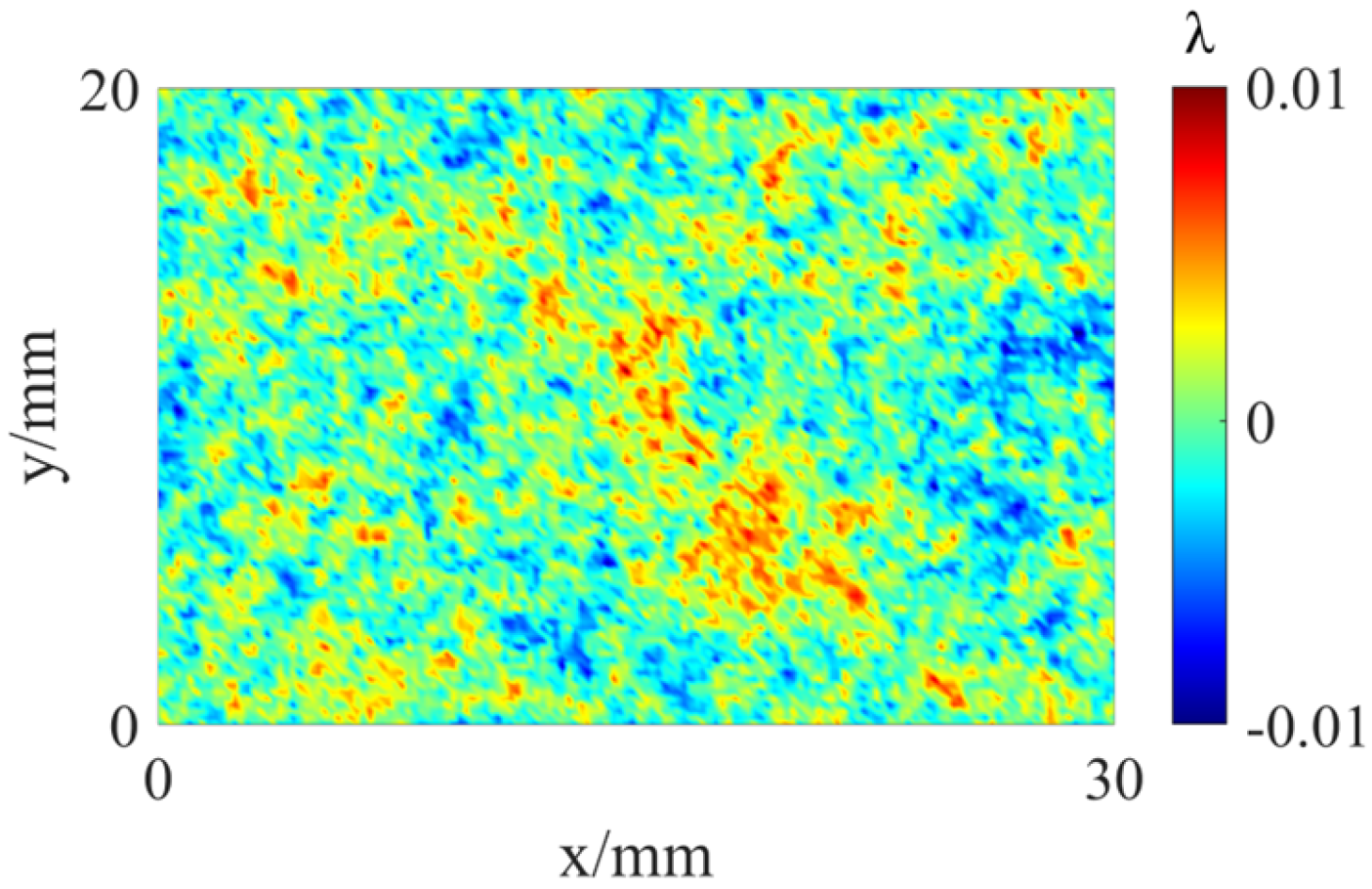
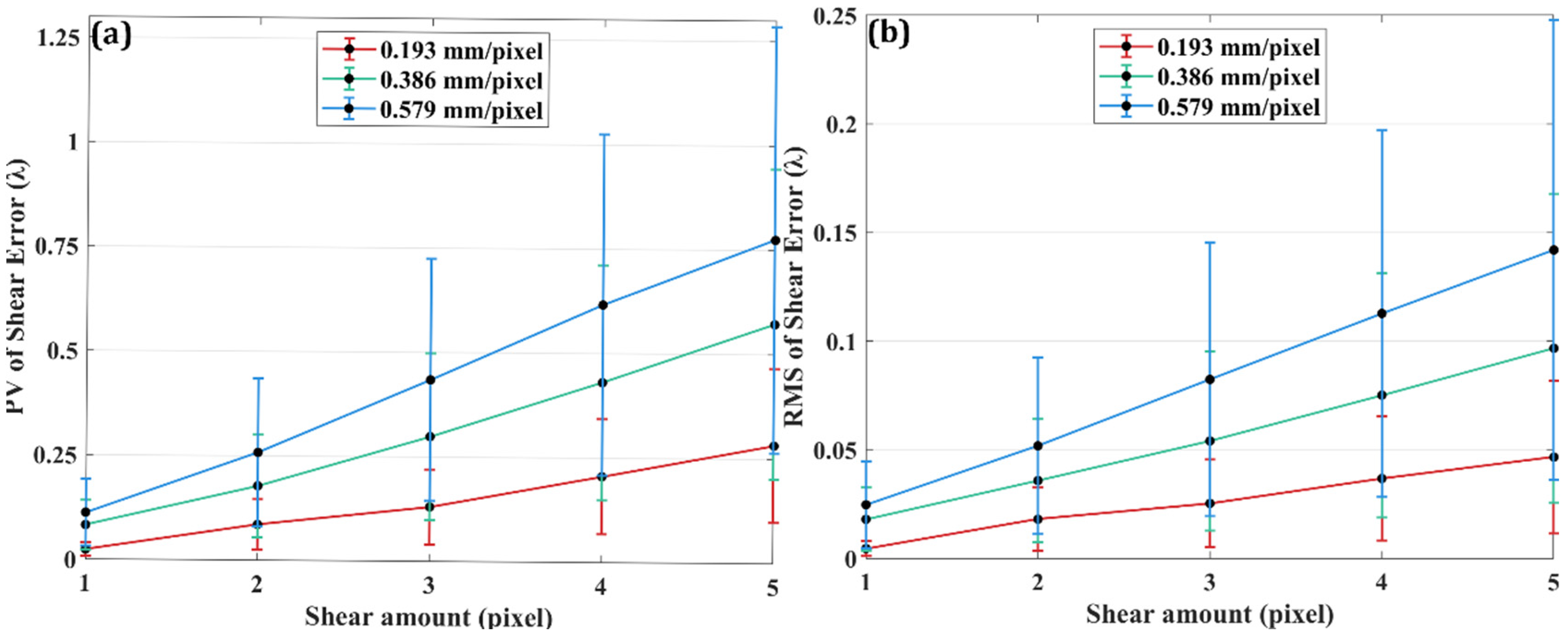
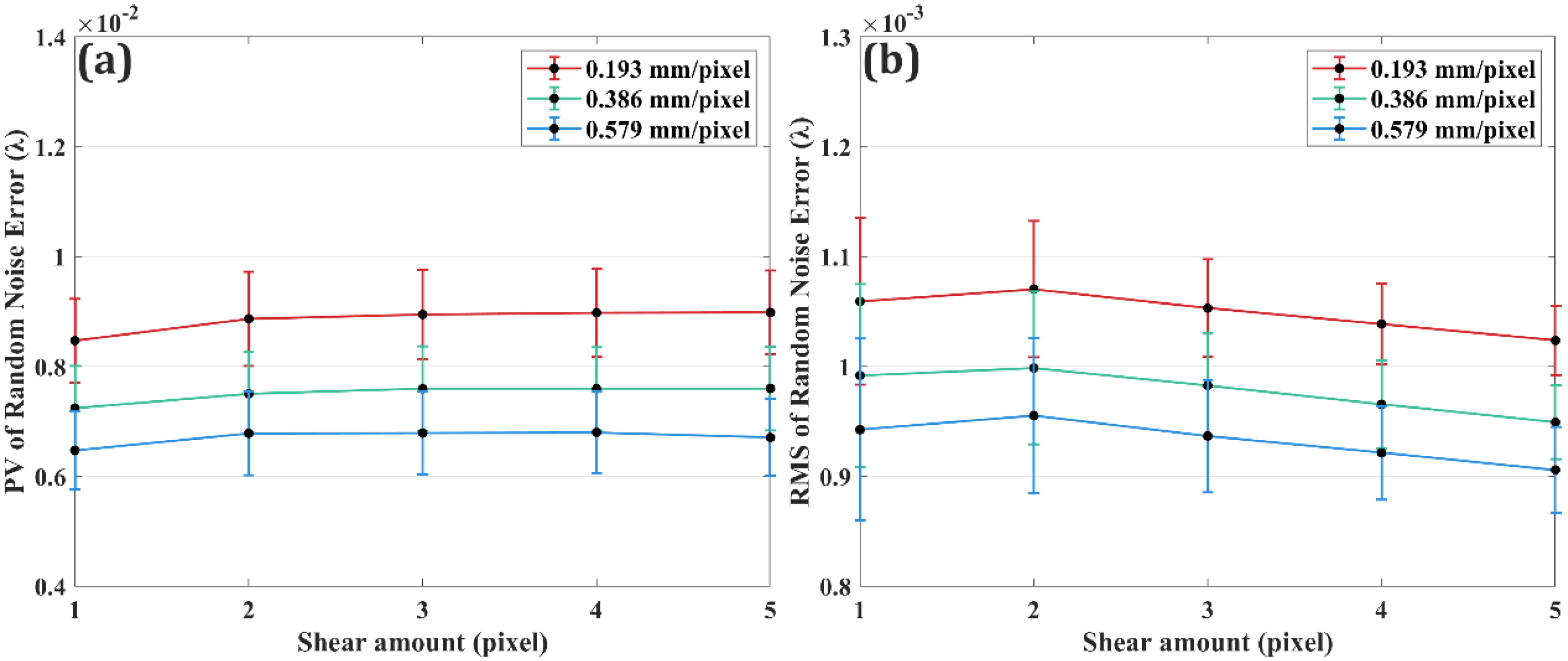
4.2. Random Error
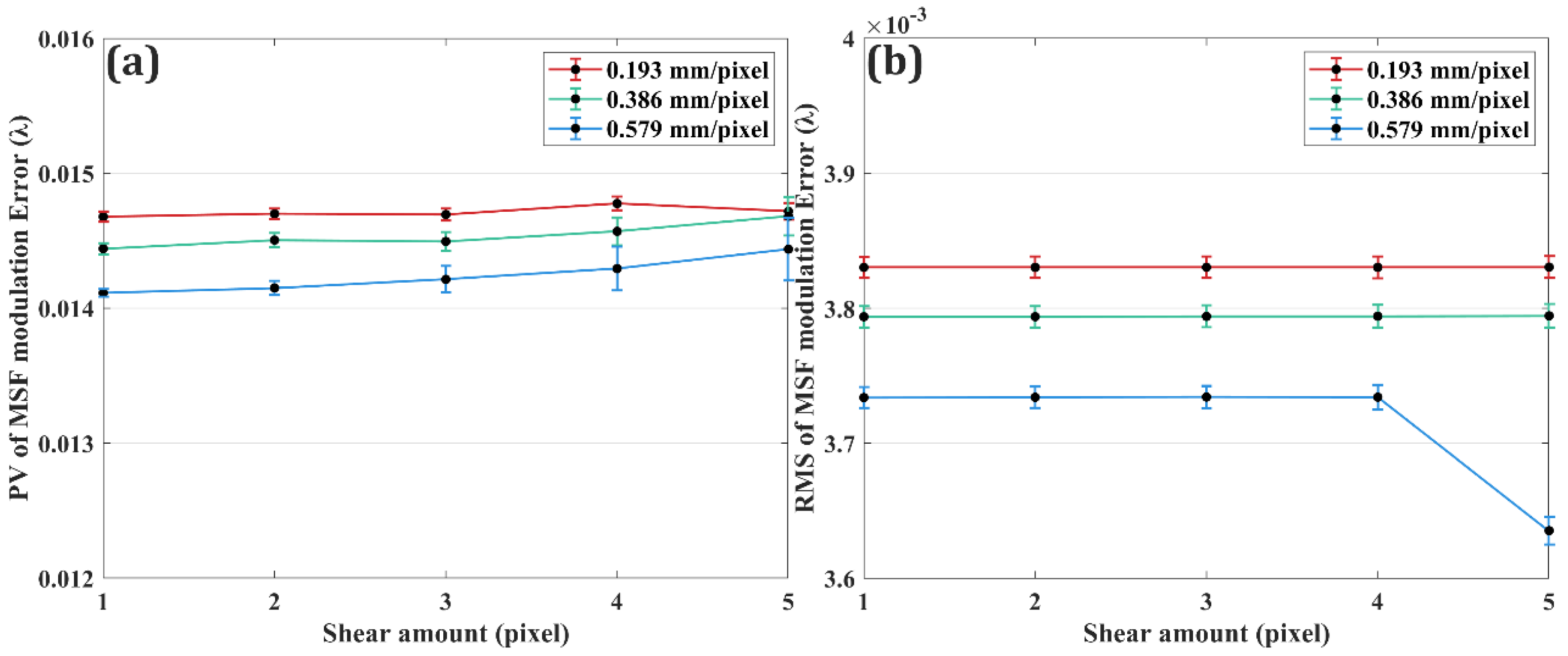
4.3. Parameter Selection of Measurement System
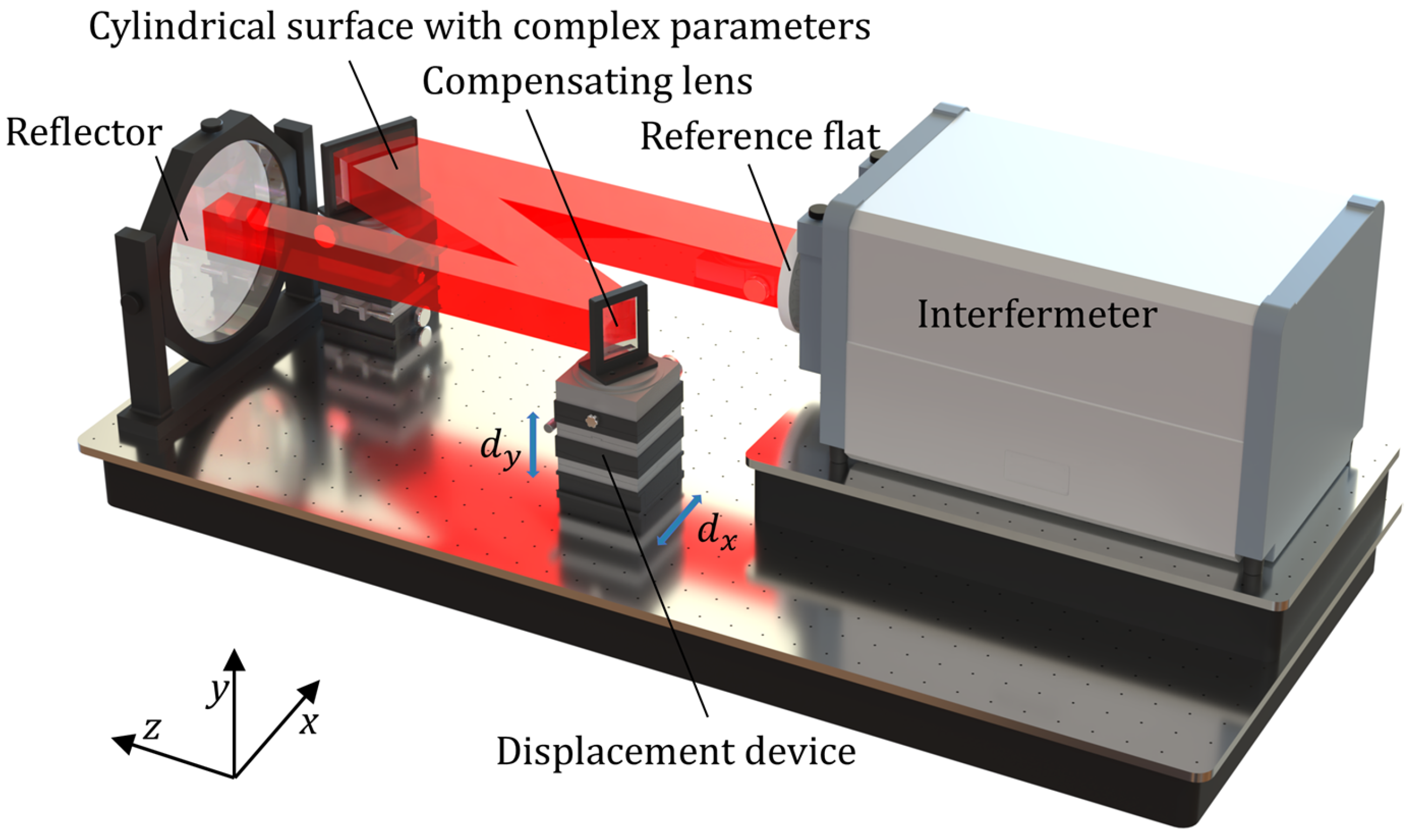
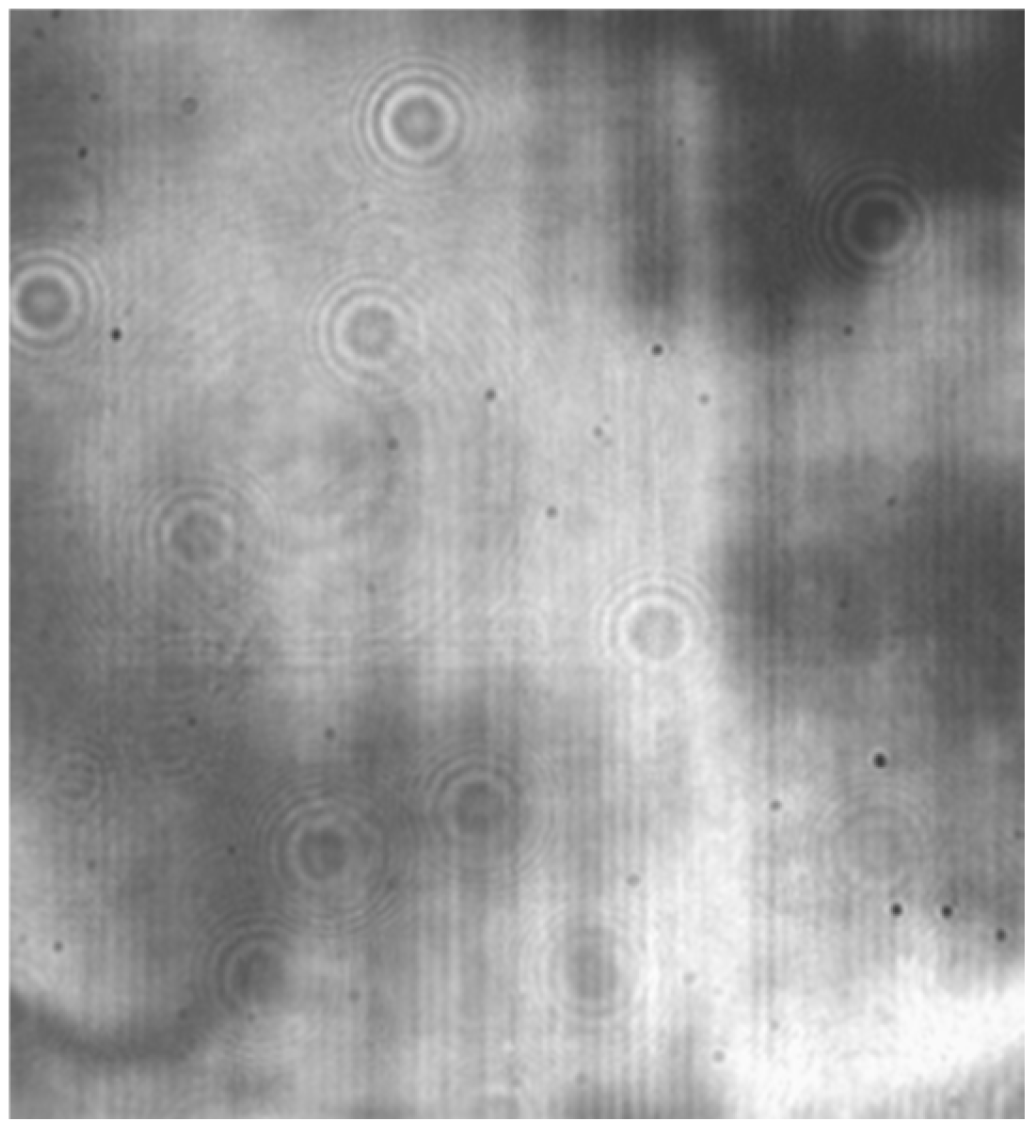
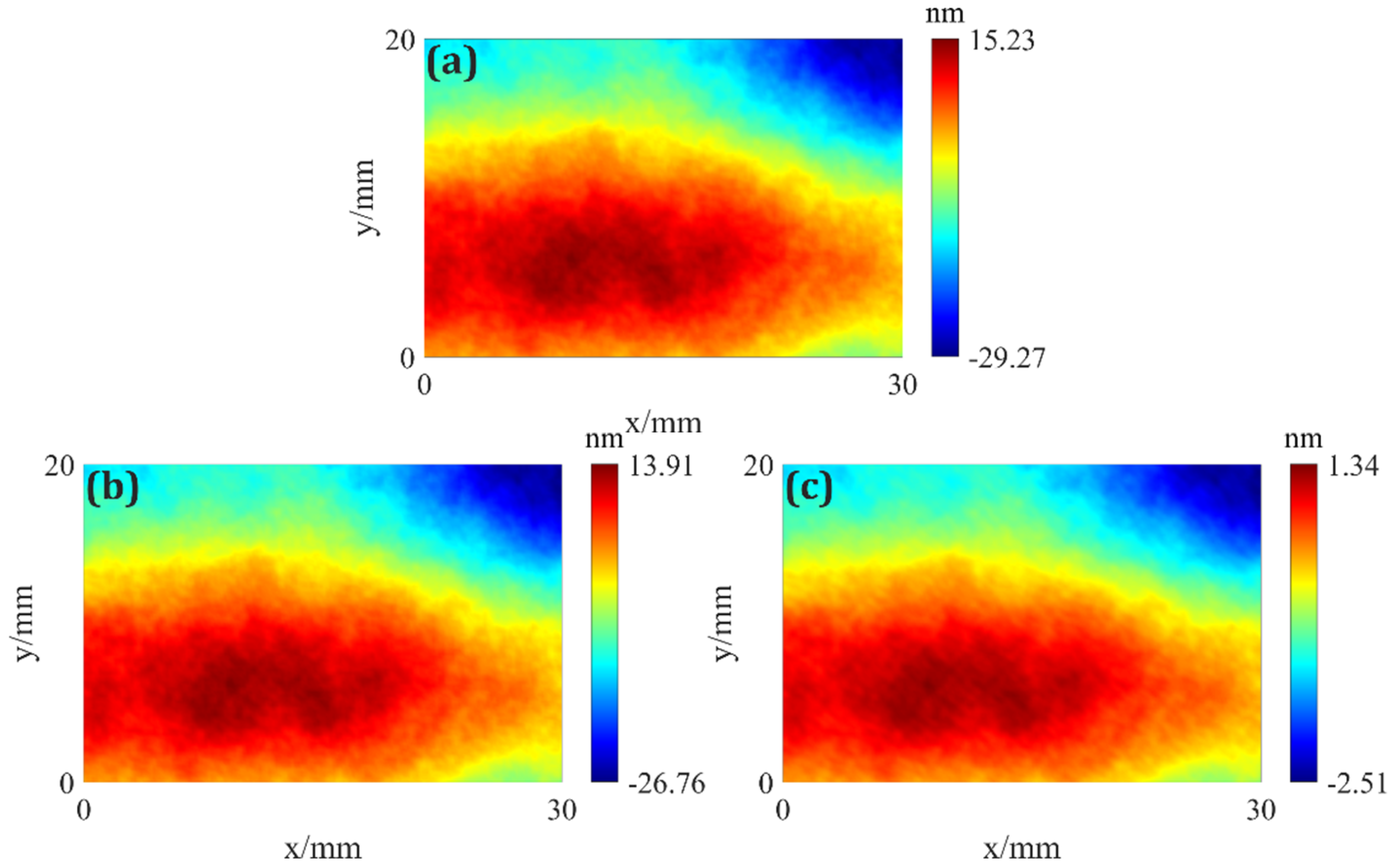
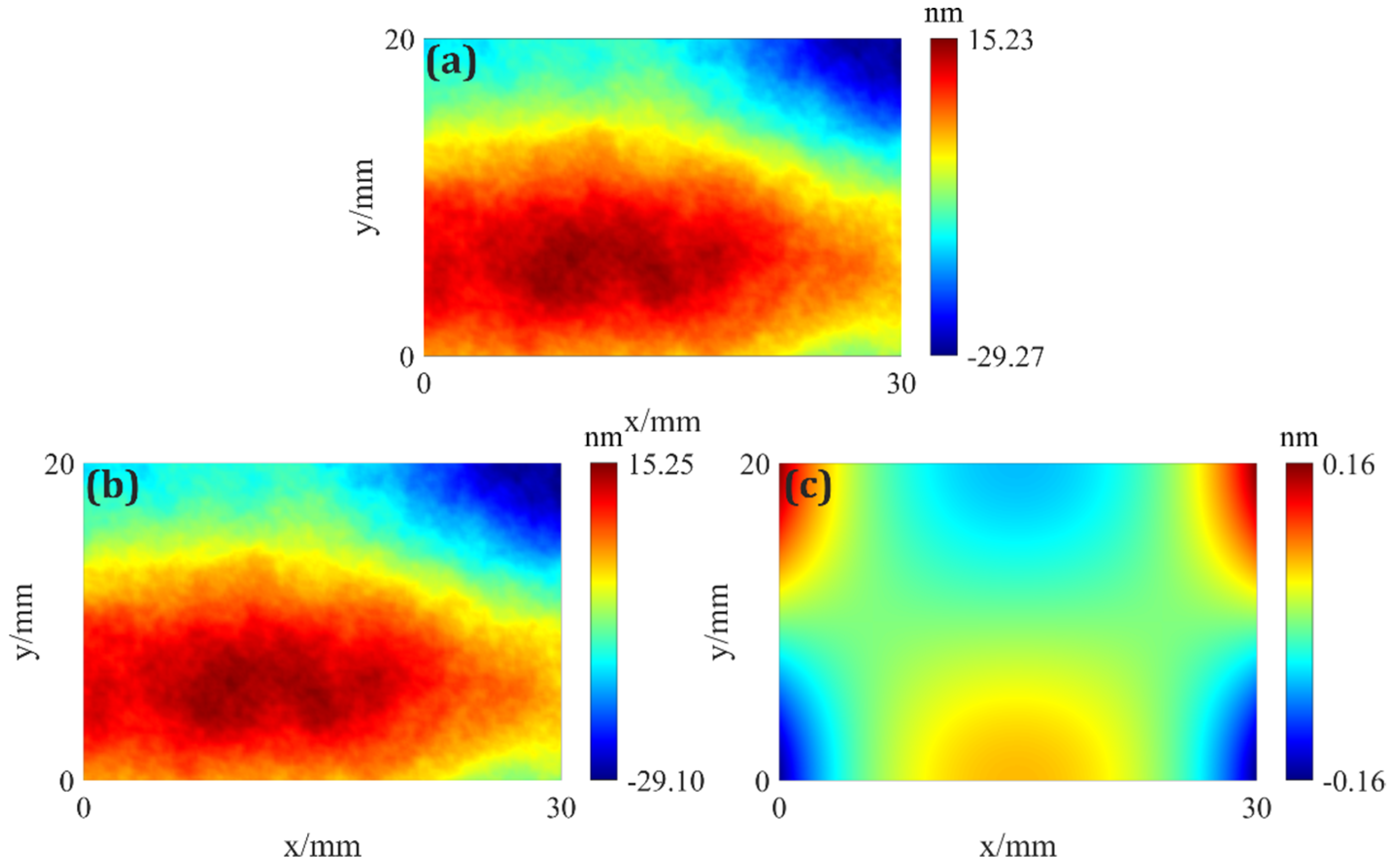
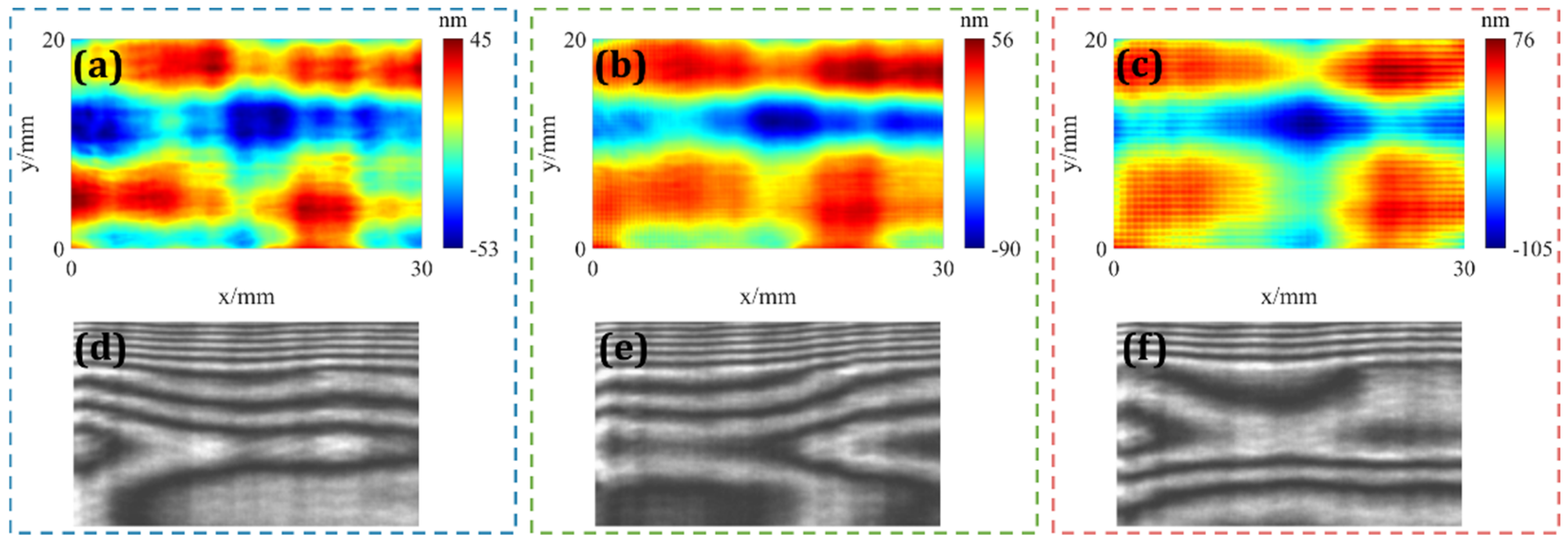
5. Experiment and Results
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malek, S.C.; Overvig, A.C.; Alu, A.; Yu, N.F. Multifunctional resonant wavefront-shaping meta-optics based on multilayer and multi-perturbation nonlocal metasurfaces. Light-Sci. Appl. 2022, 11, 246. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Kang, P.; Jeong, S.; Kwon, Y.; Yang, T.D.; Hong, J.H.; Kim, M.; Song, K.D.; Park, J.H.; Lee, J.H.; et al. High-resolution adaptive optical imaging within thick scattering media using closed-loop accumulation of single scattering. Nat. Commun. 2017, 8, 2157. [Google Scholar] [CrossRef] [PubMed]
- Delmdahl, R. The excimer laser: Precision engineering. Nat. Photonics 2010, 4, 286. [Google Scholar] [CrossRef]
- Padilla, W.J.; Averitt, R.D. Imaging with metamaterials. Nat. Rev. Phys. 2022, 4, 85–100. [Google Scholar] [CrossRef]
- Chen, B.; Chang, B.J.; Roudot, P.; Zhou, F.; Sapoznik, E.; Marlar-Pavey, M.; Hayes, J.B.; Brown, P.T.; Zeng, C.W.; Lambert, T.; et al. Resolution doubling in light-sheet microscopy via oblique plane structured illumination. Nat. Methods 2022, 19, 1419–1426. [Google Scholar] [CrossRef]
- Liu, H.Y.; Yan, L.S.; Chen, H.S.; Liu, X.; Liu, H.Y.; Chew, S.H.; Gliserin, A.; Wang, Q.; Zhang, J.W. High-order femtosecond vortices up to the 30th order generated from a powerful mode-locked Hermite-Gaussian laser. Light-Sci. Appl. 2023, 12, 207. [Google Scholar] [CrossRef]
- Gatzweiler, A.; Glatzel, H. Interferometric measurement of near-cylindrical surfaces with high amplitude resolution. Appl. Opt. 1995, 34, 7207–7212. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, J.H.; Xu, M. Interferometric method of measuring external cylindrical surfaces. Appl. Opt. 2021, 60, 47–51. [Google Scholar] [CrossRef]
- Viotti, M.R.; Albertazzi, A.; Dal Pont, A.; Fantin, A.V. Evaluation of a novel algorithm to align and stitch adjacent measurements of long inner cylindrical surfaces with white light interferometry. Opt. Lasers Eng. 2007, 45, 852–859. [Google Scholar] [CrossRef]
- León-Rodríguez, M.; Rayas, J.A.; Martínez-García, A.; Martínez-González, A.; Téllez-Quiñones, A.; Porras-Aguilar, R. Panoramic reconstruction of quasi-cylindrical objects with digital holography and a conical mirror. Opt. Lett. 2021, 46, 4749–4752. [Google Scholar] [CrossRef]
- Liu, F.; Robinson, B.M.; Reardon, P.J.; Geary, J.M. Separating misalignment from misfigure in interferograms on cylindrical optics. Opt. Express 2013, 21, 8856–8864. [Google Scholar] [CrossRef] [PubMed]
- Blinder, D.; Birnbaum, T.; Ito, T.; Shimobaba, T. The state-of-the-art in computer generated holography for 3D display. Light Adv. Manuf. 2022, 3, 572–600. [Google Scholar] [CrossRef]
- Han, S.; Zhang, L.H.; Jia, W.X. Absolute Calibration of Smooth Surface and Cylindrical Surface Measurement. In Optical Metrology and Inspection for Industrial Applications VIII; SPIE: Washington, DC, USA, 2021. [Google Scholar]
- Huang, Y.; Ma, J.; Yuan, C.J.; Pruss, C.; Sun, W.Y.; Liu, M.C.; Zhu, R.H.; Gao, Z.S.; Osten, W.G. Absolute test for cylindrical surfaces using the conjugate differential method. Opt. Eng. 2016, 55, 114104. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, X.; Hu, X.C.; Li, J.H.; Li, M.F. Stitching interferometry using Computer-Generated Hologram (CGH) based on sub-aperture adjustment aberration of 2-D Chebyshev polynomial. Opt. Lasers Eng. 2021, 143, 106618. [Google Scholar] [CrossRef]
- Hu, H.; Sun, Z.Z.; Xue, S.; Guan, C.L.; Dai, Y.F.; Liu, J.F.; Peng, X.Q.; Chen, S.Y.; Liu, Y. Self-calibration interferometric stitching test method for cylindrical surfaces. Opt. Express 2022, 30, 39188–39206. [Google Scholar] [CrossRef]
- Li, J.; Shen, H.; Wang, J.; Zhu, R. Common-path interferometry with tilt carrier for surface measurement of complex optics. Appl. Opt. 2019, 58, 1991–1997. [Google Scholar] [CrossRef]
- Kong, L.; Chen, S. Subaperture stitching test for large aperture mild acylinders. Opt. Commun. 2020, 455, 124526. [Google Scholar] [CrossRef]
- Chen, Y.; Hai, K.; Zhang, X.; Zhang, S.; Zheng, Y.; Liu, Q.; Su, X.; Huang, W.; Zhang, X.; Liu, D.; et al. Non-null test of cylindrical surfaces with complex parameters based on pseudo shearing interferometry. Opt. Lasers Eng. 2025, 184, 108687. [Google Scholar] [CrossRef]
- Zang, Z.; Peng, S.; Jin, W.; Zuo, Y.; Steinmeyer, G.; Dai, Y.; Liu, D. In-situ measurement and compensation of complex spatio-temporal couplings in ultra-intense lasers. Opt. Lasers Eng. 2023, 160, 107239. [Google Scholar] [CrossRef]
- Peng, S.; Xu, Z.; Zang, Z.; Li, X.; Dai, Y.; Wang, X.; Jin, B.; Li, X.; Sun, J.; Yang, B.; et al. Accuracy analysis of pseudo lateral shearing interferometry measuring complex spatio-temporal couplings. Opt. Laser Technol. 2023, 167, 109792. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, A.; Liu, B.; Wang, H. Error correction analysis of wavefront testing in quadriwave lateral shearing interferometry. J. Opt. Soc. Am. A 2024, 41, C10–C21. [Google Scholar] [CrossRef]
- Zhu, W.; Li, J.; Chen, L.; Zheng, D.; Yang, Y.; Han, Z. Systematic error analysis and correction in quadriwave lateral shearing interferometer. Opt. Commun. 2016, 380, 214–220. [Google Scholar] [CrossRef]
- Peng, L.; Feng, T.; Xiangzhao, W. Relationship between shear ratio and reconstruction accuracy in lateral shearing interferometry. Opt. Eng. 2020, 59, 034113. [Google Scholar] [CrossRef]
- Rhee, H.-G.; Ghim, Y.-S.; Lee, J.; Yang, H.-S.; Lee, Y.-W. Rotational error correction in lateral shearing interferometry for freeform surface measurement. In Optical Fabrication and Testing; Optica Publishing Group: Washington, DC, USA, 2014. [Google Scholar]
- Dai, F.; Tang, F.; Wang, X.; Sasaki, O.; Zhang, M. High spatial resolution zonal wavefront reconstruction with improved initial value determination scheme for lateral shearing interferometry. Appl. Opt. 2013, 52, 3946–3956. [Google Scholar] [CrossRef]
- Dai, F.; Tang, F.; Wang, X.; Sasaki, O. Generalized zonal wavefront reconstruction for high spatial resolution in lateral shearing interferometry. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2012, 29, 2038–2047. [Google Scholar] [CrossRef]
- Sidick, E. Power Spectral Density Specification and Analysis of Large Optical Surfaces. In Modeling Aspects in Optical Metrology II; SPIE: Washington, DC, USA, 2009. [Google Scholar]
- Williams, W.; Auerbach, J.; Hunt, J.; Lawson, L.; Manes, K. NIF optics phase gradient specfication. In US National Ignition Facility; Lawrence Livermore National Lab.: Livermore, CA, USA, 1997. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Zang, Z.; Zhang, S.; Chen, Y.; Zheng, Y.; Niu, Z.; Yu, J.; Luo, W.; Li, Z.; Kong, M.; et al. Accuracy Analysis of Measuring Cylindrical Surfaces with Complex Parameters Using Two-Dimensional Pseudo Lateral Shearing Interferometry. Photonics 2025, 12, 1059. https://doi.org/10.3390/photonics12111059
Zhao L, Zang Z, Zhang S, Chen Y, Zheng Y, Niu Z, Yu J, Luo W, Li Z, Kong M, et al. Accuracy Analysis of Measuring Cylindrical Surfaces with Complex Parameters Using Two-Dimensional Pseudo Lateral Shearing Interferometry. Photonics. 2025; 12(11):1059. https://doi.org/10.3390/photonics12111059
Chicago/Turabian StyleZhao, Le, Zhongming Zang, Siqi Zhang, Yang Chen, Yueqing Zheng, Zhitian Niu, Jing Yu, Weizhou Luo, Zhu Li, Ming Kong, and et al. 2025. "Accuracy Analysis of Measuring Cylindrical Surfaces with Complex Parameters Using Two-Dimensional Pseudo Lateral Shearing Interferometry" Photonics 12, no. 11: 1059. https://doi.org/10.3390/photonics12111059
APA StyleZhao, L., Zang, Z., Zhang, S., Chen, Y., Zheng, Y., Niu, Z., Yu, J., Luo, W., Li, Z., Kong, M., Wang, S., & Hai, K. (2025). Accuracy Analysis of Measuring Cylindrical Surfaces with Complex Parameters Using Two-Dimensional Pseudo Lateral Shearing Interferometry. Photonics, 12(11), 1059. https://doi.org/10.3390/photonics12111059




