A Wavelength-Multiplexed Dual-Frequency Mode-Locked Fiber Laser with Tunable Repetition Frequency Difference
Abstract
1. Introduction
2. Experimental Setup
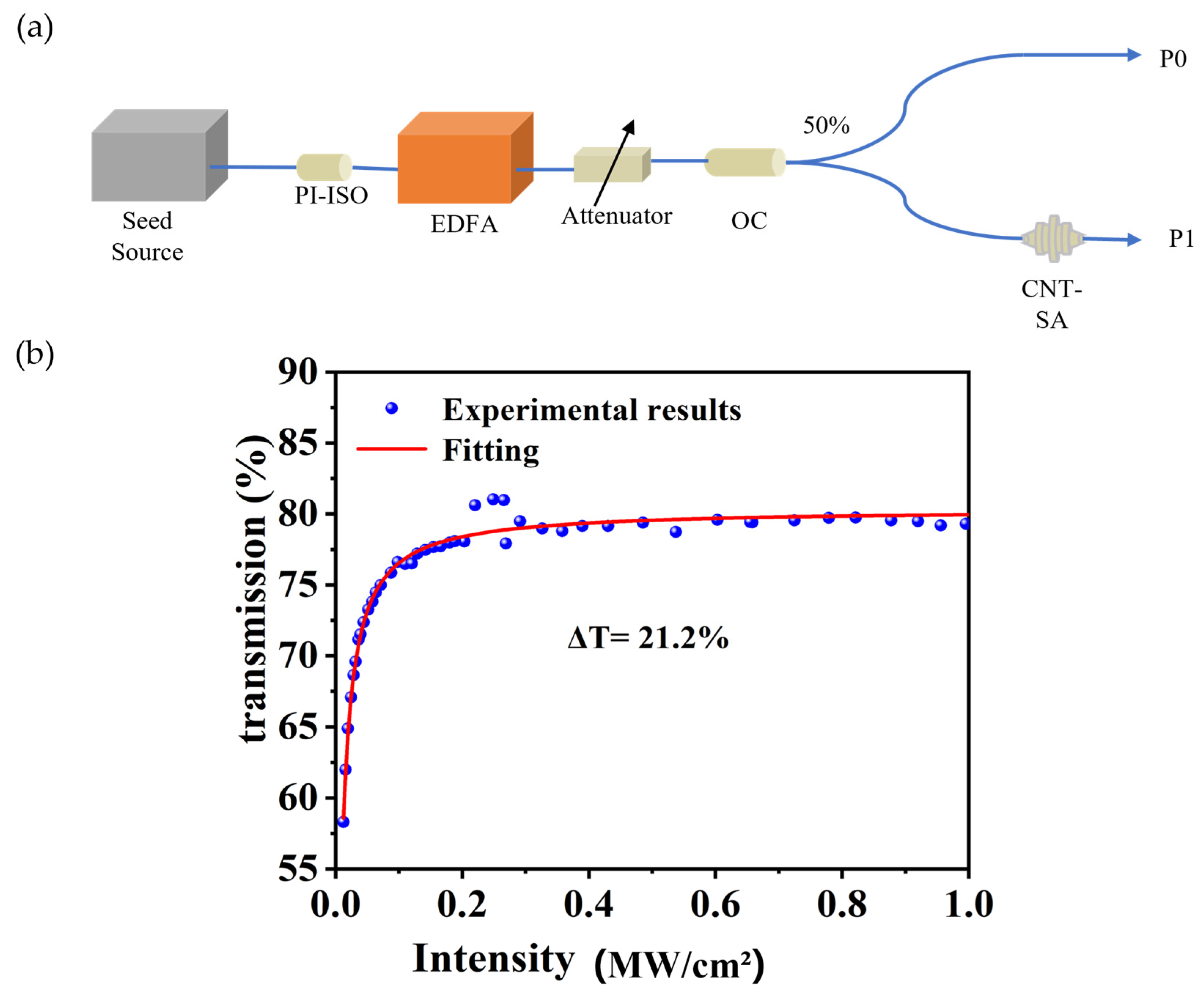
2.1. Preparation and Characterization of CNT-Based Saturable Absorber
2.2. The Principle of NPR Mechanism
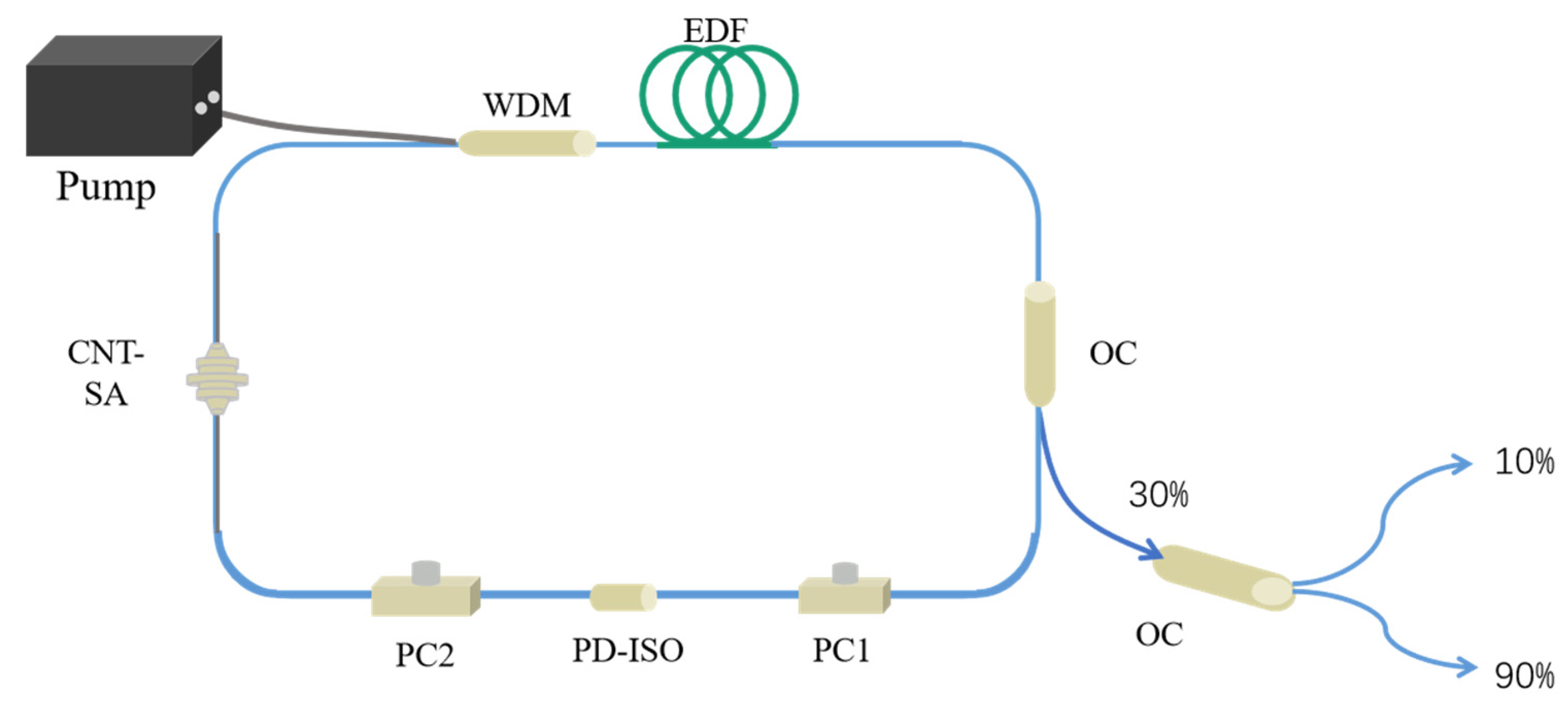
2.3. Experimental Setup of the Laser
3. Experimental Results and Analysis
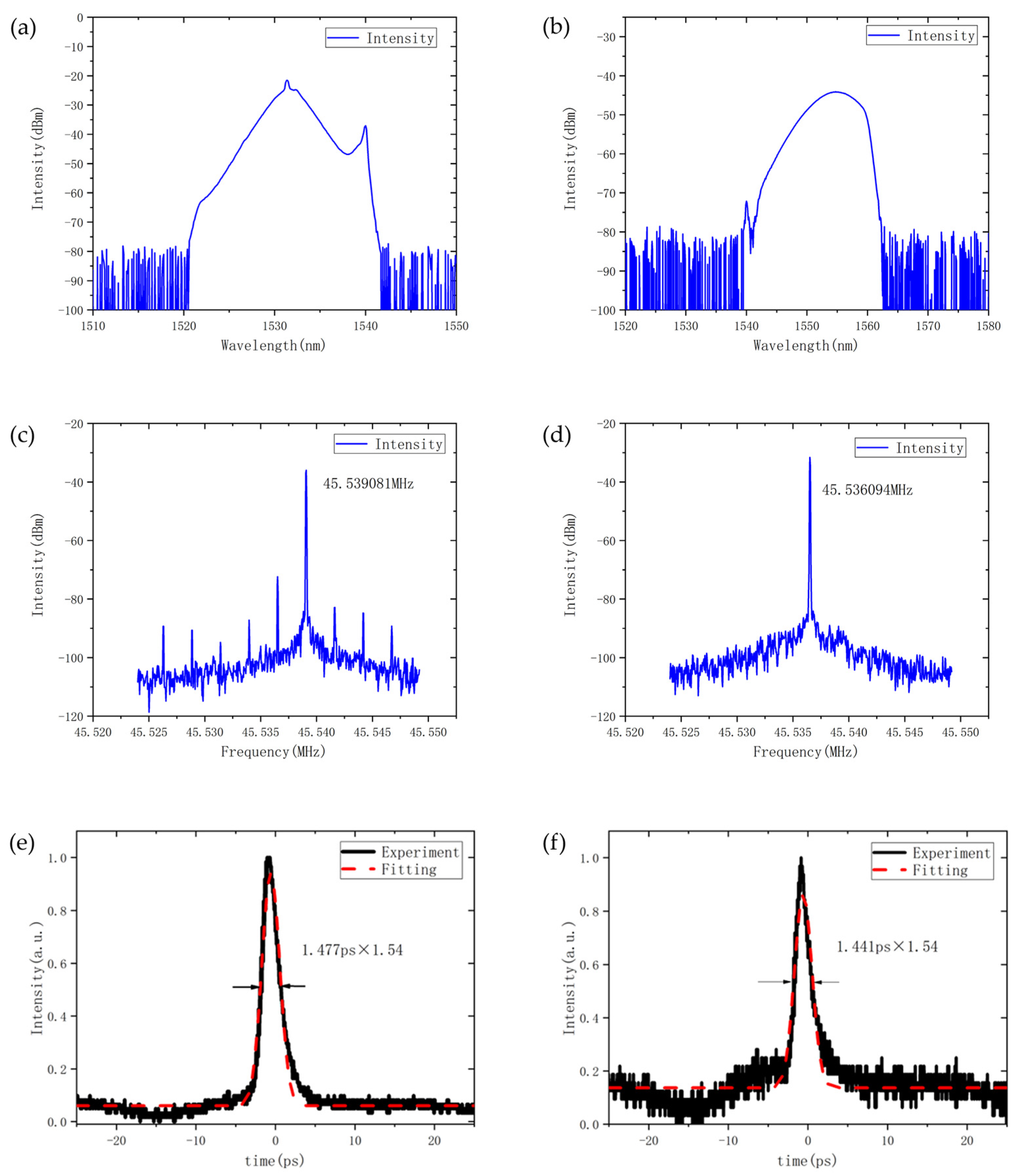
3.1. Single-Wavelength Mode-Locking
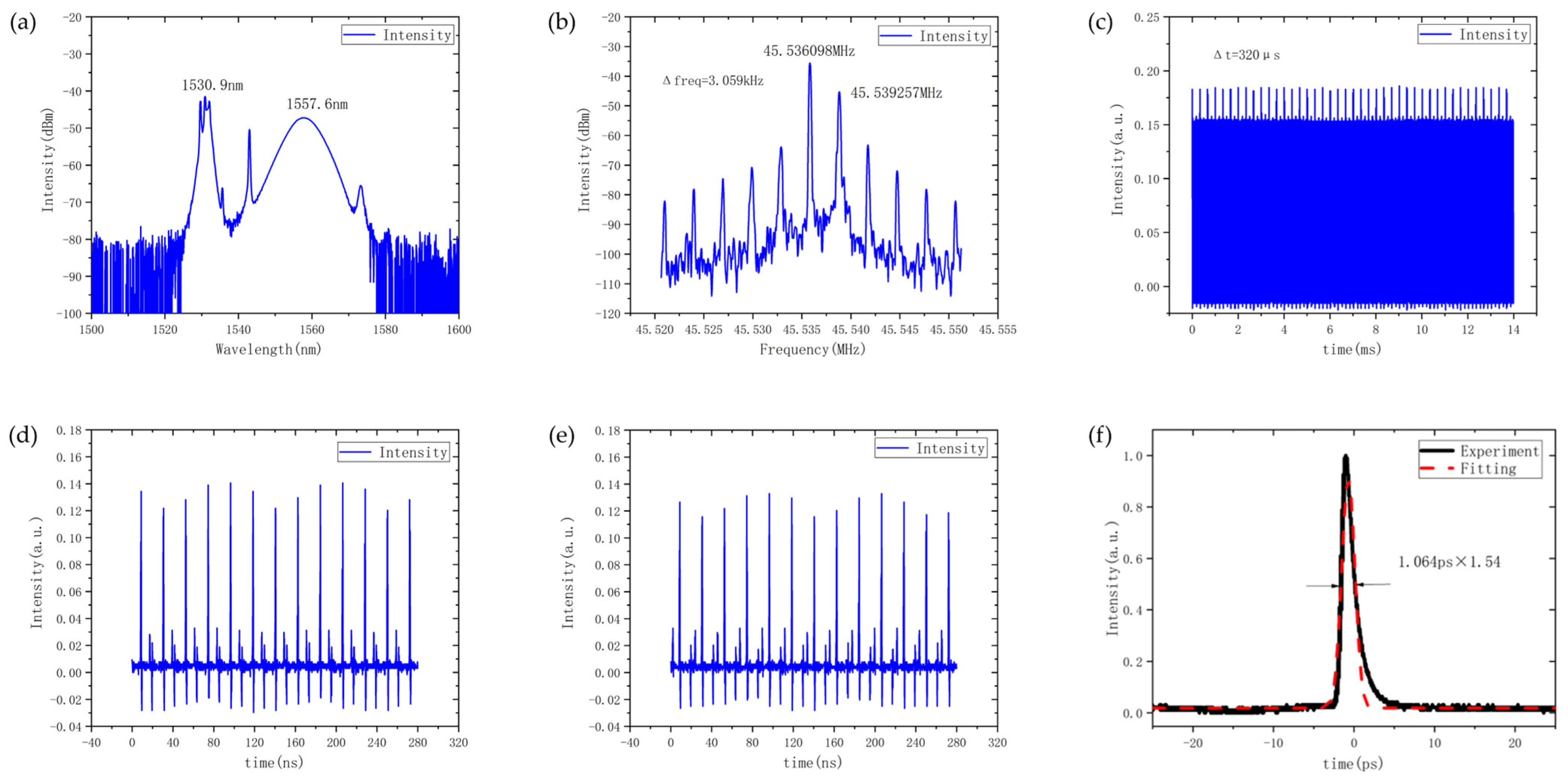
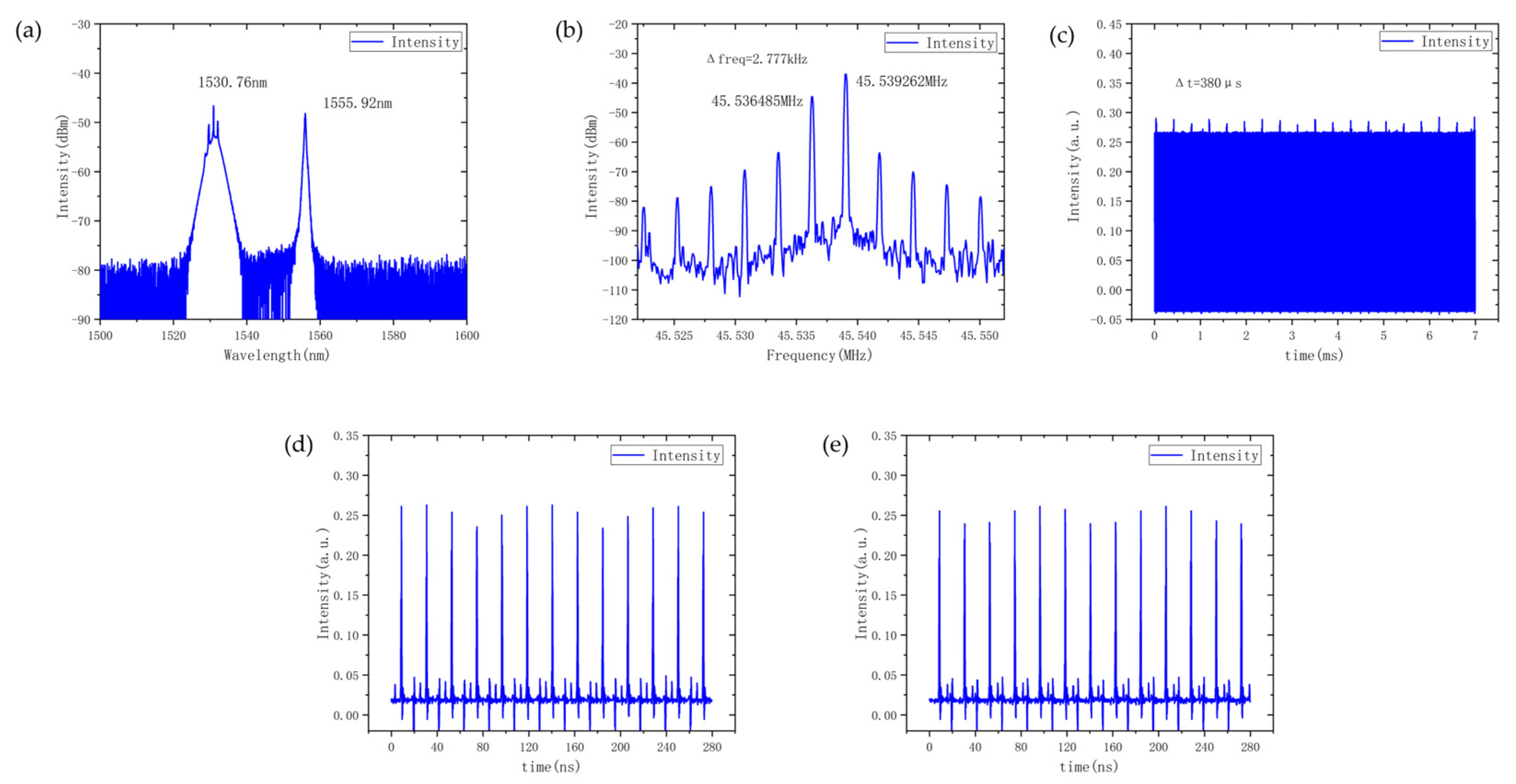
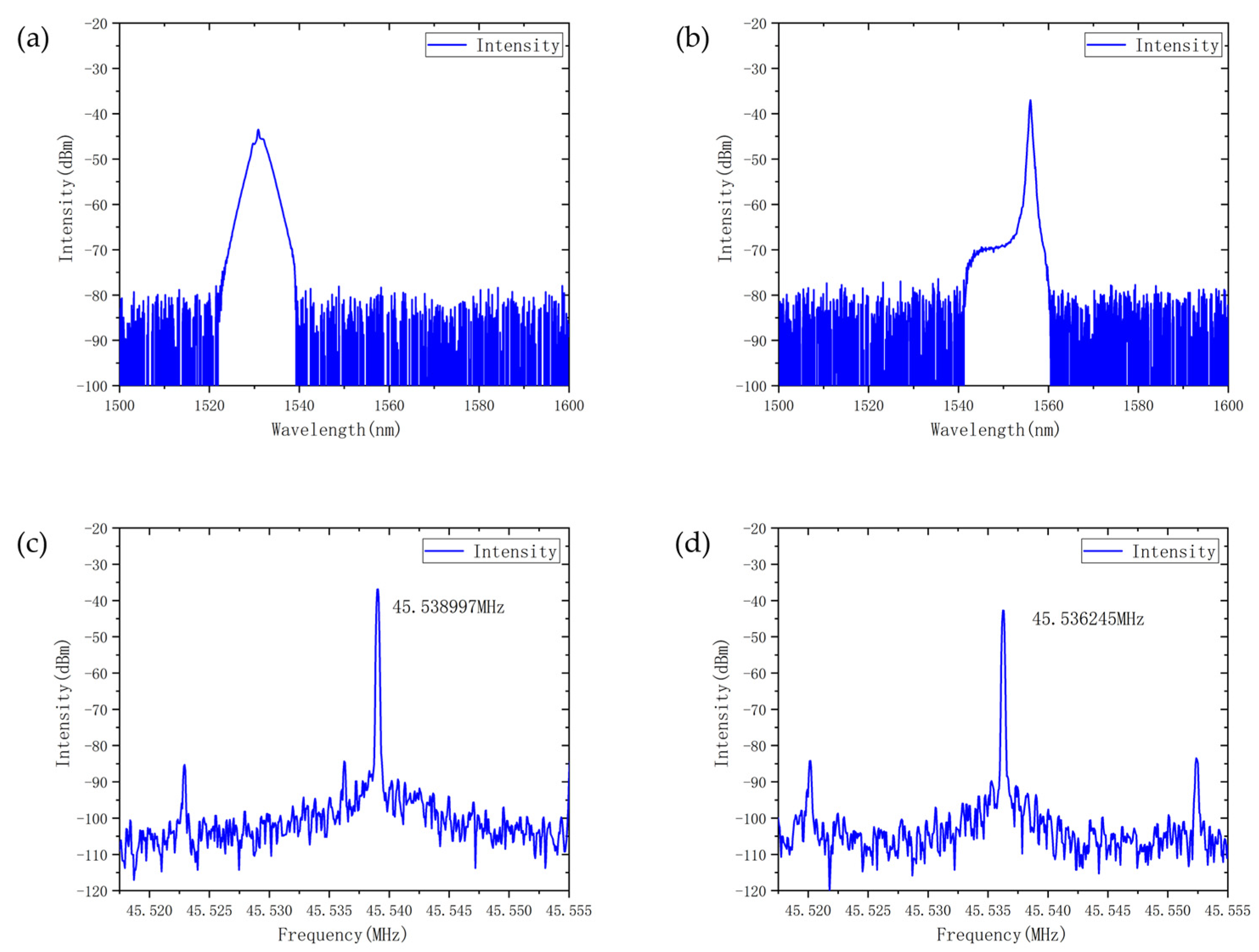
3.2. Dual-Wavelength Dual-Frequency Mode-Locking
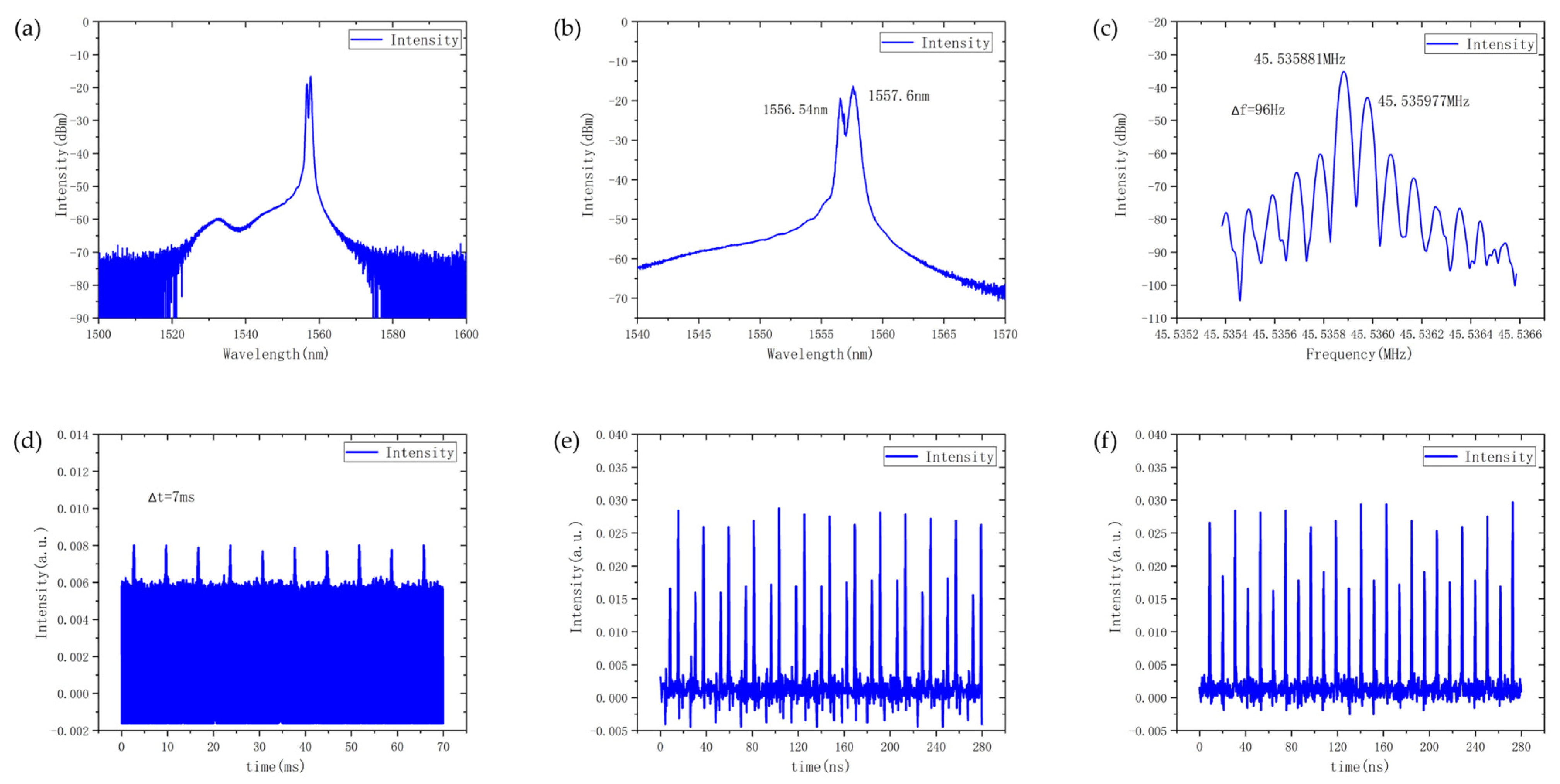
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, L.G.; Chu, P.L.; Liu, H.F. 1-GHz optical communication system using chaos in erbium-doped fiber lasers. IEEE Photonics Technol. Lett. 2000, 12, 269–271. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear fiber optics: Its history and recent progress. J. Opt. Soc. Am. B 2011, 28, A1–A10. [Google Scholar] [CrossRef]
- Liu, X.; Lagsgaard, J.; Turchinovich, D. Monolithic Highly Stable Yb-Doped Femtosecond Fiber Lasers for Applications in Practical Biophotonics. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 1439–1450. [Google Scholar] [CrossRef]
- Komarov, A.; Leblond, H.; Sanchez, F. Passive harmonic mode-locking in a fiber laser with nonlinear polarization rotation. Opt. Commun. 2006, 267, 162–169. [Google Scholar] [CrossRef]
- Li, R.; Shi, H.; Tian, H.; Li, Y.; Liu, B.; Song, Y.; Hu, M. All-polarization-maintaining dual-wavelength mode-locked fiber laser based on Sagnac loop filter. Opt. Express 2018, 26, 28302–28311. [Google Scholar] [CrossRef]
- Ning, X.; Guina, M.D.; Vainionpaa, A.M.; Lyytikainen, J.; Suomalainen, S.; Saarinen, M.J.; Okhotnikov, O.; Sajavaara, T.; Keinonen, J. Broadband semiconductor saturable absorber mirrors in the 1.55-/spl mu/m wavelength range for pulse generation in fiber lasers. IEEE J. Quantum Electron. 2002, 38, 369–374. [Google Scholar] [CrossRef]
- Dong, J.-L.; Xu, W.-C.; Luo, Z.-C.; Luo, A.-P.; Wang, H.-Y.; Cao, W.-J.; Wang, L.-Y. Tunable and switchable dual-wavelength passively mode-locked fiber ring laser with high-energy pulses at a sub-100 kHz repetition rate. Opt. Commun. 2011, 284, 5719–5722. [Google Scholar] [CrossRef]
- Sun, Z.; Hasan, T.; Torrisi, F.; Popa, D.; Privitera, G.; Wang, F.; Bonaccorso, F.; Basko, D.M.; Ferrari, A.C. Graphene Mode-Locked Ultrafast Laser. ACS Nano 2010, 4, 803–810. [Google Scholar] [CrossRef]
- Liu, X.; Han, D.; Sun, Z.; Zeng, C.; Lu, H.; Mao, D.; Cui, Y.; Wang, F. Versatile multi-wavelength ultrafast fiber laser mode-locked by carbon nanotubes. Sci. Rep. 2013, 3, 2718. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Hu, G.; Zhao, B.; Li, C.; Pan, Y.; Liu, Y.; Yasui, T.; Zheng, Z. Picometer-resolution dual-comb spectroscopy with a free-running fiber laser. Opt. Express 2016, 24, 21833–21845. [Google Scholar] [CrossRef]
- Jiang, T.; Yin, K.; Wang, C.; You, J.; Ouyang, H.; Miao, R.; Zhang, C.; Wei, K.; Li, H.; Chen, H.; et al. Ultrafast fiber lasers mode-locked by two-dimensional materials: Review and prospect. Photonics Res. 2020, 8, 78. [Google Scholar] [CrossRef]
- Zhao, X.; Zheng, Z.; Liu, L.; Wang, Q.; Chen, H.; Liu, J. Fast, long-scan-range pump-probe measurement based on asynchronous sampling using a dual-wavelength mode-locked fiber laser. Opt. Express 2012, 20, 25584–25589. [Google Scholar] [CrossRef]
- Oeri, M.; Peters, O.; Wolferstetter, M.; Holzwarth, R. Compact, high-speed sampling engine for pulsed femtosecond lasers. Proc. SPIE 2020, 11348, 18–26. [Google Scholar]
- Ghosh, S.; Eisenstein, G. Highly coherent hybrid dual-comb spectrometer. Opt. Express 2023, 31, 25093–25103. [Google Scholar] [CrossRef]
- Ideguchi, T.; Poisson, A.; Guelachvili, G.; Picqué, N.; Hänsch, T.W. Adaptive real-time dual-comb spectroscopy. Nat. Commun. 2014, 5, 3375. [Google Scholar] [CrossRef] [PubMed]
- Lv, C.; Meng, F.; Yan, Q.; Zhang, T.; Tian, Y.; Jia, Z.; Dong, W.; Qin, W.; Qin, G. Bidirectional mode-locked erbium-doped fiber laser based on an all-fiber gold nanofilm saturable absorber. Opt. Express 2024, 32, 1851–1863. [Google Scholar] [CrossRef]
- Zhao, X.; Li, T.; Liu, Y.; Li, Q.; Zheng, Z. Polarization-multiplexed, dual-comb all-fiber mode-locked laser. Photonics Res. 2018, 6, 853. [Google Scholar] [CrossRef]
- Jin, X.; Liu, R.; Zhou, J.; Li, Z.; Duan, Y.; Zhu, H. Simultaneous generation of wavelength multiplexing and polarization multiplexing from a wavelength-tunable ultrafast fiber laser. Opt. Fiber Technol. 2024, 84, 103719. [Google Scholar] [CrossRef]
- Huang, X.; Xiao, X. Harmonic mode-locking of asynchronous dual-wavelength pulses in mode-locked all-fiber lasers. Opt. Commun. 2020, 474, 126079. [Google Scholar] [CrossRef]
- Tao, J.; Fang, Y.; Song, Y.; Song, P.; Hou, L.; Lu, B.; Lin, Q.; Bai, J. Sideband-free tunable and switchable dual-wavelength mode-locked fiber laser based on the Lyot filter and spontaneous radiation peaks. Opt. Express 2022, 30, 17465–17475. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, M.; Hu, G.; Wu, Q.; Zheng, Z.; Hasan, T. Broad bandwidth dual-wavelength fiber laser simultaneously delivering stretched pulse and dissipative soliton. Opt. Express 2020, 28, 6937–6944. [Google Scholar] [CrossRef]
- Luo, X.; Tuan, T.H.; Saini, T.S.; Nguyen, H.P.T.; Suzuki, T.; Ohishi, Y. Switchable dual-wavelength mode-locked fiber laser using Saganc loop mirror. Opt. Commun. 2020, 463, 125457. [Google Scholar] [CrossRef]
- Tao, J.; Song, P.; Lv, C.; Hou, L.; Lu, B.; Bai, J. Generation of widely tunable single- and dual-wavelength in a figure-eight mode-locked fiber laser. Opt. Laser Technol. 2023, 160, 109107. [Google Scholar] [CrossRef]
- Zhao, K.; Jia, H.; Wang, P.; Guo, J.; Xiao, X.; Yang, C. Free-running dual-comb fiber laser mode-locked by nonlinear multimode interference. Opt. Lett. 2019, 44, 4323–4326. [Google Scholar] [CrossRef]
- Luo, X.; Tuan, T.H.; Saini, T.S.; Nguyen, H.P.T.; Suzuki, T.; Ohishi, Y. Tunable and switchable all-fiber dual-wavelength mode locked laser based on Lyot filtering effect. Opt. Express 2019, 27, 14635–14647. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.; Luo, Y.; Xiang, Y.; Shum, P.P.; Tang, X.; Liu, D.; Sun, Q. Coexistence of soliton singlets and molecules in a dual-wavelength mode-locked fiber laser. Opt. Commun. 2020, 457, 124700. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, T.; Ma, W.; Zhu, H.; Zhao, R. Switching and coexistence of stretched pulse and dissipative soliton in a hybrid mode-locked fiber laser. Opt. Commun. 2022, 522, 128649. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, H.; Quan, C.; Wu, Q.; Zhang, F.; Hou, L. Flexible Dual-Wavelength Mode-Locked Fiber Laser Using Spun Fiber Filter. J. Light. Technol. 2024, 42, 8875–8880. [Google Scholar] [CrossRef]
- Man, W.S.; Tam, H.Y.; Demokan, M.S.; Wai, P.K.A.; Tang, D.Y. Mechanism of intrinsic wavelength tuning and sideband asymmetry in a passively mode-locked soliton fiber ring laser. J. Opt. Soc. Am. B 2000, 17, 28–33. [Google Scholar] [CrossRef]
- Hu, G.; Liao, X.; Chen, X.; Li, H.; Chen, G.; Liu, Y.; Yan, P.; Liu, J.; Huang, H.; Li, H.; et al. Wavelength-switchable dual-wavelength pulse emission from a practical-filter-free all-fiber ring cavity. In Proceedings of the SPIE/COS Photonics Asia, Nantong, China, 12–14 October 2024; p. 132460S. [Google Scholar]

| Reference | Gain | Mode Locked Mechanism | λ (nm) | Δλ (nm) | f (MHz) | Δf (Hz) |
|---|---|---|---|---|---|---|
| [30] | EDF | SWCNT-SA+NPE | 1533.1, 1555.0 | 17.6–22 | ~28.29 | 1130–1370 |
| [23] | PM-EDF | NALM | 1558, 1581 | 23–25 | ~13.00 | 976–1164 |
| [18] | EDF | BPQDs-SA+TF | 1533.86, 1535.24 | 0.8–1.38 | ~23.3 | 188–200 |
| [28] | PM-EDF | CNT-SA+SPF | 1554, 1580 | 14.1–28.2 | ~19.7 | 507–1438 |
| [20] | PM-EDF | GO-COOH-SA | 1529, 1564 | 5–35 | ~34.82 | 444–2933 |
| This work | EDF | SWCNT-SA+NPR | 1530.9, 1557.6 | 1.02–26.7 | ~45.53 | 147~3059 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Yao, Q.; Zhang, X. A Wavelength-Multiplexed Dual-Frequency Mode-Locked Fiber Laser with Tunable Repetition Frequency Difference. Photonics 2025, 12, 1045. https://doi.org/10.3390/photonics12111045
Luo L, Yao Q, Zhang X. A Wavelength-Multiplexed Dual-Frequency Mode-Locked Fiber Laser with Tunable Repetition Frequency Difference. Photonics. 2025; 12(11):1045. https://doi.org/10.3390/photonics12111045
Chicago/Turabian StyleLuo, Lilin, Qianyu Yao, and Xinhai Zhang. 2025. "A Wavelength-Multiplexed Dual-Frequency Mode-Locked Fiber Laser with Tunable Repetition Frequency Difference" Photonics 12, no. 11: 1045. https://doi.org/10.3390/photonics12111045
APA StyleLuo, L., Yao, Q., & Zhang, X. (2025). A Wavelength-Multiplexed Dual-Frequency Mode-Locked Fiber Laser with Tunable Repetition Frequency Difference. Photonics, 12(11), 1045. https://doi.org/10.3390/photonics12111045




