Temperature-Controlled Cascaded Fabry–Pérot Filters: A Scalable Solution for Ultra-Low-Noise Stokes Photon Detection in Quantum Systems

Abstract

This study addresses the issue of cross-interference that occurs when locked continuous light and signal photons are collinear during interferometer measurements. To tackle this, a temperature-controlled Fabry–Pérot cavity filter with a heterogeneous cascaded structure is proposed and applied. The system consists of six filtering stages, created by designing Fabry–Pérot cavities of three different lengths, each used twice (to match optical frequencies), along with temperature control settings. By applying differentiated linewidth regulation, the approach effectively suppresses interference from locked light while significantly enhancing the signal-to-noise ratio in photon detection. This method overcomes the challenge of interference from same-frequency noise photons in atomic ensemble-entangled sources, achieving a noise–photon extinction ratio on the order of 10⁶ and surpassing the frequency resolution limit of a single filter. Experimental results demonstrate that the system reduces the noise floor in the detection optical path to below 10⁻¹⁶, while maintaining a photon transmission efficiency above 53% for the signal. This technology effectively addresses key challenges in noise suppression and photon state fidelity optimization in optical fiber quantum communication, offering a scalable frequency–photon noise filtering solution for long-distance quantum communication. Furthermore, its multi-parameter cooperative filtering mechanism holds broad potential applications in areas such as quantum storage and optical frequency combs.

1. Introduction

In experiments where lasers interact with quantum systems such as single atoms [1], atomic ensembles [2], ions [3], crystals [4,5], and single quantum dots [6] to generate signal photons, stray light interference has always been a key issue restricting experimental performance. This stray light mainly comes from locking lights, auxiliary lights, and read-write lights [7,8,9], with complex frequency distributions. Such interference directly reduces the signal-to-noise ratio as well as the purity and fidelity of the desired photons. Additionally, phase differences introduced by optical components during the process of creating entanglement between multiple quantum nodes further degrade the quality of the signal photons. These issues highlight the urgent need for advancements in efficient optical noise suppression, signal enhancement, and phase control techniques within the field of quantum information.

As a mainstream noise reduction solution, optical cavity filters have demonstrated significant potential in quantum systems. The design of optical cavity resonance with Stokes photons proposed by C. Simon [10] and the scheme by Lukas Heller’s team, which embeds atomic ensembles into low-finesse optical cavities [11], both achieve noise suppression through mode selection and linewidth narrowing. However, active locking schemes require the introduction of locking light with a significant frequency difference from the signal light, which not only increases the complexity of signal extraction but also further reduces system stability due to phase noise.

In recent years, tunable filtering technology has continuously evolved, providing diverse approaches for quantum noise suppression: single-cavity Fabry–Pérot filters achieve tuning through cavity length [1], refractive index [12], or angle [7] modulation—among these, piezoelectric-driven cavity length modulation can reach nanoscale precision [13], and refractive index modulation using liquid crystal materials offers advantages of low cost and miniaturization [2,14], yet the extinction ratio of single-stage structures is typically only on the order of 10⁻³ [1], which is insufficient to meet the ultra-low noise requirements of quantum systems; cascaded filtering schemes enhance performance through multi-cavity synergy, such as the homogeneous cascading design by C. Simon’s team [10] and the scheme by researchers from Shanxi University that uses 18 identical Fabry–Pérot filters to achieve an extinction ratio of 10⁻¹⁵ [15]; however, homogeneous cascading can only narrow the linewidth without expanding the free spectral range (FSR), and redundant components lead to increased insertion loss and higher system complexity [16]; heterogeneous cascading innovations break through the limitations of homogeneous cascading by combining cavities with different lengths—for instance, a three-stage Fabry–Pérot liquid crystal filter achieves 400 nm FSR expansion [14], and cascaded structures based on the Vernier effect expand the tuning range using FSR differences [17], but most existing designs are targeted at classical optical communications, leaving gaps in the specific suppression of quantum signals (e.g., an extinction ratio on the order of 10⁻¹⁶ at a frequency difference of 6.8 GHz) and the integration of passive locking.

Cascaded Fabry–Pérot configurations show significant promise for improving filter performance but are hindered by scalability challenges: for instance, four Na/Sb₂S₃/Na FP cavities have been utilized to achieve tunable near-infrared bands [18], while UV-glue-assisted cascaded Fabry–Pérot sensors have demonstrated improved accuracy in temperature and force measurement [19]. However, these approaches suffer from high complexity due to redundant components and increased insertion loss, making them unsuitable for quantum systems that require compact, low-loss integration. Fortunately, recent progress in materials and assembly techniques has established a strong foundation to overcome these issues and enhance filtering performance. Ultra-low expansion (ULE) materials effectively mitigate temperature-induced drift [20], amorphous silicon films—characterized by high refractive indices and favorable thermo-optic coefficients—optimize the design of cavity layer, and six-dimensional precision assembly combined with two-dimensional angle measurement technologies enable control of cavity mirror parallelism to the micro-radian level and cavity length precision at the nanoscale. These technological advances provide essential hardware support for the development of ultra-high extinction ratio filtering systems, offering a pathway to overcome the scalability challenges of cascaded FP designs in quantum-related applications.

Advances in materials and assembly techniques have established a basis for enhanced filtering performance: Ultra-low expansion (ULE) materials effectively minimize temperature-induced drift; amorphous silicon films with high refractive indices and thermo-optic coefficients improve the design of cavity layers; six-dimensional precision assembly combined with two-dimensional angle measurement technologies achieve micro-radian level parallelism of cavity mirrors and nanoscale accuracy in cavity length [13]. These developments provide the necessary hardware foundation for ultra-high extinction ratio filtering systems. However, current technologies still encounter three main challenges: First, the complex frequency distribution of stray light—which includes broad-spectrum noise such as locking and read-write light—makes it difficult for a single filtering method to simultaneously achieve a wide tuning range and high suppression ratio. Second, the extra optical paths introduced by active locking increase phase noise and enlarge the system size [11]. Third, achieving a balance between transmission efficiency and extinction ratio in cascaded systems remains difficult.

Notably, based on the findings from Stavrou [21] and Singh [22], quantum dot systems require stricter filter performance compared to traditional atomic ensembles. Single-cavity filters do not have sufficient extinction ratio/FSR to suppress broad-spectrum stray light or avoid signal-noise overlap; homogeneous cascades improve extinction ratio but not FSR, increasing insertion loss and exacerbating reflection-induced coherence loss. Thus, a novel cascaded filter with ultra-high extinction ratio, broad FSR, and high transmission efficiency is needed for quantum dot systems.

To overcome these challenges, this paper presents a passive-locking, temperature-controlled six-stage cascaded filtering approach: a heterogeneous cascaded structure is formed by double-passing three Fabry–Pérot cavities of varying lengths. Combining the stability of ULE materials and high-precision assembly technology, an extinction ratio on the order of 10⁻¹⁶ is achieved at a frequency difference of 6.8 GHz, while maintaining a 53% signal transmission efficiency. This scheme eliminates the need for additional locking light and resolves the core issues of stray light suppression and phase stability in quantum systems through the synergy of multiplicative noise suppression effect and spectral selectivity. Moreover, the filter integrates polarization pre-filtering to match quantum dot polarization requirements, suppresses stray light, and uses expanded FSR to avoid signal-noise overlap, supporting high-fidelity detection in quantum dot systems.

2. Theoretical Basis and Methods

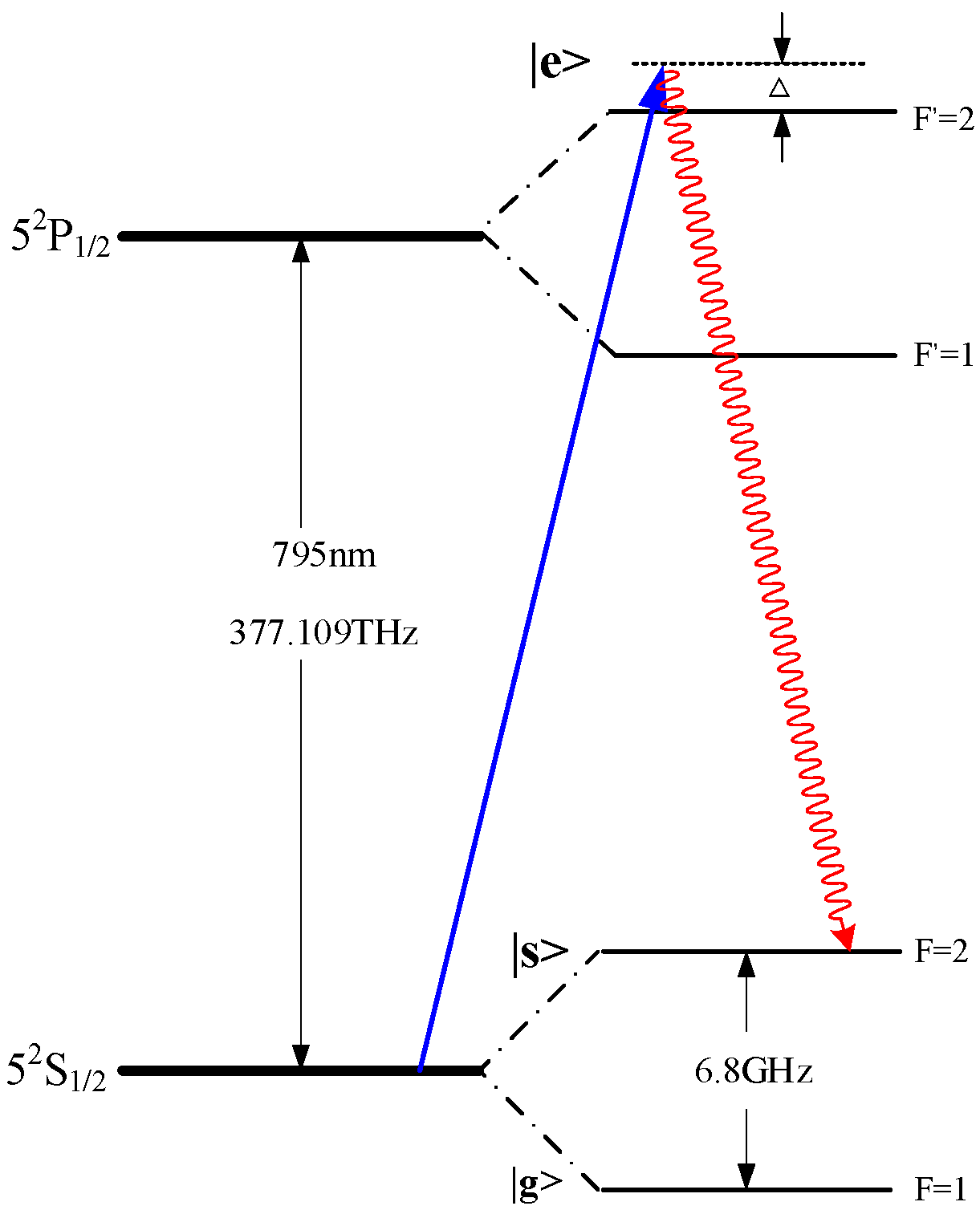
The atomic ensemble utilized in this study consists of a cloud of cold ⁸⁷Rb atoms, which serves as the medium for the generation of wave packet-tunable photons, and the relevant atomic levels are as shown in Figure 1, where $|g⟩=|5^2{S}_{1/2},F=1$, $|e⟩=|5^2{P}_{1/2},F^{\prime }=2⟩$, and $|s⟩=|5^2{S}_{1/2},F=2$. The ⁸⁷Rb atomic ensemble is prepared to be in the ground state $|g⟩$, at the initial time. The write laser beam is sourced from a DLC Pro laser (Toptica Photonics AG, Gräfelfing, Germany), which is stabilized on the saturation absorption line D1. Write pulses of varying durations are produced through the on–off timing control of the Acousto-Optic Modulator (AOM), managed by a Field-Programmable Gate Array (FPGA). The write laser beam is subsequently directed through the Polarizing Beam Splitter PBS that has been confided for V polarization, which is ∆ = 20 MHz blue-detuned to the $|g⟩\to |e⟩$ transition. The write pulse also induces the spontaneous Raman transition $|g⟩\to |s⟩$ via $|e⟩$, thereby generating the Stokes photons transition $|e⟩\to |s⟩$ and storing a spin wave simultaneously. Here, the laser frequency differs from the Stokes photon frequency by 6.8 GHz.

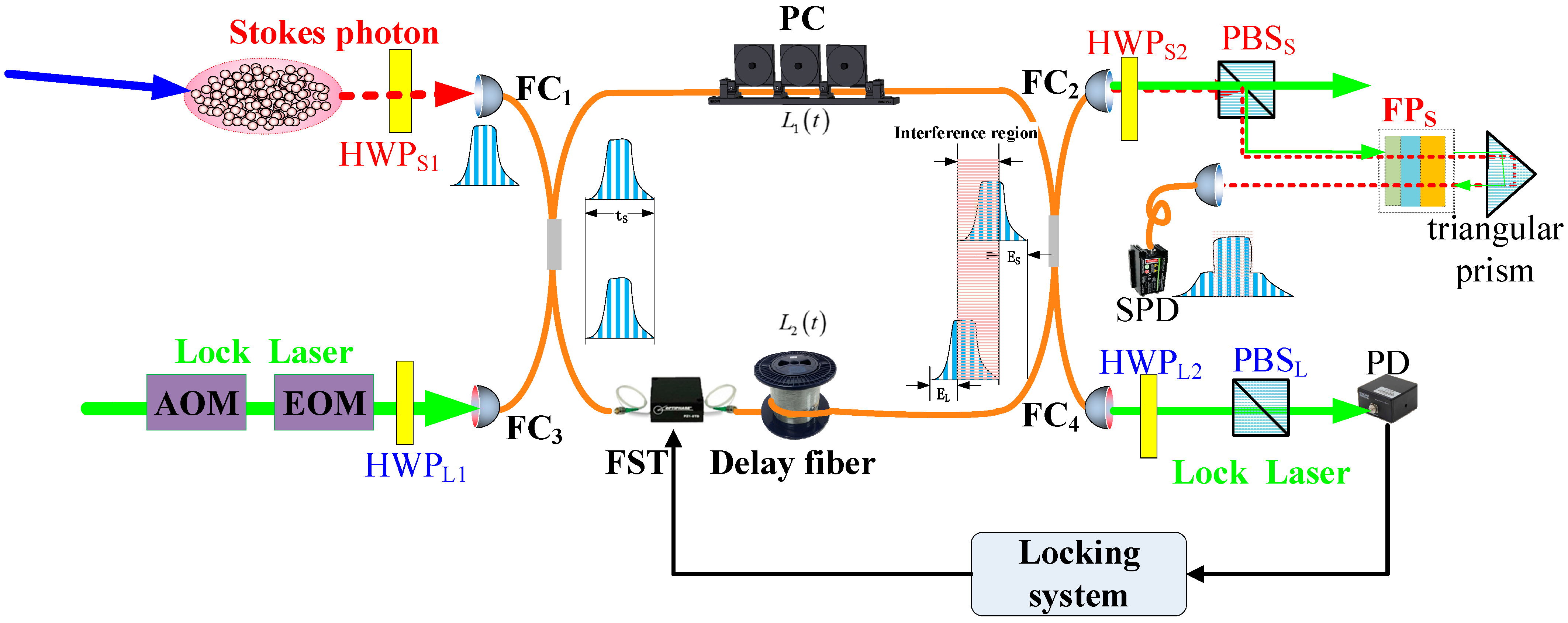
The Stokes photons generated create phase differences after traveling long distances through optical fibers. We then feed this phase difference signal into an interferometer to achieve phase locking. In quantum optics experiments, if the locking light and the signal light come from two separate lasers, their inherent differences in frequency stability and linewidth cause extra phase noise, which significantly reduces the accuracy of phase locking. To prevent this problem, this study uses the write light directly as the locking light, ensuring both the locking and signal lights come from the same source. This approach fundamentally removes the additional phase deviations caused by using two different light sources and establishes a basis for precise phase control. The detailed experimental setup is shown in Figure 2.

The lock laser output from FC₄ at the $\mathsf{\mu }\mathrm{W}$ level can be used for injection. PD achieves the locking of the optical path phase by entering the optical fiber stretcher through the locking system. The phase difference between the lock laser and the Stokes photons is adjusted by the electro-optic modulator EOM to achieve the measurement of the interference area photon number during the interference of constructive and destructive phases, thereby obtaining the interference contrast. Due to the use of two separate optical fibers, the FC₂ port will output the lock laser and Stokes photons. The width of the photon detection window is 100 ns, where 1 mW contains the number of photons $n=Pt/hv$, $P$ is the read light power, $t$ is the time of the write window, and $hv$ is the energy of a single photon. The calculation shows that the number of photons in 1 $\mathsf{\mu }\mathrm{W}$ of writing light within a 100 ns window is approximately 4 × 10⁵. To only detect the Stokes photons, the detection optical path uses PBS and FPs to suppress the lock laser and achieve efficient output of the signal photons. At FC₂, PBS polarization filtering can suppress the lock laser by one-thousandth level. Only the light at the $\mathrm{p}\mathrm{W}$ level will flow to the single-photon detection path. At this time, the cascaded temperature control filter system can achieve noise suppression at the 10⁻¹⁶ level. In addition, polarization filtering is used to perform further separation of the Stokes photons and the locking light with an extinction ratio of the order of 10⁻³, and PBS_S and HWP_S1 (HWP_S2) are used to ensure that the horizontally polarized Stokes photons are transmitted to the SPD in the horizontal direction. PBS_L and HWP_L1 (HWP_L2) are used to ensure that the vertically polarized locking light is directed to the oscilloscope in the vertical orientation.

Even lasers of identical models may demonstrate a phase discrepancy; consequently, we employ locking laser light that is sourced from the same write laser utilized for photon generation. According to the principles governing energy-level transitions, the frequency disparity between the Stokes photon and the locking laser is approximately 6.8 GHz. The signal laser beam is also derived from the write laser through an Acousto-Optic Modulator (AOM), which introduces a frequency shift of 6.8 GHz, as shown in Figure 1, allowing this beam to resonate with the Stokes photon at the same frequency. Thus, this beam can serve as an auxiliary light source to enhance photon transmission efficiency and to regulate the temperature control point of Fabry–Pérot cavities for the effective operation of the filters. To facilitate the separation of the Stokes photon (signal laser) and the locking light at the locations of FC₁ and FC₄, six-stage Fabry–Pérot (FP) filters are strategically positioned along the detection and locking paths, as shown in Figure 2. The FPs filter is utilized to isolate the locking light to extract the write light or the Stokes photon. The transfer function of the cascade filters $T$ can be articulated as follows:

$$T={\displaystyle \prod _{i=1}^n{T}_i},$$

(1)

$$T_i={\displaystyle \frac{1}{1+\frac{4R}{{\left(1-R\right)}^2}{\sin }^2\frac{\delta }{2}}},$$

(2)

where $T_i$ denotes the transfer function of the i th Fabry-Pérot (FP) filter cavity. $\delta =4\pi fnL/c$ is the phase difference caused by the optical path difference of two adjacent light beams, the frequency of the incident laser $f$ and the length of the etalon satisfy L. The standing wave condition $f=kc/2nL(k=0,1,2\dots )$, where $n$ represents the refractive index in the medium, and $L$ represents the thickness of the standard piece.

Based on the quantitative relationship between the resonant frequency and cavity length of a Fabry–Pérot (FP) cavity as described in Equation (1), precise control of the cavity length is required to achieve efficient transmission of light at the central frequency through the FP cavity. In this experiment, the TEC temperature controller (with a temperature stability of ≤0.002 °C) was used to drive a Peltier element, enabling temperature regulation of the ULE glass cavity. It should be noted that in practical operation, the transmittance of light at the central frequency cannot reach the ideal maximum efficiency of 100% due to optical losses such as cavity mirror reflection loss and medium absorption.

When the temperature changes by $∆T$, the length of the material changes to:

$$∆L=\alpha L\Delta T,$$

(3)

where $\alpha$ is the linear coefficient of thermal expansion, $∆T$ represents temperature difference, thus the offset of the corresponding frequency can be expressed as follows:

$$∆f\approx \nu \alpha \Delta T,$$

(4)

Due to the precision constraints of the temperature control system, the experiment restricts the transmittance of six-stage Fabry–Pérot cascade filters to 53%, and the extinction ratio of the cascaded Fabry–Pérot filters is of the order of 10⁻¹⁶, which significantly surpasses that of a single filter, which is approximately 10⁻³.

The frequency difference range corresponding to two half-maximum transmission points is defined as the transmission bandwidth (FWHM):

$$FWHM\approx {\displaystyle \frac{c}{2\pi nL}}{\displaystyle \frac{1-R}{\sqrt{R}}},$$

(5)

The frequency interval between adjacent transmission peaks is defined as the free spectral range (FSR):

$$FSR\approx {\displaystyle \frac{c}{2nL}},$$

(6)

The Full width at half maximum (FWHM) decreases as the length of the Fabry–Pérot cavity increases, and the spacing in the Free Spectral Range (FSR) also increases. The filter is an ultra-low expansion (ULE) material, the reflectivity $R$ is 0.9, with three cavity lengths of $L=5.4 \mathrm{mm},7.5 \mathrm{mm} \mathrm{and} 21 \mathrm{mm}$, and the refractive index $n$ is 1.5; thus, the fineness (FSR/FWHM) of the Fabry–Pérot filter resonator is 30.

The core reason for selecting ULE glass (ultra-low expansion titania-silicate glass) lies in its unique compositional design—through the combination of a titania and silicate system, this material exhibits excellent ultra-low thermal expansion properties: under extreme temperature fluctuation conditions, its linear expansion coefficient is extremely low (typically reaching the order of $\alpha \simeq {10}^{-8}/°\mathrm{C}$), resulting in minimal and highly controllable changes in cavity dimensions. Relying on this characteristic and combining it with the high-precision regulation capability of the TEC temperature controller, precise temperature control of the ULE glass-based FP filter can effectively suppress fluctuations in the physical length of the cavity caused by temperature drift, thereby achieving long-term stability of the cavity length.

According to the Fabry–Pérot resonance principle, the resonant frequency (including the central resonant frequency) and cut-off frequency band of the filter are directly determined by its cavity length (or optical length). Therefore, through precise control of the temperature-dimension correlation characteristics of the ULE glass-based filter via the temperature control system, high-stability dynamic manipulation of the filter’s transmission frequency (with a focus on the central resonant frequency) and cut-off frequency band can be further achieved. Ultimately, this provides critical frequency stability support for precision optical filtering scenarios such as quantum communication and high-resolution spectral analysis.

3. Results

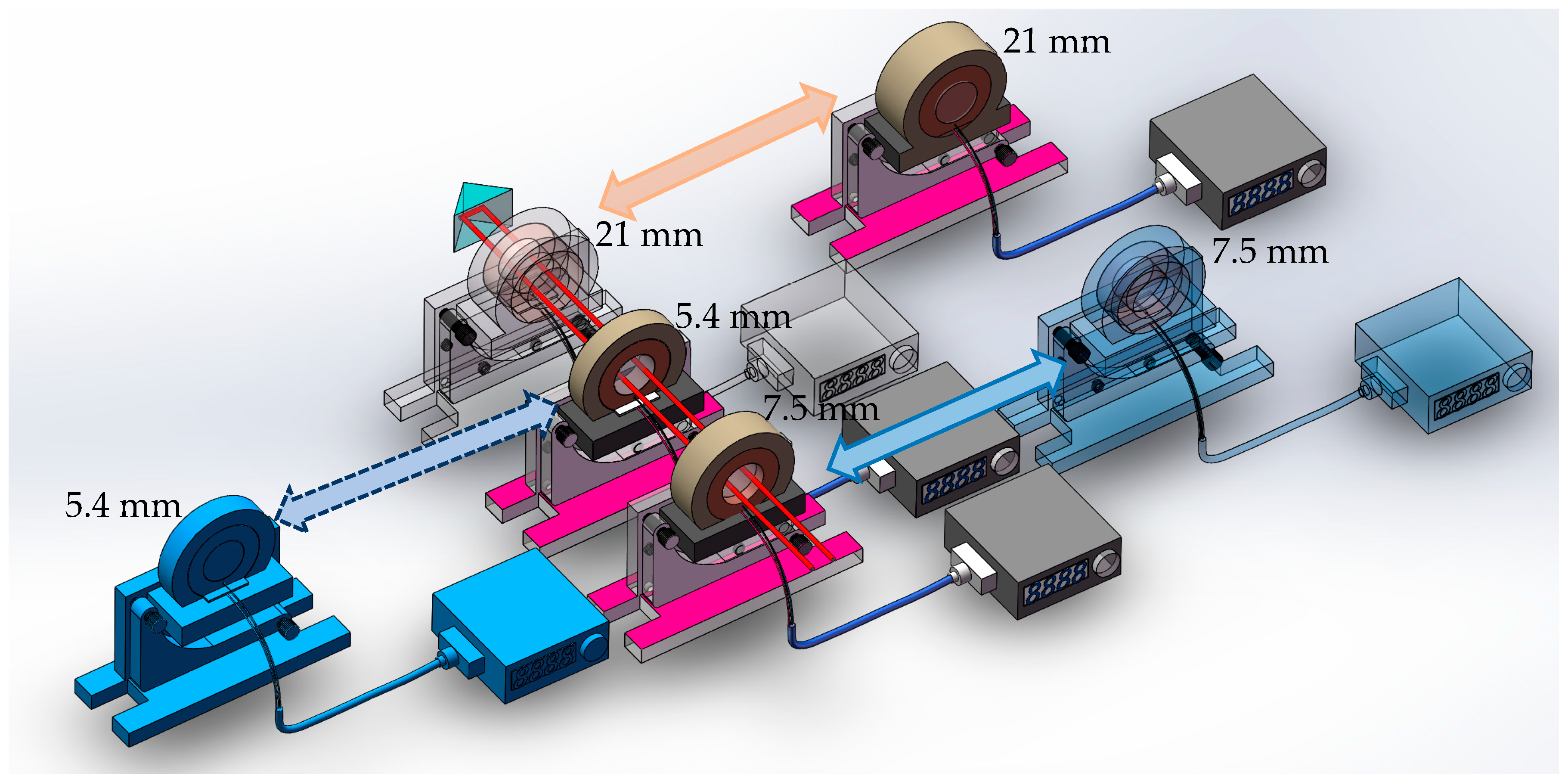
High-precision clamps are used for each Fabry–Pérot cavity, preventing cavity length deviations that could distort resonant frequencies. Figure 3 shows a device equipped with thermistors and a temperature controller, detailing the features of FPs presented in Figure 2. The thermistors collect temperature information in real time and feed it back to the temperature controller. The temperature controller then controls the Peltier elements in the cascaded filtering device to achieve temperature control. Combined with the ultra-low linear thermal expansion coefficient of ULE glass material, under constant temperature conditions, this precise temperature control can maintain the stable and efficient output of the standard device length for specific frequency bands. The stability of the cavity length is crucial for the resonance characteristics of the Fabry–Pérot cavity. Only when the cavity length is stable can light of a specific frequency pass efficiently, while light of other frequency bands is effectively suppressed, thus achieving precise filtering. This is a stable performance that is difficult to achieve with single-stage filtering. The device adopts a structure in which multiple Fabry–Pérot cavities with different cavity lengths (such as 21 mm, 5.4 mm, and 7.5 mm) are cascaded. The Fabry–Pérot cavities with different cavity lengths have different resonance characteristics. Through cascading, they can work synergistically to perform more refined screening of light of different frequencies. Compared with single-stage filtering, this multi-stage structure can provide more complex and comprehensive filtering functions and achieve effective suppression of noise of multiple frequencies.

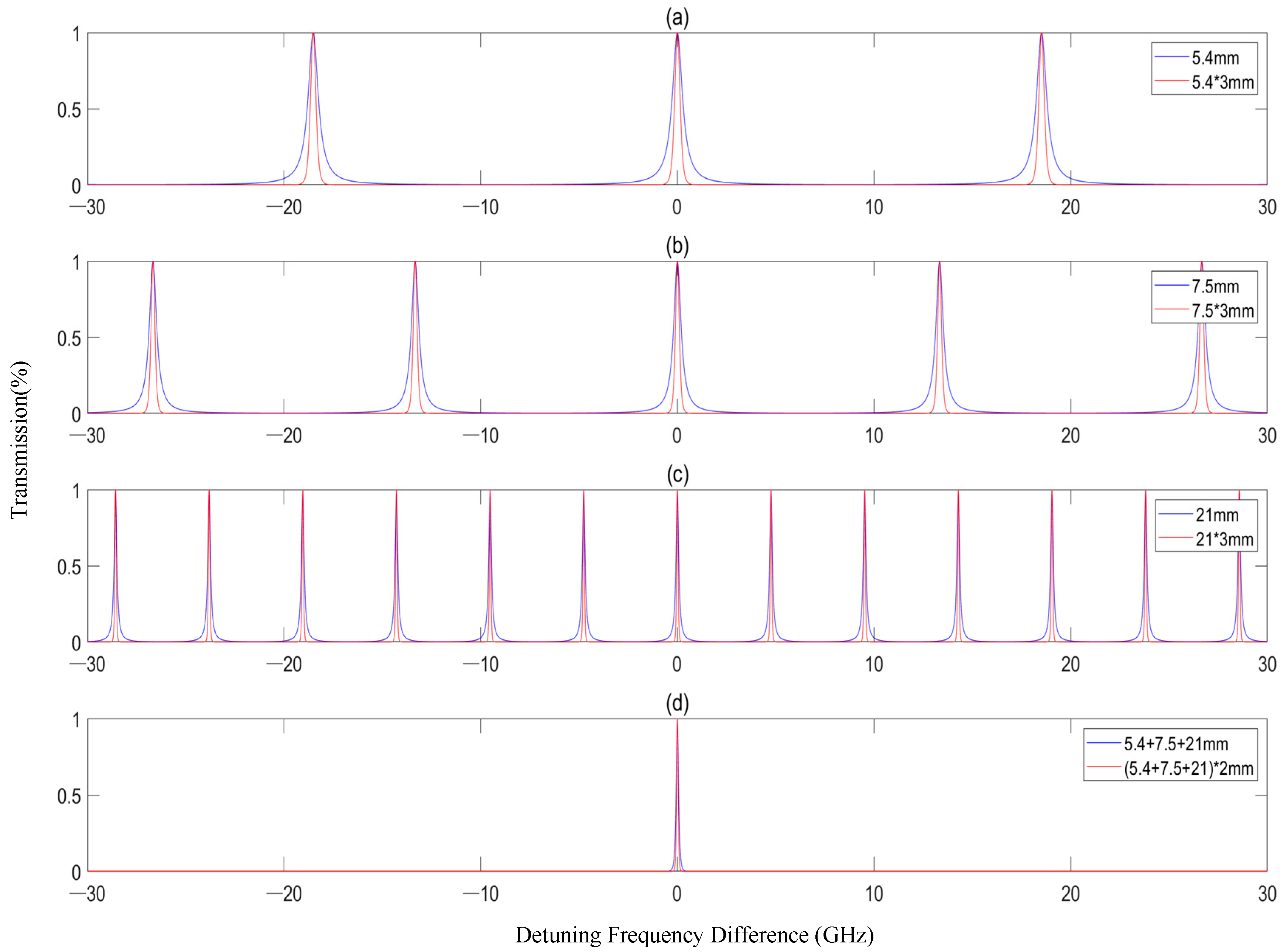
In Figure 4a–c, there are obvious differences in the number and spacing of transmission peaks as the cavity length changes. For example, when the cavity length is 5.4 mm, the spectral lines show a distribution of a few peaks with relatively wide spacing; when the cavity length is 21 mm, the number of peaks increases and the spacing becomes narrower. This reflects the direct influence of the cavity length on the resonance characteristics (transmission peak distribution) of the filter, which is consistent with the fact that the cavity length of the filter determines the resonance mode. Compared with a single cavity length, the number and distribution of transmission spectral peaks change further, reflecting the regulation of the filtering characteristics by the combination of multiple cavity lengths. It verifies that through the design of the cavity length, the transmission spectral lines of the filter can be customized to meet the specific filtering requirements in the experimental environment of this paper. Cavities with varying lengths (5.4 mm, 7.5 mm, 21 mm) possess unique resonance behaviors: their differing free spectral ranges (FSR) and transmission peak distributions enable synergistic filtering when cascaded, which is the key to expanding FSR (to 1475 MHz) while narrowing linewidth (to 50 MHz), as shown in Figure 4d. In contrast, cascading identical cavities only narrowed the FWHM without expanding FSR (Figure 4a–c), limiting their ability to avoid noise overlap with signal frequencies. Despite ultrahigh noise suppression, the six-stage filter maintained a signal photon transmission efficiency of 53% (constrained by temperature control precision), ensuring that over half of the Stokes photons were retained for detection. This balance between noise reduction and signal preservation is critical for quantum applications, where photon loss directly degrades entanglement fidelity.

The six-stage cascaded filtering system, constructed by double-passing three Fabry-Pérot cavities of distinct lengths (5.4 mm, 7.5 mm, 21.0 mm), exhibited exceptional noise suppression and spectral selectivity. Key performance parameters are summarized in

Table 1. FWHM (FSR) and extinction ratio (6.8 GHz) with different cavity lengths.

Cavity Length (mm)	FWHM (MHz)	FSR (MHz) (Peak Spacing)	Extinction Ratio (6.8 GHz)	Corresponding to Figure 4
5.4	622	18,519	3.27 × 10−3	Blue line in Figure 4a
7.5	448	13,333	2.74 × 10−3	Blue line in Figure 4b
21.0	160	4762	2.86 × 10−3	Blue line in Figure 4c
5.4 × 3	207	6173	3.49 × 10−8	Red line in Figure 4a
7.5 × 3	149	4444	2.05 × 10−8	Red line in Figure 4b
21 × 3	81	4762	2.39 × 10−8	Red line in Figure 4c
5.4 + 7.5 + 21	99	2950	2.56 × 10−8	Bule line in Figure 4d
(5.4 + 7.5 + 21) × 2	50	1475	6.57 × 10−16	Red line in Figure 4d

. At a frequency difference of 6.8 GHz (matching the offset between Stokes photons and lock laser), the six-stage combinations [(5.4 + 7.5 + 21) × 2 mm] achieved an extinction ratio of 6.57 × 10⁻¹⁶. This value is five orders of magnitude better than that of three-stage combinations (e.g., 5.4 + 7.5 + 21 mm, 2.56 × 10⁻⁸) and nine orders of magnitude superior to that of single-stage filters (e.g., 5.4 mm, 3.27 × 10⁻³). This finding confirms that multi-stage cascading of diverse cavity lengths enables cumulative noise suppression, far exceeding the capabilities of single or homogeneous cascades. The full-width at half-maximum (FWHM) of the six-stage filter was 50 MHz, which is significantly narrower than that of single-stage (160–622 MHz) or three-stage (81–207 MHz) combinations.

When filters of the same length are cascaded, they can only narrow the line width but cannot change the spacing of the transmitted spectral lines shown in Figure 4a–c. By using filters of different lengths cascaded, the free spectral region can be expanded while narrowing the line width shown in Figure 4d.

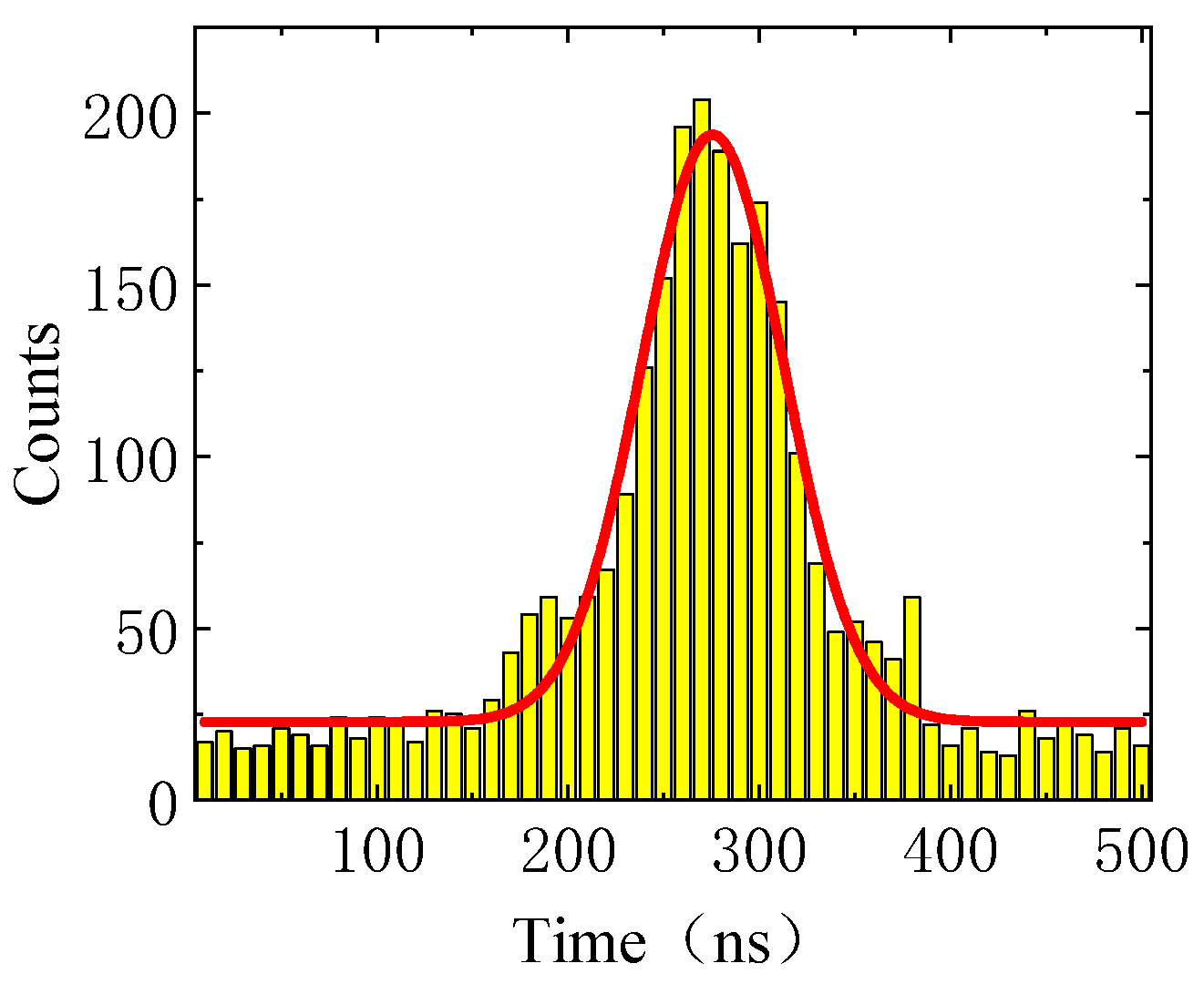
The signal output from FC₂ comprises signal photons and locking light. Following polarization filtering and cascaded filtering, the photon distribution detected by the single-photon detector (SPD) is presented in Figure 5. A concentrated distribution of signal photons is observable within the 200–400 ns acquisition window, while regions outside this window are dominated by noise. Through cascaded filtering, the locking light with a frequency difference of 6.8 GHz is efficiently suppressed, providing a guarantee for the effective measurement of photon interference signals.

4. Discussion

This research focuses on the significant problem of cross-interference between locked continuous light and signal photons in interferometric measurements. It tackles this issue using a six-stage cascaded Fabry–Pérot filtering system with temperature control. The key innovation is a double-pass setup involving three Fabry–Pérot cavities of different lengths (5.4 mm, 7.5 mm, and 21.0 mm). This heterogeneous design overcomes the constraints of conventional uniform cascades and single-cavity filters, enabling an effective balance between noise reduction and signal transmission efficiency.

4.1. Mechanisms of Superior Performance

The system’s exceptional performance originates from two interconnected key mechanisms. First, the multiplicative noise suppression effect of heterogeneous cascades: each stage of the Fabry–Pérot cavity independently contributes to noise reduction, and the total extinction ratio approximates the product of the extinction ratios of individual stages. This leads to an ultrahigh extinction ratio of 6.57 × 10⁻¹⁶ at a 6.8 GHz frequency difference (matching the offset between Stokes photons and lock laser)—far outperforming single-stage filters (10⁻³) and homogeneous cascades (10⁻⁸), and effectively resolving the bottleneck of same-frequency noise photon interference in atomic ensemble-entangled sources. Second, the expanded spectral selectivity enabled by heterogeneous cavity lengths: combining cavities of different lengths narrows the full-width at half-maximum (FWHM) to 50 MHz while expanding the free spectral range (FSR) to 1475 MHz. This avoids spectral overlap between signal and noise—a critical limitation of homogeneous cascades, which only narrow linewidth without adjusting FSR and thus risk noise–signal crosstalk in complex quantum environments.

4.2. Experimental Workflow and Technical Advantages

The system’s noise reduction workflow is designed for both efficiency and reliability. First, the cold ⁸⁷Rb atomic ensemble, driven by a Toptica DLC Pro laser (blue-detuned by 20 MHz and polarized via PBS), stably generates tunable Stokes photon wave packets while storing spin waves, ensuring a high-quality initial signal. Second, polarization pre-filtering at the FC₂ port suppresses the co-propagating lock laser by three orders of magnitude (to the pW level), reducing the dynamic range required for subsequent cascaded filtering and preventing Fabry–Pérot system saturation—an essential prerequisite for achieving ultrahigh noise rejection.

When performing a comparative analysis with existing methods in prior research—such as an 18-stage identical Fabry–Pérot filter system achieving a 10⁻¹⁵ extinction ratio—our design delivers superior noise suppression (extinction ratio down to 6.57 × 10⁻¹⁶) while using fewer components, which significantly reduces system complexity and insertion loss. Beyond this, our passive locking scheme—leveraging a common write laser for both photon generation and locking—eliminates the need for external locking light with large frequency offsets, simplifying integration and improving phase coherence. This directly addresses a major flaw of active locking schemes (increased phase noise and system volume) highlighted in the introduction, further enhancing practicality for quantum applications. In addition to these advantages, our comprehensive comparative analysis with other existing techniques in the literature underscores three key strengths of our approach: higher measurement precision enabled by heterogeneous cavity length combinations, a simplified experimental setup (e.g., single-laser configuration vs. multi-laser systems), and enhanced stability via phase-locking technology. We also objectively acknowledge current limitations, including fiber length constraints that amplify phase noise and potential laser frequency drift, and propose targeted improvements—such as integrating ultra-low expansion materials to mitigate drift and optimizing fiber routing to reduce length-related noise—to address these challenges.

4.3. Adaptability and Practical Value

Our proposed cascaded filtering system, underpinned by a multi-parameter cooperative mechanism—integrating polarization pre-filtering, heterogeneous Fabry–Pérot cascading, and precise temperature control (via ultra-low expansion (ULE) materials, thermistors, and Peltier elements)—boasts broad adaptability. By tuning cavity lengths or temperature setpoints, it can target diverse frequency offsets, making it applicable to quantum systems beyond atomic ensembles (e.g., quantum dots, ion traps) with varying spectral characteristics. Notably, it maintains a signal photon transmission efficiency above 53% (currently constrained by temperature control precision), striking a critical balance between ultrahigh noise suppression and practical photon collection—an essential requirement for quantum communication, where photon loss directly degrades entanglement fidelity and link performance.

This design also carries substantial practical and industrial value: in quantum communication, it improves the fidelity of quantum state transmission by optimizing the filter’s transmission spectrum; in quantum information processing, it provides stable frequency references for quantum bits. Moreover, its simplified experimental setup facilitates integration into compact optical devices, laying the groundwork for industrialization. For follow-up research, we plan to verify the cascaded cavity structure’s performance in a cryogenic environment to further enhance stability and explore its application in multi-channel optical filtering—efforts aimed at expanding the system’s extensibility.

4.4. Limitations and Future Directions

The current design faces key limitations: the trade-off between transmission efficiency (max. 53%) and extinction ratio is constrained by thermoelectric control precision, and its applicability to higher frequency offsets is limited by cavity free spectral range (FSR).

Future advancements could address these: sub-millikelvin thermoelectric stability would improve both efficiency and extinction ratio; broader FSR cavities would expand use in frequency comb research and quantum spectroscopy. These improvements, combined with ultra-stable lasers and enhanced noise suppression, would extend coherence times—critical for high-fidelity quantum communication and information processing—strengthening the design’s utility in quantum technologies.

5. Conclusions

This study successfully develops and validates a six-stage heterogeneous cascaded structure temperature-controlled Fabry–Pérot filtering system, delivering key contributions to quantum photon noise suppression and practical quantum communication:

• Advanced noise suppression performance: With a frequency difference of 6.8 GHz, the system attains an extinction ratio of 6.57 × 10⁻¹⁶ and reduces the detection noise floor to below the 10⁻¹⁶ level. This outperforms current simplified filtering methods and overcomes the persistent challenge of same-frequency noise photon interference in atomic ensemble-entangled sources, fulfilling the stringent ultra-low noise requirements for quantum photon detection.
• Balanced signal preservation: Despite extreme noise suppression, the system maintains a signal photon transmission efficiency above 53%, ensuring sufficient photon collection for high-fidelity quantum operations (e.g., long-distance entanglement distribution). This balance addresses a core challenge in quantum filtering—avoiding excessive photon loss while suppressing noise.
• Practical and scalable technical design: The passive locking scheme eliminates external locking light, reducing complexity and improving phase coherence; ultra-low expansion (ULE) materials for Fabry–Pérot cavities, combined with real-time temperature feedback, ensure long-term cavity length stability and reliable resonance with target Stokes photons. The multi-parameter cooperative mechanism also enables adaptation to diverse quantum systems, supporting applications in quantum storage, optical frequency combs, and hybrid quantum networks.

In conclusion, this technology provides a robust, scalable solution for frequency-domain noise suppression in quantum communication, overcoming core issues of noise interference and photon state fidelity optimization. It lays a critical foundation for the development of high-fidelity long-distance quantum technologies, with broad implications for advancing quantum information science and engineering.