High-Performance 3D Point Cloud Image Distortion Calibration Filter Based on Decision Tree

Abstract

Structured Light LiDAR is susceptible to lens scattering and temperature fluctuations, resulting in some level of distortion in the captured point cloud image. To address this problem, this paper proposes a high-performance 3D point cloud Least Mean Square filter based on Decision Tree, which is called the D−LMS filter for short. The D−LMS filter is an adaptive filtering compensation algorithm based on decision tree, which can effectively distinguish the signal region from the distorted region, thus optimizing the distortion of the point cloud image and improving the accuracy of the point cloud image. The experimental results clearly demonstrate that our proposed D−LMS filtering algorithm significantly improves accuracy by optimizing distorted areas. Compared with the 3D point cloud least mean square filter based on SVM, the accuracy of the proposed D−LMS filtering algorithm is improved from 86.17% to 92.38%, the training time is reduced by 1317 times and the testing time is reduced by 1208 times.

1. Introduction

Structural Light LiDAR faces multiple challenges when capturing point cloud images, with lens scattering and temperature variations standing out prominently among the adverse factors. These factors often result in imperfect data acquisition by the LiDAR system [1,2,3].

Specifically, lens scattering causes the laser beam to scatter during the transmission process, which will affect the accuracy results of structural light lidar in measuring the distance and position of the target object. In addition, temperature variations can cause fluctuations in the performance of internal optical components of structural light lidar, further affecting the stability of data collection. The combination of these factors leads to significant distortion in the final point cloud image, particularly around the edges. This distortion not only reduces the accuracy and reliability of the image, but also poses considerable challenges for subsequent data analysis and processing [4,5]. In addition, limited statistical frame data and atmospheric sheltering can also lead to significant backscattering, which substantially limits the depth imaging capability of LiDAR systems in strong scattering environments [6,7,8,9,10]. Therefore, effectively addressing these challenges is crucial for improving the performance of structured light lidar.

To address these challenges, researchers have designed various point cloud distortion correction methods. In the process of calibrating the data collected by Kinect sensor [11,12,13,14,15], Kourosh Khoshelham established a mathematical model of depth measurement, and analyzed the systematic error and random error [16]. However, traditional error models assume a homogeneous noise distribution, whereas the noise in structured-light LiDAR follows a Poisson-Gaussian hybrid model with spatially varying parameters [17,18,19], thereby invalidating classical calibration approaches in edge regions. As the distance between the target and the sensor increases, the measurement error will also increase. Among them, the correction of systematic error is the prerequisite for aligning depth data and color data, while random error is crucial in further processing depth data [20]. In order to reduce the negative impact of image distortion, Hong-Xiang Chen proposed a distortion-tolerant omnidirectional depth estimation algorithm using a dual-cubemap [21]. By introducing a distortion-aware module and a plug-and-play spherical perception weight matrix, the algorithm addresses the issue of uneven distribution of regions projected from a sphere, helping to reduce the supervision deviation caused by distortion. In solving geometric distortion problems such as rotation, scaling, and translation, Navnath S. Narawade proposed a method for correcting geometric distortion in images based on pixel and size [22]. This method effectively enhances the ability to correct geometric distortion by combining spy pixel technology and size geometric distortion correction module. In the scanning process of precision instruments, hysteresis and thermal drift can cause the actual position of the scanning points to deviate from the expected position, thereby significantly affecting imaging results [23,24]. To address this issue, Yinan Wu designed a hysteresis compensation algorithm based on B-spline curve fitting to correct the distortion region. In addition, the team proposed a novel off-line drift correction algorithm based on cross diagonal scanning to rectify the captured distorted images [24].

When depth images are compressed, severe boundary distortion may occur. Linear filtering can result in excessive smoothing of the edges in depth images, while non-linear filtering can preserve edge features through non-linear operations. For example, De Silva proposed a bilateral filter with adaptive filtering parameters, which can preserve the edge features by non-linear combination of adjacent pixel values through spatial distance and pixel similarity [25,26]. Additionally, Shujie Liu proposed a trilateral filtering method, which takes into account the spatial correlation and luminance similarity of the depth image and the color image [27]. Furthermore, Kwan-Jung Oh put forward a depth boundary reconstruction filter, which can be used as an in-loop filter for depth video coding [28]. Xuyuan Xu presented a low-complexity adaptive deep truncation filter that can significantly reduce compression artifacts in depth images [29]. However, a drawback of this method is the distortion and deformation it may cause in certain uneven regions, such as slope distortion and surface deformation. Considering that the previous work only utilizing spatial correlation and statistic property of local windows [30], Lijun Zhao proposed a global approach to address the problem of generating high-resolution range images by Markov Random Field (MRF) model, which can be used to eliminate artifacts in discontinuous regions of distorted depth images [31].

The above distortion calibration algorithms are overly complex, and the majority of them focus on two-dimensional image distortion calibration. To overcome these challenges, this paper proposes a high-performance 3D point cloud least mean square filter based on decision tree, which is called D−LMS filter for short. Firstly, the decision tree model can be used to extract features from the point cloud image, complete the segmentation of signal region and distortion region, and detect the positions of all points in the distortion region. Secondly, the adaptive least mean square filter is implemented to correct the points in the distorted region, thereby optimizing the distortion of the point cloud image and enhancing its accuracy.

To sum up, the D−LMS filter combines the classification and prediction ability of decision tree and the optimization performance of the adaptive least mean square filter, which makes it more accurate and robust when dealing with complex non-linear signals. In addition, the D−LMS filter has strong adaptive capabilities, and can automatically adjust the filtering parameters according to the changes in signals, resulting in even better filtering performance.

The rest of this paper is organized as follows: Section 2 lays out the principle of the proposed high-performance 3D point cloud Least Mean Square filter based on Decision Tree. Section 3 analyzes the training time and testing time of the D−LMS filtering model. Section 4 describes the performance of point cloud image distortion calibration in the experiment. Finally, conclusions are drawn.

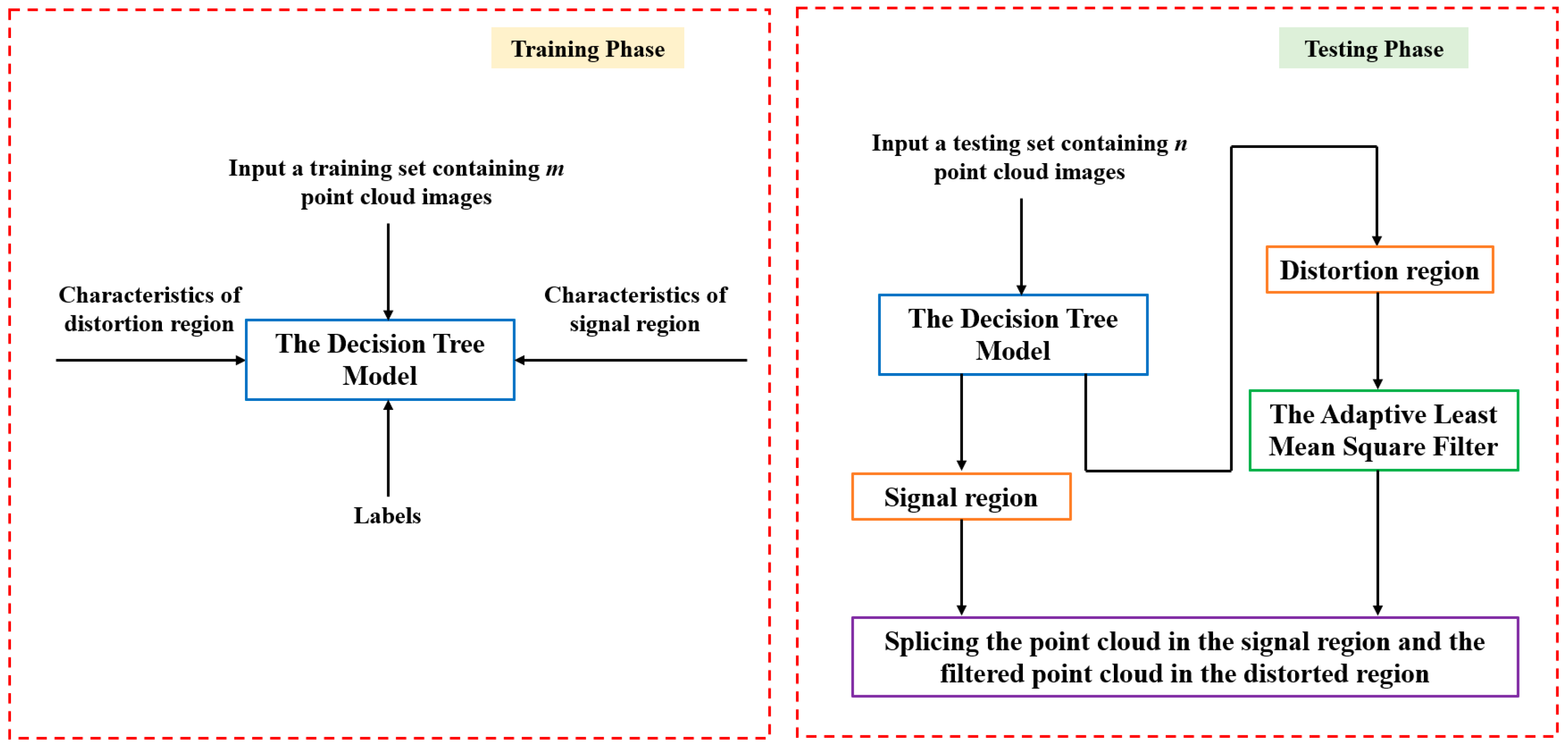
2. High-Performance 3D Point Cloud Least Mean Square Filter Based on Decision Tree

The logic of the proposed high-performance 3D point cloud least mean square filter based on decision tree is outlined in Figure 1, which encompasses two primary phases: the training phase and the testing phase.

In the training phase, the proposed D−LMS algorithm utilizes a decision tree model to learn and identify the distorted regions in 3D point cloud images. The ultimate goal of this learning process is to divide the point cloud image into signal region and distortion region, so as to extract the corresponding point data. In the testing phase, an adaptive least mean squares (LMS) filter is used to refine the points within the distorted region. This process aims to reduce distortion present in the point cloud image, thereby significantly enhancing its overall accuracy and fidelity.

2.1. Training Phase

In the training phase, this article introduces a decision tree model to complete the training process of point cloud data. The decision tree is a supervised learning algorithm used for classification and regression tasks. It makes decisions based on a tree structure and has a very fast classification speed [32].

The algorithm primarily consists of three key steps: feature selection, where important variables are identified; decision tree generation, where the structure of tree is constructed based on these variables; and decision tree pruning, where the tree is optimized for better performance and simpler interpretation. These steps work together to create a powerful tool that can help solve complex problems in various fields. In our background, it is used to classify points in 3D point cloud into signal regions or distorted regions.

Assuming that the training dataset contains $m$ point cloud images, with each image having $p$ points, the training dataset $D$ can be represented as

$$\mathit{D}=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_M,y_M\right)\right\}$$

(1)

where $x_i$ (i = 1, 2…, M) is a column vector containing three-dimensional coordinates and intensity values, $y_i$ is the corresponding signal label or distortion label, and $M=mp$ is the number of points included in the training dataset $\mathit{D}$.

The attribute set $\mathit{A}$ defined in this paper includes the following five core features:

(1)

Point Density: $\rho \left(p_i\right)={\displaystyle \frac{N}{\pi r^2}}$. It reflects the richness of data in local regions, where distorted areas typically exhibit abnormal density due to sensor errors.

(2)

The normal vector: $\theta \left(p_i\right)={\displaystyle \frac{1}{N}}\sum _{j=1}^{N}cos〈\overrightarrow{n_i}, \overrightarrow{n_j}〉$. The normal vectors in signal regions tend to be consistent, whereas those in distorted regions tend to be scattered.

(3)

Neighborhood Variance: ${\sigma }^2\left(p_i\right)={\displaystyle \frac{1}{N}}{\sum }_{j=1}^N{\left(z_j-\overline{z}\right)}^2$. The variance in distorted regions is significantly higher than that in signal regions due to noise interference.

(4)

Local Curvature: $\kappa \left({\rho }_i\right)={\displaystyle \frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2+{\lambda }_3}}$. The curvature in signal regions tends to be close to zero, whereas regions along edges or areas with distortion exhibit higher curvature values.

(5)

Intensity Gradient: $\nabla I\left(p_i\right)=\sqrt{{\left({\displaystyle \frac{\partial I}{\partial x}}\right)}^2+{\left({\displaystyle \frac{\partial I}{\partial y}}\right)}^2+{\left({\displaystyle \frac{\partial I}{\partial z}}\right)}^2}$. Abnormal fluctuations in reflection intensity may occur in distortion areas due to sensor errors.

Algorithm 1 lays out the main principle of the decision tree model. Initially, the information gain of all features is calculated from the root node, and the feature with the largest information gain is selected as the feature of the node. Then, a child node is established according to the feature result, and the above method is called recursively for the child node. Finally, a decision tree is constructed until all features are selected. The goal is to construct a decision tree model $\mathit{T}$ according to the given training dataset $\mathit{D}$, so that it can correctly classify the target point cloud into signal point cloud and distorted point cloud, and the loss function needs to be minimized in the learning process.

To prevent the degradation of generalization performance caused by overfitting to noisy data during the training process of the decision tree model, this paper adopts a strategy that combines pre-pruning and post-pruning to optimize the tree structure.

During the growth process of the decision tree, pre-pruning terminates branch expansion in advance based on the following criteria. The purpose is to limit the depth of the tree to prevent over-fitting, while preserving the key features (such as high curvature and high variance) in the distorted regions of the point cloud.

(1)

Minimum sample size threshold: the splitting is stopped when the number of samples contained in the current node is less than ${\tau }_{min}$.

(2)

Information gain threshold: If the information gain after splitting is less than ${\tau }_{gain}$, the split is rejected.

For post-pruning, Cost-Complexity Pruning can be used to prune the subtree recursively after the decision tree has fully grown. Post-pruning can address the issue of underfitting that may result from pre-pruning, particularly in scenarios where the boundary between the distorted area and the normal area is ambiguous. Throughout the entire process, it is necessary to calculate the cost complexity difference $∆C$ before and after pruning, followed by traversing all non-leaf nodes from bottom to top. If $∆C>0$, pruning is performed, and then the subtree with the lowest cost is retained.

Algorithm 1 The Decision Tree Model

Input: Training dataset $\mathit{D}=\left\{\left({\mathit{x}}_1,y_1\right),\left({\mathit{x}}_2,y_2\right),\cdots ,\left({\mathit{x}}_{\mathit{M}},y_M\right)\right\}$

Attribute set $\mathit{A}=\left\{a_1, a_2, \cdots , a_d\right\}$

Process$: \mathrm{Function} \mathrm{T}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\left(\mathit{D}, \mathit{A}\right)$

Output$: \mathrm{The} \mathrm{decision} \mathrm{tree} \mathit{T}$

1: Generating node.

2: if the samples in $\mathit{D}$ all belong to the same category $\mathit{C}$ then

3:  Mark the node as a C-class leaf node.

4: end if

5: if $\mathit{A}=\varnothing$ or $\mathrm{the} \mathrm{samples} \mathrm{in} \mathit{D}$$\mathrm{have} \mathrm{the} \mathrm{same} \mathrm{value} \mathrm{on} \mathit{A}$ then

6:  Mark the node as a leaf node.

7:  Mark its category as the class with the largest number of samples in $\mathit{D}$.

8: end if

9: Select the optimal partition attribute $a_{*}$ from $\mathit{A}$.

10: for $a_{*}^v$ in $a_{*}$ do

11:  Generate a branch for node.

12:  Let ${\mathit{D}}_{\mathit{v}}$ represent a subset of samples in $\mathit{D}$ that take the value $a_{*}^v$.

13:  if ${\mathit{D}}_{\mathit{v}}=\varnothing$ then

14:    Mark a branch node as a leaf node.

15:    Mark its category as the class with the largest number of samples in $\mathit{D}$.

16:  else

17:    Take $\mathrm{T}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\left({\mathit{D}}_{\mathit{v}}, \mathit{A}\backslash \left\{a_{*}\right\}\right)$ as a branch node.

18:  end if

19: end for

20: Output a decision tree with node as the root node.

2.2. Testing Phase

In the testing phase, it is necessary to apply the trained decision tree model to accurately classify the point cloud data in the testing dataset, and then complete the detailed segmentation of signal region and distortion region.

Specifically, we can efficiently extract key features from point cloud images by using the branching structure of decision trees, laying a crucial foundation for accurately distinguishing between signal regions and distortion regions. Through the classification ability of decision tree, we can accurately identify the signal regions in point cloud images, which are those areas that are not affected by distortion or have a low degree of distortion, as well as distorted areas, which experience significant changes in shape, position, color, and other attributes due to various factors.

Among them, the points in the distorted region can be expressed as

$$\mathit{Z}=\left\{{\mathit{z}}_{\mathbf{1}}, {\mathit{z}}_{\mathbf{2}},\cdots ,{\mathit{z}}_{\mathit{\tau }}\right\}$$

(2)

where ${\mathit{z}}_{\mathit{i}}$ (i = 1, 2…, $\tau$) is a column vector containing three-dimensional coordinates and intensity values, and $\tau$ is the number of points included in the distorted region.

After successfully segmenting the distorted regions of the point cloud, we introduce the Adaptive Least Mean Square (ALMS) filter to accurately correct the points in the distorted regions [33,34,35]. ALMS is well-known for its exceptional optimization performance, allowing for automatic adjustment of filtering parameters based on the actual distribution of distortion points to achieve optimal distortion correction.

Algorithm 2 lays out the main principle of the adaptive least mean square filter.

Algorithm 2 The Adaptive Least Mean Square (ALMS) filter

Input$: \mathrm{The} \mathrm{point} \mathrm{cloud} \mathrm{dataset} \mathit{Z}$ in the distorted region

The filter order K

Step factor $\mu$

Output$: \mathrm{The} \mathrm{corrected} \mathrm{point} \mathrm{cloud} \mathrm{dataset} \mathit{Z}\prime$

$1:\hspace{1em}\mathrm{Set} \mathrm{an} \mathrm{initial} \mathrm{weight} \mathrm{coefficient} W_k$.

2: for ${\mathit{z}}_{\mathit{k}} \mathbf{in} \mathit{Z}$ do

3:  ${\mathit{z}}_{\mathit{k}}\prime =\sum _{i=0}^{\tau -1}{W}_k·{\mathit{z}}_{\mathit{k}-\mathit{i}}$

4:  ${\mathit{e}}_{\mathit{k}}={\mathit{\theta }}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}}\prime$

5:  $J\left(W_k\right)=E\left[{{\mathit{e}}_{\mathit{k}}}^{\mathbf{2}}\right]=E\left[{\left({\mathit{\theta }}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}}\prime \right)}^{\mathbf{2}}\right]$

6:  $\nabla \left(J\left(W_k\right)\right)={\displaystyle \frac{\partial \left[{{\mathit{e}}_{\mathit{k}}}^{\mathbf{2}}\right]}{\partial W_k}}$

7:  $W_{k+1}=W_k-{\displaystyle \frac{1}{2}}\mu \left[-\nabla \left(J\left(W_k\right)\right)\right]$

8: end for

$9:\hspace{1em}\mathrm{Output} \mathrm{the} \mathrm{correct} \mathrm{point} \mathrm{cloud} \mathrm{dataset} \mathit{Z}\prime$.

Set an initial weight coefficient $W_k$, where $k=\mathrm{1,2},\cdots ,\tau$, and the initial weight coefficient is 0. Then, the input signal ${\mathit{z}}_{\mathit{k}}$ becomes the output signal ${\mathit{z}}_{\mathit{k}}\prime$ after being processed by a digital filter with adjustable parameters. The output signal ${\mathit{z}}_{\mathit{k}}\prime$ can be expressed as:

$${\mathit{z}}_{\mathit{k}}\prime =W_k·\sum _{i=0}^{\tau -1}{\mathit{z}}_{\mathit{k}-\mathit{i}}.$$

(3)

Next, the error signal is the difference between the expected response ${\mathit{\theta }}_{\mathit{k}}$ and the output signal ${\mathit{z}}_{\mathit{k}}\prime$, which can be expressed as

$${\mathit{e}}_{\mathit{k}}={\mathit{\theta }}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}}\prime .$$

(4)

Afterwards, the filter parameters are dynamically adjusted using an adaptive filtering algorithm, ultimately leading to the minimization of $E\left[{{\mathit{e}}_{\mathit{k}}}^{\mathbf{2}}\right]$. The weight coefficient and the output of the filter are recalculated, and this process is iteratively repeated until the termination condition is satisfied.

Finally, the corrected point cloud dataset can be obtained:

$$\mathit{Z}\prime =\left\{{\mathit{z}}_{\mathbf{1}}\prime , {\mathit{z}}_{\mathbf{2}}\prime ,\cdots ,{\mathit{z}}_{\mathit{\tau }}\prime \right\}$$

(5)

where ${\mathit{z}}_{\mathit{i}}\prime$ (i = 1, 2…, $\tau$) is a column vector corrected by the ALMS filter.

Throughout the entire process, the filter order $k$ determines the number of preceding iterations utilized in the adaptive filtering process. A higher $k$ incorporates more historical data, which can enhance estimation accuracy but also increases computational complexity. Conversely, a lower $k$ reduces latency but may compromise performance in highly dynamic environments.

During the noise reduction process for LiDAR point clouds, the $k$ value is typically set within the range of 20 to 100. This parameter requires dynamic adjustment based on the characteristics of the point cloud data, the types of noise present, and the available hardware conditions.

The step factor $\mu$ controls the adaptation rate of the ALMS algorithm. A larger $\mu$ accelerates convergence but may result in overshooting or instability, whereas a smaller $\mu$ ensures stability at the expense of reduced adaptation speed. In general, the $\mu$ value can be set to 0.001 in the experiment, which ensures convergence in real-world scenarios while maintaining the capability for rapid adaptation.

Through the fine processing of the ALMS filter, the points in the distorted region will be effectively pulled back to their proper positions, thus significantly optimizing the overall quality of the point cloud image and improving its accuracy and reliability.

3. Complexity Analysis

In this section, we delve into the complexity analysis of the 3D point cloud least mean square filter based on SVM and the proposed 3D point cloud least mean square (D−LMS) filter based on decision tree. The computer processor is an Intel(R) Core (TM) i7-14700KF, operating at a frequency of 3400 MHZ. This powerful processor boasts an array of 20 cores and 28 logical processors, delivering exceptional computational capabilities. The Graphics Processing Unit (GPU) is the GeForce RTX 4070 SUPER, which is a high-end graphics card device released by NVIDIA on 17 January 2024. With such a robust configuration, it enables us to handle complex computations and large datasets with ease.

Table 1. Complexity Analysis of Different Methods.

Algorithm	Training Time	Testing Time
3D point cloud least mean square filter based on SVM	1726.25 s	72.52 s
The proposed D−LMS filtering algorithm	1.31 s	0.06 s

compares the complexities of different point cloud distortion calibration methods in the detection area 1.9 m away from lidar. Compared with the 3D point cloud least mean square filter based on SVM, the proposed D−LMS filtering algorithm reduces the model training time by 1317 times and the testing time by 1208 times. These results highlight the excellent efficiency and effectiveness of the proposed D−LMS method in processing and correcting point cloud distorted data.

4. Performance Analysis

In our experiment, we used a structured light LiDAR to collect point cloud depth images at 30 different distances. These images were utilized to create a comprehensive training dataset. Furthermore, we prepared a testing dataset consisting of point cloud depth images captured at specific distances of 0.6 m, 0.9 m, 1.2 m, 1.6 m, and 1.9 m, ensuring diverse and representative evaluation of the performance of our proposed method. In order to ensure the stability of data acquisition, we adopt a temperature-controlled environment to reduce the influence of temperature fluctuation on the performance of LiDAR.

Figure 2 presents an overview of part of our training dataset, which consists of 14 meticulously captured point cloud depth images. The distances between these point clouds and the structured light LiDAR vary across a range of 0.6 m to 1.9 m, with each image corresponding to a distance interval of 0.1 m. In these images, the left side of the image is the original point cloud depth image, and the right side of the image is the point cloud depth image segmented by the decision tree model, in which the red-marked regions represent signal point clouds that require no filtering or correction. Conversely, the green-marked regions indicate distorted areas composed of incorrect point cloud data. The experiment has a total of five test datasets, each with a different distance from the structured light LiDAR. The number of points in the signal region and distortion region for these test datasets can be found in

Table 2. The number of points in the signal region and the distortion region for different test datasets.

The Testing Dataset	Distance	Number of Points in Signal Region	Number of Points in Distorted Region
Dataset 1	0.6 m	231,651	9646
Dataset 2	0.9 m	211,051	29,800
Dataset 3	1.2 m	199,536	41,316
Dataset 4	1.6 m	175,473	64,782
Dataset 5	1.9 m	172,829	64,940

.

Figure 3 displays the original point cloud images of the five test datasets, revealing that the distortion around the edges becomes increasingly severe as the distance from the structured light LiDAR increases. Specifically, the contour edge of the object in the point clouds exhibit increasing distortion, highlighting the challenges of maintaining data accuracy in areas far from the sensor.

Figure 4 shows the point cloud images of five test datasets corrected by the 3D point cloud least mean square filter based on SVM. Through observation, it can be found that the SVM model only draws two boundaries between the signal region and the distorted region, which is rough and fails to accurately distinguish each point, meaning it cannot identify which points are signal points and which ones are distortion points.

Figure 5 shows the point cloud images of five test datasets corrected by the proposed D−LMS filtering algorithm. Under the guidance of the decision tree model for partitioning, the signal regions and distorted regions are intricately interleaved, allowing for precise identification of all distorted point clouds. Subsequently, these distorted point clouds can be accurately corrected using the adaptive least mean squares filter, ultimately yielding a high-precision point cloud image.

Table 3. The accuracy of different methods under five testing datasets.

Algorithm	Dataset 1	Dataset 2	Dataset 3	Dataset 4	Dataset 5
Without algorithm processing	96.00%	87.63%	82.85%	73.04%	72.69%
3D point cloud least mean square filter based on SVM	98.87%	95.78%	92.39%	87.54%	86.17%
The proposed D−LMS filtering algorithm	99.52%	97.25%	95.03%	93.55%	92.38%

summarizes the accuracy of different methods under five testing datasets. In this context, accuracy is defined as the ratio of the number of correct points to the total number of points. It takes into account both the original signal points that were accurately retained and the distorted points that were successfully corrected to their true positions. This provides a comprehensive measure of how well each method performs in terms of accuracy.

The experimental result shows that the D−LMS filtering algorithm can effectively improve the accuracy of point cloud images under five testing datasets, which demonstrates the superiority of the D−LMS filtering algorithm in terms of its ability to accurately correct point cloud data. Compared with the original point cloud image without algorithm processing, the accuracy of the proposed D−LMS filtering algorithm is improved from 72.69% to 92.38%. Compared with the 3D point cloud least square filter based on SVM, the accuracy of the proposed D−LMS filtering algorithm is improved from 86.17 to 92.38%. These results emphasize the effectiveness and efficiency of D−LMS filtering algorithm, which indicates that it can be widely used in the field of distortion calibration of 3D point cloud images.

5. Conclusions

In summary, this paper proposes a high-performance 3D point cloud Least Mean Square filter based on Decision Tree, which can address the challenges of distortion in point cloud images captured by Structured Light LiDAR. The proposed D−LMS filtering algorithm can effectively address the problems of lens scattering and temperature fluctuation, which are the primary factors causing distortion in the collected data. By utilizing the classification and prediction capabilities of the decision tree model, the D−LMS filtering algorithm can accurately differentiate between signal regions and distortion regions, and can automatically adjust its filtering parameters through the adaptive least mean square filter to accurately correct the distortion point. Compared with the original point cloud image, the D−LMS filter has significantly improved the accuracy of the point cloud image from 72.69% to 92.38%, which represents a significant advancement in the field of 3D point cloud image distortion calibration. Its high performance, adaptability and robustness make it a promising solution to improve the accuracy of point cloud data obtained by structured light lidar system.