Improving the High-Pressure Sensing Characteristics of Y2MoO6:Eu3+ Using a Machine Learning Approach
Abstract
1. Introduction
2. Materials and Methods
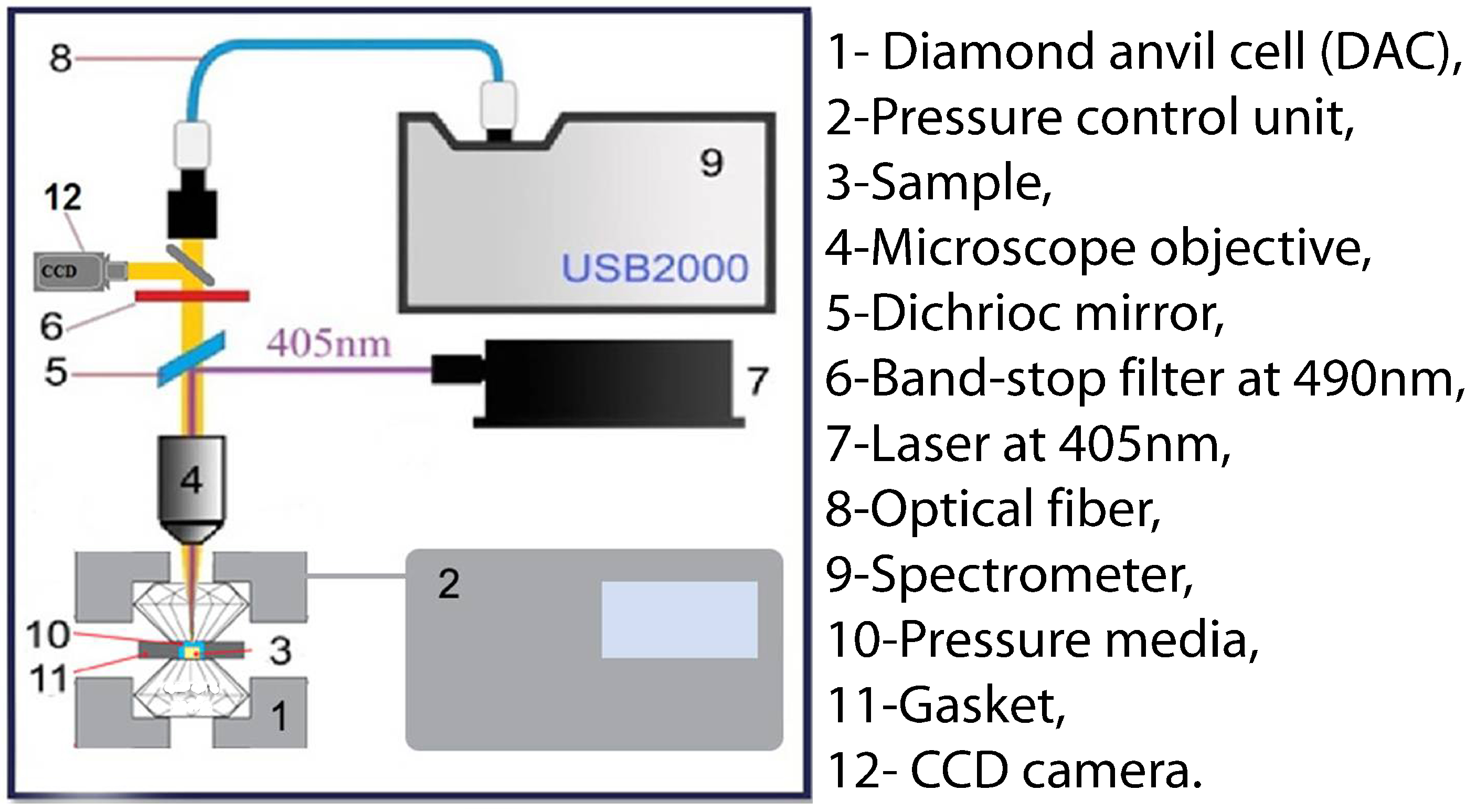
2.1. Experimental Setup for High-Pressure Measurements
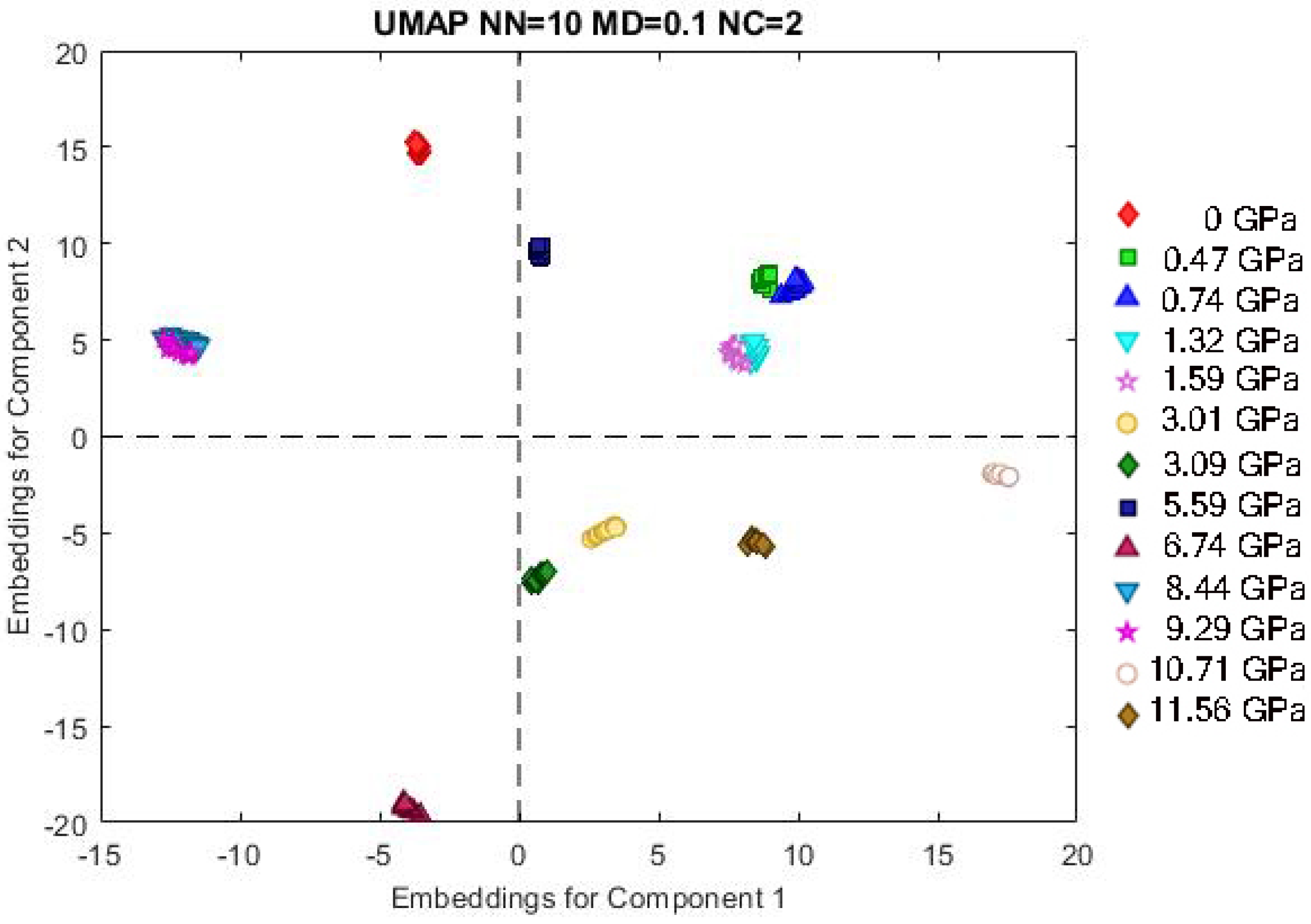
2.2. Machine Learning Analysis
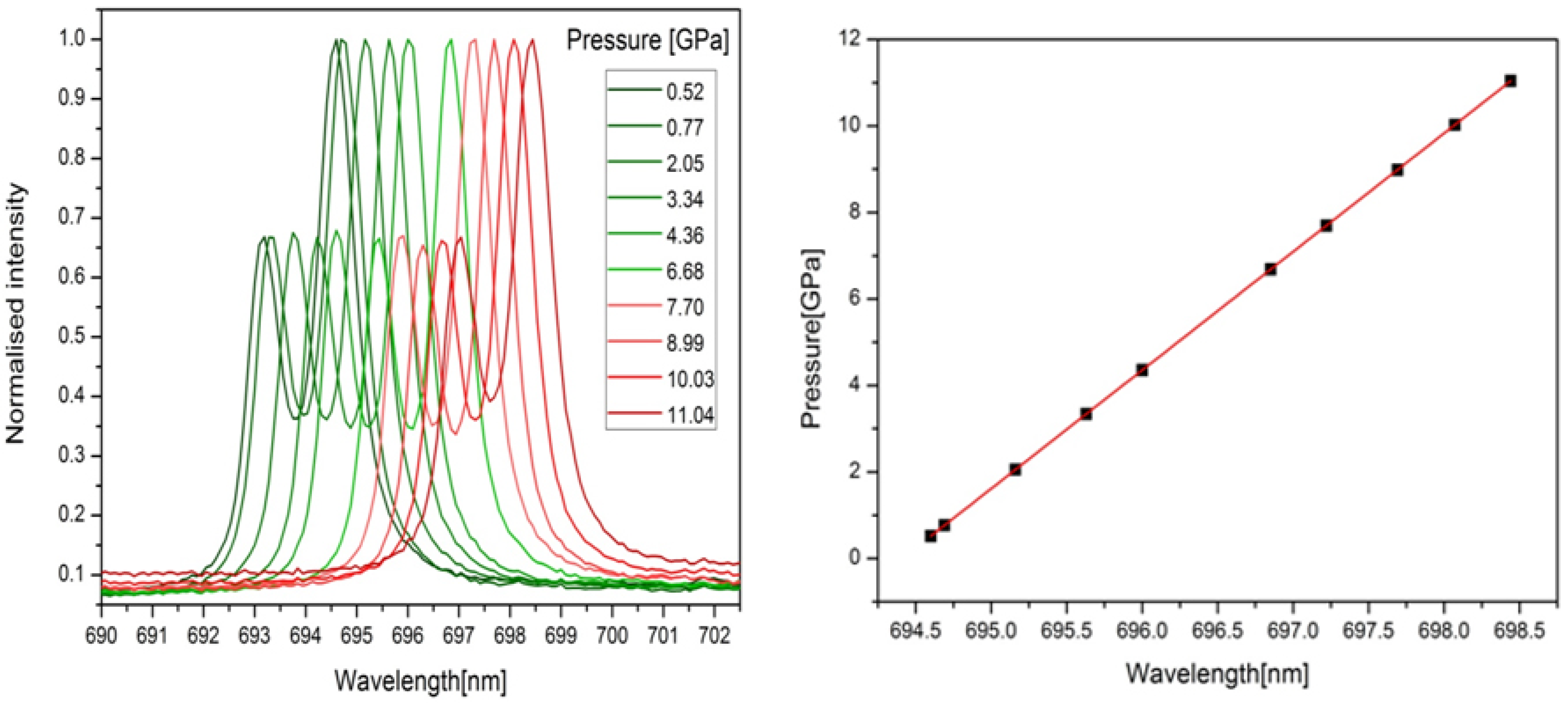
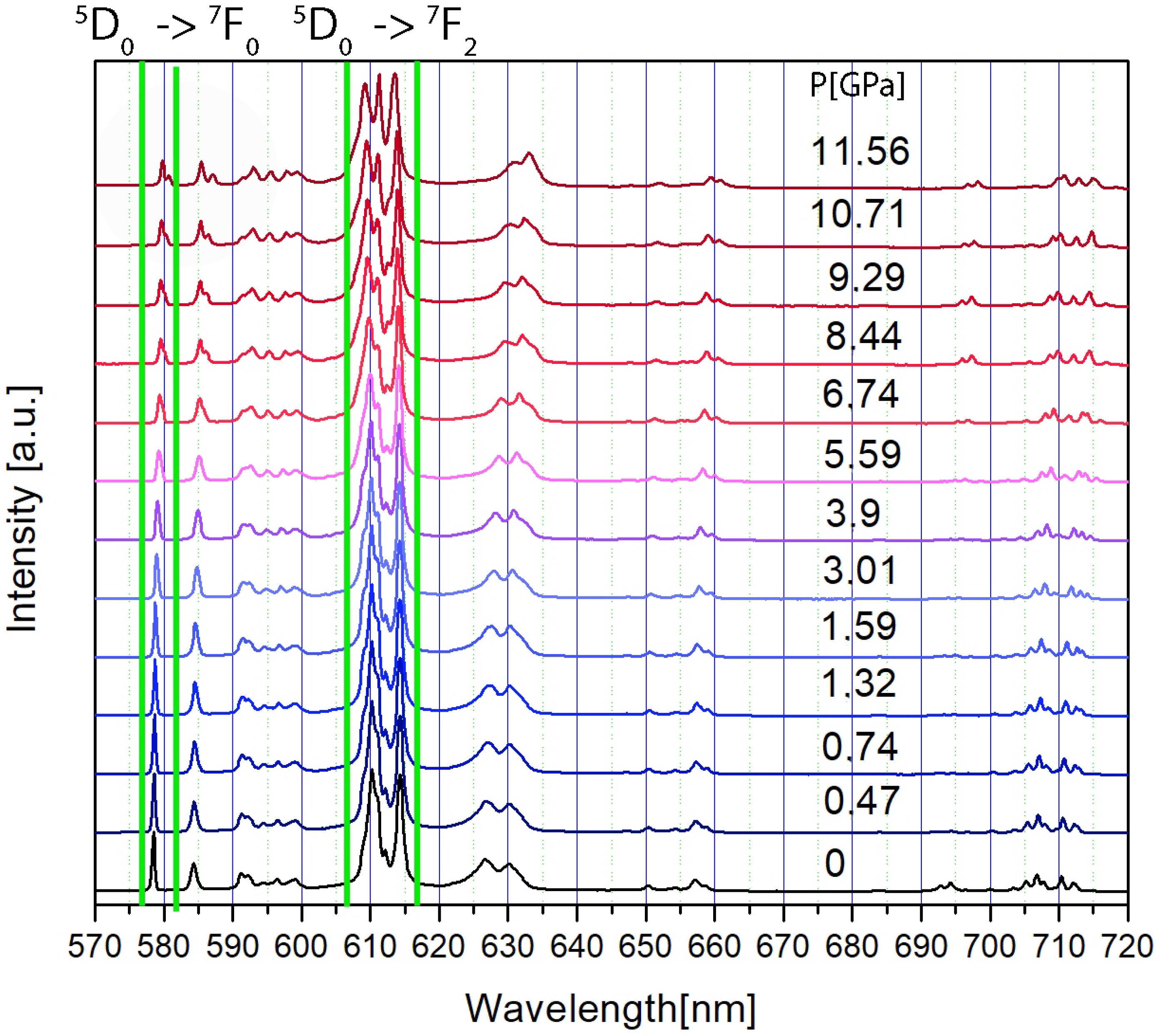
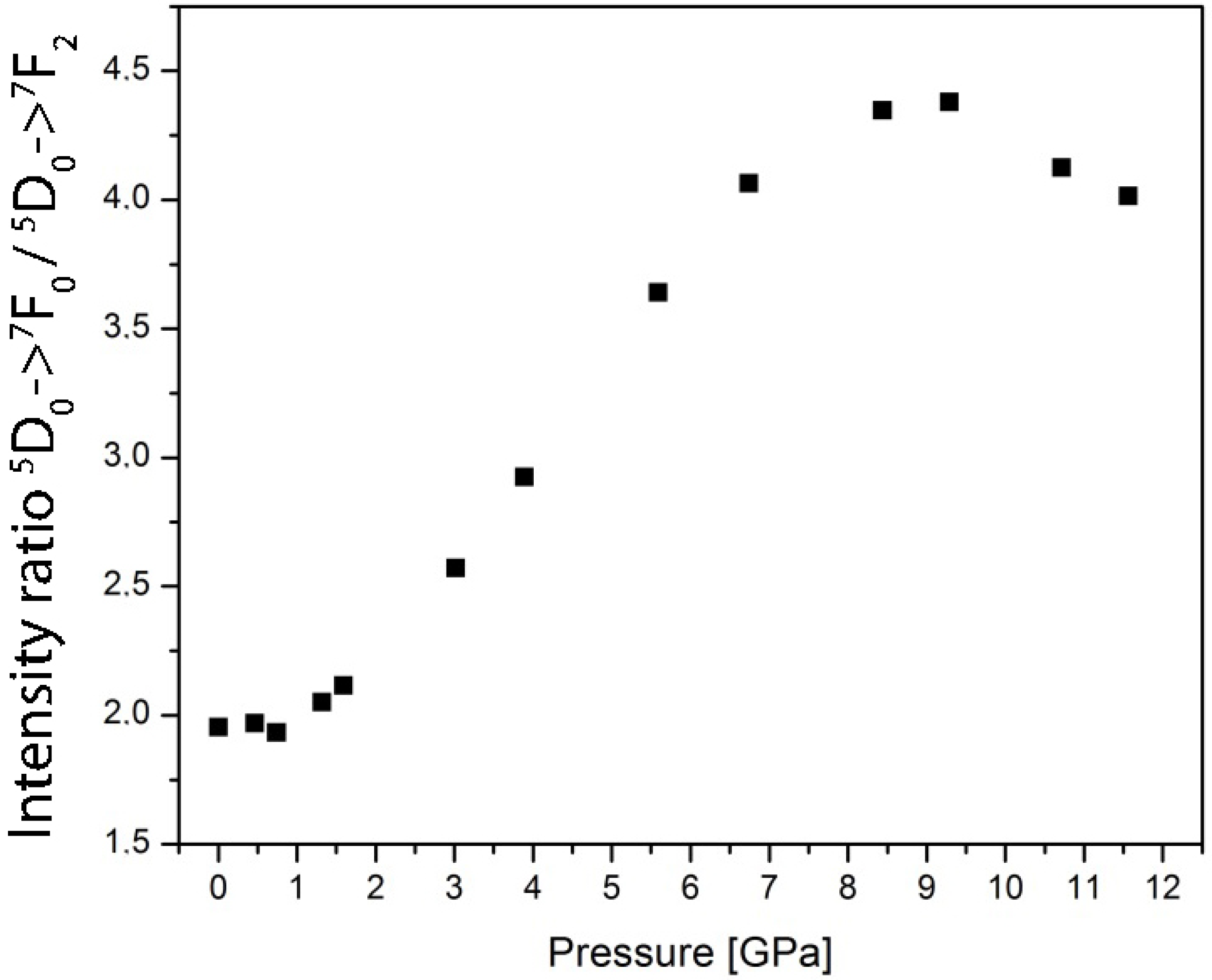
3. Results
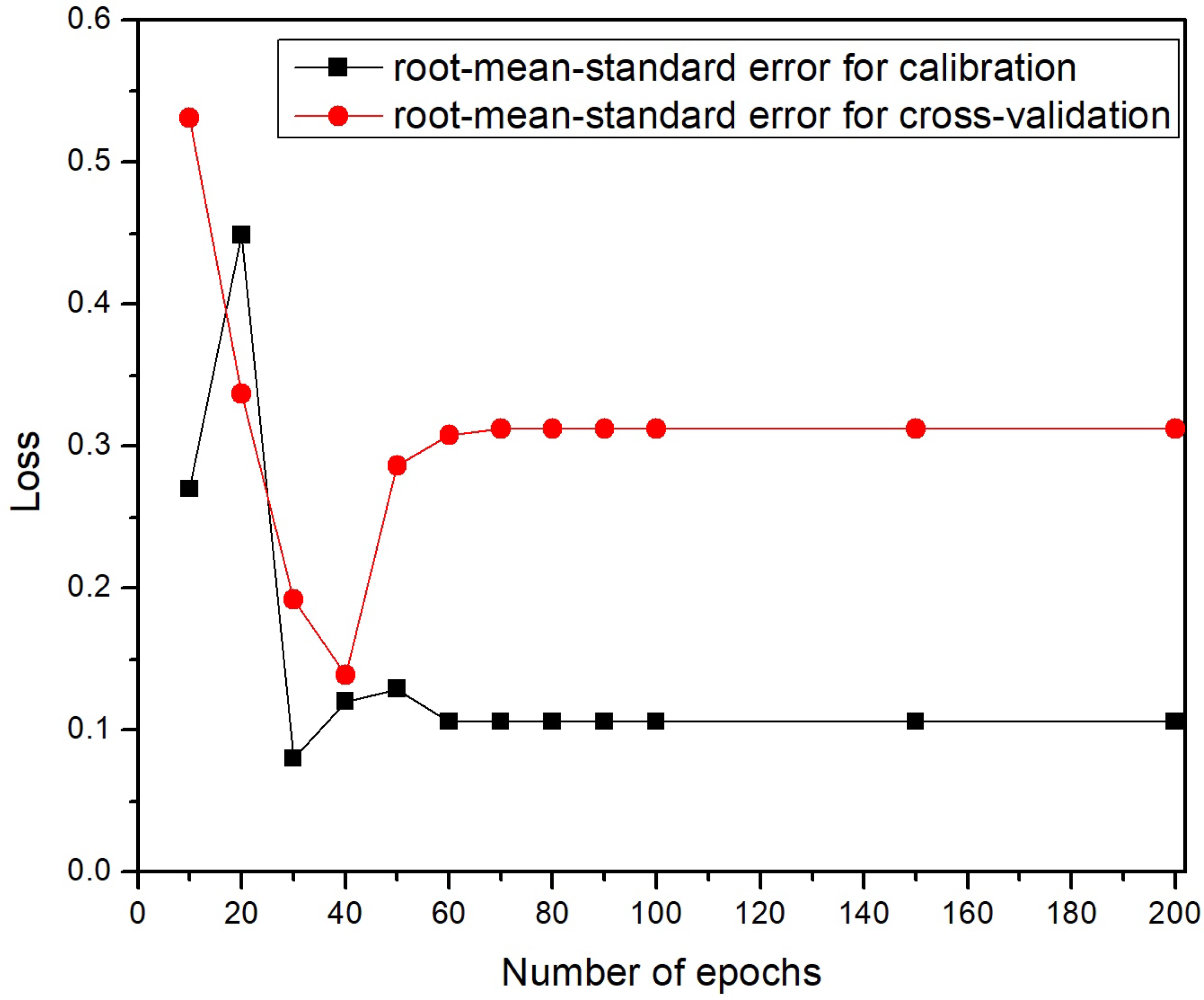
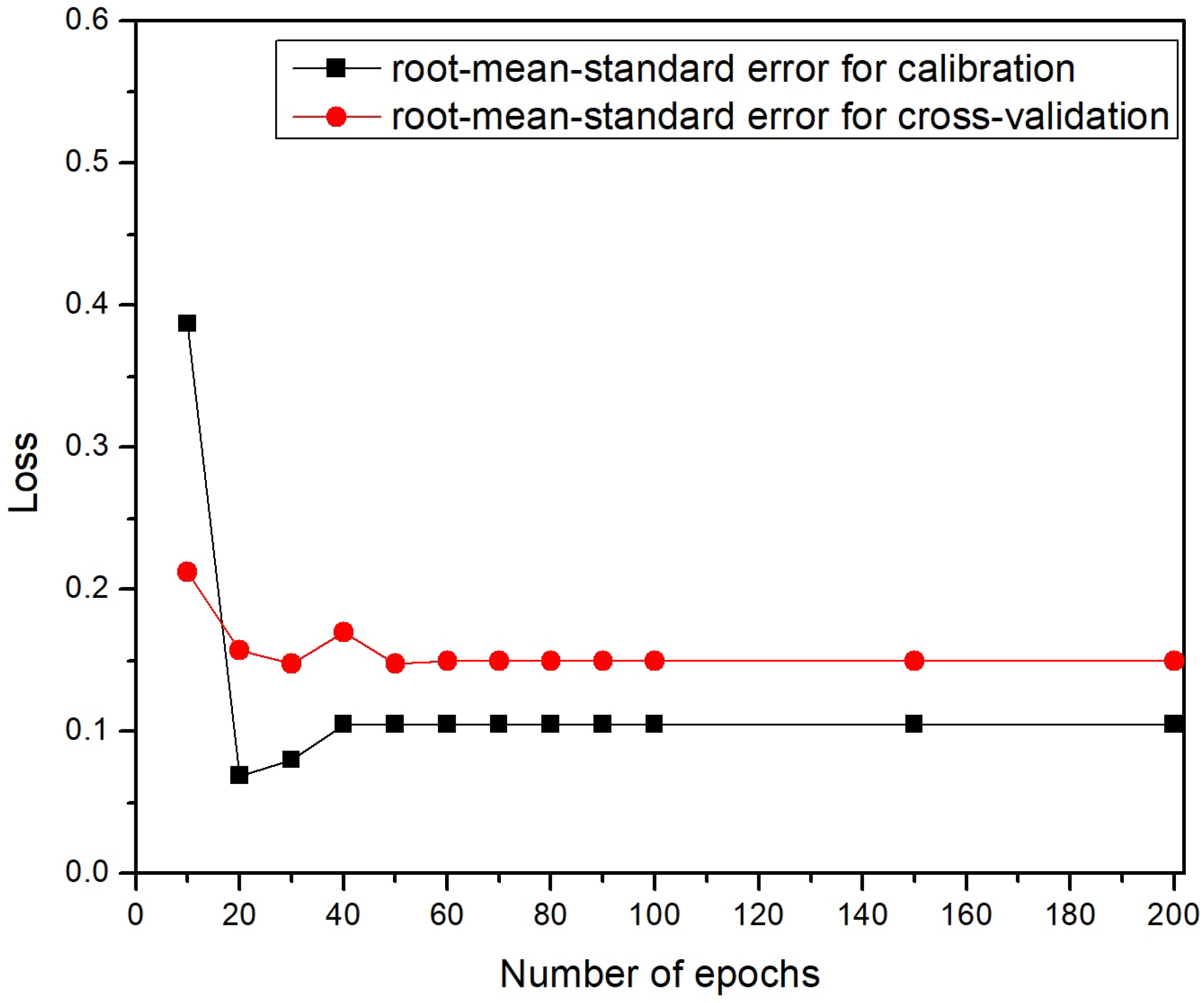
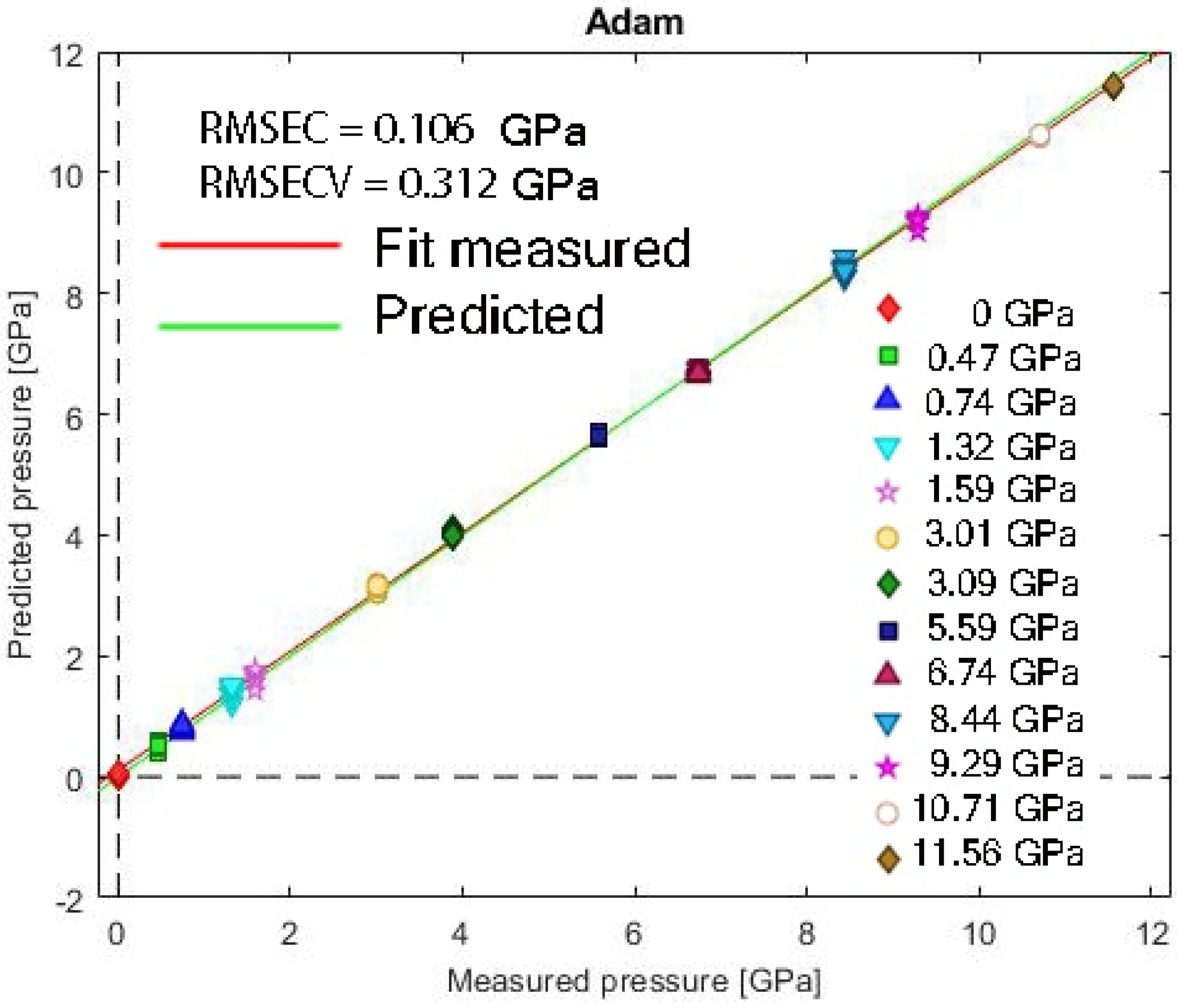
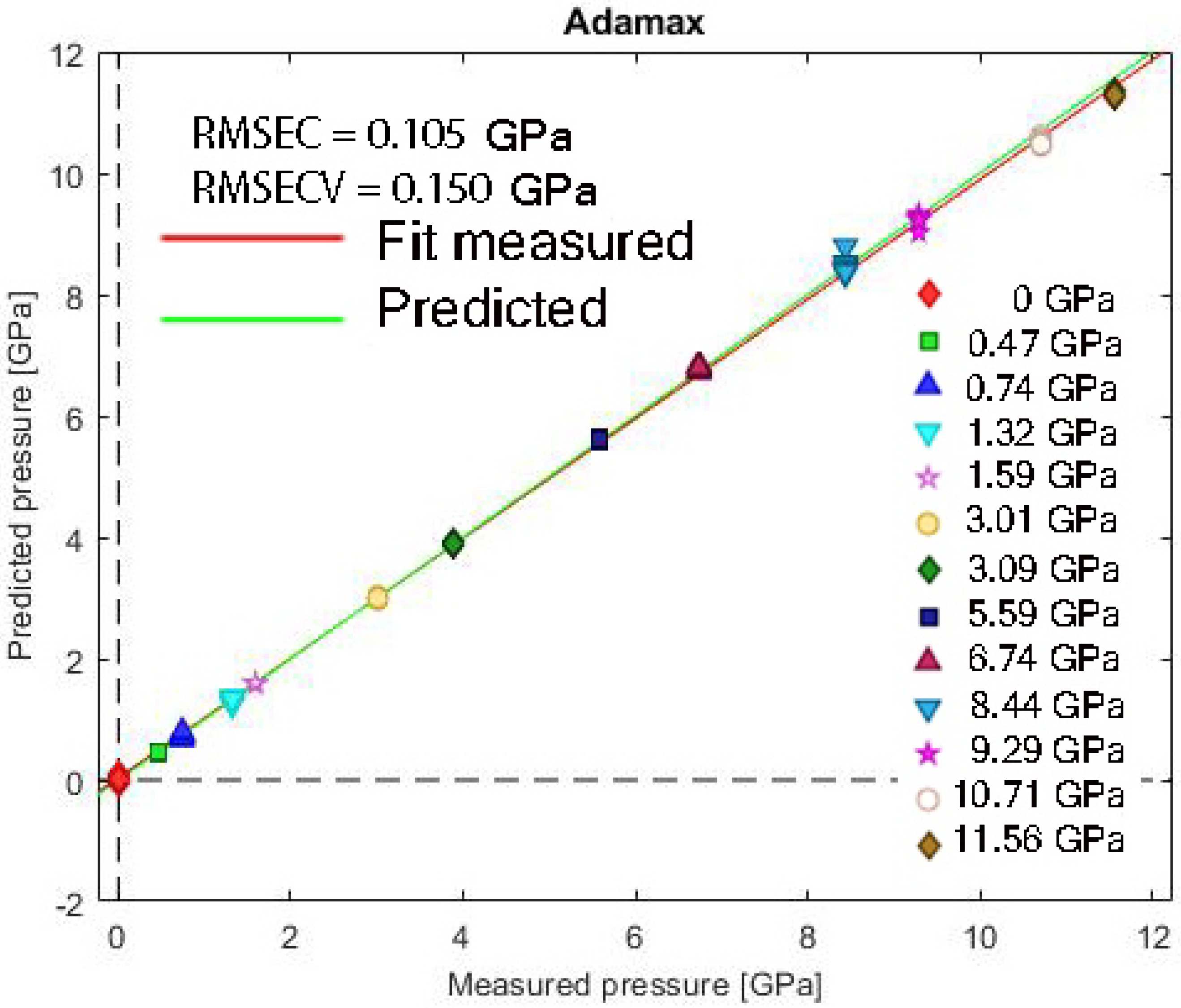
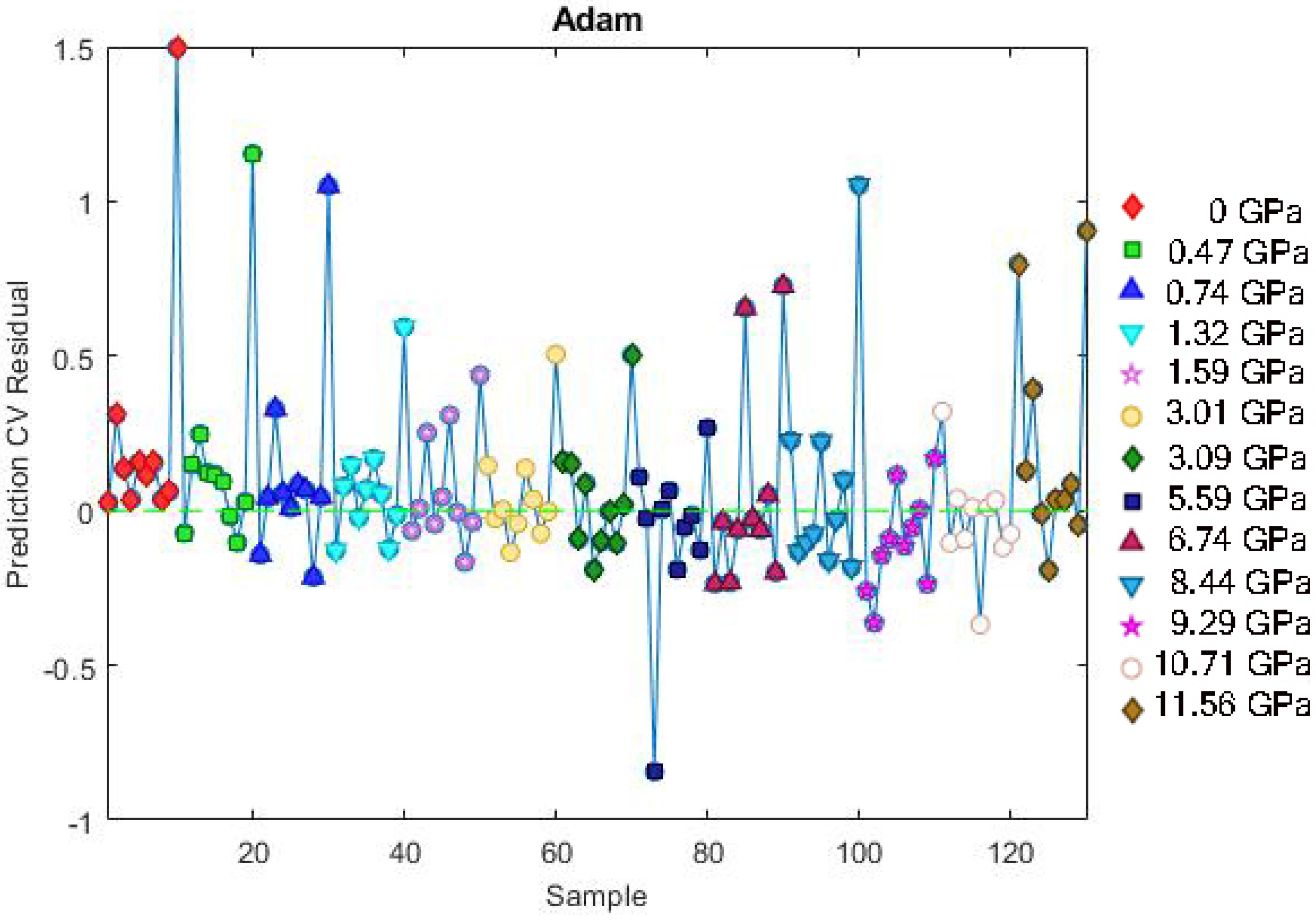
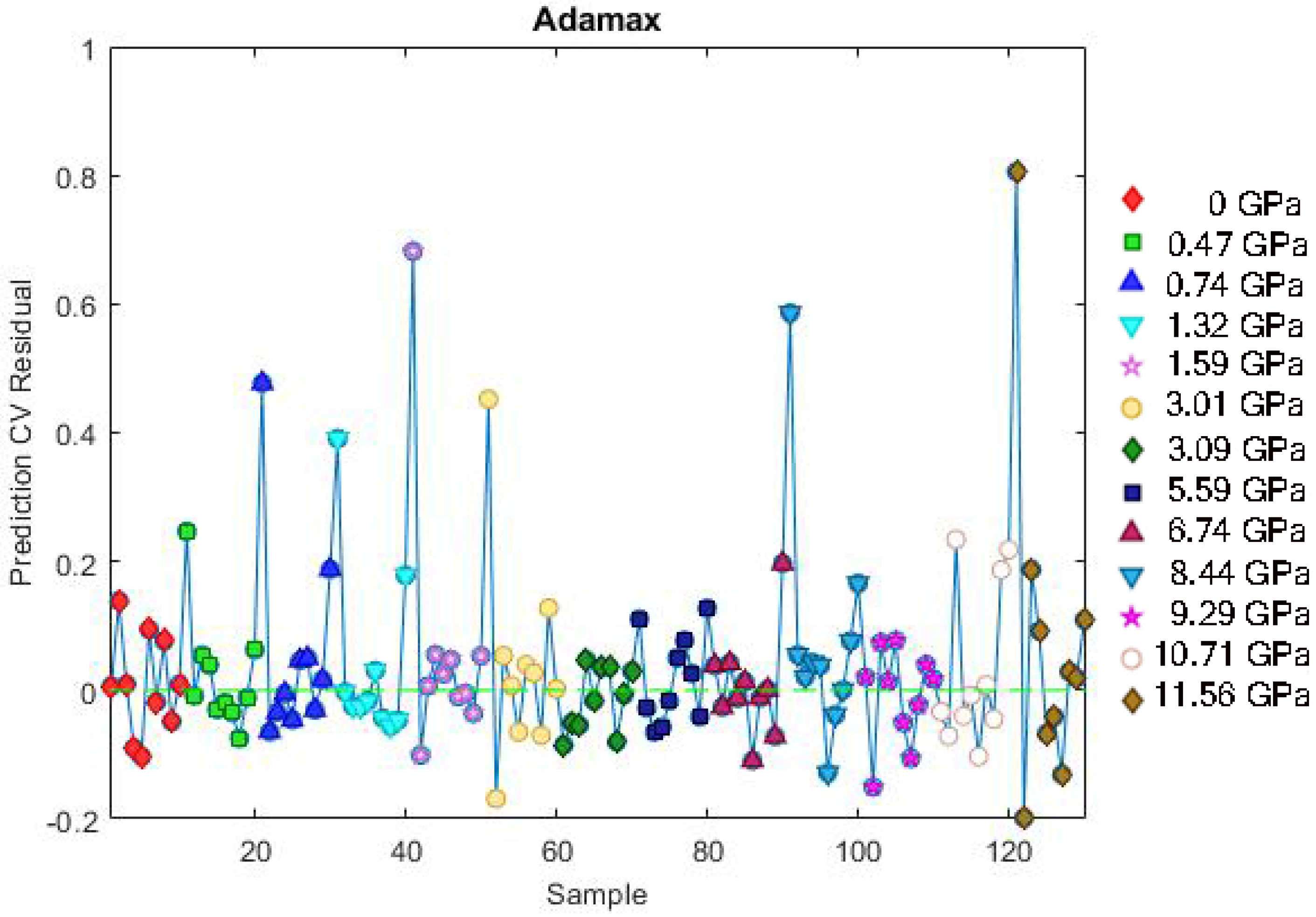
3.1. Model and Training Configuration
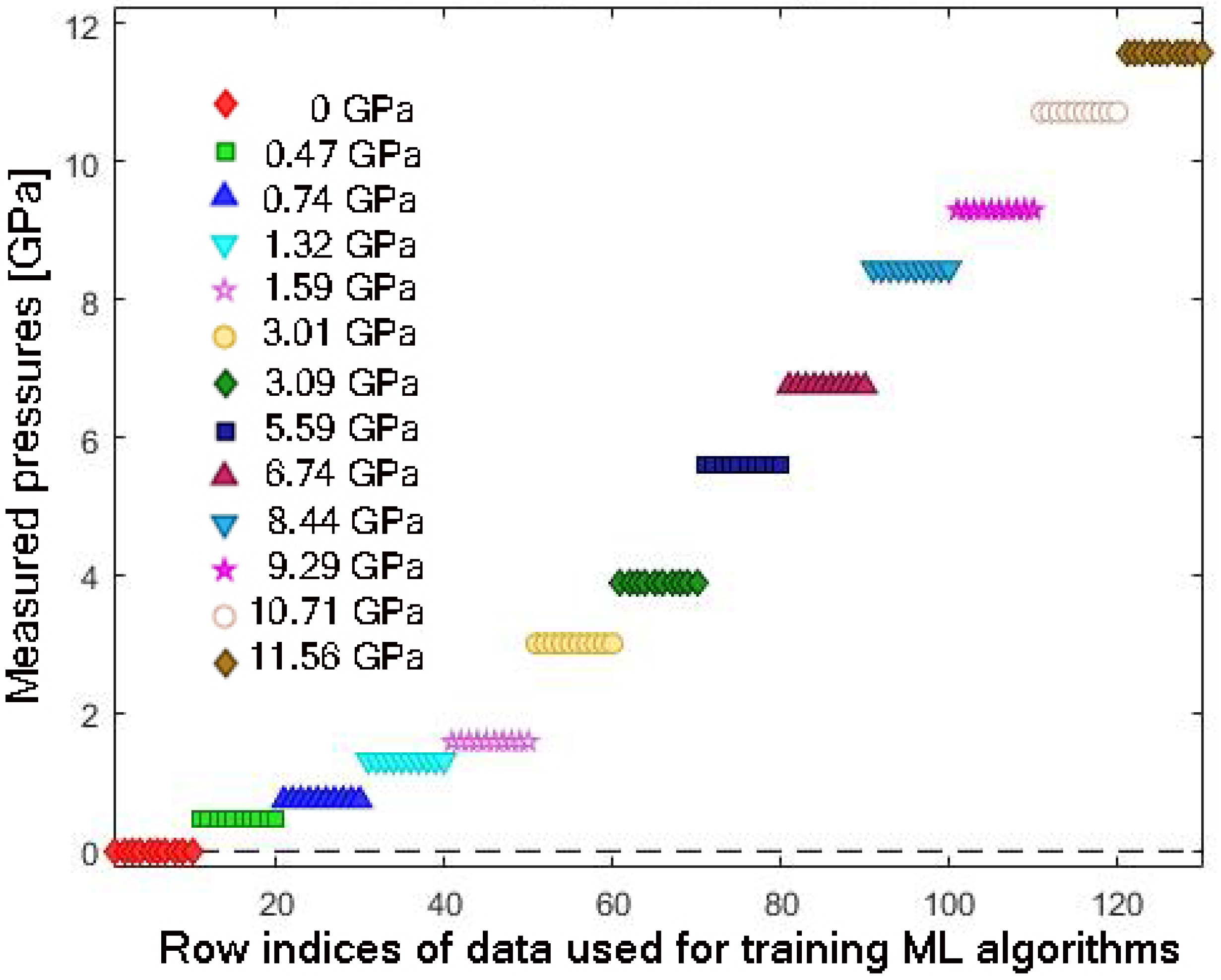
3.2. Data Preprocessing
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lv, Q.; Wang, C.; Chen, S.; Zheng, H.; Dong, E.; Zhu, G. Ultrasensitive Pressure-Induced Optical Materials: Europium-Doped Hafnium Silicates with a Khibinskite Structure for Optical Pressure Sensors and WLEDs. Inorg. Chem. 2021, 61, 3212–3222. [Google Scholar] [CrossRef]
- Runowski, M.; Zheng, T.; Woźny, P.; Du, P. NIR emission of lanthanides for ultrasensitive luminescence manometry—Er3+-activated optical sensor of high pressure. Dalton Trans. 2021, 50, 14864–14871. [Google Scholar] [CrossRef] [PubMed]
- Antoniak, M.A.; Zelewski, S.J.; Oliva, R.; Żak, A.; Kudrawiec, R.; Nyk, M. Combined Temperature and Pressure Sensing Using Luminescent NaBiF4:Yb,Er Nanoparticles. ACS Appl. Nano Mater. 2020, 3, 4209–4217. [Google Scholar] [CrossRef]
- Goderski, S.; Runowski, M.; Woźny, P.; Lavín, V.; Lis, S. Lanthanide Upconverted Luminescence for Simultaneous Contactless Optical Thermometry and Manometry–Sensing under Extreme Conditions of Pressure and Temperature. ACS Appl. Mater. Interfaces 2020, 12, 40475–40485. [Google Scholar] [CrossRef]
- Runowski, M.; Woźny, P.; Stopikowska, N.; Guo, Q.; Lis, S. Optical Pressure Sensor Based on the Emission and Excitation Band Width (fwhm) and Luminescence Shift of Ce3+-Doped Fluorapatite—High-Pressure Sensing. ACS Appl. Mater. Interfaces 2019, 11, 4131–4138. [Google Scholar] [CrossRef] [PubMed]
- Runowski, M.; Woźny, P.; Lavin, V.; Lis, S. Optical pressure nano-sensor based on lanthanide doped SrB2O4:Sm2+ luminescence—Novel high-pressure nanomanometer. Sens. Actuators B Chem. 2018, 273, 585–591. [Google Scholar] [CrossRef]
- Matovic, B.; Nikolic, M.; Prekajski Djordjevic, M.; Dmitrovic, S.; Lukovic, J.; Maletaskic, J.; Jelenkovic, B. Luminescence Properties of Eu3+ Doped Mayenite Under High Pressure. J. Innov. Mater. Extrem. Cond. 2020, 1, 12–14. [Google Scholar]
- Zhang, J.; Cui, H.; Zhu, P.; Ma, C.; Wu, X.; Zhu, H.; Ma, Y.; Cui, Q. Photoluminescence studies of Y2O3:Eu3+ under high pressure. J. Appl. Phys. 2014, 115, 023502. [Google Scholar] [CrossRef]
- Baran, A.; Mahlik, S.; Grinberg, M.; Zych, E. High pressure and time-resolved luminescence spectra of Ca3Y2(SiO4)3 doped with Eu2+ and Eu3+. J. Phys. Condens. Matter 2013, 25, 025603. [Google Scholar] [CrossRef]
- He, X.; Bian, D.; Wang, H.; Xu, J. Eu3+ activated Y2MoO6 A narrow band red-emitting phosphor with strong near-UV absorption. Luminescence 2013, 28, 973–976. [Google Scholar] [CrossRef]
- Han, B.; Zhang, J.; Wang, Z.; Liu, Y.; Shi, H. Investigation on the concentration quenching and energy transfer of red-light-emitting phosphor Y2MoO6:Eu3+. J. Lumin. 2014, 149, 150–154. [Google Scholar] [CrossRef]
- Wu, L.; Tian, X.; Deng, K.; Liu, G.; Yin, M. Site selective spectroscopic study of an efficient red-emitting phosphor Y2MoO6:Eu. Opt. Mater. 2015, 45, 28–31. [Google Scholar] [CrossRef]
- Stankovic, N.; Nikolic, G.M.; Jelenkovic, B.; Daneu, N.; Maletaskic, J.; Prekajski DJordjevic, M.; Matovic, B. Luminescence properties of Eu3+ activated Y2MoO6 powders calcined at different temperatures. Process. Appl. Ceram. 2020, 14, 71–76. [Google Scholar] [CrossRef]
- Ofelt, G.S. Intensities of Crystal Spectra of Rare-Earth Ions. J. Chem. Phys. 1962, 37, 511–520. [Google Scholar] [CrossRef]
- Judd, B.R. Optical Absorption Intensities of Rare-Earth Ions. Phys. Rev. 1962, 127, 750–761. [Google Scholar] [CrossRef]
- Yu, L.; Song, H.; Lu, S.; Liu, Z.; Yang, L.; Kong, X. Luminescent Properties of LaPO4:Eu Nanoparticles and Nanowires. J. Phys. Chem. B 2004, 108, 16697–16702. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, S.; Liu, Q.; Wang, Y.; Wang, S.; Chen, J.; Xu, R.; Luo, L. Y2O3:Eu3+ microstructures: Hydrothermal synthesis and photoluminescence properties. Mat. Res. Bull. 2009, 44, 2201–2205. [Google Scholar] [CrossRef]
- Halevy, I.; Carmon, R.; Winterrose, M.L.; Yeheskel, O.; Tiferet, E.; Ghose, S. Pressure-induced structural phase transitions in Y2O3 sesquioxide. J. Phys. Conf. Ser. 2010, 215, 012003. [Google Scholar] [CrossRef]
- Forman, R.A.; Piermarini, G.J.; Barnett, J.D.; Block, S. Pressure measurement made by the utilization of ruby sharp-line luminescence. Science 1972, 176, 284–285. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, Q.; Zhang, C.; Li, L.; Li, X.; Li, F. Fluorescence pressure sensors: Calibration of ruby, Sm2+:SrB4O7, and Sm3+: YAG to 55 GPa and 850 K. J. Appl. Phys. 2024, 135, 105902. [Google Scholar] [CrossRef]
- Shen, G.; Smith, J.S.; Kenney-Benson, C.; Klotz, S. Calibration of ruby (Cr3+:Al2O3) and Sm2+:SrFCl luminescence lines from the melting of mercury: Constraints on the initial slopes. High Press. Res. 2021, 41, 175–183. [Google Scholar] [CrossRef]
- Marciniak, L.; Woźny, P.; Szymczak, M.; Runowski, M. Optical pressure sensors for luminescence manometry: Classification, development status, and challenges. Coord. Chem. Rev. 2024, 507, 215770. [Google Scholar] [CrossRef]
- Sangiorgio, M. Deep Learning in Multi-Step Forecasting of Chaotic Dynamics; Special Topics in Information Technology; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Scalia, G. Machine Learning for Scientific Data Analysis; Special Topics in Information Technology; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Sayin, B.; Krivosheev, E.; Yang, J.; Passerini, A.; Casati, F. A review and experimental analysis of active learning over crowdsourced data. Artif. Intell. Rev. 2021, 54, 5283–5305. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.; Wu, Z.; Xu, H.; Zhu, L. Two-step learning for crowdsourcing data classification. Multimed. Tools Appl. 2022, 81, 34401–34416. [Google Scholar] [CrossRef]
- Chatzidakis, M.; Botton, G.A. Towards calibration-invariant spectroscopy using deep learning. Sci. Rep. 2019, 9, 2126. [Google Scholar] [CrossRef] [PubMed]
- Weng, S.; Yuan, H.; Zhang, X.; Li, P.; Zheng, L.; Zhao, J.; Huanga, L. 2020 Deep learning networks for the recognition and quantitation of surface-enhanced Raman spectroscopy. Analyst 2020, 145, 4827–4835. [Google Scholar] [CrossRef]
- Ranamukhaarachchi, S.A.; Peiris, R.H.; Moresoli, C. Fluorescence spectroscopy and principal component analysis of soy protein hydrolysate fractions and the potential to assess their antioxidant capacity characteristics. Food Chem. 2017, 217, 469–475. [Google Scholar] [CrossRef]
- Dramicanin, T.; Zekovic, I.; Perisa, J.; Dramicanin, M.D. The Parallel Factor Analysis of Beer Fluorescence. J. Fluoresc. 2019, 29, 1103–1111. [Google Scholar] [CrossRef]
- Ximendes, E.; Marin, R.; Carlos, L.D.; Jaque, D. Less is more: Dimensionality reduction as a general strategy for more precise luminescence thermometry. Light Sci. Appl. 2022, 11, 237. [Google Scholar] [CrossRef]
- Barbon, S.; da Costa Barbon, A.P.A.; Mantovani, R.G.; Barbin, D.F. Machine Learning Applied to Near-Infrared Spectra for Chicken Meat Classification. J. Spectrosc. 2018, 2018, 8949741. [Google Scholar] [CrossRef]
- Geronimo, B.C.; Mastelini, S.M.; Carvalho, R.H.; Barbon Júnior, S.; Barbin, D.F.; Shimokomaki, M.; Ida, E.I. Computer vision system and near-infrared spectroscopy for identification and classification of chicken with wooden breast, and physicochemical and technological characterization. Infrared Phys. Technol. 2019, 96, 303–310. [Google Scholar] [CrossRef]
- Junior, S.B.; Mastelini, S.M.; Barbon, A.P.A.; Barbin, D.F.; Calvini, R.; Lopes, J.F.; Ulrici, A. Multi-target prediction of wheat flour quality parameters with near infrared spectroscopy. Inf. Process. Agric. 2020, 7, 342–354. [Google Scholar] [CrossRef]
- Nolasco Perez, I.M.; Badaró, A.T.; Barbon, S.; Barbon, A.P.A.; Pollonio, M.A.R.; Barbin, D.F. Classification of Chicken Parts Using a Portable Near-Infrared (NIR) Spectrophotometer and Machine Learning. Appl. Spectrosc. 2018, 72, 1774–1780. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Xu, W.; Yao, M.; Zheng, L.; Hu, C.; Zhang, Z.; Sun, Z. Convolutional neural networks open up horizons for luminescence thermometry. J. Lumin. 2023, 256, 119637. [Google Scholar] [CrossRef]
- Vlasic, A.; Sevic, D.; Rabasovic, M.S.; A Krizan, J.; Savic-Sevic, S.; Rabasovic, M.D.; Mitric, M.; Marinkovic, B.P.; Nikolic, M.G. Effects of temperature and pressure on luminescent properties of Sr2CeO4:Eu3+ nanophosphor. J. Lumin. 2018, 199, 285–292. [Google Scholar] [CrossRef]
- Chijioke, A.D.; Nellis, W.J.; Soldatov, A.; Silvera, I.F. The ruby pressure standard to 150GPa. J. Appl. Phys. 2005, 98, 114905. [Google Scholar] [CrossRef]
- Wise, B.M.; Gallagher, N.B.; Bro, R.; Shaver, J.M.; Windig, W.; Koch, R.S. Chemometrics Tutorial for PLS Toolbox and Solo; Eigenvector Research, Inc.: Manson, WA, USA, 2006; ISBN 0-9761184-1-6. [Google Scholar]
- Wise, B.M.; Gallagher, N.B.; Bro, R.; Shaver, J.M.; Windig, W.; Koch, R.S. Solo Software User’s Guide Version 1.1; Eigenvector Research, Inc.: Manson, WA, USA, 2010; Available online: https://www.software.eigenvector.com/user/Solo_Software_UsersGuide.pdf (accessed on 13 October 2025).
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Jelic, J.Z.; Dencevski, A.; Rabasovic, M.D.; Krizan, J.; Savic-Sevic, S.; Nikolic, M.G.; Aguirre, M.H.; Sevic, D.; Rabasovic, M.S. Improving the Two-Color Temperature Sensing Using Machine Learning Approach: GdVO4:Sm3+ Prepared by Solution Combustion Synthesis (SCS). Photonics 2024, 11, 642. [Google Scholar] [CrossRef]
- Blasse, G.; Grabmaier, B.C. A general introduction to luminescent materials. In Luminescent Materials; Springer: Berlin/Heidelberg, Germany, 1994; pp. 1–9. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar] [CrossRef]
- Mei, S.; Guo, Y.; Lin, X.; Dong, H.; Sun, L.D.; Li, K.; Yan, C.H. Experimental and simulation insights into local structure and luminescence evolution in Eu3+-doped nanocrystals under high pressure. J. Phys. Chem. Lett. 2020, 11, 3515–3520. [Google Scholar] [CrossRef]
- Zhang, C.C.; Zhang, Z.M.; Dai, R.C.; Wang, Z.P.; Zhang, J.W.; Ding, Z.J. High-pressure raman and luminescence study on the phase transition of GdVO4: Eu3+ microcrystals. J. Phys. Chem. C 2010, 114, 18279–18282. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Chen, S.; Li, Y.; Lv, Q.; Shao, B.; Zhao, L. A novel high efficiency and ultra-stable red emitting europium doped pyrophosphate phosphor for multifunctional applications. Inorg. Chem. Front. 2021, 8, 3984–3997. [Google Scholar] [CrossRef]
- Chen, X.; Lou, H.; Zeng, Z.; Cheng, B.; Zhang, X.; Liu, Y.; Xu, D.; Yang, K.; Zeng, Q. Structural transitions of 4:1 methanol–ethanol mixture and silicone oil under high pressure. Matter Radiat. Extrem. 2021, 6, 038402. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, Z.; Zhang, H.; Ren, Y.; Zhu, X.; Yang, K. Structural stability and phonon anharmonicity of Y2MoO6 Raman spectroscopic and XRD studies. Phys. B Condens. Matter 2017, 521, 43–48. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolic, M.G.; Sevic, D.; Rabasovic, M.S. Improving the High-Pressure Sensing Characteristics of Y2MoO6:Eu3+ Using a Machine Learning Approach. Photonics 2025, 12, 1024. https://doi.org/10.3390/photonics12101024
Nikolic MG, Sevic D, Rabasovic MS. Improving the High-Pressure Sensing Characteristics of Y2MoO6:Eu3+ Using a Machine Learning Approach. Photonics. 2025; 12(10):1024. https://doi.org/10.3390/photonics12101024
Chicago/Turabian StyleNikolic, Marko G., Dragutin Sevic, and Maja S. Rabasovic. 2025. "Improving the High-Pressure Sensing Characteristics of Y2MoO6:Eu3+ Using a Machine Learning Approach" Photonics 12, no. 10: 1024. https://doi.org/10.3390/photonics12101024
APA StyleNikolic, M. G., Sevic, D., & Rabasovic, M. S. (2025). Improving the High-Pressure Sensing Characteristics of Y2MoO6:Eu3+ Using a Machine Learning Approach. Photonics, 12(10), 1024. https://doi.org/10.3390/photonics12101024




