Inverse Judd–Ofelt Formalism Based on Radiative Lifetime for Comparative Spectroscopy of RE3+ Ions in Glass
Abstract
1. Introduction
2. Theory and Notation
2.1. JO Relations (ED Line Strength, Radiative Rate, Branching)
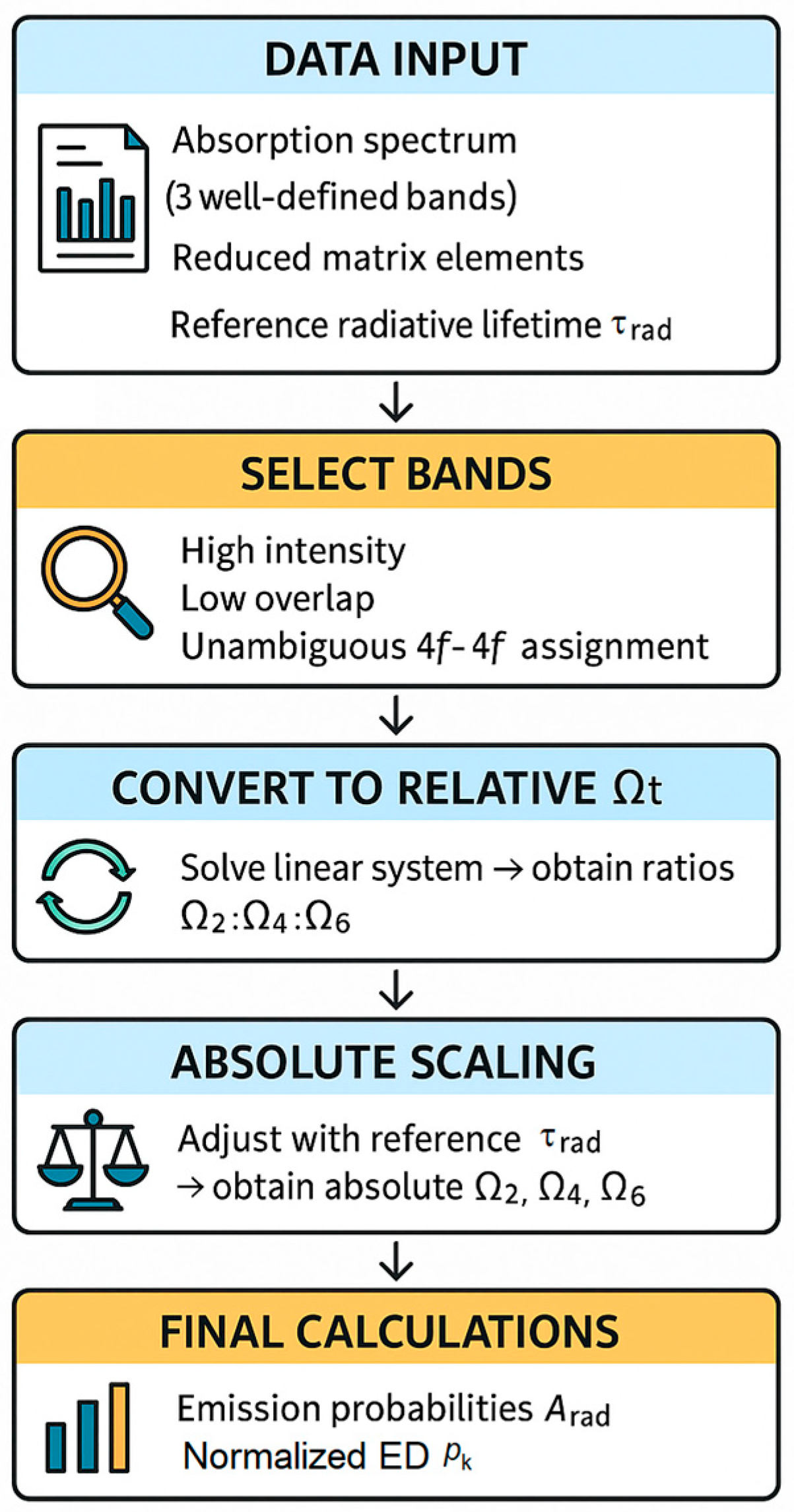
2.2. Inverse JO from Relative Absorption: Ratios and Absolute Scaling
2.3. Fixing the Absolute Scale by a Lifetime Constraint
Summary of Scaling Logic
2.4. Assumptions and Physical Validity
- Physical grounding of the inverse JO approach: The inverse route does not modify JO physics; it only changes the data normalization. The integrated absorbance areas Sk of ground-state bands are proportional to the same electric–dipole line strengths that underlie classical JO, i.e., Sk ∝ , up to a single global prefactor (thickness, dopant density, detector gain, local-field). That prefactor multiplies all bands equally and therefore sets only the absolute scale of (Ω2, Ω4, Ω6). Ratios such as h = Ω2/(Ω4 + Ω6) and χ = Ω4/Ω6, and within-set normalized fractions pk, remain invariant and retain their physical meaning (e.g., hypersensitivity, medium-range rigidity, branching trends). Selection rules, local-field modeling, and Einstein relations are exactly those of classical JO; we simply exploit the scale-independence of the ratios to work with relative spectra.
- Electric–dipole (ED) dominance: The three bands per ion are ED-allowed in these hosts; magnetic–dipole (MD) terms are neglected within the chosen windows. This is standard for the selected manifolds in oxide/oxyfluoride glasses and within our uncertainty budget [8,9,10,25]. For the selected bands in these oxyfluoride glasses, magnetic–dipole (MD) contributions are estimated to remain below ~10% [8,9,10,25]. Within this uncertainty budget they are neglected here, although the framework allows their inclusion whenever significant.
- Small Stokes shift: For intra-4f transitions we take λem ≈ λabs in the λ−3 factor of Equation (2); the resulting bias is sub-dominant relative to baseline/window choices used to form Srel,k (Section 3.1.1). The Einstein-rate scaling with λ−3 follows standard radiative-rate formulas [27].
- Local-field model: We adopt the virtual-cavity factor , with a representative visible-wavelength refractive index n = 1.52 for these oxyfluoride glasses [28], consistent with typical values in related hosts and borosilicate-crown standards [29,30]. Varying n within 1.50–1.55 changes L (n) by ≈ 11% (about +4% from 1.50→1.52), which only rescales absolute Arad; the normalized fractions and the JO ratios are unaffected.
- Minimal determinacy and stability: With three bands and three Ωt, Equation (6) is minimally determined. Stability relies on the linear independence of the rows of U (each defined by ); conditioning is verified before scaling. Solver choices and diagnostics (non-negative least squares, residual norms, condition numbers) are detailed in Section 3.1.
3. Experimental
3.1. Computational Methodology
3.1.1. Spectral Preprocessing and Band Integration
3.1.2. Inverse JO Analysis from Normalized Areas
3.1.3. Scaling and Uncertainty Analysis
- (i)
- baseline fits were jittered within the local noise;
- (ii)
- integration half-widths were randomly varied by ±(5–10) nm;
- (iii)
- peak centers were dithered by ±2 nm to emulate discrete sampling.
3.2. Glass Preparation and Absorption Measurements
4. Results and Discussion
4.1. Absorption Features
4.2. JO Intensity Parameters: Trends and Host Interpretation
4.3. Radiative Probabilities and Normalized ED Fractions Pk
4.4. Cross-Ion Comparison Under Uniform Optical Assumptions
- (i)
- Site asymmetry/covalency: Ω2 follows Dy3+ > Er3+ > Sm3+ (see Section 4.2; Table 4);
- (ii)
- Intermediate- vs. long-range response: The empirical rule Ω4 > Ω6 holds for all ions (see Section 4.2; Table 4);
- (iii)
- Radiative partitioning within the selected triplets: The normalized ED fractions pk (Table 5) summarize how each ion distributes ED strength under identical assumptions. In brief, Er3+ is dominated by the blue–green 4I15/2 →2H11/2 branch with 4I15/2 → 4F7/2 secondary and 4I11/2 minor; Sm3+ partitions more evenly across the near-IR set, led by 6F5/2 with contributions from 6F3/2 and 6F7/2; Dy3+ is most asymmetric, with the longest-wavelength mixed (6F11/2 + 6H9/2) feature leading, followed by the mixed (6F7/2 + 6H5/2) line and 6F5/2. For numerical values and uncertainties, see Section 4.3 and Table 5.
- (iv)
- Link to glass composition: In the 60SiO2–20Al2O3–10Na2O–10BaF2 matrix, an oxide-leaning backbone (Si–O–Al cross-linking) promotes Ω4 > Ω6, while F− coordination tends to lower covalency and suppress Ω2. The very small Ω2 of Sm3+ is therefore consistent with more ionic, more symmetric local fields (greater RE–F share/fewer nearby NBOs), whereas the large Ω2 of Dy3+ suggests O-richer, asymmetry-enhancing neighborhoods (modifier/NBO influence). Er3+ combines moderate Ω2 with the largest χ, consistent with stiffer intermediate-range environments in this aluminosilicate-rich glass [30,35,36,44,45].
- (v)
- Robustness: These qualitative rankings persist within the 95% confidence intervals reported in Table 5. Treating Dy3+ mixed features as single bands (with summed ⟨U(t)⟩2) preserves the linear model and does not change the ordering of Ωt or the pk patterns; changes to n or τref rescale Arad, but leave Ω-ratios and pk unchanged [19,38,39,40,41,42].
4.5. Practical Implications
4.6. Limitations and Sensitivity
4.7. Where This Approach Helps—And Where It Does Not
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Symbols (by Workflow)
| Symbol/Term | Meaning (Concise) | Where Defined |
| S = {1, 2, 3} | Set of the three selected ground-state transitions per ion | Section 2 |
| Srel,k | Normalized band strength from absorption (unitless) | Section 3.1.1 |
| Uk,t | Squared reduced matrix element for band k and rank t ∈ {2,4,6} | Section 2 |
| JO | Judd–Ofelt theory/parameters | Section 2 |
| Scale-free JO parameters from inverse NNLS | Section 2.3 | |
| NNLS | Non-negative least squares (solver for Equation (6)) | Section 3.1.2 |
| SED | Electric–dipole (ED) line strength | Section 2 |
| κ(n, Ju) | Prefactor in Equation (2) (includes local-field and degeneracy terms) | Section 2.4 |
| Virtual-cavity local-field factor | Section 2.4 | |
| Relative Einstein coefficient from Equation (2) with Ω(rel) | Section 2.3 | |
| τref | Lifetime anchor used to set the absolute scale | Section 2.3 |
| α | Global scaling factor converting relative → absolute (Ωt,Arad) | Section 2.3 |
| Arad, Arad,tot | Absolute Einstein rate; sum over S equals 1/τref | Section 2.3 |
| τrad | Radiative lifetime computed from Arad | Section 2.3 |
| ED/MD | Electric–dipole/magnetic–dipole | Section 2 |
| β | Branching ratio (single emitting manifold only) | Section 2.1 |
| pk | Normalized fraction within S (not an oscillator strength) | Section 2.1 |
| MC | Monte Carlo resampling for uncertainties | Section 3.1.3 |
| CI 95% | Percentile-based 95% confidence interval | Section 3.1.3 |
Appendix A. Invariance of Omega-Ratios and Normalized Fractions
Statement and Proof
References
- Auzel, F. Upconversion and anti-Stokes processes with f and d ions in solids. Chem. Rev. 2004, 104, 139–173. [Google Scholar] [CrossRef] [PubMed]
- Binnemans, K. Interpretation of europium(III) spectra. Coord. Chem. Rev. 2015, 295, 1–45. [Google Scholar] [CrossRef]
- Hong, Z.; Yue, H.; Lin, Z.; Luo, X.; Hou, H.; Wu, S.; Lai, F.; Wang, W.; You, W.; Huang, J. Photoluminescence properties of Dy3+/Sm3+ co-doped gallium silicate glass–ceramics for solid-state warm white lighting. J. Non-Cryst. Solids 2024, 628, 122837. [Google Scholar] [CrossRef]
- Blanc, W.; Choi, Y.G.; Zhang, X.; Nalin, M.; Richardson, K.A.; Righini, G.C.; Ferrari, M.; Jha, A.; Massera, J.; Jiang, S.; et al. The past, present and future of photonic glasses: A review in homage to the United Nations International Year of glass 2022. Prog. Mater. Sci. 2023, 134, 101084. [Google Scholar] [CrossRef]
- Judd, B.R. Optical absorption intensities of rare-earth ions. Phys. Rev. 1962, 127, 750–761. [Google Scholar] [CrossRef]
- Ofelt, G.S. Intensities of crystal spectra of rare earth ions. J. Chem. Phys. 1962, 37, 511–520. [Google Scholar] [CrossRef]
- Reisfeld, R.; Jørgensen, C.K. Lasers and Excited States of Rare Earths; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Weber, M.J. Spontaneous emission probabilities for Sm3+, Eu3+, and Gd3+ in LaF3. Phys. Rev. 1967, 157, 262–272. [Google Scholar] [CrossRef]
- Jorgensen, C.K.; Reisfeld, R. Judd–Ofelt parameters and chemical bonding in lanthanide complexes and glasses. J. Less Common Met. 1983, 93, 107–112. [Google Scholar] [CrossRef]
- Carnall, W.T.; Goodman, G.L.; Rajnak, K.; Rana, R.S. A systematic analysis of the spectra of the lanthanides doped into single crystal LaF3. J. Chem. Phys. 1989, 90, 3443–3457. [Google Scholar] [CrossRef]
- Hehlen, M.P.; Brik, M.G.; Krämer, K.W. 50th anniversary of the Judd–Ofelt theory: An experimentalist’s view of the formalism and its application. J. Lumin. 2013, 136, 221–239. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, Y.; Zhang, D.-L. Comment on “A universal approach for calculating the Judd–Ofelt parameters of RE3+ in powdered phosphors and its application for the β-NaYF4:Er3+/Yb3+ phosphor derived from auto-combustion-assisted fluoridation”. Phys. Chem. Chem. Phys. 2019, 21, 10834–10839. [Google Scholar] [CrossRef]
- Ćirić, A.; Stojadinović, S.; Sekulić, M.; Dramićanin, M.D. JOES: An application software for Judd–Ofelt analysis from Eu3+ emission spectra. J. Lumin. 2019, 205, 351–356. [Google Scholar] [CrossRef]
- Ćirić, A.; Marciniak, Ł.; Dramićanin, M.D. Self-referenced method for the Judd–Ofelt parametrisation of the Eu3+ excitation spectrum. Sci. Rep. 2022, 12, 563. [Google Scholar] [CrossRef] [PubMed]
- Neto, J.A.M.; Hewak, D.W. Application of a modified Judd–Ofelt theory to Pr3+ doped fluoride glasses. J. Non-Cryst. Solids 1995, 183, 201–207. [Google Scholar] [CrossRef]
- Goldner, P.; Auzel, F. Application of standard and modified Judd–Ofelt theories to a praseodymium-doped fluorozirconate glass. J. Appl. Phys. 1996, 79, 7972–7977. [Google Scholar] [CrossRef]
- Hien, N.T.; Kien, N.T.; Yen, V.H.; Ngoc, T.; Do, P.V.; Phuc, V.X.; Ca, N.X. Optical properties and Judd–Ofelt analysis of Dy3+ doped CoAl2O4 nanocrystals. J. Lumin. 2023, 249, 117245. [Google Scholar] [CrossRef]
- Xue, S.-D.; Liu, M.-H.; Zhang, P.; Wong, W.-H.; Zhang, D.-L. Validity of Judd-Ofelt spectroscopy based on diffuse reflectance spectrum and fluorescence lifetime of phosphor. J. Lumin. 2020, 224, 117304. [Google Scholar] [CrossRef]
- Vega, M.; Alemany, P.; Martín, I.R.; Llanos, J. Structural properties, Judd–Ofelt calculations, and near infrared to visible photon up-conversion in Er3+/Yb3+ doped BaTiO3 phosphors under excitation at 1500 nm. RSC Adv. 2017, 7, 10529–10536. [Google Scholar] [CrossRef]
- Hrabovsky, J.; Varak, P.; Krystufek, R. LOMS.cz computational platform for high-throughput classical and combinatorial Judd-Ofelt analysis and rare-earth spectroscopy. Sci. Rep. 2025, 15, 28945. [Google Scholar] [CrossRef] [PubMed]
- Kumar, G.M.; Rao, D.N.; Agarwal, G.S. Measurement of Local Field Effects of the Host on the Lifetimes of Embedded Emitters. Phys. Rev. Lett. 2003, 91, 203903. [Google Scholar] [CrossRef]
- Babu, S.; Balakrishna, A.; Rajesh, D.; Ratnakaram, Y.C. Dy3+ doped oxy-fluoride phosphate glasses for laser materials: A photoluminescence study. Int. J. ChemTech Res. 2014, 6, 3276–3279. [Google Scholar]
- Pradeesh, K.; Oton, C.J.; Agotiya, V.K.; Raghavendra, M.; Vijaya Prakash, G. Optical properties of Er3+ doped alkali chlorophosphate glasses for optical amplifiers. Opt. Mater. 2008, 31, 155–160. [Google Scholar] [CrossRef]
- Pugliese, D.; Boetti, N.G.; Lousteau, J.; Ceci-Ginistrelli, E.; Bertone, E.; Geobaldo, F.; Milanese, D. Concentration quenching in an Er-doped phosphate glass for compact optical lasers and amplifiers. J. Alloys Compd. 2016, 657, 678–683. [Google Scholar] [CrossRef]
- Pisarski, W.A. Judd–Ofelt Analysis and Emission Properties of Dy3+ Ions in Borogermanate Glasses. Materials 2022, 15, 9042. [Google Scholar] [CrossRef] [PubMed]
- Praveena, R.; Venkatramu, V.; Babu, P.; Jayasankar, C.K. Fluorescence spectroscopy of Sm3+ ions in P2O5–PbO–Nb2O5 glasses. Phys. B Condens. Matter 2008, 403, 3527–3534. [Google Scholar] [CrossRef]
- Hilborn, R.C. Einstein coefficients, cross sections, f values, dipole moments, and all that. Am. J. Phys. 1982, 50, 982–986. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, Y.; Zheng, R.-L.; Shen, J.-P.; Guo, H.-T.; Liu, C.-X. Optical characteristics of an oxyfluoride glass waveguide formed by a proton implantation. Results Phys. 2018, 10, 200–204. [Google Scholar] [CrossRef]
- SCHOTTAG. N-BK7® Optical Glass Data Sheet (nd = 1.51680 at 587.6 nm); SCHOTTAG: Mainz, Germany, 2023. [Google Scholar]
- RP Photonics Encyclopedia. (s.d.). Crown Glasses (BK7 nd = 1.5168, nd = 1.5168, nd = 1.5168). Available online: https://www.rp-photonics.com/crown_glasses.html (accessed on 13 August 2025).
- Dieke, G.H. Spectra and Energy Levels of Rare Earth Ions in Crystals; Interscience Publishers: New York, NY, USA, 1968. [Google Scholar]
- Poonam Shivani Anu Kumar, A.; Sahu, M.K.; Rani, P.R.; Deopa, N.; Punia, R.; Rao, A.S. Judd–Ofelt parameterization and luminescence characterization of Dy3+ doped oxyfluoride lithium zinc borosilicate glasses for lasers and w-LEDs. J. Non-Cryst. Solids 2020, 544, 120187. [Google Scholar] [CrossRef]
- Naresh, V.; Buddhudu, S. Analysis of visible–NIR emission and photoluminescence quenching in Er3+:Bi2O3–AlF3–TeO2–B2O3 glasses. Phys. Chem. Glas. Eur. J. Glass Sci. Technol. B 2015, 56, 255–262. [Google Scholar] [CrossRef]
- Kirdsiri, K.; Raja Ramakrishna, R.; Damdee, B.; Kim, H.J.; Kaewjaeng, S.; Kothan, S.; Kaewkhao, J. Optical and luminescence features of Sm3+-doped Li2O–MO–B2O3 (M = Mg/Ca/Sr/Ba) glasses for orange emission in WLEDs. J. Alloys Compd. 2018, 749, 197–204. [Google Scholar] [CrossRef]
- Naresh, V.; Buddhudu, S. Energy-transfer-based emission spectra of (Sm3+, Dy3+):Li2O–LiF–B2O3–CdO glasses. J. Lumin. 2014, 147, 63–71. [Google Scholar] [CrossRef]
- Boudchicha, N.; Iezid, M.; Goumeidane, F.; Legouera, M.; Prasad, P.S.; Rao, P.V. Judd–Ofelt Analysis and Spectroscopy Study of Tellurite Glasses Doped with Rare-Earth (Nd3+, Sm3+, Dy3+, and Er3+). Materials 2023, 16, 6832. [Google Scholar] [CrossRef]
- Tanabe, S.; Ohyagi, T.; Soga, N.; Hanada, T. Compositional dependence of Judd–Ofelt parameters of Er3+ ions in alkali-metal borate glasses. Phys. Rev. B 1992, 46, 3305–3310. [Google Scholar] [CrossRef]
- Ebendorff-Heidepriem, H.; Ehrt, D.; Bettinelli, M.; Speghini, A. Effect of glass composition on Judd–Ofelt parameters and radiative decay rates of Er3+ in fluoride phosphate and phosphate glasses. J. Non-Cryst. Solids 1998, 240, 66–78. [Google Scholar] [CrossRef]
- Duan, Z.; Zhang, J.; Hu, L. Spectroscopic properties Judd-Ofelt theory analysis of doped oxyfluoride silicate glass. J. Appl. Phys. 2007, 101, 043110. [Google Scholar] [CrossRef]
- Mukamil, S.; Shahid, N.; Sarumaha, C.; Khattak, S.A.; Wabaidur, S.M.; Islam, M.A.; Kothan, S.; Shoaib, M.; Khan, I.; Ullah, I.; et al. Spectroscopic investigation of dysprosium doped bismuth-borate glasses for white light application. Opt. Mater. 2022, 127, 112291. [Google Scholar] [CrossRef]
- Heo, J. 1.3-μm-emission properties and local structure of Dy3+ in chalcohalide glasses. Comptes Rendus. Chimie 2002, 5, 739–749. [Google Scholar] [CrossRef]
- Joseph, P.A.J.; Maheshvaran, K.; Rayappan, I.A. Structural and optical studies on Dy3+ ions doped alkali lead borophosphate glasses for white light applications. J. Non-Cryst. Solids 2021, 557, 120652. [Google Scholar] [CrossRef]
- Szymański, D.; Sobczyk, M. Optical and structural investigation of dysprosium doped-Y2Te4O11. J. Lumin. 2016, 173, 11–18. [Google Scholar] [CrossRef]
- Jørgensen Chr, K.; Judd, B.R. Hypersensitive pseudoquadrupole transitions in lanthanides. Mol. Phys. 1964, 8, 281–290. [Google Scholar] [CrossRef]
- Van Deun, R.; Binnemans, K.; Görller-Walrand, C.; Adam, J.L. Judd–Ofelt intensity parameters of trivalent lanthanide ions in a NaPO3–BaF2-based fluorophosphate glass. J. Alloys Compd. 1999, 283, 59–65. [Google Scholar] [CrossRef]
- Lalla, E.A.; Konstantinidis, M.; De Souza, I.; Daly, M.G.; Martín, I.R.; Lavín, V.; Rodríguez-Mendoza, U.R. Judd–Ofelt parameters of RE3+-doped fluorotellurite glass (RE3+ = Pr3+, Nd3+, Sm3+, Tb3+, Dy3+, Ho3+, Er3+, and Tm3+). J. Alloys Compd. 2020, 845, 156028. [Google Scholar] [CrossRef]
- Lu, K.; Liu, Z.; Wang, Y.; Yang, W.; Peng, H.; Ye, Y.; Shi, Y.; Qi, J.; Lu, T. Optical transmission and transition properties of lanthanide doped highly transparent Y2Zr2O7 ceramics. J. Alloys Compd. 2022, 905, 164133. [Google Scholar] [CrossRef]
- Takebe, H.; Nageno, Y.; Morinaga, K. Compositional Dependence of Judd-Ofelt Parameters in Silicate, Borate, and Phosphate Glasses. J. Am. Ceram. Soc. 1995, 78, 1161–1168. [Google Scholar] [CrossRef]
- Kesavulu, C.R.; Yoo, M.Y.; Lee, J.H.; Lim, K.-S.; Dharmaiah, P.; Jayasankar, C.K.; Babu, P. Optical and upconversion properties of Er3+-doped oxyfluoride transparent glass-ceramics containing SrF2 nanocrystals. J. Mater. Res. 2013, 28, 1481–1489. [Google Scholar] [CrossRef]
- Bansal, K.; Mishra, N.K.; Abdullahi, I.; Singh, P.J.; Tyagi, M.; Singh, S. Studies of luminescence traits and Judd–Ofelt analysis of Sm3+-activated oxyfluoride glasses. Opt. Mater. 2024, 147, 114579. [Google Scholar] [CrossRef]
- Chen, F.; Wei, T.; Jing, X.; Tian, Y.; Zhang, J.; Xu, S. Investigation of mid-infrared emission characteristics and energy transfer dynamics in Er3+ doped oxyfluoride tellurite glass. Sci. Rep. 2015, 5, 10676. [Google Scholar] [CrossRef] [PubMed]
- Yamsuk, Y.; Yasaka, P.; Kaewkhao, J.; Sangwaranatee, N. Sm3+ ions doped zinc barium tellurite oxyfluoride glasses for laser materials. J. Met. Mater. Miner. 2020, 30, 10. [Google Scholar] [CrossRef]
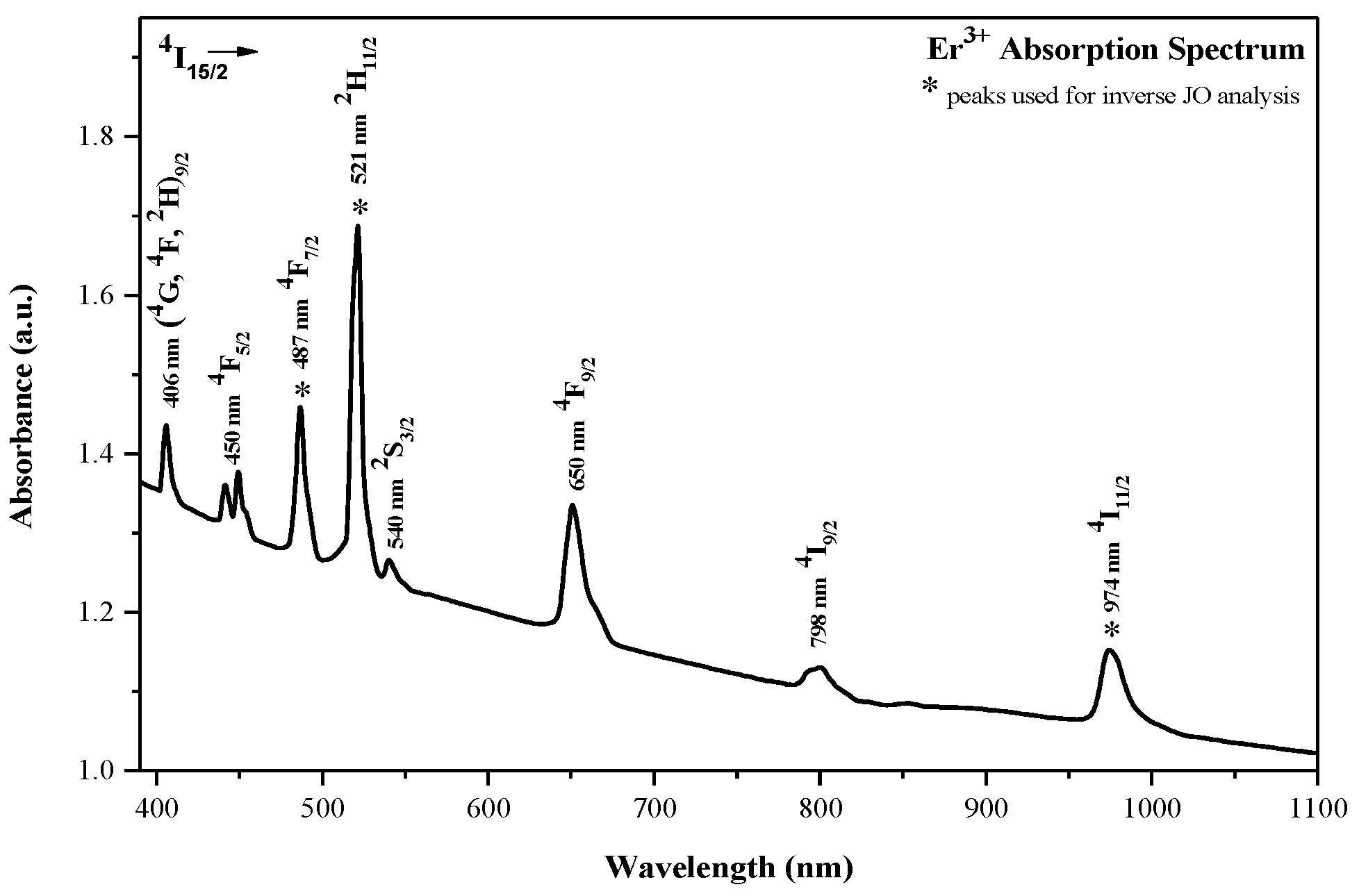

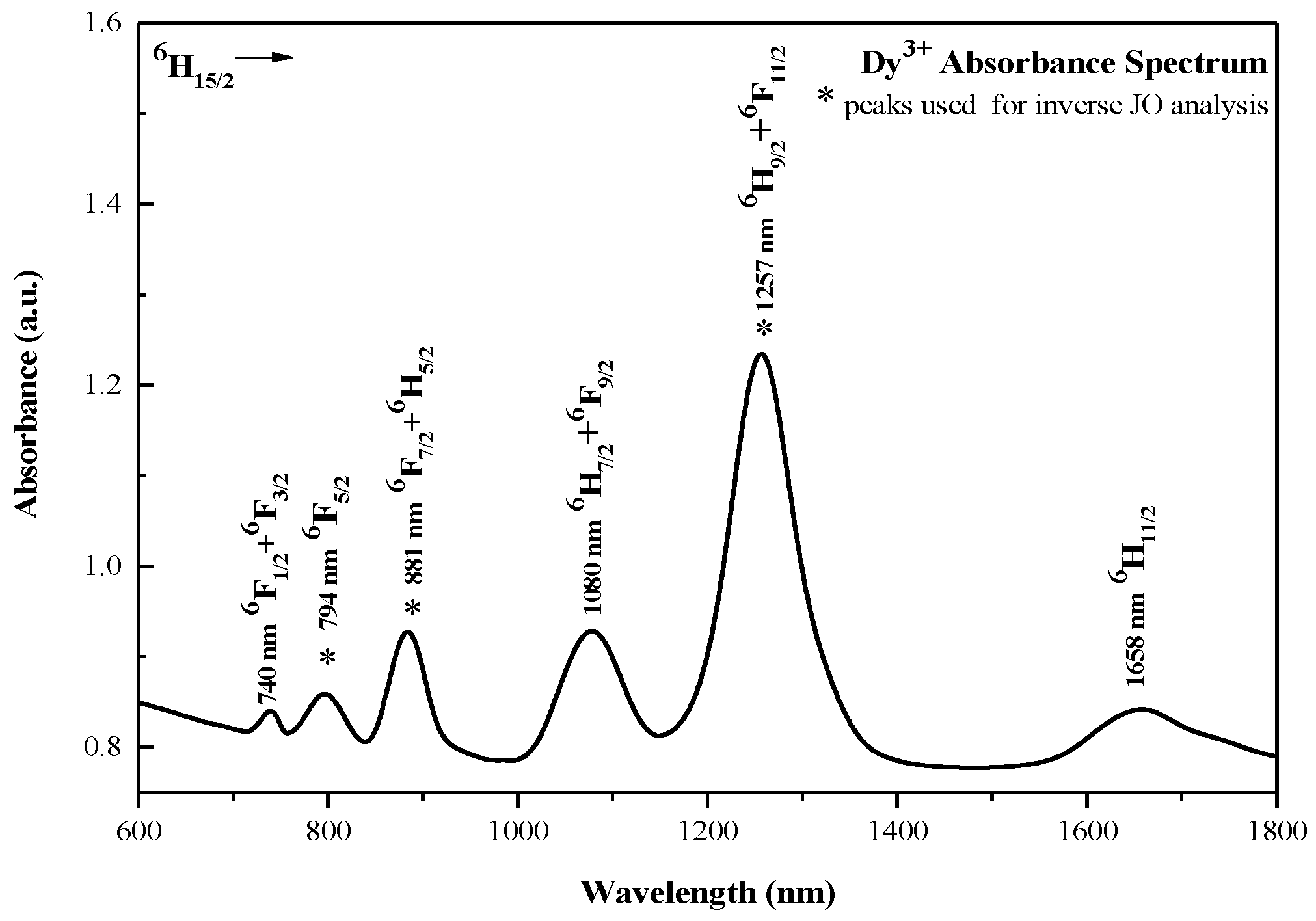
| Peak | l (nm) | Electronic Transition | ) (×10−6 a.u./nm) | Srel,k | ⟨U(2)⟩2 | ⟨U(4)⟩2 | ⟨U(6)⟩2 |
|---|---|---|---|---|---|---|---|
| 1 | 487 | 4I15/2→4F7/2 | 3.224 | 0.467 | 0.0 | 0.1465 | 0.6272 |
| 2 | 521 | 4I15/2→2H11/2 | 6.908 | 1.00 | 0.7158 | 0.4138 | 0.0927 |
| 3 | 974 | 4I15/2→4I11/2 | 1.169 | 0.169 | 0.0276 | 0.0002 | 0.3942 |
| Peak | l (nm) | Electronic Transition | ) (×10−6 a.u./nm) | Srel,k | ⟨U(2)⟩2 | ⟨U(4)⟩2 | ⟨U(6)⟩2 |
|---|---|---|---|---|---|---|---|
| 1 | 1232 | 6H5/2→6F7/2 | 1.843 | 1.0 | 0.0020 | 0.1429 | 0.4301 |
| 2 | 1380 | 6H5/2→6F5/2 | 0.822 | 0.446 | 0.0331 | 0.2844 | 0.0 |
| 3 | 1487 | 6H5/2→6F3/2 | 0.706 | 0.383 | 0.1444 | 0.1365 | 0.0 |
| Peak | l (nm) | Electronic Transition | ) (×10−6 a.u./nm) | Srel,k | ⟨U(2)⟩2 | ⟨U(4)⟩2 | ⟨U(6)⟩2 |
|---|---|---|---|---|---|---|---|
| 1 | 794 | 6H15/2→6F5/2 | 0.154 | 0.092 | 0.0 | 0.0 | 0.3446 |
| 2 | 881 | 6H15/2→6F7/2+6H5/2 | 0.412 | 0.246 | 0.0 | 0.1352 | 0.7164 |
| 3 | 1257 | 6H15/2→6F11/2+6H9/2 | 1.673 | 1.0 | 0.9394 | 0.8465 | 0.4078 |
| Ion | Ω2 (×10−20 cm2) | Ω4 (×10−20 cm2) | Ω6 (×10−20 cm2) |
|---|---|---|---|
| Dy3+ | 4.910 | 3.368 | 2.246 |
| Sm3+ | 0.193 | 2.040 | 1.388 |
| Er3+ | 2.257 | 3.380 | 0.700 |
| Ion | Electronic Transition | λ (nm) | SED (×10−20 cm2) | Arad (s−1) | 95% CI on Arad | pk | 95% CI on pk | Arad,tot (s−1) |
|---|---|---|---|---|---|---|---|---|
| Er3+ | 4I15/2→4F7/2 | 487 | 0.934 | 133.9 | 116.3–153.2 | 0.268 | 0.233–0.306 | 500 |
| Er3+ | 4I15/2→2H11/2 | 521 | 3.079 | 360.1 | 340.2–378.0 | 0.720 | 0.680–0.756 | |
| Er3+ | 4I15/2→4I11/2 | 974 | 0.339 | 6.0 | 4.5–7.6 | 0.012 | 0.009–0.015 | |
| Sm3+ | 6H5/2→6F7/2 | 1232 | 0.889 | 102.3 | 91.1–113.6 | 0.205 | 0.182–0.227 | 500 |
| Sm3+ | 6H5/2→6F5/2 | 1380 | 0.587 | 258.7 | 246.0–270.9 | 0.517 | 0.492–0.542 | |
| Sm3+ | 6H5/2→6F3/2 | 1487 | 0.306 | 139.0 | 124.0–154.0 | 0.278 | 0.248–0.308 | |
| Dy3+ | 6H15/2→6F5/2 | 794 | 0.774 | 88.3 | 75.0–102.3 | 0.177 | 0.150–0.205 | 500 |
| Dy3+ | 6H15/2→6F7/2+6H5/2 | 881 | 2.064 | 171.7 | 152.6–190.8 | 0.343 | 0.305–0.382 | |
| Dy3+ | 6H15/2→6F11/2+6H9/2 | 1257 | 8.379 | 240.0 | 218.7–260.9 | 0.480 | 0.437–0.522 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasconcelos, H.C.; Meirelles, M.G.; Özmenteş, R. Inverse Judd–Ofelt Formalism Based on Radiative Lifetime for Comparative Spectroscopy of RE3+ Ions in Glass. Photonics 2025, 12, 1011. https://doi.org/10.3390/photonics12101011
Vasconcelos HC, Meirelles MG, Özmenteş R. Inverse Judd–Ofelt Formalism Based on Radiative Lifetime for Comparative Spectroscopy of RE3+ Ions in Glass. Photonics. 2025; 12(10):1011. https://doi.org/10.3390/photonics12101011
Chicago/Turabian StyleVasconcelos, Helena Cristina, Maria Gabriela Meirelles, and Reşit Özmenteş. 2025. "Inverse Judd–Ofelt Formalism Based on Radiative Lifetime for Comparative Spectroscopy of RE3+ Ions in Glass" Photonics 12, no. 10: 1011. https://doi.org/10.3390/photonics12101011
APA StyleVasconcelos, H. C., Meirelles, M. G., & Özmenteş, R. (2025). Inverse Judd–Ofelt Formalism Based on Radiative Lifetime for Comparative Spectroscopy of RE3+ Ions in Glass. Photonics, 12(10), 1011. https://doi.org/10.3390/photonics12101011






