Tunable Graphene Plasmonic Sensor for Multi-Component Molecular Detection in the Mid-Infrared Assisted by Machine Learning
Abstract
1. Introduction
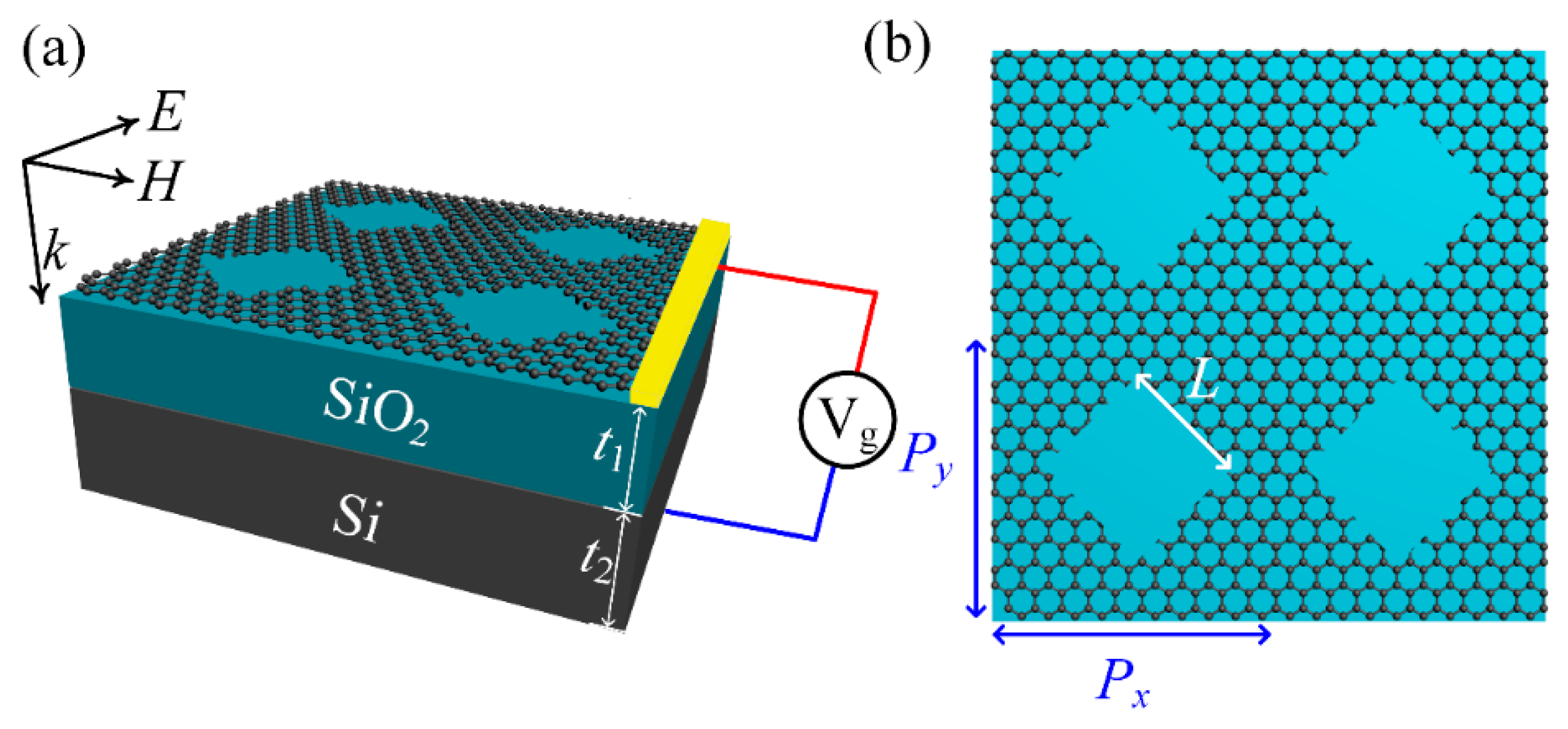
2. Materials and Methods
3. Results and Discussion
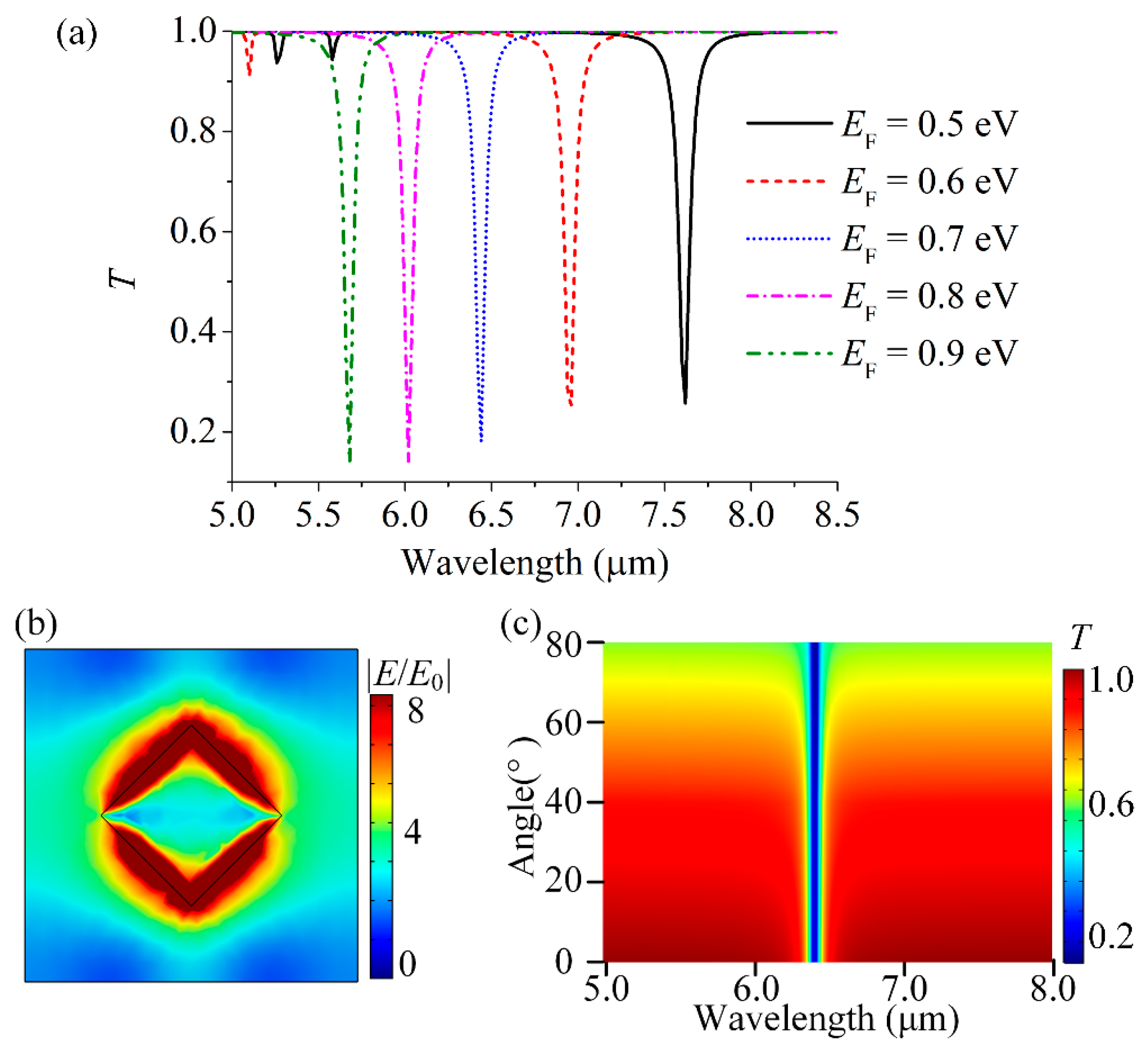
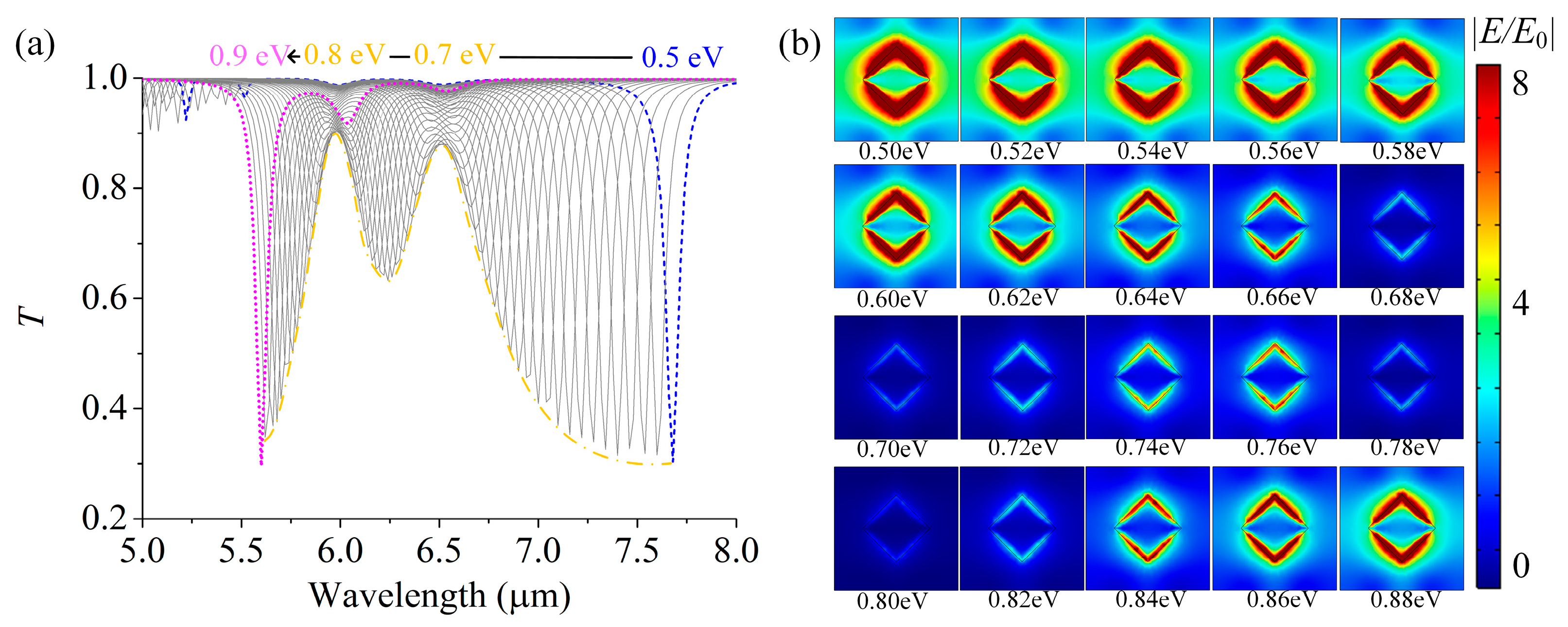
3.1. Surface Plasmon Properties of Single-Layer GSA Arrays
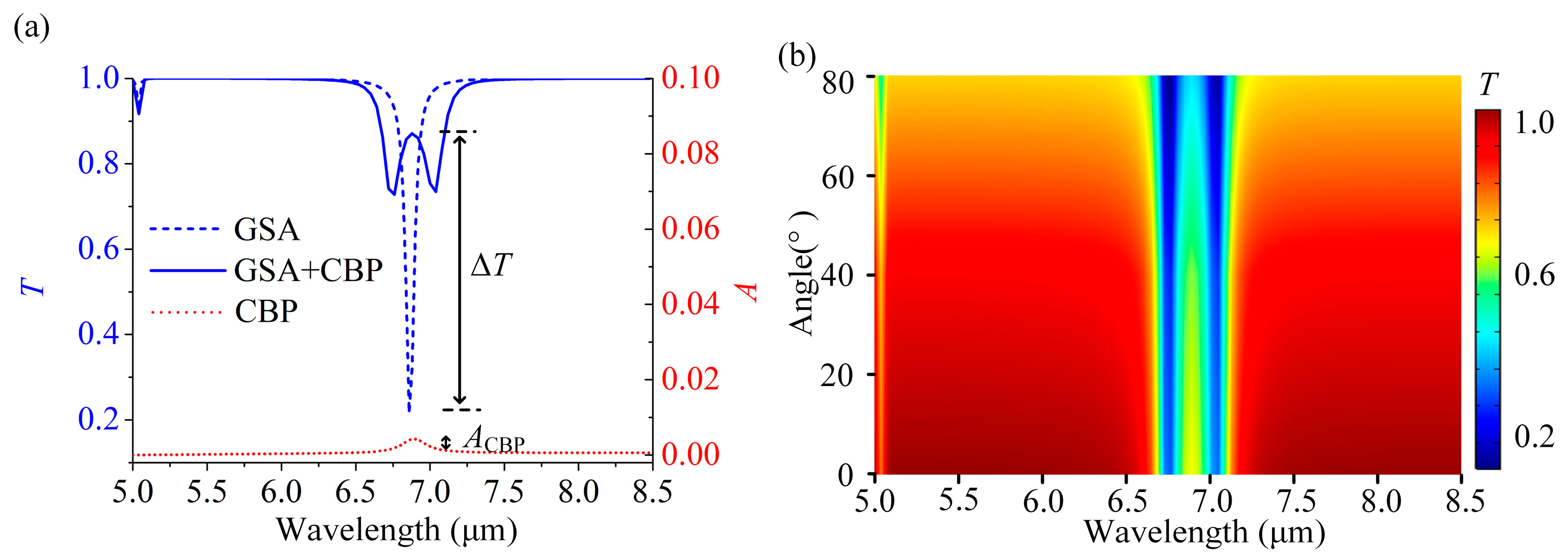
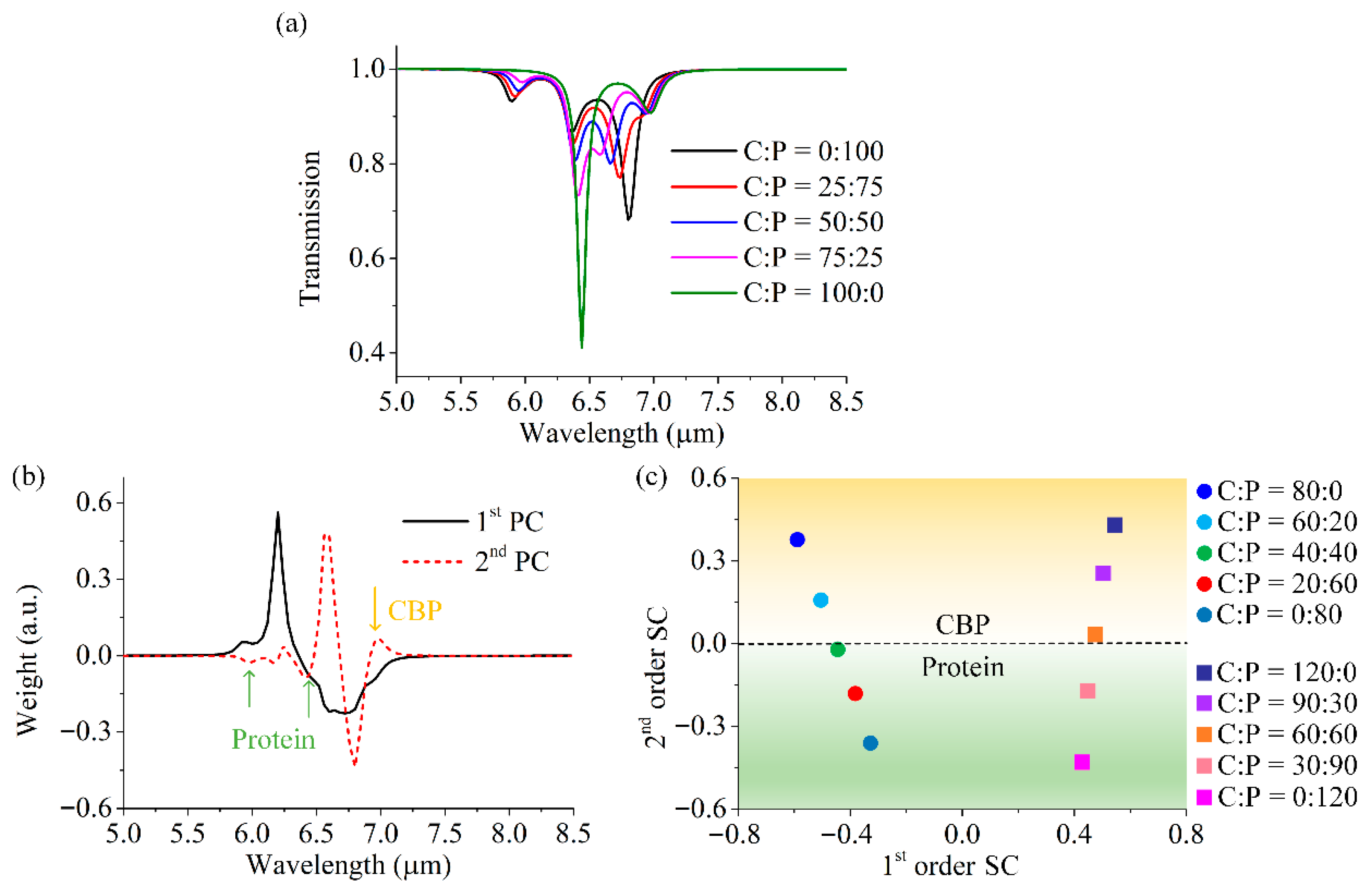
3.2. Molecular Qualitative Detection Based on the GSA Arrays
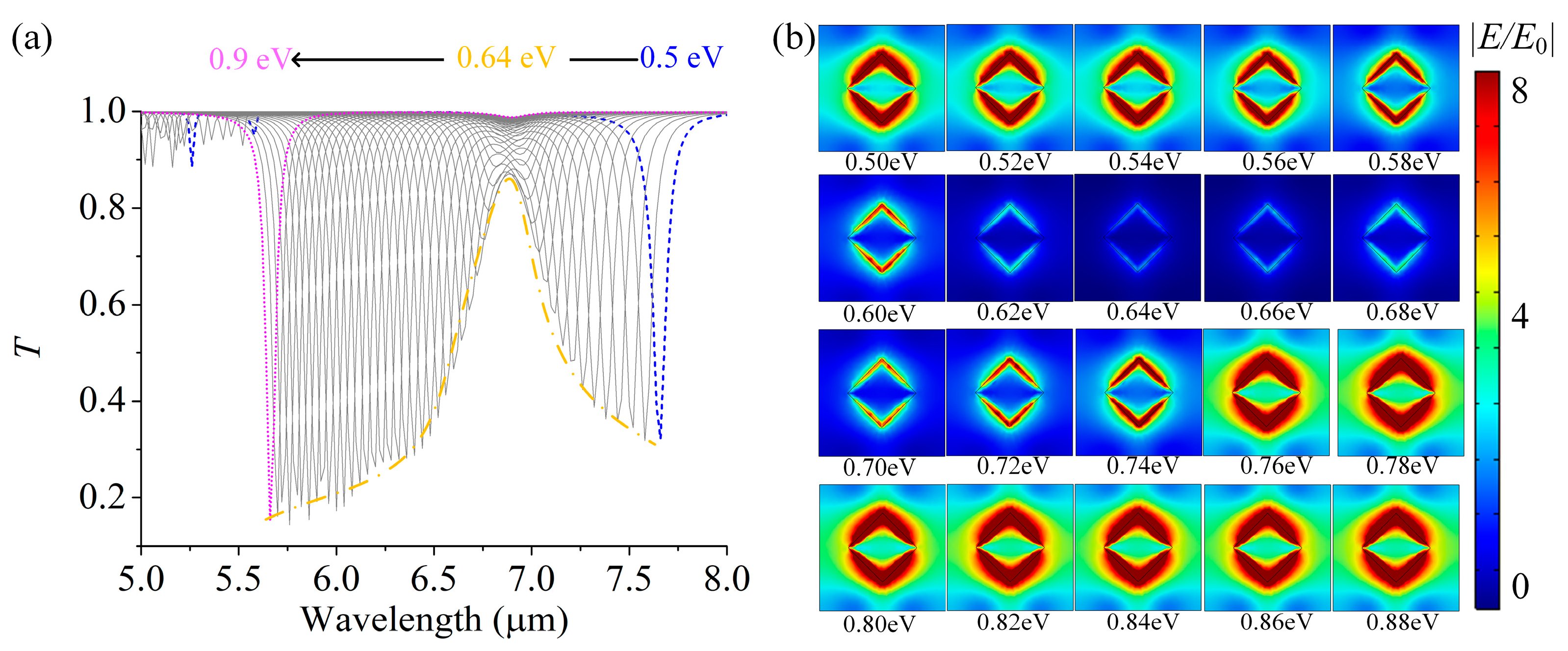
3.3. Molecular Quantitative Detection Based on the GSA Arrays and PCA Algorithm
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rangel, G.F.; Martínez, L.D.D.; Walter, L.S.; Mizaikoff, B. Recent advances and trends in mid-infrared chem/bio sensors. Trends Anal. Chem. 2024, 180, 117916. [Google Scholar] [CrossRef]
- Brolo, A.G. Plasmonics for Future Biosensors. Nat. Photonics 2012, 6, 709–713. [Google Scholar] [CrossRef]
- Jain, P.K.; Huang, X.; El-Sayed, I.H.; El-Sayed, M.A. Noble metals on the nanoscale: Optical and photothermal properties and some applications in imaging, sensing, biology, and medicine. Acc. Chem. Res. 2008, 41, 1578–1586. [Google Scholar] [CrossRef]
- Qu, W.-G.; Deng, B.; Zhong, S.-L.; Shi, H.-Y.; Wang, S.-S.; Xu, A.-W. Plasmonic resonance energy transfer-based nanospectroscopy for sensitive and selective detection of 2,4,6-trinitrotoluene (TNT). Chem. Commun. 2011, 47, 1237–1239. [Google Scholar] [CrossRef]
- Willets, K.A.; Van Duyne, R.P. Localized Surface Plasmon Resonance Spectroscopy and Sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef]
- Mayerhofer, T.G.; Popp, J. Periodic Array-Based Substrates for Surface-Enhanced Infrared Spectroscopy. Nanophotonics 2018, 7, 39–79. [Google Scholar] [CrossRef]
- Maleki, M.J.; Soroosh, M.; AL-Shammri, F.K.; Alkhayer, A.G.; Mondal, H. Design and Simulation of a Compact Subwavelength Graphene Based Switch for Surface Plasmon Polariton Transmission in Integrated Optoelectronic Circuits. Plasmonics 2025, 20, 3605–3617. [Google Scholar] [CrossRef]
- Mcoyi, M.P.; Mpofu, K.T.; Sekhwama, M.; Mthunzi-Kufa, P. Developments in Localized Surface Plasmon Resonance. Plasmonics 2025, 20, 5481–5520. [Google Scholar] [CrossRef]
- Mejía-Salazar, J.R.; Oliveira, O.N., Jr. Plasmonic biosensing: Focus review. Chem. Rev. 2018, 118, 10617–10625. [Google Scholar] [CrossRef] [PubMed]
- Neubrecht, F.; Huck, C.; Weber, K.; Pucci, A.; Giessen, H. Surface-enhanced infrared spectroscopy using resonant nanoantennas. Chem. Rev. 2017, 117, 5110–5145. [Google Scholar] [CrossRef] [PubMed]
- Jahn, M.; Patze, S.; Hidi, I.J.; Knipper, R.; Radu, A.I.; Mühlig, A.; Yüksel, S.; Peksa, V.; Weber, K.; Mayerhöfer, T.; et al. Plasmonic nanostructures for surface enhanced spectroscopic methods. Analyst 2016, 141, 756–793. [Google Scholar] [CrossRef] [PubMed]
- Aksu, S.; Yanik, A.A.; Adato, R.; Artar, A.; Huang, M.; Altug, H. High-throughput nanofabrication of infrared plasmonic nanoantenna arrays for vibrational nanospectroscopy. Nano Lett. 2010, 10, 2511–2518. [Google Scholar] [CrossRef]
- Zeng, S.; Sreekanth, K.V.; Shang, J.; Yu, T.; Chen, C.-K.; Yin, F.; Baillargeat, D.; Coquet, P.; Ho, H.-P.; Kabashin, A.V.; et al. Graphene-Gold Metasurface Architectures for Ultrasensitive Plasmonic Biosensing. Adv. Mater. 2015, 27, 6163–6169. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, Y.; Xu, C.; Han, X.; Yan, X. Tunable light trapping and absorption enhancement with graphene ring arrays. Phys. Chem. Chem. Phys. 2016, 18, 26661–26669. [Google Scholar] [CrossRef]
- Li, H.; Ji, C.; Ren, Y.; Hu, J.; Qin, M.; Wang, L. Investigation of multiband plasmonic metamaterial perfect absorbers based on graphene ribbons by the phase-coupled method. Carbon 2019, 141, 481–487. [Google Scholar] [CrossRef]
- Chen, K.; Adato, R.; Altug, H. Dual-band perfect absorber for multispectral plasmon-enhanced infrared spectroscopy. ACS Nano 2012, 6, 7998–8006. [Google Scholar] [CrossRef]
- Aouani, H.; Šipová, H.; Rahmani, M.; Navarro-Cia, M.; Hegnerová, K.; Homola, J.; Hong, M.; Maier, S.A. Ultrasensitive broadband probing of molecular vibrational modes with multifrequency optical antennas. ACS Nano 2013, 7, 669–675. [Google Scholar] [CrossRef]
- Bao, Q.; Loh, K.P. Graphene photonics, plasmonics, and broadband optoelectronic devices. ACS Nano 2012, 6, 3677–3694. [Google Scholar] [CrossRef]
- Liu, C.; Liu, P.; Yang, C.; Lin, Y.; Zha, S. Dynamic electromagnetically induced transparency based on a metal-graphene hybrid metamaterial. Opt. Mater. Express 2018, 8, 1132–1142. [Google Scholar] [CrossRef]
- Yan, H.; Low, T.; Zhu, W.; Wu, Y.; Freitag, M.; Li, X.; Guinea, F.; Avouris, P.; Xia, F. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat. Photonics 2013, 7, 394–399. [Google Scholar] [CrossRef]
- Li, Y.; Yan, H.; Farmer, D.B.; Meng, X.; Zhu, W.; Osgood, R.M.; Heinz, T.F.; Avouris, P. Graphene plasmon enhanced vibrational sensing of surface-adsorbed layers. Nano Lett. 2014, 14, 1573–1577. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 2009, 80, 245435. [Google Scholar] [CrossRef]
- Rodrigo, D.; Tittl, A.; John-Herpin, A.; Limaj, O.; Altug, H. Self-similar multiresonant nanoantenna arrays for sensing from near-to mid-infrared. CS Photonics 2018, 5, 4903–4911. [Google Scholar] [CrossRef]
- Liu, X.; Galfsky, T.; Sun, Z.; Xia, F.; Lin, E.-C.; Lee, Y.-H.; Kéna-Cohen, S.; Menon, V.M. Strong light–matter coupling in two-dimensional atomic crystals. Nat. Photonics 2015, 9, 30–34. [Google Scholar] [CrossRef]
- Zhang, Z.; Lee, Y.; Haque, M.F.; Leem, J.; Hsieh, E.Y.; Nam, S.W. Plasmonic sensors based on graphene and graphene hybrid materials. Nano Converg. 2022, 9, 28. [Google Scholar] [CrossRef]
- Yager, T.; Chikvaidze, G.; Wang, Q.; Fu, Y. Graphene Hybrid Metasurfaces for Mid-Infrared Molecular Sensors. Nanomaterials 2023, 13, 2113. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, H.Y.; Pei, J.Y. Fabrication of nanopore in graphene by electron and ion beam irradiation: Influence of graphene thickness and substrate. Comput. Mater. Sci. 2015, 102, 258–266. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, B.; Liao, S.; Xu, Z. Vibrational strong coupling of organic molecules embedded within graphene plasmon nanocavities facilitated by perfect absorbers. J. Chem. Phys. 2024, 161, 234703. [Google Scholar] [CrossRef] [PubMed]
- Han, Q.; Zhang, H.; Kaplan, A.; Fan, S.; Xu, Y.; Zhang, C.; Gao, W.; He, E.; Dong, J. Synthesis of flexible SERS sensing platform of graphene/Ag-popcorns/PMMA for ultrasensitive detection. Spectrochim. Acta A 2026, 347, 126888. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Hang, Y.; Zhou, Y.; Zhu, J.; Yang, J.; Wang, X. Graphene-based biosensors for detection of composite vibrational fingerprints in the Mid-infrared region. Nanomaterials 2019, 9, 1496. [Google Scholar] [CrossRef]
- Zhu, J.; Cheng, J.; Zhang, L.; Liu, Q. Modeling of 2D graphene material for plasmonic hybrid waveguide with enhanced near-infrared modulation. Mater. Lett. 2017, 186, 53–56. [Google Scholar] [CrossRef]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; García de Abajo, F.J.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Liu, Z.Q.; Liu, X.S.; Liu, G.Q.; Fu, G.L.; Wang, J.Q.; Shen, Y. Multi-functional polarization conversion manipulation via graphene-based metasurface reflectors. Opt. Express 2021, 29, 70–81. [Google Scholar] [CrossRef]
- Guo, X.D.; Hu, H.; Zhu, X.; Yang, X.X.; Dai, Q. Higher order Fano graphene metamaterials for nanoscale optical sensing. Nanoscale 2017, 9, 14998–15004. [Google Scholar] [CrossRef]
- Jiang, X.P.; Zhang, Z.J.; Wen, K.; Li, G.F.; He, J.; Yang, J.B. A Triple-Band Hybridization Coherent Perfect Absorber Based on Graphene Metamaterial. Appl. Sci. 2020, 10, 1750. [Google Scholar] [CrossRef]
- Rodrigo, D.; Tittl, A.; Ait-Bouziad, N.; John-Herpin, A.; Limaj, O.; Kelly, C.; Yoo, D.; Wittenberg, N.J.; Oh, S.-H.; Lashuel, H.A.; et al. Resolving molecule-specific information in dynamic lipid membrane processes with multi-resonant infrared metasurfaces. Nat. Commun. 2018, 9, 2160. [Google Scholar] [CrossRef] [PubMed]
- Limaj, O.; Etezadi, D.; Wittenberg, N.J.; Rodrigo, D.; Yoo, D.; Oh, S.-H.; Altug, H. Infrared plasmonic biosensor for real-time and label-free monitoring of lipid membranes. Nano Lett. 2016, 16, 1502–1508. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of plasmonic waves in graphene by guided-mode resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef]
- Ju, L.; Geng, B.; Horng, J.; Girit, C.; Martin, M.; Hao, Z.; Bechtel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R.; et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630–634. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Yang, X.; Gao, J. Strong coupling between mid-infrared localized plasmons and phonons. Opt. Express 2016, 24, 12367–12374. [Google Scholar] [CrossRef]
- Pérez-González, O.; Aizpurua, J.; Zabala, N. Optical transport and sensing in plexcitonic nanocavities. Opt. Express 2013, 21, 15847–15858. [Google Scholar] [CrossRef]
- Chen, H.; Shao, L.; Woo, K.C.; Wang, J.; Lin, H.-Q. Plasmonic-molecular resonance coupling: Plasmonic splitting versus energy transfer. J. Phys. Chem. C 2012, 116, 14088–14095. [Google Scholar] [CrossRef]
- Balci, S.; Kucukoz, B.; Balci, O.; Karatay, A.; Kocabas, C.; Yaglioglu, G. Tunable plexcitonic nanoparticles: A model system for studying plasmon—Exciton interaction from the weak to the ultrastrong coupling regime. ACS Photonics 2016, 3, 2010–2016. [Google Scholar] [CrossRef]
- Kühner, L.; Semenyshyn, R.; Hentschel, M.; Neubrech, F.; Tarín, C.; Giessen, H. Vibrational sensing using infrared nanoantennas: Toward the noninvasive quantitation of physiological levels of glucose and fructose. ACS Sens. 2019, 4, 1973–1979. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Zhang, Z.; Wan, Z.; Bian, A.; Li, B.; Chang, Y.; Hu, Y. Tunable Graphene Plasmonic Sensor for Multi-Component Molecular Detection in the Mid-Infrared Assisted by Machine Learning. Photonics 2025, 12, 1000. https://doi.org/10.3390/photonics12101000
Zhao Z, Zhang Z, Wan Z, Bian A, Li B, Chang Y, Hu Y. Tunable Graphene Plasmonic Sensor for Multi-Component Molecular Detection in the Mid-Infrared Assisted by Machine Learning. Photonics. 2025; 12(10):1000. https://doi.org/10.3390/photonics12101000
Chicago/Turabian StyleZhao, Zhengkai, Zhe Zhang, Zhanyu Wan, Ang Bian, Bo Li, Yunwei Chang, and Youyou Hu. 2025. "Tunable Graphene Plasmonic Sensor for Multi-Component Molecular Detection in the Mid-Infrared Assisted by Machine Learning" Photonics 12, no. 10: 1000. https://doi.org/10.3390/photonics12101000
APA StyleZhao, Z., Zhang, Z., Wan, Z., Bian, A., Li, B., Chang, Y., & Hu, Y. (2025). Tunable Graphene Plasmonic Sensor for Multi-Component Molecular Detection in the Mid-Infrared Assisted by Machine Learning. Photonics, 12(10), 1000. https://doi.org/10.3390/photonics12101000




