High-Stability PGC-EKF Demodulation Algorithm Integrated with a Phase Delay Compensation Module
Abstract
1. Introduction
2. Theory
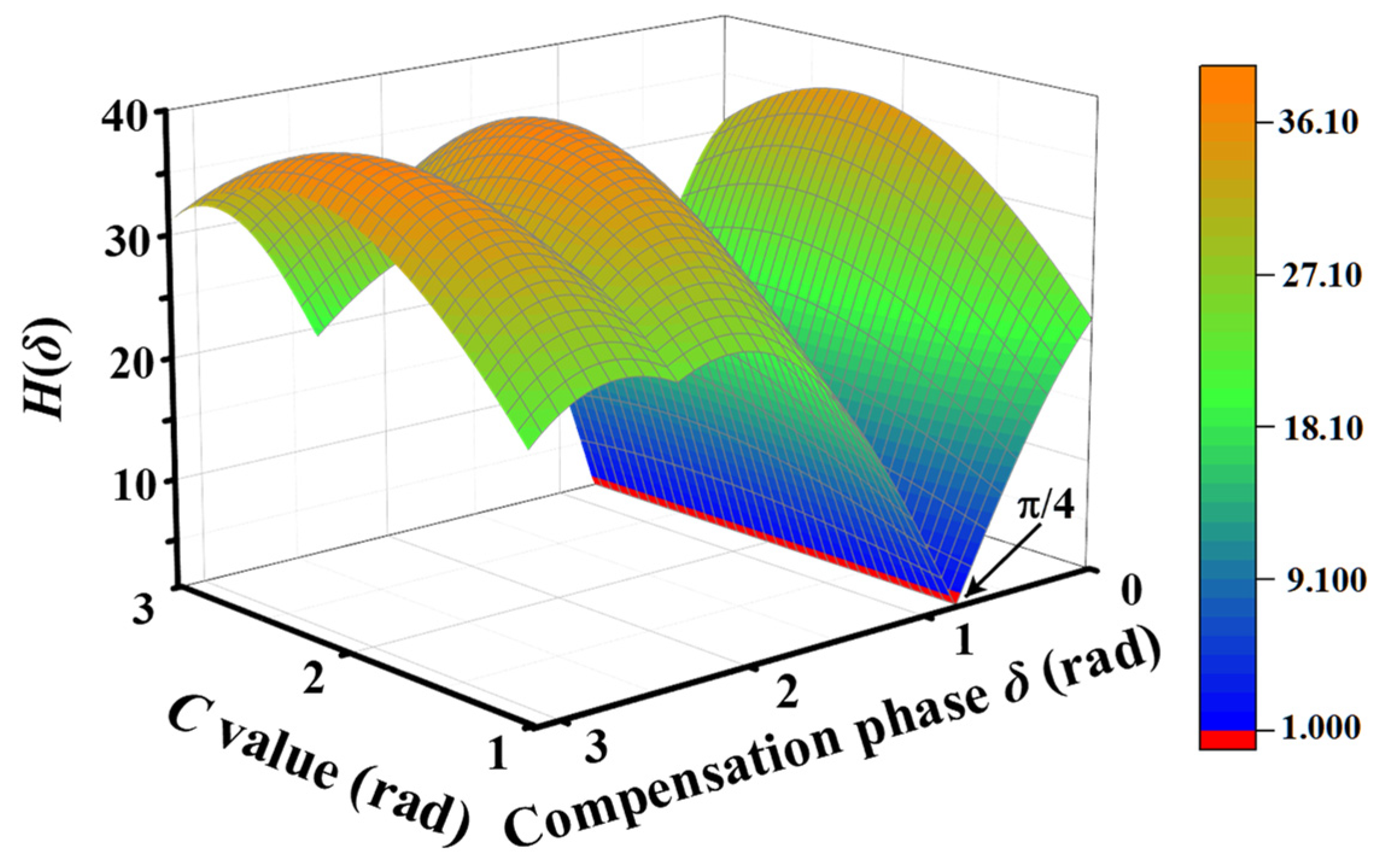
2.1. The Influence of C Value and θ on the Demodulation Result
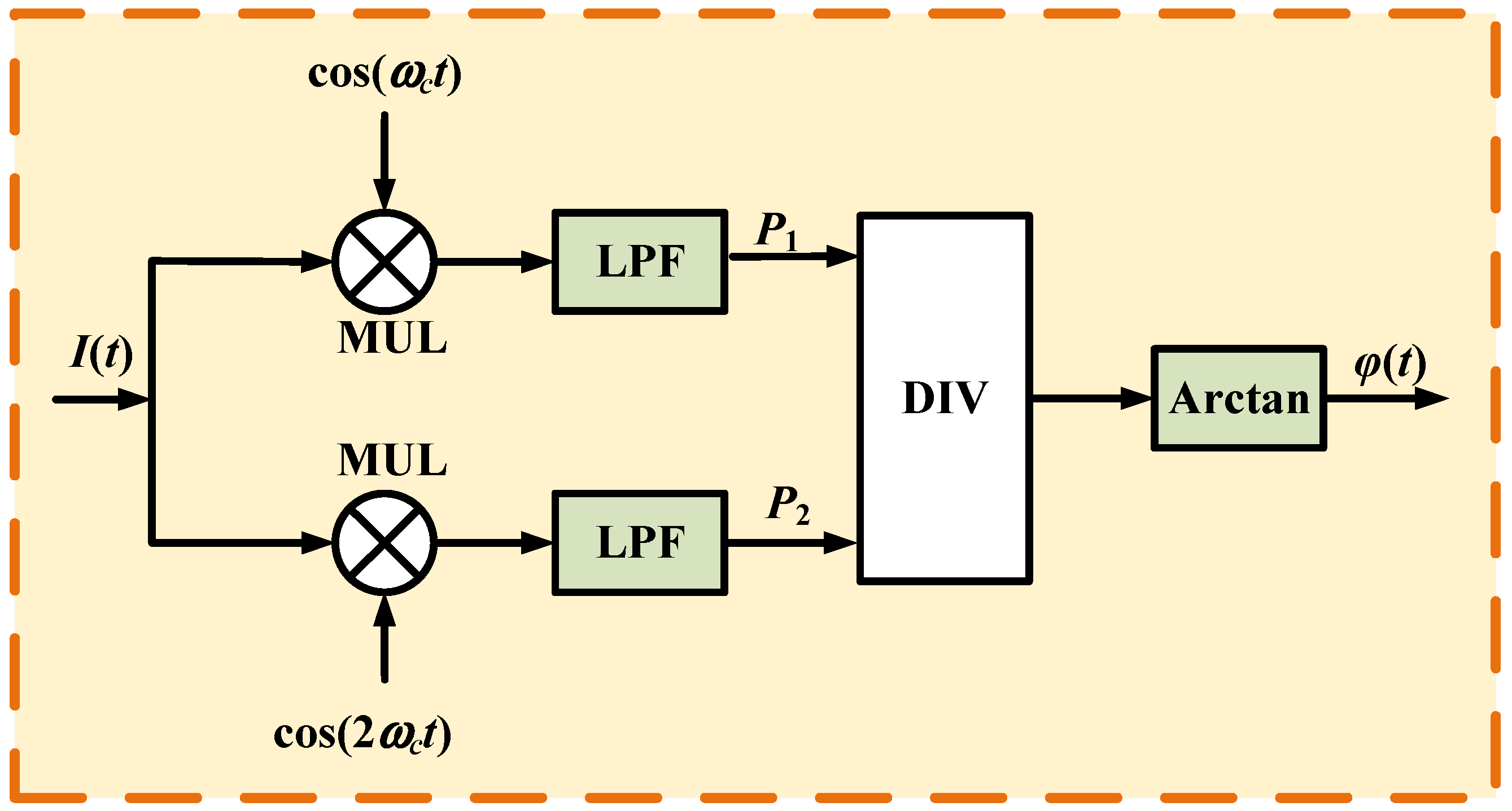
2.2. The Principle of PGC-PDC-EKF Demodulation Scheme
3. Simulation and Analysis
3.1. Performance Analysis of the PDC Module
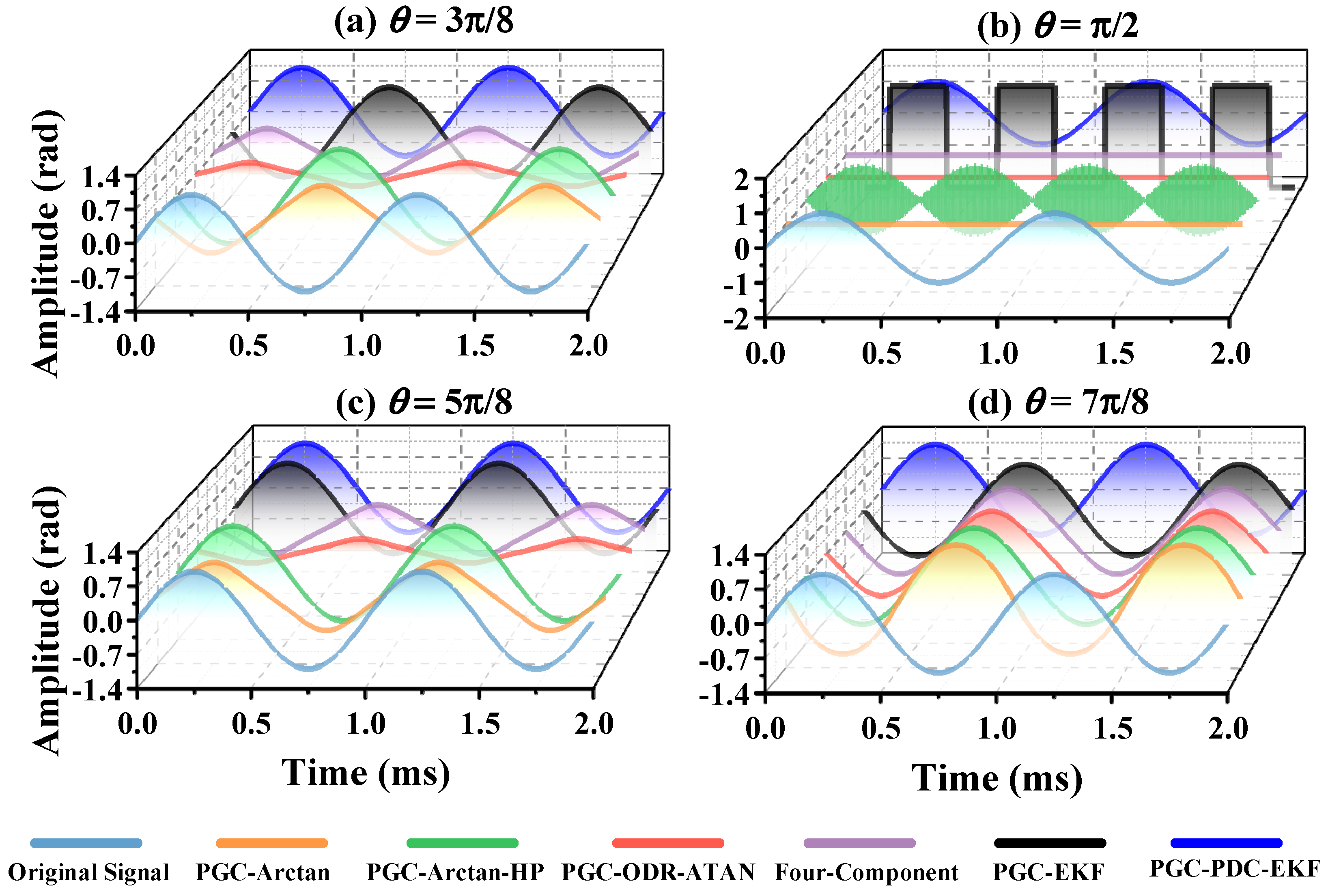
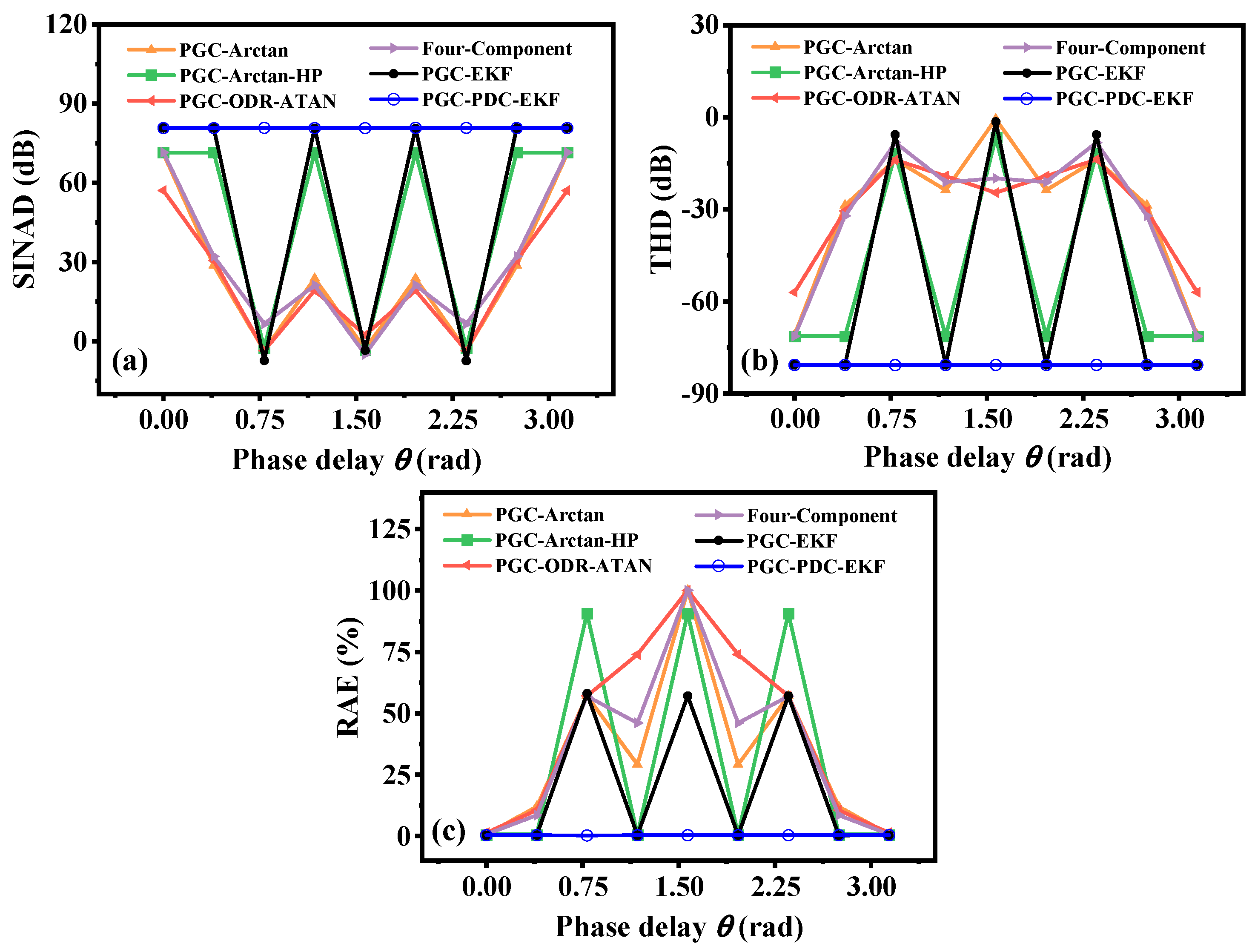
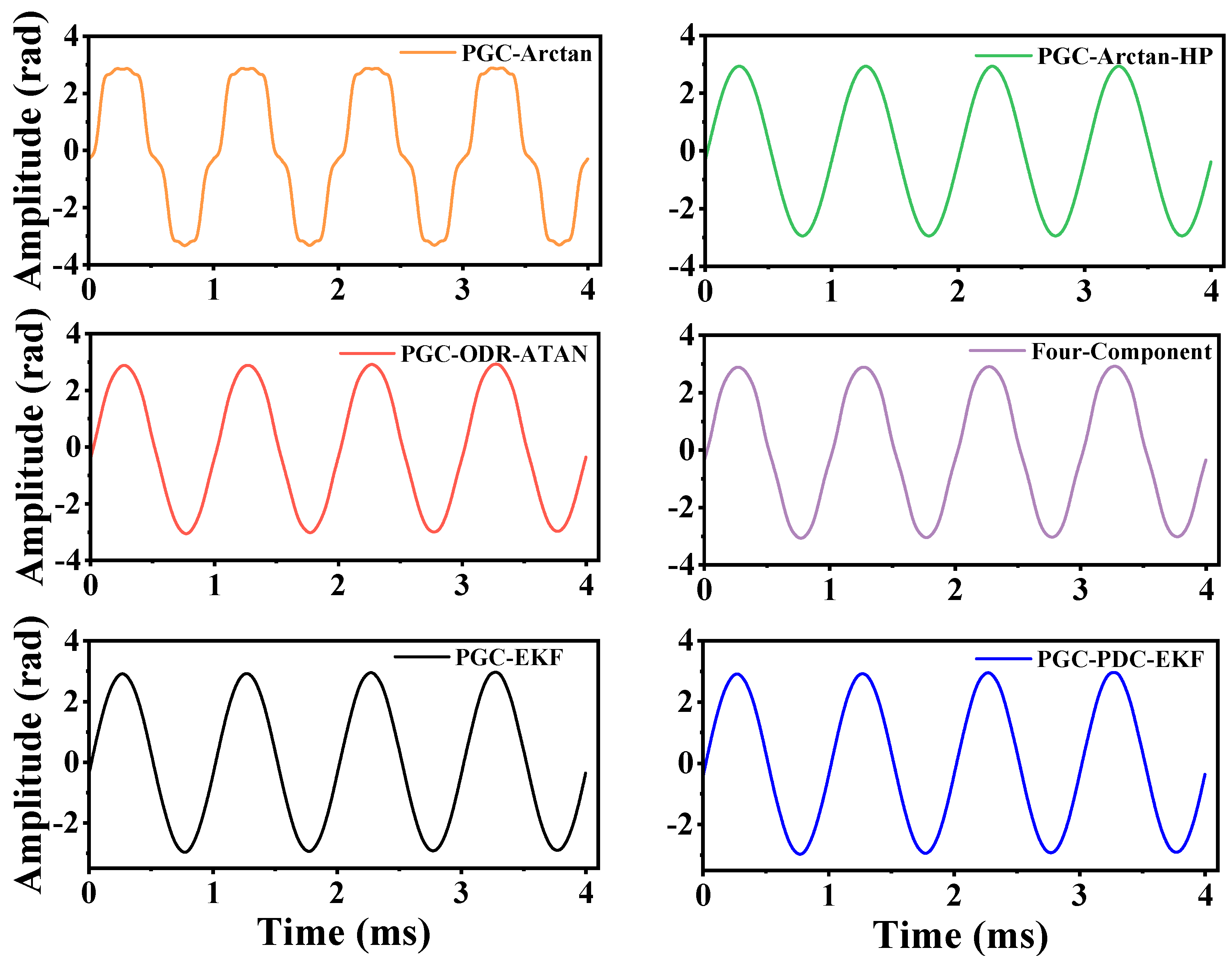
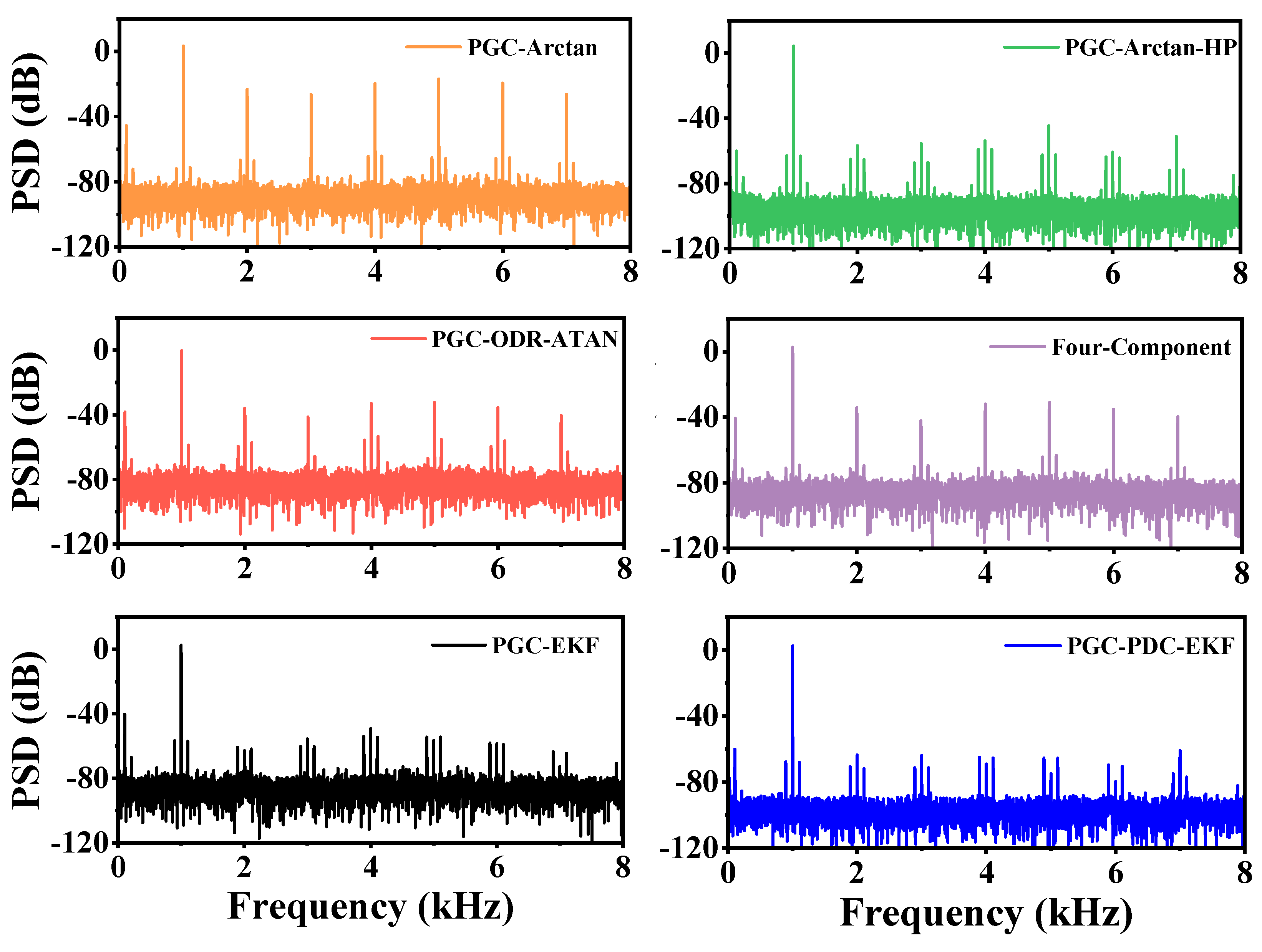
3.2. Performance Comparison of Demodulation Algorithms at Different Phase Delays
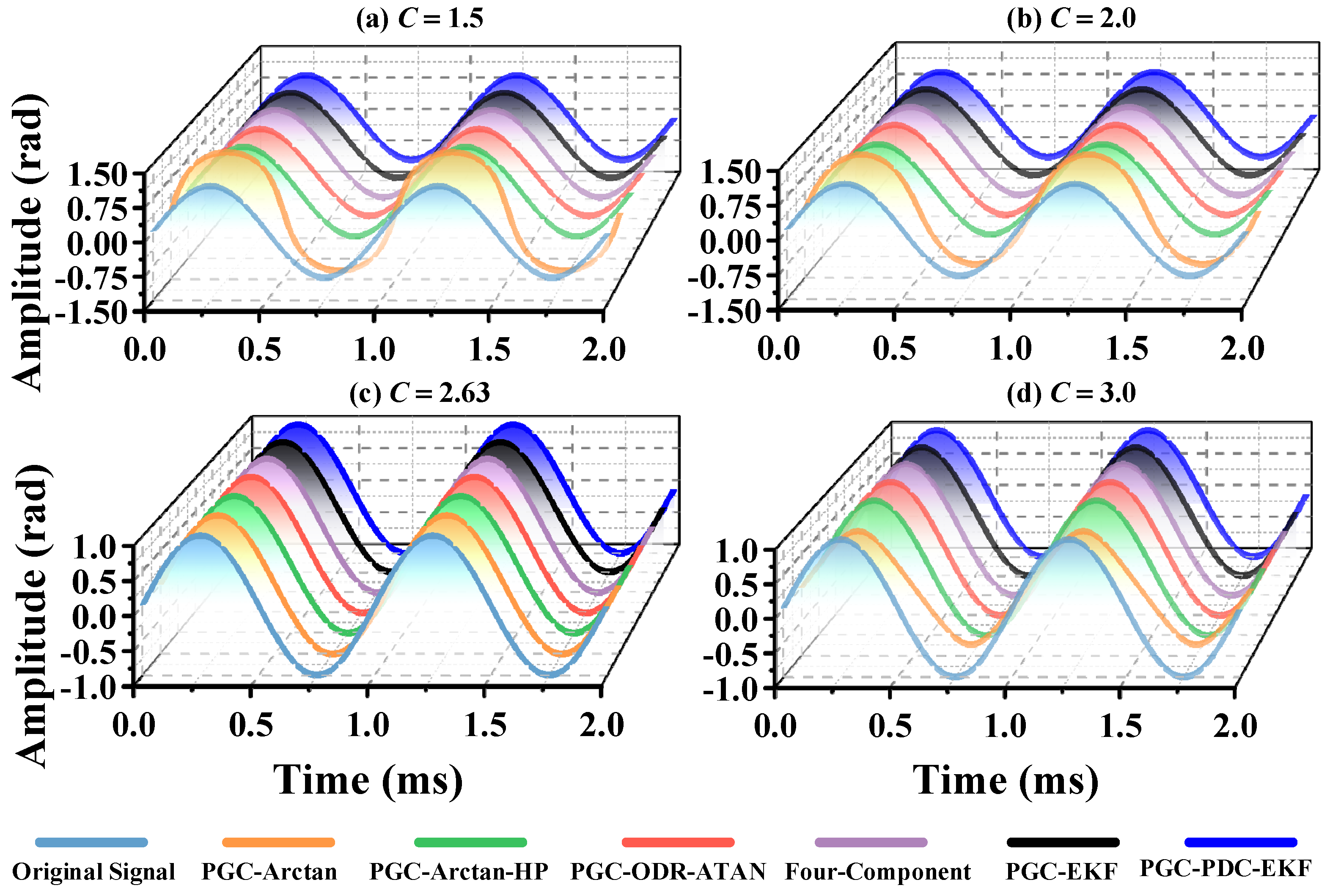
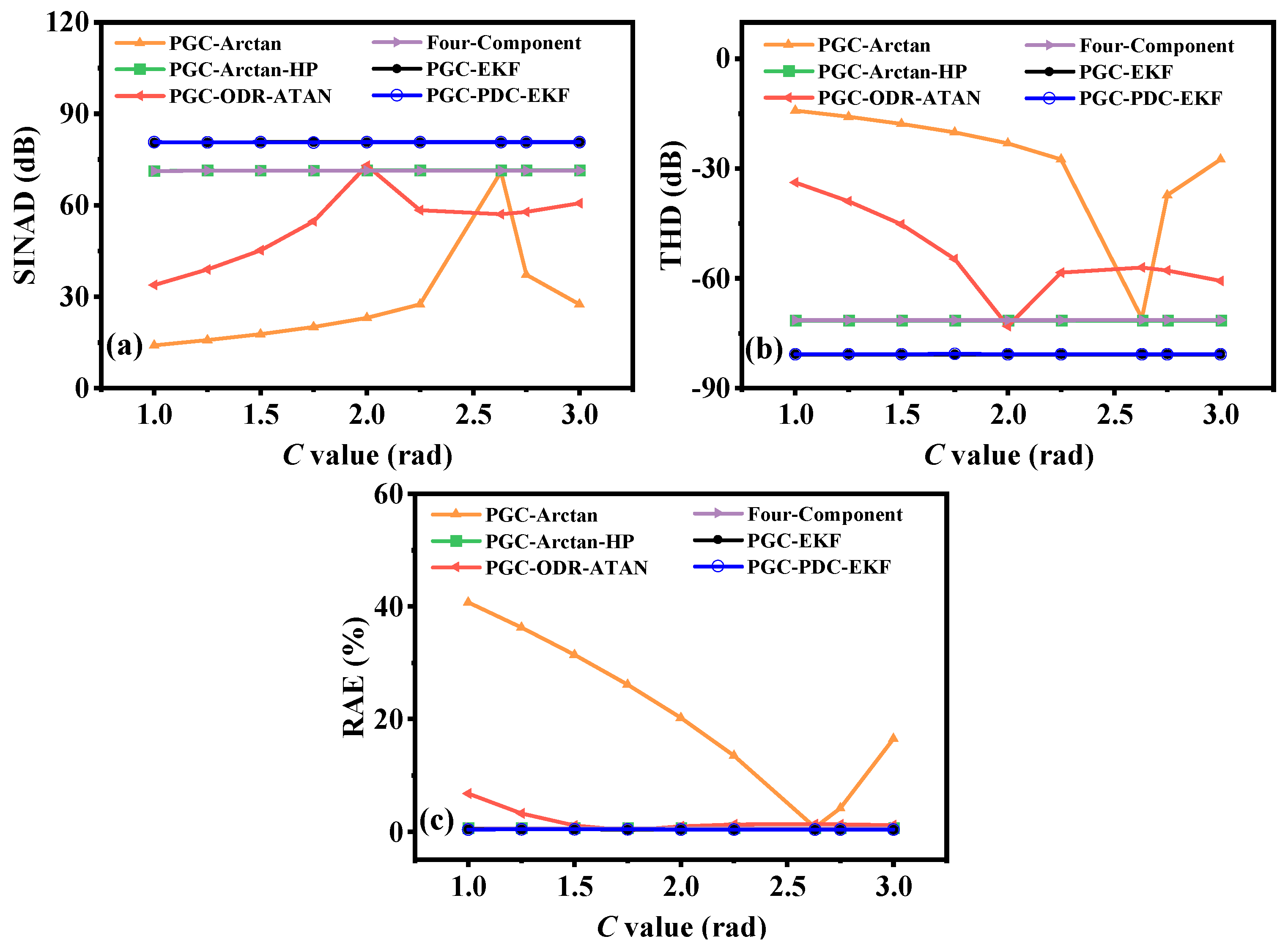
3.3. Performance Comparison of Demodulation Algorithms at Different C Value
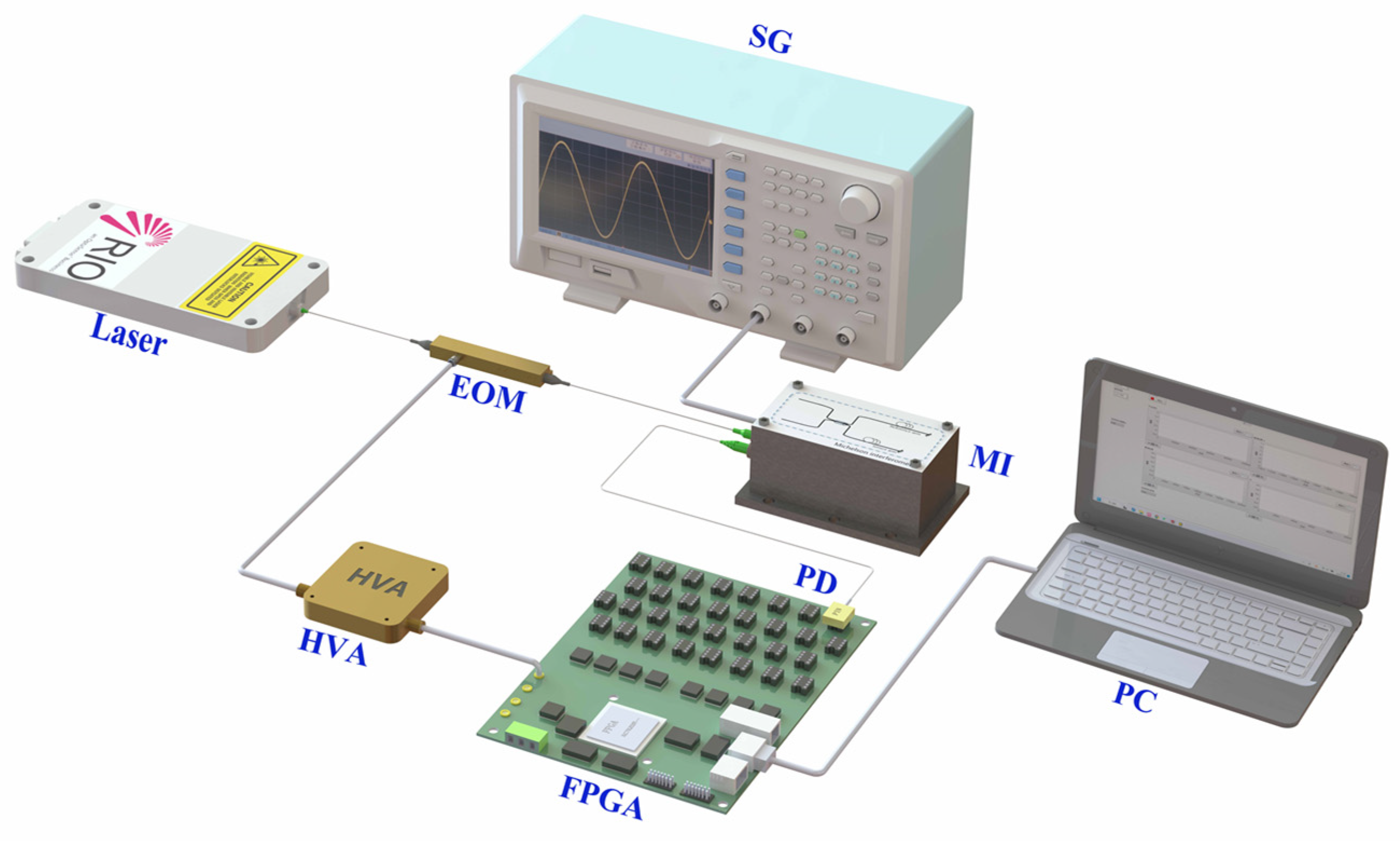
4. Experiments and Results
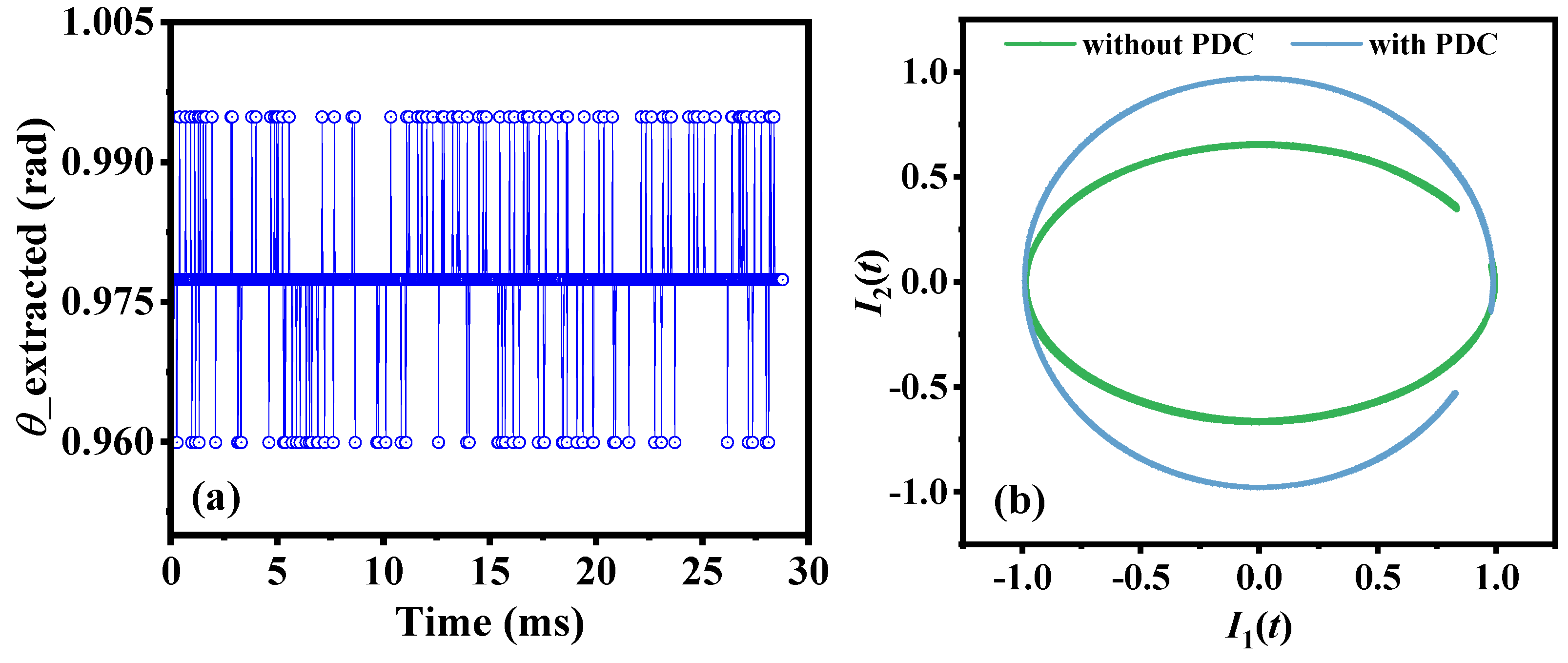
4.1. Performance Analysis of PDC Module
4.2. Linearity of the Demodulated Signal
4.3. Performance Comparison of Different Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marin, Y.; Velha, P.; Oton, C.J. Distortion-corrected phase demodulation using phase-generated carrier with multitone mixing. Opt. Express 2020, 28, 36849–36861. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Zhang, Q.; Zhang, M.; Dai, H.; Zhang, J.; Liu, L.; Zhang, L.; Jin, X.; Wang, G.; Qi, G. Distributed optical fiber vibration sensing using phase-generated carrier demodulation algorithm. Appl. Phys. 2018, 124, 84. [Google Scholar] [CrossRef]
- He, J.; Wang, L.; Li, F.; Liu, Y. An ameliorated phase generated carrier demodulation algorithm with low harmonic distortion and high stability. J. Light. Technol. 2010, 28, 3258–3265. [Google Scholar]
- Zhang, A.; Li, D. Interferometric sensor with a PGC-AD-DSM demodulation algorithm insensitive to phase modulation depth and light intensity disturbance. Appl. Opt. 2018, 57, 7950–7955. [Google Scholar] [CrossRef]
- Azmi, A.I.; Leung, I.; Chen, X.; Zhou, S.; Zhu, Q.; Gao, K.; Childs, P.; Peng, G. Fiber laser-based hydrophone systems. Photon. Sens. 2011, 1, 210–221. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Tian, C.; Zhang, M.; Liao, Y. Analysis and optimization of the PGC method in all digital demodulation systems. J. Light. Technol. 2018, 26, 3225–3233. [Google Scholar] [CrossRef]
- Gui, L.; Wu, X.; Yu, B.; Guang, D.; Shi, J.; Zuo, C. High-stability PGC demodulation algorithm based on a reference fiber-optic interferometer with insensitivity to phase modulation depth. J. Light. Technol. 2021, 39, 6968–6975. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Zhao, L.; Fu, Z.; Zhang, J.; Li, Z.; Qiao, X. Improved PGC demodulation algorithm to eliminate modulation depth and intensity disturbance. Appl. Opt. 2022, 61, 5722–5727. [Google Scholar] [CrossRef]
- Volkov, A.V.; Plotnikov, M.Y.; Mekhrengin, M.V.; Miroshnichenko, G.P.; Aleynik, A.S. Phase modulation depth evaluation and correction technique for the PGC demodulation scheme in fiber-optic interferometric sensors. IEEE Sens. J. 2017, 17, 4143–4150. [Google Scholar] [CrossRef]
- Gong, Y.; Shi, J.; Guang, D.; Zhou, M.; Mu, S.; Wu, X. Improved algorithm for phase generation carrier to eliminate the influence of modulation depth with multi-harmonics frequency mixing. J. Light. Technol. 2023, 41, 1357–1363. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, L.; Chen, B.; Xu, Z.; Xie, J. Real-time phase delay compensation of PGC demodulation in sinusoidal phase-modulation interferometer for nanometer displacement measurement. Opt. Express 2017, 25, 472–485. [Google Scholar] [CrossRef]
- Nikitenko, A.N.; Plotnikov, M.Y.; Volkov, A.V.; Mekhrengin, M.V.; Kireenkov, A.Y. PGC-Atan demodulation scheme with the carrier phase delay compensation for fiber-optic interferometric sensors. IEEE Sens. J. 2018, 18, 1985–1992. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, Y.; Xie, J.; Lou, Y.; Chen, B.; Zhang, S. Nonlinear error compensation of PGC demodulation with the calculation of carrier phase delay and phase modulation depth. J. Light. Technol. 2021, 39, 2327–2335. [Google Scholar] [CrossRef]
- Xie, J.; Yan, L.; Chen, B.; Lou, B. Extraction of carrier phase delay for nonlinear errors compensation of PGC demodulation in an SPM interferometer. J. Light. Technol. 2019, 37, 3422–3430. [Google Scholar] [CrossRef]
- Hou, C.; Liu, G.; Guo, S.; Tian, S.; Yuan, Y. Large dynamic range and high sensitivity PGC demodulation technique for tri-component fiber optic seismometer. IEEE Access 2020, 8, 15085–15092. [Google Scholar] [CrossRef]
- Ni, C.; Zhang, M.; Zhu, Y.; Hu, C.; Ding, S.; Jia, Z. Sinusoidal phase modulating interferometer with ellipse fitting and a correction method. Appl. Opt. 2017, 56, 3895–3899. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Xu, L.; Ge, Q.; Wu, X.; Yu, B. High precision and stabilization PGC demodulation scheme for fiber optic interferometric sensors. J. Light. Technol. 2023, 41, 6615–6620. [Google Scholar] [CrossRef]
- Shapiro, R. Smoothing, filtering, and boundary effects. Rev. Geophys. 1970, 8, 359–387. [Google Scholar] [CrossRef]
- Zhe, Y.; Lian, B.; Tong, K.; Chen, S. Novel strong tracking square-root cubature kalman filter for GNSS/INS integrated navigation system. IET Radar Sonar Navig. 2019, 13, 976–982. [Google Scholar]
- Yan, L.; Chen, Z.; Chen, B.; Xie, J.; Zhang, S.; Lou, Y.; Zhang, E. Precision PGC demodulation for homodyne interferometer modulated with a combined sinusoidal and triangular signal. Opt. Express 2018, 26, 4818–4831. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, X.; Chang, J.; Zhou, H. Improved PGC demodulation algorithm for fiber optic interferometric sensors. Opt. Express 2024, 32, 2162–2178. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Yu, B.; Zhang, J.; Shi, J.; Guang, D.; Zuo, C.; Mu, S.; Liu, Y.; Lin, Z.; Wu, X. Ameliorated PGC demodulation technique based on the ODR algorithm with insensitivity to phase modulation depth. Opt. Express 2023, 31, 7175–7186. [Google Scholar] [CrossRef] [PubMed]
- Chang, N.; Huang, X.; Wang, H. Phase generated carrier demodulation approach in fiber-optic hydrophone based on extended Kalman filter parameter estimation. Chin. J. Lasers 2022, 49, 103–114. [Google Scholar]


| Step Size l (Rad) | Set θ (Rad) | Calculated δx (Rad) | Error (%) | Resolution (Rad) | Time (s) |
|---|---|---|---|---|---|
| π/45 | 1.55338 | 1.53589 | 1.1259 | 0.06981 | 0.086 |
| π/90 | 1.55338 | 1.57080 | 1.1214 | 0.03490 | 0.088 |
| π/180 | 1.55338 | 1.55334 | 0.0025 | 0.01745 | 0.093 |
| π/360 | 1.55338 | 1.55334 | 0.0025 | 0.00873 | 0.144 |
| Algorithm | Phase Singularities | ||||
|---|---|---|---|---|---|
| PGC-Arctan | − | π/4 | π/2 | 3π/4 | − |
| PGC-Arctan-HP | − | π/4 | π/2 | 3π/4 | − |
| PGC-ODR-ATAN | π/6 | π/4 | π/2 | 3π/4 | 5π/6 |
| Four-Component | π/6 | π/4 | π/2 | 3π/4 | 5π/6 |
| PGC-EKF | − | π/4 | π/2 | 3π/4 | − |
| PGC-PDC-EKF | − | − | − | − | − |
| Algorithm | RAE (%) | SINAD (dB) | THD (dB) |
|---|---|---|---|
| PGC-Arctan | 13.4742 | 35.98 | −36.24 |
| PGC-Arctan-HP | 1.6145 | 46.18 | −49.77 |
| PGC-ODR-ATAN | 4.3530 | 39.27 | −41.47 |
| Four-Component | 3.9106 | 40.12 | −42.53 |
| PGC-EKF | 0.9870 | 47.96 | −54.86 |
| PGC-PDC-EKF | 0.0374 | 54.01 | −62.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhu, F.; Xu, X.; Zhao, Z.; Deng, C. High-Stability PGC-EKF Demodulation Algorithm Integrated with a Phase Delay Compensation Module. Photonics 2025, 12, 44. https://doi.org/10.3390/photonics12010044
Zhao H, Zhu F, Xu X, Zhao Z, Deng C. High-Stability PGC-EKF Demodulation Algorithm Integrated with a Phase Delay Compensation Module. Photonics. 2025; 12(1):44. https://doi.org/10.3390/photonics12010044
Chicago/Turabian StyleZhao, Hengyang, Feng Zhu, Xiaoxiao Xu, Zongling Zhao, and Chuanlu Deng. 2025. "High-Stability PGC-EKF Demodulation Algorithm Integrated with a Phase Delay Compensation Module" Photonics 12, no. 1: 44. https://doi.org/10.3390/photonics12010044
APA StyleZhao, H., Zhu, F., Xu, X., Zhao, Z., & Deng, C. (2025). High-Stability PGC-EKF Demodulation Algorithm Integrated with a Phase Delay Compensation Module. Photonics, 12(1), 44. https://doi.org/10.3390/photonics12010044




