The Application of Digital Holographic Speckle Pattern Interferometry to the Structural Condition Study of a Plaster Sample

Abstract

We use non-destructive Digital Holographic Speckle Pattern Interferometry (DHSPI), post-processing image analysis and one-dimensional exponential analysis to visualize, map and describe the structural condition of a plaster-based material. The body is heated by infrared radiation for two different time windows and the cooling process that follows is monitored in time by the so-called interferograms that are developed and are the result of the superposition of the holographic recordings of the sample prior to the thermal load and at variable time intervals during the cooling process. The fringe patterns in the interferometric images reveal features and characteristics of the interior of the material, with the experimental method and the post-process analysis adopted in this work offering accuracy, sensitivity and full-field diagnosis, in a completely non-destructive manner, without the need of sampling.

1. Introduction

In the last years, the technological developments in applied sciences and relevant industrial fields demand cost-effective, accurate and sensitive testing and diagnostic techniques that allow for prompt, on-site and minimally invasive characterization of materials and structures. In this context, optical diagnostic methods provide a wide spectrum of detection schemes and sensing platforms, from optical fiber sensors to laser-based remote material characterization techniques, that can be applied to photonics, microelectronics, engineering and relevant disciplines, with the strong advantage of non-destructive evaluation in real time [1,2,3,4]. Such optical systems provide precision and repeatability, while they frequently constitute an integrated part of the ongoing operation and/or the production line, as monitoring and continuous assessment of the material’s condition is demanded during the course of the application.

Laser-based diagnostic tools have been optimized in the last years providing excellent capabilities in terms of testing of structural integrity, non-contact measurement and characterization of materials and reliable operation. Recently, the potential of determining the size and shape of randomly distributed sub-micrometer silica microspheres using laser interferometry has been demonstrated [5]. In microelectronics, laser interferometry has been successfully applied to the in-situ control of the fabrication and engineering of complicated Si-based multilayer systems, allowing for the control and quantification of the parameters involved in their fabrication (such as the effective optical thickness or porosity of the semiconductor layer) and enabling calibration and optimization of the manufacturing process [6]. Very impressively, laser-based optical metrology techniques span the range from micro- and nanometer scale platforms such as quality control and/or the study of biological samples [7] to the study of larger scale objects such as the detection of structural defects and damages in engineering and industrial applications [8,9].

Laser-based Digital Holographic Speckle Pattern Interferometry (DHSPI) constitutes a well-established technique for the evaluation of the structural condition of various objects, measuring sub-micrometer mechanical displacements with a resolution determined by the source wavelength in use [10]. The method is based on digitally recording and processing the outcome of the interference of two coherent electromagnetic waves, each being in fact associated with a hologram of the object under study in a corresponding state [11]. This interference results in the so-called interferograms which exhibit specific fringe pattern formations, reflecting the structural condition of the body, and allow for the characterization of the construction. The interaction of the laser light with the object takes place at pre-specified time intervals in a non-contact, non-destructive and full-field manner, all of which offer great advantages to in-situ, real-time measurements of the response to an external stimulus, without any shape or surface roughness limitations [12]. With the DHSPI technique, out-of-plane surface displacements of samples that are associated with the layer condition and characteristics of their inner parts, possible inhomogeneities, damages, alterations and/or different constituent layers are bound to be assessed and accounted for, within a variety of materials and geometries [12,13].

In this work, the response of a lime-plaster sample is studied with the DHSPI technique after external thermal excitation in an attempt to assess its structural condition. Lime-plaster complexes constitute a mixture of sand, water and inorganic material, called lime, which is composed largely of calcium oxides and hydroxides. Parameters such as porosity, moisture content or chemical composition have been studied with respect to their influence on the mechanical, thermal and elastic characteristics of lime plaster [14,15]. Lime plaster allows for the diffusion and evaporation of moisture and thus is less affected by water, less prone to soften and dissolve compared to other types of plaster [16]; plaster made of hydrated lime is less brittle, more durable against crack formation and detachment from the body of a structure when subjected to mechanical stress due to solar radiation and/or moisture resulting in expansion [16]. Lime plaster and lime-based composite materials containing polymer, ceramics or other additives exhibit properties that favor their use on a large scale as building and engineering materials, in environment-friendly applications and energy-efficient solutions in manufacturing technology, as well as in cultural constructions and cultural heritage [17,18,19,20]. In this context, besides the chemical properties assessed by means of sampling, employing chemical processes and analytical techniques, the mechanical and structural in-situ, real-time non-destructive investigation of lime-plaster products are of high impact and can be carried out by means of optical metrology techniques on site.

Here, we apply the DHSPI technique employing optical interaction of the laser beam with the sample surface and full-field image capture for the evaluation of the thermomechanical response of a lime-plaster-based object after thermal loading. We use a portable optical platform connected to an automated recording system to obtain two-dimensional real-time interferometric images, which are post-processed and analyzed in terms of the number and type of fringe patterns. The fringe patterns of the interferograms reveal information on the out-of-plane displacement of the sample, and their evolution in time is then analyzed and discussed with respect to extracted exponential decay time constants. This real-time imaging of the off-axis deformation, combined with the one-dimensional exponential decay analysis of the induced displacement, enables us to track the sample’s structural condition, changes inside the material, voids and/or cracks through the attempt to follow the paths of energy and strain release during cooling down, after the initial energy deposition [12].

This approach aims to identify internal discontinuities in a fully non-contact and non-destructive manner, with high resolution, experimental simplicity and repeatability, with the purpose of application to various materials and layered geometries, without the strict necessity of tuning the laser wavelength or other parameters of the laser beam, as opposed to other monitoring techniques where, for example, the central wavelength must be tuned close to an optical resonance [1,3]. Most importantly, the DHSPI technique has been successfully established for in-situ measurements and applied to numerous on-site examinations with the portable optical geometry that has been developed [21]. The portable experimental set-up, along with the interferometric image post-processing and the one-dimensional exponential analysis proposed here, serve as a sensitive and accurate non-invasive optical metrology platform, which has the potential for in-situ characterization of sub-millimeter and micro-meter structures over a wide range of bulk structures, without the use of a complementary experimental diagnostic technique and/or a complex time-consuming theoretical analysis.

2. Materials and Methods

2.1. Plaster Sample

The sample under investigation consists of a baked-brick support, a coarse plaster layer and a painted fine plaster layer. The brick support is lighter than stone, with material properties that favor compactness and durability. The dimensions of the sample are 19.7 cm × 19.7 cm × 3 cm, with the total thickness of the support and the two layers being 3 cm. The coarse plaster layer has a thickness of 1 cm and is composed of lime mixed with washed and sieved sand of 1–2 mm size (lime/sand ratio: 1/3), while the fine plaster layer has a thickness of about 0.5 cm and consists of lime mixed with even finer grain sand (ratio lime/sand: 1/2.5). The known defect in the subsurface structure represents a common type and size of defect that can develop underneath historical fresco wall decorations and is simulated by inserting a cyclic organic material, soluble in water, to the interior of the object, below the surface area; the defect is of circular shape, with a diameter of 8 cm, as highlighted in Figure 1a.

After its construction, the sample with its purposefully made defected area was stored, studied and naturally aged in the laboratory, where it was exposed to the laboratory environment and the everyday so-called “laboratory conditions”. These are characterized by constant temperature T = 18–21 °C and relative humidity 35–45% during winter, or T = 23–25 °C and relative humidity 45–55% during summer. The topography of the induced defect is shown schematically in Figure 1.

2.2. Holographic Interferometry

In Digital Holographic Speckle Pattern Interferometry two temporally separated waves/holograms of two different states A₁ and A₂ of the object are considered. Each of the two holograms results from the superposition of the beam scattered from the object A_o1 and A_o2 with the reference beam A_r, and corresponds to the object under study before (state 1) and after the influence of an external load e.g., temperature (state 2). The external load results in a deformed scattering object surface, a variation of the optical path for the scattered A_o2 beam and, thus, in phase variations which manifest themselves with the formation of interference fringes when the two holograms are superimposed for producing the so-called interferograms and comparing the two different states.

The process of A₁ (x, y) and A₂ (x, y) wave superposition at the recording x–y plane is presented in detail in [22] may be expressed mathematically as

$$\mathrm{I}\left(\mathrm{x},\mathrm{y}\right)=2{\mathrm{a}}^2\left(\mathrm{x},\mathrm{y}\right)\left\{1+{\mathrm{e}}^{\mathrm{i}\mathsf{\Delta }\mathsf{\phi }\left(\mathrm{x},\mathrm{y}\right)}+{\mathrm{e}}^{-\mathrm{i}\mathsf{\Delta }\mathsf{\phi }\left(\mathrm{x},\mathrm{y}\right)}\right\}=2{\mathrm{a}}^2\left(\mathrm{x},\mathrm{y}\right)\left\{1+\cos \mathsf{\Delta }\mathsf{\phi }(\mathrm{x},\mathrm{y})\right\}$$

(1)

where I denotes the intensity of the generated superposition, a the amplitude of the waves of wavelength 532 nm, and Δφ(x, y) = 2d π/λ the phase difference of the two waves, resulting from the displacement d of the object surface. Bright and dark fringes N (constructive and destructive interference) result from Δφ being even or odd multiples N = 2d/λ of π, respectively, and form isotopic curves which indicate surface points of constant values of Δφ and so of equal displacement values d. The number N of interference fringes allows for the surface displacement along the z-axis developed between two object states to be quantified and can be from several tens to fractions of micrometers. For one pair of bright and dark fringes (N = 1) Δφ = π and the relative displacement is then d = λ/2 = 266 nm, which denotes the system’s resolution along the z-direction, determined by the laser wavelength. Details of the method and the mathematical formulation of DHSPI can be found in [22].

With DHSPI, a comparison of two temporally separated holograms of the same object is achieved at any selected time interval between two states. Under conditions for interference fringe formation, the appearance of a single pair of fringes indicates that a dimensional change has taken place. The highest density and/or complexity in the fringe patterns is observed directly after excitation by the external load; the number of fringes is then gradually reduced during relaxation, towards the complete absence of fringes at the end of the process and the equilibrium state. Material inhomogeneities, construction defects and variations that respond to the external stimulus and displace the surface in a different manner than the intact part of the object manifest themselves as distinct local discontinuities in the fringe patterns and are marked by differences in the inclination and/or the number of fringes.

2.3. Experimental

Figure 2a shows the experimental set-up employed in the current study. The set-up is designed for the purpose of acquiring real-time holographic recordings and the corresponding interferograms of the sample surface and of monitoring its mechanical behavior after thermal excitation by infrared light.

The external load comes from IR light-induced temperature rise. The light originates from two infrared lamps of 175 W, placed symmetrically at approximately 30 cm from the sample, forming an angle of 35° with the surface normal. This distance is chosen as the optimum for a homogeneous thermal effect over the examined surface, after measuring the thermal distribution on the surface at variable positions. The two lamps are always switched on simultaneously and the sample is thermally loaded for a total time of 60 s or 180 s, achieving a thermal increase over the whole surface of approximately ΔΤ = 2 °C and 4 °C, respectively [23]. The excitation process results in a final temperature value for the sample that depends on the material’s thermal properties. After the excitation time window, the lamps are switched off and the detector starts recording the interferograms and monitoring the cooling-down process. The duration of the IR thermal lamps’ operation, as well as the time interval between the interferogram recordings, is pre-specified and controlled throughout the whole measurement by a custom-developed software. All initial values, technical and geometrical parameters of the experiment are stored and each measurement can be reproduced at any time.

The DHSPI optical system constitutes a compact optical configuration, based on the principles and characteristics of off-axis phase-shifted holographic interferometry [11]. The optical scheme inside the DHSPI system is presented in Figure 2b and details can be found in [12]. The laser in use is a diode-pumped, solid-state CW laser, with a 532 nm, 300 mW, TEM₀₀-mode output beam, >30 m coherence length and a divergence of approximately 30 cm at 1 m. A 50/50 beam splitter (BS) placed after the source splits the laser beam to the reference (RB) and object beams (OB). After the OB reaches the object, a C-mount converging combination lens (CL) collects the back-scattered light from the illuminated surface and a beam combiner (BC) ensures it interferes with the reference beam, as shown in Figure 2b. In a typical 25 mm lens, as the one used here, the Field of View (FOV) is 30 cm at 1 m.

The system comprises a CCD camera (5 megapixel, pixel size of 4.4 μm) for digital acquisition and recording, at the image plane, of the holographic diffraction grating formed by the interfering reference and object beams. The intensity of each pixel varies from 0 to 255, based on the 8-bit system, while pixel saturation from laser light corresponds to the 255 value. To avoid saturation and improve the quality of the acquired images the relative intensity of the two beams directed onto the CCD array is carefully controlled. The RB intensity is controlled by a variable attenuator (VA) filter wheel, while the OB intensity is controlled by a shutter indication, which corresponds to the time the photosensitive sensor inside the camera is exposed to light. For the best fringe visibility, the intensities I on the recording x–y plane are set so that the I_RB/I_OB ratios take values in the range 1:1–1:10 [11]. After thermal loading, there is practically no shift of the imaged point relative to the pixel of the CCD sensor. The only considered impact of the surface displacement is the change of the speckle intensity, which is recorded and processed in order to extract the phase difference between holograms and generate the corresponding interferograms.

After every time interval within the cooling-down measuring time, the object possesses a different mechanical state. For each state 1, 2, … i, a 5-step phase-shifting software calculates the light phase φ_i(x, y, t) from 5 shifted positions of the movable PZT piezoelectric mirror of Figure 2b, providing the digital hologram n (state n), starting from n = 0. In every subsequent recording at a time interval t_n, the phase φ_i(x, y, t) is calculated afresh from a 5-position newly acquired set of the PZT positioner, the object’s surface response is represented by the hologram n and the interferogram m, m = 1, 2… is generated from the comparison of every hologram with the initial one n = 0 at the beginning of the recording. Consequently, subtraction of the phases of the two holograms results in the requested phase difference Δφ_n and then leads to the interferograms and the final images.

The system in automated mode starts recording and processes the first exposure before the excitation lamps and the thermal loading are on, in order to set the appropriate fringe contrast on the images and calibrate the optical system by acquiring a fringe-free interferogram, ensuring also the vibration-free stability of the experimental set-up. This first hologram with the initial values of the surface position is set as the reference state of the sample. During the increase of the object temperature, the recording system is off and no interferograms are collected during thermal loading to avoid possible camera over-exposure. Once the IR lamps are off, the recording restarts and the system follows the cooling-down process of the sample. Each new hologram is recorded at a certain time interval t_n and the phase φn is extracted; the phase difference Δφ_n of the phase of every new hologram from the phase of the reference hologram is directly linked to the displacement occurring during t_n and reveals the fringe patterns in the resulting interferograms. The intervals t_n in the case of the current measurements are of 8 s duration; in other words, the interferograms are recorded every 8 s, starting from t = 0 s. The interferograms are subject to further analysis and provide calibrated relative displacement values of the surface normal, determined in an absolute fashion between indicated points.

3. Results and Discussion

The intensity recordings captured by the CCD camera are further processed. The data processing software that has been developed allows for the generation of the wrapped-phase digital interferometric images; these images take the form of the fringe patterns shown in Figure 3 and reveal qualitative and quantitative information on the structural condition of the sample to be extracted. The most relevant information regards the localization and sizing of the inhomogeneities accumulated. It should be noted that the sample is clamped steadily in the x and y directions, in order to minimize displacement contributions along the x and y axes due to unwanted vibrations, as well as from the thermal load originating from the IR lamps, which results in mechanical deformation on the x-plane.

The IR lamps are used to heat the sample. Heat conduction then results in energy being transferred to the interior of the sample as well as the environment; the thermomechanical properties of the material and/or the defect area influence heat conduction and the cooling-down process, this being reflected on the spatially differentiated temperature values over the sample surface. In other words, a differentiated displacement d is experienced by the different locations and/or points of the sample surface.

The number of fringes N inferred from the interferometric images are the result of this temperature-induced surface displacement d along the z-axis. Therefore, d is derived from the fringes N multiplied by the factor (1/2)λ, d = N × (1/2)λ, and ranges from 266 nm for N = 1 to some micrometers. This displacement points to the z-axis direction; that is, out of the x–y plane. The longer the exposure to the temperature load and/or the higher the temperature, the greater the deformation of the object and the number of the generated fringes, due to the greater optical path difference traveled by the interfering beams before and after the exposure.

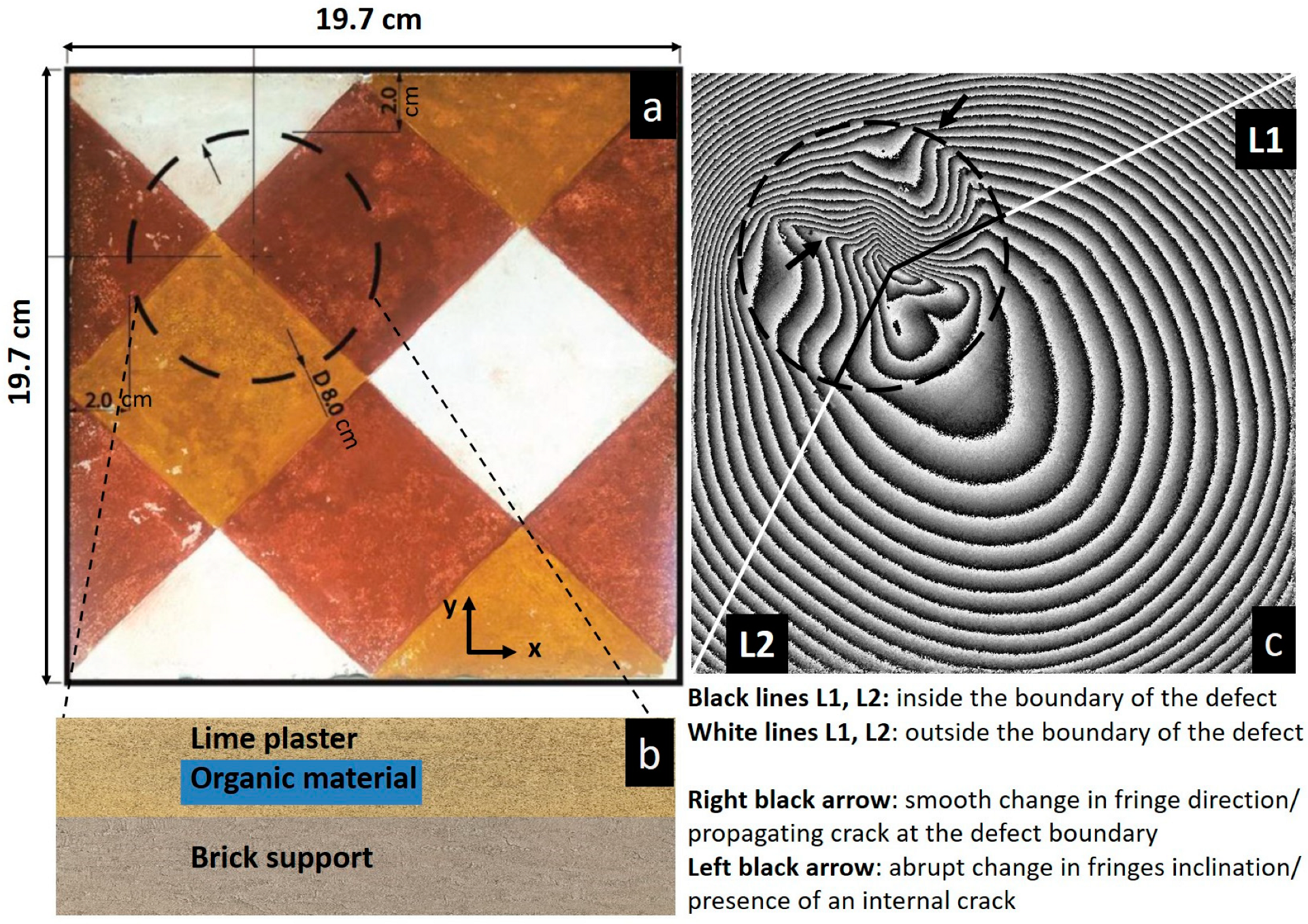
The asymmetry shown in the developed fringe pattern in Figure 1 indicates the area of the inner insertion (or detachment), which induces both material and structural variations. This inhomogeneity together with defects and cracks developed through time generate temperature gradients and displace the surface in a different manner compared to their surrounding locations. Therefore, the association of the certain fringe morphologies with internal defect types are of high importance and the classification and validation of such by means of experiments and numerical simulations on various samples has been presented in [10].

In Figure 1 the black arrow on the right points to dead-end fringes and the smooth change of the fringe direction towards the intact area; this is associated with a crack evolution along the dashed-line circle (crossed by Line 1 on the right-side area). The abrupt changes in fringe inclination inside the defect boundaries, marked by the black arrow on the left, indicate the presence of an enclosed internal crack (crossed by Line 2 on the left-side area) [10]. These types of fringe patterns describing detachments and cracks are characteristic of the irregularities found in a wide spectrum of bulk combination structures, independent of the material and application.

Figure 3 shows four interferograms for two different exposure times to the infrared radiation, i.e., (a) t = 60 s and (b) t = 180 s, directly after thermal loading (time zero), at t = 250 s, at t = 500 s and at the end of the recording time, t = 730 s. Higher exposure time means a greater thermal load experienced by the sample, resulting in greater displacement values. From the interferograms of Figure 3 qualitative information can be derived with respect to the size, positioning and condition of the discontinuities below the sample surface in the x–y plane. The defect manifests itself as a distinct, well-defined circular topology with an interferometric pattern of the highest fringe density; the latter arises from the excess accumulation of thermal energy and the varied response of this part compared to the rest of the sample, due to the presence of the organic film and its different thermal properties. Indeed, it is at the point where the two lines L1 and L2 meet that the highest measured temperature has been recorded by the temperature sensor in previous IR thermography experiments on the same sample [23], despite the symmetry of the sample combined with the placement of the IR lamps. The highest-temperature point lies very close to the diagonal of the square surface. Inside and outside the defect boundaries additional discontinuities can be observed. This is due to the damage and deterioration that has been experienced over time [10]. For the assessment of the thermomechanical energy transfer evolution, the lines L1 and L2 on the interferogram of Figure 1 are chosen for the displacement analysis; they extend to both the defected and non-defected areas, crossing the boundary of the defect. Each line starts from the point of highest temperature and is split into two parts; that is, to a line lying exclusively “inside” the defected area (black) and a line from the defect boundary towards the vertices of the sample surface (white) [23].

Despite even thermal excitation of the whole surface and the inner parts, the two sets of interferograms differ in the overall density of fringes. This is expected given that the longer-exposed sample experiences a larger induced deformation; differences in the relaxation behavior are also to be expected. The images of Figure 3 reveal the known circular defect area through the distinct localized fringe pattern, which exhibits a higher number of fringes in the case of longer exposure. Similarly, the highlighted discontinuities developed below the surface, inside, outside and/or at the boundary of the defect location are also visualized, the longer exposure resulting in more distinct fringe features. On the other hand, the fringe features attributed to specific inhomogeneities, as well as their evolution over time, share similarities for the two thermal loads, both for the areas inside and outside the circular boundary. The type of these fringe patterns is qualitatively reproduced, pointing to the fact that the initial energy penetrates to the interior of the sample and the defects are “reached” for both exposure times, enabling detection in both sets of interferograms. Finally, after observation and comparison of the interferograms, it is evident that the fringe patterns are clearly differentiated along L1 and L2 for both exposure times. The evolution of the interferograms (Figure 3) shows that in longer times L1 comes across a greater number of fringes than L2. A greater number of fringes is related to larger displacement values, longer cooling-down times and, therefore, accumulation of energy and dissipation towards the respective part of the sample can be postulated.

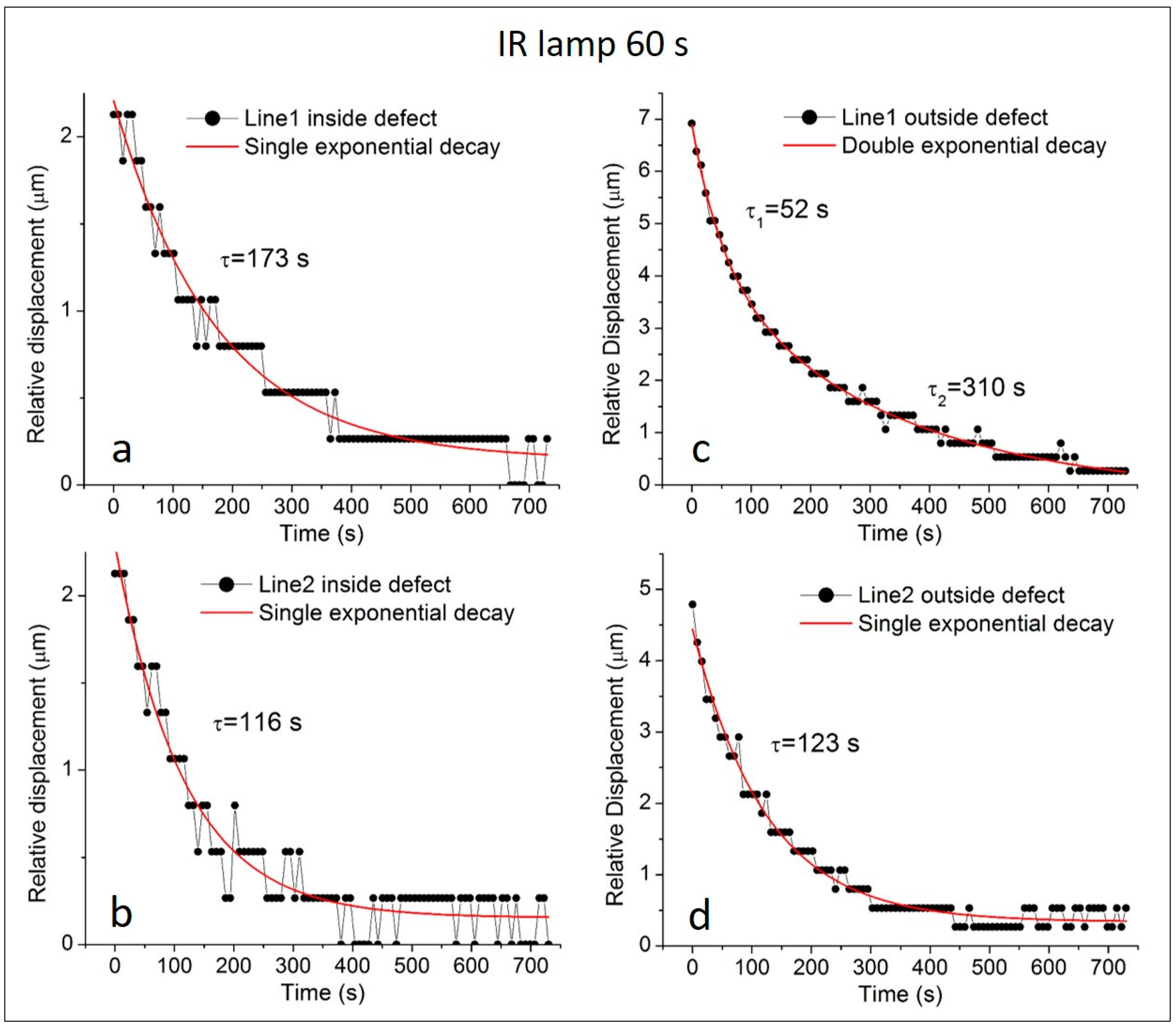
Figure 4 shows the progression of the relative displacement values with time between the two end points of each line under consideration, after exposure of the sample for t₁ = 60 s to the IR light. Each point on the graphs is extracted from the corresponding interferogram produced by the post-processing procedure for the specific time interval (for the whole measurement window, 730 s) and more specifically it is extracted from the number of fringes encountered for Lines 1 and 2 on the interferograms (Figure 1) as follows: a total of 100 interferometric images are loaded by our custom-developed software, on the first image of which the lines in question are marked and the number of fringes crossed by this line are given by the system, minimizing the possible ambiguities introduced by manual “counting”; without altering the drawn lines, the whole sequence of images follow automatically one by one and two data columns are produced, showing the number of fringes corresponding to the time interval between interferograms, which are translated to displacement vs. time. It should be noted that fringe pattern visibility and fringe contrast constitute the key points for precision and accuracy of these generated displacement results. Therefore, obtaining preliminary test interferograms for different laser, imaging and other technical parameters allows for a final measurement (one series of interferograms) to be obtained for the desired experimental conditions (thermal load, time of measurement window, chosen areas for determining the number fringes, etc.).

An exponential function of the mathematical form

$$\mathrm{y}={\mathrm{y}}_0+{\sum }_{\mathrm{n}=1}{\mathrm{A}}_{\mathrm{n}}{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }\mathrm{n}}}}$$

(2)

is used for fitting the experimental data and is also shown in Figure 4; A_n is the amplitude and τ_n the exponential time constant with which the displacement is decaying, while y₀ reproduces an offset signal, reflecting an exponential decay of a longer time constant compared to the time window of the measurement. These parameters are used for best fitting the experimental data and are given by the fitting program (OriginLab). It should be pointed out that, as the displacement is determined in reference to the lines L1 and L2, the experimental data, as well as the exponential fitting curves, provide information on the evolution of the displacement difference between the two ends of each line. The relative displacement decays monotonically for the cases of both L1 and L2 until the end of the recording time; the time constants extracted are τ = 173 s and τ₁ = 52 s/τ₂ = 310 s for L1 inside the defect and L1 outside the defect, respectively, and τ = 116 s and τ = 123 s for L2 inside the defect and L2 outside the defect, respectively. The fact that the decay time constants are longer for L1 indicates that the thermomechanical energy is mainly directed and accumulated to the areas surrounding this direction and followingly released towards adjacent paths and/or to the corresponding interior and the environment of the plaster sample. This outcome was visualized already by the non-symmetric fringe patterns with respect to the defect geometry on the images of Figure 3 and the higher fringe density developed on the right.

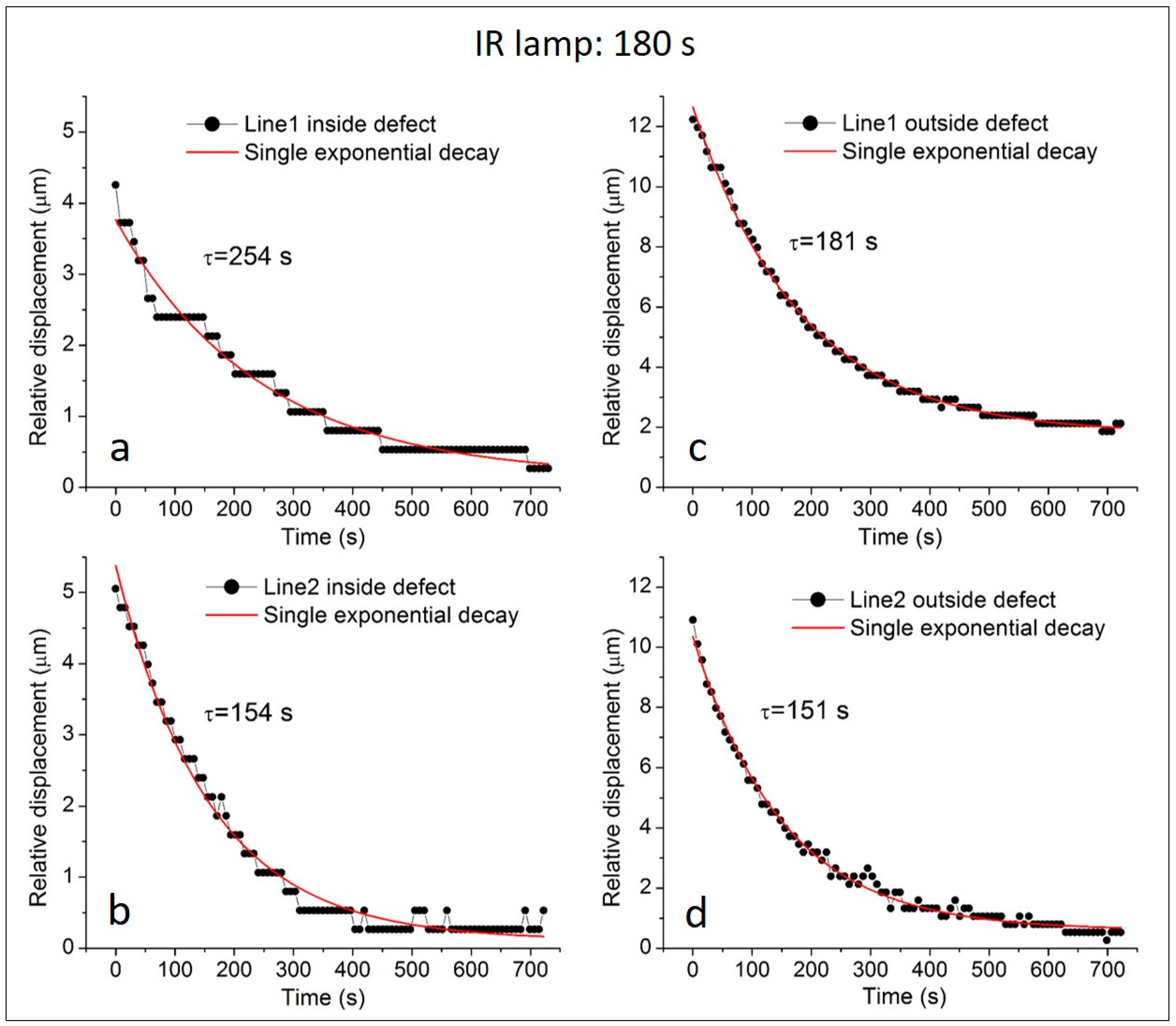
Similar conclusions can be drawn from the experimental outcomes depicted in Figure 5; that is, for exposure time t = 180 s. Also in this case, the area of the longer lasting fringe pattern and the highest density of fringes surrounds the location crossed by Line 1; the corresponding time constants extracted for the two lines L1 and L2 read τ = 254 s and τ = 181 s for L1 inside the defect and L1 outside the defect, respectively, and τ = 154 s and τ = 151 s for L2 inside the defect and L2 outside the defect, respectively. It is worth noting that the relative displacement values at time 0 s are higher in this case of longer exposure and higher energy load, while the remaining values of displacement for L2 outside are stabilized within the time window of the measurement at the value of 0.532 μm, while this value was 0.266 μm for the case of the lower energy load. What is more, the displacement evolution along L1 outside can be fitted with exponential functions of either τ₁ = 181 s and τ₂ > 1000 s or τ₁ = 181 s and a high-value offset of about y₀ = 3 μm, both reflecting a condition of a long-lasting relative displacement, a preserved mechanical energy cumulation in this area and a slower cooling-down process that extends beyond the measurement time window.

From the observations of Figure 4 and Figure 5 it can be confirmed that higher energy load results in higher displacement values and longer lasting offset, as it is expected. What is more, the higher energy load influences the time constants, which in the case of longer exposure become longer. Following the thermal load, heat conduction takes place from the surface to the interior region of the sample; it is known from IR-thermography metrology techniques that the temperature of the sample after time t at a given location of depth z and thermal diffusivity α is proportional to the input energy E multiplied by the exponential ${\mathrm{e}}^{(-{\mathrm{z}}^2/4\mathsf{\alpha }\mathrm{t})}$, and is influenced by the thermomechanical parameters of the material [24,25]. The spatial distribution of the displacements experienced by the surface points as a result of the thermal expansion of the different regions of the sample is, therefore, expected to vary for the points over defect-free regions compared to defected regions. As a consequence, it can be postulated that longer exposure to the radiation of the IR lamps and higher energy load result in the input energies reaching diverse material parts inside the specimen, cracks and/or defects of variable thermomechanical properties and responses during the energy transfer and the cooling-down process; the relative displacement between the same surface points should vary with the input energy, in accordance to the higher displacement values and the different time constants observed.

The layered plaster material, the organic insertion and the internal cracks that have been developed over time constitute paths for channeling energy to their immediate vicinities until it is eventually dissipated to the ambient surroundings and the body cools down. For ambient laboratory conditions, where there is a uniform application of the thermal load and small temperature gradients inside the body (as presumed by the small initial temperature rise), heat conduction inside the body can be described by the equation of Newton’s law of cooling [26].

$$\mathsf{\Delta }\mathsf{{\rm T}}(\mathrm{t})=\mathsf{\Delta }\mathsf{{\rm T}}(0){\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }}}}$$

(3)

where ΔΤ(t) = T(t) − T_env denotes the temporal evolution of the temperature difference between one point of interest and the environment, and takes the value ΔT(0) = T(0) − T_env at time 0 s. The time constant τ = mc/(hA) is connected to the material properties through the mass m, the specific heat capacity c, the heat transfer coefficient h and the surface A of the object. For the two end points a and b of each line L1 and L2, the exponential functions (2) associated with Newton’s law of cooling become the following:

$$\begin{array}{c}\mathsf{\Delta }{\mathsf{{\rm T}}}_{\mathrm{a}}\left(\mathrm{t}\right)-\mathsf{\Delta }{\mathsf{{\rm T}}}_{\mathrm{b}}\left(\mathrm{t}\right)={[\mathsf{{\rm T}}}_{\mathrm{a}}\left(0\right)-{\mathsf{{\rm T}}}_{\mathrm{e}\mathrm{n}\mathrm{v}}]{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }1}}}-{[\mathsf{{\rm T}}}_{\mathrm{b}}\left(0\right)-{\mathsf{{\rm T}}}_{\mathrm{e}\mathrm{n}\mathrm{v}}]{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }2}}}\hfill \\ {\Rightarrow [\mathsf{{\rm T}}}_{\mathrm{a}}\left(\mathrm{t}\right)-{\mathsf{{\rm T}}}_{\mathrm{b}}(\mathrm{t})]={[\mathsf{{\rm T}}}_{\mathrm{a}}\left(0\right)-{\mathsf{{\rm T}}}_{\mathrm{e}\mathrm{n}\mathrm{v}}]{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }1}}}-{[\mathsf{{\rm T}}}_{\mathrm{b}}\left(0\right)-{\mathsf{{\rm T}}}_{\mathrm{e}\mathrm{n}\mathrm{v}}]{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }2}}}\hfill \\ \Rightarrow {[\mathsf{{\rm T}}}_{\mathrm{a}}\left(\mathrm{t}\right)-{\mathsf{{\rm T}}}_{\mathrm{b}}(\mathrm{t})]={\mathrm{B}}_1{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }1}}}+{\mathrm{B}}_2{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{\mathsf{\tau }2}}}\hfill \end{array}$$

(4)

If it is assumed that the relative displacement d of each considered pair a-b follows the relative temperature difference progression of decay rate 1/τ [23,27], the time constants τ extracted from the fitting curves (Equation (2)) of Figure 4 and Figure 5 can be linked to those of the Equation (4) describing Newton’s law of cooling; in the cases studied here a maximum of n = 2 exponential time constants are obtained from fitting the data. A second time constant reflects dissimilar thermomechanical properties for the vicinities around points a and b, while a matching cooling-down response can be suggested for the two areas when only one exponential time constant is extracted from the fitting curves.

The purposefully inserted material in the plaster sample interior, as well as the developed structural discontinuities, result in residual air gaps and less effective thermal contact between the constituent parts of the construction. Propagating cracks, gaps and voids are of sub-millimeter and micrometer dimensions and they appear in the interferograms as discontinuities of linear-like or circular shape. For air density ρ = 1.225 kg/m³ the above-mentioned thermal parameters read c = 1000 J kg⁻¹ K⁻¹, h = 2.5–25 Wm⁻²K⁻¹ [26,28,29] and short time constants of the order of τ = 10–100 s are expected. It should be noted that the unambiguous determination of short time constants in the range 10 s – 100 s is restricted by the 8 s step size with which the successive interferograms are attained, which might additionally conceal the presence of more than one short time constant within this decay window.

For the plaster material composition, studies report for the specific heat capacity the range c = 585–820 Jkg⁻¹K⁻¹ and for the thermal conductivity k = 0.7–2 Wm⁻¹K⁻¹ [30,31]. The heat transfer coefficient h is calculated by dividing thermal conductivity k by a length scale of the order of 10 cm = 0.1 m and so h = 7–20 Wm⁻²K⁻¹. The sample under study has a mass of m = 0.4 kg and a heat-transferring area inside the body which lies in the range A ≤ 0.0388 m², depending on the geometrical cut, with the largest area corresponding to the nominal dimensions of the plaster. These values yield a time constant τ ≥ 300 s; this longer time constant, together with the non-zero offset y₀ that is present more dominantly in the displacement values of L1 outside and L2 outside, is related to the plaster material’s natural non-conducting character, which does not favor the dissipation of heat and is in accordance to the fringes still visible on these sides on the interferograms. Similar experiments and exponential analysis on wood-type marquetry samples revealed a long time constant of the order of t > 1000 s, in agreement with the thermomechanical parameters and the insulating properties of wood [12].

Besides the impact of the material properties, the type of geometry of the present defects and discontinuities also affects the values of the exponential time constants derived from the evolution of the number of fringes, with the energy being channeled and preserved towards the direction of the L1 location, in accordance with the higher temperature values measured by IR thermography on the plaster sample surface [23]. Thermal energy flow in the presence of defects has been studied in detail and it was concluded in this work that, in the presence of structural discontinuities such as cracks and detachments, the direction of energy flow is influenced by the type and geometry of the developed structure [23]; the propagating crack at the boundary of the circular insertion was related to a path favoring thermomechanical energy flow, while the internal crack inside the circular area boundaries was connected to a thermal barrier, directing the propagation of energy to other paths. The longer decay time of the L1 inside relative displacement compared to the corresponding of L2 inside is in line with this finding, similar to the considerably longer cooling times observed for L1 outside for both exposure times.

Regarding the cooling-down behavior of the defect area, it is worth mentioning that during the cooling-down process the distinct pattern of the highest fringe density appearing at t = 0 s starts to merge to the overall fringe pattern developed after t = 200 s, as observed by the recorded interferograms. However, it is only with the exponential analysis that clear evidence of the existence of variable paths of energy flow can be deduced. On the other hand, these exponential values are influenced by both the structural discontinuities and the organic material properties, making the isolation of the contribution of the thermal parameters of the organic material to the extracted time constants values complicated. A decay process from the area of an organic insertion of similar size and polyester material inside the marquetry sample was reported to exhibit a time constant of the order of 20 s, a value close to τ = 52 s found here for the 60 s IR thermal load [12].

An advantage arising from the exponential analysis followed in this work is related to the fact that it can be directly applied to the interferograms without the necessity of a special phase analysis software or demanding and time-consuming post-processing of the obtained images. Moreover, it can be exploited for characterizing the structural condition and response in intermediate time windows, providing evidence on the material state together with the interferograms at variable stages of the measurement. Structural monitoring can be achieved and characteristic time scales can shed light on the type and features of the materials and defects, regardless of the origin of the cause (humidity, thermal load, etc.) and under real conditions. Other technologies that have been exploited for the analysis of lime-based plaster materials include the Digital Imaging Correlation (DIC) technique, Nuclear Magnetic Resonance (NMR), optical and electron (SEM–EDS) microscopy and X-ray diffractometry (XRD) [32,33,34]; our laboratory has developed Digital Holographic Speckle Pattern Interferometry for the extensive study of lime plasters and other materials utilized in engineering and other applications.

4. Conclusions

In this work, the response of a plaster-based material has been investigated after the deposition of thermal load in the form of infrared radiation from an incoherent infrared light source. The approach adopted in the study is applied to the evaluation of the thermomechanical behavior of the plaster sample subject to the radiation for two different exposure times t = 60 s and t = 180 s, and is based on the combination of the experimental technique of Digital Holographic Speckle Pattern Interferometry DHSPI with the post-processing of the recorded interferograms and the formation, visualization and processing of fringe-pattern images together with the exponential analysis of the fringe-pattern evolution in selected areas, providing insight on the mechanical response of the material in time.

Time constants in the range 50 s–1000 s are extracted, which are attempted to be correlated with the thermal parameters of the plaster material and existent structural discontinuities, as well as a purposefully inserted organic material called the defect. Long time constants > 300 s are postulated to arise from the nature of the plaster material, while shorter time constants are attributed to the existence of air gaps originating from cracks, detachments and layer joints and/or to the organic material. Very importantly, the nature of the defects in the interior of the object are shown to favor the distribution of energy following initial thermal load towards specific areas. Similar findings on a spectrum of structures can be potentially be exploited in order to complementary characterize irregularities before further analysis or experimental assessment with other methods come into play.

The present work aims at the realization of a non-invasive optical characterization platform that attempts to characterize variable materials and structural geometries, comprising different layer materials and various forms of inhomogeneities.