The Designed Phase Mask for Suppressing the Inter-Pixel Crosstalk Noise in Intensity-Modulated Multilevel Holographic Data Storage Systems
Abstract
1. Introduction
2. Principle of Detected Signal-Quality Improvement
2.1. Inter-Pixel Crosstalk Noise
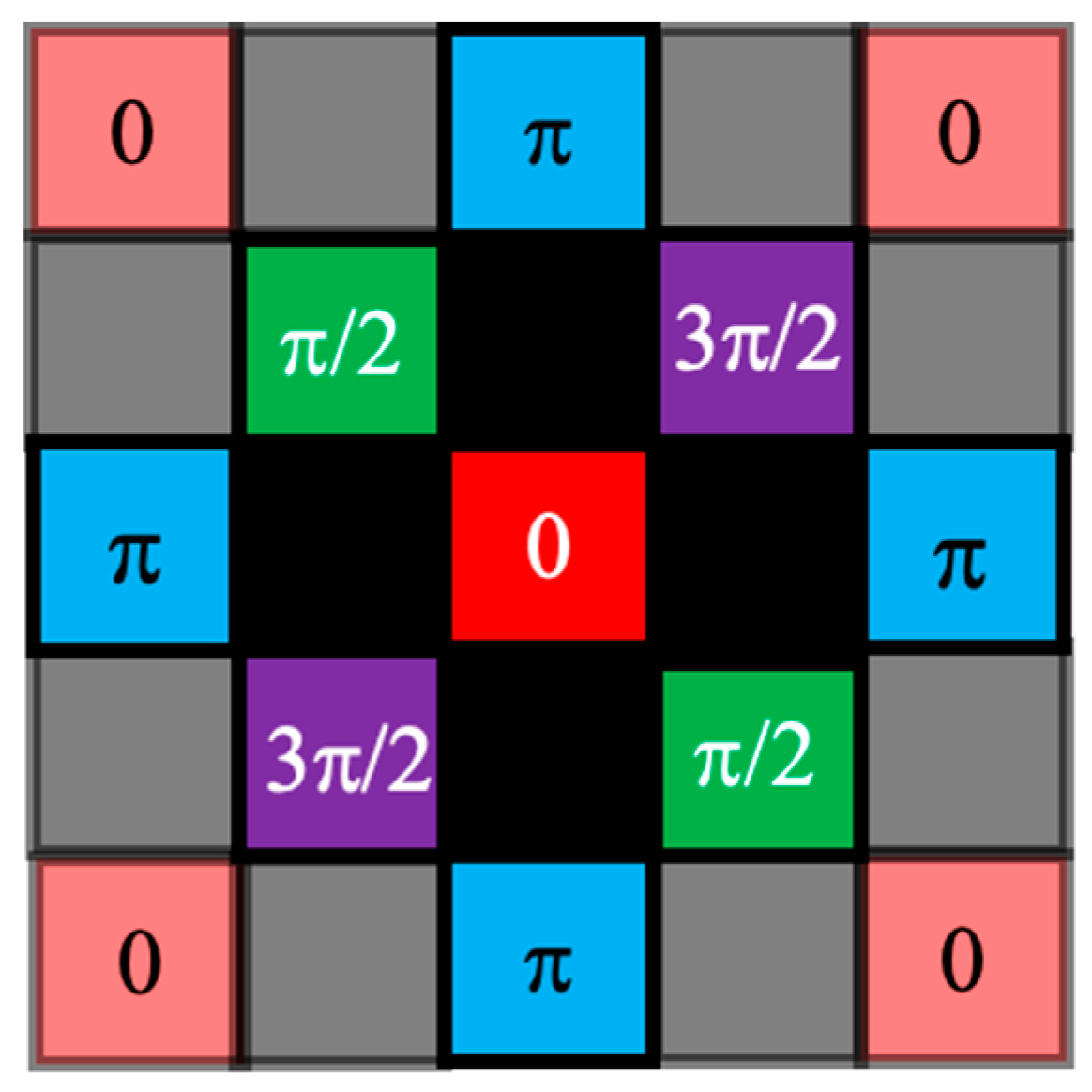
2.2. Crosstalk Noise-Suppression Method
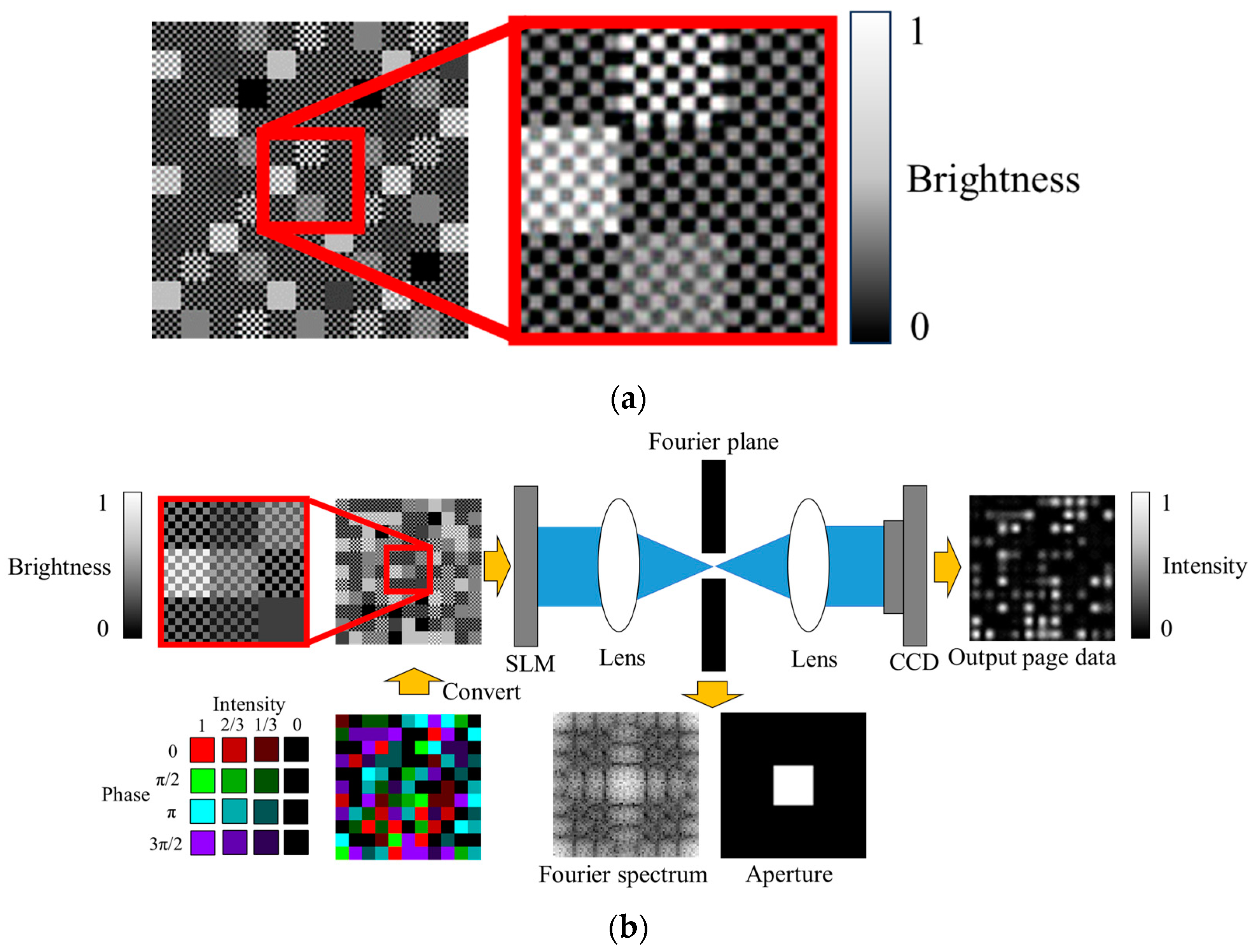
2.3. Signal Image to Be Input
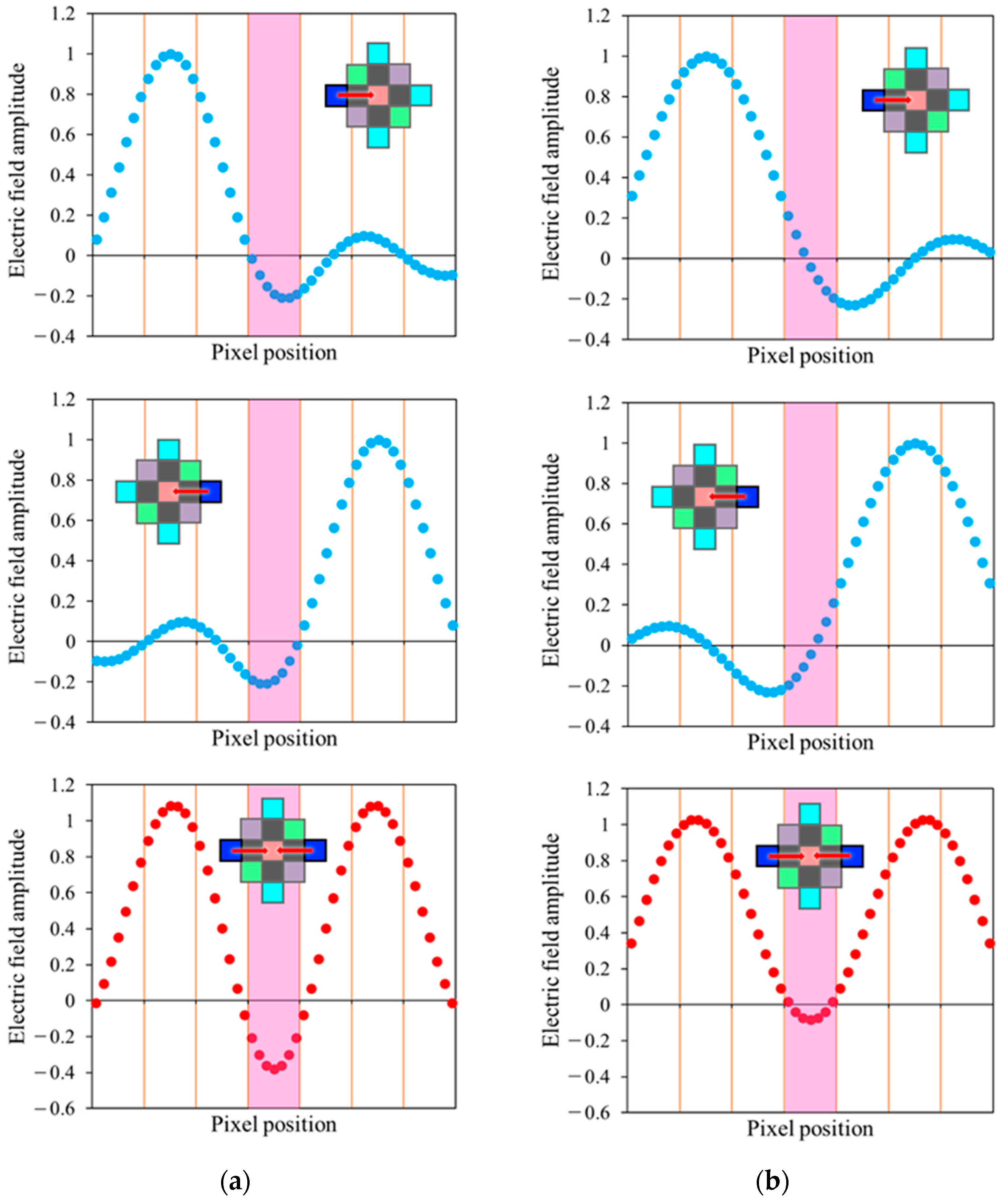
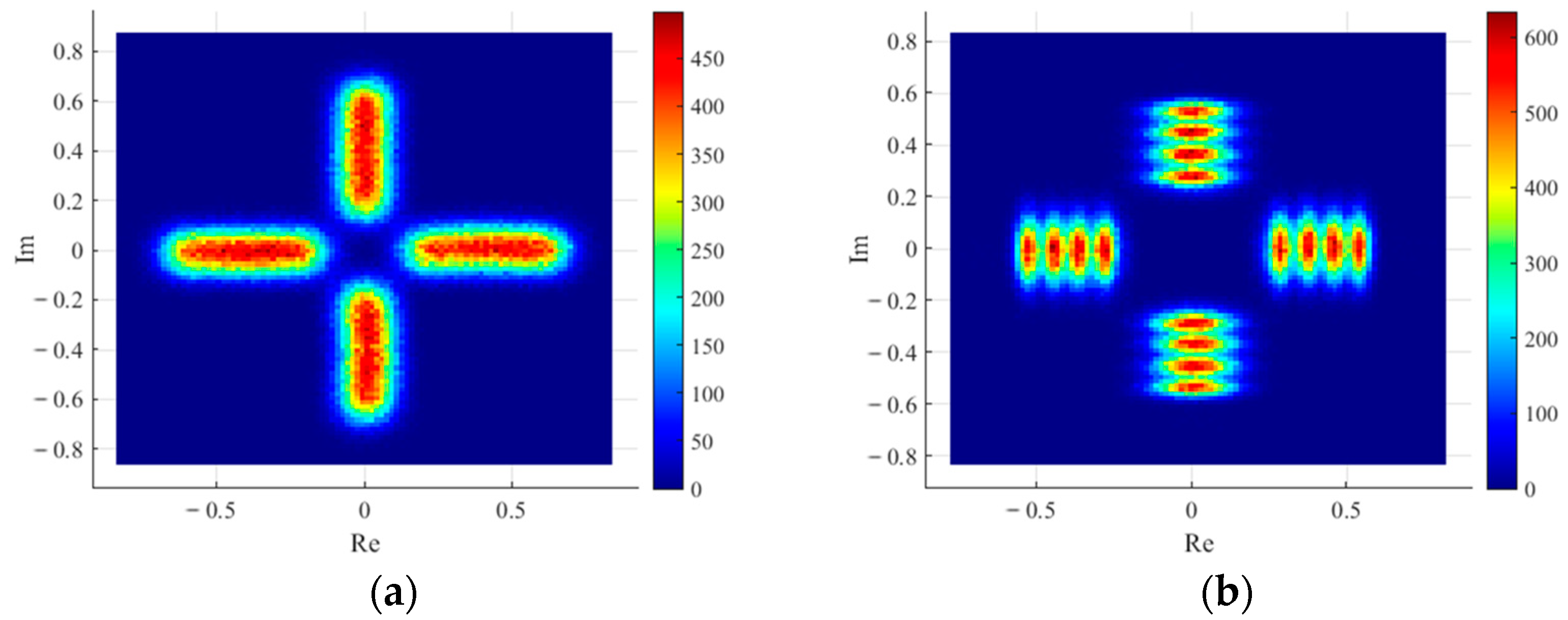
3. Simulation
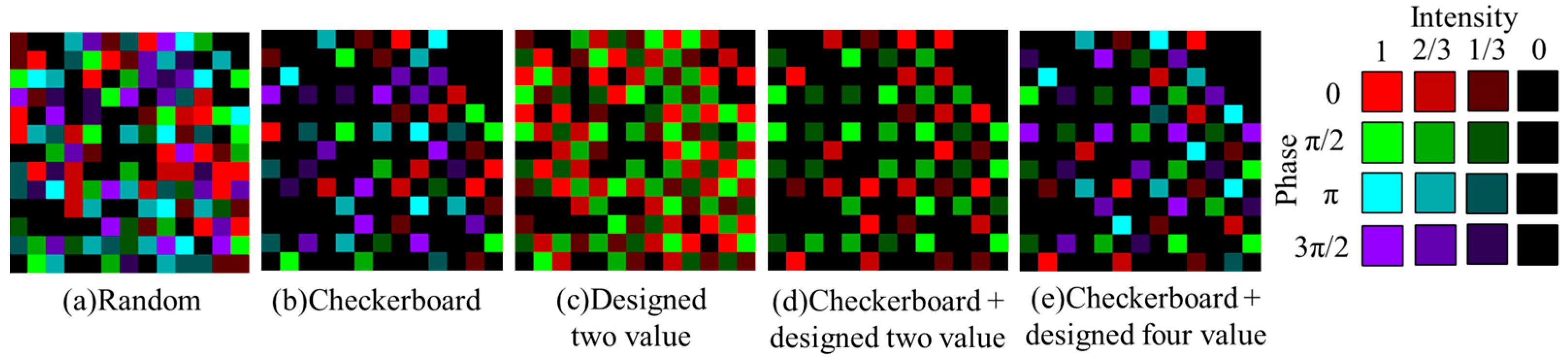
3.1. Simulation Method
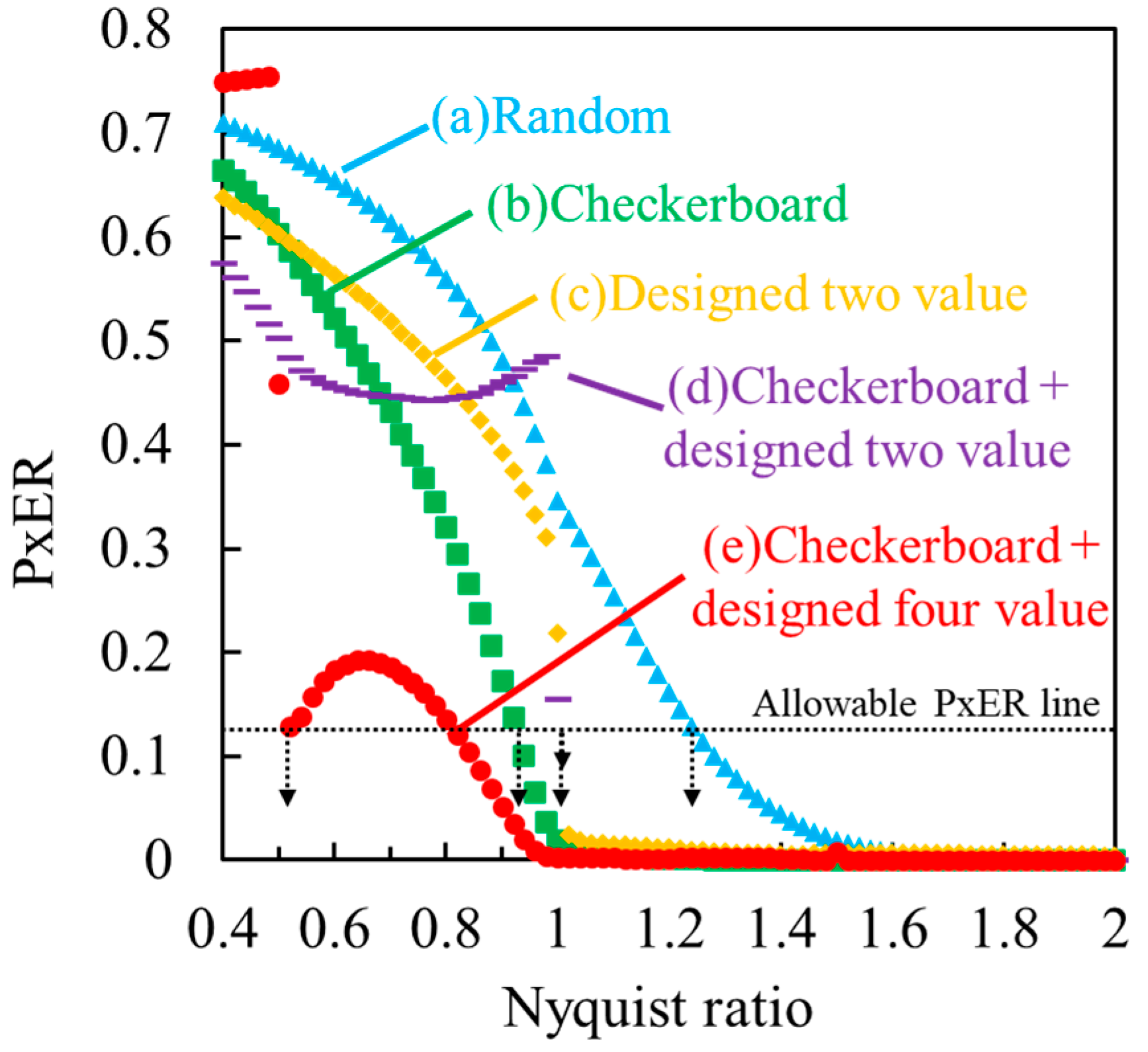
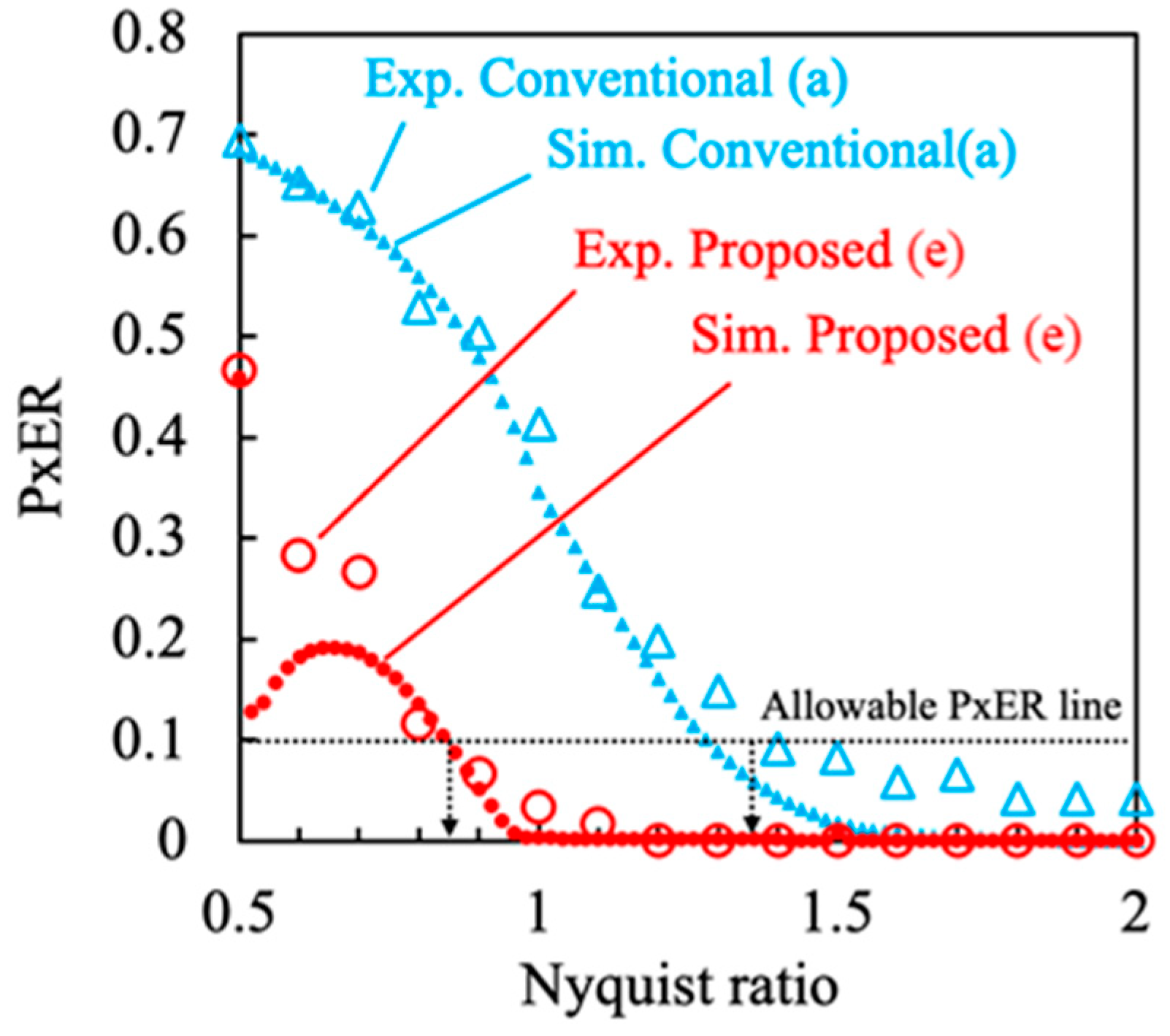
3.2. Simulation Results and Discussion
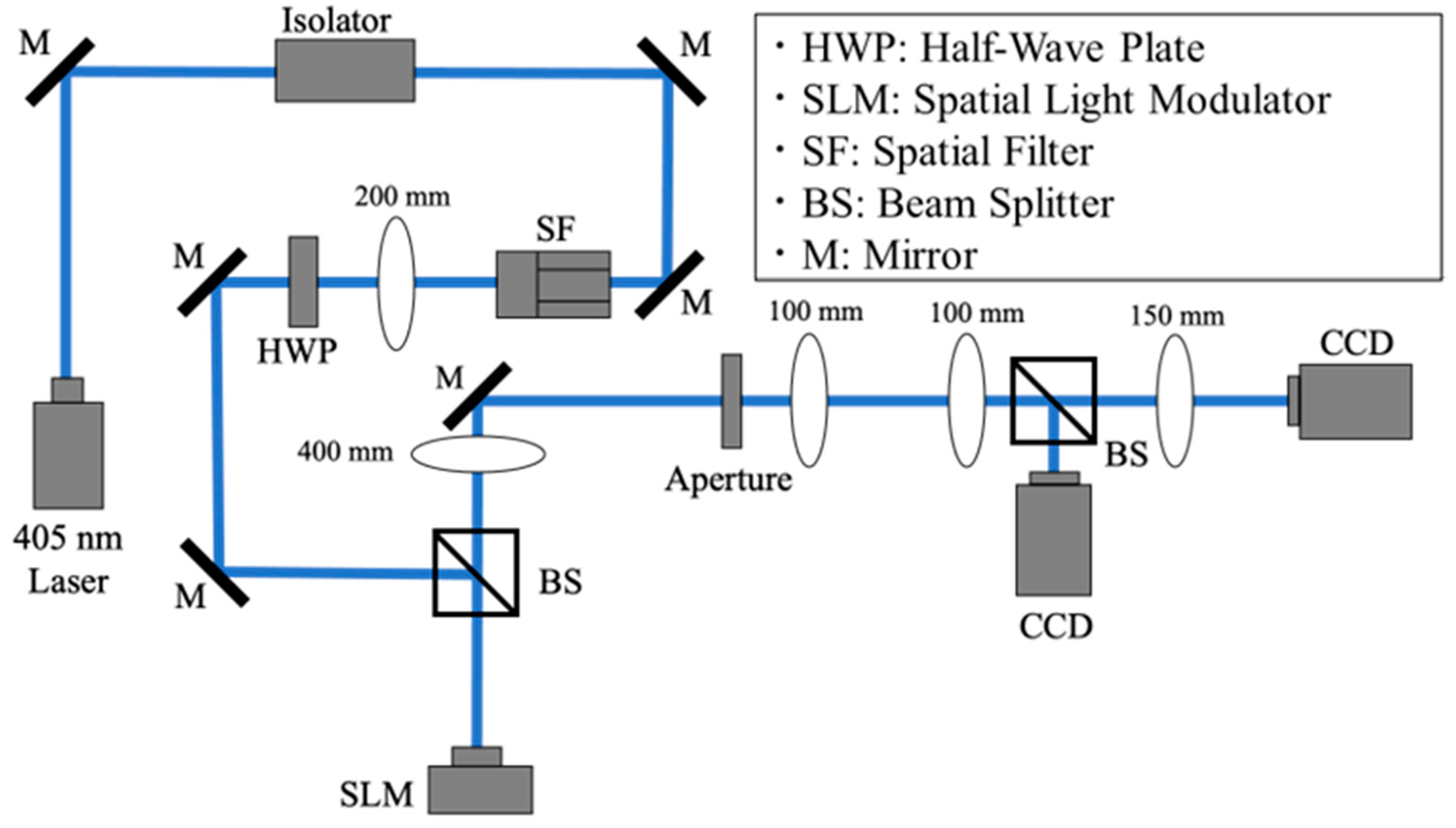
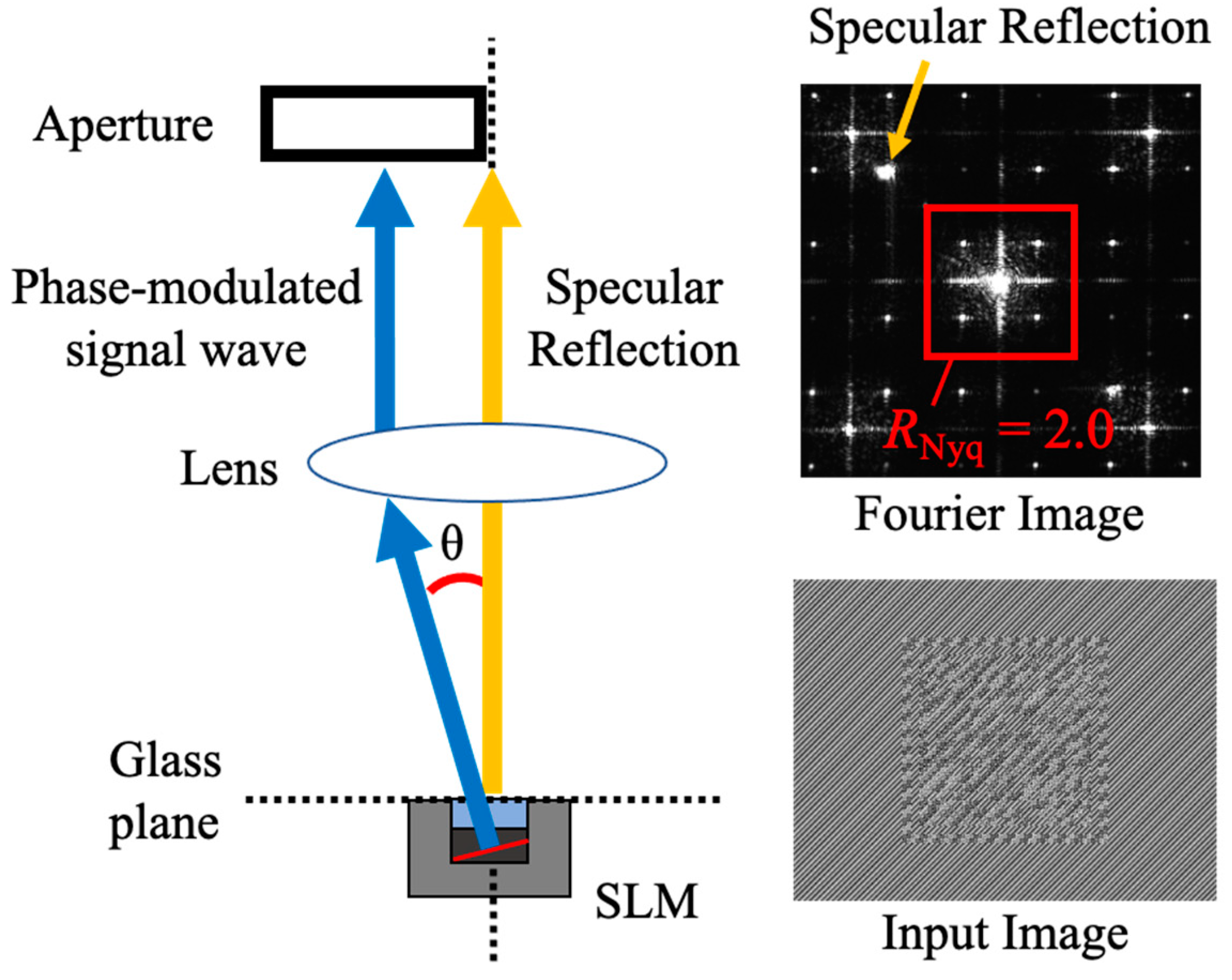
4. Experiments
4.1. Experimental Method
4.2. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coufal, H.J.; Psaltis, D.; Sincerbox, G.T. Holographic Data Storage; Springer: Berlin, Germany, 2000. [Google Scholar]
- Curtis, K.; Dhar, L.; Hill, A.; Wilson, W.; Ayres, M. Holographic Data Storage: From Theory to Practical Systems; Wiley: New York, NY, USA, 2010. [Google Scholar]
- Anderson, K.; Curtis, K. Polytopic Multiplexing. Opt. Lett. 2004, 29, 1402–1404. [Google Scholar] [CrossRef] [PubMed]
- Mok, F.H. Angle-Multiplexed Storage of 5000 Holograms in Lithium Niobate. Opt. Lett. 1993, 18, 915–917. [Google Scholar] [CrossRef]
- Shimura, T.; Ichimura, S.; Fujimura, R.; Kuroda, K.; Xiaodi, T.; Horimai, H. Analysis of a Collinear Holographic Storage System: Introduction of Pixel Spread Function. Opt. Lett. 2006, 31, 1208–1210. [Google Scholar] [CrossRef] [PubMed]
- Sato, M.; Ogasawara, M.; Ito, Y.; Tanaka, S.; Iida, T. New Coaxial Interference Method for Consumer Holographic Memory. Jpn. J. Appl. Phys. 2007, 46, 3850–3854. [Google Scholar] [CrossRef]
- Tanaka, K.; Hara, M.; Tokuyama, K.; Hirooka, K.; Ishioka, K.; Fukumoto, A.; Watanabe, K. Improved Performance in Coaxial Holographic Data Recording. Opt. Express 2007, 15, 16196–16209. [Google Scholar] [CrossRef]
- Burr, G.W.; Barking, G.; Coufal, H.; Hoffnagle, J.A.; Jefferson, C.M.; Neifeld, M.A. Gray-Scale Data Pages for Digital Holographic Data Storage. Opt. Lett. 1998, 23, 1218–1220. [Google Scholar] [CrossRef]
- Okamoto, A.; Kunori, K.; Takabayashi, M.; Tomita, A.; Sato, K. Holographic Diversity Interferometry for Optical Storage. Opt. Express 2011, 19, 13436. [Google Scholar] [CrossRef]
- Nobukawa, T.; Nomura, T. Multilevel Recording of Complex Amplitude Data Pages in a Holographic Data Storage System Using Digital Holography. Opt. Express 2016, 24, 21001. [Google Scholar] [CrossRef]
- John, R.; Joseph, J.; Singh, K. Holographic Digital Data Storage Using Phase-Modulated Pixels. Opt. Lasers Eng. 2005, 43, 183–194. [Google Scholar] [CrossRef]
- Bunsen, M.; Umetsu, S.; Takabayashi, M.; Okamoto, A. Method of Phase and Amplitude Modulation/Demodulation Using Datapages with Embedded Phase-Shift for Holographic Data Storage. Jpn. J. Appl. Phys. 2013, 52, 09LD04. [Google Scholar] [CrossRef]
- Nobukawa, T.; Nomura, T. Linear Phase Encoding for Holographic Data Storage with a Single Phase-Only Spatial Light Modulator. Appl. Opt. 2016, 55, 2565–2573. [Google Scholar] [CrossRef] [PubMed]
- Nobukawa, T.; Nomura, T. Digital Super-Resolution Holographic Data Storage Based on Hermitian Symmetry for Achieving High Areal Density. Opt. Express 2017, 25, 1326–1338. [Google Scholar] [CrossRef] [PubMed]
- Muroi, T.; Katano, Y.; Kinoshita, N.; Ishii, N. Dual-Page Reproduction to Increase the Data Transfer Rate in Holographic Memory. Opt. Lett. 2017, 42, 2287–2290. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-T.; Cho, B.-C.; Kim, E.-S.; Gil, S.-K. Performance Analysis of Phase-Code Multiplexed Holographic Memory. Appl. Opt. 2000, 39, 4160–4167. [Google Scholar] [CrossRef] [PubMed]
- Takabayashi, M.; Okamoto, A.; Tomita, A.; Bunsen, M. Symbol Error Characteristics of Hybrid-Modulated Holographic Data Storage by Intensity and Multi Phase Modulation. Jpn. J. Appl. Phys. 2011, 50, 09ME05. [Google Scholar] [CrossRef]
- Schwider, J.; Burow, R.; Elssner, K.-E.; Grzanna, J.; Spolaczyk, R.; Merkel, K. Digital Wave-Front Measuring Interferometry: Some Systematic Error Sources. Appl. Opt. 1983, 22, 3421–3432. [Google Scholar] [CrossRef] [PubMed]
- Fujimura, R. Investigation of Noise Characteristics of Multivalued Signals and Estimation of Single-Page Storage Density in Holographic Data Storage. ITE Trans. Media Technol. Appl. 2021, 9, 144–152. [Google Scholar] [CrossRef]
- Ishii, T.; Fujimura, R. Interpixel Crosstalk Cancellation on Holographic Memory. Jpn. J. Appl. Phys. 2017, 56, 09NA10. [Google Scholar] [CrossRef]
- Nobukawa, T.; Barada, D.; Nomura, T.; Fukuda, T. Orthogonal Polarization Encoding for Reduction of Interpixel Cross Talk in Holographic Data Storage. Opt. Express 2017, 25, 22425. [Google Scholar] [CrossRef]
- Hong, J.; McMichael, I.; Ma, J. Influence of phase masks on cross talk in holographic memory. Opt. Lett. 1996, 21, 1694–1696. [Google Scholar] [CrossRef]
- Bernal, M.-P.; Burr, G.W.; Coufal, H.; Grygier, R.K.; Hoffnagle, J.A.; Jefferson, C.M.; Oesterschulze, E.; Shelby, R.M.; Sincerbox, G.T.; Quintanilla, M. Effects of multilevel phase masks on interpixel cross talk in digital holographic storage. Appl. Opt. 1997, 36, 3107–3115. [Google Scholar] [CrossRef] [PubMed]
- Saito, M.; Fujimura, R. Noise Suppression in Intensity-Modulated Multivalued Holographic Memory. In Proceedings of the International Workshop on Photonics Polymer for Innovation, Suwa, Nagano, Japan, 16 October 2018. [Google Scholar]
- Göröcs, Z.; Erdei, G.; Sarkadi, T.; Ujhelyi, F.; Reményi, J.; Koppa, P.; Lorincz, E. Hybrid Multinary Modulation Using a Phase Modulating Spatial Light Modulator and a Low-Pass Spatial Filter. Opt. Lett. 2007, 32, 2336. [Google Scholar] [CrossRef] [PubMed]
- Bernal, M.-P.; Burr, G.W.; Coufal, H.; Quintanilla, M. Balancing Interpixel Cross Talk and Detector Noise to Optimize Areal Density in Holographic Storage Systems. Appl. Opt. 1998, 37, 5377. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-H.; Lim, S.-Y.; Kim, N.; Park, N.-C.; Yang, H.; Park, K.-S.; Park, Y.-P. Increasing the Storage Density of a Page-Based Holographic Data Storage System by Image Upscaling Using the PSF of the Nyquist Aperture. Opt. Express 2011, 19, 12053–12065. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Hao, J.; Wang, K.; Zhang, Y.; Li, H.; Tan, X. Frequency Expanded Non-Interferometric Phase Retrieval for Holographic Data Storage. Opt. Express 2020, 28, 511–518. [Google Scholar] [CrossRef] [PubMed]
- Ishii, N.; Katano, Y.; Muroi, T.; Kinoshita, N. Spatially Coupled Low-Density Parity-Check Error Correction for Holographic Data Storage. Jpn. J. Appl. Phys. 2017, 56, 09NA03. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.Y.; Zhou, Z.; Zhang, H.; Wei, Y.; Yu, H.G.; Hu, W.; Chen, W.; Dai, H.T.; Ma, L.L.; Qiu, C.W.; et al. Vectorial liquid-crystal holography. eLight 2024, 4, 5. [Google Scholar] [CrossRef]




| Number of data pixels | 1001 × 1001 data pixels |
| Number of pixels within one data pixel | 7 × 7 pixels |
| Nyquist size | 1001 ×1001 pixels |
| Nyquist ratio | 0.5–2.0 |
| Pattern Name | Amplitude Pattern | Phase Pattern |
|---|---|---|
| (a) Random | (A) All pixels 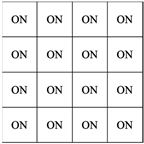 | (I) Random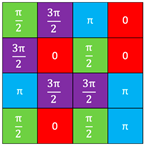 |
| (b) Checkerboard | (B) Checkerboard | (II) Random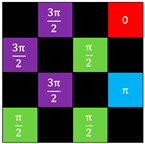 |
| (c) Designed two value | (A) All pixels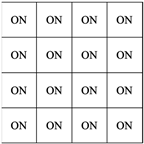 | (III) Regular (0, π/2)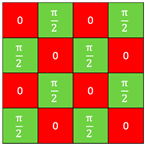 |
| (d) Checkerboard + Designed two value | (B) Checkerboard | (IV) Regular (0, π/2)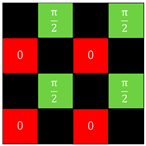 |
| (e) Checkerboard + Designed four value | (B) Checkerboard | (V) Regular (0, π/2, π, 3π/2)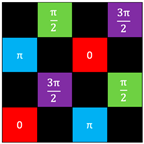 |
| Size of the data pixel | 560 μm |
| Nyquist size | 289 μm |
| Number of signal data pixels within a page | 60 data pixels |
| Number of detector pixels within one data pixel | 44 × 44 detector pixels |
| Nyquist ratio | 0.5–2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nonaka, T.; Hirayama, S.; Shimura, T.; Fujimura, R. The Designed Phase Mask for Suppressing the Inter-Pixel Crosstalk Noise in Intensity-Modulated Multilevel Holographic Data Storage Systems. Photonics 2024, 11, 507. https://doi.org/10.3390/photonics11060507
Nonaka T, Hirayama S, Shimura T, Fujimura R. The Designed Phase Mask for Suppressing the Inter-Pixel Crosstalk Noise in Intensity-Modulated Multilevel Holographic Data Storage Systems. Photonics. 2024; 11(6):507. https://doi.org/10.3390/photonics11060507
Chicago/Turabian StyleNonaka, Takuya, Soki Hirayama, Tsutomu Shimura, and Ryushi Fujimura. 2024. "The Designed Phase Mask for Suppressing the Inter-Pixel Crosstalk Noise in Intensity-Modulated Multilevel Holographic Data Storage Systems" Photonics 11, no. 6: 507. https://doi.org/10.3390/photonics11060507
APA StyleNonaka, T., Hirayama, S., Shimura, T., & Fujimura, R. (2024). The Designed Phase Mask for Suppressing the Inter-Pixel Crosstalk Noise in Intensity-Modulated Multilevel Holographic Data Storage Systems. Photonics, 11(6), 507. https://doi.org/10.3390/photonics11060507





