Design of a High-Frame-Rate and Large-Grayscale Simulation Projection System Based on Digital Micromirror Devices
Abstract
1. Introduction
2. Principle
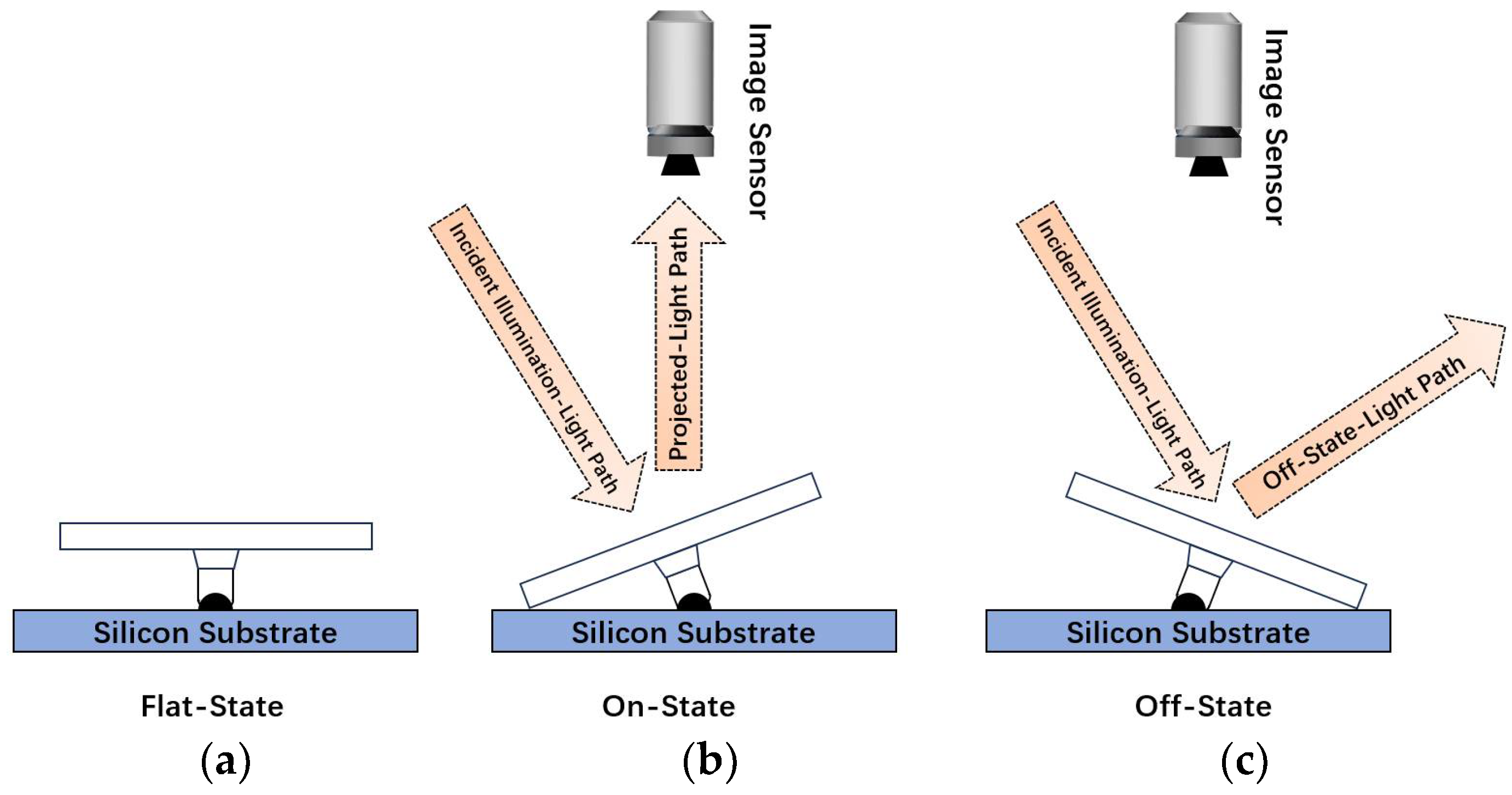
2.1. Basic Working Principle of DMD
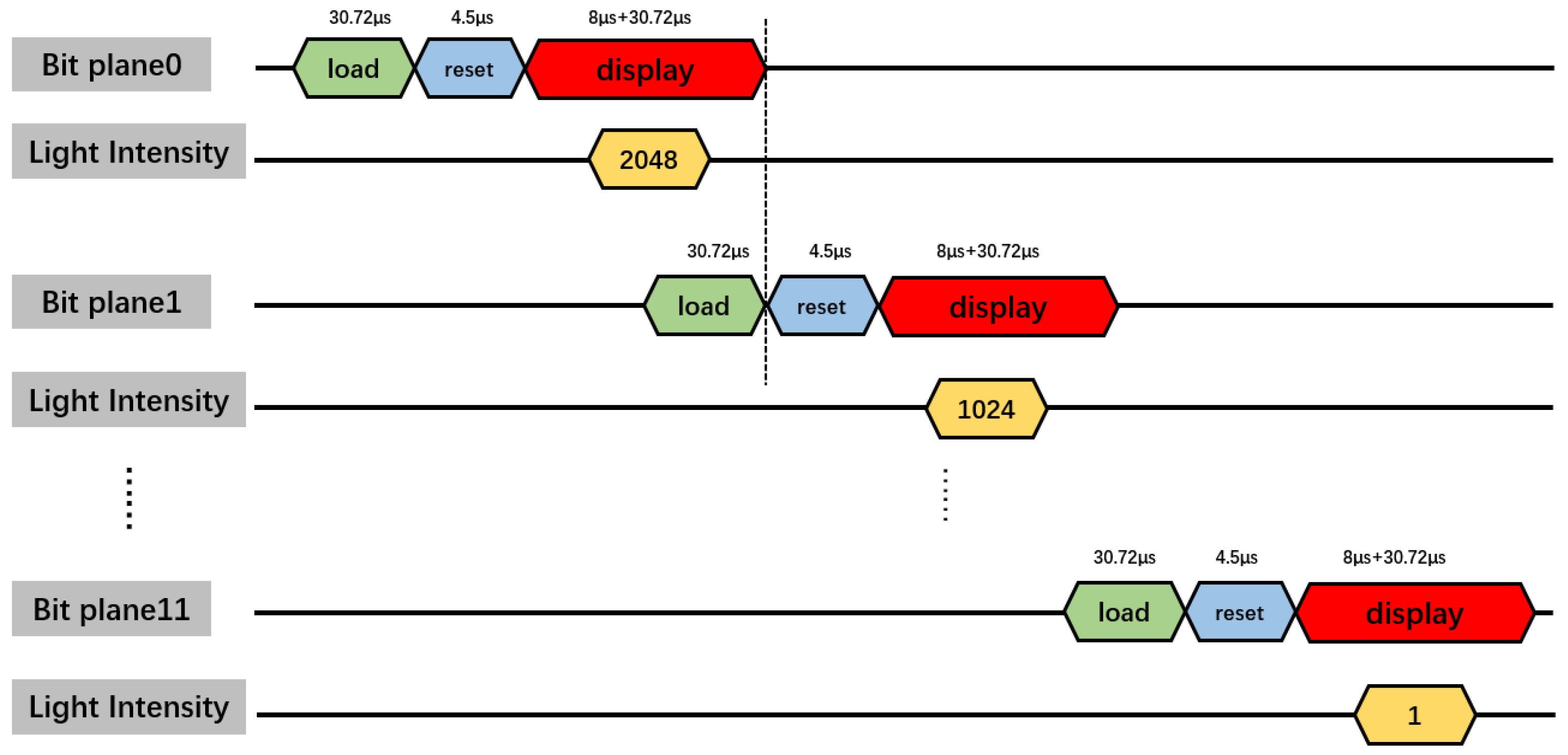
2.2. Bit Plane Decomposition
2.3. Traditional DMD Grayscale Modulation
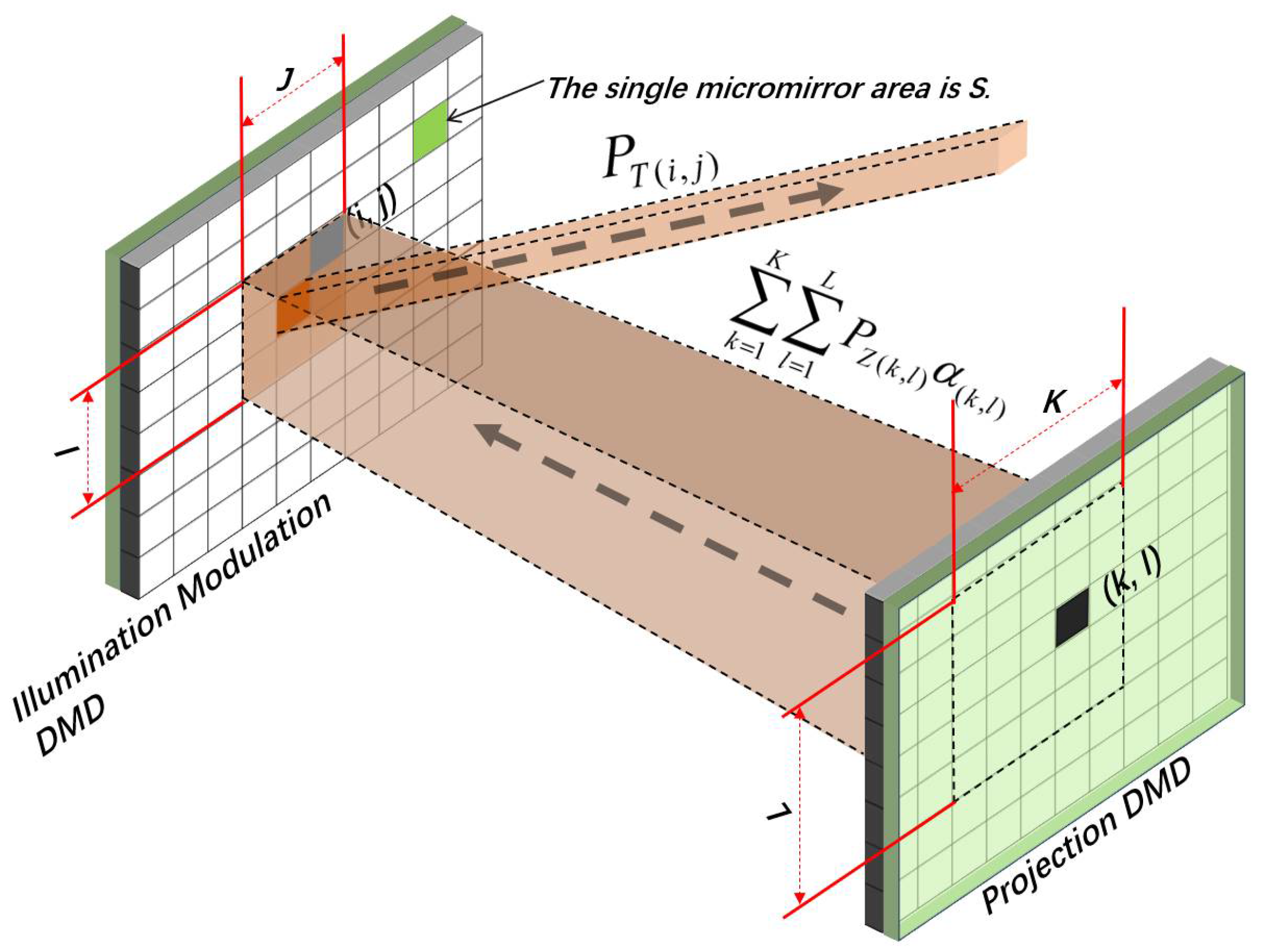
2.4. Dual DMD Synchronous Modulation
3. Materials and Methods
3.1. Projection Experiment Protocol
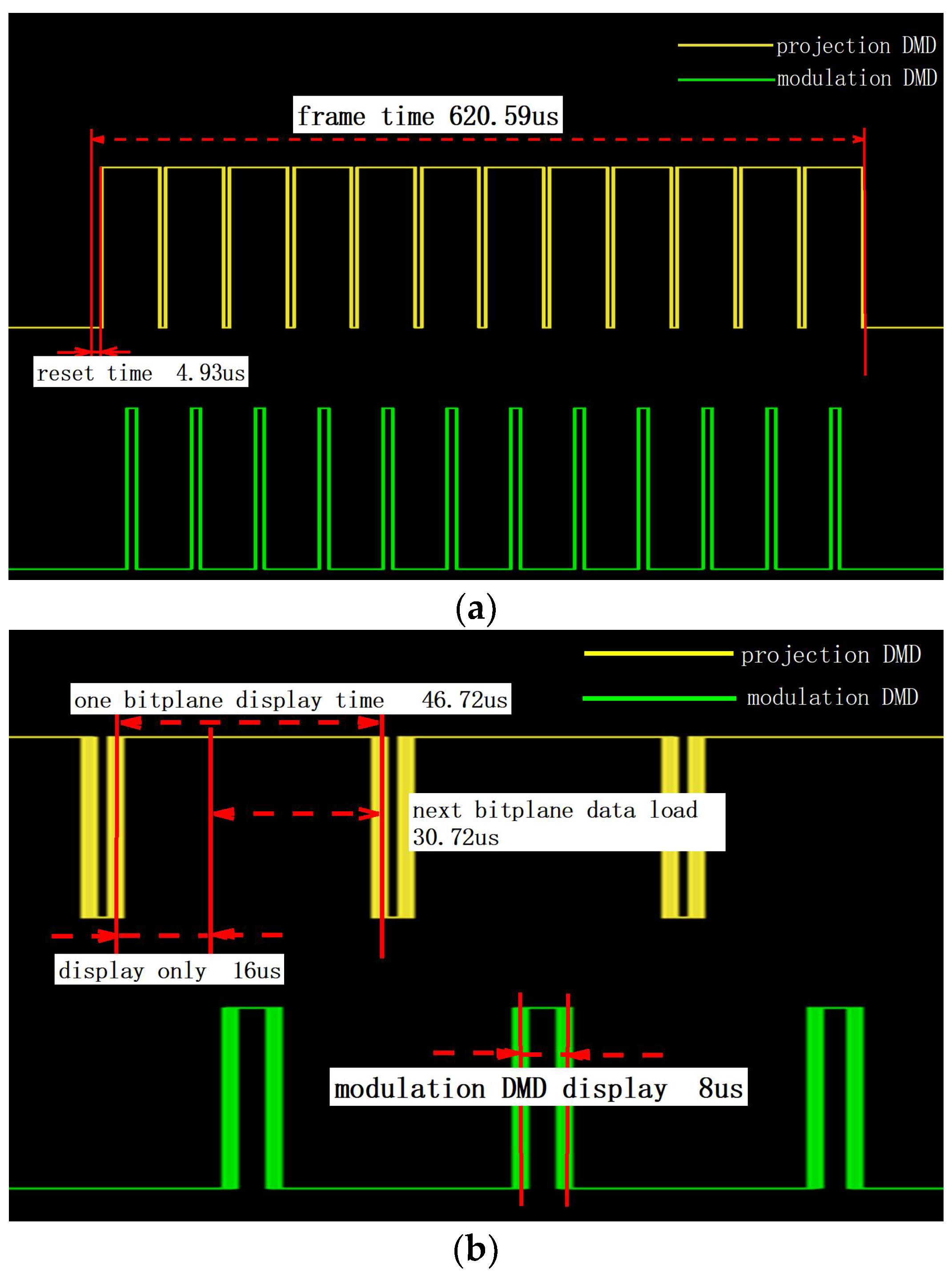
3.2. Frame Rate Calculation
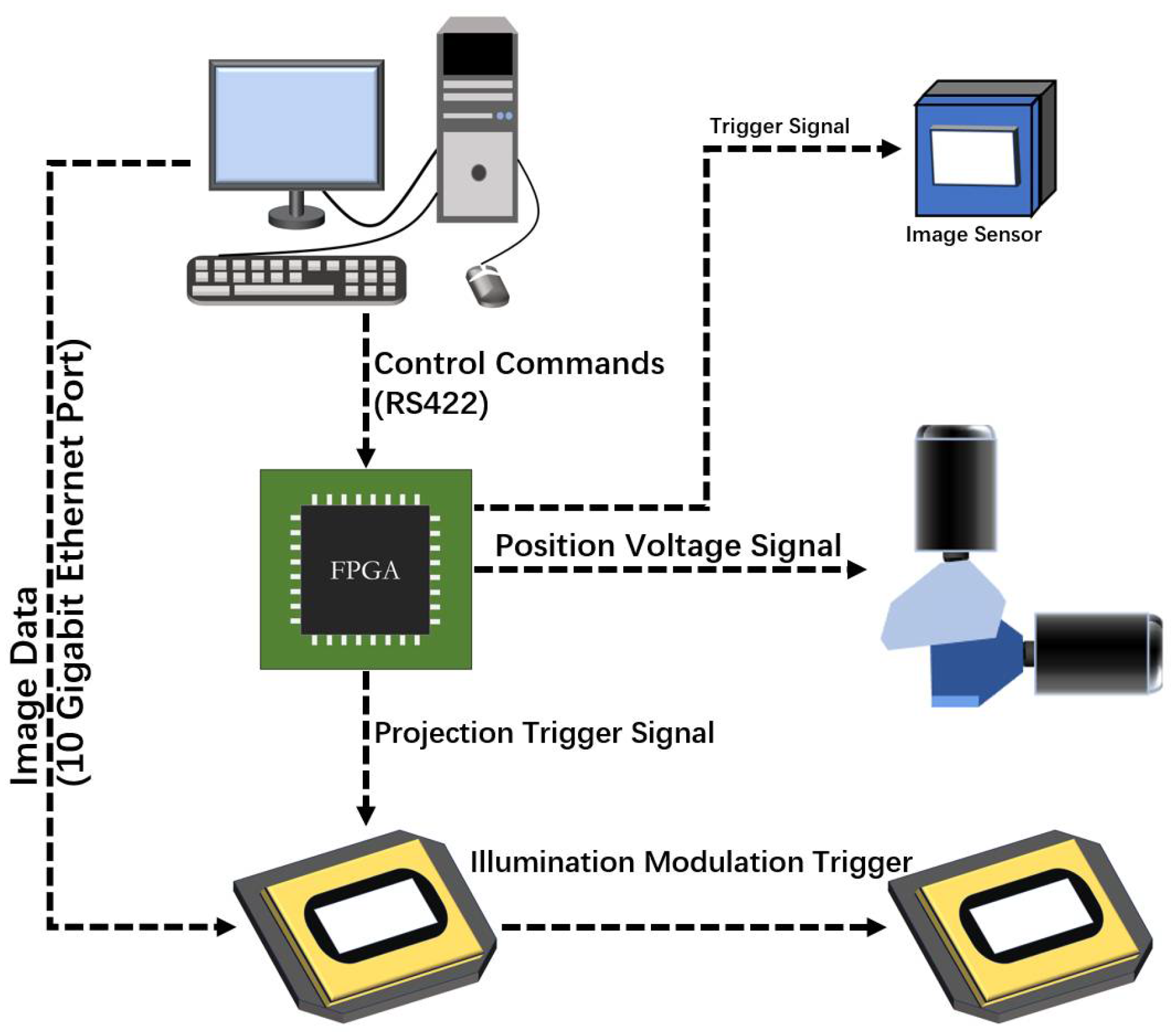
3.3. Experimental System Construction
4. Results and Discussion
4.1. Landscape Projection Test
4.2. Experimental Verification
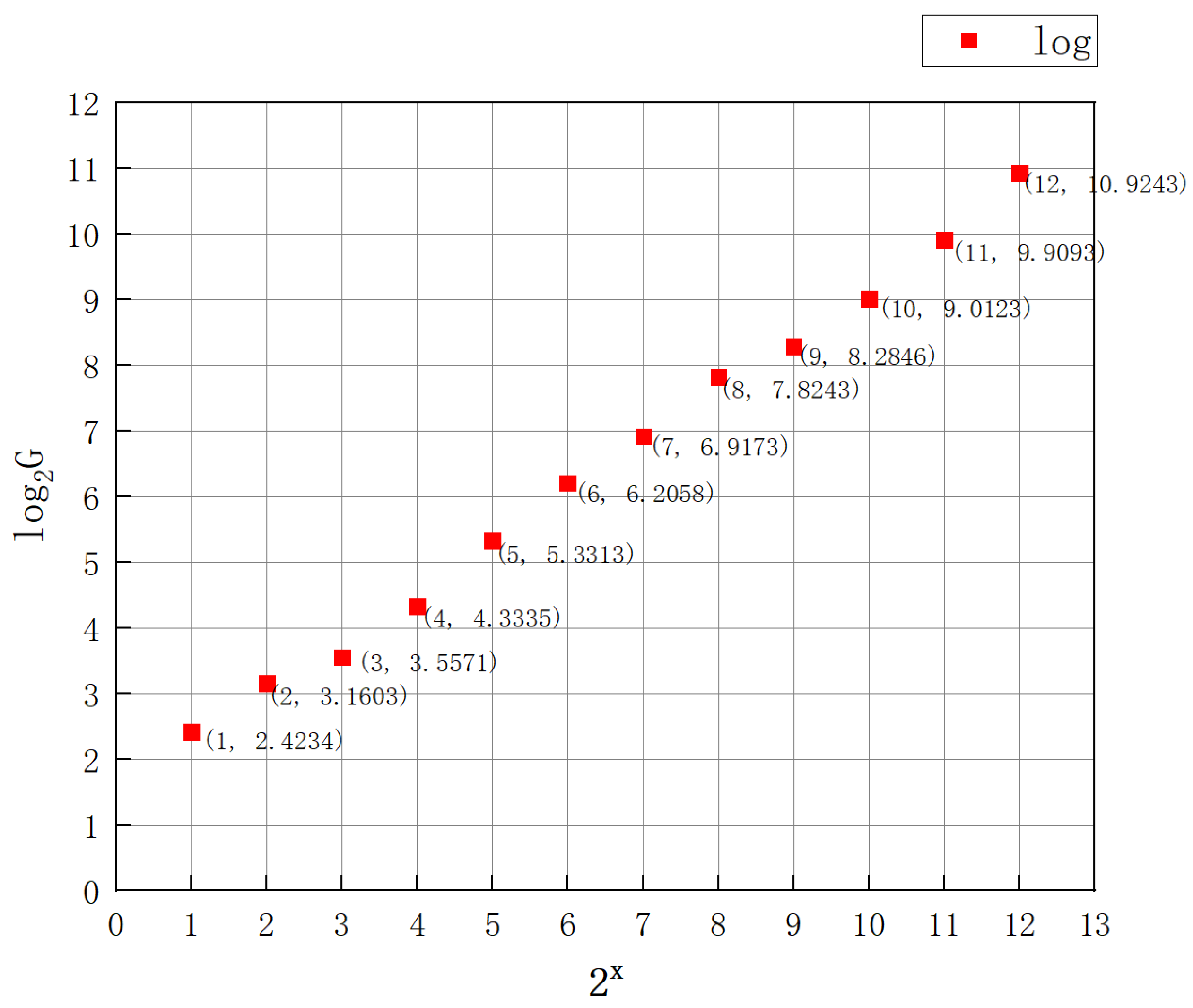
4.2.1. Grayscale Test
4.2.2. Frame Rate Test
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Introduction to ±12 Degree Orthogonal Digital Micromirror Devices (DMDs). Available online: https://www.ti.com/lit/pdf/dlpa008?keyMatch=DMD&tisearch=search-everything (accessed on 16 April 2024).
- Cheng, Z.; Toshiyoshi, H. CMOS-MEMS Micro-Mirror Arrays by Post-Processing ASMC 0.35-μm CMOS Chips. J. Microelectromech. Syst. 2017, 26, 1435–1441. [Google Scholar] [CrossRef]
- Gong, C.; Hogan, T. CMOS compatible fabrication processes for the digital micromirror device. IEEE J. Electron. Devi. 2014, 2, 27–32. [Google Scholar] [CrossRef]
- Wang, J.; Huffman, J.; Pinheiro, P.; Hall, J. An embedded reset driver for digital micromirror devices (DMDs). J. Soc. Inf. Disp. 2010, 18, 868–872. [Google Scholar] [CrossRef]
- Yu, W.-K.; Yang, Y.; Liu, J.-R.; Wei, N.; Wang, S.-F. Secondary Complementary Balancing Compressive Imaging with a Free-Space Balanced Amplified Photodetector. Sensors 2022, 22, 3801. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, J.; Li, C.; Xu, R.; Zhang, Y.; Liu, S.; Wang, J. MEMS-based super-resolution remote sensing system using compressive sensing. Opt. Commun. 2018, 426, 410–417. [Google Scholar] [CrossRef]
- Li, D.; Wei, H.; Fang, H.; Gao, Y. Group Control of Photo-Responsive Colloidal Motors with a Structured Light Field. Photonics 2024, 11, 421. [Google Scholar] [CrossRef]
- Kang, E.; Choi, H.; Hellman, B.; Rodriguez, J.; Smith, B.; Deng, X.; Liu, P.; Lee, T.L.-T.; Evans, E.; Hong, Y.; et al. All-MEMS Lidar Using Hybrid Optical Architecture with Digital Micromirror Devices and a 2D-MEMS Mirror. Micromachines 2022, 13, 1444. [Google Scholar] [CrossRef]
- Dudley, D.; Duncan, W.; Slaughter, J. Emerging digital micromirror device (DMD) applications. In Proceedings of the MOEMS Display and Imaging Systems, San Jose, CA, USA, 28–29 January 2003. [Google Scholar]
- Zhu, L.; Cao, Z.; Fu, S.; Wang, Y.; Qin, Y. Double-light-path multiplexing enabled light shaping efficiency enhancement for digital micromirror device. In Proceedings of the 2020 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 24–27 October 2020. [Google Scholar]
- Ketchum, R.S.; Blanche, P.-A. Diffraction Efficiency Characteristics for MEMS-Based Phase-Only Spatial Light Modulator with Nonlinear Phase Distribution. Photonics 2021, 8, 62. [Google Scholar] [CrossRef]
- Wan, Z.; Shi, Z.; Liu, Q.; Fu, X. Holographic Tailoring of Structured Light Field with Digital Device. Photonics 2022, 9, 506. [Google Scholar] [CrossRef]
- Lin, C.; Xu, W.; Liu, B.; Wang, H.; Xing, H.; Sun, Q.; Xu, J. Three-Dimensional Printing of Large Objects with High Resolution by Dynamic Projection Scanning Lithography. Micromachines 2023, 14, 1700. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Kim, K.; Yoon, J.; Yoon, J.; Park, Y.K. Active illumination using a digital micromirror device for quantitative phase imaging. Opt. Lett. 2015, 40, 5407–5410. [Google Scholar] [CrossRef]
- Yang, S.; Yan, X.; Qin, H.; Zeng, Q.; Liang, Y.; Arguello, H.; Yuan, X. Mid-Infrared Compressive Hyperspectral Imaging. Remote Sens. 2021, 13, 741. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhou, J.; Chen, Q.; Lei, L.; Wen, K.; Hu, Y. Rapid prototyping of a dammann grating in DMD-based maskless lithography. IEEE Photonics J. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Jun, J. A comprehensive methodology for optimizing read-out timing and reference DAC offset in high frame rate image sensing systems. Sensors 2023, 23, 7048. [Google Scholar] [CrossRef] [PubMed]
- Etoh, T.G.; Nguyen, A.Q.; Kamakura, Y.; Shimonomura, K.; Le, T.Y.; Mori, N. The Theoretical Highest Frame Rate of Silicon Image Sensors. Sensors 2017, 17, 483. [Google Scholar] [CrossRef] [PubMed]
- Mansur, D.J.; Vaillancourt, R.; Benedict, -G.R.; Newbry, S.P.; Dupuis, J.R. High-dynamic range DMD-based IR scene projector. In Proceedings of the Emerging Digital Micromirror Device Based Systems and Applications V (SPIE MOEMS-MEMS), San Francisco, CA, USA, 15 March 2013. [Google Scholar]
- Song, J.; Gao, Y.; Li, Z.; Li, J.; Zhang, X.; Zhou, L.; Shi, Q. Research on high frame rate scene projection method based on digital micromirror device (DMD). In Proceedings of the 2019 International Conference on Optical Instruments and Technology: Optoelectronic Imaging/Spectroscopy and Signal Processing Technology, Beijing, China, 12 March 2020. [Google Scholar]
- Hassan, N.B.; Dehkhoda, F.; Xie, E.; Herrnsdorf, J.; Strain, M.J.; Henderson, R.; Dawson, M.D. Ultrahigh frame rate digital light projector using chip-scale LED-on-CMOS technology. Photonics Res. 2022, 10, 2434–2446. [Google Scholar] [CrossRef]
- DLP® 0.7 XGA 2×LVDS TYPE-A DMD. Available online: https://www.ti.com/lit/gpn/DLP7000 (accessed on 15 April 2024).
- Jiang, Y.; Liu, Z.; Li, Y.; Li, J.; Lian, Y.; Liao, N.; Li, Z.; Zhao, Z. A digital grayscale generation equipment for image display standardization. Appl. Sci. 2020, 10, 2297. [Google Scholar] [CrossRef]
- Yuan, C.; Yan, Q.; Wu, Y.; Wang, Y.; Wang, Y. Single photon compressive imaging based on digital grayscale modulation method. Photonic Sens. 2021, 11, 350–361. [Google Scholar] [CrossRef]
- Kai, Z.; Yong, H.; Jie, Y.; Li, S. Dynamic infrared scene simulation using grayscale modulation of digital micro-mirror device. Chinese J. Aeronaut. 2013, 26, 394–400. [Google Scholar]
- DLPC410 DMD Digital Controller. Available online: https://www.ti.com/lit/gpn/DLPC410 (accessed on 15 April 2024).
- Jeong, J.-Y.; Shim, J.; Hong, S.-K.; Kwon, O.-K. A high-speed and energy-efficient multi-bit cyclic ADC using single-slope quantizer for CMOS image sensors. IEEE T CIRCUITS-II 2021, 68, 2322–2326. [Google Scholar] [CrossRef]
- Liang, Y.; Ding, R.; Zhu, Z. A 9.1 ENOB 200MS/s asynchronous SAR ADC with hybrid single-ended/differential DAC in 55-nm CMOS for image sensing signals. IEEE Sens. J. 2018, 18, 7130–7140. [Google Scholar] [CrossRef]








| Indicator | Value |
|---|---|
| RMSE | 13.83 |
| PSNR | 23.27 |
| SSIM | 0.747 |
| Original Gray Value | Imaging Gray Value (G) |
|---|---|
| 21 | 5.3645 |
| 22 | 8.9403 |
| 23 | 11.7708 |
| 24 | 20.1608 |
| 25 | 40.2593 |
| 26 | 73.8108 |
| 27 | 120.8696 |
| 28 | 226.6397 |
| 28 | 29.7324 |
| 29 | 40.9083 |
| 210 | 67.7453 |
| 211 | 126.1512 |
| 212 | 254.9373 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, L.; Yang, Y.; Li, H.; Tang, Y.; Li, Z.; Qu, Y.; Zhao, M.; Li, J. Design of a High-Frame-Rate and Large-Grayscale Simulation Projection System Based on Digital Micromirror Devices. Photonics 2024, 11, 793. https://doi.org/10.3390/photonics11090793
Meng L, Yang Y, Li H, Tang Y, Li Z, Qu Y, Zhao M, Li J. Design of a High-Frame-Rate and Large-Grayscale Simulation Projection System Based on Digital Micromirror Devices. Photonics. 2024; 11(9):793. https://doi.org/10.3390/photonics11090793
Chicago/Turabian StyleMeng, Lingxuan, Yongqiang Yang, Hongyu Li, Yanfu Tang, Zhongming Li, Ying Qu, Min Zhao, and Junlin Li. 2024. "Design of a High-Frame-Rate and Large-Grayscale Simulation Projection System Based on Digital Micromirror Devices" Photonics 11, no. 9: 793. https://doi.org/10.3390/photonics11090793
APA StyleMeng, L., Yang, Y., Li, H., Tang, Y., Li, Z., Qu, Y., Zhao, M., & Li, J. (2024). Design of a High-Frame-Rate and Large-Grayscale Simulation Projection System Based on Digital Micromirror Devices. Photonics, 11(9), 793. https://doi.org/10.3390/photonics11090793





