Abstract
The objective of this study, which is divided into two parts, is twofold: to address long-standing challenges in the sensing of atmospheric turbulence-induced wavefront aberrations under strong scintillation conditions via a comparative analysis of several basic scintillation-resistant wavefront sensing (SR-WFS) architectures and iterative phase retrieval (IPR) techniques (Part I, this paper), and to develop a framework for the potential integration of SR-WFS techniques into practical closed-loop non-astronomical atmospheric adaptive optics (AO) systems (Part II). In this paper, we consider basic SR-WFS mathematical models and phase retrieval algorithms, tradeoffs in sensor design and phase retrieval technique implementation, and methodologies for WFS parameter optimization and performance assessment. The analysis is based on wave-optics numerical simulations imitating realistic turbulence-induced phase aberrations and intensity scintillations, as well as optical field propagation inside the SR-WFSs. Several potential issues important for the practical implementation of SR-WFS and IPR techniques, such as the requirements for phase retrieval computational grid resolution, tolerance with respect to optical element misalignments, and the impact of camera noise and input light non-monochromaticity, are also considered. The results demonstrate that major wavefront sensing requirements desirable for AO operation under strong intensity scintillations can potentially be achieved by transitioning to novel SR-WFS architectures, based on iterative phase retrieval techniques.
1. Introduction
The operational principles of wavefront sensors (WFS) used in astronomical adaptive optics (AO) applications, including Shack–Hartmann wavefront sensors (SH) [1,2], curvature sensors [3,4], lateral shearing interferometers [5,6], pyramid WFSs [7,8], etc., are based on the assumption of relatively weak intensity inhomogeneities (scintillations) in the entering WFS optical field. For this reason, it is not surprising that these sensors are not efficient in the AO applications associated with laser beam propagation over near-horizontal or slant atmospheric paths, which are commonly characterized by moderate-to-strong intensity scintillations [9]. This drawback precludes the efficient utilization of AO techniques in such rapidly growing atmospheric optics areas as directed energy (DE) [10,11], remote laser power beaming [12], laser communications [13], and active (laser illumination-based) imaging [14].
Efforts have been undertaken in recent years to develop wavefront sensors that are less affected by scintillations (scintillation-resistant WFS) and hence, can be used for turbulence-induced aberration sensing in various non-astronomical atmospheric AO systems [15,16]. Despite some progress in tackling the scintillation problem, the scintillation resistant wavefront sensing (SR-WFS) approaches have not yet (to our knowledge) been implemented in practical closed-loop non-astronomical atmospheric AO systems.
One of the reason for this outcome is that in addition to scintillation resistance, such sensors should meet several additional criteria, i.e., they must exhibit: (a) a high closed-loop operational bandwidth (typically close to or above 1.0 kHz); (b) sufficiently high spatial resolution regarding phase aberration sensing (e.g., ranging from about 102 to 103 resolvable phase values); (c) cost efficiency; (d) robust operation under a wide range of turbulence and environmental conditions; (e) easy alignment and maintenance; (f) operation at a low signal-to-noise ratio (SNR) and with a non-monochromatic light source; and (g) high accuracy in aberration sensing, with errors not exceeding a small fraction of the operational wavelength.
This list of desired WFS characteristics may require modification and/or extension for certain, specific atmospheric AO applications. However, it is quite challenging to meet even a portion of the previously mentioned criteria using a single WFS instrument. Furthermore, some requirements may be at odds with each other. For example, increasing the WFS operational bandwidth will most likely only be achieved at the expense of wavefront sensing resolution and accuracy, and vice versa. On the other hand, the classical SH sensor represents an excellent example of a wavefront sensing system that meets nearly all of the criteria outlined above, with the exception of resistance to scintillations, as well as inadequate spatial resolution for some AO applications. In this study, the SH sensor is considered as the model to be followed in the development of scintillation-resistant wavefront sensing techniques for atmospheric AO applications.
In this paper, we demonstrate that most of the wavefront sensing characteristics desired for atmospheric AO can potentially be achieved by transitioning to WFS architectures based on iterative phase retrieval (IPR) techniques.
In Section 2, we provide a synopsis of basic WFS configurations and IPR algorithms that may be considered as candidates for turbulence-induced phase aberration sensing and AO mitigation under strong scintillations. These sensors can be described in terms of a generic SR-WFS model introduced here. This model is further applied to derive iterative phase and complex field (phase and magnitude) retrieval algorithms based on the gradient descent optimization of a fidelity (error) metric—analogues of the classical Gerchberg–Saxton (GS) and Fienup error reduction and hybrid input–output (HIO) phase retrieval algorithms [17,18,19,20]. We also outline the similarity between the iterative phase retrieval techniques and algorithms used for the synthesis of programmable diffractive optics elements (DOE) in laser beam shaping applications [21,22]. This section also provides a description of the IPR computational steps and metrics that can be utilized for phase and complex field retrieval accuracy assessment.
In Section 3, we analyze the general properties of optical field transformation in basic SR-WFS configurations which are “favorable” for achieving high performance in closed-loop operation under a wide range of turbulence conditions. This analysis is further applied to the SR-WFS optical configuration introduced here and referred to as the scintillation-resistant advanced phase contrast (SAPCO) sensor that, like the SH-WFS, is composed of a single optical element—a specifically designed phase mask. In this section, we also outline and discuss several tradeoffs that should be considered in designing SR-WFS instruments for atmospheric AO applications, including tradeoffs between phase retrieval accuracy and required computational time.
Section 3 concludes with a description of the numerical simulation setting used for analysis and parameter optimization of SR-WFSs and IPR-based wave front sensing techniques. Numerical simulations were conducted using a conventional wave-optics (split-step operator-based [23]) numerical simulation approach. To imitate realistic turbulence-induced wavefront aberrations and intensity scintillations, the modeling and simulation (M&S) setting included laser beacon beam propagation over 5 km to the SR-WFS input plane through atmospheric turbulence uniformly distributed along the path.
Section 4 provides examples of parameter selection and optimization for basic SR-WFS types, with special emphasis on the SAPCO sensor. Optimization of WFS parameters was based on the computation of the phase retrieval error in the course of the HIO algorithm iterations. The corresponding dependencies (phase retrieval error evolution curves) were obtained from a set of numerical simulation trials conducted for statistically independent atmospheric turbulence realizations, using specific WFS parameter values, and under different turbulence conditions. The trial results were averaged over turbulence realizations, and the corresponding atmospheric-averaged phase retrieval error evolution curves were used for parameter optimization and for the comparative performance assessment of basic SR-WFS types. This methodology was applied to address issues important for practical (hardware) implementation of SR-WFS architectures based on the IPR technique such as tolerance, with respect to SR-WFS parameter deviations unaccounted for in the mathematical model used for phase retrieval, and the impact of WFS photo-array (camera) noise and laser source non-monochromaticity.
In the concluding remarks (Section 5), we consider the future path for SR-WFS technique integration into closed-loop AO systems. A framework for this integration, with specific examples of SR-WFS-based AO architectures and performance analysis, are presented in a subsequent paper (Part II).
2. Scintillation Resistant Wavefront Sensing for Atmospheric AO
2.1. Intensity Scintillation Impact on Zonal and Modal WFSs
Due to the point-to-point (or zonal) mapping of input and output field characteristics in conventional WFSs, the spatial modulation of the input field intensity is practically “imprinted” into the sensor output intensity used for input field phase computation (retrieval), where is a coordinate vector in the WFS input and output planes. Correspondingly, under strong scintillations, the output intensity distribution in these sensors may contain low-intensity (“dark”) regions, with an SNR unacceptably low for accurate phase retrieval.
At the same time, intensity inhomogeneities (e.g., resulting from turbulence-induced scintillations) are not a major concern for modal-type WFSs, where input intensity “dark” regions are dispersed across the sensor output plane. The term “modal WFS” is used here, in spite of the fact that it most commonly refers to holographic-type WFSs performing input field transformation (mapping) on a set of highly localized spots associated with phase aberration components, which can be directly (without phase reconstruction) utilized for closed loop AO control [24]. The transformation of the optical field in these WFSs can be considered non-localized.
A simple lens, with a photo-array (camera) located at its focal plane, represents a canonic example of a modal-type optical system that provides non-localized mapping of the input and output fields. Referred to here as the lens-based WFS, this optical system is illustrated in Figure 1. In lens-based and other modal-type WFSs the output intensity is predominantly defined by the input field phase and is only weakly influenced by input field intensity inhomogeneities—the major reason why modal-type wavefront sensing systems are more resilient to intensity scintillations. This low sensitivity (resilience) with respect to intensity scintillations comes at the price of significantly more complicated and time-consuming (in comparison with conventional WFSs) signal processing requirements for phase function retrieval from output intensity measurements.
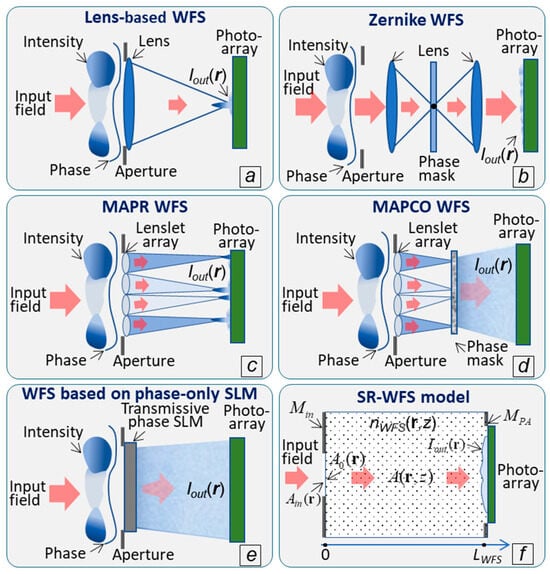
Figure 1.
Examples of single-camera-based modal type WFS configurations: (a) lens-based WFS, (b) multi-aperture phase retrieval (MAPR) WFS, (c) WFS based on a phase-only spatial light modulator (SLM), (d) WFS based on a phase contrast (Zernike) filter, (e) multi-aperture phase contrast (MAPCO) WFS, and (f) the generic SR-WFS model.
Potential utilization of SR-WFSs for atmospheric AO is contingent upon how efficiently (rapidly and accurately) phase retrieval can be performed. This, in turn, largely depends on both the SR-WFS type (WFS optical configuration) defining the input-to-output field transformation, and the phase retrieval algorithm utilized. Both the WFS optical configuration (optical design) and the phase retrieval algorithm should be jointly optimized, while accounting for input field phase and intensity characteristics specific for A-AO applications. The following sections include discussions of both of these key matters.
2.2. Basic SR-WFS Architectures
Examples of WFS types weakly affected by scintillations and considered in this paper are represented in Figure 1 by notional schematics of: (a) the lens-based WFS; (b) a classical Zernike filter (Zernike WFS) [25,26,27]; (c) multi-aperture phase reconstruction (MAPR) sensor [15]; (d) multi-aperture phase contrast (MAPCO) WFS [16]; and (e) a WFS based on a phase-only spatial light modulator (SLM) used for imposing a high-resolution random phase modulation pattern onto the optical field entering the sensor [28,29,30].
The optical schematics of the Zernike and MAPCO WFSs in Figure 1b,d include phase-shifting elements (phase masks). The Zernike sensor phase mask represents a diffraction-limited circular region (Zernike phase dot) at the lens focus that introduces a π/2 radian phase shift into the optical wave passing through the phase dot [25]. The corresponding phase mask of the MAPCO WFS is composed of a large number of differently configured Zernike phase dots that impose a π radian phase shift [16].
In the SR-WFSs in Figure 1, phase masks, and a phase-only SLM that can also be considered as a phase mask, provide non-localized input-to-output optical field transformation enabling mitigation of the input field intensity scintillations (dark regions) impact on sensor output intensity. Note that in the case of lens-based and MAPR WFSs, non-localized optical field transformation is achieved via the positioning of the photo-array in the focal plane of the corresponding lens and lenslet array.
Characteristic output intensity patterns for the modal-type basic SR-WFS configurations in Figure 1 are illustrated in Figure 2 for relatively weak (top row), moderate-to-strong (middle row), and strong (bottom row) turbulence conditions. These intensity patterns were computed using the input field intensity and phase distributions shown in Figure 3, which are identical for all WFSs. Note that the phase patterns in this figure (bottom row) exhibit characteristic topological singularities (branch points [31]) and 2π phase cuts, which increase in number when turbulence strength is increased.

Figure 2.
Examples of output intensity patterns corresponding to the basic SR-WFS configurations in Figure 1. The input field complex amplitudes entering the sensors were obtained through numerical simulations of monochromatic (λ = 1064 nm) plane wave propagation over L = 5 km in homogeneously distributed (volume) turbulence under relatively weak (top row, , ), moderate-to-strong (middle row, , ), and strong (bottom row, , ) conditions. The yellow squares indicate the sensor aperture of size DWFS = D/M = 3.55 mm, where D is the input field aperture size (D = 15 cm), and M = 42.2 is the demagnification factor of the optical receiver telescope in front of the WFS. The optical wave propagation length inside the WFSs (between the input and output planes) was LWFS = 100 cm for the lens-based WFS and LWFS = 28 cm for all other WFS configurations. A densely packed array of 4 × 4 square lenses (lenslet array) was used in the M&S of both the MAPR and MAPCO WFSs. The phase mask of the MAPCO sensor with size Dmask = 2DWFS was composed of randomly distributed Ndot = 3600 identical phase dots of ddot = 100 μm diameter. Gray-scale images in this and all subsequent figures correspond to the 2DWFS × 2DWFS square at the WFS input and output planes, corresponding with the 2D × 2D square at the receiver telescope pupil plane.

Figure 3.
Input field intensity (top row) and phase patterns (bottom row) used in the computation of the SR-WFS output intensity distributions shown in Figure 2: (left column), (middle column), and (right column). The yellow squares indicate the sensor aperture. Phase functions are shown module 2π.
The impact of turbulence is characterized in Figure 2 and elsewhere in this paper by the following commonly used parameters: the ratio of the WFS aperture size D to the Fried parameter (the measure of the input field phase aberration correlation length) and the Rytov variance , describing the input field intensity scintillation strength [32,33,34].
For the numerical analysis in this paper, the following expressions for and were utilized: and [33]. Here, is the defining turbulence strength refractive index structure parameter, is the wavenumber for a monochromatic optical wave of wavelength , and L is the atmospheric propagation path length.
Comparing the input and output intensity distributions in Figure 2 and Figure 3 reveals the lack of correlation between the corresponding intensity patterns, which is typical for modal-type wavefront sensors. Note that some similarity between and can still be observed in Figure 2 for the Zernike WFS, but only under relatively weak turbulence .
It is worth pointing out a distinguishing characteristic (which will be discussed later on) of the output intensity distributions in Figure 2 that is important for selecting the SR-WFS type for atmospheric AO applications. As seen from Figure 2, when the turbulence strength is increased, the output intensity patterns for the lens-based WFS, MAPR, and Zernike WFS undergo quite a significant transformation. Conversely, the corresponding intensity distributions for phase contrast-type sensors, such as MAPCO and phase-SLM-based sensors, preserve a similar spatial structure (randomly scattered spots) when the turbulence strength is increased. For these sensors, we would expect (as further discussed in Section 3.1 and Section 4.3) that the phase retrieval efficiency would be less affected by turbulence strength—an important advantage for closed-loop wavefront sensing and AO control under diverse turbulence conditions.
2.3. Generic Scintillation Resistance WFS: Mathematical Model
Consider a generic SR-WFS model, as illustrated in Figure 1f. This model provides a general framework for the analysis of different WFS architectures. The transformation of a coherent monochromatic (quasi-monochromatic) input optical field with complex amplitude is described in this model by accounting for the following effects: (a) input field diffraction at the WFS aperture diaphragm [pupil-plane mask ]; (b) propagation through SR-WFS phase-only optical element(s) located between the input (z = 0) and output () planes; and (c) propagation along optical path segments between these elements. Additionally, we assume that optical power losses inside the SR-WFS are negligibly small and can be neglected.
The impact of phase-only optical elements (e.g., lenses, lenslets, phase masks, etc.) on the optical field complex amplitude , where , is described in the SR-WFS model using the refractive index dependence on the transversal and longitudinal (along the sensor optical axis) coordinates, corresponding to and z.
For example, a thin phase-only optical element (e.g., a phase mask, lens, or lenslet array) located at the plane , where , is described by the function , where is a delta function, and is the phase modulation introduced by the phase-only optical element. It is easy to see that the generic SR-WFS model can be applied for the analysis of optical field transformation performed in all of the sensing systems shown in Figure 1.
In general terms, the transformation of the optical field complex amplitude inside the generic SR-WFS can be described in the framework of the Fresnel approximation of diffraction theory using the following parabolic (quasi-optics propagation) equation [34]:
where is the Laplacian operator, is the undisturbed refractive index, and . The boundary condition for Equation (1) is defined by the input field complex amplitude , where is the input field magnitude within the aperture diaphragm .
In the generic SR-WFS model considered here, it is assumed that retrieval of the input field phase inside the WFS aperture is solely based on the processing of the output intensity distribution inside the photo-array region, as described by the aperture function . For simplicity, we assume that and are window functions equal to one inside and zero outside of the corresponding squares of size and . It is also convenient to assume that exceeds the characteristic output field footprint size, and that the camera pixel size can be considered as infinitely small. This implies that .
The SR-WFS model introduced here can be applied to describe input-to-output optical field transformation for a wide range of wavefront sensing architectures (including WFSs that are not necessarily resilient to intensity scintillations). In the following sections, this SR-WFS model is utilized in the derivation of the IPR algorithms used in the efficiency analysis of the wavefront sensing of atmospheric turbulence-induced aberrations.
2.4. Phase Retrieval via Optimization of an SR-WFS Output Field Fidelity Metric
The phase retrieval problem can be formulated as a minimization problem for the following fidelity metric (also referred to as an error metric and cost function) [20,35]:
Here, and are, correspondingly, the SR-WFS output field intensity and complex amplitude computed using the input field estimation for the “true” input field complex amplitude inside the WFS aperture diaphragm. Here, and are corresponding estimations of the true magnitude and phase (A diacritic tilde symbol is used to distinguish optical field characteristics associated with input field estimation).
The complex amplitude estimation defines the boundary condition
for propagation Equation (1), which is used for computation of the output field intensity estimation and the corresponding value of the fidelity metric [Equation (2)].
Fidelity metric minimization is considered here using iterative modification (“shaping”) of the phase and magnitude estimations aimed at the retrieval of the true phase function . Note that the minimization of a fidelity metric analogous to Equation (2) is commonly used for the synthesis of phase-only diffractive optics elements (DOE-based beam shapers) that perform the transformation of a laser beam with a known input intensity distribution into a beam with output intensity that is maximally “close” [optimal in terms of Metric (2)] to the desired intensity at a pre-defined distance from the beam shaper [21,22].
Similar to the beam shaping problem statement mentioned above, both the input and output intensity distributions are assumed to be known in the classical GS error reduction iterative phase retrieval algorithm originally developed for the reconstruction of astronomical images [17,18,36]. Note that the original GS technique requires the utilization of two cameras, enabling the synchronous measurement of both the input and output intensity distributions.
The core GS algorithm concept was further exploited to include complex field (both phase and magnitude) retrieval based on the processing of both a single and multiple intensity distributions (e.g., error-reduction iterative Fourier transform [18,20], phase diversity [36], incremental binary random sampling [37], beam-propagation-based random phase modulation [38], coded diffraction patterns [39], etc.).
In the single-camera-based wavefront sensing configurations considered here, the input field intensity is assumed to be unknown. Although knowledge of this intensity distribution is not required for AO operation, the function still needs to be retrieved, since the error metric (2) absolute minimum value can only be achieved when both the input field intensity and the phase distributions are correctly determined. Thus, in the case of single-camera-based SR-WFS, we “unavoidably” deal with the complex field retrieval problem. By keeping this in mind, in this paper, we interchangeably refer to either “phase” or “complex field” retrieval.
2.5. Complex Field Retrieval for the Generic SR-WFS Model
To further proceed with phase (complex field) retrieval algorithms for the SR-WFS model, it is convenient to represent the error metric (2) in the following equivalent form:
where
is the complex function corresponding to the formal replacement of the magnitude in by the true output field magnitude .
Assume that the selected input field intensity estimation is defined within the aperture diaphragm , and the function obeys the following condition describing preservation of the optical power inside the SR-WFS:
Under this condition, the minimization of the fidelity metric (4) is equivalent to the maximization of the following expression (referred to as the overlapping integral [40] or the interference metric [41]):
Assume now that the function in Equation (5) defines the boundary condition for the complex amplitude of an auxiliary “optical wave” propagating along the SR-WFS optical axis in the reverse direction (from the output to the input plane). Correspondingly, the propagation (back-propagation) of this auxiliary wave can be described by the following quasi-optics equation, similar to Expression (1):
Note that the term “propagating” or “back-propagating” wave is applied to the solution (numerical solution) of either Equation (1) or Equation (8), rather than to the propagation of real optical waves.
Using Equations (1) and (8) for the counter-propagating waves with complex amplitudes and , one can derive the following relationship, coupling integral characteristics of these complex amplitudes at the SR-WFS input and output planes [41,42]:
where denotes the complex amplitude corresponding to the solution of Equation (1) with boundary condition (3). Note that Expression (9) is valid for the arbitrary boundary conditions for both Equations (1) and (8). Using Expressions (3) and (5), Relationship (9) can be represented in the form:
where .
Consider now an iterative procedure of metric [Equation (10)] maximization with respect to estimations of the input field phase and magnitude . Define these estimations at the n-th iteration (n = 0, …,) as and , correspondingly. In the introduced notations, the right-hand side of Equation (10) is given by:
where and are, correspondingly, the complex amplitude and the phase of the back-propagating wave at the SR-WFS input plane, computed based on the estimations and .
The functions and in Expression (11) denote the input field phase and the magnitude estimations that should be selected at the next (n + 1-st) iteration. It is easy to see that metric in Equation (11) can be increased by choosing the n + 1-st input field phase estimation as the following:
The derived iterative procedure [Equation (12)] formally coincides with the original GS phase retrieval algorithm, assuming that both the input and output intensity distributions are known. In the single-camera-based SR-WFS model considered here, the input intensity or, equivalently, the magnitude , is the unknown function that should be retrieved jointly with the input field phase .
To derive the corresponding algorithm for input field magnitude retrieval, substitute from Equation (12) into Expression (11), which now reads
It can be shown that the metric in Equation (13) can be increased by selecting, at the next (n + 1-st) iteration, the input field magnitude estimation in the form:
Here, we used optical power conservation condition (6) and the assumption that the input field estimation is defined inside the aperture diaphragm .
The update rules for input phase [Equation (12)] and magnitude [Equation (14)] estimations can be represented in the form of a single iterative equation:
where the notation defines a complex function conjugated with respect to .
Expression (15) describes an iterative procedure of back-propagating wave complex amplitude conjugation inside the aperture diaphragm . It can be shown that the complex field retrieval iterative algorithm (15) is directly related to error metric (2) minimization via the conditional gradient search technique [35,43]. Corresponding derivations are analogous to those presented in Ref. [44].
Iterative Equation (15) represents a formal analog of the known in AO complex field conjugation (CFC) control algorithm, in which the function is associated with the complex amplitude of an optical wave scattered off a remotely located target and propagated back to the laser beam projection transceiver aperture (target-return wave) [44]. This resemblance between the phase (complex field) retrieval and AO CFC control algorithms is further discussed in Part II. Referring to this formal analogy between the AO CFC control and the iterative algorithm for complex field retrieval via the auxiliary function conjugation (AFC), as described by iterative Equation (15), the latter expression is referred to here as the AFC algorithm.
The iterative procedures described by Equations (12) and (15) belong to a wide framework of Fienup phase and complex field retrieval algorithms originally developed [20,45] for astronomical imaging. One of the major issues with the practical application of these algorithms for wavefront sensing in atmospheric AO systems is their relatively slow convergence, resulting in a potentially unacceptably low closed-loop operational bandwidth. As shown in Section 4.3, complex field retrieval convergence can be significantly improved using the AFC algorithm clone, referred to as the hybrid input–output (HIO) iterative scheme, introduced by Fienup [18].
The iterative procedure to achieve a complex amplitude estimation update in the HIO algorithm is given by:
where is a tuning parameter (), and is a window function, which is zero inside the aperture diaphragm, and one otherwise. When compared with Equation (15), the HIO algorithm contains an additional term on the right-hand side of Expression (16), which affects complex amplitude estimations outside the aperture diaphragm [within the window-function ]. While the origin of this term, referred to here as Fienup’s complex field retrieval acceleration term, still lacks rigorous justification (as pointed out in Ref. [46]), its presence commonly results in a noticeable acceleration of complex field retrieval process convergence [16,18,28].
2.6. Complex Field Retrieval Computational Steps
Consider now the computational steps associated with the utilization of the AFC [Equation (15)], and HIO [Equation (16)] complex field retrieval algorithms.
In both cases, the iterations start from the selection of an initial (defined by the superscript n = 0) estimation for the input field complex amplitude . In the modeling and simulations (M&S) described in Section 4 and Section 5, the magnitude was always set to be equal to a constant inside the SR-WFS aperture diaphragm , and zero otherwise. At the same time, the initial phase estimation was represented by a random realization of a delta-correlated field, with zero mean and a uniform probability distribution inside the interval [−π, π].
In the analysis of the closed-loop wavefront sensing and adaptive optics (AO) control described in the paper that follows this study (Part II), the initial estimation was changed at each step of the AO control variable update (at each AO control cycle). In this case, to accelerate convergence, the initial complex field estimation was set to be equal to the retrieved complex amplitude obtained during the preceding AO control cycle.
In both cases the initial estimation was utilized as the boundary condition for propagation Equation (1), which describes the evolution of the complex amplitude along the SR-WFS optical axis from to .
The computational steps associated with subsequent (ranging from n = 1 to Nit) iterations are identical for both the AFC [Equation (15)] and HIO [Equation (16)] algorithms and include:
- (1)
- Numerical integration of Equation (1) with the boundary condition , enabling computation of the complex amplitude at the sensor output plane.
- (2)
- Setting the boundary condition [Equation (5)] for the auxiliary complex amplitude .
- (3)
- Numerical integration of Equation (8) from to to obtain the complex amplitude at the SR-WFS input plane.
- (4)
- Computation of the input field complex amplitude estimation at the n + 1-st iteration using either the AFC [Equation (15)] or HIO [Equation (16)] update rule.
Steps (1) through (4) are repeated utilizing the complex field estimation as the boundary condition for Equation (1).
The complex amplitude retrieval trial ends with the computation of the complex field estimation after completing the set of Nit iterations. The number of required iterations Nit depends on the metric selected for the evaluation of the phase and/or complex field retrieval quality. Note that in the case of closed-loop WFS operation, the number of iterations Nit may be constrained by the duration of the AO control cycle and the computational time needed to perform a single phase retrieval iteration.
2.7. Complex Field and Phase Retrieval Quality Metrics
For phase retrieval quality assessment, it is necessary to account for the 2π phase ambiguity [31,47]. This implies that the phase estimation functions , which are distinguished from the true phase function by points or regions having a modulo 2π difference, should be considered as equivalent. For this reason, the performance evaluation of phase retrieval algorithms should be based on metrics that are insensitive to modulo 2π phase value jumps. This requirement is satisfied for the following metrics that can be used for phase retrieval accuracy evaluation at each nth iteration:
where and are, correspondingly, the WFS input aperture area and the residual phase computed at the nth phase retrieval iteration. Note that ideal retrieval of the true phase corresponds to and . Metric (17a) can be associated with the well-known Strehl ratio that is applied here for an optical wave with uniform intensity [] and phase aberration . The metric in Equation (17b) is referred to here as the phase retrieval error. This metric is convenient for estimating the number of iterations required to reach a pre-selected phase retrieval error threshold [16].
For the quality assessment of complex field retrieval, the following metrics characterizing “matching” of the true and the retrieved complex amplitudes can be used:
Ideal input field complex amplitude retrieval (both phase and magnitude) corresponds to and .
The spatial distribution of the retrieved phase error within the WFS aperture may play an important role in AO beam projection applications in which a larger error is more “acceptable” (causes a smaller impact on AO system performance) within laser beam footprint areas with lower intensity, e.g., within the tail section of a truncated Gaussian-shaped beam formed by an off-axis type transmitter telescope (beam director). For this reason, the projected beam intensity distribution (beam “shape”) should somehow be accounted for in the phase retrieval quality metric. This can be achieved by adding a weighting function proportional to into Expression (17a). The corresponding phase retrieval quality metrics accounting for the transmitted beam shape are given by the following:
Note that a similar beam shape weighting factor can also be applied into the corresponding Expression (18) for use in complex field retrieval quality metrics.
These introduced metrics may not be adequate for the analysis of the phase retrieval error impact on the overall performance of closed-loop atmospheric AO systems. In addition to the evaluation of phase retrieval errors, such a performance analysis may also require consideration of a number of mutually dependent factors such as beam director configuration, propagation geometry, atmospheric turbulence strength, feedback control algorithm, beam control performance measures, etc. An example of such an analysis is presented in Part II of this paper.
3. Tradeoffs in SR-WFS Design and Phase Retrieval Technique Implementation
3.1. Basic Considerations for SR-WFS Design: SAPCO WFS
The phase retrieval convergence rate, defined here as , represents one of the most important characteristics for the assessment of IPR-based wavefront sensing technique relevance for atmospheric AO. The convergence rate depends not only on the phase retrieval algorithm, pre-selected phase error threshold , and initial complex field estimation, but to large degree, on the optical configuration specific for each SR-WFS (WFS optical design/schematic) defining the input-to-output optical field transformation inside the WFS, the atmospheric turbulence strength, and the propagation geometry on which the spatiotemporal characteristics of the input field phase and intensity distributions depend.
As shown in the M&S described in Section 4, a higher phase retrieval convergence rate is expected with WFS optical designs that provide highly non-localized mapping of the input and output fields, resulting in a near homogeneous output intensity spread across the entire photo-array area, with the absence of dominating intensity spikes. Such highly non-localized input-to-output mapping leads to increased SNR and the mitigation of phase retrieval process stagnation.
For the atmospheric AO applications considered here, it is also important to achieve a uniform phase retrieval convergence rate for a wide range of turbulence conditions—from weak turbulence, characterized by the presence of smooth (low-order) phase aberrations and relatively weak intensity scintillations, to strong turbulence, for which the input field phase exhibits a complicated topological structure, with a number of branch points and highly scintillated intensity. This suggests that more uniform convergence rates are anticipated for SR-WFS optical configurations in which the variation in turbulence strength and hence, the input field characteristics, do not significantly affect the general structure of the WFS output intensity patterns.
In terms of the outlined (“favorable” for achieving a high phase retrieval convergence rate) criteria, compare the basic SR-WFS architectures shown in Figure 1. The following physics-based analysis provides general guidance for the development and optimization of the most promising SR-WFS architectures for atmospheric AO applications, such as the scintillation-resistant advanced phase contrast (SAPCO) WFS introduced here.
- Lens-based WFS (Figure 1a). The output intensity distributions in this sensor (left column in Figure 2) are highly non-uniform and are characterized by the presence of dominant (bright) intensity spots surrounded by relatively weak side-lobes under weak and moderate-to-strong turbulence. Turbulence strength increases result in side-lobe area widening and an associated diminishing of the bright spot, which practically vanishes under strong turbulence conditions. Note that input field phase aberrations predominantly affect the intensity distribution pattern within the side-lobe region. Correspondingly, in order to ensure an SNR sufficiently high for accurate phase retrieval under weak turbulence, lens-based WFS would require a photo-array (camera) with a large dynamical range. In addition, to scale the output intensity footprint into the camera chip area, the lens, or a combination of lenses used for optical field scaling, should possess a relatively long focal length F, thus leading to the implementation of WFS hardware that is potentially bulky and sensitive to vibrations.
- Multi-aperture phase retrieval (MAPR) WFS (Figure 1c). The drawbacks of the lens-based sensor are partially alleviated in the MAPR WFS design via the utilization of a 2D lenslet array composed of densely packaged lenslets of size . The lenslet array performs input field partitioning into -fold smaller zones (subregions), resulting in both a general decrease in sensor output intensity spatial nonuniformity and a decrease in the impact of turbulence strength on the output intensity spatial structure inside the subregions, as illustrated in Figure 2 (second column) for . Additionally, -fold smaller size lenslets enable a proportional decrease in the focal length , potentially providing for a more compact WFS hardware implementation. Another advantage of the MAPR WFS is the possibility for significant improvement in both the phase retrieval convergence rate and the required computational time by processing the output intensity within the subregions in parallel [15]. On the other hand, input field partitioning may lead to crosstalk between neighboring subregions (especially under strong turbulence conditions), resulting in a decline in phase retrieval accuracy (see Section 4.3).
- Zernike filter-based WFS (Figure 1b). This sensor provides for a more spatially uniform output intensity spreading across the photo-array area than either the lens-based or MAPR sensors (compare with the corresponding images in Figure 2). One of the major potential drawbacks of this sensor is its high sensitivity to turbulence-induced wavefront tilts, leading to focal spot lateral displacements with respect to the phase shifting dot. These displacements, typical for weak turbulence conditions, result in strong variations in the output intensity pattern contrast that negatively affect phase retrieval convergence. Intensity pattern contrast variations and the general decline in the contrast also occur due to fluctuations in optical power within the phase shifting dot area when the turbulence strength increases. Furthermore, Zernike WFS is even bulkier than are the lens-based and MAPR sensors.
- Multi-aperture phase contrast (MAPCO) WFS (Figure 1d). The shortcomings of the SR-WFS discussed above are addressed in the MAPCO WFS, consisting of a densely packed array of phase contrast (Zernike-type) sensors [16]. Here, the same approach as that used in the MAPR WFS is applied—input field partitioning with a lenslet array. Mitigation of the negative impact of local (inside lenslet subregions) wavefront tilts is achieved using a phase mask composed of a large (~103) number of identical phase shifting dots arranged either randomly (random-dot phase mask) or in the form of a 2D grid (grid-dot phase mask) [16]. The optical wave entering the MAPCO sensor is focused by the lenslet array onto the phase mask, and after receiving the corresponding phase modulation, it undergoes free-space propagation (diffraction) over the relatively short distance to the photo-array. The output intensity patterns of the MAPCO sensor are comprised of a large number of spots that are nearly evenly spread across the output plane, as illustrated in Figure 2 (fourth column). Note that increases in turbulence strength have little impact on the general structure and spatial extent of the output intensity patterns—a desired WFS characteristic for obtaining a comparably even phase retrieval convergence rate under a wide range of turbulence conditions.The characteristic size and configuration of spots in the MAPCO WFS output intensity depend on a set of design parameters, including the propagation length , dimension , and focal length of the lenslet array, along with the phase dot pattern characteristics, such as the phase dot size , introduced phase modulation amplitude , and the geometry and density of the dots within the phase mask. The density is defined here as the percentage of the mask area occupied by phase dots. This parameter primarily impacts the output intensity pattern contrast that reaches its maximum value when the phase dots occupy approximately 50% of the entire phase mask area, as discussed in Section 4.2.
- WFS based on phase-only SLM (Figure 1e). Note that the phase-only SLM in this SR-WFS type can be replaced by a specially designed phase mask, providing a random phase modulation pattern with analogues parameters. The characteristic output intensity distributions in this WFS consist of random structures composed of bright spots (speckles), as shown in Figure 2 (right column). The characteristic size and spatial extent (spread) of these spots depend on the overall sensor length and parameters of the random phase modulation pattern induced by the SLM, namely the phase modulation variance and correlation length . Note that increases in turbulence strength cause a noticeable increase in the characteristic speckle size and the spatial extent of the output intensity.
As shown by the numerical simulations (see Section 4), the phase retrieval convergence rate for the sensors considered here depends on the characteristic spatial structure of the output intensity distributions which can be (to some degree) engineered by turning (optimizing) the WFS optical design and/or sensor parameters. From this viewpoint, the MAPCO WFS offers the largest parameter space to be utilized for the phase retrieval convergence rate optimization.
Another important issue to be considered in the selection of SR-WFS optical configuration and parameter optimization is the strong phase retrieval error dependence on the accuracy of mathematical and computational models describing the actual (implemented in the hardware) sensor. Any discrepancy between the optical field transformation occurring in a specific WFS type and its “imitation” in the phase retrieval computations may cause uncompensated phase errors that are “invisible” for the AO controller.
This disparity between hardware-implemented WFS and its mathematical/computational model may emerge from a number of unaccounted for factors that can influence sensor output intensity, such as misalignments, unidentified phase aberrations in the optical elements, and the non-monochromaticity of the input light and/or changes in environmental conditions occurring during WFS operation.
From this viewpoint, an SR-WFS optical configuration comprised of the minimal possible numbers of optical components packaged into a compact rigid instrument certainly exhibits an obvious advantage, if such an SR-WFS can also provide a high convergence rate and accuracy in regards to input field phase retrieval.
The SR-WFS design criteria discussed above were considered for the SAPCO sensor proposed here. The optical schematic of this sensor, shown in Figure 4, is similar to that of the MAPCO WFS (Figure 1d), with the exception that the SAPCO WFS does not have a lenslet array. Both sensors include phase masks composed of large numbers of phase dots, with parameters identical or similar to those of the MAPCO sensor discussed above. In addition to the phase mask characteristics, the SAPCO sensor output intensity structure also depends on the propagation distances and , correspondingly, between the input aperture diaphragm and the phase mask, and between the phase mask and the photo-array, as shown in Figure 4. The spatial structure of the output intensity patterns for both sensors are alike (compare the corresponding output intensity distributions in Figure 2 and Figure 4). As M&S shows (see Section 4.3), the absence of the lenslet array in the SAPCO sensor scarcely impacts the phase retrieval convergence speed, while it simplifies both the WFS optical design (with fewer optical elements) and the corresponding mathematical model used in the phase retrieval computations.
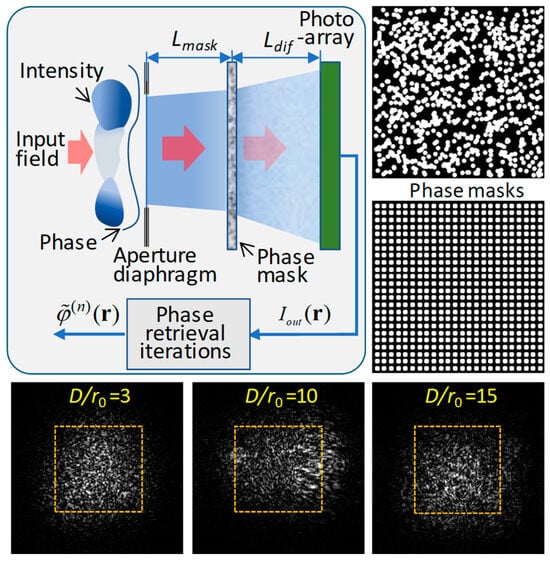
Figure 4.
Optical schematic of the scintillation-resistant advanced phase contrast (SAPCO) WFS. The sensor is composed of an aperture diaphragm, a phase mask containing large numbers of circular phase dots of diameter that are either distributed randomly or in the form of a 2D grid (shown in right inserts), and a photo-array. The SAPCO WFS output intensity (shown by grey-scale images) are computed for the numerical simulation setting and input field phase and intensity distributions (shown in Figure 3) identical to those described in Figure 2. The parameters used in the M&S are: DWFS = 3.55 mm, Dmask = 2DWFS, Lmask = Ldif = 14 cm, ddot = 100 μm, and Δdot = π rad. Simulations were conducted for a random-dot mask (top right) composed of Ndot = 3600 dots inside the Dmask × Dmask area, with approximately 50% density ().
3.2. Phase Retrieval Computational Time
In addition to optical design simplification and a potentially more rigorous mathematical model describing the optical field transformation in the actual WFS, the lower number of optical components is also desired to reduce the computational time needed to perform the single-phase retrieval iteration (iteration time). Correspondingly, decreases in lead to shortening the overall phase retrieval computation time . Here, Nit is the number of iterations associated with either the selected phase retrieval error threshold , as defined by Equation (17), or the limitation imposed by the AO control cycle duration.
In a simplified generic SR-WFS model comprised of thin phase-only optical elements, the iteration time is primarily defined by the time required for the numerical integration of Equations (1) and (8), describing the propagation of the outgoing and back-propagating (auxiliary) waves in an optically homogeneous media along consecutive non-zero-length optical path segments, defined by the optical element locations inside the SR-WFS. Note that the parameter does not account for the optical elements located at the input and output planes, e.g., the optical elements at the input plane in the SR-WFS schematics shown Figure 1 (left column), for which .
In the standard wave-optics based M&S technique [23], the numerical integration of the propagation Equations (1) and (8) includes a direct 2D fast Fourier transform (FFT), followed by the multiplication of the result by a 2D array (phase term) and further, an inverse FFT of the multiplication product [48,49]. The associated computational times required for a single FFT and multiplication by the phase term (complex 2D array) are defined, correspondingly, as and .
Similarly, the impact of a thin phase-only element (or phase mask) is accounted for by the multiplication of the ingoing complex amplitude [complex 2D array] by a complex 2D array describing the phase-only element-induced wavefront phase modulation. This operation adds an additional computational time of .
Thus, the computational time required for single phase retrieval iteration for the generic SR-WFS composed of a single phase-only element at the pupil plane (lens, lenslet array, or phase mask) and phase-only elements inside the sensor can be estimated as:
Here and are, correspondingly, the times required to compute the boundary condition for the back-propagating wave complex amplitude at the sensor’s output plane [Equation (5)] and to perform the complex amplitude estimation update, based on either auxiliary function conjugation (AFC) [Equation (15)] or hybrid input–output (HIO) [Equation (16)] algorithms. Note that the computational times in Equation (20) depend on the numerical grid size (resolution) and the specific computational hardware and software used. In most cases, the computational times , , and are significantly shorter than and can be neglected, which simplifies Expression (20):
It follows from Equation (21) that the expected phase retrieval iteration time for SR-WFS optical configurations, comprised of optical elements located between the sensor input and output planes, is a factor longer than that for the optical schematics shown in the left column in Figure 1, for which . Note that for both MAPCO and SAPCO WFSs, as both sensors have a single phase-only optical element (phase mask) inside the WFS propagation path (the lenslet array of the MAPCO WFS is not accounted for, as it is located directly at the input plane).
The results for the iteration time benchmarking for the SR-WFS optical configuration with (MAPCO and SAPCO WFS, shown in Figure 1d and Figure 4) are presented in Table 1 for a numerical grid of different resolution NPR (numerical grid with NPR × NPR pixels). The simulations were performed using different NVIDIA Geforce GPU models. Iterative phase retrieval computations were performed for the HIO algorithm. The benchmarking was conducted using the CUDA-based, GPU-optimized C# WaveJet software package [50]. Note that the presented estimates for can vary based on such factors as the specific CPU and GPU models, FFT implementation, the computer code, etc.

Table 1.
Results of phase retrieval iteration time benchmarking for MAPCO and SAPCO sensors.
Further decreases in phase retrieval iteration time are expected due to ongoing advancements in GPU technology and software optimization. More drastic phase retrieval computation acceleration, by several folds, is anticipated to be achieved via transitioning to a specialized FPGA-based signal processing hardware. This suggests (and is further discussed in Part II of this study) potential achievements exceeding one kHz of closed-loop AO control system bandwidth with the utilization of IPR techniques and the described SR-WFS architectures.
3.3. Phase Retrieval Computational Grid
As indicated in Table 1, the reduction in the iteration time desired for an increase in AO control bandwidth could potentially be achieved by minimizing the phase retrieval computational grid resolution (grid size NPR). The question to ask is, how small could NPR be without sacrificing the phase retrieval convergence rate and accuracy?
From a general AO requirement viewpoint, spatial resolution in phase aberration sensing on the order of 103 (e.g., 32 × 32) resolvable phase values would be sufficient for the majority of atmospheric AO applications. This may incite the idea that a numerical grid with NWFS = 32 (NWFS × NWFS pixels inside the SR-WFS aperture diaphragm) could be an acceptable option. However, the AO wavefront sensing resolution requirement does not imply that accurate phase retrieval computations can be performed using such a low-resolution numerical grid. There are some constraints that should be accounted for in the selection of an acceptable phase retrieval numerical grid resolution (parameter NPR) and the associated actual (physical) size DPR for the phase retrieval computational area.
First, the SR-WFS output intensity distribution may quite significantly extend beyond the sensor aperture area of size DWFS, as shown in Figure 2 and Figure 4. Correspondingly, both the photo-array size DPA and physical size DPR of the phase retrieval computational area should exceed DWFS. It is important that the parameters DPA and DPR should provide an accurate representation (approximation) of the measured intensity on the chosen numerical grid. As seen from Figure 2, the output intensity patterns do not extend beyond approximately twice the size of the DWFS for all considered SR-WFS configurations. Therefore, we may set DPA = DPR = 2DWFS, also additionally assuming that in the course of the phase retrieval computations, the complex amplitudes and do not extend beyond the selected computational area of size DPR. Note that for optimal SR-WFS performance, the phase retrieval computational grid (resolution and pixel pitch) should match the corresponding photo-array parameters.
Second, the computational grid resolution should provide a sufficiently accurate numerical representation of: (a) the SR-WFS optical elements; (b) the characteristic spatial features of the measured output intensity pattern; and (c) the complex amplitudes and within the entire phase retrieval computational volume DPR × DPR × LWFS. For the basic SR-WFS optical configurations considered (shown in Figure 1 and Figure 4), the smallest spatial scale is associated with the phase-shifting elements, i.e., the phase dots of the Zernike, MAPCO, and SAPCO WFSs, and the characteristic phase modulation correlation length of the SLM-based WFS. Note that in the course of the phase retrieval computations, the complex amplitudes and can be truncated by the phase mask boundary. In order to prevent such truncation, the phase mask size Dmask should exceed the DWFS. To be on the safe side, the following SR-WFS design parameters defining the phase retrieval computational grid size NPR were used in M&S: Dmask = DPA = DPR = 2DWFS.
For the estimation of the smallest acceptable grid size NPR, consider as an example the phase mask shown in Figure 4, composed of an array of 24 × 24 square-shaped phase dots inside the DWFS × DWFS area (48 × 48 phase dots within the entire mask of size Dmask = 2DWFS). By assuming that each phase-shifting dot can be satisfactorily represented on the numerical grid by a 4 × 4 pixel square, for the smallest possible computational grid dimension, we obtain NPR = 256. This implies that the phase retrieval computations at this grid size will provide the input field phase aberration estimation at NWFS × NWFS grid points, where NWFS = NPR/2 = 128, with significantly higher (four-fold) resolution than that required for the majority of atmospheric AO applications. As M&S shows, phase mask numerical representation using a smaller number of pixels (3 × 3 or 2 × 2) per phase dot, aiming to potentially decrease NPR, resulted in slow convergence and unacceptably high phase retrieval errors. The origin of such errors is insufficiently accurate (for such a small number of pixels per phase dot) numerical integration of parabolic Equations (1) and (8) in the course of the phase retrieval iterations.
As mentioned above, the computational grid should also provide an accurate approximation of the characteristic spatial structures for the output intensity distribution . In the case of phase contrast-type sensors (Zernike, MAPCO, SAPCO, and phase SLM-based WFSs), for which the intensity patterns contain small bright spots (speckles), as shown in Figure 2 and Figure 3, the numerical grid pixel size should be several folds smaller than the characteristic speckle size lsp. Note that for the MAPCO and SAPCO sensors, the speckle size lsp can be adjusted (scaled) by changing the distance between the phase mask and the photo-array. In the numerical simulations described here, this distance was set to cm in order to obtain approximately 4 × 4 or 5 × 5 pixels per intensity bright spot on the numerical grid, with NPR = 256. This computational grid resolution was used in M&S for all the SR-WFS types considered.
An important factor that defines the overall SR-WFS design parameter space (including the required computational grid resolution) is the photo-array size DPA. In the numerical simulations, we used DPA = DPR = 7.10 mm (256 × 256 pixels) to match the smallest dimension of a commercially available CCD camera. Correspondingly, the square WFS aperture mask was reduced by two times: DWFS = DPA/2 = 3.55 mm (128 × 128 pixels).
We also assumed the presence of a receiver telescope (beam reducer) providing reimaging of the pupil square area of size D = 15 cm into the WFS aperture diaphragm, with the demagnification factor M = D/DWFS = 42.2, as shown in Figure 5. These parameters were identical for all SR-WFS types considered here. In M&S of the phase contrast-type sensors, the physical size of the phase-shifting dots was set to ddot = 100 μm. In the case of WFS based on phase-only SLM, the introduced phase modulation was modeled using random field realizations, delta-correlated on the numerical grid, with a uniform probability distribution inside the interval [0, π]. Other parameters of the basic SR-WFS models in Figure 1 (e.g., focal distances of lenses and lenslet arrays) were selected based on a numerical analysis of phase retrieval efficiency under a wide range of atmospheric turbulence conditions.
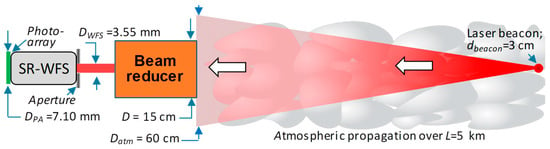
Figure 5.
Schematic diagram of the numerical simulation setting for SR-WFS performance analysis.
3.4. Numerical Modeling and Simulations Setting
For the numerical modeling of optical field realizations entering the SR-WFS typical of atmospheric AO applications, the M&S setting included a monochromatic (λ = 1064 nm) laser beacon located at a distance of L = 5 km from the beam reducer telescope, as shown in Figure 5. We assumed that the collimated Gaussian beam of width dbeacon, generated by a beacon laser source, propagates through homogeneously distributed isotropic atmospheric turbulence prior to entering the beam reducer telescope. A lens (not shown in Figure 5) with focal distance f = L/M at the beam reducer exit plane was included in the numerical model for the mitigation of static defocus-type aberrations of the optical field at the SR-WFS input plane (plane of the aperture diaphragm).
The numerical simulations of beacon beam propagation in the turbulent atmosphere were based on the conventional wave-optics (split-step operator [23,48,49]) technique using a computational grid with a resolution of 1024 × 1024 pixels. The physical size of the simulation area corresponded to a 0.6-m square, with a pixel size of around 0.58-mm. The beacon beam complex amplitude at the beam reducer input plane was rescaled to the 512 × 512 pixel grid, and the central 256 × 256 pixel section (30 × 30 cm2) was assigned as the phase retrieval computational grid, with a resolution of NPR = 256 and a pixel size ~1.17-mm (prior to demagnification by the beam reducer). The beacon optical wave reimaging achieved by the beam reducer telescope, with demagnification factor M = D/DWFS = 42.2, was modeled by simple reassignment (M-fold reduction) of the grid pixel size from ~1.17-mm to ΔWFS~27.7 μm.
Turbulence-induced refractive index inhomogeneities along the beacon beam propagation path were represented by a set of Nφ = 20 equally spaced 2D random thin phase screens corresponding to the Kolmogorov turbulence power spectrum [51]. A single set of the generated Nφ phase screens is referred to here as a “turbulence realization” [52]. Each turbulence realization was comprised of Nφ statistically uncorrelated phase screens.
Turbulence and intensity scintillation strength were correspondingly characterized by the ratio and the Rytov variance , defined in Section 2.2. The parameter D/r0 was altered (from zero to = 20) via equivalent changes in the phase screen modulation amplitudes in each turbulence realization. This enables the simulation of SR-WFS input field realizations , with Rytov variances ranging from zero to . Characteristic examples of computed input field phase and intensity distributions are shown in Figure 3.
The spatial inhomogeneity of the generated input field intensity realizations within the receiver beam reducer telescope square aperture of area SRx = D × D was characterized by the scintillation index [16], as follows:
where is the mean value of the input field intensity within the receiver aperture described by the window . In Equation (22) and elsewhere below, < >atm denotes averaging (also referred to as atmospheric averaging) corresponding to an ensemble of Natm statistically independent turbulence realizations. The parameter Natm equal to 100 was used in all M&S examples described below.
For each SR-WFS type and pre-selected value, the phase retrieval performance was evaluated in a set of Natm phase retrieval trials, resulting in the computation of the corresponding dependencies , (j = 1, …, Natm) of the phase retrieval error [Equation (17b)] on the iteration number n, which were averaged over atmospheric trials. The obtained dependencies computed for different values (referred to here as atmospheric-averaged phase retrieval error evolution curves) were used for parameter optimization and performance assessment of the basic SR-WFS types shown in Figure 1.
For comparative analysis of the SR-WFSs and phase retrieval algorithms, we also utilized the atmospheric-averaged number of iterations required for each fixed ratio to reach a pre-selected threshold level = 0.1. The values were computed by averaging the corresponding iteration numbers obtained for each phase retrieval trial, where j = 1, …, Natm.
4. SR-WFS Parameter Optimization and Performance Assessment
4.1. SR-WFS Optimization Parameter Space
As previously mentioned, phase retrieval process convergence depends on a number of parameters specific for each SR-WFS type. Correspondingly, for unbiased performance comparison of different sensors, these parameters should be independently optimized for each SR-WFS configuration. The overall parameter space for the SR-WFSs considered here is quite extensive, which makes such a comparative analysis a challenging task.
To simplify the problem, we assumed several (pre-selected) parameters common for all SR-WFS types, including phase retrieval computational grid resolution (NPR = 256) and the physical sizes of the WFS input aperture DWFS, photo-array DPR = 2DWFS, phase retrieval computational area DPA = DPR = 2DWFS, photo-array DPA = DPR = 2DWFS, and the aperture size for the beam reducer D = MDWFS.
We also employed the previously optimized parameters for the MAPCO WFS [16]: the diameter and phase modulation amplitude of the phase shifting dots (correspondingly μm and rad), and the propagation (diffraction) distance between the phase mask and photo-array ( cm). These parameters were pre-set for both the MAPCO (Figure 1d) and SAPCO (Figure 4) sensors. Lenslet arrays composed of 4 × 4 densely packed lenses were used in M&S of both MAPR and MAPCO WFS, while the optimal focal distance value was determined separately for each sensor: = 28 cm for MARP, and = 20 cm for MAPCO WFS.
As a result, the optimization parameter space was significantly reduced. It included the lens focal distance F for the lens-based and Zernike WFSs; propagation distances and between the WFS aperture diaphragm and correspondingly, the photo-array for the phase-only SLM-based WFS; and a phase mask for the SAPCO WFS. In both the SAPCO and MAPCO WFSs, we also considered random-dot and grid-dot-type phase masks of size DPA and optimized the number of phase dots (Ndot) within the phase mask.
The selection and optimization of the SR-WFS parameters were based on a comparison of atmospheric-averaged phase retrieval errors (phase retrieval error evolution curves), which were computed using the HIO algorithm. To verify that the selected SR-WFS parameter values are satisfactory under a wide range of turbulence conditions, numerical simulations were performed for weak-to-moderate turbulence (, , ), moderate-to-strong turbulence (, , ), and strong turbulence (, , ).
4.2. Parameter Optimization Methodology Examples
As an example of SR-WFS parameter optimization, consider the SAPCO sensor optical setting shown in Figure 4. The design parameters to be optimized included the distance between the WFS aperture diaphragm and the phase mask and the geometry and density of the phase shifting dots of the sensor phase mask. Corresponding numerical simulation results are presented in Figure 6 and Figure 7 by sets of atmospheric-averaged phase retrieval error evolution curves computed using the HIO algorithm for and .
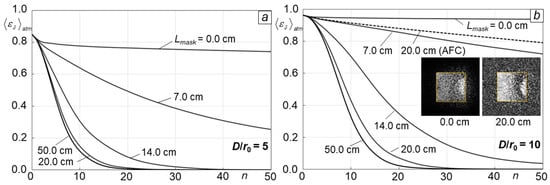
Figure 6.
Atmospheric-averaged phase retrieval error evolution curves for the SAPCO WFS configuration (Figure 4), with a phase mask composed of randomly distributed phase shifting dots with density (Ndot = 3600 dots within a square of size Dmask = 2DWFS). Results were obtained for different parameter values and turbulence conditions corresponding to = 5 (a) and = 10 (b). Phase retrieval simulations were performed using the HIO (solid lines) and AFC (dashed line) algorithms [Equations (16) and (15)]. Averaging was performed using Natm = 100 statistically independent turbulence realizations. Grayscale images illustrate the auxiliary function magnitude within the phase retrieval grid area DPR × DPR at the sensor input plane prior to the first (n = 1) complex field estimation update.
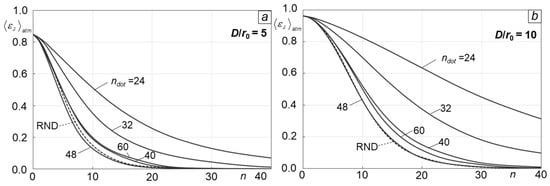
Figure 7.
Atmospheric-averaged phase retrieval error evolution curves for a SAPCO WFS with grid-dot-type phase masks having different grid pattern dimension parameter ndot values (solid lines) and with a random-dot-type mask composed of Ndot = 3600 dots randomly located across the mask area (RND dashed line) for turbulence conditions corresponding to = 5 (a) and = 10 (b).
As can be seen from the curves in Figure 6, the phase retrieval iterative process convergence speed strongly depends on the phase mask position (parameter ). It is especially slow for the SAPCO WFS with the phase mask located at the sensor pupil plane . Note that this WFS configuration coincides with that of the phase-only SLM-based WFS in Figure 1e, except that the parameters of the random phase modulation pattern for this sensor (phase modulation variance and correlation length ) are quite different from the phase mask parameters of the SAPCO WFS and could be separately optimized to improve convergence.
Gradually increasing the distance from zero to approximately 20 cm resulted in a significant acceleration of the phase retrieval convergence rate for both weak-to-moderate ( = 5) and moderate-to-strong ( = 10) turbulence conditions. With an additional increase in parameter , the iterative process convergence speed only marginally improved. This suggests that, from a practical viewpoint (WFS compactness and rigidity), the distance = 20 cm could be considered as a reasonable (optimal) option, and it was used in all numerical simulations subsequently described.
To understand why the increase in the distance between the sensor aperture diaphragm and phase mask may play such a critical role in the phase retrieval convergence speed, consider the grayscale images in Figure 6b for the back-propagating wave (auxiliary function) magnitude at the SAPCO sensor input plane for the following two cases: the phase mask located either at the WFS pupil plane ( = 0), or at a distance = 20 cm from the WFS aperture diaphragm. For = 0 (image on the left), nearly the entire back-propagated wave footprint [magnitude ] is confined within the WFS aperture diaphragm, as indicated by the yellow square in Figure 6. Correspondingly, in this case, the Fienup complex field retrieval process acceleration term in the hybrid input–output (HIO) update rule [Equation (16)], which accounts for the corresponding complex amplitudes outside the aperture diaphragm , is negligibly small. Indeed, the product in this term is zero, as the initial complex field estimate is defined solely within the window function . On the other hand, the complex amplitude in this expression is primarily confined within due to boundary condition (5) for the back-propagating wave describing outgoing field phase conjugation at the WFS output plane. With the negligibly small acceleration term, the HIO algorithm nearly coincides with the slow-converging auxiliary function conjugation (AFC) algorithm [Equation (15)].
In the second case ( = 20 cm), the back-propagated wave receives strong phase modulation after passing through the phase mask, resulting in escalated divergence and corresponding expansion to outside the input aperture diaphragm after propagation over the distance , as shown in Figure 6b (image at right). This back-propagated wave footprint broadening “activates” the convergence acceleration term of the HIO algorithm (16), resulting in faster complex field retrieval process convergence. An additional increase in distance eventually results in a disbalance between the convergence acceleration and the AFC [] terms in Equation (16) for the HIO algorithm, leading to marginal convergence speed acceleration and even slowing when the complex amplitude expands beyond the physical size DPR of the phase retrieval computational area.
To emphasize the importance of the back-propagating wave footprint expansion to outside the aperture diaphragm in the SAPCO WFS, we computed the phase retrieval error evolution curve (shown by a dashed line in Figure 6, right) for using the AFC algorithm [Equation (15)], which does not include the HIO algorithm acceleration term. This resulted in a significant drop in the phase retrieval convergence rate (compare the corresponding solid and dashed curves computed for using the HIO and ACF algorithms in Figure 6b).
The second example of SAPCO WFS design parameter optimization is illustrated in Figure 7, where the atmospheric-averaged phase retrieval error evolution curves were computed for the grid-dot- and random-dot-type phase masks (as shown in the Figure 4 right inserts), composed of different numbers Ndot of identical phase shifting dots within the mask area of size Dmask = DPR. The grid-dot-type phase masks were represented by ndot × ndot arrays of phase shifting dots occupying the entire mask. The dimension of the phase shifting dot grid pattern (parameter ndot) was varied, with the goal of optimizing the phase retrieval convergence rate. Simulations were performed for weak-to-moderate () and moderate-to-strong () turbulence conditions, with a fixed (previously optimized) distance between the WFS aperture diaphragm and the phase mask.
As shown in Figure 7, increases in the parameter ndot and consequently, in the density of the phase dots inside the phase mask (parameter ) from ndot = 24 (Ndot = 576, 10%) to ndot = 40 (Ndot =1600, 27%), resulted in rapid phase retrieval process convergence improvement for both turbulence conditions examined. The fastest convergence was observed for the grid-dot mask, with ndot = 48 (Ndot = 2304, 40%). Note that the utilization of a random-dot-type phase mask (dashed RND line in Figure 7) with Ndot = 3600 provided a nearly optimal phase retrieval convergence rate, while the use of the grid-dot-type mask with an equal number of phase dots (ndot = 60) resulted in noticeably slower convergence. This difference can be explained by the fact that the density parameter (percentage of the mask area occupied by phase dots) for the random-dot mask was nearly 50% ( 52%) vs. 61% for the corresponding grid-dot mask with an equal number of phase dots. Since the sensor output intensity distribution is formed by the interference of light components passing through and missing the phase shifting dots, the highest interference pattern visibility and hence, the highest output intensity pattern contrast, can be achieved with the phase dot density factor 50%. Apparently, as confirmed in M&S, a higher output intensity contrast leads to faster HIO phase retrieval algorithm convergence. In the example considered here, the random arrangement of Ndot = 3600 phase dots resulted in their occasional overlapping and a corresponding decrease in the density factor from 61% for the 60 × 60 grid (ndot = 60) to 52%, which is closer to the optimal (50%) density factor value. Based on this analysis, in the following M&S of SAPCO and MAPCO WFSs, we exclusively used a random-dot-type mask, with Ndot = 3600 phase shifting dots.
4.3. Comparative Performance Analysis of Basic SR-WFS Configurations
The methodology of WFS parameter optimization described in Section 4.2 for the SAPCO sensor was applied to the basic SR-WFS configurations shown in Figure 1. For a fair comparison of phase retrieval performance for these sensors, several parameters were identically set for all SR-WFS configurations (pre-selected parameters discussed previously in Section 4.1).
Additionally, note that the phase retrieval convergence rate can be strongly affected by wavefront tip and tilt (tip/tilt) aberrations in the optical field entering the WFS. In practical atmospheric AO systems, this type of aberration is commonly mitigated using a separate AO control subsystem utilizing a fast-steering mirror, which typically operates with a significantly higher closed-loop frequency bandwidth, enabling mitigation (or complete removal) of tip/tilt aberrations from the entering WFS optical field. In the analysis of such AO system architectures, tip/tilt aberrations can be considered as absent (actively removed). In the M&S presented here, we also included an SR-WFS performance analysis for the case of preliminarily removed tip/tilt aberrations. Corresponding results [atmospheric-averaged phase retrieval error evolution curves ] computed using Natm = 100 statistically independent turbulence realizations are presented in Figure 8.
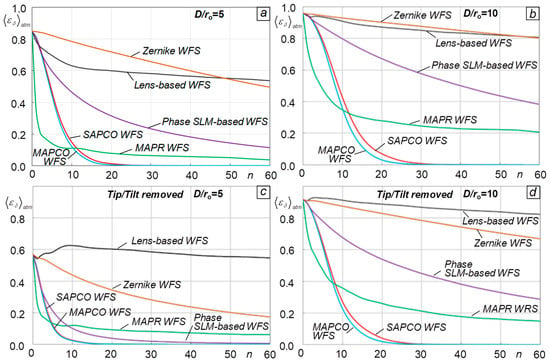
Figure 8.
Atmospheric-averaged phase retrieval error evolution curves for the basic SR-WFS types (Figure 1) computed for turbulence conditions corresponding to = 5 (a,c) and = 10 (b,d), without (a,b) and with (c,d) wavefront tip and tilt aberration removal from the input optical fields.
First, compare the phase retrieval iterative process convergence in the absence of tip/tilt removal (top panels). Under both the weak-to-moderate and moderate-to-strong turbulence conditions examined, both the MAPCO and SAPCO sensors significantly outperformed other sensor types, providing significantly faster phase retrieval convergence and accuracy. Separately, also note the relatively poor performance of both the Zernike- and lens-based WFSs.
Although the initial stage of phase retrieval computations for the MAPR sensor resulted in the most rapid (among all sensors) decrease in the error , which is due to processing of output intensity within the subregions in parallel (as mentioned in Section 3.1 and Ref. [15]), the iterative process quickly slowed down and nearly stagnated at approximately for = 5 and for = 10, as can be seen in Figure 8a,b.
The removal of wavefront tip and tilt aberrations [Figure 8c,d] clearly resulted in phase retrieval process convergence acceleration for all sensors, although this does not change the overall conclusion regarding the dominant performance superiority of MAPCO and SAPCO WFS. The most noticeable convergence speed improvements achieved using tip/tilt aberration removal are observed for Zernike- and phase SLM-based sensors in the case of weak-to-medium turbulence ( = 5). This result is expected for the Zernike WFS, considering the high sensitivity of this sensor to input field tip/tilt aberrations, as previously mentioned in Section 3.1. Note that under strong turbulence conditions [Figure 8d], the impact of tip/tilt aberration removal on the performance of both Zernike- and SLM-based WFSs is less pronounced.
Based on the apparent advantage (clearly seen in Figure 8) of the MAPCO and SAPCO WFS architectures for potential practical use in atmospheric AO systems, subsequent analysis was narrowed down to further study only these SR-WFS configurations.
To compare the performance of MAPCO and SAPCO WFSs in more detail, consider the dependencies shown in Figure 9 describing the atmospheric-averaged number of iterations required to reach a 10% residual phase retrieval error threshold as a function of , with and without tip/tilt aberration removal. As can be seen from the presented curves, for (under weak-to-moderate turbulence conditions) the number of iterations is nearly equal for both WFS types. With an increase in turbulence strength (up to in Figure 9), is smaller for the MAPCO WFS, but the difference compared with that for the SAPCO WFS is within the standard deviation range (shown in Figure 9 by vertical error bars).
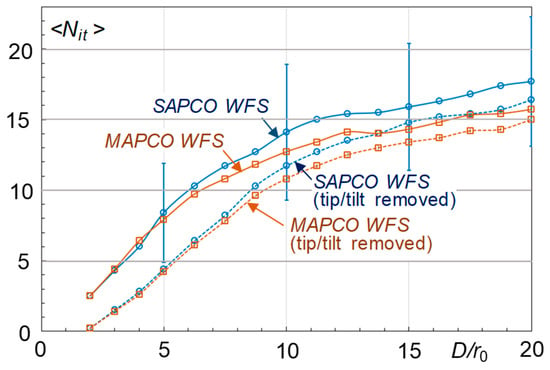
Figure 9.
Average number of iterations <Nit> required to reach a phase retrieval residual error threshold of (10% error) vs. a ratio for MAPCO and SAPCO WFS configurations, with (dotted lines) and without (solid lines) removal of tip/tilt phase aberration components from the entering WFS input field. Vertical bars indicate the standard deviation, characterizing fluctuations in iteration numbers computed for Natm = 100 phase retrieval trials for the SAPCO WFS, with no tip/tilt aberration removal. Error bars are virtually identical for all other curves and thus, are omitted here.
The removal of tip/tilt aberrations resulted in a significant acceleration in phase retrieval convergence, leading to a nearly two-fold decrease in for values ranging from to . Under strong turbulence (), tip/tilt aberration removal is noticeably less beneficial for both WFSs, with the difference in , with and without tip/tilt aberration removal, being smaller than the standard deviation of the mean.
In general, the results presented in Figure 9 demonstrate a relatively small difference in phase retrieval performance between the SAPCO and MAPCO (Figure 1d) sensors. Since, from a practical viewpoint, the SAPCO WFS configuration is simpler and hence, easier to align and ruggedize, this sensor may exhibit a better (among the SR-WFS types considered here) potential for atmospheric AO applications. These factors prompted the selection of the SAPCO WFS for further analysis.
4.4. SR-WFS Tolerance Analysis Examples
In this section, we consider examples of SR-WFS “tolerance” analysis in assessing the impact of the potential discrepancy between optical field transformation in a hardware-implemented SR-WFS vs. one described in mathematical and/or numerical sensor models used for phase retrieval computations.
The questions to address are, how sensitive are phase retrieval computations to relatively small, unaccounted for deviations in the WFS parameters in the SR-WFS model, and how can errors resulting from these deviations be minimized by tuning the WFS mathematical/numerical model and/or improving the accuracy of sensor component alignment. Since the overall WFS parameter space is quite extensive, the tolerance analysis presented here is limited to only the SAPCO WFS (Figure 4) and a specified set of parameters.
Consider first the impact of an unrevealed in the SAPCO WFS mathematical model possible longitudinal (along the sensor optical axis) deviation ΔCCD in the photo-array (CCD camera) position with respect to its prescribed in the model (nominal) location a distance Ldif from the phase mask. Such a deviation may occur due to insufficiently accurate WFS alignment, and/or environmental factors (temperature variations, mechanical jitter, etc.).
With photo-array longitudinal shift ΔCCD, the measured sensor output intensity corresponds to the distance LCCD = Ldif + ΔCCD. At the same time, phase retrieval computations are performed based on the mathematical model of the sensor, which does not account for the photo-array position deviation (misalignment), i.e., assuming ΔCCD = 0. In the course of phase retrieval iterations, this misalignment, which is unaccounted for in the mathematical model, results in residual phase retrieval error , (n = 0, 1, …), which is dependent upon the photo-array displacement ΔCCD. Here, is the true input field phase, and is the phase function computed at the nth phase retrieval iteration performed, based on the measured intensity .
The impact of SAPCO WFS photo-array misalignment was evaluated in numerical simulations using the phase retrieval error metric , defined by Equation (17b). Note that, with perfect WFS alignment, coincides with the phase error metric , as previously discussed.
An analogous approach was applied to evaluate the tolerance requirements with respect to the longitudinal displacement Δaper of the sensor aperture diaphragm and the lateral shift Δmask of the phase mask by computing the corresponding phase errors and . The corresponding results are presented in Figure 10, represented by sets of atmospheric-averaged phase retrieval error evolution curves [dependencies , , and ], which were computed for different misalignment parameter values: ΔCCD, Δaper, and Δmask. The pre-selected phase retrieval residual error threshold (shown in Figure 10 by horizontals dashed lines) was considered as the maximum permissible misalignment level.
Figure 10.
Atmospheric-averaged phase retrieval error evolution curves for the SAPCO WFS (Figure 4), computed for turbulence conditions corresponding to = 10 in the presence of longitudinal deviations ΔCCD and Δaper in the WFS photo-array (a) and the aperture diaphragm (b), with respect to the nominal distances Ldif = 14 cm [for (a)] and Lmask = 20 cm [for (b)], and the phase mask lateral shift over the distance Δmask, without (c) and with (d) removal of tip/tilt aberrations from the input wave entering the WFS.
By comparing the phase error evolution curves in Figure 10a–c, one can see that phase mask lateral positioning requires significantly higher accuracy than does longitudinal positioning of the photo-array and aperture diaphragm. Also, note that in the case of phase mask lateral displacement [Figure 10c,d], the smallest phase retrieval error is achieved after approximately the first n = 15 iterations, and the error only increases with successive iterations. For the phase dot size ddot = 100 μm used in simulations, a phase retrieval error below 10% can be obtained, with a phase mask lateral displacement Δmask not exceeding approximately 5 μm. The corresponding tolerances in the positioning of the photo-array (ΔCCD 0.3 mm) and aperture diaphragm (Δaper 2.0 mm) are significantly more relaxed.The required alignment accuracy (including phase mask lateral positioning) can be fulfilled using commercial opto-mechanical positioners. Note that the alignment tolerance results presented are specific to the SAPCO sensor parameters selected in M&S (see Section 3.4) and the turbulence strength, and may vary when these parameters change.
Compare the phase retrieval error evolution curves in Figure 10c,d corresponding to phase mask lateral misalignment, computed without and with tip/tilt aberration removal using an external fast steering mirror-based control system. The results clearly indicate that tip/tilt aberration mitigation results in a noticeably lower alignment accuracy requirement. This difference is quite easy to understand from a physics viewpoint, as tip/tilt aberrations at the sensor aperture diaphragm lead to overall optical field footprint shifts in the phase mask plane, hence causing an effect analogous to a phase mask lateral shift.
Notice that the phase retrieval convergence rate for the perfectly aligned WFS in Figure 10c,d is nearly two-fold higher than the corresponding convergence rate in Figure 10a,b, while they are expected to be identical. The reason for this difference is that in the analysis of phase mask lateral misalignment, the numerical grid size NPR was doubled (from NPR = 256, which was used in all previously described simulations, to NPR = 512) to increase the number of pixels per phase dot and hence, the accuracy of phase mask lateral misalignment in M&S. This increase in phase retrieval computation grid resolution also resulted in more accurate numerical integration of the propagation Equations (1) and (8) for the outgoing and back-propagating (auxiliary) waves in the HIO iterative algorithm [Equation (16)], thus decreasing digital noise and accelerating phase retrieval process convergence. This phase retrieval convergence improvement does not come without a price—there is a noticeable increase in the iteration time (see Table 1) and a potential decline in AO control bandwidth. The optimal choice, from an AO control perspective, between phase retrieval convergence acceleration via the increase in the phase retrieval computational grid resolution at the expense of the increase in iteration time vs. the decrease in when transitioning to a lower numerical grid resolution, is an important subject to be further investigated.
Phase retrieval computations may offer useful tools for SR-WFS alignment and calibration, while utilizing a plane (reference) input optical wave for this purpose. For example, as numerical simulations show, in the presence of the WFS misalignment ΔCCD or Δaper, phase retrieval computations result in a clearly seen random uncorrelated phase component (phase noise) vs. a spatially uniform phase function for the perfectly aligned sensor. The amplitude of the phase noise component gradually increases with an increase in either parameter ΔCCD or Δaper. Correspondingly, the variation in the random fluctuations in the retrieved phase patterns can be used as a metric to be minimized in the course of WFS alignment.
Similarly, the retrieved phase patterns can also be used for phase mask lateral alignment. As M&S shows, retrieved phase patterns exhibit characteristic (dependent on lateral shift amplitude Δmask) striped spatial structures, which can provide guidance for phase mask lateral alignment during WFS calibration.
4.5. Impact of Camera Noise and Laser Beacon Linewidth
“Photon-hungry” (low input field photon flux level) operational conditions, characterized by a relatively low SNR, are common for atmospheric optics applications. Correspondingly, phase retrieval “resilience” with respect to photo-array (camera) noise is an important matter to be considered. Camera noise impact is analyzed here for the SAPCO WFS configuration, which perhaps possesses the lowest optical power losses and hence, potentially the highest SNR among the basic SR-WFS architectures considered above and shown in Figure 1. Note that in the analysis, we neglect potential optical power losses in the SAPCO sensor related to imperfections in the phase mask glass plate antireflection coatin.
Camera noise inside the photo-array area of size DPA = 2DWFS was represented in M&S by statistically independent delta-correlated 2D random fields (n = 1, …, Natm), with uniform probability distribution inside the [0, 1] interval. After scaling by the factor ν, each noise realization was superimposed with a corresponding realization of the WFS output intensity distribution prior to conducting the phase retrieval computations. SNR was defined as the ratio of atmospheric-averaged (averaged over Natm = 100 turbulence and noise realizations) optical and camera noise powers inside the WFS photo-array area: .
Phase retrieval computations with “noisy” WFS output intensity distributions were repeated for a set of pre-selected SNR values. The computed dependencies of the atmospheric-averaged phase retrieval error on iteration number n for = 5 and = 10 are presented in Figure 11 for several SNR values.
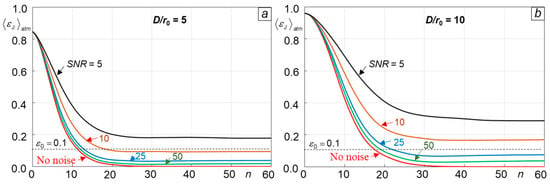
Figure 11.
Atmospheric-averaged phase retrieval error evolution curves for the SAPCO WFS, computed for turbulence conditions corresponding to = 5 (a) and = 10 (b) in the presence of photo-array noise for different SNR values. Numerical simulation parameters are presented in Figure 5 and are described in Section 3.4, Section 4.1, and Section 4.2.
As might be expected, photo-array noise results in a decreased phase retrieval convergence rate and lower accuracy, which are more pronounced for stronger turbulence ( = 10 in Figure 11b). For the chosen acceptable phase retrieval error , the SNR should be approximately above ten for weak-to-moderate ( = 5) and nearly twice that for moderate-to-strong ( = 10) turbulence conditions.
Thus far in our previous analysis, the light source (laser beacon light) was considered monochromatic. This assumption may not be applicable for a number of atmospheric AO applications, including directed energy and remote laser power beaming, based on spectral beam combining (see [53]), and the utilization of short-pulse or wide-linewidth laser systems for laser beacon generation and active imaging [54].
The question to ask is, how might the non-monochromaticity (non-zero spectral linewidth) of the input optical field entering the SR-WFS potentially impact phase retrieval process accuracy and convergence speed? To address this question, as an example, we consider the phase retrieval efficiency for the SAPCO WFS operating with a non-monochromatic laser beacon light.
In numerical simulations, a non-monochromatic laser beacon was represented by a set of Nλ = 11 monochromatic collimated Gaussian beams (laser beacon spectral components) with identical widths dbeacon and different wavelengths {λn}, (n = 1, …, Nλ). It is assumed that the wavelengths {λn} are equidistantly distributed within a spectral band (laser beacon linewidth) centered at the wavelength λc = 1060 nm, corresponding to the largest peak intensity value among the Nλ laser beacon monochromatic components.
In the laser beacon model considered here, the wavelengths (spectral lines) are symmetrical with respect to the central wavelength λc, and the peak intensity values of the corresponding laser beacon spectral components are described by the Gaussian function of width Δλ (laser beacon linewidth), dependent on the wavelength. The linewidth is commonly defined as the full-width at half-maximum (FWHM) of the spectral band, where the peak intensity value drops to half its maximum value. In the example of a Gaussian spectral intensity distribution considered here, the wavelength difference between two adjacent laser beacon spectral components was equal to Δλ/6.
The output intensity at the SAPCO sensor photo-array was obtained via averaging the Nλ output intensity distributions {}, which were computed by considering the atmospheric propagation of individual monochromatic laser beacon components of the WFS input plane and the subsequent propagation from the sensor aperture diaphragm to the photo-array plane. The output intensity distribution was further utilized for phase retrieval computations, based on the WFS mathematical model corresponding to a monochromatic input light with central wavelength λc = 1060 nm, and the HIO algorithm [Equation (16)].
In the M&S of individual laser beacon component propagation, the wavelength difference was accounted for via the corresponding change in phase screen modulation amplitudes for each turbulence realization. A similar phase modulation amplitude scaling was applied to the SAPCO sensor phase mask (scaling of the phase dot introduced phase shift). Note that the M&S parameters for both the SAPCO sensor and atmospheric turbulence were computed for the central laser beacon wavelength λc.
The impact of the laser beacon linewidth Δλ on the phase retrieval accuracy and the convergence rate is illustrated in Figure 12 by the dependence of the atmospheric-averaged phase retrieval error on the iteration number for = 5 and = 10.
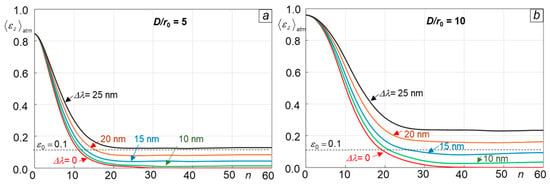
Figure 12.
Atmospheric-averaged phase retrieval error evolution curves for the SAPCO WFS, operating with a non-monochromatic laser beacon of linewidth Δλ, computed for atmospheric turbulence conditions corresponding to = 5 (a) and = 10 (b). M&S parameters are presented in Figure 5 and described in Section 3.4, Section 4.1, and Section 4.2.
Analogous to the impact of photo-array noise (see Figure 11), laser source linewidth broadening resulted in a decline in both the phase retrieval convergence rate and the accuracy, which is more evident under stronger turbulence conditions ( = 10 in Figure 12). In order to quantify the potential decline in WFS performance, consider (as before) the 10% phase retrieval error as an acceptable criterion (), shown in Figure 12 by horizontal dashed lines. This criterion is met for laser sources, with linewidth Δλ of approximately 22 nm for weak-to-moderate ( = 5) and 15 nm for moderate-to-strong ( = 10) turbulence conditions.
The results obtained indicate the potential applicability of the SAPCO WFS and the iterative phase retrieval technique discussed here for atmospheric AO systems operating with broadband (several hundred GHz) continuous wave and picosecond pulse laser sources.
5. Concluding Remarks
Recent advances in the development of GPU- and FPGA-based signal processing hardware have opened up the real prospect for the practical employment of computationally expensive iterative phase retrieval (IPR) techniques in closed-loop atmospheric AO applications. On the other hand, these possibilities cannot be fully realized without the parallel development of novel wavefront sensing architectures that are no longer constrained by the phase retrieval computational time and are uniquely suitable for addressing one of the most challenging atmospheric AO problems related to closed-loop wavefront sensing control under the strong scintillation conditions typical of near-ground propagation scenarios.
In this paper, we provide a general framework for the analysis of such scintillation-resistant wavefront sensing (SR-WFS) architectures based on IPR algorithms, which can be considered as candidates for turbulence-induced phase aberration sensing and AO control under strong scintillations. It was shown that these sensors can be described in terms of a generic SR-WFS model that was further applied for the derivation of iterative phase and complex field retrieval algorithms—analogues to the classical Gerchberg–Saxton and Fienup hybrid input–output (HIO) iterative algorithms. This general phase retrieval framework was utilized for the optimization and comparative performance analysis of basic SR-WFS architectures. This analysis led to the introduction of the scintillation-resistant advanced phase-contrast (SAPCO) WFS. The major advantages of the SAPCO sensor are its simplicity, from a practical implementation viewpoint, and its efficiency of phase retrieval under a wide range of turbulence conditions. The numerical simulation results provided for the SAPCO WFS tolerance, with respect to optical component misalignment, and its ability to operate using both non-monochromatic light and under relatively low SNR, open attractive opportunities for the potential utilization of this IPR technique-based sensor for closed-loop AO control under strong input field intensity scintillations, as described in Part II.
Author Contributions
Conceptualization, derivations, and manuscript-writing, M.A.V.; computer code development and numerical simulations, E.P.; analysis and discussions of obtained results, M.A.V. and E.P.; preparation of the manuscript for submission, M.A.V. and E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by Optonica LLC projects.
Data Availability Statement
No new data were generated in this study.
Acknowledgments
We thank Jennifer C. Ricklin for her careful review and helpful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hardy, J.W. Adaptive Optics for Astronomical Telescopes; Oxford Series in Optical and Imaging Sciences; Oxford University Press: New York, NY, USA, 1998; ISBN 978-0-19-509019-2. [Google Scholar]
- Platt, B.C.; Shack, R. History and Principles of Shack-Hartmann Wavefront Sensing. J. Refract. Surg. 2001, 17, 573. [Google Scholar] [CrossRef] [PubMed]
- Roddier, F. Curvature Sensing and Compensation: A New Concept in Adaptive Optics. Appl. Opt. 1988, 27, 1223. [Google Scholar] [CrossRef] [PubMed]
- Rousset, G. Wave-Front Sensors. In Adaptive Optics in Astronomy; Roddier, F., Ed.; Cambridge University Press: Cambridge, UK, 1999; p. 91. ISBN 978-0-521-55375-9. [Google Scholar]
- Hardy, J.W.; Lefebvre, J.E.; Koliopoulos, C.L. Real-Time Atmospheric Compensation. J. Opt. Soc. Am. 1977, 67, 360. [Google Scholar] [CrossRef]
- Sandler, D.G.; Cuellar, L.; Lefebvre, M.; Barrett, T.; Arnold, R.; Johnson, P.; Rego, A.; Smith, G.; Taylor, G.; Spivey, B. Shearing Interferometry for Laser-Guide-Star Atmospheric Correction a Large D/r0. J. Opt. Soc. Am. A 1994, 11, 858. [Google Scholar] [CrossRef]
- Ragazzoni, R. Pupil Plane Wavefront Sensing with an Oscillating Prism. J. Mod. Opt. 1996, 43, 289. [Google Scholar] [CrossRef]
- Esposito, S.; Riccardi, A. Pyramid Wavefront Sensor Behavior in Partial Correction Adaptive Optic Systems. Astron. Astrophys. 2001, 369, L9. [Google Scholar] [CrossRef]
- Barchers, J.D.; Fried, D.L.; Link, D.J.; Tyler, G.A.; Moretti, W.; Brennan, T.J.; Fugate, R.Q. Performance of Wavefront Sensors in Strong Scintillation. In Proceedings of the Adaptive Optical System Technologies II 2003, Waikoloa, HI, USA, 1 February 2003; Wizinowich, P.L., Bonaccini, D., Eds.; SPIE: California, UK; p. 217. [Google Scholar] [CrossRef]
- Perram, G.P.; Cusumano, S.J.; Hengehold, R.L.; Fiorino, S.T. An Introduction to Laser Weapon Systems, 1st ed.; Directed Energy Professional Society: Albuquerque, NM, USA, 2010; ISBN 978-0-9793687-4-5. [Google Scholar]
- Varshney, A.K.; Mainuddin; Singhal, G.; Nayak, J. High Power Lasers for Directed Energy Applications: Developments and Challenges. Infrared Phys. Technol. 2024, 136, 105064. [Google Scholar] [CrossRef]
- Soref, R.; De Leonardis, F.; Daligou, G.; Moutanabbir, O. Directed High-Energy Infrared Laser Beams for Photovoltaic Generation of Electric Power at Remote Locations. APL Energy 2024, 2, 026101. [Google Scholar] [CrossRef]
- Majumdar, A.K.; Ricklin, J.C. Free-Space Laser Communications: Principles and Advances; Springer: New York, NY, USA, 2008; ISBN 978-0-387-28652-5. [Google Scholar]
- Göhler, B.; Lutzmann, P.; Anstett, G. 3D Imaging with Range Gated Laser Systems Using Speckle Reduction Techniques to Improve the Depth Accuracy. In Proceedings of the Electro-Optical and Infrared Systems: Technology and Applications V, Cardiff, UK, 15–18 September 2008; Huckridge, D.A., Ebert, R.R., Eds.; SPIE: California, UK, 2008; p. 711307. [Google Scholar] [CrossRef]
- Aubailly, M.; Vorontsov, M.A. Scintillation Resistant Wavefront Sensing Based on Multi-Aperture Phase Reconstruction Technique. J. Opt. Soc. Am. A 2012, 29, 1707. [Google Scholar] [CrossRef]
- Bordbar, B.; Vorontsov, M.A. Complex Field Sensing in Strong Scintillations with Multi-Aperture Phase Contrast Techniques. J. Opt. 2020, 22, 10LT01. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. A Practical Algorithm for the Determination of Phase from Image and Diffraction Plane Pictures. Optik 1972, 35, 237. [Google Scholar]
- Fienup, J.R. Phase Retrieval Algorithms: A Comparison. Appl. Opt. 1982, 21, 2758. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase-Retrieval Algorithms for a Complicated Optical System. Appl. Opt. 1993, 32, 1737. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Phase Retrieval Algorithms: A Personal Tour [Invited]. Appl. Opt. 2013, 52, 45. [Google Scholar] [CrossRef]
- Soifer, V.A.; Kotlar, V.; Doskolovich, L. Iterative Methods for Diffractive Optical Elements Computation; CRC Press: Boca Raton, FL, USA, 1997; ISBN 978-1-4822-7291-8. [Google Scholar]
- Vorontsov, M.A.; Matveev, A.N.; Sivokon’, V.P. Optimal Guiding of the Wave Front in the Focusing of Radiation into an Arbitrary Region. Sov. Phys. Dokl. 1986, 31, 829. [Google Scholar]
- Fleck, J.A.; Morris, J.R.; Feit, M.D. Time-Dependent Propagation of High Energy Laser Beams through the Atmosphere. Appl. Phys. 1976, 10, 129. [Google Scholar] [CrossRef]
- Ghebremichael, F.; Andersen, G.P.; Gurley, K.S. Holography-Based Wavefront Sensing. Appl. Opt. 2008, 47, A62. [Google Scholar] [CrossRef]
- Zernike, F. How I Discovered Phase Contrast. Science 1955, 121, 345. [Google Scholar] [CrossRef]
- Vorontsov, M.A.; Justh, E.W.; Beresnev, L.A. Adaptive Optics with Advanced Phase-Contrast Techniques: Part I. High-Resolution Wave-Front Sensing. J. Opt. Soc. Am. A 2001, 18, 1289. [Google Scholar] [CrossRef]
- Bloemhof, E.E.; Wallace, J.K. Phase Contrast Techniques for Wavefront Sensing and Calibration in Adaptive Optics. In Proceedings of the Astronomical Adaptive Optics Systems and Applications, San Diego, CA, USA, 31 December 2003; Tyson, R.K., Lloyd-Hart, M., Eds.; SPIE: California, UK, 2003; p. 309. [Google Scholar]
- Wu, Y.; Sharma, M.K.; Veeraraghavan, A. WISH: Wavefront Imaging Sensor with High Resolution. Light Sci. Appl. 2019, 8, 44. [Google Scholar] [CrossRef]
- Wang, C.; Dun, X.; Fu, Q.; Heidrich, W. Ultra-High Resolution Coded Wavefront Sensor. Opt. Express 2017, 25, 13736. [Google Scholar] [CrossRef]
- Li, X.; Liu, K.; Liu, Z.; Guo, J. High-Precision Phase Retrieval Method for Speckle Suppression Based on Optimized Modulation Masks. Opt. Express 2023, 31, 18824. [Google Scholar] [CrossRef] [PubMed]
- Fried, D.L. Branch Point Problem in Adaptive Optics. J. Opt. Soc. Am. A 1998, 15, 2759. [Google Scholar] [CrossRef]
- Fried, D.L. Optical Resolution Through a Randomly Inhomogeneous Medium for Very Long and Very Short Exposures. J. Opt. Soc. Am. 1966, 56, 1372. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media, 2nd ed.; SPIE Publications: Bellingham, WA, USA, 2005; ISBN 978-1-5106-4370-3. [Google Scholar]
- Ahmanov, S.A.; Nikitin, S.Y. Physical Optics; Oxford University Press: Oxford, UK, 1997; ISBN 978-0-19-851795-5. [Google Scholar]
- Vorontsov, M.A.; Shmalgauzen, V.I. The Principles of Adaptive Optics; Izdatel’stvo Nauka: Moscow, Russia, 1985. [Google Scholar]
- Paxman, R.G.; Schulz, T.J.; Fienup, J.R. Joint Estimation of Object and Aberrations by Using Phase Diversity. J. Opt. Soc. Am. A 1992, 9, 1072. [Google Scholar] [CrossRef]
- Wang, B.-Y.; Han, L.; Yang, Y.; Yue, Q.-Y.; Guo, C.-S. Wavefront Sensing Based on a Spatial Light Modulator and Incremental Binary Random Sampling. Opt. Lett. 2017, 42, 603. [Google Scholar] [CrossRef] [PubMed]
- Almoro, P.F.; Pedrini, G.; Gundu, P.N.; Osten, W.; Hanson, S.G. Enhanced Wavefront Reconstruction by Random Phase Modulation with a Phase Diffuser. Opt. Lasers Eng. 2011, 49, 252. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Soltanolkotabi, M. Phase Retrieval from Coded Diffraction Patterns. Appl. Comput. Harmon. Anal. 2015, 39, 277. [Google Scholar] [CrossRef]
- Zel’dovich, B.Y.; Pilipetsky, N.F.; Shkunov, V.V. Principles of Phase Conjugation; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 1985; Volume 42, ISBN 978-3-662-13573-0. [Google Scholar]
- Vorontsov, M.A.; Shmal’gauzen, V.I. Interference Criteria for the Focusing of Light. Sov. J. Quantum Electron. 1980, 10, 285. [Google Scholar] [CrossRef]
- Minet, J.; Vorontsov, M.A.; Polnau, E.; Dolfi, D. Enhanced Correlation of Received Power-Signal Fluctuations in Bidirectional Optical Links. J. Opt. 2013, 15, 022401. [Google Scholar] [CrossRef]
- Levitin, E.S.; Polyak, B.T. Constrained Minimization Methods. USSR Comput. Math. Math. Phys. 1966, 6, 1. [Google Scholar] [CrossRef]
- Vorontsov, M.A.; Kolosov, V.V.; Kohnle, A. Adaptive Laser Beam Projection on an Extended Target: Phase- and Field-Conjugate Precompensation. J. Opt. Soc. Am. A 2007, 24, 1975. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R.; Marron, J.C.; Schulz, T.J.; Seldin, J.H. Hubble Space Telescope Characterized by Using Phase-Retrieval Algorithms. Appl. Opt. 1993, 32, 1747. [Google Scholar] [CrossRef] [PubMed]
- Bauschke, H.H.; Combettes, P.L.; Luke, D.R. Phase Retrieval, Error Reduction Algorithm, and Fienup Variants: A View from Convex Optimization. J. Opt. Soc. Am. A 2002, 19, 1334. [Google Scholar] [CrossRef] [PubMed]
- Gass, J.; Dakoff, A.; Kim, M.K. Phase Imaging without 2π Ambiguity by Multi-wavelength Digital Holography. Opt. Lett. 2003, 28, 1141. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE: Bellingham, WA, USA, 2010; ISBN 978-0-8194-8326-3. [Google Scholar]
- Roggemann, M.C.; Welsh, B.M. Imaging Through Turbulence, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-0-203-75128-2. [Google Scholar]
- Lachinova, S.; Maynard, M.; Vorontsov, M.A.; Filimonov, G.; Spencer, M. WaveJET Software Modeling and Simulation Platform for HEL DE Applications: Overview. In Proceedings of the 21st Annual Directed Energy S&T Symposium Proceedings, Destin, FL, USA, 20 November 2019. [Google Scholar]
- Kolmogorov, A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akad. Nauk. SSSR Dokl. 1941, 30, 301. [Google Scholar]
- Vorontsov, M.; Filimonov, G.; Ovchinnikov, V.; Polnau, E.; Lachinova, S.; Weyrauch, T.; Mangano, J. Comparative Efficiency Analysis of Fiber-Array and Conventional Beam Director Systems in Volume Turbulence. Appl. Opt. 2016, 55, 4170. [Google Scholar] [CrossRef]
- Walbaum, T.; Plötner, M.; Strecker, M.; Heinzig, M.; Liem, A.; Ehrhardt, S.; Möller, F.; Damm, C.; Trautmann, S.; Rothhardt, C.; et al. Spectral Beam Combining for Security as Well as Terrestrial, Satellite, and Deep Space Communication. In Proceedings of the Fiber Lasers XXI: Technology and Systems, San Francisco, CA, USA, 27 January–1 February 2024; Jollivet, C., Ed.; SPIE: San Francisco, CA, USA, 2024; p. 25. [Google Scholar] [CrossRef]
- DiComo, G.; Helle, M.; Kaganovich, D.; Schmitt-Sody, A.; Elle, J.; Peñano, J. Nonlinear Self-Channeling of High-Power Lasers through Controlled Atmospheric Turbulence. J. Opt. Soc. Am. B 2020, 37, 797. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).