Grating Coupler Design for Low-Cost Fabrication in Amorphous Silicon Photonic Integrated Circuits
Abstract
1. Introduction
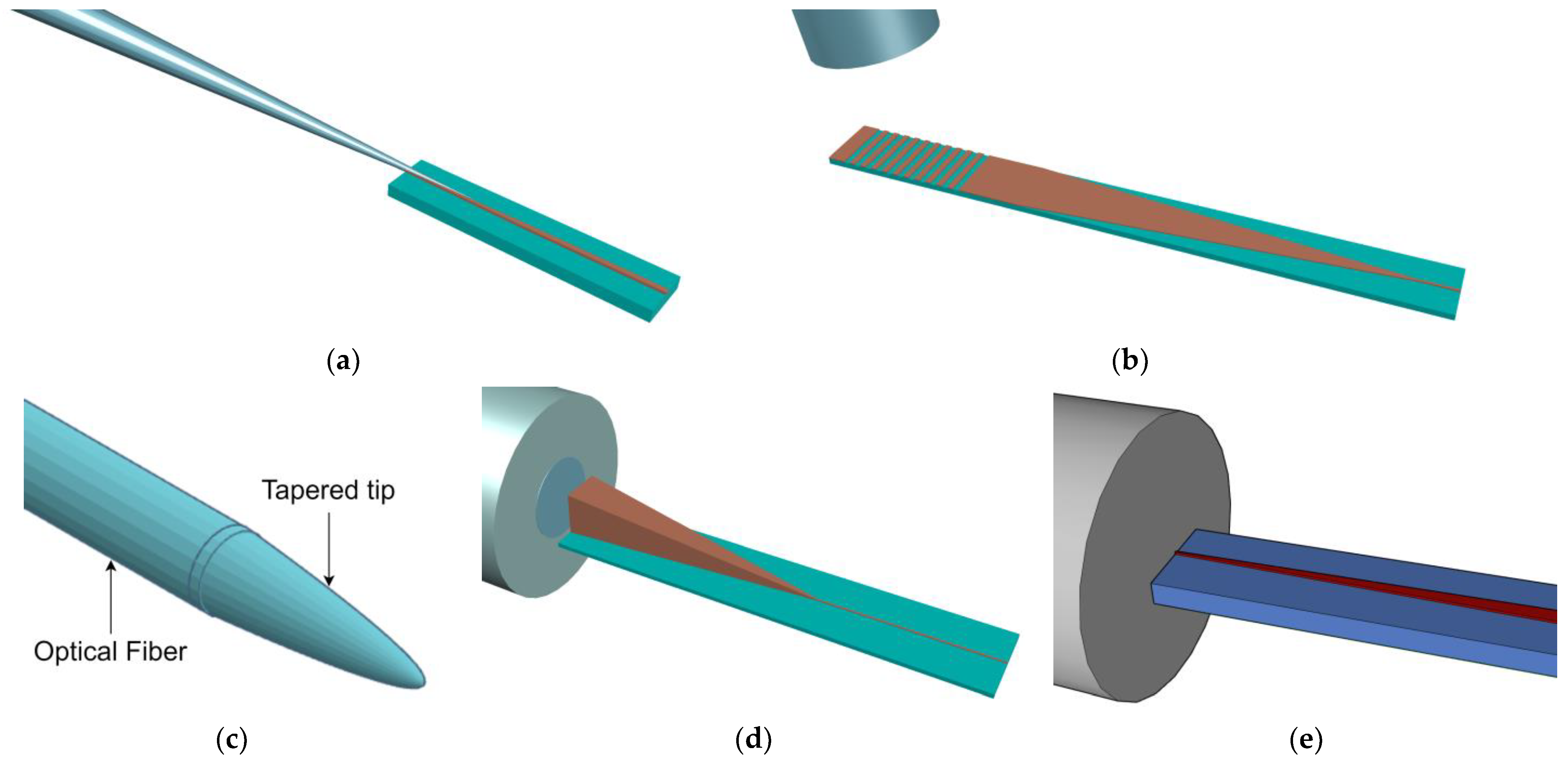
2. Brief Review of Light-Coupling Methods
- Lensed fibers [43];
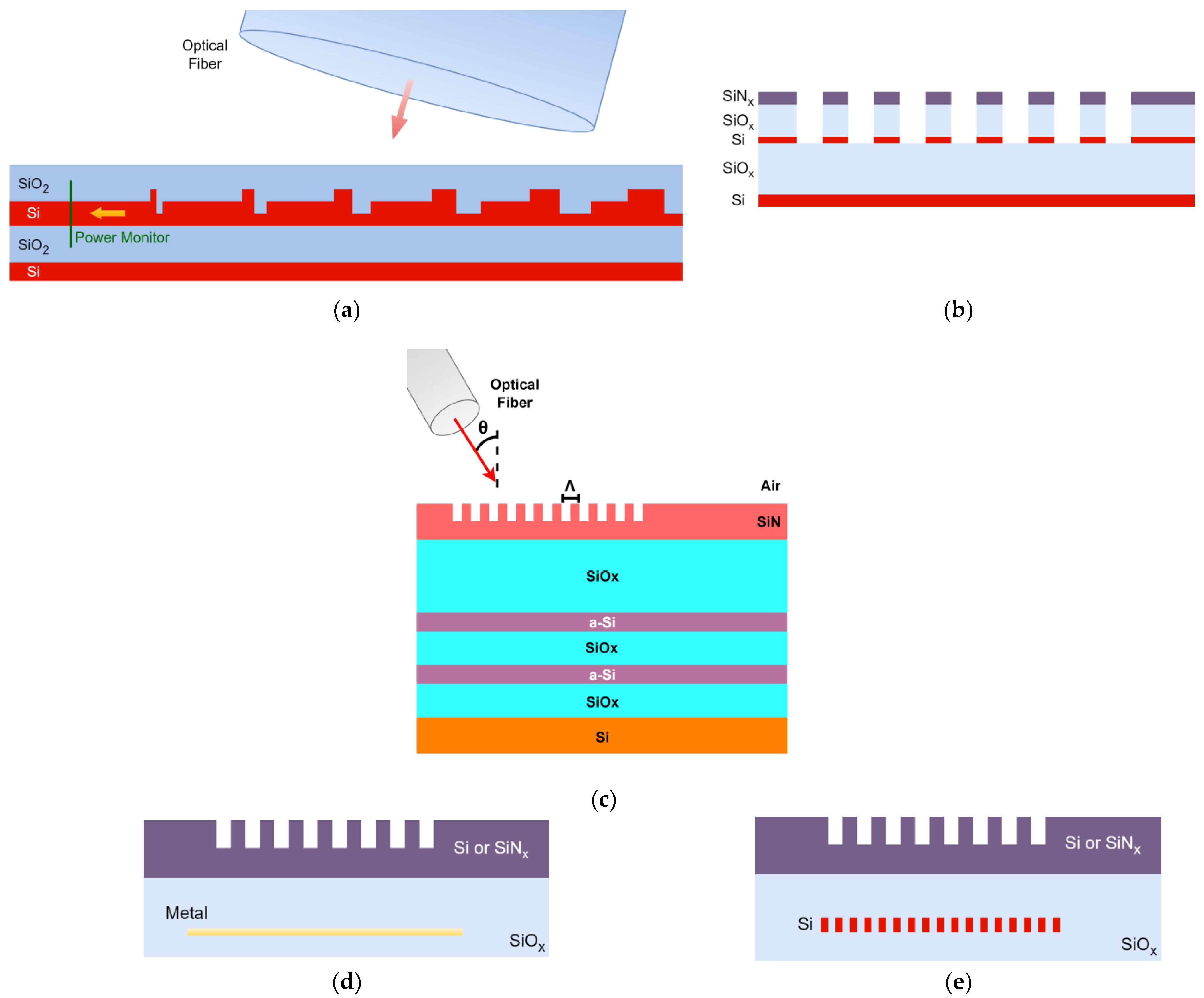
Grating Couplers
3. Materials and Methods
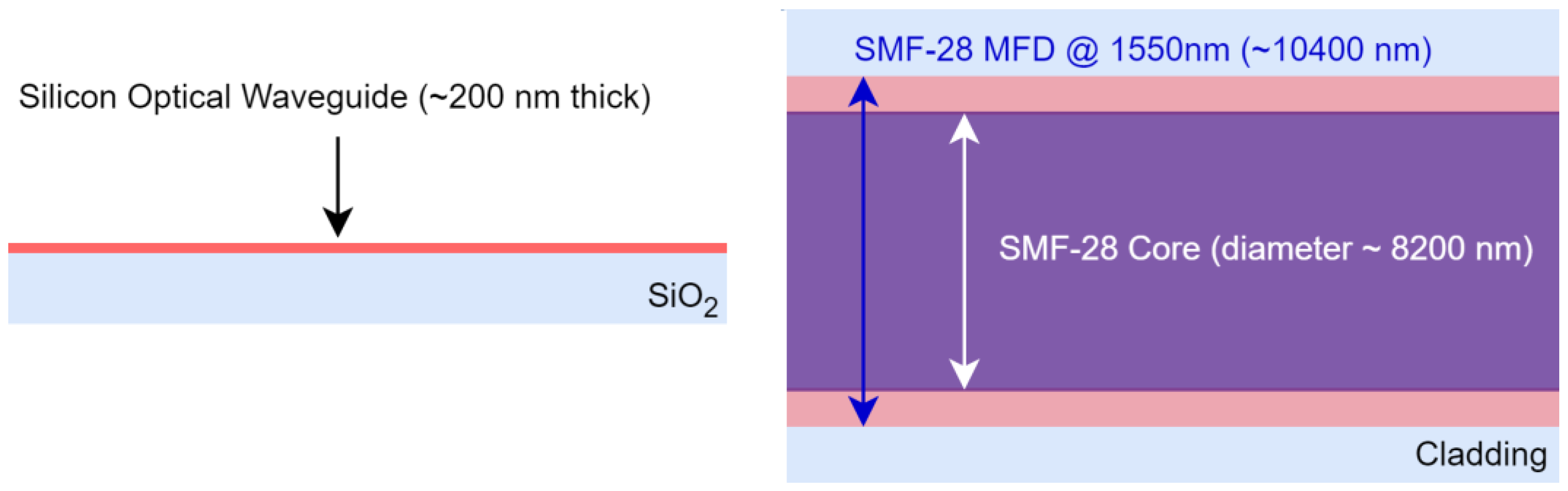
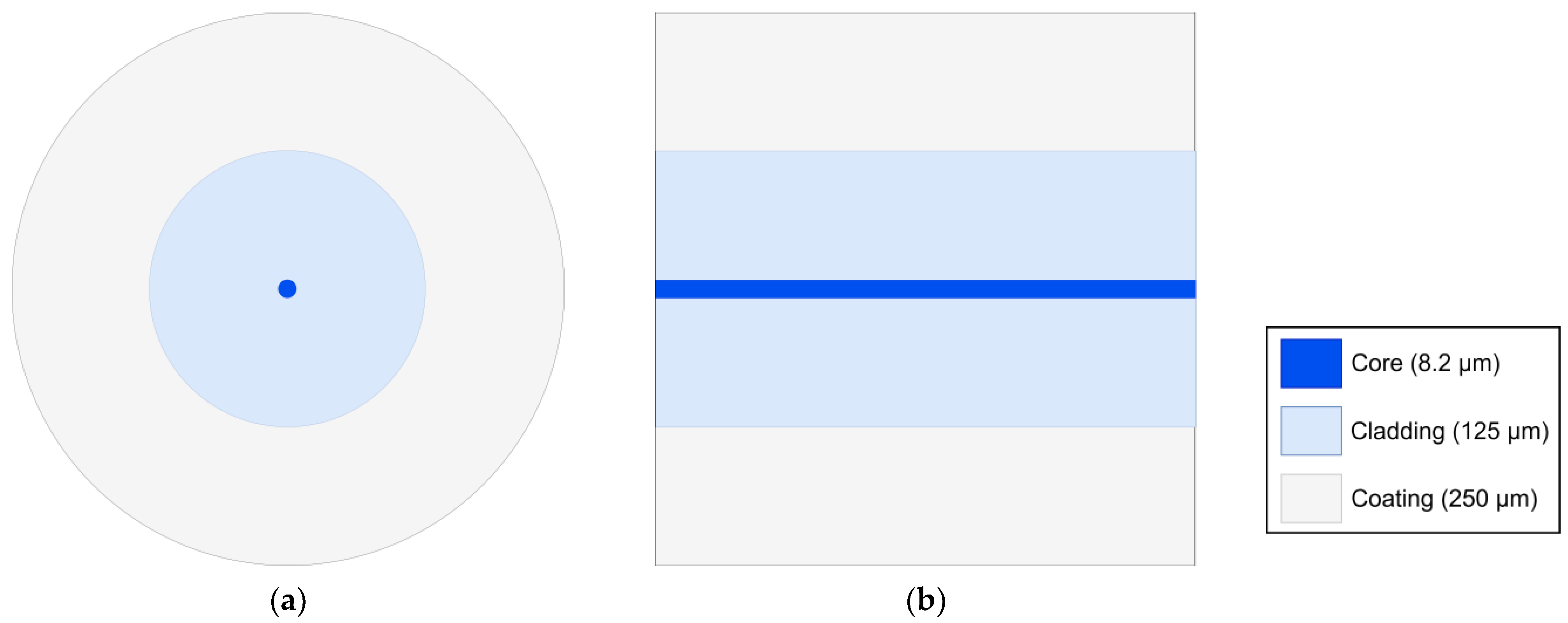
3.1. Single-Mode Optical Fiber
3.2. Single-Mode Waveguide
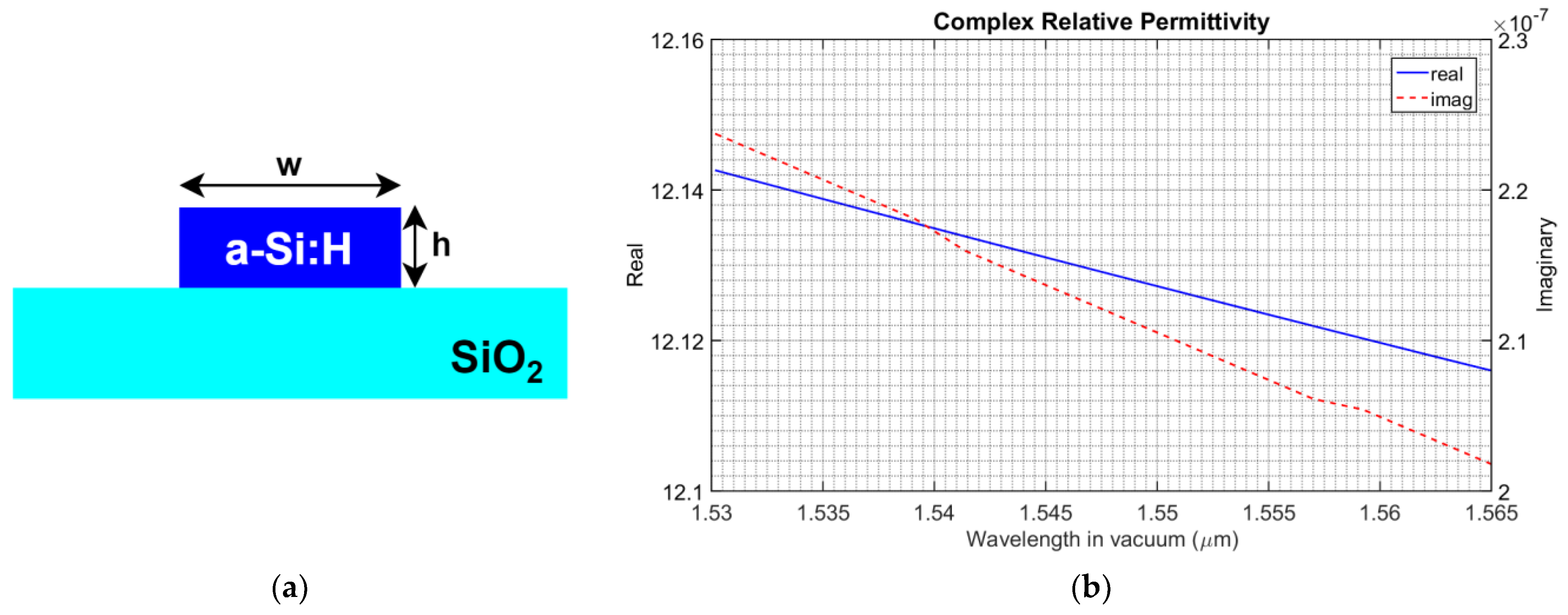
3.3. Grating Coupler Design
3.4. Grating-Coupler Optimization
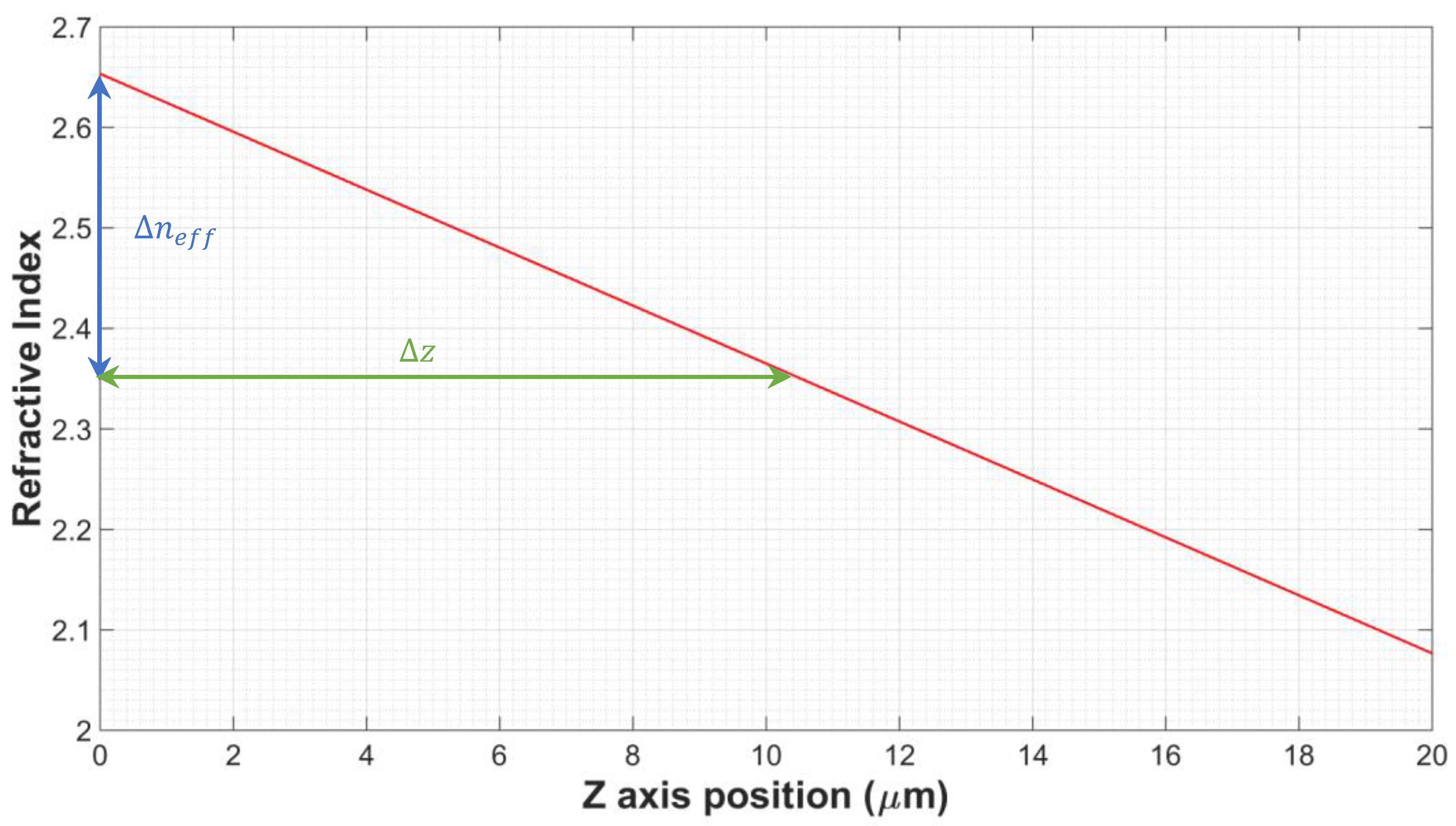
3.5. Linear Refractive-Index Variation
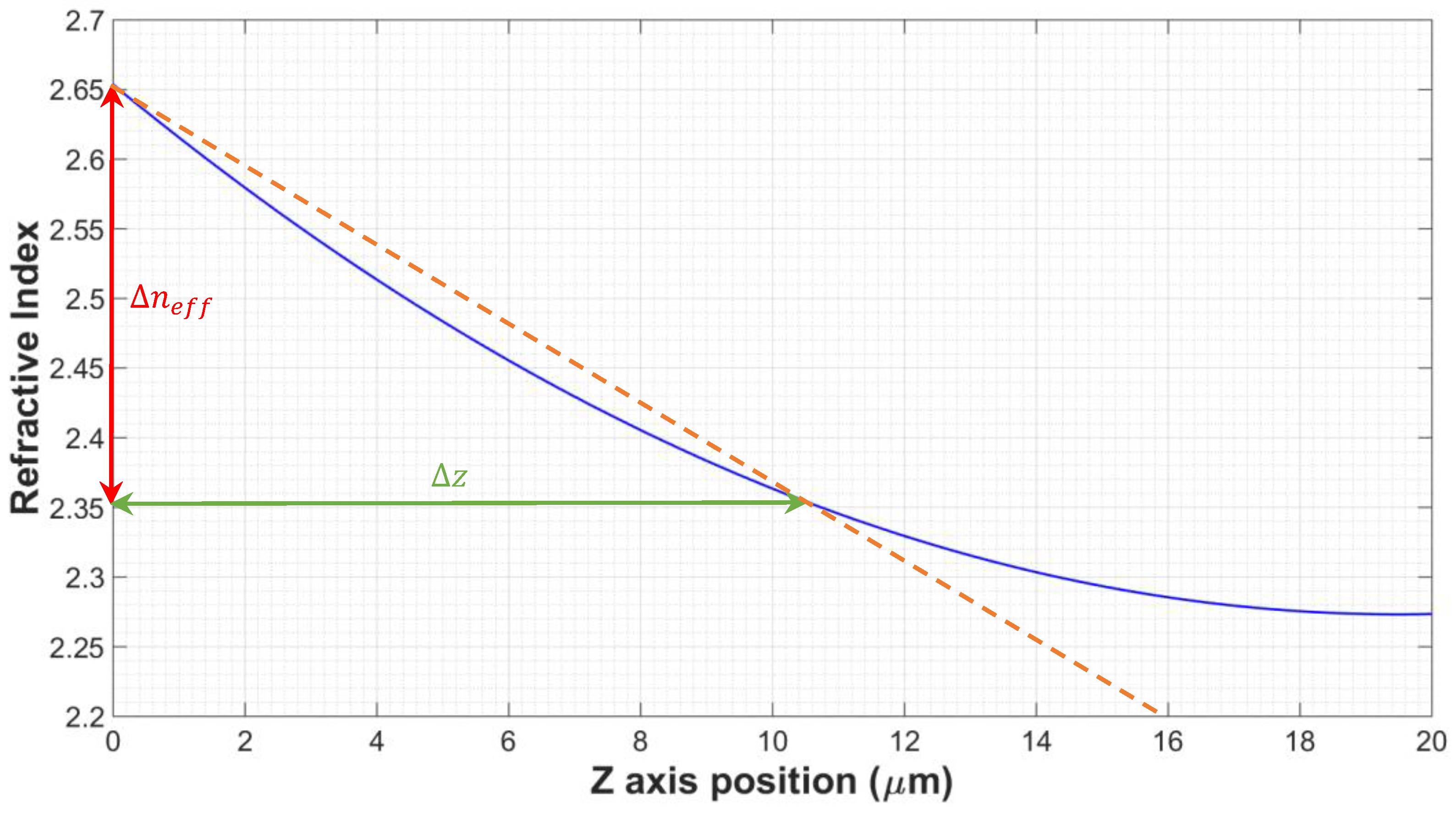
3.6. Quadratic Refractive-Index Variation
3.7. Fill Factor Greater than 50%
3.8. Overlapped-Grating Design
3.9. Random-Distribution Overlapped Grating Design
4. Results
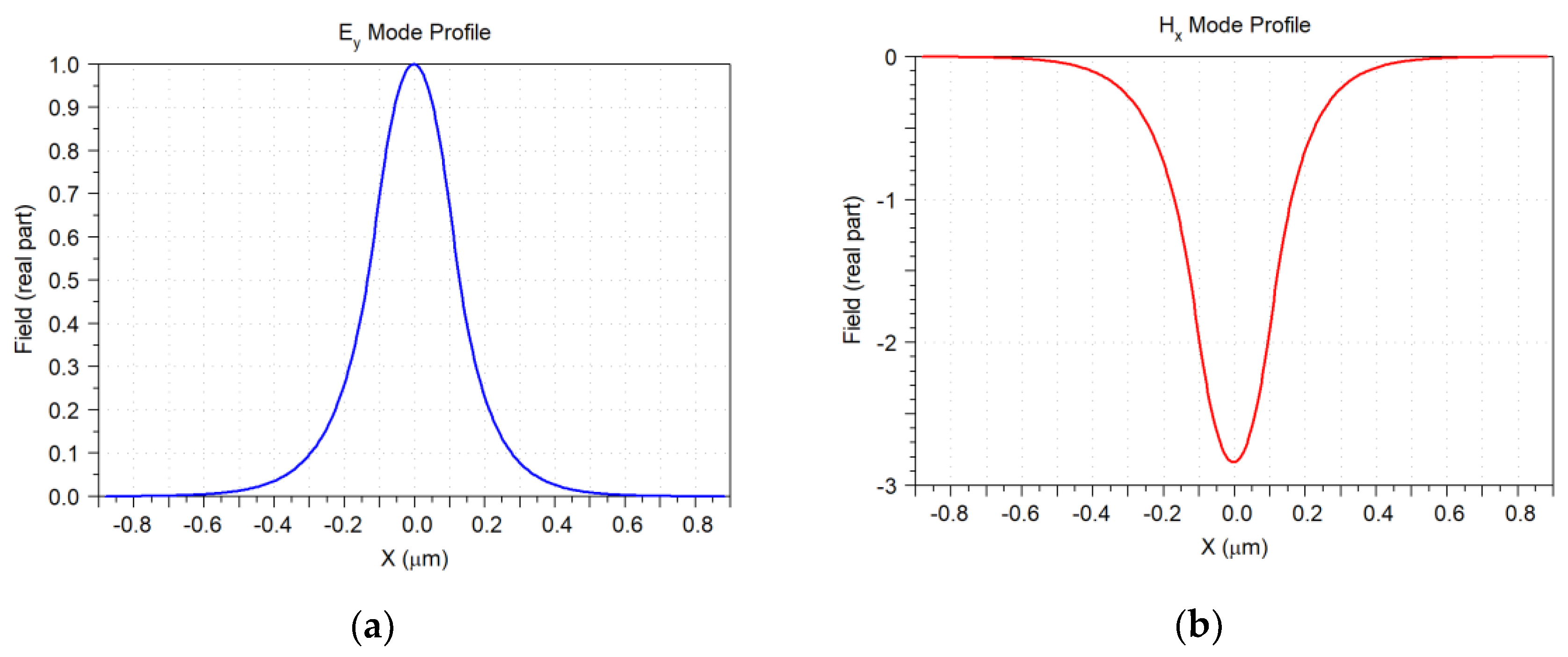
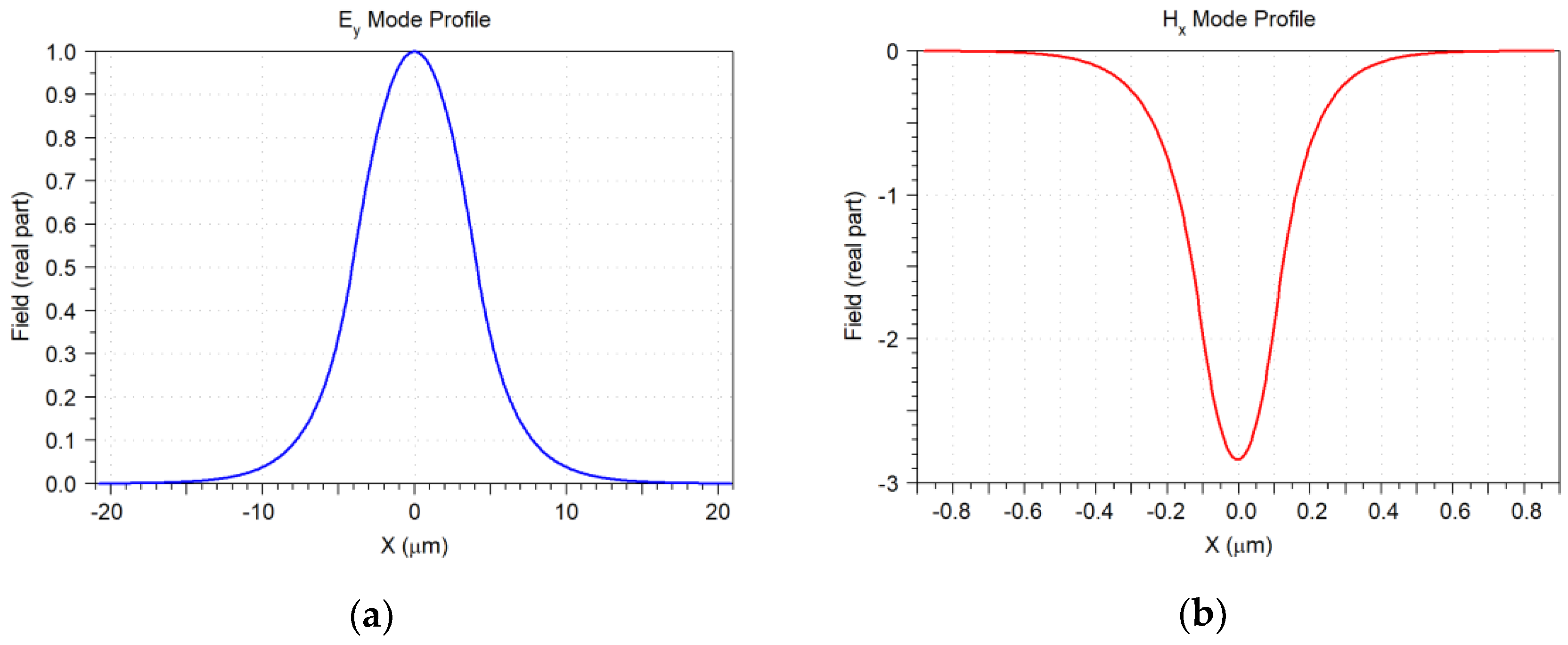
4.1. Fundamental Mode of the Waveguide
4.2. Simulated Single-Mode-Fiber Fundamental Mode
4.3. Non-Optimized Grating-Coupler Performance
4.4. Constant Refractive Index and Fill Factor Greater than 50%
4.5. Linear Effective-Refractive-Index Variation
4.6. Quadratic Effective-Refractive-Index Variation
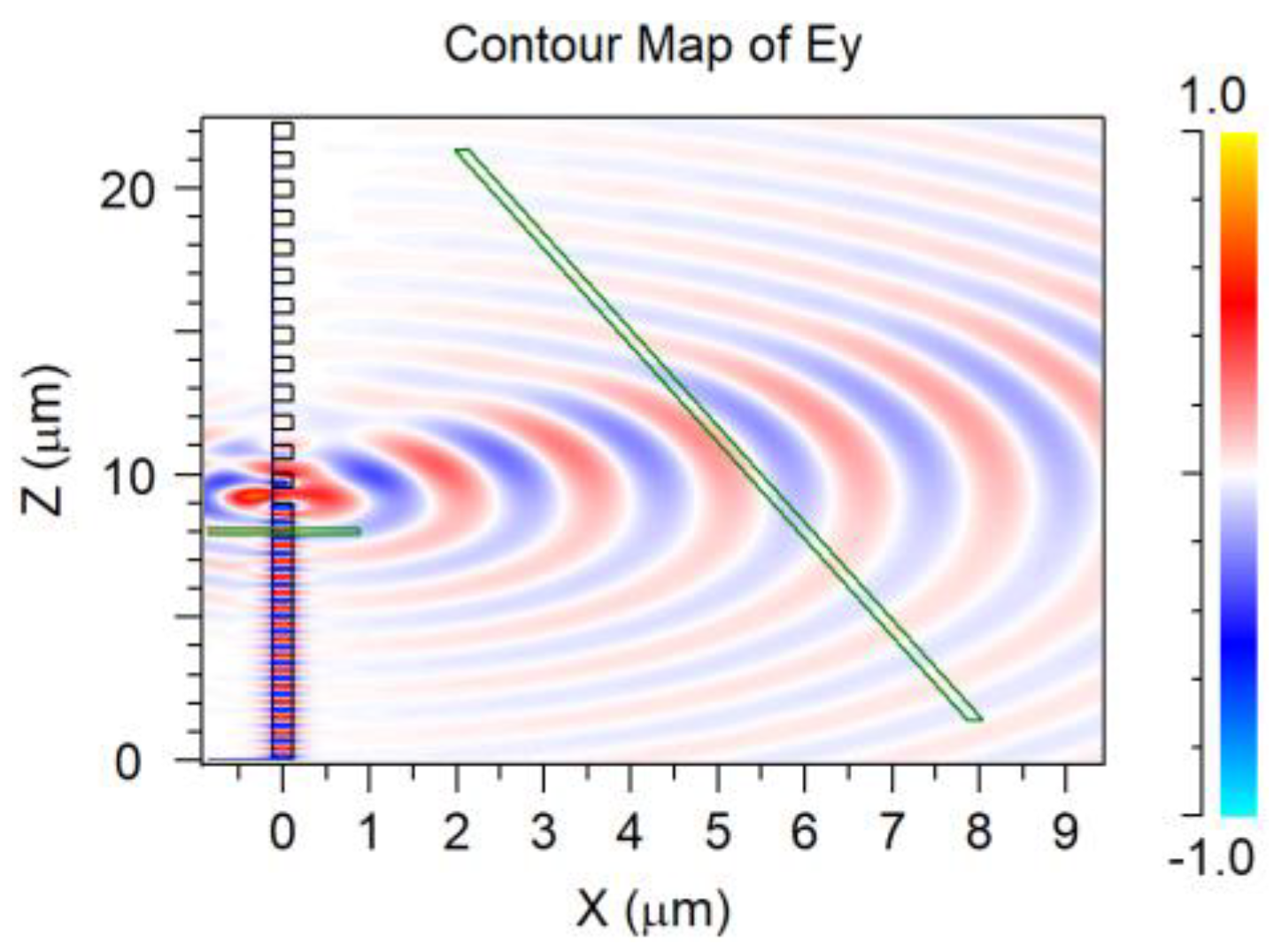
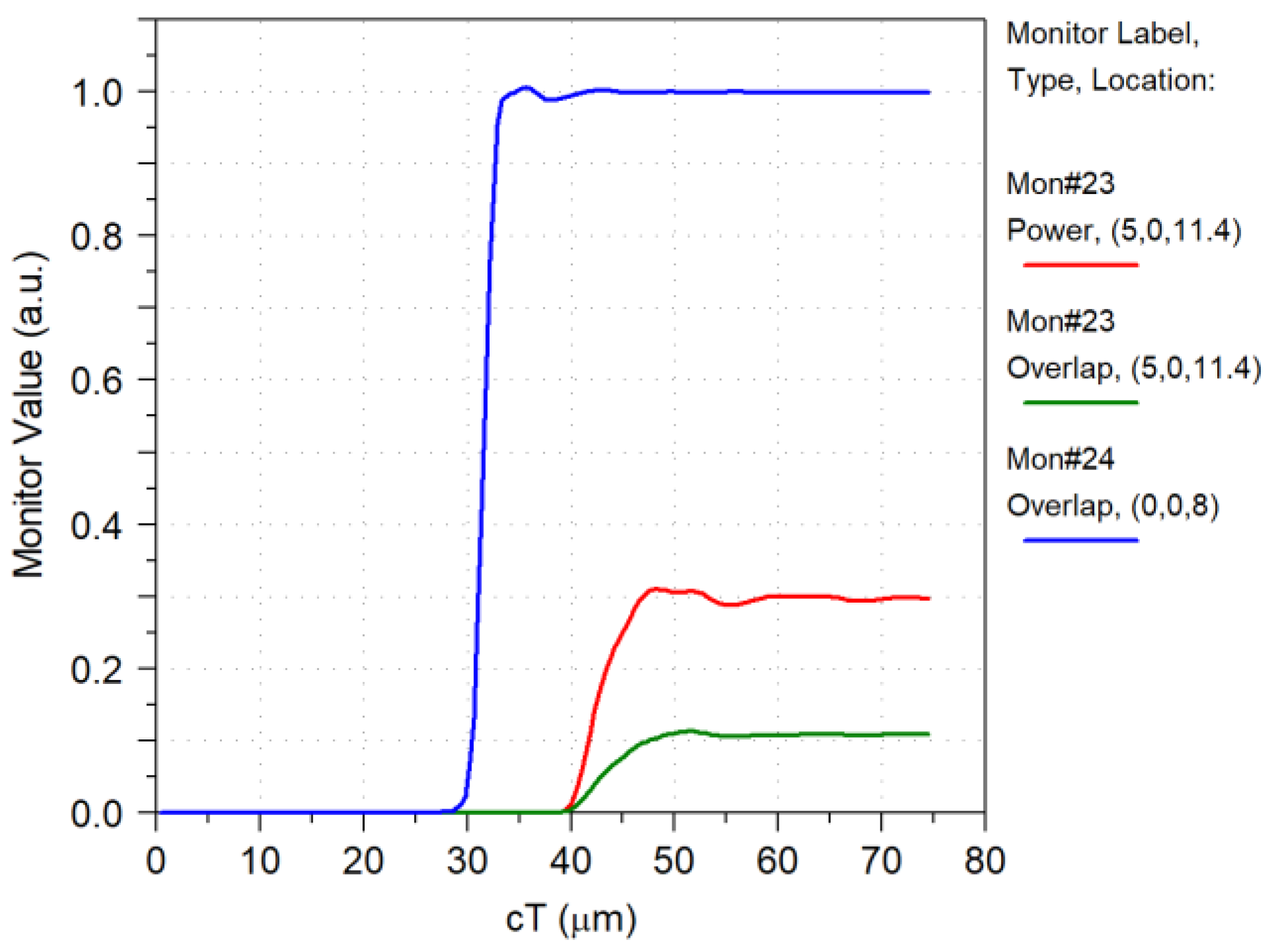
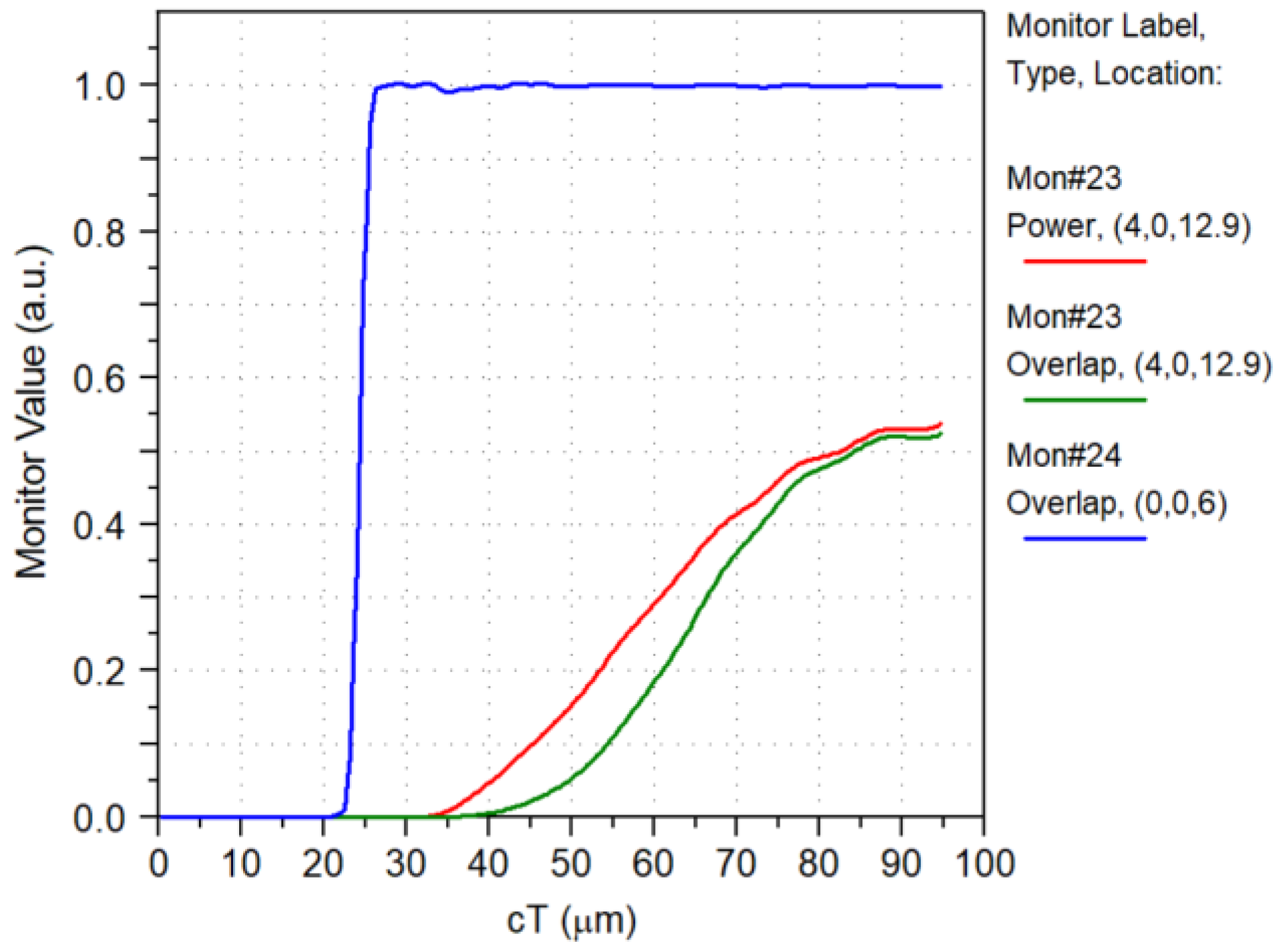
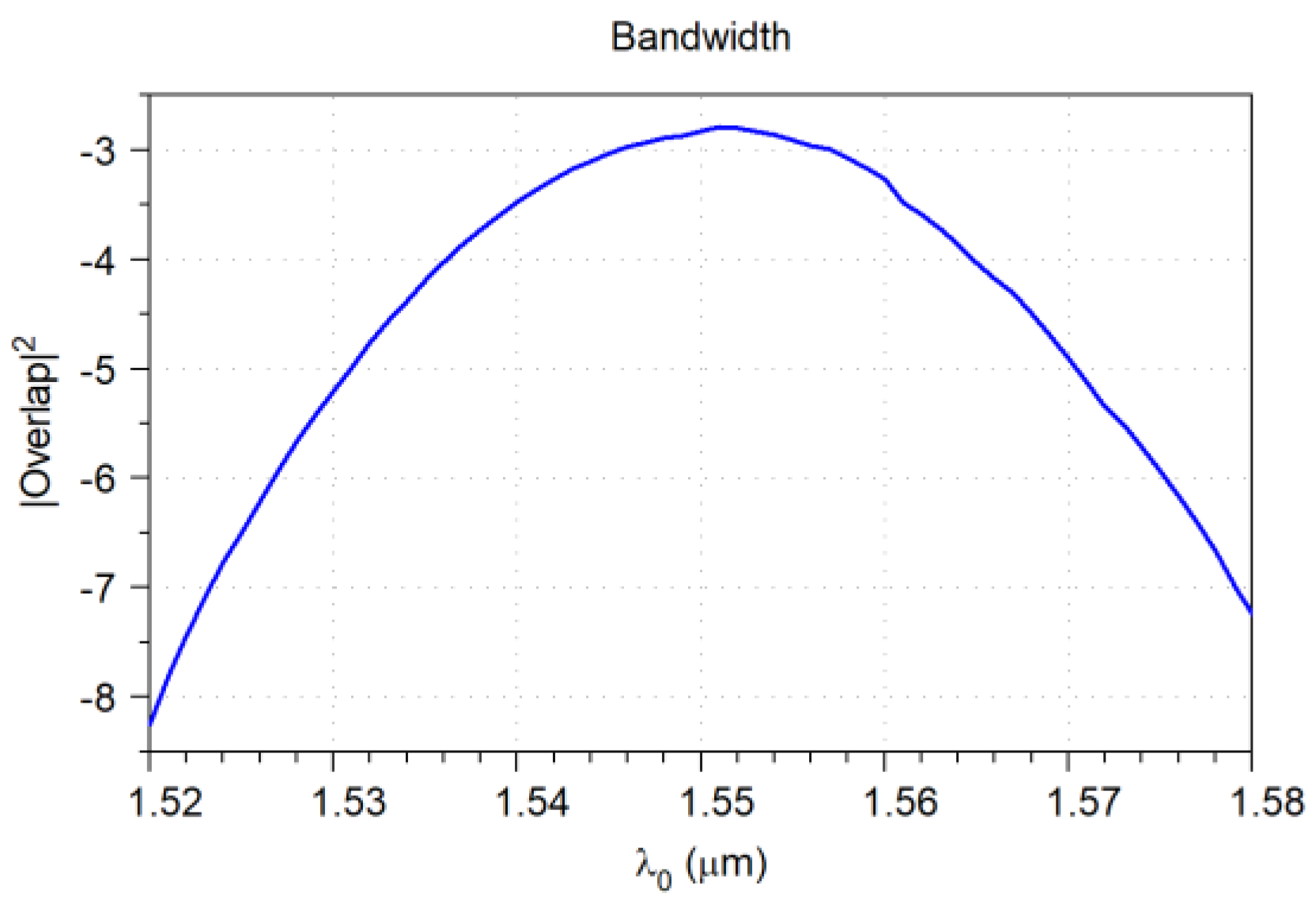
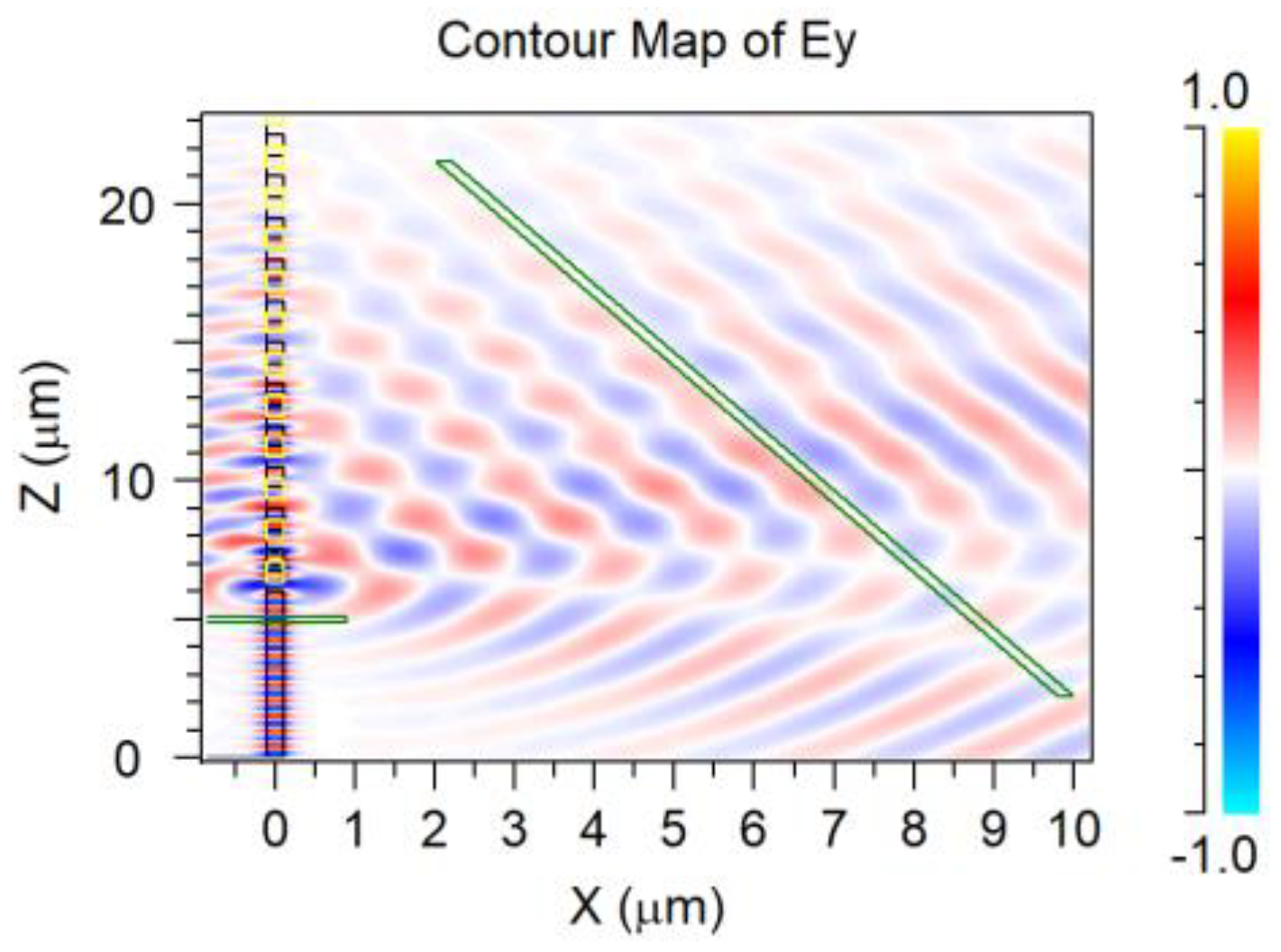
4.7. Overlapped Micrometric Design
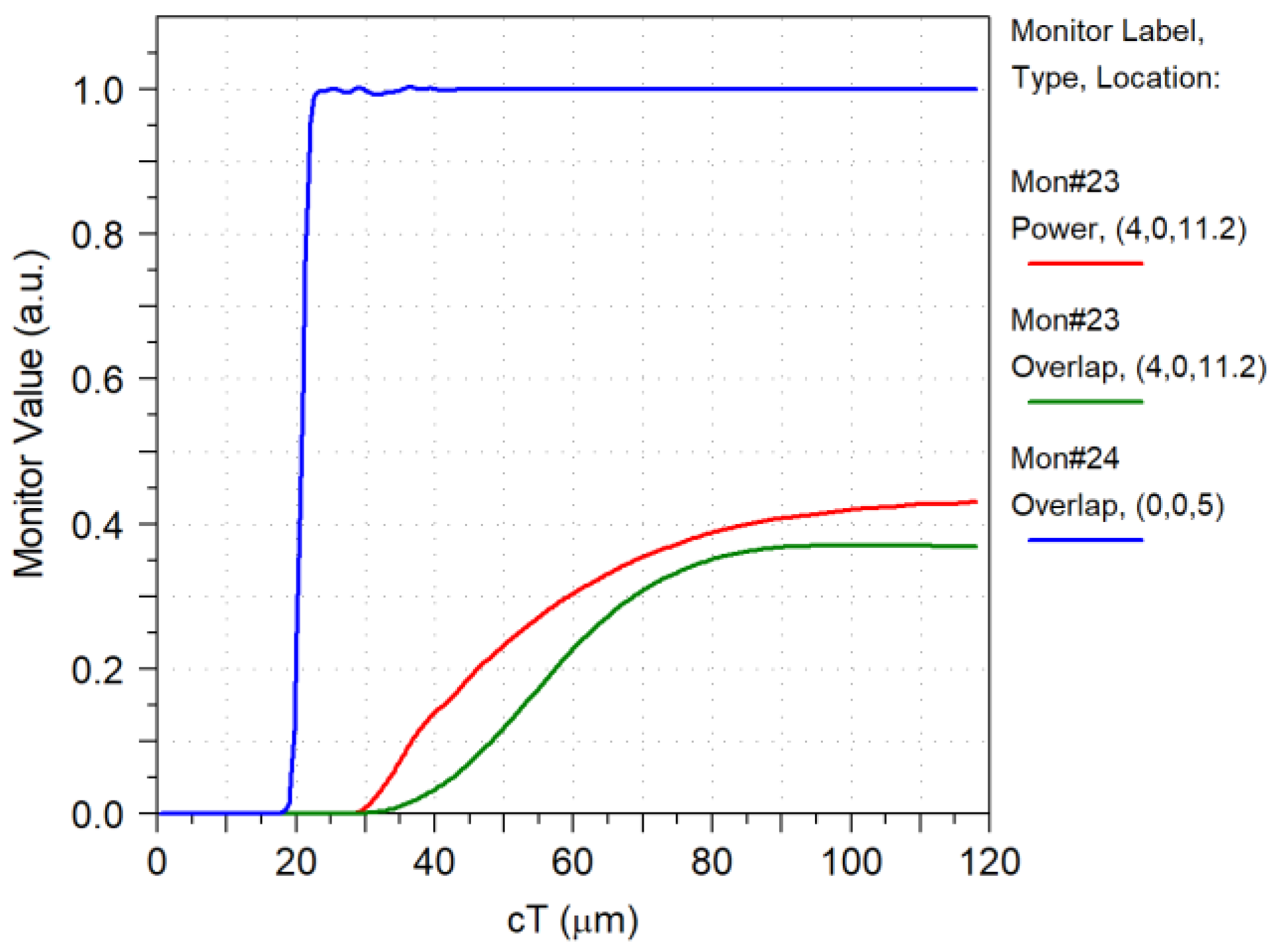
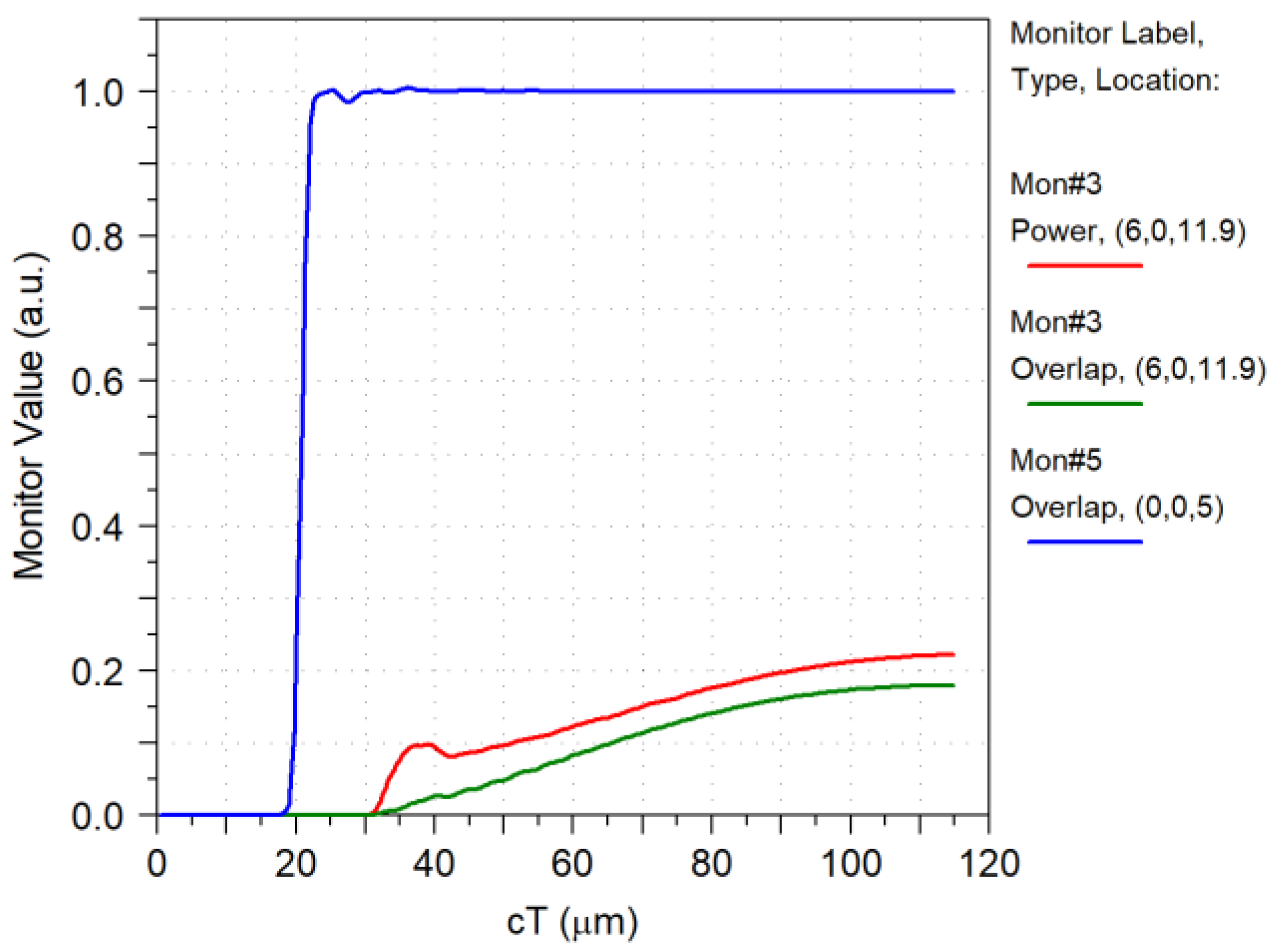
4.8. Random Distribution
5. Discussion
6. Conclusions
7. Future Work and Improvement
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
gratingLength = 20;//micrometer delta_neff = −0.3;//1/micrometer delta_z = 10.4;//micrometer (SMF-28 MFD) m = delta_neff/delta_z; neff0 = 2.65348;//F = 0.9 theta = deg2rad(15);//15 deg ne = 1;//air nu = 2.8372;//220 nm aSiH strip waveguide (2D-FEM) lambda0 = 1.55;//micrometer z = 0; neff = 0; GP = 0; F = 0; num = 1; while (z < gratingLength){ neff = m*z + neff0; GP = lambda0/(neff − sin(theta));//GP = Grating period (micrometer) F = (neff − ne)/(nu − ne); print(“GP”+num2str(num)+” = “+num2str(GP,3)+“\r\n”);//round to nm print(“F”+num2str(num)+” = “+num2str(F,3) + “\r\n”);//round to nm z = z + GP; num = num + 1; }
Appendix B
a = 0.001;
b = −0.039;
gratingLength = 20;//micrometer
neff0 = 2.65348;//F = 0.9
theta = deg2rad(15);//15 deg
ne = 1;//air
nu = 2.8372;//220 nm aSiH strip waveguide (2D-FEM)
lambda0 = 1.55;//micrometer
z = 0;
neff = 0;
GP = 0;
F = 0;
num = 1;
while (z < gratingLength){
neff = a*z^2 + b*z + neff0;
GP = lambda0/(neff - sin(theta));//GP = Grating period (micrometer)
F = (neff - ne)/(nu - ne);
print([“GP”+num2str(num)+” = “+num2str(GP,3)+“\r\n”]);//round to nm
print([“F”+num2str(num)+” = “+num2str(F,3)+“\r\n”]);//round to nm
z = z + GP;
num = num + 1;
}
References
- Sengupta, K.; Nagatsuma, T.; Mittleman, D.M. Terahertz integrated electronic and hybrid electronic–photonic systems. Nat. Electron. 2018, 1, 622–635. [Google Scholar] [CrossRef]
- Thraskias, C.A.; Lallas, E.N.; Neumann, N.; Schares, L.; Offrein, B.J.; Henker, R.; Plettemeier, D.; Ellinger, F.; Leuthold, J.; Tomkos, I. Survey of photonic and plasmonic interconnect technologies for intra-datacenter and high-performance computing communications. IEEE Commun. Surv. Tutor. 2018, 20, 2758–2783. [Google Scholar] [CrossRef]
- Pelucchi, E.; Fagas, G.; Aharonovich, I.; Englund, D.; Figueroa, E.; Gong, Q.; Hannes, H.; Liu, J.; Lu, C.Y.; Matsuda, N.; et al. The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 2022, 4, 194–208. [Google Scholar] [CrossRef]
- Lukin, D.M.; Guidry, M.A.; Vučković, J. Integrated Quantum Photonics with Silicon Carbide: Challenges and Prospects. PRX Quantum 2020, 1, 020102. [Google Scholar] [CrossRef]
- Pinske, J.; Teuber, L.; Scheel, S. Highly degenerate photonic waveguide structures for holonomic computation. Phys. Rev. A 2020, 101, 062314. [Google Scholar] [CrossRef]
- Huang, C.; Sorger, V.J.; Miscuglio, M.; Al-Qadasi, M.; Mukherjee, A.; Lampe, L.; Nichols, M.; Tait, A.N.; Ferreira de Lima, T.; Marquez, B.A.; et al. Prospects and applications of photonic neural networks. Adv. Phys. X 2022, 7, 1981155. [Google Scholar] [CrossRef]
- Wu, C.; Yu, H.; Lee, S.; Peng, R.; Takeuchi, I.; Li, M. Programmable phase-change metasurfaces on waveguides for multimode photonic convolutional neural network. Nat. Commun. 2021, 12, 96. [Google Scholar] [CrossRef]
- Bai, B.; Shu, H.; Wang, X.; Zou, W. Towards silicon photonic neural networks for artificial intelligence. Sci. China Inf. Sci. 2020, 63, 160403. [Google Scholar] [CrossRef]
- Moughames, J.; Porte, X.; Thiel, M.; Ulliac, G.; Larger, L.; Jacquot, M.; Kadic, M.; Brunner, D. Three-dimensional waveguide interconnects for scalable integration of photonic neural networks. Optica 2020, 7, 640–646. [Google Scholar] [CrossRef]
- Torrijos-Morán, L.; Lisboa, B.D.; Soler, M.; Lechuga, L.M.; García-Rupérez, J. Integrated optical bimodal waveguide biosensors: Principles and applications. Results Opt. 2022, 9, 100285. [Google Scholar] [CrossRef]
- Kumaar, P.; Sivasubramanian, A. Optimization of the Transverse Electric Photonic Strip Waveguide Biosensor for Detecting Diabetes Mellitus from Bulk Sensitivity. J. Healthc. Eng. 2021, 2021, 6081570. [Google Scholar] [CrossRef]
- Voronin, K.V.; Stebunov, Y.V.; Voronov, A.A.; Arsenin, A.V.; Volkov, V.S. Vertically coupled plasmonic racetrack ring resonator for biosensor applications. Sensors 2020, 20, 203. [Google Scholar] [CrossRef]
- Leuermann, J.; Fernández-Gavela, A.; Torres-Cubillo, A.; Postigo, S.; Sánchez-Postigo, A.; Lechuga, L.M.; Halir, R.; Molina-Fernández, Í. Optimizing the limit of detection of waveguide-based interferometric biosensor devices. Sensors 2019, 19, 3671. [Google Scholar] [CrossRef]
- Luan, E.; Shoman, H.; Ratner, D.M.; Cheung, K.C.; Chrostowski, L. Silicon photonic biosensors using label-free detection. Sensors 2018, 18, 3519. [Google Scholar] [CrossRef]
- Niu, D.; Zhang, D.; Wang, L.; Lian, T.; Jiang, M.; Sun, X.; Li, Z.; Wang, X. High-resolution and fast-response optical waveguide temperature sensor using asymmetric Mach-Zehnder interferometer structure. Sens. Actuators A Phys. 2019, 299, 111615. [Google Scholar] [CrossRef]
- Jin, T.; Zhou, J.; Lin, P.T. Real-time and non-destructive hydrocarbon gas sensing using mid-infrared integrated photonic circuits. RSC Adv. 2020, 10, 7452–7459. [Google Scholar] [CrossRef]
- Hänsel, A.; Heck, M.J.R. Opportunities for photonic integrated circuits in optical gas sensors. J. Phys Photonics 2020, 2, 012002. [Google Scholar] [CrossRef]
- Consani, C.; Ranacher, C.; Tortschanoff, A.; Grille, T.; Irsigler, P.; Jakoby, B. Mid-infrared photonic gas sensing using a silicon waveguide and an integrated emitter. Sens. Actuators B Chem. 2018, 274, 60–65. [Google Scholar] [CrossRef]
- Lipka, T.; Moldenhauer, L.; Müller, J.; Trieu, H.K. Photonic integrated circuit components based on amorphous silicon-on-insulator technology. Photonics Res. 2016, 4, 126–134. [Google Scholar] [CrossRef]
- Bucio, T.D.; Lacava, C.; Clementi, M.; Faneca, J.; Skandalos, I.; Baldycheva, A.; Galli, M.; Debnath, K.; Petropoulos, P.; Gardes, F. Silicon Nitride Photonics for the Near-Infrared. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–13. [Google Scholar] [CrossRef]
- Wilmart, Q.; El Dirani, H.; Tyler, N.; Fowler, D.; Malhouitre, S.; Garcia, S.; Casale, M.; Kerdiles, S.; Hassan, K.; Monat, C.; et al. A versatile silicon-silicon nitride photonics platform for enhanced functionalities and applications. Appl. Sci. 2019, 9, 255. [Google Scholar] [CrossRef]
- Muñoz, P.; Micó, G.; Bru, L.A.; Pastor, D.; Pérez, D.; Doménech, J.D.; Fernández, J.; Baños, R.; Gargallo, B.; Alemany, R.; et al. Silicon nitride photonic integration platforms for visible, near-infrared and mid-infrared applications. Sensors 2017, 17, 2088. [Google Scholar] [CrossRef] [PubMed]
- Porcel, M.A.G.; Hinojosa, A.; Jans, H.; Stassen, A.; Goyvaerts, J.; Geuzebroek, D.; Geiselmann, M.; Dominguez, C.; Artundo, I. Silicon nitride photonic integration for visible light applications. Opt. Laser Technol. 2019, 112, 299–306. [Google Scholar] [CrossRef]
- Costa, J.; Almeida, D.; Fantoni, A.; Lourenço, P.; Vieira, M. Silicon Nitride Interferometers for Optical Sensing with Multi-micron Dimensions. J. Phys. Conf. Ser. 2022, 2407, 012005. [Google Scholar] [CrossRef]
- Almeida, D.; Costa, J.; Fantoni, A.; Vieira, M. Rib Waveguide Plasmonic Sensor for Lab-on-Chip Technology. IFIP Adv. Inf. Commun. Technol. 2022, 649, 187–196. [Google Scholar] [CrossRef]
- Costa, J.; Fantoni, A.; Lourenço, P.; Vieira, M. Optimisation of a plasmonic parallel waveguide sensor based on amorphous silicon compounds. In Proceedings of the Optical Sensing and Detection VI, Online, 6–10 April 2020; p. 11354. [Google Scholar] [CrossRef]
- Costa, J.; Almeida, D.; Fantoni, A.; Lourenço, P. Performance of an a-Si:H MMI multichannel beam splitter analyzed by computer simulation. In Proceedings of the Silicon Photonics XVI, Online, 5 March 2021; p. 1169106. [Google Scholar] [CrossRef]
- Domínguez Bucio, T.; Tarazona, A.; Khokhar, A.Z.; Mashanovich, G.Z.; Gardes, F.Y. Low temperature silicon nitride waveguides for multilayer platforms. In Proceedings of the Silicon Photonics and Photonic Integrated Circuits V, Brussels, Belgium, 13 May 2016; p. 9891. [Google Scholar] [CrossRef]
- Suda, S.; Tanizawa, K.; Sakakibara, Y.; Kamei, T.; Nakanishi, K.; Itoga, E.; Ogasawara, T.; Takei, R.; Kawashima, H.; Namiki, S.; et al. Pattern-effect-free all-optical wavelength conversion using a hydrogenated amorphous silicon waveguide with ultra-fast carrier decay. Opt. Lett. 2012, 37, 1382–1384. [Google Scholar] [CrossRef] [PubMed]
- Takei, R.; Manako, S.; Omoda, E.; Sakakibara, Y.; Mori, M.; Kamei, T. Sub-1 dB/cm submicrometer-scale amorphous silicon waveguide for backend on-chip optical interconnect. Opt. Express 2014, 22, 4779–4788. [Google Scholar] [CrossRef]
- Oo, S.Z.; Tarazona, A.; Khokhar, A.Z.; Petra, R.; Franz, Y.; Mashanovich, G.Z.; Reed, G.T.; Peacock, A.C.; Chong, H.M.H. Hot-wire chemical vapor deposition low-loss hydrogenated amorphous silicon waveguides for silicon photonic devices. Photonics Res. 2019, 7, 193–200. [Google Scholar] [CrossRef]
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips [Invited]. Photonics Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Son, G.; Han, S.; Park, J.; Kwon, K.; Yu, K. High-efficiency broadband light coupling between optical fibers and photonic integrated circuits. Nanophotonics 2018, 7, 1845–1864. [Google Scholar] [CrossRef]
- Sethi, P.; Kallega, R.; Haldar, A.; Selvaraja, S.K. Compact broadband low-loss taper for coupling to a silicon nitride photonic wire. Opt. Lett. 2018, 43, 3433–3436. [Google Scholar] [CrossRef]
- Tiecke, T.G.; Nayak, K.P.; Thompson, J.D.; Peyronel, T.; de Leon, N.P.; Vuletić, V.; Lukin, M.D. Efficient fiber-optical interface for nanophotonic devices. Optica 2015, 2, 70–75. [Google Scholar] [CrossRef]
- Fang, N.; Yang, Z.; Wu, A.; Chen, J.; Zhang, M.; Zou, S.; Wang, X. Three-dimensional tapered spot-size converter based on (111) silicon-on-insulator. IEEE Photonics Technol. Lett. 2009, 21, 820–822. [Google Scholar] [CrossRef]
- Synopsys Inc. RSoft Photonic Device Tools. Available online: https://www.synopsys.com/photonic-solutions/rsoft-photonic-device-tools/rsoft-products.html (accessed on 20 August 2024).
- Almeida, D.; Rossi, M.; Lourenço, P.J.P.S.; Fantoni, A.; Costa, J.; Vieira, M. Amorphous silicon grating couplers based on random and quadratic variation of the refractive index. In Proceedings of the SPIE 12880, Physics and Simulation of Optoelectronic Devices XXXII, 128800J, San Francisco, CA, USA, 11 March 2024. [Google Scholar] [CrossRef]
- Zhou, X.; Tsang, H.K. Photolithography Fabricated Sub-Decibel High-Efficiency Silicon Waveguide Grating Coupler. IEEE Photonics Technol. Lett. 2023, 35, 43–46. [Google Scholar] [CrossRef]
- Vitali, V.; Domínguez Bucio, T.; Lacava, C.; Marchetti, R.; Mastronardi, L.; Rutirawut, T.; Churchill, G.; Faneca, J.; Gates, J.C.; Gardes, F.; et al. High-efficiency reflector-less dual-level silicon photonic grating coupler. Photonics Res. 2023, 11, 1275–1283. [Google Scholar] [CrossRef]
- Lourenço, P.; Fantoni, A.; Costa, J.; Fernandes, M. Design and optimization of a waveguide/fibre coupler in the visible range. In Proceedings of the Physics and Simulation of Optoelectronic Devices XXIX, Online, 5 March 2021; p. 1168019. [Google Scholar] [CrossRef]
- Ong, E.W.; Fahrenkopf, N.M.; Coolbaugh, D.D. SiNx bilayer grating coupler for photonic systems. OSA Contin. 2018, 1, 13–25. [Google Scholar] [CrossRef]
- Yoshida, T.; Omoda, E.; Atsumi, Y.; Nishi, T.; Tajima, S.; Miura, N.; Mori, M.; Sakakibara, Y. Vertically Curved Si Waveguide Coupler with Low Loss and Flat Wavelength Window. J. Light. Technol. 2016, 34, 1567–1571. [Google Scholar] [CrossRef]
- Mu, X.; Wu, S.; Cheng, L.; Fu, H.Y. Edge couplers in silicon photonic integrated circuits: A review. Appl. Sci. 2020, 10, 1538. [Google Scholar] [CrossRef]
- Sure, A.; Dillon, T.; Murakowski, J.; Lin, C.; Pustai, D.; Prather, D. Fabrication and characterization of three-dimensional silicon tapers. Opt. Express 2003, 11, 3555–3561. [Google Scholar] [CrossRef]
- Shiraishi, K.; Yoda, H.; Ohshima, A.; Ikedo, H.; Tsai, C.S. A silicon-based spot-size converter between single-mode fibers and Si-wire waveguides using cascaded tapers. Appl. Phys. Lett. 2007, 91, 141120. [Google Scholar] [CrossRef]
- Fritze, M.; Knecht, J.; Bozler, C.; Keast, C.; Fijol, J.; Jacobson, S.; Keating, P.; LeBlanc, J.; Fike, E.; Kessler, B.; et al. Fabrication of three-dimensional mode converters for silicon-based integrated optics. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2003, 21, 2897–2902. [Google Scholar] [CrossRef]
- Cheng, L.; Mao, S.; Li, Z.; Han, Y.; Fu, H.Y. Grating Couplers on Silicon Photonics: Design Principles, Emerging Trends and Practical Issues. Micromachines 2022, 13, 606. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, Y.; Shao, Z.; Liu, L.; Zhou, L.; Yang, C.; Chen, Y.; Yu, S. High-efficiency wideband SiN_x-on-SOI grating coupler with low fabrication complexity. Opt. Lett. 2017, 42, 3391–3394. [Google Scholar] [CrossRef]
- Marchetti, R.; Lacava, C.; Khokhar, A.; Chen, X.; Cristiani, I.; Richardson, D.J.; Reed, G.T.; Petropoulos, P.; Minzioni, P. High-efficiency grating-couplers: Demonstration of a new design strategy. Sci. Rep. 2017, 7, 16670. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, S. Design Principles of Apodized Grating Couplers. J. Light. Technol. 2020, 38, 4435–4446. [Google Scholar] [CrossRef]
- Sacher, W.D.; Huang, Y.; Ding, L.; Taylor, B.J.F.; Jayatilleka, H.; Lo, G.-Q.; Poon, J.K.S. Wide bandwidth and high coupling efficiency Si3N4-on-SOI dual-level grating coupler. Opt. Express 2014, 22, 10938–10947. [Google Scholar] [CrossRef]
- Hong, J.; Spring, A.M.; Qiu, F.; Yokoyama, S. A high efficiency silicon nitride waveguide grating coupler with a multilayer bottom reflector. Sci. Rep. 2019, 9, 12988. [Google Scholar] [CrossRef]
- Singh, R.; Singh, R.R.; Priye, V. Parametric optimization of fiber to waveguide coupler using Bragg gratings. Opt. Quantum Electron. 2019, 51, 256. [Google Scholar] [CrossRef]
- Tan, H.; Liu, W.; Zhang, Y.; Yin, S.; Dai, D.; Gao, S.; Guan, X. High-Efficiency Broadband Grating Couplers for Silicon Hybrid Plasmonic Waveguides. Photonics 2022, 9, 550. [Google Scholar] [CrossRef]
- Nambiar, S.; Ranganath, P.; Kallega, R.; Selvaraja, S.K. High efficiency DBR assisted grating chirp generators for silicon nitride fiber-chip coupling. Sci. Rep. 2019, 9, 18821. [Google Scholar] [CrossRef]
- Ding, Y.; Peucheret, C.; Ou, H.; Yvind, K. Fully etched apodized grating coupler on the SOI platform with −0.58 dB coupling efficiency. Opt. Lett. 2014, 39, 5348–5350. [Google Scholar] [CrossRef] [PubMed]
- Romero-García, S.; Merget, F.; Zhong, F.; Finkelstein, H.; Witzens, J. Visible wavelength silicon nitride focusing grating coupler with AlCu/TiN reflector. Opt. Lett. 2013, 38, 2521–2523. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, J.; Xie, W.; Tian, B.; Li, Y.; Brainis, E.; Jiao, Y.; Van Thourhout, D. Ultra-compact silicon nitride grating coupler for microscopy systems. Opt. Express 2017, 25, 33297–33304. [Google Scholar] [CrossRef]
- Lin, T.; Yang, H.; Li, L.; Yun, B.; Hu, G.; Li, S.; Yu, W.; Ma, X.; Liang, X.; Cui, Y. Ultra-broadband and highly efficient silicon nitride bi-layer grating couplers. Opt. Commun. 2023, 530, 129209. [Google Scholar] [CrossRef]
- Saktioto; Zairmi, Y.; Veriyanti, V.; Candra, W.; Syahputra, R.F.; Soerbakti, Y.; Asyana, V.; Irawan, D.; Okfalisa; Hairi, H.; et al. Birefringence and Polarization Mode Dispersion Phenomena of Commercial Optical Fiber in Telecommunication Networks. J. Phys. Conf. Ser. 2020, 1655, 012160. [Google Scholar] [CrossRef]
- Corning Inc. Corning® SMF-28TM Optical Fiber. Available online: https://brightspotcdn.byu.edu/c5/a3/eaf794ab47889d39559a4fac1e68/smf28.pdf (accessed on 20 August 2024).
- Fantoni, A.; Lourenco, P.; Vieira, M. A model for the refractive index of amorphous silicon for FDTD simulation of photonics waveguides. In Proceedings of the 2017 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Copenhagen, Denmark, 24–28 July 2017; pp. 167–168. [Google Scholar] [CrossRef]
- Vitali, V.; Lacava, C.; Domínguez Bucio, T.; Gardes, F.Y.; Petropoulos, P. Highly efficient dual-level grating couplers for silicon nitride photonics. Sci. Rep. 2022, 12, 15436. [Google Scholar] [CrossRef]
- Hong, J.; Qiu, F.; Spring, A.M.; Yokoyama, S. Silicon waveguide grating coupler based on a segmented grating structure. Appl. Opt. 2018, 57, 3301–3305. [Google Scholar] [CrossRef]
- Van Laere, F.; Claes, T.; Schrauwen, J.; Scheerlinck, S.; Bogaerts, W.; Taillaert, D.; O’Faolain, L.; Van Thourhout, D.; Baets, R. Compact focusing grating couplers for silicon-on-insulator integrated circuits. IEEE Photonics Technol. Lett. 2007, 19, 1919–1921. [Google Scholar] [CrossRef]
- Zhang, Z.; Shan, X.; Huang, B.; Zhang, Z.; Cheng, C.; Bai, B.; Gao, T.; Xu, X.; Zhang, L.; Chen, H. Efficiency enhanced grating coupler for perfectly vertical fiber-to-chip coupling. Materials 2020, 13, 2681. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; He, Y. Resolution technology of lithography machine. J. Phys. Conf. Ser. 2022, 2221, 012041. [Google Scholar] [CrossRef]











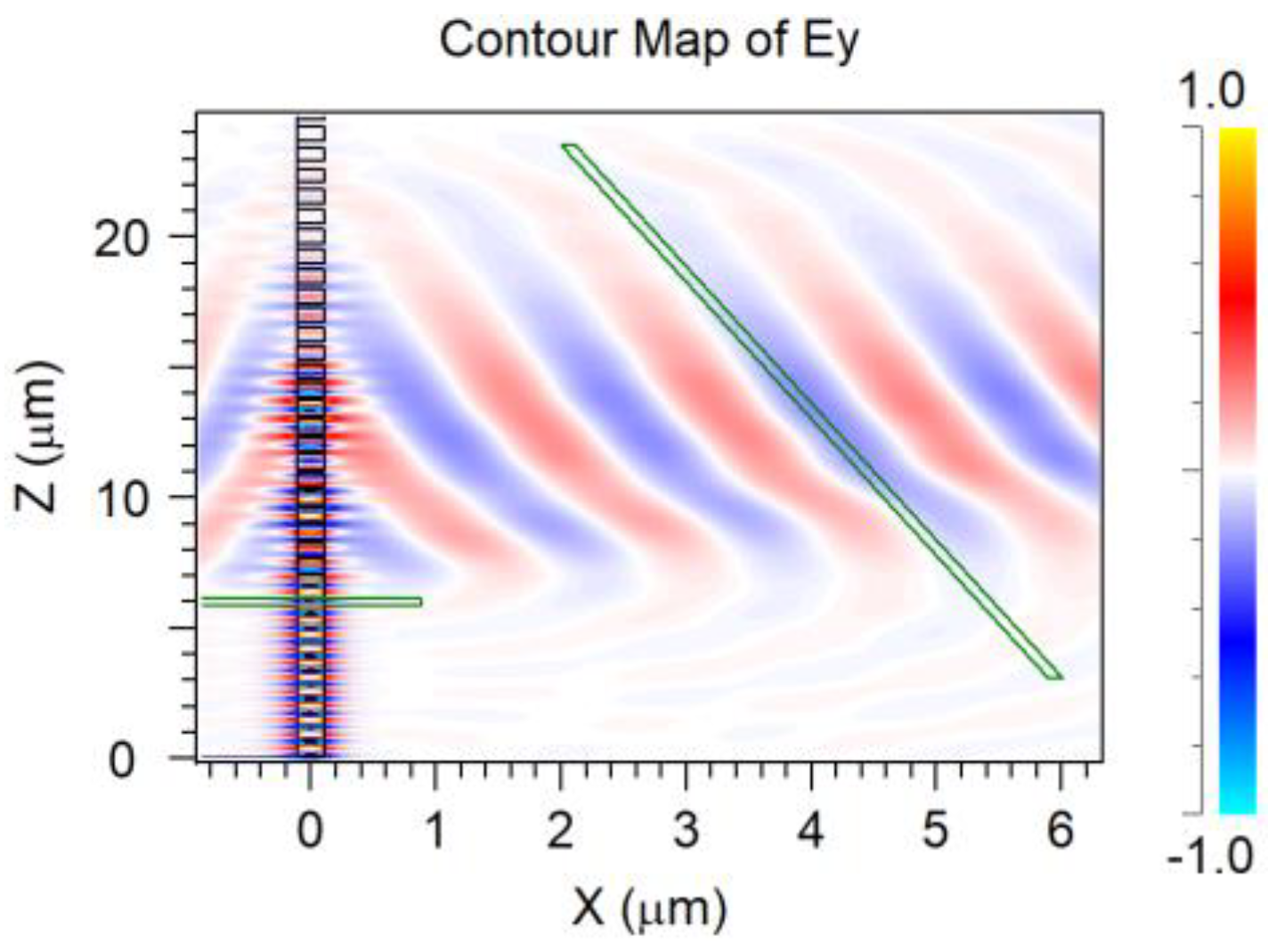
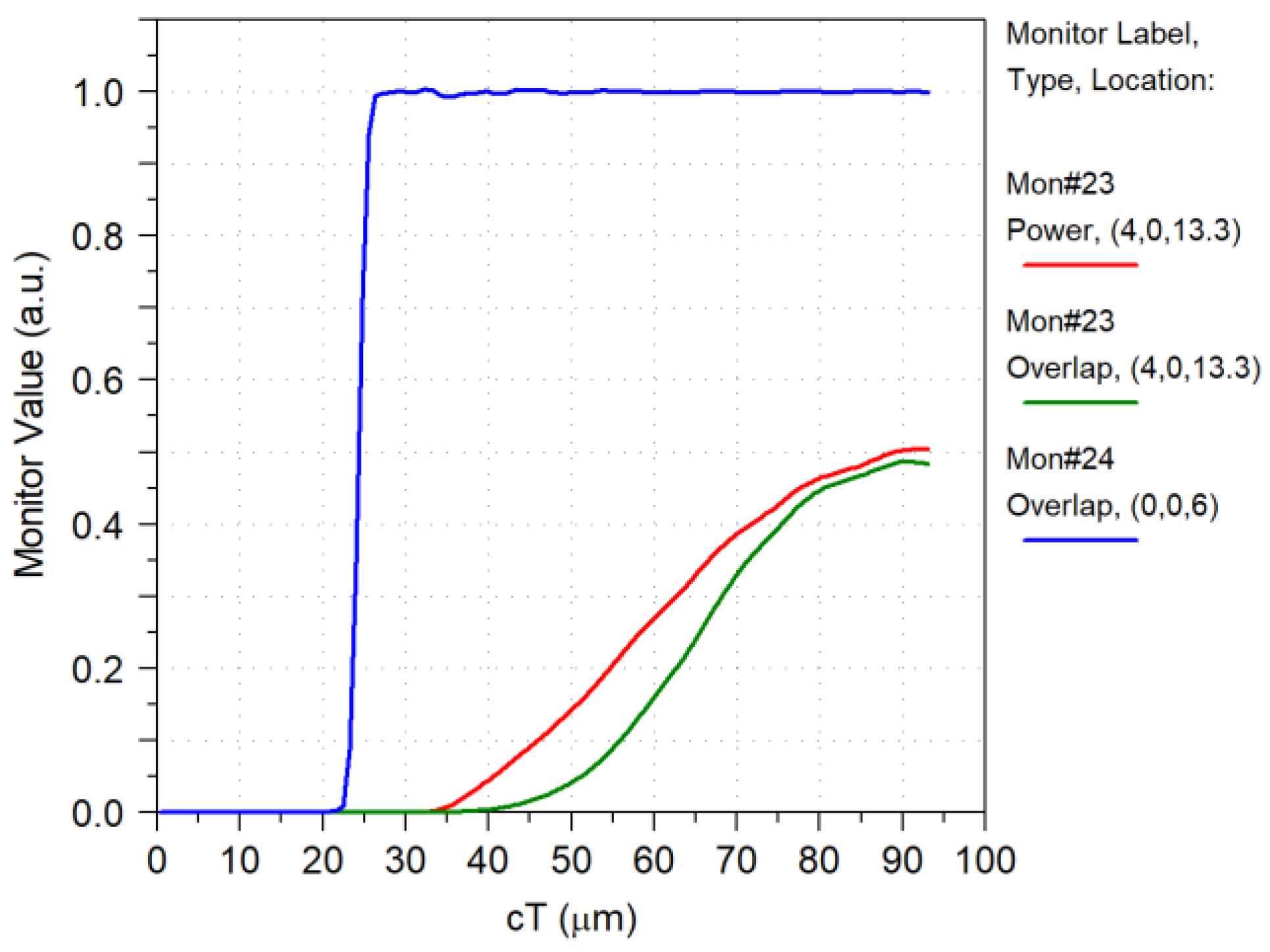
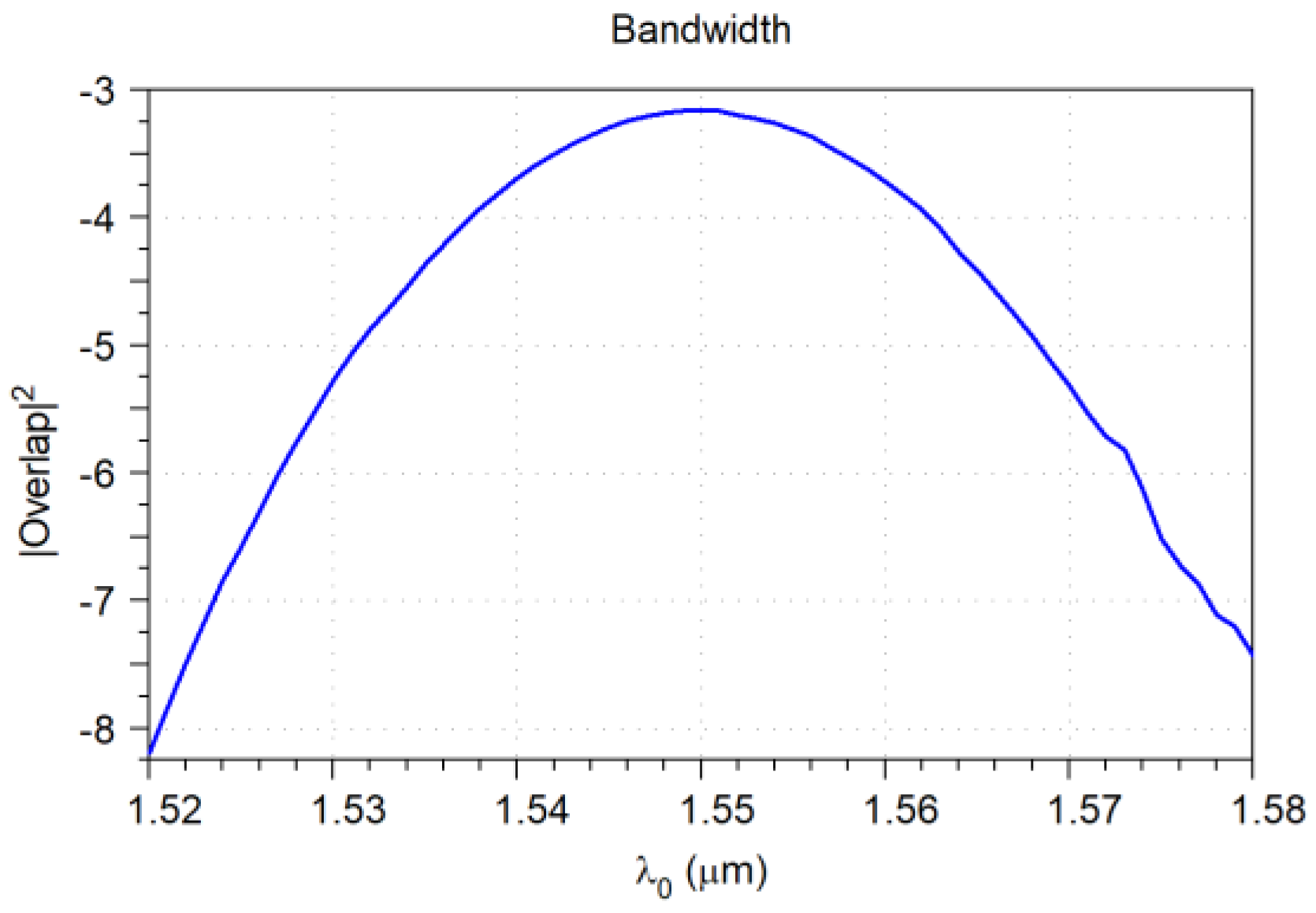
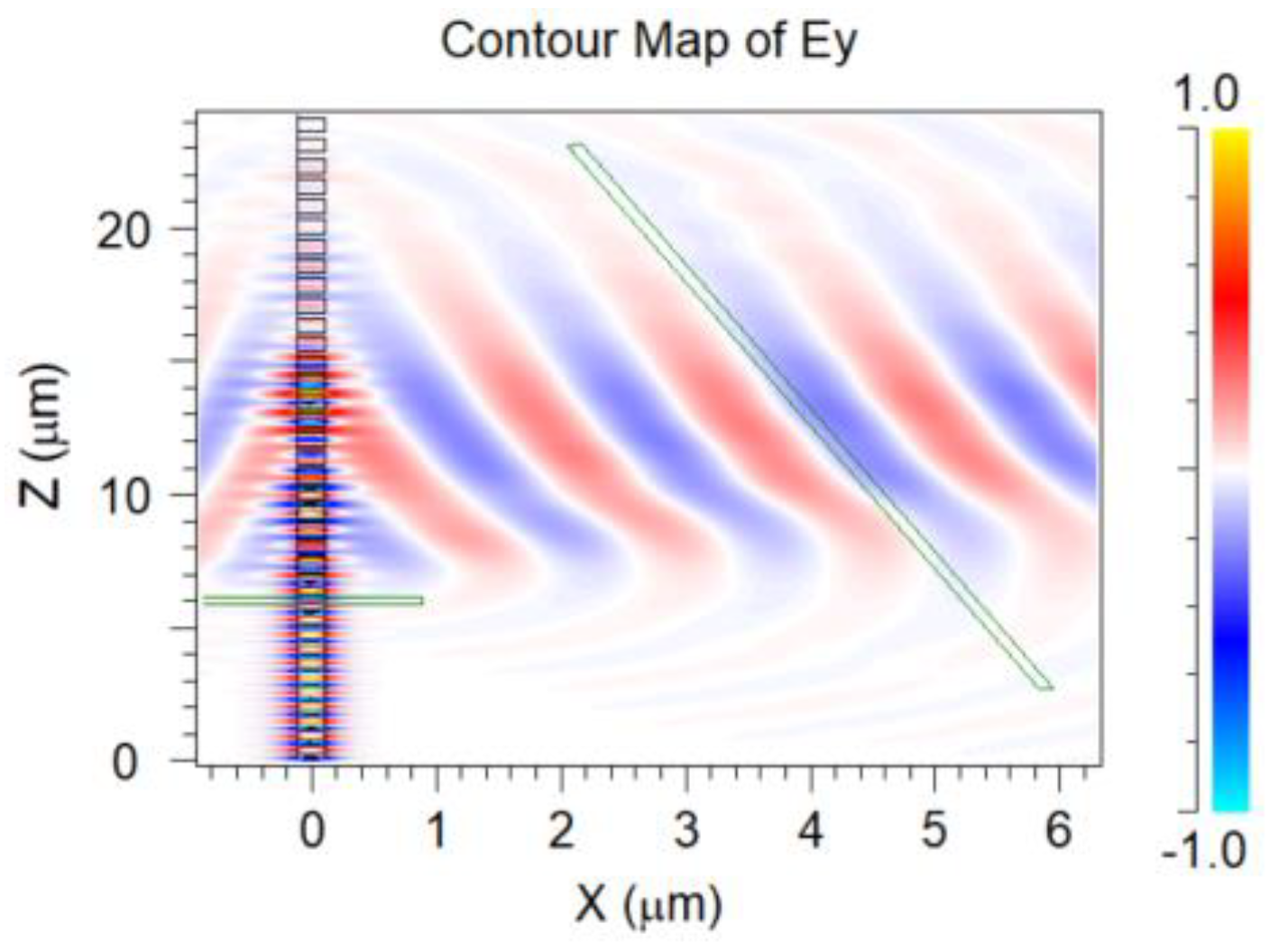

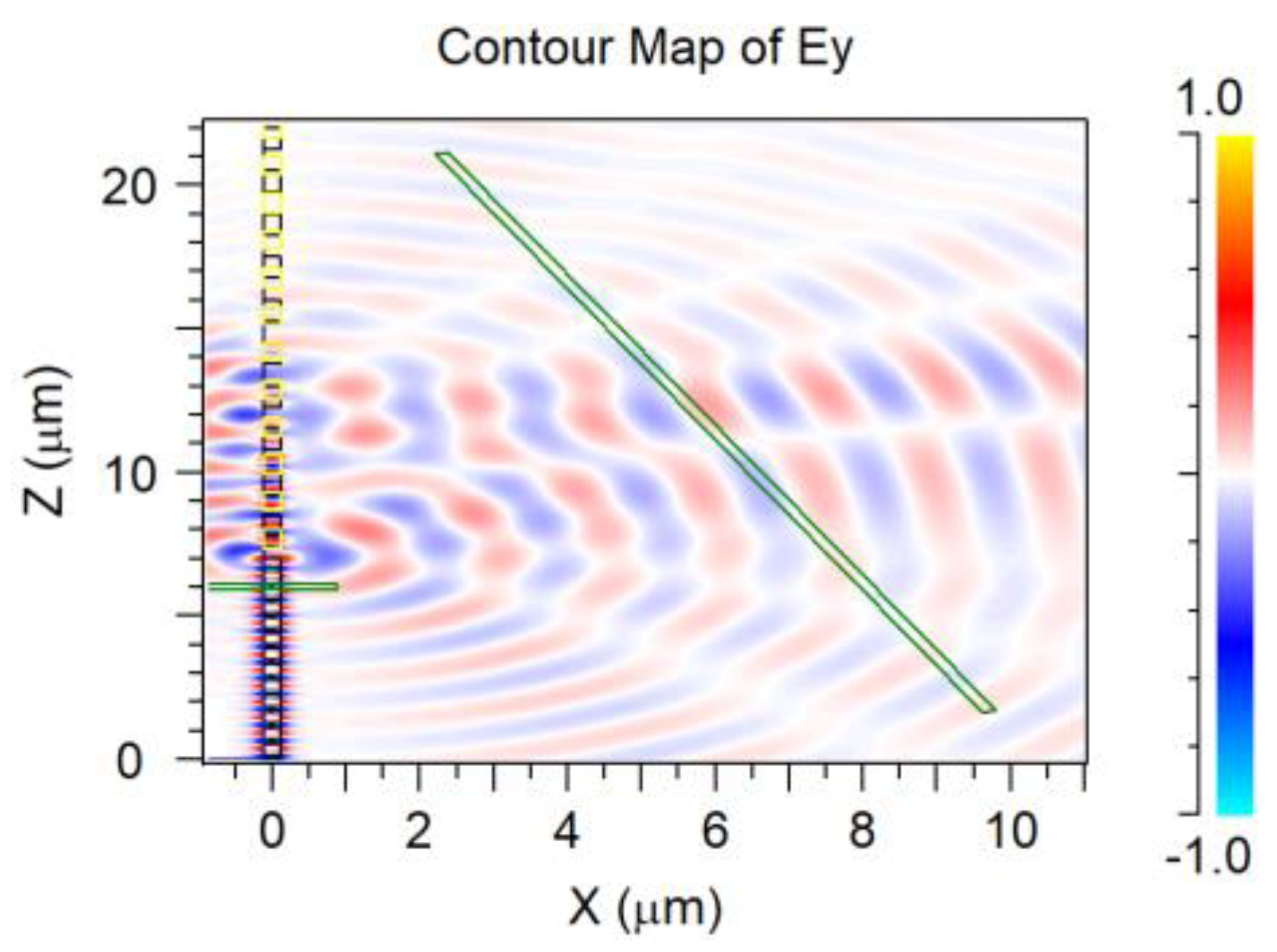
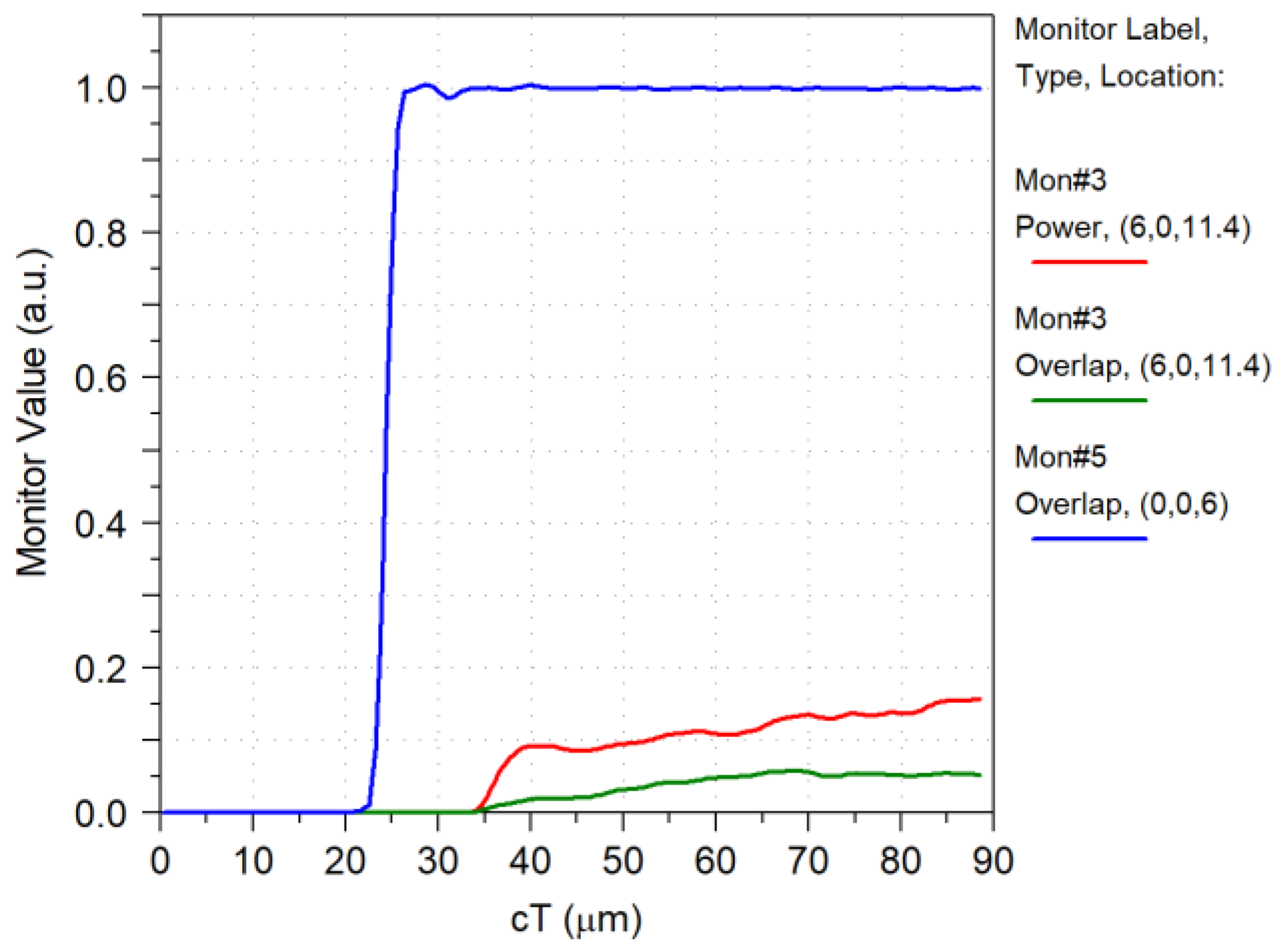
| Parameter | Value |
|---|---|
| Attenuation | ≤0.22 dB/km |
| Mode Field Diameter (MFD) | 10.4 ± 0.8 µm |
| Core Diameter | 8.2 µm |
| Cladding Diameter | 125 ± 0.7 µm |
| Coating Diameter | 245 ± 5 µm |
| Effective Refractive Index (Neff at rated MFD) | 1.4682 |
| Refractive Index Difference | 0.36% |
| Segment Number | Λ [nm] | F (LE/Λ) | Segment Number | Λ [nm] | F (LE/Λ) |
|---|---|---|---|---|---|
| 1 | 647 | 0.900 | 15 | 732 | 0.750 |
| 2 | 652 | 0.890 | 16 | 739 | 0.738 |
| 3 | 658 | 0.880 | 17 | 747 | 0.727 |
| 4 | 663 | 0.869 | 18 | 754 | 0.715 |
| 5 | 668 | 0.859 | 19 | 763 | 0.703 |
| 6 | 674 | 0.848 | 20 | 771 | 0.691 |
| 7 | 680 | 0.838 | 21 | 779 | 0.679 |
| 8 | 686 | 0.827 | 22 | 788 | 0.667 |
| 9 | 692 | 0.816 | 23 | 798 | 0.654 |
| 10 | 698 | 0.805 | 24 | 807 | 0.642 |
| 11 | 704 | 0.795 | 25 | 817 | 0.629 |
| 12 | 711 | 0.783 | 26 | 827 | 0.616 |
| 13 | 718 | 0.772 | 27 | 838 | 0.603 |
| 14 | 725 | 0.761 | 28 | 849 | 0.590 |
| Segment Number | Λ [nm] | F (LE/Λ) | Segment Number | Λ [nm] | F (LE/Λ) |
|---|---|---|---|---|---|
| 1 | 647 | 0.900 | 15 | 734 | 0.746 |
| 2 | 654 | 0.886 | 16 | 739 | 0.738 |
| 3 | 661 | 0.873 | 17 | 744 | 0.731 |
| 4 | 668 | 0.860 | 18 | 748 | 0.725 |
| 5 | 674 | 0.848 | 19 | 752 | 0.719 |
| 6 | 681 | 0.836 | 20 | 755 | 0.713 |
| 7 | 687 | 0.824 | 21 | 759 | 0.709 |
| 8 | 694 | 0.813 | 22 | 761 | 0.705 |
| 9 | 700 | 0.802 | 23 | 764 | 0.701 |
| 10 | 706 | 0.791 | 24 | 766 | 0.698 |
| 11 | 712 | 0.781 | 25 | 767 | 0.696 |
| 12 | 718 | 0.772 | 26 | 769 | 0.694 |
| 13 | 724 | 0.763 | 27 | 769 | 0.693 |
| 14 | 729 | 0.754 | 28 | 769 | 0.693 |
| GC Design | GC Material | GC Feature Size * | Coupling Efficiency | −1 dB Bandwidth | Bottom Reflector | Required Masks ** | Reference |
|---|---|---|---|---|---|---|---|
| Silicon Nitride Top Layer | Si | 266 nm | −1.7 dB | 64 nm | No | 3 | [67] |
| Fully Etched Apodized | Si | 100 nm | −0.6 dB | (71 nm, −3 dB) | Yes, Al layer | 1 | [57] |
| Shift-pattern Overlay | Si/Poly-Si | 171 nm | −0.9 dB | 35 nm | No | 3 | [39] |
| Dual-level GC | Si | 60 nm | −0.8 dB | 31.3 nm | No | 3 | [40] |
| Bilayer GC | Si3N4 | N/A | −1.0 dB | 117 nm | Yes, DBR | 2 | [60] |
| Dual-level GC | Si3N4/Si | 200 nm | −1.3 dB | 80 nm | Yes, GC | 2 | [52] |
| Chirped GC | Si | 26 nm | −0.1 dB | (35 nm, −3 dB) | Yes, DBR | 2 | [54] |
| Multilayer Bottom Reflector | SiNx | 86 nm | −1.8 dB | 52.5 nm | Yes, DBR | 1 | [53] |
| Bilayer GC | SiNx | N/A | −2.7 dB | 47.9 nm | No | 2 | [42] |
| Compact Focusing GC | Si | 315 nm | −7.0 dB *** | 41 nm | No | 2 | [66] |
| Uniform GC | Si | 270 nm | −5.8 dB | (48.5 nm, −3 dB) | No | 2 | [65] |
| Segmented GC | Si | 190 nm | −2.9 dB | (71.4 nm, −3 dB) | No | 2 | [65] |
| Non-optimized GC | a-Si:H | 510 nm | −9.7 dB | N/A | No | 1 | This work |
| Fill factor > 50% | a-Si:H | 120 nm | −4.3 dB | 25 nm | No | 1 | This work |
| Linear R.I. Variation | a-Si:H | 60 nm | −3.1 dB | 26 nm | No | 1 | This work |
| Quadratic R.I. Variation | a-Si:H | 60 nm | −2.8 dB | 25 nm | No | 1 | This work |
| Overlapped Micrometric | a-Si:H | 750 nm | −7.5 dB | 22 nm | No | 2 | This work |
| Random Distribution | a-Si:H | 650 nm | −12.8 dB | N/A | No | 2 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, D.; Lourenço, P.; Fantoni, A.; Costa, J.; Vieira, M. Grating Coupler Design for Low-Cost Fabrication in Amorphous Silicon Photonic Integrated Circuits. Photonics 2024, 11, 783. https://doi.org/10.3390/photonics11090783
Almeida D, Lourenço P, Fantoni A, Costa J, Vieira M. Grating Coupler Design for Low-Cost Fabrication in Amorphous Silicon Photonic Integrated Circuits. Photonics. 2024; 11(9):783. https://doi.org/10.3390/photonics11090783
Chicago/Turabian StyleAlmeida, Daniel, Paulo Lourenço, Alessandro Fantoni, João Costa, and Manuela Vieira. 2024. "Grating Coupler Design for Low-Cost Fabrication in Amorphous Silicon Photonic Integrated Circuits" Photonics 11, no. 9: 783. https://doi.org/10.3390/photonics11090783
APA StyleAlmeida, D., Lourenço, P., Fantoni, A., Costa, J., & Vieira, M. (2024). Grating Coupler Design for Low-Cost Fabrication in Amorphous Silicon Photonic Integrated Circuits. Photonics, 11(9), 783. https://doi.org/10.3390/photonics11090783






