Transmission Characteristics Analysis of a Twin-Waveguide Cavity
Abstract
1. Introduction
2. Simulation
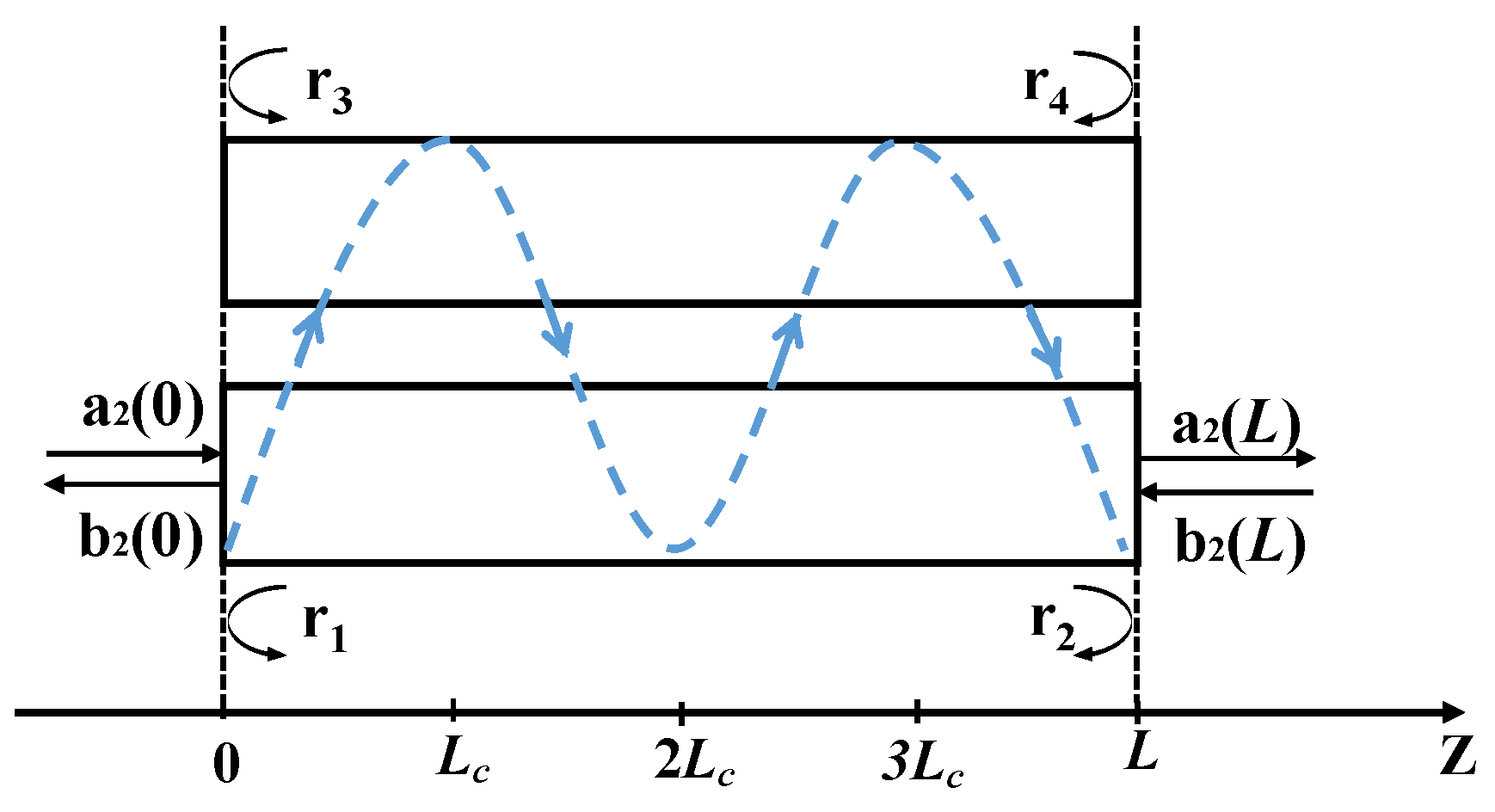
2.1. Transmission Model
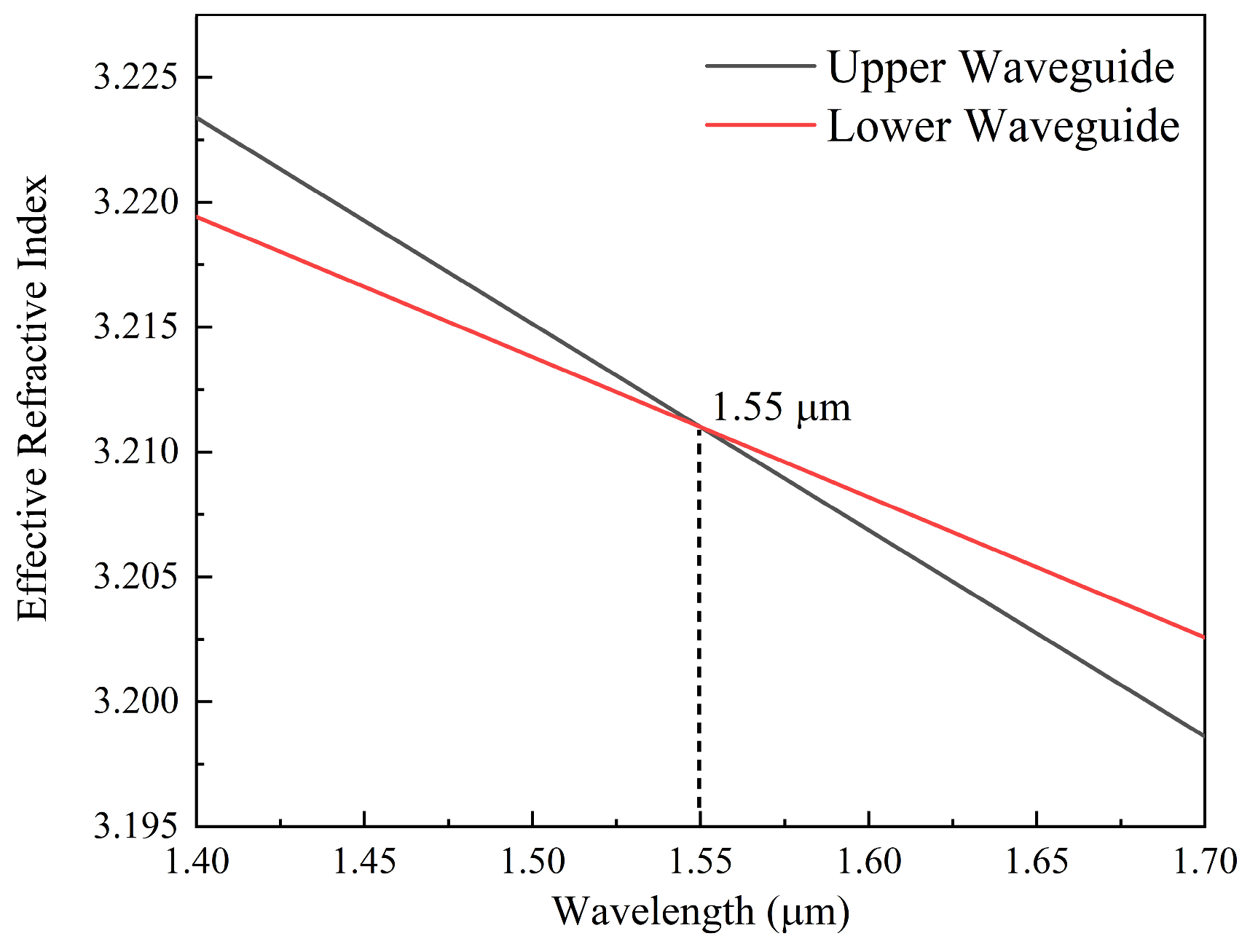
2.2. Parameters
3. Results and Discussion
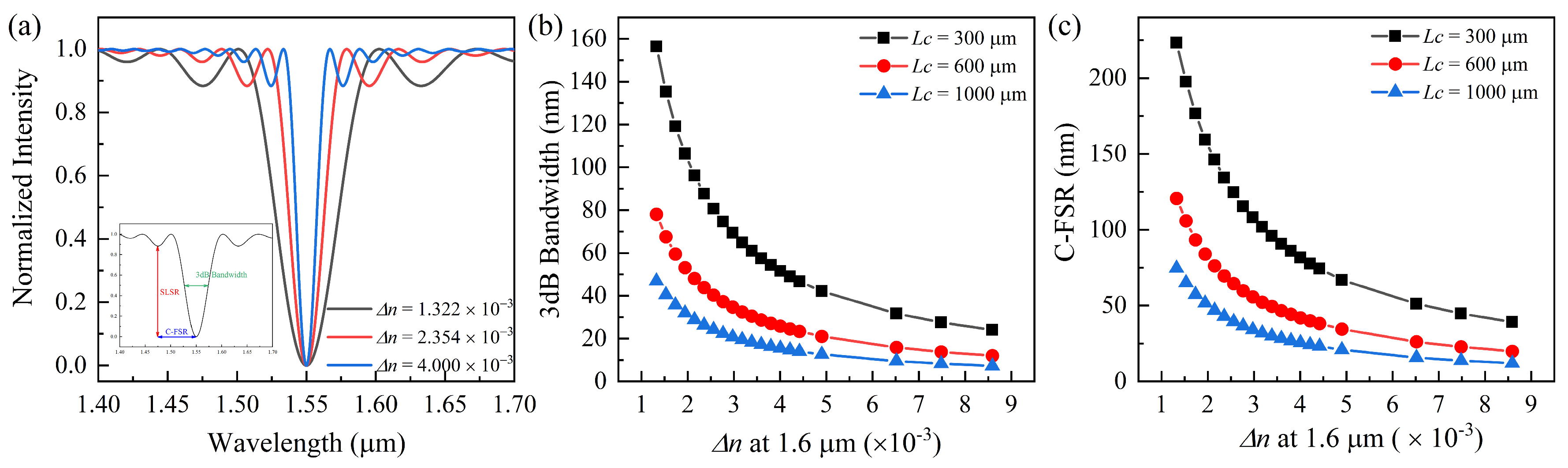
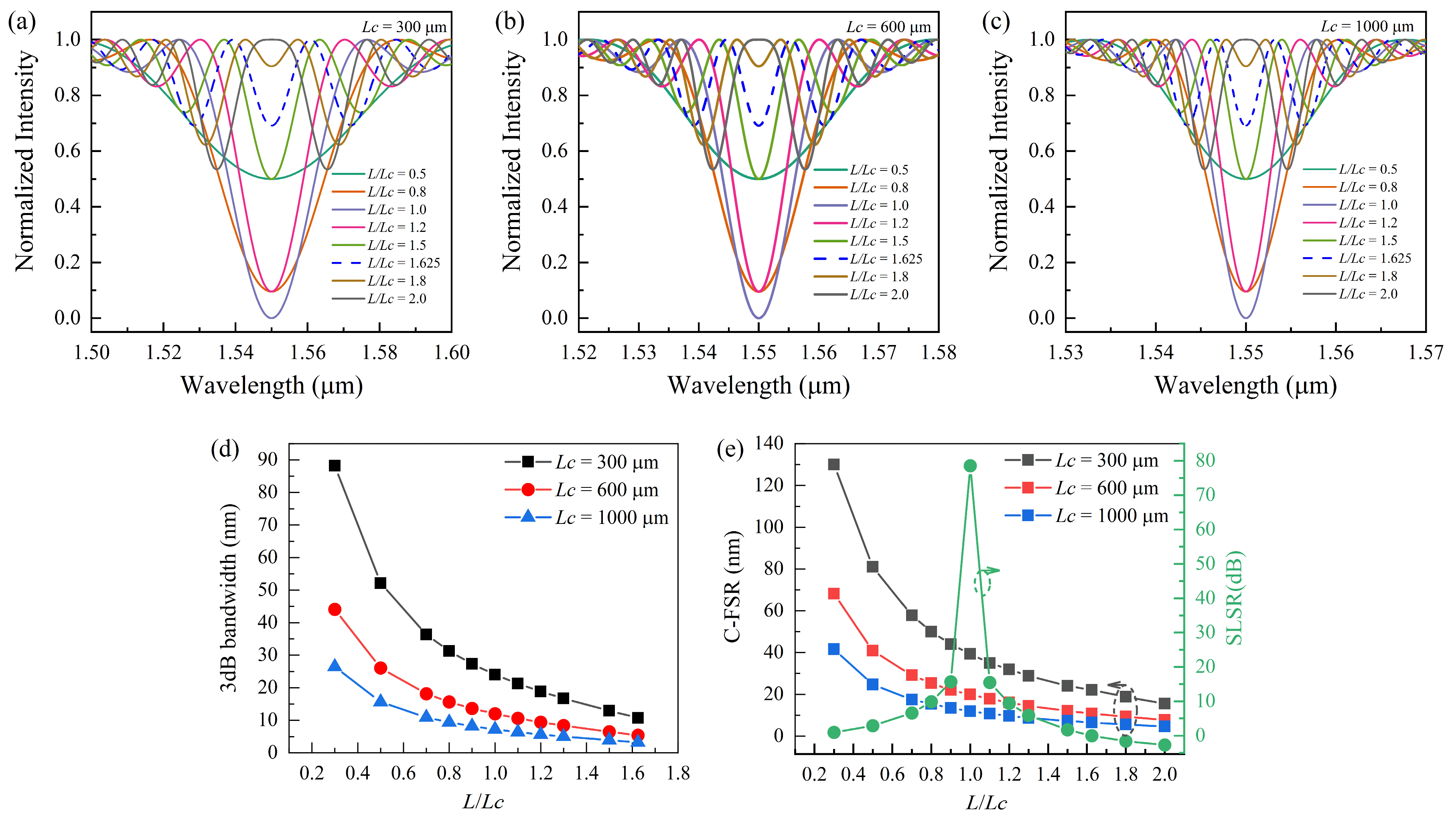
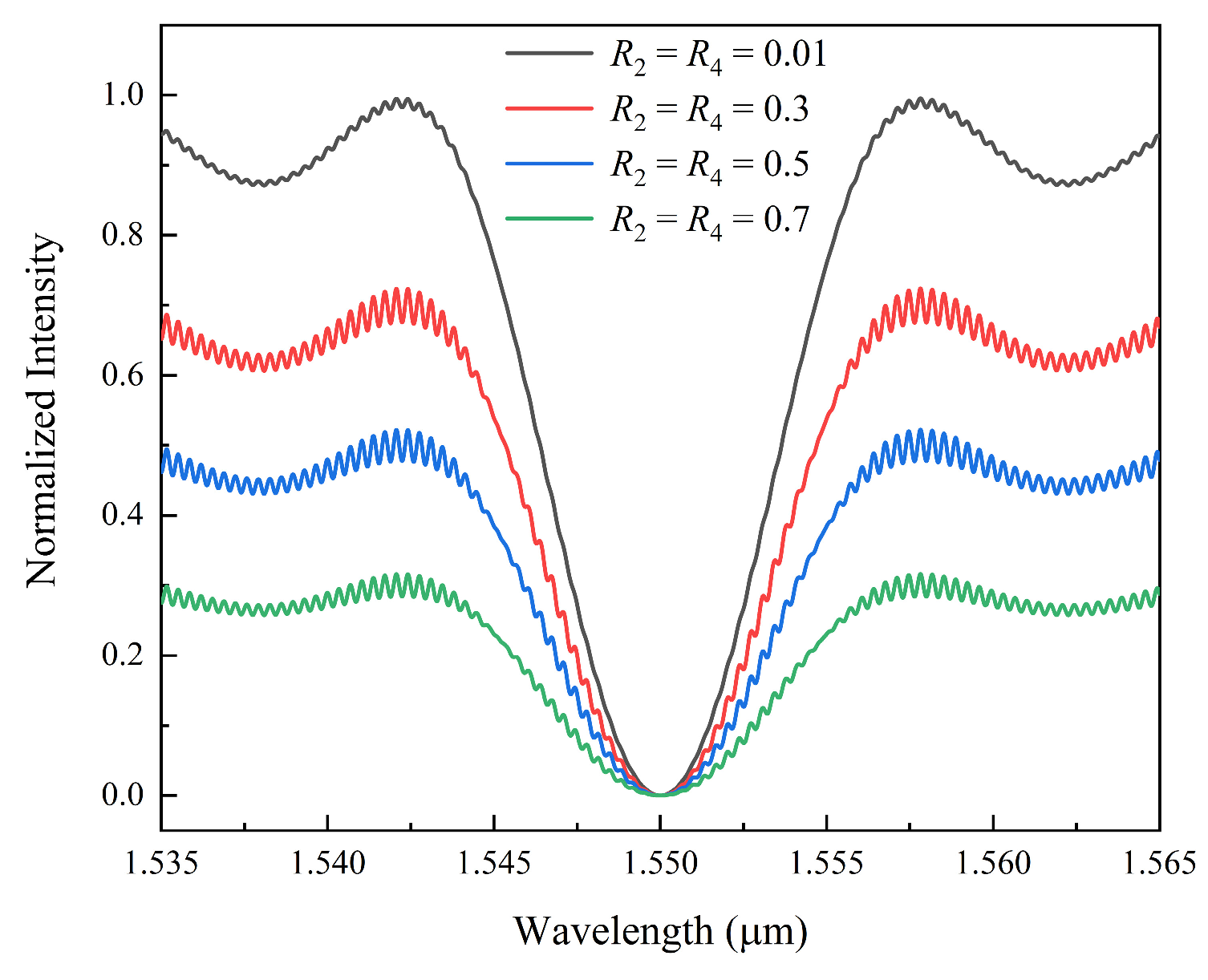
3.1. Without Facet Reflection
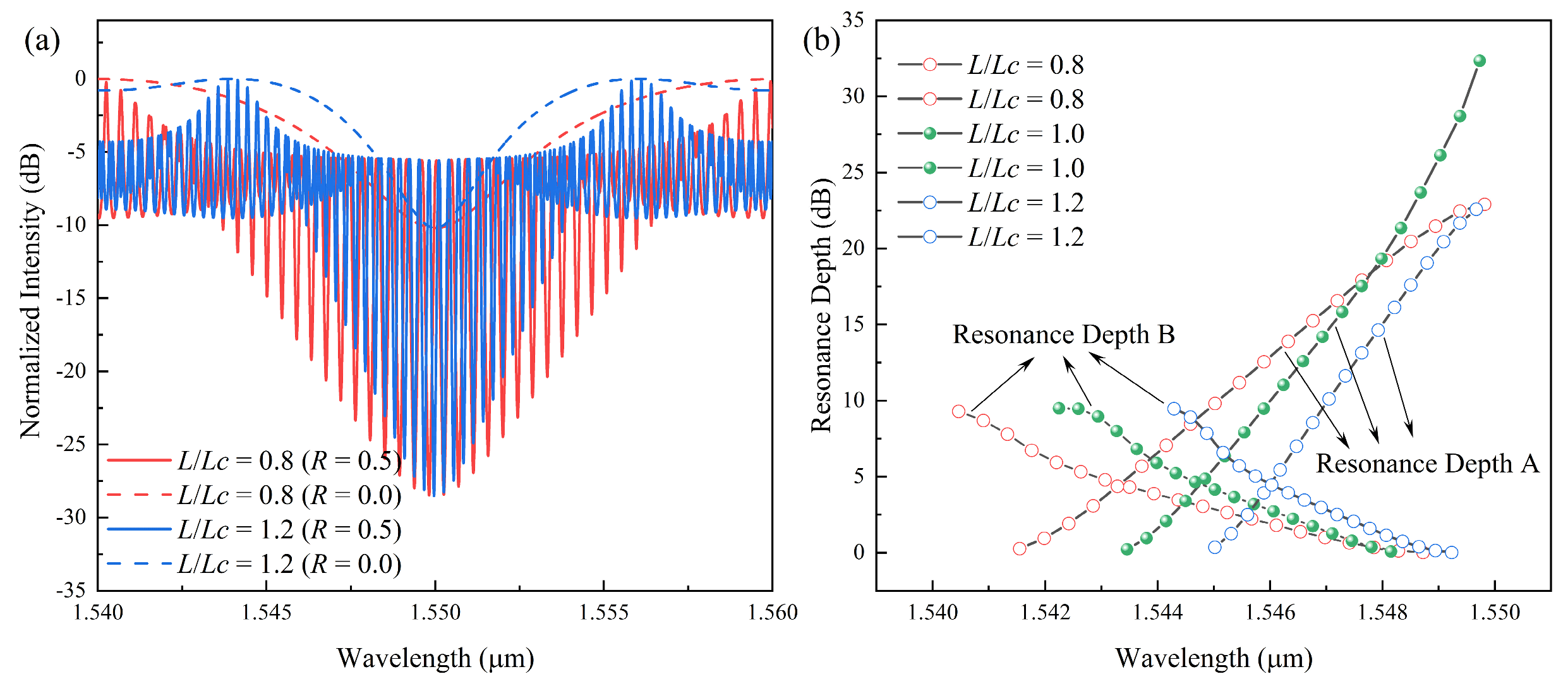
3.2. With Facet Reflection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, X.-Y.; Jin, X.-M. Integrated photonic computing beyond the von Neumann architecture. Photonics 2023, 10, 1027–1036. [Google Scholar] [CrossRef]
- Chen, Q.; Hu, X.; Wen, L.; Yu, Y.; Cumming, D.R.S. Nanophotonic image sensors. Small 2016, 12, 4922–4935. [Google Scholar] [CrossRef] [PubMed]
- Chovan, J.; Uherek, F. Photonic integrated circuits for communication systems. Radioengineering 2018, 27, 357–363. [Google Scholar] [CrossRef]
- Paraiso, T.K.; Roger, T.; Marangon, D.G.; Marco, I.D.; Sanzaro, M.; Woodward, R.I.W.; Dynes, J.F.; Yuan, Z.L.; Shields, A.J. A photonic integrated quantum secure communication system. Nat. Photonics 2021, 15, 850–856. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.A.R.; Ram-Mohan, L.R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Xia, F.; Menon, V.M.; Forrest, S.R. Photonic integration using asymmetric twin-waveguide (ATG) technology: Part I-concepts and theory. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 17–29. [Google Scholar] [CrossRef]
- Xiao, F.; Han, Q.; Ye, H.; Wang, S.; Lu, A.Q.; Xiao, F. Butt-joint regrowth method by MOCVD for integration of evanescent wave coupled photodetector and multi-quantum well semiconductor optical amplifier. Chin. Phys. 2022, 31, 048101. [Google Scholar] [CrossRef]
- Wang, B.; Zeng, Y.; Song, Y.; Wang, Y.; Liang, L.; Qin, L.; Zhang, J.-W.; Jia, P.; Lei, Y.-X.; Qiu, C.; et al. Principles of Selective Area Epitaxy and Applications in III–V Semiconductor Lasers Using MOCVD: A Review. Crystals 2022, 12, 1011. [Google Scholar] [CrossRef]
- Malik, D.; Das, U. A novel highly-efficient compact 3D-spot size converter using quantum-well intermixing. J. Light. Technol. 2022, 40, 5615–5621. [Google Scholar] [CrossRef]
- Kazi, M.; Ghosh, S.; Sugiyama, M.; Nakano, Y. Offset-Quantum-Well-Based Integrated Stokes Vector Modulator on InP. IEEE Photonics Technol. Lett. 2019, 31, 1233–1236. [Google Scholar] [CrossRef]
- Jiao, Y.-Q.; van der Tol, J.; Pogoretskii, V.; van Engelen, J.; Abbas Kashi, A.; Reniers, A.; Wang, Y.; Zhao, X.R.; Yao, W.M.; Liu, T.R.; et al. Indium phosphide membrane nanophotonic integrated circuits on silicon. Phys. Status Solidi A 2020, 217, 1900606. [Google Scholar] [CrossRef]
- Hou, L.; Marsh, J. Photonic Integrated Circuits: From Techniques to Devices. In Proceedings of the 2019 Asia Communications and Photonics Conference (ACP 2019), Chengdu, China, 2–5 November 2019. [Google Scholar]
- Wang, H.-S.; Li, C.-Q.; Forrest, S. A fully integratable 1.55-μm wavelength, continuously tunable asymmetric twin-waveguide distributed Bragg reflector laser. IEEE Photonics Technol. Lett. 2003, 15, 1189–1191. [Google Scholar] [CrossRef]
- Gokhale, M.; Xia, F.-N.; Thomson, J.; Studenkov, P.; Forrest, S. High quantum efficiency, 40 GHz InGaAs twin waveguide PIN photodetectors. In Proceedings of the Annual Meeting of the IEEE Lasers and Electro-Optics Society (LEOS 2001), San Diego, CA, USA, 12–13 November 2001; pp. 885–886. [Google Scholar] [CrossRef]
- Galarza, M.; Thourhout, D.V.; Baets, R.; Lopez-Amo, M. Compact and highly-efficient polarization independent vertical resonant couplers for active-passive monolithic integration. Opt. Express 2008, 16, 8350–8358. [Google Scholar] [CrossRef] [PubMed]
- Chin, M.-K.; Lee, C.-W.; Shen, J. Polarization-independent vertical coupler for photonics integration. Opt. Express 2004, 12, 117–123. [Google Scholar] [CrossRef]
- López, O.; Lasaosa, D.; López-Amo, M.; Galarza, M. Highly-efficient fully resonant vertical couplers for InP active-passive monolithic integration using vertically phase matched waveguides. Opt. Express 2013, 21, 22717–22727. [Google Scholar] [CrossRef]
- Liang, X.-J.; Mu, J.-W.; Li, X.; Xi, Y.-P. Efficient Active-to-Passive Light Coupling of InGaAsP/InP Laser Using Subwavelength Coupler. IEEE Photonics J. 2013, 5, 6602408. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, G.; Fan, Y.; Lu, Q.-Y.; Guo, W.-H. Design of Compact but Fabrication-Tolerant Vertical Coupler for Active-Passive Integration. J. Light. Technol. 2018, 36, 755–762. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Yang, Y.Y. Low-loss switching fabric design for recirculating buffer in WDM optical packet switching networks using arrayed waveguide grating routers. IEEE Trans. Commun. 2006, 54, 1469–1472. [Google Scholar] [CrossRef]
- Suematsu, Y.; Yamada, M.; Hayashi, K. Integrated twin-guide AlGaAs laser with multiheterostructure. IEEE J. Quantum Electron. 1975, 11, 457–460. [Google Scholar] [CrossRef]
- Yamada, M.; Suematsu, Y. Analysis of an integrated twin-guide laser with coupled-wave theory. IEEE J. Quantum Electron. 1977, 13, 201–206. [Google Scholar] [CrossRef]
- Suematsu, Y.; Kishino, K.; Kambayashi, T. Axial-mode selectivities for various types of integrated twin-guide lasers. IEEE J. Quantum Electron. 1977, 13, 619–622. [Google Scholar] [CrossRef]
- Adams, M.J. Theory of twin-guide Fabry-Perot laser amplifiers. IEE Proc. J. 1989, 136, 287–292. [Google Scholar] [CrossRef]
- Studenkov, P.V.; Xia, F.; Gokhale, M.R.; Forrest, S.R. Asymmetric twin-waveguide 1.55-μm wavelength laser with a distributed Bragg reflector. IEEE Photonics Technol. Lett. 2000, 12, 468–470. [Google Scholar] [CrossRef]
- Thylen, L. Wavelength and noise filtering characteristics of coupled active and passive waveguides. IEEE J. Quantum Electron. 1987, 23, 1956–1961. [Google Scholar] [CrossRef]
- Broberg, B.; Lindgren, B.S.; Oberg, M.; Jiang, H. A novel integrated optics wavelength filter in InGaAsP-InP. J. Lightwave Technol. 1986, 4, 196–203. [Google Scholar] [CrossRef]
- Wu, C.; Rolland, C.; Puetz, N.; Bruce, R.; Chik, K.D.; Xu, J.-M. A vertically coupled InGaAsP/InP directional coupler filter of ultranarrow bandwidth. IEEE Photonics Technol. Lett. 1991, 3, 519–521. [Google Scholar] [CrossRef]
- Wu, C.; Rolland, C.; Shepherd, F.; Larocque, C.; Puetz, N.; Chik, K.D.; Xu, J.-M. InGaAsP/InP vertical directional coupler filter with optimally designed wavelength tunability. IEEE Photonics Technol. Lett. 1993, 5, 457–459. [Google Scholar] [CrossRef]
- Han, S.K.; Ramaswamy, R.V.; Tavlykaev, R.F. Narrow-band vertically stacked filters in InGaAlAs/InP at 1.5 μm. J. Light. Technol. 1996, 14, 77–83. [Google Scholar] [CrossRef]
- Liu, B.; Shakouri, A.; Abraham, P.; Chiu, Y.J.; Zhang, S.; Bowers, J. Fused InP-GaAs vertical coupler filters. IEEE Photon. Technol. Lett. 1999, 11, 9–95. [Google Scholar] [CrossRef]
- Luo, C.-C.; Wang, J.; Qiu, B.-C.; Zhang, R.-Y. Gain spectral narrowing of semiconductor laser based on dual-core vertical coupler structure. Opt. Commun. 2020, 474, 126166. [Google Scholar] [CrossRef]
- Safaai-Jazi, A.; Chang, C.-C. Spectral characteristics of coupled-waveguide Fabry-Perot resonators and filters. IEEE J. Quantum Electron. 1996, 32, 1063–1069. [Google Scholar] [CrossRef]
- Hardy, A.A. A unified approach to coupled-mode phenomena. IEEE J. Quantum Electron. 1998, 34, 1109–1116. [Google Scholar] [CrossRef]
- Coldren, L.A.; Corzine, S.W.; Masanovic, M.L. Diode Lasers and Photonic Integrated Circuits, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 360–366. [Google Scholar] [CrossRef]


| Material | Refractive Index | Thickness (µm) |
|---|---|---|
| InGaAsP | 3.3548 | 0.2921 |
| InP | 3.169 | 2 |
| InGaAsP | 3.2887 | 0.45 |
| Twin-Waveguide Cavity | Meaning | Symbol | Value | Units |
|---|---|---|---|---|
| Central wavelength | λ0 | 1.55 | µm | |
| Effective refractive index at λ0 | 3.211 | - | ||
| Coupling length | Lc | 1000 | µm | |
| Cavity length | L | 1000 | µm | |
| Upper Waveguide | Group refractive index | ng1 | 3.339 | - |
| Facet reflection coefficient | r3, r4 | 0 | - | |
| Facet power reflectivity | R3, R4 | 0 | - | |
| Lower Waveguide | Group refractive index | ng2 | 3.298 | - |
| Facet reflection coefficient | r1, r2 | 0 | - | |
| Facet power reflectivity | R1, R2 | 0 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Zhang, R.; Zhang, B.; Qin, B.; Zhao, Y.; Qiu, B.; Liu, B.; Zhao, X. Transmission Characteristics Analysis of a Twin-Waveguide Cavity. Photonics 2024, 11, 777. https://doi.org/10.3390/photonics11080777
Luo C, Zhang R, Zhang B, Qin B, Zhao Y, Qiu B, Liu B, Zhao X. Transmission Characteristics Analysis of a Twin-Waveguide Cavity. Photonics. 2024; 11(8):777. https://doi.org/10.3390/photonics11080777
Chicago/Turabian StyleLuo, Chanchan, Ruiying Zhang, Ben Zhang, Bisheng Qin, Yanshuang Zhao, Bocang Qiu, Bohan Liu, and Xiaoming Zhao. 2024. "Transmission Characteristics Analysis of a Twin-Waveguide Cavity" Photonics 11, no. 8: 777. https://doi.org/10.3390/photonics11080777
APA StyleLuo, C., Zhang, R., Zhang, B., Qin, B., Zhao, Y., Qiu, B., Liu, B., & Zhao, X. (2024). Transmission Characteristics Analysis of a Twin-Waveguide Cavity. Photonics, 11(8), 777. https://doi.org/10.3390/photonics11080777





