Optical Frequency References at 1542 nm: Precision Spectroscopy of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 Lines of 127I2 at 514 nm
Yokohama National University, 79-5 Tokiwadai, Hodogaya-ku, Yokohama 240-8501, Japan
*
Author to whom correspondence should be addressed.
Photonics 2024, 11(8), 770; https://doi.org/10.3390/photonics11080770
Submission received: 20 June 2024
/
Revised: 1 August 2024
/
Accepted: 16 August 2024
/
Published: 19 August 2024
(This article belongs to the Special Issue Optical Communication, Sensing and Network)
Abstract
:Frequency-stabilized lasers are fundamental topics in research relating to optical frequency and wavelength standards. The absolute frequencies and hyperfine structures of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 lines of molecular iodine (127I2) at 514 nm were measured using a frequency-stabilized laser based on modulation transfer spectroscopy. The hyperfine splitting of each line was fitted to a four-term Hamiltonian with an uncertainty of several kilohertz to obtain the hyperfine constants for the line. A total of 97 hyperfine transitions of the six lines were measured with an uncertainty of 5.6 kHz (fractionally 9.6 × 10−12). They can provide new optical frequency references for telecommunication and other applications.
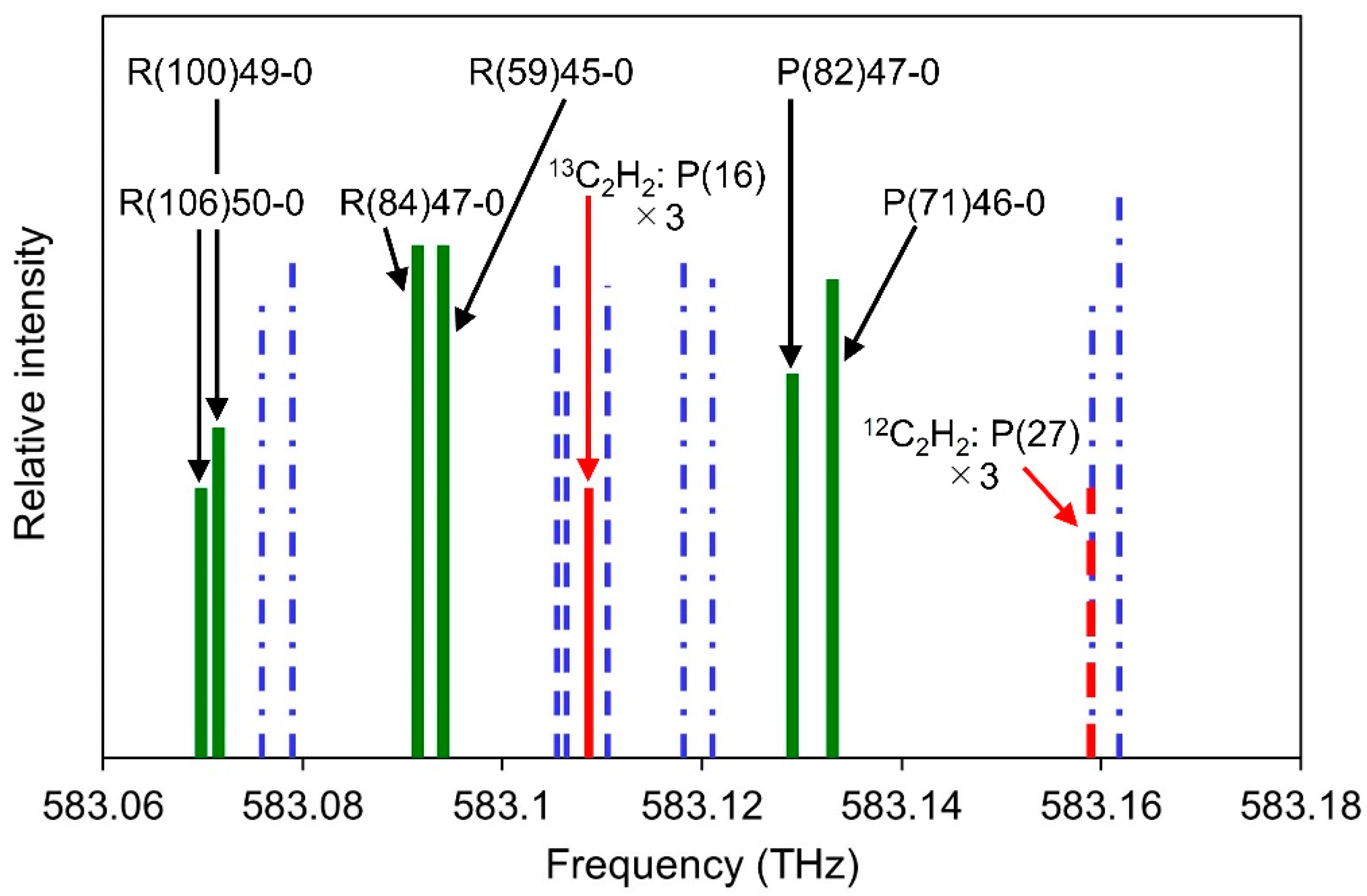
1. Introduction
Optical frequency standards [1] in telecommunication wavelength bands are useful not only for the management of the channel frequency of Dense Wavelength Division Multiplexing (DWDM) systems but also for other applications, including precision measurement and satellite communication. Besides acetylene [2,3,4] and Rb [5,6] optical frequency (or wavelength) standards, optical frequency standards at telecommunication wavelengths have recently been developed using frequency-stabilized lasers based on the precision spectroscopy of molecular iodine [7]. The acetylene optical frequency standard uses an optical cavity in the spectroscopic system. Therefore, this system is not reliable enough for long-term operation because the optical cavity is sensitive to environmental vibration. The Rb optical frequency standard uses a magnetic shield in the spectroscopic system, which is relatively difficult to handle, to reduce the frequency shift of the spectrum due to the magnetic field in the environment. The iodine-based optical frequency standard at the telecommunication wavelength has the advantages of a simple setup and reliability (without an optical cavity or magnetic shield in the spectroscopic system) over acetylene and Rb standards. Precision spectroscopy was performed on three iodine lines [8] (blue dashed lines in Figure 1) close to the tripled frequency of the P(16) line of 13C2H2 (red line in Figure 1), which is recommended by the International Committee for Weights and Measures (CIPM) as an optical frequency standard at telecommunication wavelengths [9]. We also measured the hyperfine structure of the seven iodine lines in the same wavelength region (six of them have the same excited-state vibrational quantum number v′ = 44) to study the rotation dependence of the excited state hyperfine constants [10]. These seven lines are shown in Figure 1 as blue dot-dashed lines (two of them are close and overlap in Figure 1). As shown in Figure 1, there are several other iodine lines with excited-state vibrational quantum numbers other than v′ = 44 and, in some cases, relatively low intensity (green lines in Figure 1) [11]. They are the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 lines of 127I2 at 514 nm. These lines have not been investigated using Doppler-free laser spectroscopy, and their hyperfine structures have not yet been resolved. The absolute frequencies of these lines were only measured for the Doppler-limited line (an overlap of all the Doppler-broadened hyperfine structures in the line) center using Fourier transform spectroscopy with an uncertainty of several tens of megahertz [11].
In this study, we performed Doppler-free laser spectroscopy based on modulation transfer spectroscopy [12,13] for the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 lines of 127I2 at 514 nm. This study is a continuation of our previous works [8,10] and focuses on some relatively weak iodine lines. The absolute frequencies and hyperfine transitions of the lines were measured with an uncertainty of 5.6 kHz, which is an improvement of approximately four orders of magnitude compared to that of the Doppler-limited measurement [11]. The hyperfine constants for each line were obtained by fitting the observed hyperfine structure to a four-term Hamiltonian equation [14]. The observed 97 hyperfine transitions of the six iodine lines provide new optical frequency references for telecommunications and other applications, including optical frequency combs. In telecommunication applications, the obtained new optical frequency references can be used for DWDM channels where no frequency reference is available. In the frequency comb system, the obtained frequency-stabilized laser in the telecom wavelength region can serve as the frequency reference for Er-fiber combs [7].
2. Experiment
In this study, an external-cavity diode laser at 1542 nm (RIO PLANEX) was used for spectroscopy and laser frequency stabilization. The output of the laser light was injected into an Er-doped fiber amplifier for power amplification. The amplified laser output was sent to a periodically poled lithium niobate (PPLN) waveguide [7] for the third-harmonic generation (THG) at 514 nm. The generated THG light was used for Doppler-free spectroscopy of molecular iodine based on modulation transfer spectroscopy [12,13]. The iodine spectrometer contained a 30 cm-long iodine cell. In the modulation transfer spectroscopy, a pump beam with phase modulation was used to saturate the iodine absorption. The phase modulation was set to 220 kHz using an acousto-optic modulator. A probe laser beam was used to detect the saturation dip through modulation transfer [12,13]. The modulation on the pump beam was transferred to the probe beam only when saturation occurred. The probe beam was sent to a photodetector to generate first-derivative-like modulation transfer signals through demodulation. Laser frequency stabilization was achieved by using the observed modulation transfer signal as an error signal. Possible error signal offset from feedback electronics was minimized by adjusting the lock point to the averaged level of the off-resonance spectral baseline. Servo control was achieved by the feedback control of the laser current and temperature. For the laser frequency measurement, we conducted a beat frequency measurement between the frequency-locked laser and Er-doped fiber comb [15]. An iodine-stabilized Nd:YAG laser [16] was used as an optical frequency reference for the Er-doped fiber comb. Further details of the experimental setup and method can be found elsewhere [8,10].
Figure 2 shows the observed hyperfine structures of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 lines of 127I2. The laser frequency was swept to observe hyperfine structures by gradually changing the laser temperature. The cold-finger temperature of the iodine cell was maintained at −10 °C, which corresponds to an iodine pressure of approximately 1.4 Pa. The optical powers of the pump and probe beams were 1.8 and 0.28 mW, respectively, except for the P(71)46-0 line, where the probe beam power was 0.15 mW. The diameters of both the beams were approximately 1.7 mm. The hyperfine transitions of the R(84)47-0 and R(59)45-0 lines are shown as the “a” and “b” series, respectively, in the same graph [Figure 2c]. For the R(106)50-0, R(100)49-0, P(82)47-0 and R(84)47-0 lines, whose ground state J″ is even (106, 100, 82, and 84, respectively), 15 hyperfine transitions were observed [Figure 2a,b,d, and “a” series of Figure 2c, respectively]. On the other hand, 21 hyperfine transitions were observed for the P(71)46-0 and R(59)45-0 lines, whose ground state J″ is odd (71 and 59, respectively) [Figure 2e and “b” series of Figure 2c]. The weak components in the spectra of the R(106)50-0, R(100)49-0, and P(82)47-0 lines belonged to nearby rovibrational lines. Several close hyperfine transitions that were not resolved in Figure 2 were resolved on an enlarged scale and could be locked separately: (i) the a2 transition of the R(100)49-0 line and the nearby transition of another line, (ii) the b7 and b8 transitions of the R(59)45-0 line, and (iii) the a6 and a7 transitions of the P(82)47-0 line.
The diode laser was stabilized to all 15 or 21 hyperfine transitions of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0 and P(71)46-0 lines. The absolute frequency of the laser locked to each hyperfine transition was determined by the beat measurement between the iodine-stabilized diode laser and the frequency comb. The measured absolute frequencies of the laser locked to the a1(b1) transitions of the six lines are summarized in Table 1. The statistical uncertainty of the measurement was estimated to be 0.4 kHz from the repeatability (lock and unlock) of the frequency-stabilized laser. The total systematic uncertainty was evaluated to be 5.6 kHz in our previous studies [8,10], where the largest systematic uncertainty was 5 kHz, owing to cell impurities. By combining the statistical and systematic uncertainties, the uncertainty of the measured absolute frequency was determined to be 5.6 kHz (fractional uncertainty of 9.6 × 10−12).
In Table 2 and Table 3, the “Obs.” columns represent the measured values for the hyperfine splittings of the six lines, which were obtained by taking the frequency difference between each hyperfine transition and the a1(b1) transition. Because the frequency shift is similar for each hyperfine transition, the measurement uncertainty of the hyperfine splitting interval is not affected by systematic uncertainties, such as optical power and iodine pressure shifts. The measurement uncertainty of the hyperfine splittings was mainly contributed by the repeatability (0.4 kHz) of the stabilized diode laser and was calculated to be 0.6 kHz ( kHz).
3. Calculation and Discussion
The measured intervals of the hyperfine transitions were fitted to a four-term Hamiltonian [14] to calculate the hyperfine constants of the iodine lines. The four-term Hamiltonian includes the electric quadrupole, spin–rotation, tensor spin–spin, and scalar spin–spin interactions, where eQq, C, d, and δ are the respective hyperfine constants corresponding to these interactions [14]. In the present calculation, a nonlinear least-squares fit was performed using the ROOT analysis libraries of CERN [17]. The detailed procedure and parameters of the fitting are described elsewhere [18,19]. The hyperfine splitting calculated from the fit was compared with the measured hyperfine splitting. The differences between the measurement and calculation are listed in the columns “Obs.-Cal.” in Table 2 and Table 3. The measured frequencies of the a2 transition of the R(100)49-0 line, the b7 and b8 transitions of the R(59)45-0 line, and the a6 and a7 transitions of the P(82)47-0 line were excluded from the fitting because they were too close to each other or to other hyperfine transitions. The residual slope on the error signal from adjacent transitions will introduce an offset in the signal and hence shift the line center when the lock point is set to the averaged level of the off-resonance spectral baseline. The standard deviation of the theoretical fit was approximately 2 or 3 kHz, except for the R(106)50-0, R(100)49-0 lines. The larger standard deviation of the fit for the R(106)50-0, R(100)49-0 lines (8.6 and 5.0 kHz, respectively) is caused by overlapping with other relatively weak lines, as shown in Figure 2a,b. Through the theoretical fit, hyperfine constants ΔeQq, ΔC, Δd, and Δδ, which are the differences in the hyperfine constants between the upper and lower states, were obtained. The calculated hyperfine constants of the six iodine lines are listed in Table 4.
The uncertainties in the values for the main hyperfine constant, ΔeQq, were <10 kHz, except for the R(106)50-0 line. The slightly larger uncertainty of ΔeQq (17 kHz) of the R(106)50-0 line obtained from fitting is due to slightly larger measurement uncertainties caused by the overlapping with other lines. Furthermore, the intensity of the R(106)50-0 line was the lowest among the observed lines. Small uncertainties were also observed for ΔC, Δd, and Δδ. Accurate hyperfine constants were used to reproduce the hyperfine spectra of iodine. Therefore, formulae for predicting hyperfine constants are essential for spectroscopy [20]. In our previous work, we derived formulae to express the rotational dependence of the ground state eQq″ (v″ = 0) [21] and excited states eQq′ (v′ = 32 and 44) [10,19]. The hyperfine constants obtained in this study can be used to improve our understanding of the rotational dependence of the excited-state hyperfine constants for v′ = 45, 46, 47, 49, and 50.
We observed 97 hyperfine transitions in six lines with an uncertainty of 5.6 kHz over a range greater than 64 GHz. By combining the absolute frequencies presented in Table 1 and the hyperfine splittings in Table 2 and Table 3, we can determine the frequencies of all the hyperfine transitions, except for the unresolved and excluded transitions. Such a grid of iodine reference lines was already investigated in the 571–596 nm wavelength region, with an uncertainty of approximately 2 MHz in an early stage of Doppler-free spectroscopy [22]. However, the present study has achieved a measurement uncertainty approximately 400 times smaller than that in Ref. [22]. Because our iodine-stabilized laser outputs at a fundamental wavelength of 1542 nm, these transitions can serve as new optical frequency references for telecommunications and other applications. As indicated in Figure 1, the acetylene optical frequency standard next to the P(16) line of 13C2H2 is the P(27) line of 12C2H2 [9]. The transitions observed in this study provide new candidates for frequency standards at telecom wavelengths to fill the gap in existing CIPM-recommended standards. In particular, when an iodine-stabilized diode laser is used as a frequency reference for an optical frequency comb, the variation in its laser frequency is useful in finding a suitable beat frequency for frequency locking. An iodine-stabilized diode laser at 1542 nm [7] was used as the optical frequency reference in the astrocomb [23].
4. Conclusions
In conclusion, we measured the absolute frequency and studied the hyperfine structure of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 lines of molecular iodine at 514 nm using high-resolution spectroscopy and a narrow-linewidth diode laser. The hyperfine splitting of each line was fitted to a four-term Hamiltonian with an uncertainty of several kilohertz to obtain accurate hyperfine constants for the line. The measurement of absolute frequencies and hyperfine structures of these lines are valuable for practical applications, such as telecommunication and optical frequency combs.
Author Contributions
Conceptualization, F.-L.H.; methodology, S.M., D.A. and F.-L.H.; investigation, S.M., Y.I. and F.-L.H.; data curation, Y.I., D.A. and F.-L.H.; writing—original draft preparation, S.M. and F.-L.H.; writing—review and editing, D.A.; funding acquisition, F.-L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI 24K01382 and the Japan Science and Technology Agency (JST) Moonshot R&D (Grant No. JPMJMS226C).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors thank M. Yoshiki for her technical assistance with the experiments.
Conflicts of Interest
The authors have no conflicts of interest to declare.
References
- Hong, F.-L. Optical frequency standards for time and length applications. Meas. Sci. Technol. 2016, 28, 012002. [Google Scholar] [CrossRef]
- Nakagawa, K.; de Labachelerie, M.; Awaji, Y.; Kourogi, M. Accurate optical frequency atlas of the 1.5-µm bands of acetylene. J. Opt. Soc. Am. B 1996, 13, 2708–2714. [Google Scholar] [CrossRef]
- Onae, A.; Okumura, K.; Yoda, J.; Nakagawa, K.; Yamaguchi, A.; Kourogi, M.; Imai, K.; Widiyatomoko, B. Toward an accurate frequency standard at 1.5 µm based on the acetylene overtone band transition. IEEE Trans. Instrum. Meas. 1999, 48, 563–566. [Google Scholar] [CrossRef]
- Hong, F.-L.; Onae, A.; Jiang, J.; Guo, R.; Inaba, H.; Minoshima, K.; Schibli, T.R.; Matsumoto, H. Absolute frequency measurement of an acetylene-stabilized laser at 1542 nm. Opt. Lett. 2003, 28, 2324–2326. [Google Scholar] [CrossRef] [PubMed]
- Bernard, J.E.; Madej, A.A.; Siemsen, K.J.; Marmet, L.; Latrasse, C.; Touahri, D.; Poulin, M.; Allard, M.; Têtu, M. Absolute frequency measurement of a laser at 1556 nm locked to the 5S1/2–5D5/2 two-photon transition in 87Rb. Opt. Commun. 2000, 173, 357–364. [Google Scholar] [CrossRef]
- Ye, J.; Swartz, S.; Jungner, P.; Hall, J.L. Hyperfine structure and absolute frequency of the 87Rb 5P3/2 state. Opt. Lett. 1996, 21, 1280–1282. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, K.; Okubo, S.; Wada, M.; Kashiwagi, K.; Yoshii, K.; Inaba, H.; Hong, F.-L. Iodine-stabilized laser at telecom wavelength using dual-pitch periodically poled lithium niobate waveguide. Opt. Express 2020, 28, 2166–2178. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, K.; Kobayashi, T.; Yoshiki, M.; Akamatsu, D.; Hong, F.-L. Hyperfine structure and absolute frequency of 127I2 transitions at 514 nm for wavelength standards at 1542 nm. J. Opt. Soc. Am. B 2022, 39, 2264–2271. [Google Scholar] [CrossRef]
- Recommended Values of Standard Frequencies. Available online: https://www.bipm.org/en/publications/mises-en-pratique/standard-frequencies (accessed on 15 August 2024).
- Yoshiki, M.; Matsunaga, S.; Ikeda, K.; Akamatsu, D.; Hong, F.-L. Rotation dependence of v′ = 44 excited-state hyperfine constants obtained via precise measurements of the hyperfine structures of 127I2 lines near 514 nm. Eur. Phys. J. D 2023, 77, 140. [Google Scholar] [CrossRef]
- Gerstenkorn, S.; Luc, P. Atlas du Spectre d’Absorption de la Molecule d’Iode; Editions de CNRS: Paris, France, 1978. [Google Scholar]
- Shirley, J.H. Modulation transfer processes in optical heterodyne saturation spectroscopy. Opt. Lett. 1982, 7, 537–539. [Google Scholar] [CrossRef] [PubMed]
- Camy, G.; Bordé, C.J.; Ducloy, M. Heterodyne saturation spectroscopy through frequency modulation of the saturating beam. Opt. Commun. 1982, 41, 325–330. [Google Scholar] [CrossRef]
- Bordé, C.J.; Camy, G.; Decomps, B.; Descoubes, J.-P.; Vigué, J. High precision saturation spectroscopy of 127I2 with argon lasers at 5 145 Å and 5 017 Å: I—Main resonances. J. Phys. Fr. 1981, 42, 1393–1411. [Google Scholar] [CrossRef]
- Asahina, Y.; Yoshii, K.; Yamada, Y.; Hisai, Y.; Okubo, S.; Wada, M.; Inaba, H.; Hasegawa, T.; Yamamoto, Y.; Hong, F.-L. Narrow-linewidth and highly stable optical frequency comb realized with a simple electro-optic modulator system in a mode-locked Er:fiber laser. Jpn. J. Appl. Phys. 2019, 58, 038003. [Google Scholar] [CrossRef]
- Hong, F.-L.; Ishikawa, J. Hyperfine structures of the R(122)35-0 and P(84)33-0 transitions of 127I2 near 532 nm. Opt. Commun. 2000, 183, 101–108. [Google Scholar] [CrossRef]
- Brun, R.; Rademakers, F. ROOT—An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. A 1997, 389, 81–86. [Google Scholar] [CrossRef]
- Kobayashi, T.; Akamatsu, D.; Hosaka, K.; Inaba, H.; Okubo, S.; Tanabe, T.; Yasuda, M.; Onae, A.; Hong, F.-L. Absolute frequency measurements and hyperfine structures of the molecular iodine transitions at 578 nm. J. Opt. Soc. Am. B 2016, 33, 725–734. [Google Scholar] [CrossRef]
- Sakagami, H.; Yoshii, K.; Kobayashi, T.; Hong, F.-L. Absolute frequency and hyperfine structure of 127I2 transitions at 531.5 nm by precision spectroscopy using a narrow-linewidth diode laser. J. Opt. Soc. Am. B 2020, 37, 1027–1034. [Google Scholar] [CrossRef]
- Bodermann, B.; Knöckel, H.; Tiemann, E. Widely usable interpolation formulae for hyperfine splittings in the 127I2 spectrum. Eur. Phys. J. D 2002, 19, 31–44. [Google Scholar] [CrossRef]
- Hong, F.-L.; Ye, J.; Ma, L.-S.; Picard, S.; Bordé, C.J.; Hall, J.L. Rotation dependence of electric quadrupole hyperfine interaction in the ground state of molecular iodine by high-resolution laser spectroscopy. J. Opt. Soc. Am. B 2001, 18, 379–387. [Google Scholar] [CrossRef]
- Velchev, I.; Dierendonck, R.; Hogervorst, W.; Ubachs, W. A dense grid of reference iodine lines for optical frequency calibration in the range 571–596 nm. J. Mol. Spectrosc. 1998, 187, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Okubo, S.; Nakamura, K.; Schramm, M.; Yamamoto, H.; Ishikawa, J.; Hong, F.-L.; Kashiwagi, K.; Minoshima, K.; Tsutsui, H.; Kambe, E.; et al. Erbium-Fiber-Based Visible Astro-Comb with 42-GHz Mode Spacing. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), OSA, San Jose, CA, USA, 13–18 May 2018. paper STu3P.1. [Google Scholar] [CrossRef]
Figure 1.
Frequency atlas of the 127I2 absorption lines (blue and green lines) near the tripled frequency of acetylene lines (red lines) at 514 nm. The blue dashed and dot-dashed lines are the iodine lines investigated in Refs. [8,10], respectively. The green lines are the iodine lines investigated in the present study. The relative intensity of iodine lines was taken from Ref. [11]. The intensity of the acetylene lines is not on the same scale as the iodine lines.
Figure 1.
Frequency atlas of the 127I2 absorption lines (blue and green lines) near the tripled frequency of acetylene lines (red lines) at 514 nm. The blue dashed and dot-dashed lines are the iodine lines investigated in Refs. [8,10], respectively. The green lines are the iodine lines investigated in the present study. The relative intensity of iodine lines was taken from Ref. [11]. The intensity of the acetylene lines is not on the same scale as the iodine lines.
Figure 2.
Observed hyperfine structures of the 127I2 lines near 514 nm. The vertical scales are the same for all graphs. The R(84)47-0 (“a” series) and R(59)45-0 (“b” series) lines overlap and are shown in the same graph.
Figure 2.
Observed hyperfine structures of the 127I2 lines near 514 nm. The vertical scales are the same for all graphs. The R(84)47-0 (“a” series) and R(59)45-0 (“b” series) lines overlap and are shown in the same graph.
Table 1.
Measured absolute frequencies of the 127I2 transitions.
| Transition | Frequency (kHz) |
|---|---|
| R(106)50-0:a1 | 583,069,385,497.5 (5.6) |
| R(100)49-0:a1 | 583,071,194,338.3 (5.6) |
| R(84)47-0:a1 | 583,092,689,333.5 (5.6) |
| R(59)45-0:b1 | 583,093,530,646.8 (5.6) |
| P(82)47-0:a1 | 583,128,690,994.0 (5.6) |
| P(71)46-0:a1 | 583,132,532,647.7 (5.6) |
Table 2.
Observed and calculated hyperfine splittings of the even J number transitions, where all values are in kHz, and SD denotes the standard deviation of the fit.
Table 2.
Observed and calculated hyperfine splittings of the even J number transitions, where all values are in kHz, and SD denotes the standard deviation of the fit.
| R(106)50-0 | R(100)49-0 | R(84)47-0 | P(82)47-0 | |||||
|---|---|---|---|---|---|---|---|---|
| Obs. | Obs.-Cal. | Obs. | Obs.-Cal. | Obs. | Obs.-Cal. | Obs. | Obs.-Cal. | |
| a1 | 0.0 | −0.6 | 0.0 | −0.3 | 0.0 | 0.1 | 0.0 | −0.3 |
| a2 | 106,679.4 | 10.6 | 133,636.6 * | 20.1 | 180,615.0 | 4.4 | 186,005.2 | 2.0 |
| a3 | 241,694.6 | −11.3 | 248,832.0 | −6.9 | 261,646.6 | −4.9 | 263,087.9 | −3.6 |
| a4 | 287,194.3 | −2.8 | 307,368.9 | 4.6 | 303,297.8 | 3.7 | 301,900.2 | 2.8 |
| a5 | 321,834.8 | 10.3 | 315,171.8 | 6.2 | 342,167.7 | −2.0 | 346,140.8 | −1.9 |
| a6 | 335,920.0 | −9.0 | 349,683.2 | −3.8 | 373,765.7 | −3.1 | 376,498.3 * | 2.1 |
| a7 | 455,458.3 | −11.0 | 428,980.4 | −4.9 | 383,039.2 | −5.0 | 377,690.8 * | −14.7 |
| a8 | 508,736.3 | 12.3 | 495,666.6 | 6.5 | 472,932.5 | 4.5 | 470,257.7 | 2.4 |
| a9 | 556,748.7 | 3.2 | 537,316.3 | 2.4 | 504,020.2 | 3.2 | 500,110.5 | −1.8 |
| a10 | 563,631.1 | 0.2 | 564,090.1 | −1.9 | 564,983.0 | 0.0 | 565,021.9 | 0.8 |
| a11 | 615,902.0 | 0.1 | 629,677.7 | 3.8 | 653,574.1 | 0.8 | 656,264.3 | 0.3 |
| a12 | 658,122.7 | −3.6 | 665,218.9 | −3.3 | 677,414.0 | −1.6 | 678,746.6 | −0.2 |
| a13 | 750,756.8 | 1.6 | 744,818.7 | −1.5 | 734,877.9 | 0.3 | 733,643.8 | 1.1 |
| a14 | 794,627.6 | −0.4 | 781,947.8 | −0.9 | 760,263.5 | −1.0 | 757,680.9 | −2.2 |
| a15 | 846,558.6 | 0.5 | 847,196.5 | 0.0 | 848,449.5 | 0.6 | 848,507.5 | 0.5 |
| SD | 8.6 | 5.0 | 3.6 | 2.4 | ||||
* Values excluded from the fit.
Table 3.
Observed and calculated hyperfine splittings of the odd J number transitions, where all values are in kHz, and SD denotes the standard deviation of the fit.
Table 3.
Observed and calculated hyperfine splittings of the odd J number transitions, where all values are in kHz, and SD denotes the standard deviation of the fit.
| R(59)45-0 | P(71)46-0 | ||||
|---|---|---|---|---|---|
| Obs. | Obs.-Cal. | Obs. | Obs.-Cal. | ||
| b1 | 0.0 | 3.6 | a1 | 0.0 | 4.0 |
| b2 | 83,603.1 | 1.8 | a2 | 101,327.1 | 0.6 |
| b3 | 163,631.9 | −1.5 | a3 | 199,012.9 | −3.6 |
| b4 | 279,747.0 | −1.0 | a4 | 286,598.2 | −0.1 |
| b5 | 357,652.8 | −2.6 | a5 | 370,322.1 | −3.2 |
| b6 | 375,380.5 | 1.8 | a6 | 397,768.6 | 2.4 |
| b7 | 449,748.8 * | −0.0 | a7 | 460,292.4 | −1.4 |
| b8 | 452,019.3 * | −2.9 | a8 | 478,039.8 | −0.1 |
| b9 | 478,373.9 | −3.4 | a9 | 488,201.7 | −3.8 |
| b10 | 536,505.4 | 0.4 | a10 | 561,763.0 | 2.6 |
| b11 | 558,578.1 | −0.1 | a11 | 586,521.9 | 2.0 |
| b12 | 586,575.4 | −1.2 | a12 | 595,357.3 | −0.5 |
| b13 | 649,336.5 | −1.6 | a13 | 666,749.0 | −0.6 |
| b14 | 714,116.2 | −1.0 | a14 | 739,068.0 | −0.2 |
| b15 | 735,632.0 | −2.2 | a15 | 749,684.8 | −1.1 |
| b16 | 769,617.0 | −0.1 | a16 | 784,372.6 | −0.2 |
| b17 | 810,264.1 | 1.9 | a17 | 830,673.5 | 2.0 |
| b18 | 842,749.7 | 1.1 | a18 | 863,660.5 | 1.5 |
| b19 | 908,277.9 | 0.9 | a19 | 923,297.9 | −0.8 |
| b20 | 930,226.5 | 1.1 | a20 | 947,820.3 | 0.3 |
| b21 | 955,688.4 | 2.0 | a21 | 975,243.0 | 0.1 |
| SD | 2.1 | 2.2 | |||
* Values excluded from the fit.
Table 4.
Hyperfine constants obtained from fitting.
| Line | ΔeQq (MHz) | ΔC (kHz) | Δd (kHz) | Δδ (kHz) |
|---|---|---|---|---|
| R(106)50-0 | 1886.649 (17) | 398.308 (10) | −221.07 (56) | 55.12 (45) |
| R(100)49-0 | 1887.605 (9) | 355.587 (7) | −199.36 (43) | 38.10 (45) |
| R(84)47-0 | 1889.559 (8) | 284.410 (5) | −158.50 (23) | 15.97 (21) |
| R(59)45-0 | 1891.696 (3) | 228.863 (3) | −126.39 (7) | 3.80 (5) |
| P(82)47-0 | 1889.654 (4) | 281.774 (4) | −156.49 (13) | 15.16 (13) |
| P(71)46-0 | 1890.699 (3) | 252.942 (2) | −140.33 (12) | 8.56 (9) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Matsunaga, S.; Isawa, Y.; Akamatsu, D.; Hong, F.-L. Optical Frequency References at 1542 nm: Precision Spectroscopy of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 Lines of 127I2 at 514 nm. Photonics 2024, 11, 770. https://doi.org/10.3390/photonics11080770
AMA Style
Matsunaga S, Isawa Y, Akamatsu D, Hong F-L. Optical Frequency References at 1542 nm: Precision Spectroscopy of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 Lines of 127I2 at 514 nm. Photonics. 2024; 11(8):770. https://doi.org/10.3390/photonics11080770
Chicago/Turabian StyleMatsunaga, Shogo, Yuta Isawa, Daisuke Akamatsu, and Feng-Lei Hong. 2024. "Optical Frequency References at 1542 nm: Precision Spectroscopy of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 Lines of 127I2 at 514 nm" Photonics 11, no. 8: 770. https://doi.org/10.3390/photonics11080770
APA StyleMatsunaga, S., Isawa, Y., Akamatsu, D., & Hong, F.-L. (2024). Optical Frequency References at 1542 nm: Precision Spectroscopy of the R(106)50-0, R(100)49-0, R(84)47-0, R(59)45-0, P(82)47-0, and P(71)46-0 Lines of 127I2 at 514 nm. Photonics, 11(8), 770. https://doi.org/10.3390/photonics11080770
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
