Research on a Near-Field Millimeter Wave Imaging Algorithm and System Based on Multiple-Input Multiple-Output Sparse Sampling

Abstract

In order to reduce the hardware cost and data acquisition time in near-field scenarios, such as airport security imaging systems, this paper discusses the layout of a multiple-input multiple-output (MIMO) radar array. In view of the existing multi-input multiple-output imaging algorithm, the reconstructed image artifacts and aliasing problems caused by sparse sampling are discussed. In this paper, a multi-station radar array and a corresponding sparse MIMO imaging algorithm based on combined sparse sub-channels are proposed. By studying the wave–number spectrum of backscattered MIMO synthetic aperture radar (SAR) data, the nonlinear relationship between the wave number spectrum and reconstructed image is established. By selecting a complex gain vector, multiple channels are coherently combined effectively, thus eliminating aliasing and artifacts in the reconstructed image. At the same time, the algorithm can be used for the MIMO–SAR configuration of arbitrarily distributed transmitting and receiving arrays. A new multi-station millimeter wave imaging system is designed by using a frequency-modulated continuous wave (FMCW) chip and sliding rail platform as a planar SAR. The combination of the hardware system provides reconfiguration, convenience and economy for the combination of millimeter wave imaging systems in multiple scenes.

1. Introduction

In the field of millimeter wave near-field imaging, there are many challenges in antenna array design, such as excessive array elements, high design complexity, high manufacturing cost, and the resulting problems, such as limited sampling rate, uneven array performance, difficult delay correction, complex system detection, and maintenance [1]. Therefore, millimeter wave near-field imaging research has been focused on optimizing antenna array size, improving sampling efficiency, and reducing design and manufacturing difficulties [2].

In recent years, the MIMO radar has attracted much attention as a cutting-edge radar technology which uses a multi-channel transceiver radar system. The MIMO radar can combine each observation channel to form a virtual plane aperture, so as to capture the three-dimensional echo signal, which provides a broader application prospect for radar detection [3]. It is worth mentioning that the MIMO radar can complete data acquisition in a very short time. Compared with the traditional single-shot single-harvest image system, the acquisition speed of the MIMO radar is better [4]. Due to its small array number and fast sampling speed, the MIMO radar has shown great application potential in near-field imaging fields such as human security screening [5].

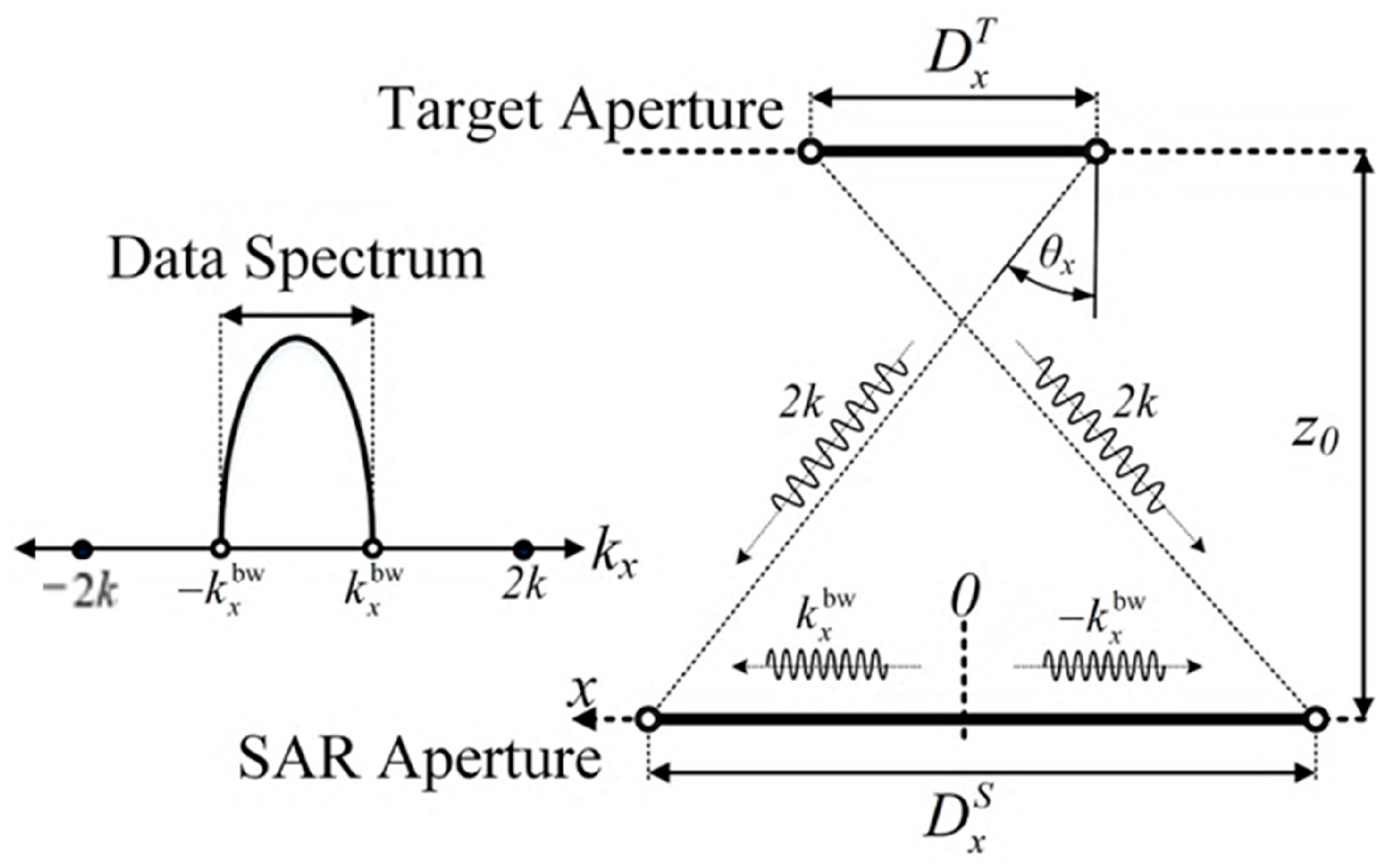
The MIMO imaging algorithm plays an important role in the research field of MIMO radar. In the far-field environment, the concept of virtual array is used to simplify the processing of echo signals [6]. Through this method, the complex array combination can be effectively regarded as a single-send single-receive mode, so that the traditional radar-imaging algorithm can be more convenient for image reconstruction. However, in the near-field environment, although this method satisfies the Nyquist sampling theorem, the undersampling problem will lead to the frequency aliasing of backscattered data, which will introduce grating lobes into the reconstructed image and seriously affect the imaging accuracy [7]. In 2019, Muhammet Yanik proposed a low-cost high-resolution MIMO millimeter wave imager prototype for concealed object detection. The synthetic aperture radar (SAR) in a target scene is realized by using the horizontal and vertical slide system [8,9,10]. The study validates the great potential of low-cost FMCW radar sensors for high-resolution imaging tasks in security applications. In 2018, the Beijing Institute of Technology solved the problem of not being able to load heavier hardware equipment and power supply equipment in lightweight radar systems. A new design scheme for a miniature SAR system was proposed [11] which greatly reduced the burden and was more efficient. In 2022, Chenyin Wu proposed that a millimeter wave radar based on a frequency-modulated continuous wave (FMCW) modulation technology has advantages in simplifying image reconstruction implementation [12]. Compared with the traditional reconstruction process, the signal-to-noise ratio (SNR) is limited. The team simulated the image reconstruction process of a 77 GHz FMCW radar combined with synthetic aperture radar (SAR) technology. In order to overcome the disadvantage of a low signal-to-noise ratio, the coherence effect is realized to reduce noise. In 2022, Hao Pei of Southeast University, for the first time, proposed a salience visual attention algorithm [13] to suppress background noise when foreground objects are highlighted. After the saliency map is generated, a SAR image segmentation algorithm is used to calculate the candidate regions. Finally, a morphological analysis and connectivity component analysis are used to reduce false positives and detect vehicles in the imaging scene. In 2019, Xiao Dong carried out short-range synthetic aperture radar (SAR)-imaging experiments by using a commercial monolithic millimeter wave radar and conducted experiments on SAR and ISAR [14]. The results show that the application of SAR technology to a monolithic millimeter wave radar can improve the range resolution of radar. Therefore, it is urgent to develop an efficient and accurate MIMO imaging algorithm for near-field environments.

Compressed sensing imaging can also achieve sparse sampling imaging. Compressed sensing mainly relies on two basic criteria to achieve compressed sampling: sparsity and incoherence. In general, most of the pixel values of an image are not zero, but according to the image compression theory, after many specific transformations, most of the coefficients are close to zero. The traditional sampling method does not consider image sparsity. After, the image is sampled according to the sampling theorem, in order to speed up transmission and save storage space. For any imaging mode, the observation matrix method can be used to design the down-sampling matrix, and the coherence between the observation matrix and the sparse basis used in reconstruction should be ensured. A random matrix is largely irrelevant to any sparse basis, so a random down-sampling matrix can be introduced into millimeter wave direct compression holography. In this imaging mode, two-dimensional random sampling can be directly introduced, and the sampling time can be reduced by optimizing the scanning path, such as using the travelling salesman algorithm (TSA) to calculate the optimal path.

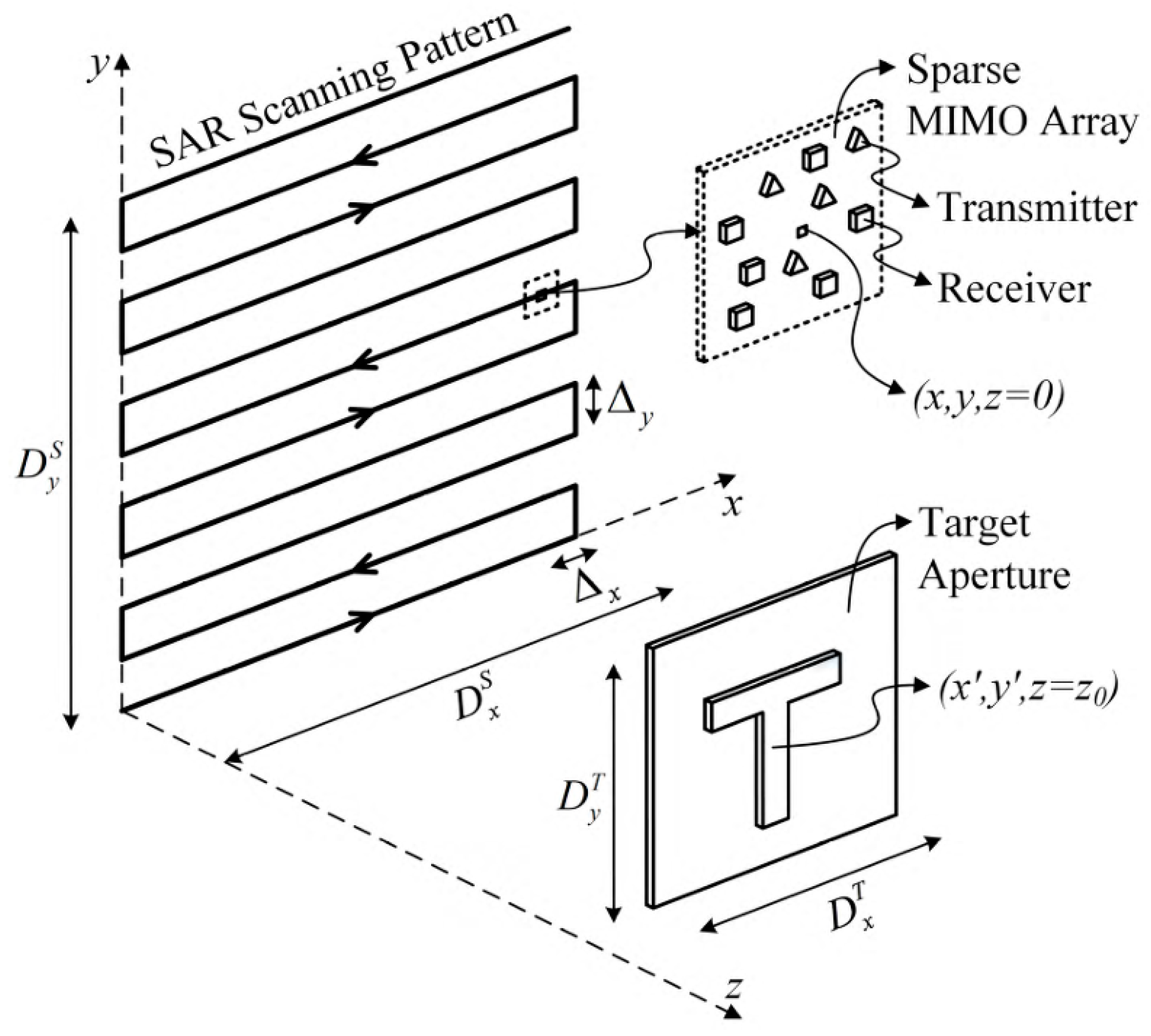
In view of the artifacts and aliasing problems caused by sparse sampling in existing multi-station imaging algorithms, this paper proposes a multi-station radar array form and a corresponding sparse MIMO imaging algorithm based on combined sparse sub-channels. By studying the wave–number spectrum of backscattered MIMO–SAR data, the nonlinear relationship between the wave number spectrum and the reconstructed image is established. By selecting the complex gain vector, multiple channels are coherently combined effectively, thus eliminating aliasing and artifacts in the reconstructed image. At the same time, the algorithm can be used for MIMO–SAR configuration of arbitrarily distributed transmitting and receiving arrays. A new multi-station millimeter wave imaging system is designed by using a FMCW chip and sliding rail platform as a planar SAR. The combination of the hardware systems provides reconfiguration, convenience, and economy in the multi-scene.

2. MIMO Sparse Sampling Imaging Algorithm Based on Multi-Channel Coherent Superposition

2.1. Echo Signal Model

When TDM–MIMO mode is used, the transceiver array cannot be directly equivalent to the virtual array. Assume that a transmitting array sends a signal at the (x_u, y_u, 0) position, the signal propagates to the $(x^{\prime },y^{\prime },z_0)$ position in space, and then its reflected echo is captured by the receiving array at the (x_v, y_v, 0) position, thus constituting the overall transmission path of the signal [15]:

$$\begin{array}{cc}{R}_{\ell }=R_u+R_v=& \sqrt{{\left(x_u-x^{\prime }\right)}^2+{\left(y_u-y^{\prime }\right)}^2+z_0^2}\\ & +\sqrt{{\left(x_v-x^{\prime }\right)}^2+{\left(y_v-y^{\prime }\right)}^2+z_0^2}\end{array}$$

(1)

According to the principle of equivalent phase center, this set of transceiver arrays can be regarded as a virtual array located at (x, y), that is, its phase center is located at (x, y). Assume that the transmitting and receiving arrays are separated by $d_l^y$ in height and $d_l^x$ in orientation. Using Formula (1), combined with the electromagnetic wave propagation theory and geometric relations, it can be expressed as a new form through Taylor expansion:

$$R_{\ell }\approx 2R+{\displaystyle \frac{{\left(d_{\ell }^x\right)}^2+{\left(d_{\ell }^y\right)}^2}{4R}}-{\displaystyle \frac{{\left(\left(x-x^{\prime }\right)d_{\ell }^x+\left(y-y^{\prime }\right)d_{\ell }^y\right)}^2}{4R^3}}$$

(2)

In this formula, R represents the distance from the equivalent virtual phase center to the target.

To create this virtual array architecture, the receiving antennas must separate the signals corresponding to different transmitting antennas. Therefore, the orthogonality between transmitting antennas is realized by using time division multiplexing (TDM) technology. The imaging system proposed in this paper utilizes sparse MIMO arrays to move continuously and parallel in the xy plane, assuming that the target is a two-dimensional object parallel to the scanning plane, as shown in Figure 1.

2.2. Wave Number Spectrum Analysis and Spatial Sampling Rate Analysis of Plane Aperture

In order to reconstruct alix-free images, this section studies the relationship between spectral and spatial domains in the sparsely sampled MIMO–SAR imaging system. The one-dimensional wave number domain spectrum is first analyzed to determine the relationship between the size of the target and the continuously finite SAR aperture, thus completing the MIMO–SAR configuration.

Set the target area to be centered relative to the scanning system, as shown in Figure 2. At this time, the analysis of wave number spectrum is limited to the x axis, and the expression obtained can also be extended to the y axis. This method is based on the known total size of the area to be measured.

Suppose θ_x is the limit of the angle of motion on the X-axis, i.e., the smaller angle that the antenna’s beamwidth or aperture covers on the corresponding axis.

Assuming that the angle covered by the aperture is less than the beam width of the antenna, it can be expressed as follows:

$$\sin {\theta }_x={\displaystyle \frac{\left(D_x^S+D_x^T\right)/2}{\sqrt{{\left(D_x^S+D_x^T\right)}^2/4+z_0^2}}}$$

(3)

As shown in Figure 2, D^Sx and D^Tx are the dimensions of the synthetic aperture and the target aperture. Taking into account the size of the synthetic aperture and the target aperture, the echo signal spectrum along the X-axis will be limited to the range [−k^bwx, k^bwx], where k^bwx is the highest wave number component:

$$k_x^{\mathrm{bw}}\approx 2k\sin \theta$$

(4)

By substituting (3) into (4), the bandwidth of echo data collected along the X-axis is as follows:

$$k_x^{\mathrm{bw}}\approx {\displaystyle \frac{2\pi \left(D_x^S+D_x^T\right)}{\lambda \sqrt{{\left(D_x^S+D_x^T\right)}^2/4+z_0^2}}}$$

(5)

In the MIMO–SAR imaging system, the echo signal is spatially sampled by the transmitting and receiving antennas. The system adopts sparse sampling, and the spatial sampling needs to meet the Nyquist criterion to avoid aliasing. The maximum theoretical value in space is λ/4, where λ is the wavelength. However, the spectrum of echo data captured in a finite SAR aperture is limited by its size, the spatial range of the target aperture, and the distance between the two planes. The continuous spatial domain signal s(x) and its Fourier transform are assumed to be S(k_x). As shown in (5), S(k_x) is limited to the range |k_x| ≤ k^bwx. The corresponding minimum sampled wave number along the x-axis is as follows:

$$k_x^s\ge 2k_x^{\mathrm{bw}}={\displaystyle \frac{4\pi \left(D_x^S+D_x^T\right)}{\lambda \sqrt{{\left(D_x^S+D_x^T\right)}^2/4+z_0^2}}}$$

(6)

Therefore, when the sampling conditions meet the following conditions, the reconstructed image will not be aliased:

$${\Delta }_x\le {\Delta }_x^{\mathrm{Nyq}}={\displaystyle \frac{\pi }{k_x^{\mathrm{bw}}}}={\displaystyle \frac{\lambda \sqrt{{\left(D_x^S+D_x^T\right)}^2/4+z_0^2}}{2\left(D_x^S+D_x^T\right)}}$$

(7)

2.3. MIMO Sparse Sampling Imaging Algorithm

The main task of image reconstruction is to process the phase correctly, and the amplitude variation with distance attenuation has little effect on the reconstructed image. Therefore, the signal received by the nth single station virtual element can be expressed as follows:

$$s_{\mathrm{n}}(k)\approx s(k){\displaystyle \frac{e^{jk{R}_{\mathrm{n}}}}{R^2}}=s(k)e^{j{\varphi }_{\mathrm{n}}(k)}$$

(8)

where s(k) is the signal received by the physical unit located at the same midpoint between the actual transmitter and receiver antenna and:

$${\varphi }_{\mathrm{n}}(k)=k{\displaystyle \frac{{\left(d_{\mathrm{n}}^x\right)}^2+{\left(d_{\mathrm{n}}^y\right)}^2}{4z_0}}$$

(9)

ϕ_n(k) is the nonlinear phase term in near-field imaging. The MIMO array is converted into a virtual array, and the continuous SAR aperture spatial sampling data are represented by the nth virtual channel:

$$s_{\mathrm{n}}(x,y)=s(x,y)e^{j{\varphi }_{\mathrm{n}}}{\displaystyle \sum _{p\in \mathbb{Z}}{\displaystyle \sum _{q\in \mathbb{Z}}\delta }}\left(x-p{\Delta }_x-x_{\mathrm{n}},y-q{\Delta }_y-y_{\mathrm{n}}\right)$$

(10)

where ∆x and ∆y are the sampling intervals in the x and y dimensions, respectively, and S(x, y) represents the backscatter data received on the aperture. To simplify the calculation, the k variable of the original backscatter data is ignored. x_n and y_n are the midpoint offsets of the virtual array on the x and y axes, respectively. The two-dimensional wave number spectrum of the correlated sampled signal on channel n is expressed as follows:

$$S_{\mathrm{n}}\left(k_x,k_y\right)={\displaystyle \frac{e^{j\varphi }}{{\Delta }_x{\Delta }_y}}{\displaystyle \sum {\displaystyle \sum S}}\left(k_x-m{k}_x^s,k_y-n{k}_y^s\right)e^{-j\left(m{k}_x^{s}x+n{k}_y^{s}y\right)}$$

(11)

In the above formula, (mk^sx, nk_sy) is the pseudo-spectral center of the target image when aliasing occurs.

The relationship between the wave number spectrum of the sampled echo data and the reconstructed image is nonlinear. The influence of the aliasing components in the sampled data spectrum on the reconstructed image can be deduced by analyzing the nonlinear relationship. According to (9), assume that the aliasing spectral component of the hth channel is as follows:

$$S_{mn}^{\mathrm{h}}\left(k_x,k_y\right)=\underset{C_{mn}^{\mathrm{h}}}{\underbrace{{\displaystyle \frac{e^{j\left(\varphi -\left(m{k}_x^s{x}_x+n{k}_y^{\delta }y\right)\right)}}{{\Delta }_x{\Delta }_y}}}}S\left({\widehat{k}}_x,{\widehat{k}}_y\right)$$

(12)

where:

$${\widehat{k}}_x=k_x-m{k}_x^s,\hspace{1em}{\widehat{k}}_y=k_y-n{k}_y^s$$

(13)

According to the relationship between the backscatter data and the image spectrum, Equation (10) becomes the following:

$$S_{mn}^{\mathrm{h}}\left(k_x,k_y\right)=C_{mn}^{\mathrm{h}}P\left({\widehat{k}}_x,{\widehat{k}}_y\right){\displaystyle \frac{e^{j{\widehat{k}}_z{z}_0}}{{\widehat{k}}_z}}$$

(14)

The wave number spectrum of reconstructed image artifacts generated by aliasing components is obtained as follows:

$$P_{mn}^{\mathrm{h}}\left(k_x,k_y\right)=S_{mn}^{\mathrm{h}}\left(k_x,k_y\right)k_z{e}^{-j{k}_z{z}_0}=C_{mn}^{\mathrm{h}}P\left({\widehat{k}}_x,{\widehat{k}}_y\right){\displaystyle \frac{k_z}{{\widehat{k}}_z}}{e}^{j\left({\widehat{k}}_z-k_z\right)z_0}$$

(15)

It can be seen from the above formula that the artifacts caused by the aliasing component in the sampled wave number spectrum are translated by non-aliasing images with nonlinear operations. If the spatial sampling intervals ∆x and ∆y do not satisfy Nyquist’s theorem, aliasing will occur during image reconstruction. In this paper, a sparse MIMO–SAR reconstruction algorithm is proposed to reconstruct non-aliasing images by selecting complex gain for multi-channel combination. The aliasing component in the Formula (10) can be offset by the correct selection of the complex gain vector, thus eliminating the aliasing image in (12). Set the compound gain as follows:

$$w={\left[\begin{array}{llll}{w}_0\hfill & w_1\hfill & \dots \hfill & w_{L-1}\hfill \end{array}\right]}^T$$

(16)

Including L virtual channels, T stands for vector transpose; the MIMO–SAR sampling process and image reconstruction process are shown in Figure 3. Set the image reconstruction filter h(x, y) as follows:

$$h(x,y)={\mathrm{IFT}}_{2D}\left[k_z{e}^{-j{k}_z{z}_0}\right]$$

(17)

IFT_2D represents the two-dimensional inverse Fourier transform operation over the xy field. Combine the complex gain vector with the virtual channel spectrum:

$$\tilde{S}\left(k_x,k_y\right)={\displaystyle \sum _0^{L-1}w}S\left(k_x,k_y\right)={\displaystyle \frac{1}{{\Delta }_x{\Delta }_y}}{\displaystyle \sum _0^{L-1}w}{e}^{j\varphi }\times {\displaystyle \sum {\displaystyle \sum S}}\left(k_x-m{k}_x^s,k_y-n{k}_y^s\right)e^{-j\left(m{k}_x^{s}x+n{k}_y^{s}y\right)}$$

(18)

According to the above analysis, the translation component in the wave number spectrum must be eliminated in order to reconstruct an alix-free image. Since Equation (9) covers all translation components in the visible region, the total number of aliasing items to be eliminated in (14) is limited by parameters m and n:

$$\left|m{k}_x^s\right|\le 2k_x^{\mathrm{bw}},\hspace{1em}\left|n{k}_y^s\right|\le 2k_y^{\mathrm{bw}}$$

(19)

where k^bwx and k^bwy are the largest wave number components on the x and y axes, respectively, and the vector symbol are defined as follows:

$${\mathrm{H}}_{m,n}=\left[\begin{array}{ll}m{k}_x^s\hfill & n{k}_y^s\hfill \end{array}\right],\hspace{1em}\mathrm{I}={\left[\begin{array}{ll}x\hfill & y\hfill \end{array}\right]}^T$$

(20)

Rearrange Equation (14) as follows:

$$\begin{array}{l}\tilde{S}\left(k_x,k_y\right)={\displaystyle \frac{1}{{\Delta }_x{\Delta }_y}}[\left({\displaystyle \sum _0^{L-1}w}{e}^{j\varphi }\right)S\left(k_x,k_y\right)+\left({\displaystyle \sum _0^{L-1}w}{e}^{j\left(\varphi -H_{0,1}I\right)}\right)S\left(k_x,k_y-k_y^s\right)\\ +\left({\displaystyle \sum _0^{L-1}w}{e}^{j\left(\varphi -H_{0,2}I\right)}\right)S\left(k_x,k_y-2k_y^s\right)+\dots +\left({\displaystyle \sum _0^{L-1}w}{e}^{j\left(\varphi -H_{1,0}I\right)}\right)S\left(k_x-k_x^s,k_y\right)+\dots ]\end{array}$$

(21)

Using the following vector notation:

$${\alpha }_{m,n}=\left[\begin{array}{ll}m{k}_x^s\hfill & n{k}_y^s\hfill \end{array}\right],\hspace{1em}{\beta }_{\mathrm{h}}={\left[\begin{array}{ll}{x}_{\mathrm{h}}\hfill & y_{\mathrm{h}}\hfill \end{array}\right]}^T$$

(22)

Assuming that there is a solution to the vector w, all aliasing terms are eliminated, so that the backscattering wavenumber spectrum S(k_x, k_y) without aliasing in (17) can be obtained:

$$\underset{H}{\underbrace{\left[\begin{array}{cccc}{e}^{j{\varphi }_0}& e^{j{\varphi }_1}& \dots & e^{j{\varphi }_{L-1}}\\ e^{j\left({\varphi }_0-{\alpha }_{0,1}{\beta }_0\right)}& e^{j\left({\varphi }_1-{\alpha }_{0,1}{\beta }_1\right)}& \dots & e^{j\left({\varphi }_{L-1}-{\alpha }_{0,1}{\beta }_{L-1}\right)}\\ e^{j\left({\varphi }_0-{\alpha }_{0,2}{\beta }_0\right)}& e^{j\left({\varphi }_1-{\alpha }_{0,2}{\beta }_1\right)}& \dots & e^{j\left({\varphi }_{L-1}-{\alpha }_{0,2}{\beta }_{L-1}\right)}\\ ⋮& ⋮& ⋮& ⋮\\ e^{j\left({\varphi }_0-{\alpha }_{1,0}{\beta }_0\right)}& e^{j\left({\varphi }_1-{\alpha }_{1,0}{\beta }_1\right)}& \dots & e^{j\left({\varphi }_{L-1}-{\alpha }_{1,0}{\beta }_{L-1}\right)}\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]}}\underset{W}{\underbrace{\left[\begin{array}{c}{w}_0\\ w_1\\ ⋮\\ w_{L-1}\end{array}\right]}}=\underset{e}{\underbrace{{\Delta }_x{\Delta }_y\left[\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right]}}$$

(23)

By expanding the reconstruction formula, the solution of the complex gain vector is as follows:

$$w={\left(H^{T}H\right)}^{-1}{H}^{T}e$$

(24)

Finally, the reconstruction result of MIMO sparse sampling image is as follows:

$$p(x,y)={\mathrm{IFT}}_{2D}\left[w^{T}S\left(k_x,k_y\right)k_z{e}^{-j{k}_z{z}_0}\right]$$

(25)

$$S\left(k_x,k_y\right)={\left[\begin{array}{lll}{S}_0\left(k_x,k_y\right)\hfill & \dots \hfill & S_{L-1}\left(k_x,k_y\right)\hfill \end{array}\right]}^T$$

(26)

3. Results and Analysis

3.1. MIMO Imaging System Design

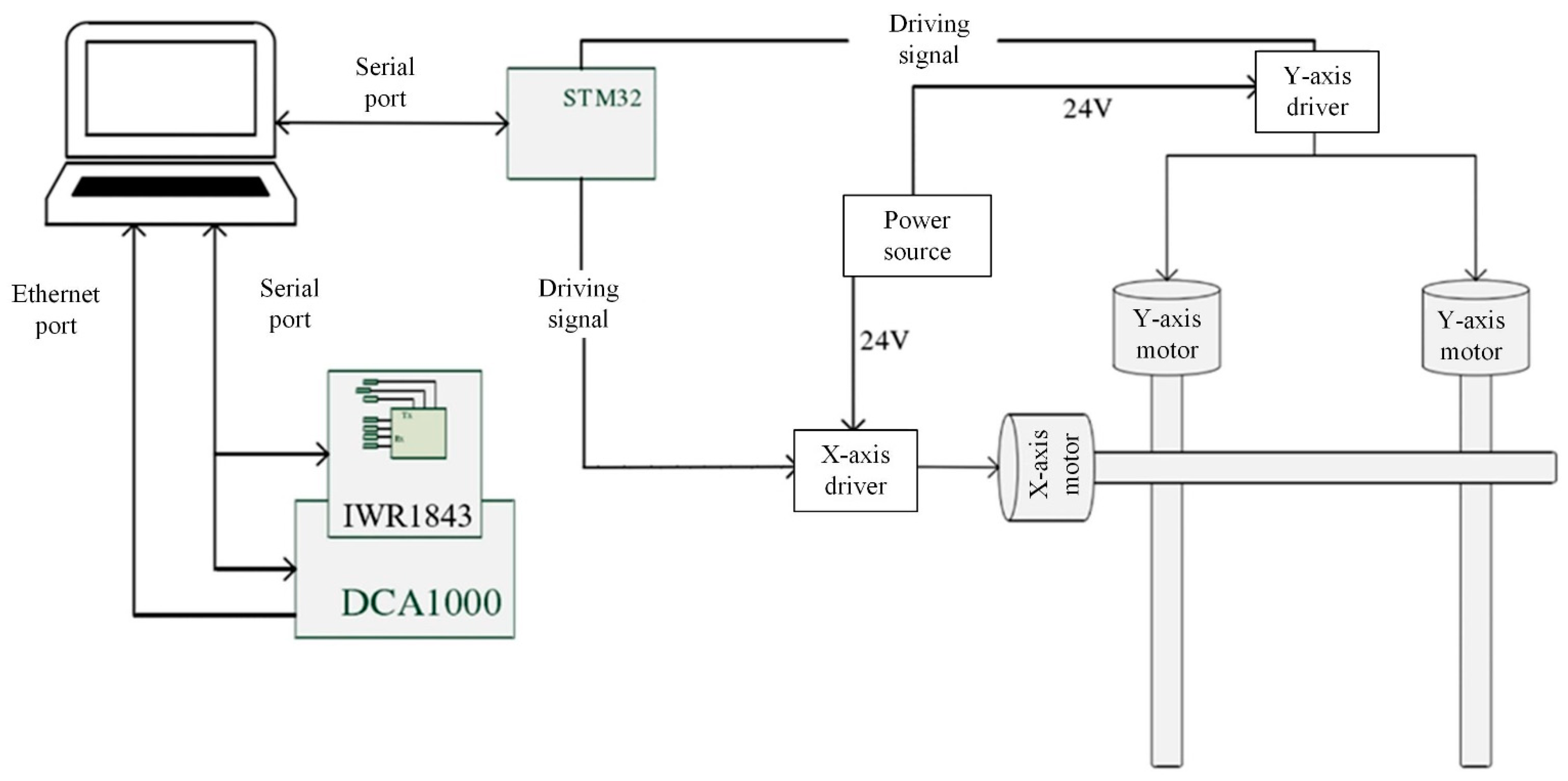
This section focuses on multi-station millimeter wave imaging technology and designs a MIMO millimeter wave imaging system by using an FM continuous wave chip and integrating a slide platform to construct a planar synthetic aperture radar.

This combination method significantly simplifies the hardware structure, reduces the system cost, and provides convenience and economy for the rapid construction of the MIMO millimeter wave near-field imaging system in multiple scenes. The prototype system consists of a millimeter wave sensor and scanning module, which uses a common industry standard communication architecture to ensure a high degree of reconfigurability for the system.

This section uses TI’s IWR1843 millimeter wave radar chip integration board, a hardware integration board that operates in the 76–81 GHz band. As shown in Figure 4, the integrated chip is equipped with three transmitting antennas and four receiving antennas, demonstrating excellent anti-interference capability. The main control task is carried out by the ARM-Cortex and the C674x-DSP, which have a RAM capacity of 1526 KB.

This radar chip not only has low power consumption, high precision, and fast processing speed, these advantages together ensure the real-time imaging of the system. At present, the radar has been widely used in many fields, such as vehicle obstacle detection, and the main performance indicators are shown in

Table 1. IWR1843 parameters.

Parameter Name	Parameter Value	Parameter Name	Parameter Value
Frequency range	77–82 GHz	Maximum sampling interval	13 MHz
Number of receiving units	4	Horizontal angular resolution	30°
Number of transmitting units	3	Vertical angular resolution	30°
Working power	13 dBm	Range resolution	3.8 cm

.

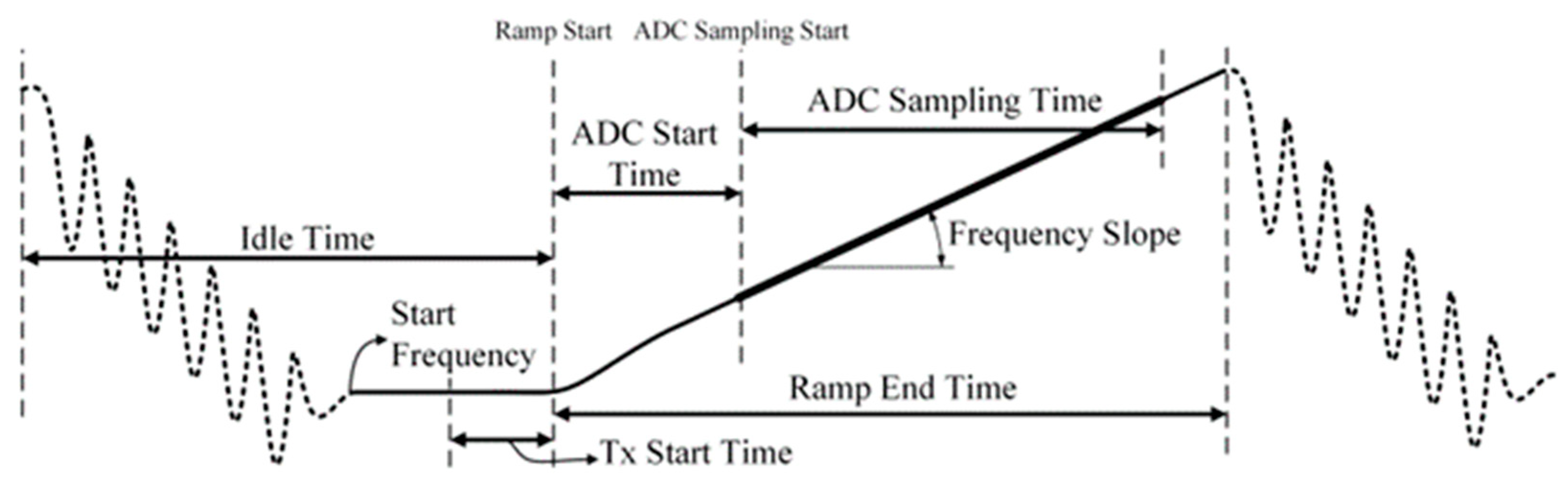
Using the combination of this radar and DCA1000, this device can realize real-time data acquisition and efficient transmission of dual-channel and four-channel low-voltage differential signals of radar sensors. The collected data are quickly transmitted to the computer via Ethernet, which greatly simplifies the subsequent analysis of the data and is suitable for diversified development scenarios such as image processing. The chirp slope is the slope of frequency computed from the sweep bandwidth of B and the chirp duration of T (K = B/T). The FMCW signal configuration parameters are shown in Figure 5.

In order to verify the effectiveness of the proposed algorithm in practical applications, the IWR1843 FM CW radar chip with an operating frequency of 77 GHz is used for experiments in this section. In the experiment, this paper uses the movement of the slide platform to simulate the synthetic aperture, and the radar is embedded in the slider as the hardware basis to realize the synthetic aperture. The IWR1843 radar chip is connected to the DCA1000 data processing board in the mobile module, and the captured data are uploaded to the computer instantaneously, with the help of Ethernet technology. In addition, the computer side also has the control function of the radar movement mode and can conduct in-depth processing of the subsequent collected data.

The motion trajectory of the moving module is designed as follows: first, it is stably fixed at a certain height, and then it moves gradually on the azimuth dimension to achieve the effect of synthetic aperture. After completing this step, it transitions to the next height dimension at the same raised height, and repeats the above operations until the cumulative distance traveled by the height dimension reaches the pre-set standard. The working block diagram of the imaging system platform and the imaging process are shown in Figure 6.

The MIMO imaging platform developed in this paper is shown in Figure 7.

3.2. Experimental Results and Analysis

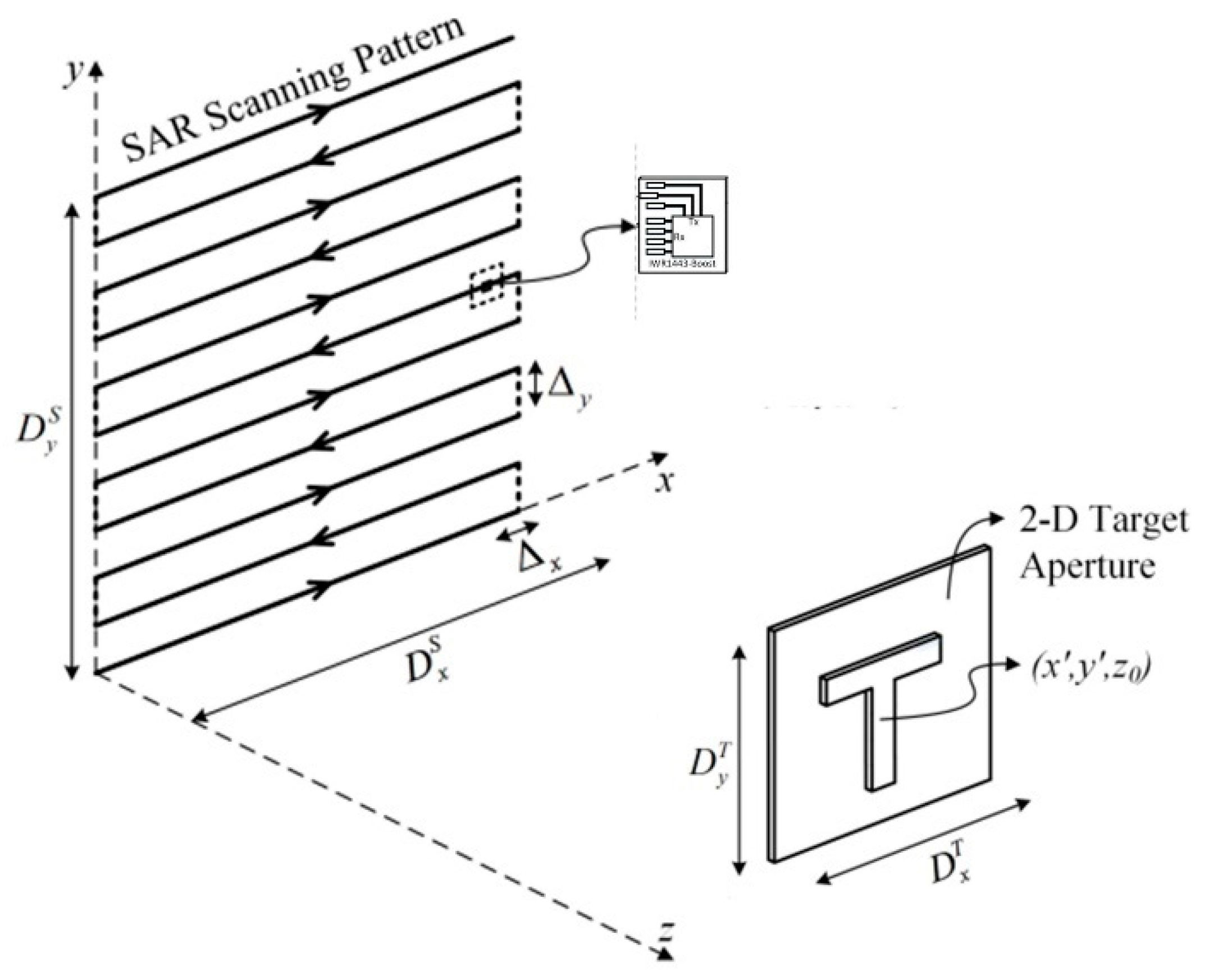
The scanning diagram of the imaging system is shown in Figure 8. Based on the data model, algorithm, and spatial sampling conditions proposed in this paper, combined with the hardware parameters of the IWR1843 millimeter wave radar chip, the experimental parameters are designed as shown in

Table 2. Experimental parameters of MIMO imaging.

Parameter Name	Parameter Value	Parameter Name	Parameter Value
X-direction scanning aperture	500 mm	Starting frequency	77 GHz
Y-direction scanning aperture	200 mm	Bandwidth	4 GHz
X-direction scanning interval	0.6 mm	Chirp Sampling number	512
Y-direction scanning interval	8 mm	Chirp slope	67
Number of antenna arrays	3 × 4

:

The hollow metal plate is taken as the imaging target, as shown in Figure 9. Its size is 200 mm × 100 mm, and the imaging distance is 400 mm.

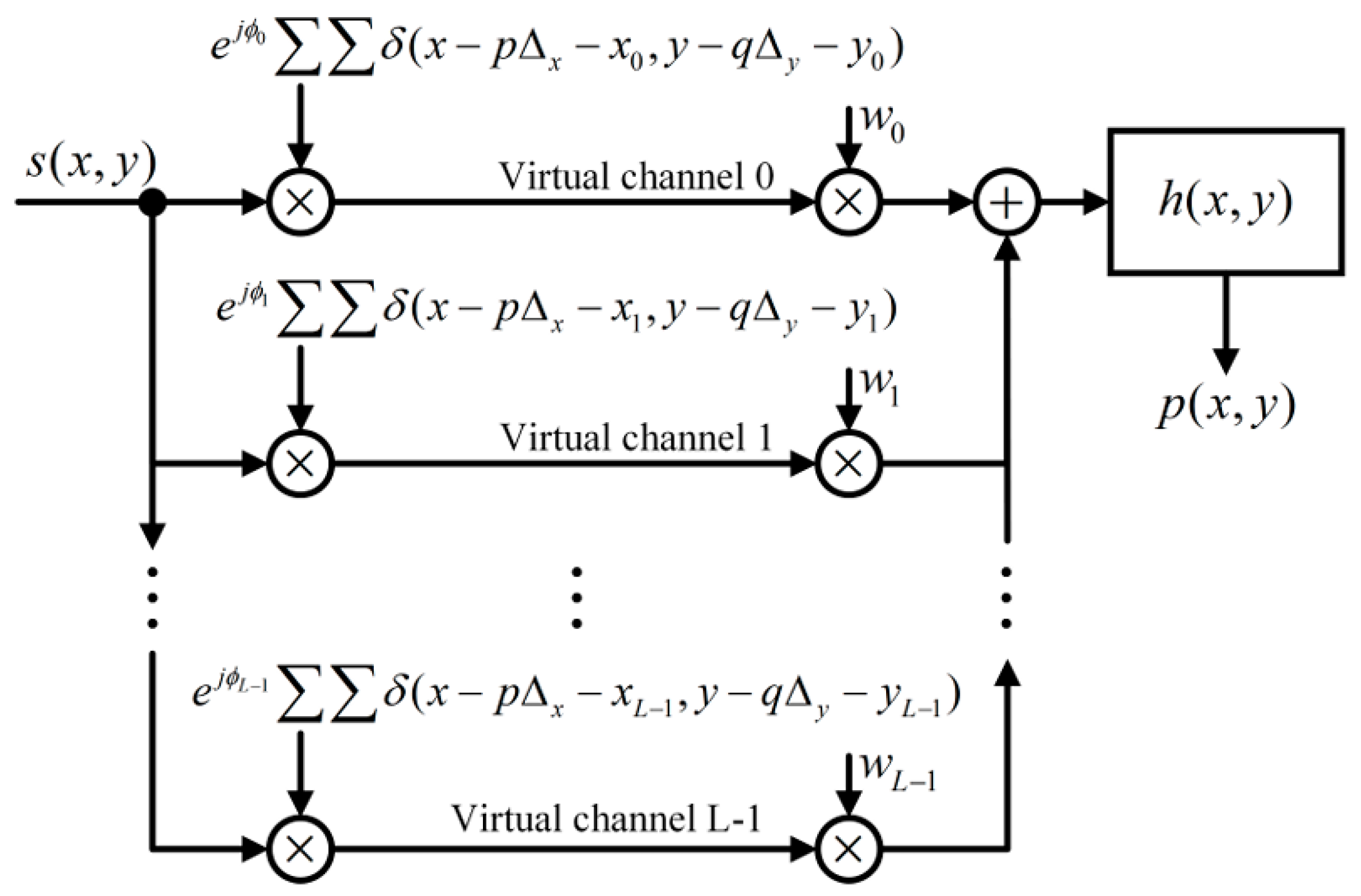
In the experiment of TDM–MIMO, the imaging effect of single-channel imaging under sparse sampling conditions, uncorrected MIMO virtual array imaging, and multi-channel coherent combination with complex gain vector w are compared. Imaging results are shown in Figure 9.

Through the analysis of Figure 10a, the single-channel algorithm fails to meet the requirements of the spatial Nyquist sampling law in the imaging process because the sampling is too sparse, so that the frequency spectrum aliasing occurs in the height dimension. This phenomenon directly leads to the reduction in the clarity of the target image, and the geometric shape features become blurred, making it difficult to clearly identify the geometric features of the three letters HIT. Specifically, the HIT letters are compressed and part of the information is lost. However, when the virtual array imaging algorithm under MIMO is adopted, it can clearly be seen that the geometric characteristics of the target have been significantly improved compared with the single-channel algorithm, which is more visible, but the boundary is still unclear, and some artifacts caused by aliasing are partially removed but still exist. At this time, the complex gain vector w is introduced for multi-channel coherent combination. The imaging results are shown in Figure 10d. The results of the compressed sensing imaging algorithm (TSA) are shown in Figure 10c. When one-half, two-dimensional random sampling is introduced, the hollow part of the letter has a very good sparse expression. Compared with the coherent superposition sampling algorithm proposed in this paper, the edge of the hollow part is somewhat fuzzy.

When the multi-channel spectrum and the complex gain vector are coherently combined, all artifacts are eliminated, the hollow letter geometry is clear, and the target size in the imaging results is completely consistent with the actual target parameters, which verifies the imaging effect and performance of the algorithm.

This shows that in an under-sampled scenario (∆y = 8 mm > 2λ), the image can be reconstructed without aliasing by using sparse virtual array. The reconstruction time of image slices at each frequency is not more than 100 ms, and the delay introduced by MATLAB is taken into account in the real-time implementation.

In the second imaging experiment, the experimental target size is 100 mm × 150 mm. In order to effectively account for the distortion of the reconstructed image caused by aliasing, the target distance z₀ = 275 mm, and the horizontal resolution is about 1.6 mm. The spatial sampling interval ∆x = 0.6 mm and ∆y = 8 mm. The sheet metal target is shown in Figure 11.

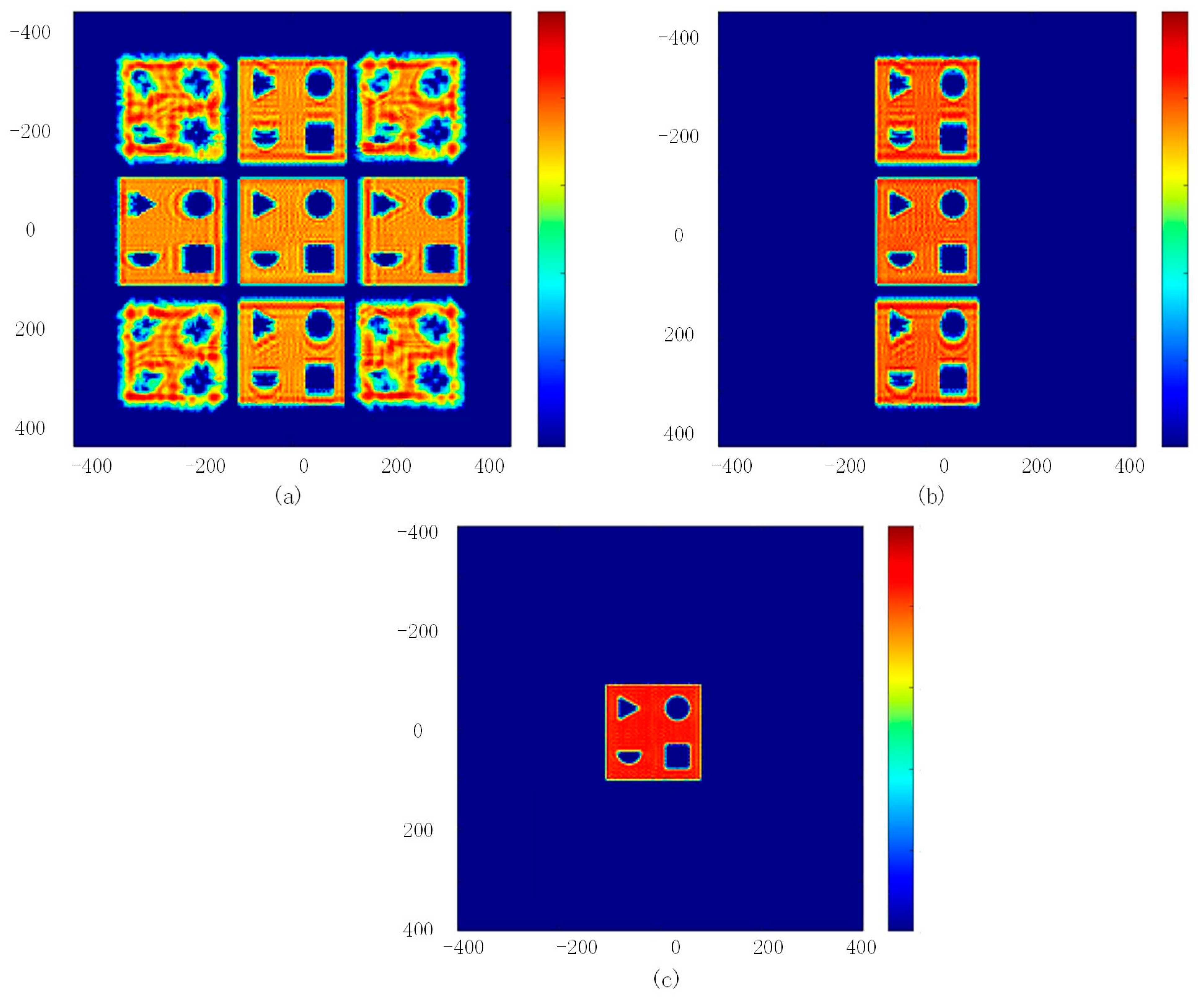
The sampling interval along the x axis satisfies the Nyquist criterion, and the aperture is under-sampled along the y axis. It can be seen from theoretical analysis that when the equivalent single-send single-receive decomposition virtual array imaging is used (single-channel imaging), L virtual channels will produce L-1 aliasing terms, the complex gain vector is used for coherent superposition, and L-1 aliasing terms can be offset by L subchannels. In Figure 10, this paper uses the IWR radar chip and adopts three transmitting and three receiving units for imaging. According to the theoretical analysis, the single-transmitting and single-receiving virtual channel is decomposed into nine virtual elements, and eight artifacts will be obtained in the single-channel imaging, as shown in Figure 12a. The six artifacts on the left and right sides will be eliminated by coherent combination of 1, 5, and 9 channels and selecting w gain in Figure 12b. When 1, 3, 5, 7, and 9 channels are selected for coherent superposition, the upper and lower artifacts are completely eliminated, as shown in Figure 12c.

In the case of under-sampling, high-precision, high-quality, and high-resolution imaging can still be maintained. The multi-channel coherent superposition algorithm can not only guarantee the imaging quality but also greatly reduce the imaging time, which opens up a broader application field for the construction of a near-field imaging system and algorithm.

4. Conclusions

MIMO imaging can greatly reduce the number of required physical arrays, shorten the sampling time, and reduce the difficulty of imaging system design and manufacturing. In order to eliminate the aliasing phenomenon in the MIMO equivalent virtual array imaging process, this paper studies the wave number spectrum of backscattered MIMO–SAR data, and establishes the nonlinear relationship between the wave number spectrum and reconstructed image. A sparse MIMO–SAR imaging algorithm based on the combined sparse sub-channel spectrum is proposed to reconstruct alix-free images. The algorithm can be used for the MIMO–SAR configuration of arbitrarily distributed transmitting and receiving arrays. It greatly simplifies the system structure and reduces the system cost. At the same time, this paper designs a new MIMO millimeter wave imaging system by using the FMCW chip and the slide platform as a planar synthetic aperture radar. Through theoretical reasoning and experimental verification, the sparse MIMO–SAR imaging algorithm is integrated with the imaging platform, and the near-field MIMO radar imaging can be efficiently and accurately realized. The system consists of modular millimeter wave sensors, which makes the system highly reconfigurable due to the common industry standard communication architecture used in this paper. The system can be used to validate new technologies and algorithms in the field of millimeter wave MIMO–SAR imaging.