Low-Bit-Depth Detection for Phase Retrieval with Higher Efficiency in Holographic Data Storage
Abstract
1. Introduction
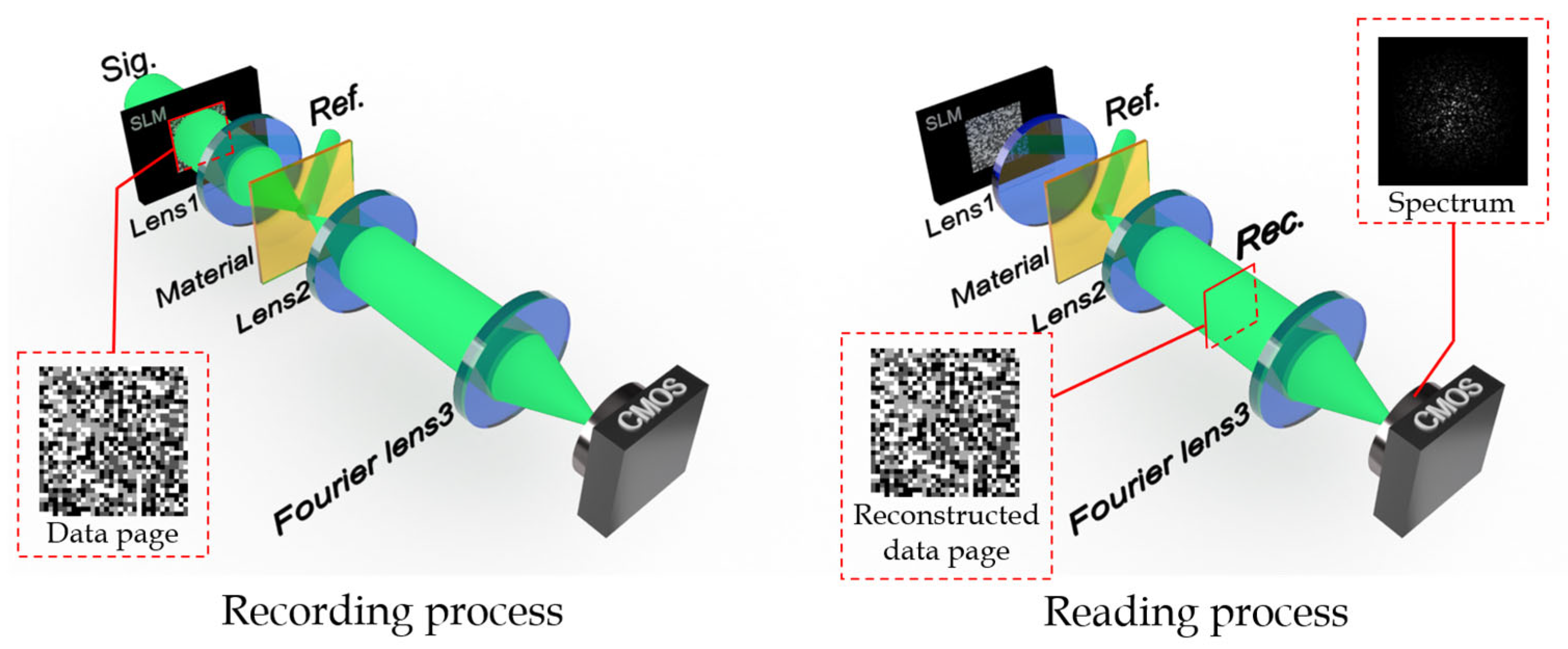
2. Theory and Methods
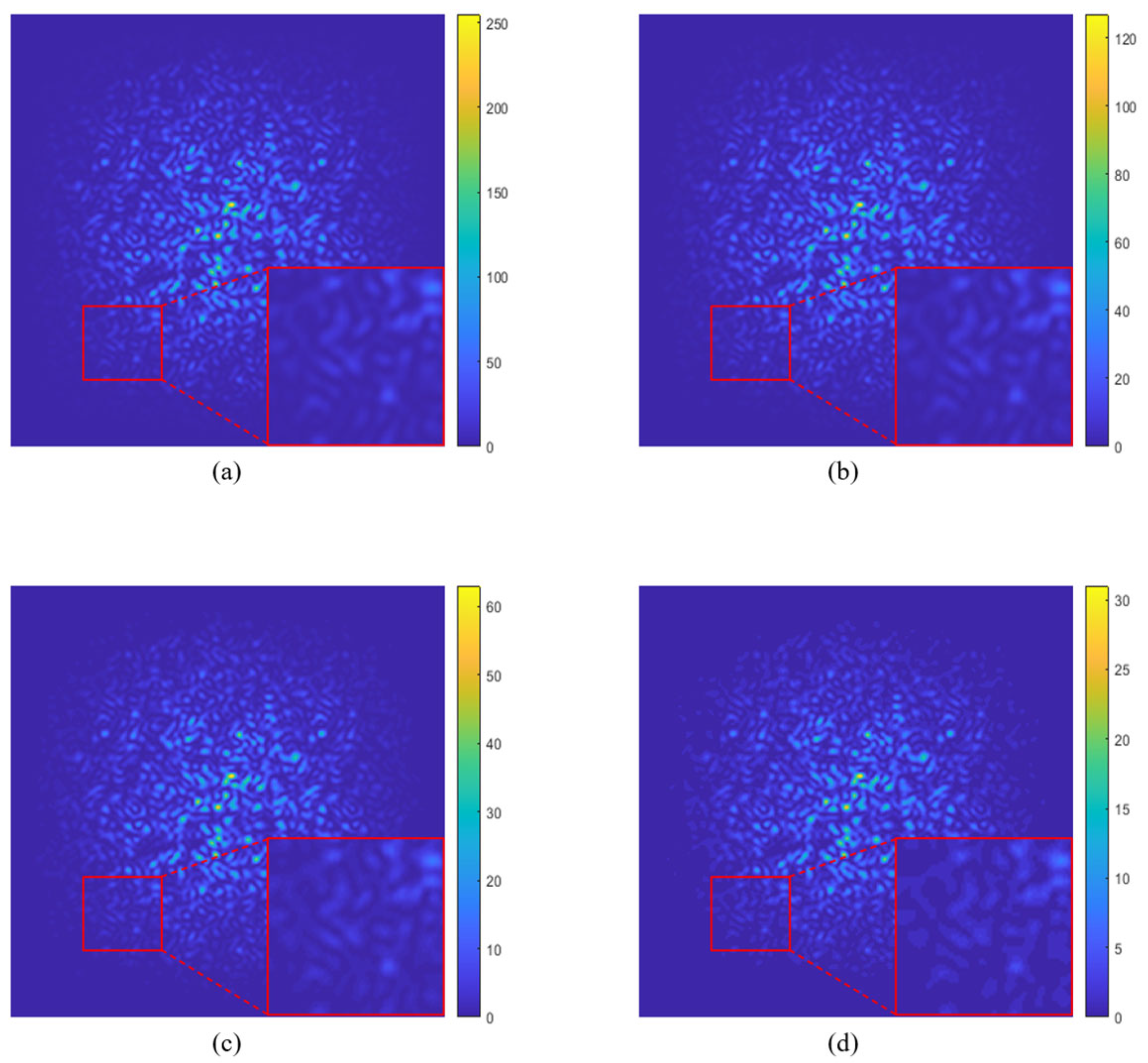
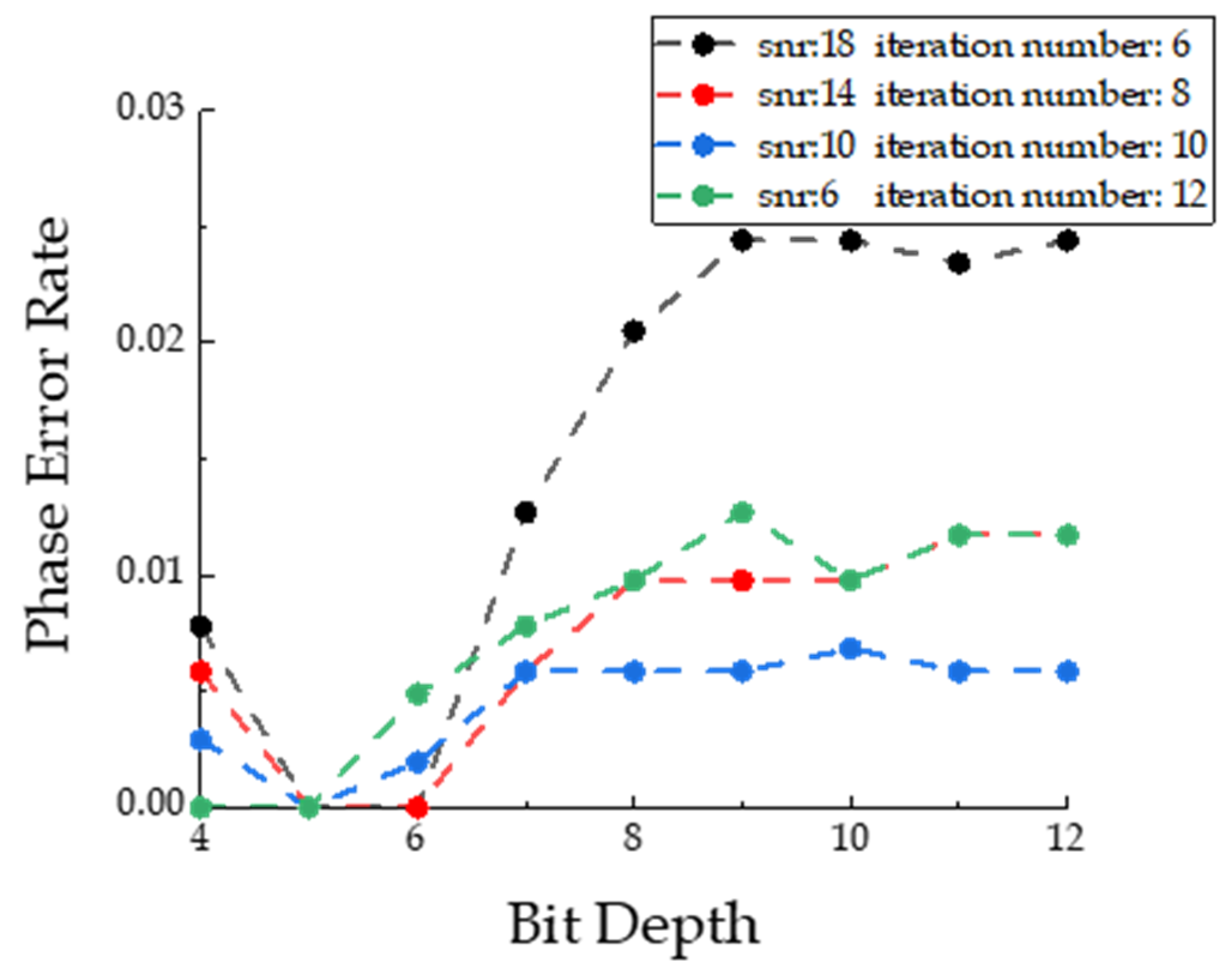
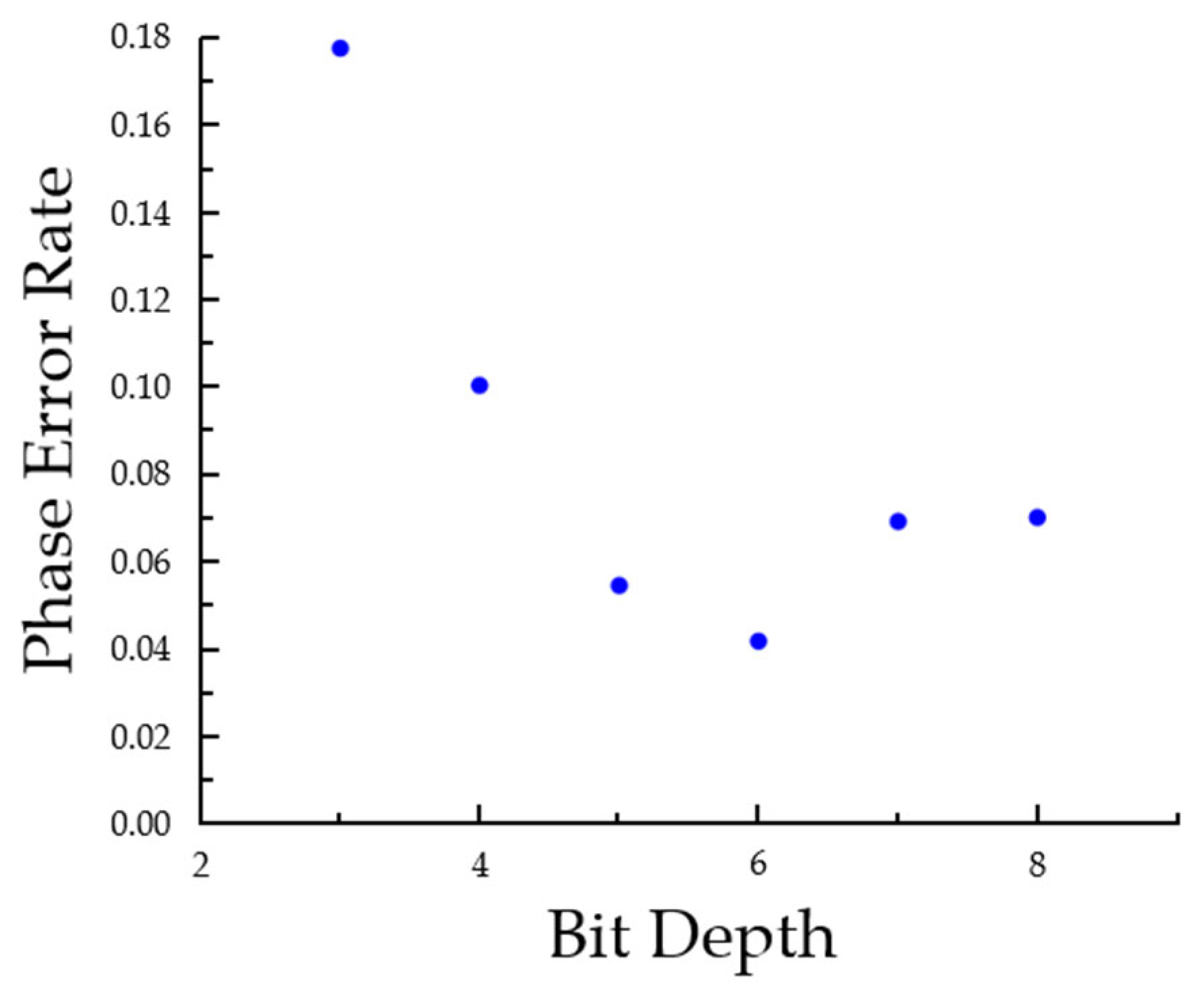
3. Simulation and Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reinsel, D.; Gantz, J.; Rydning, J. The Digitization of the World from Edge to Core. Available online: https://www.seagate.com/files/www-content/our-story/trends/files/idc-seagate-dataage-whitepaper.pdf (accessed on 16 July 2024).
- Sony, Panasonic. White Paper: Archival Disc Technology. Available online: https://panasonic.cn/wp-content/uploads/2020/05/Archival-Disc-Technology-%EF%BC%9A2nd-Edition.pdf (accessed on 16 July 2024).
- Lin, X.; Hao, J.; Zheng, M.; Dai, T.; Li, H.; Ren, Y. Optical holographic data storage-The time for new development. Opto-Electron. Eng. 2019, 46, 180642. [Google Scholar]
- Van Heerden, P.J. Theory of optical information storage in solids. Appl. Opt. 1963, 2, 393–400. [Google Scholar] [CrossRef]
- Pasltis, D.; Levene, M.; Pu, A.; Barbastathis, G.; Curtis, K. Holographic digital data storage using shift multiplexing. Opt. Lett. 1995, 20, 782. [Google Scholar] [CrossRef] [PubMed]
- Takabayashi, M.; Okamoto, A.; Eto, T.; Okamoto, T. Shift-multiplexed self-referential holographic data storage. Appl. Opt. 2014, 53, 4375–4381. [Google Scholar] [CrossRef] [PubMed]
- Rakuljic, G.; Leyva, V.; Yariv, A. Optical data storage by using orthogonal wavelength-multiplexed volume holograms. Opt. Lett. 1992, 17, 1471–1473. [Google Scholar] [CrossRef] [PubMed]
- Mok, F. Angle-multiplexed storage of 5000 holograms in lithium niobite. Opt. Lett. 1993, 18, 915–917. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Wang, Z.; Zhang, H.; Jin, G.; Gu, C. Volume holographic printing using unconventional angular multiplexing for three-dimensional display. Appl. Opt. 2016, 55, 6046. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, X.; Xu, Y.; Xian, M.; Feng, Z.; Zhu, L.; Cao, Y.; Lan, S.; Guan, B.; Qiu, C.; Gu, M.; et al. Synthetic helical dichroism for six-dimensional optical orbital angular momentum multiplexing. Nat. Photonics 2021, 15, 901–907. [Google Scholar] [CrossRef]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Wang, Q.; Eric, P.; Yang, Q.; Zhang, X.; Quan, X.; Xu, Y.; Han, J.; Zhang, W. Reflective chiral meta-holography: Multiplexing holograms for circularly polarized waves. Light Sci. Appl. 2018, 7, 25. [Google Scholar] [CrossRef]
- Guo, J.; Wang, T.; Quan, B.; Zhao, H.; Gu, C.; Li, J.; Wang, X.; Situ, G.; Zhang, Y. Polarization multiplexing for double images display. Opto-Electron. Adv. 2019, 2, 180029. [Google Scholar] [CrossRef]
- Khonina, S.; Kazanskiy, N.; Butt, M.; Karpeev, S. Optical multiplexing techniques and their marriage for on-chip and optical fiber communication: A review. Opto-Electron. Adv. 2022, 5, 210127. [Google Scholar] [CrossRef]
- Tang, D.; Shao, Z.; Xie, X.; Zhou, Y.; Zhang, X.; Fan, F.; Wen, S. Flat multifunctional liquid crystal elements through multi-dimensional information multiplexing. Opto-Electron. Adv. 2023, 6, 220063. [Google Scholar] [CrossRef]
- Haw, M. Holographic data storage: The light fantastic. Nature 2003, 422, 556–558. [Google Scholar] [CrossRef] [PubMed]
- Yoneda, N.; Nobukawa, T.; Morimoto, T.; Saita, Y.; Nomura, T. Common-path angular-multiplexing holographic data storage based on computer-generated holography. Opt. Lett. 2021, 46, 2920–2923. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Liu, J.; Hao, J.; Wang, K.; Zhang, Y.; Li, H.; Horimai, H.; Tan, X. Collinear holographic data storage technologies. Opto-Electron. Adv. 2020, 3, 19000401–19000408. [Google Scholar] [CrossRef]
- Nobukawa, T.; Nomura, T. Multilevel recording of complex amplitude data pages in a holographic data storage system using digital holography. Opt. Express 2016, 24, 21001–21011. [Google Scholar] [CrossRef] [PubMed]
- Nobukawa, T.; Nomura, T. Linear phase encoding for holographic data storage with a single phase-only spatial light modulator. Appl. Opt. 2016, 55, 2565–2573. [Google Scholar] [CrossRef]
- Yan, X.; Liu, X.; Li, J.; Zhang, Y.; Chang, H.; Jing, T.; Hu, H.; Qu, Q.; Wang, X.; Jiang, X. Generating multi-depth 3d holograms using a fully convolutional neural network. Adv. Sci. 2024, 2308886. [Google Scholar] [CrossRef]
- Hao, J.; Lin, X.; Lin, Y.; Chen, M.; Chen, R.; Situ, G.; Horimai, H.; Tan, X. Lensless complex amplitude demodulation based on deep learning in holographic data storage. Opto-Electron. Adv. 2023, 6, 220157. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Lee, J. A Nonlinear Convolutional Neural Network-Based Equalizer for Holographic Data Storage Systems. Appl. Sci. 2023, 13, 13029. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, F.; Wang, L.; Lu, X.; Zhao, S. Multiplexing Perfect Optical Vortex for Holographic Data Storage. Photonics 2023, 10, 720. [Google Scholar] [CrossRef]
- Wang, J.; Tan, X.; Qi, P.; Wu, C.; Huang, L.; Xu, X.; Huang, Z.; Zhu, L.; Zhang, Y.; Lin, X.; et al. Linear polarization holography. Opto-Electron. Sci. 2022, 1, 210009. [Google Scholar] [CrossRef]
- Neifeld, M.; Chou, W. Information theoretic limits to the capacity of volume holographic optical memory. Appl. Opt. 1997, 36, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Takabayashi, M.; Okamoto, A.; Tomita, A.; Bunsen, M. Symbol Error Characteristics of Hybrid-Modulated Holographic Data Storage by Intensity and Multi Phase Modulation. Jpn. J. Appl. Phys. 2011, 50, 09ME05. [Google Scholar] [CrossRef]
- Li, Z.; Yan, M.; Zeng, T.; Zhang, G. Phase retrieval from incomplete data via weighted nuclear norm minimization. Pattern Recognit. 2022, 125, 108537. [Google Scholar] [CrossRef]
- Jeon, S.; Gil, S. 2-step Phase-shifting Digital Holographic Optical Encryption and Error Analysis. J. Opt. Soc. Korea 2011, 15, 244–251. [Google Scholar] [CrossRef][Green Version]
- Maiden, A.; Rodenburg, J. An improved psychographic phase retrieval algorithm for diffractive imaging. Ultramicroscopy 2009, 109, 1256–1262. [Google Scholar] [CrossRef]
- Pan, X.; Liu, C.; Lin, Q.; Zhu, J. Ptycholographic iterative engine with self-positioned scanning illumination. Opt. Express 2013, 21, 6162–6168. [Google Scholar] [CrossRef]
- Volkov, V.; Zhu, Y.; Graef, M. A new symmetrized solution for phase retrieval using the transport of intensity equation. Micron 2002, 33, 411–416. [Google Scholar] [CrossRef]
- Fienup, J. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Memmolo, P.; Ferraro, P.; Cao, L. Dual-plane coupled phase retrieval for non-prior holographic imaging. PhotoniX 2022, 3, 3. [Google Scholar] [CrossRef]
- Shu, Y.; Sun, J.; Lyu, J.; Fan, Y.; Zhou, N.; Ye, R.; Zheng, G.; Chen, Q.; Zuo, C. Adaptive optical quantitative phase imaging based on annular illumination Fourier ptychographic microscopy. PhotoniX 2022, 3, 24. [Google Scholar] [CrossRef]




| Phase Level | Amount of Data | Oversampling | PER | ||||
|---|---|---|---|---|---|---|---|
| 8-bit | 7-bit | 6-bit | 5-bit | 4-bit | |||
| 3 phase level | 16 × 16 | 3 × 3 | 0.004 | 0 | 0 | 0.004 | 0.019 |
| 4 × 4 | 0 | 0 | 0 | 0 | 0.008 | ||
| 5 × 5 | 0 | 0 | 0 | 0 | 0 | ||
| 32 × 32 | 3 × 3 | 0.019 | 0.018 | 0.005 | 0.022 | 0.077 | |
| 4 × 4 | 0.017 | 0.017 | 0.012 | 0.024 | 0.063 | ||
| 5 × 5 | 0.087 | 0.084 | 0.069 | 0.077 | 0.127 | ||
| 48 × 48 | 3 × 3 | 0.087 | 0.084 | 0.068 | 0.065 | 0.095 | |
| 4 × 4 | 0.195 | 0.192 | 0.180 | 0.178 | 0.185 | ||
| 5 × 5 | 0.265 | 0.263 | 0.264 | 0.262 | 0.265 | ||
| 4 phase level | 16 × 16 | 3 × 3 | 0.027 | 0.019 | 0.011 | 0.07 | 0.152 |
| 4 × 4 | 0.012 | 0.012 | 0.004 | 0.016 | 0.089 | ||
| 5 × 5 | 0.012 | 0.008 | 0.008 | 0.019 | 0.070 | ||
| 32 × 32 | 3 × 3 | 0.052 | 0.047 | 0.017 | 0.057 | 0.115 | |
| 4 × 4 | 0.07 | 0.069 | 0.041 | 0.055 | 0.099 | ||
| 5 × 5 | 0.109 | 0.107 | 0.084 | 0.113 | 0.167 | ||
| 48 × 48 | 3 × 3 | 0.153 | 0.146 | 0.125 | 0.134 | 0.182 | |
| 4 × 4 | 0.250 | 0.250 | 0.238 | 0.235 | 0.248 | ||
| 5 × 5 | 0.321 | 0.319 | 0.321 | 0.317 | 0.326 | ||
| 5 phase level | 16 × 16 | 3 × 3 | 0.167 | 0.160 | 0.078 | 0.086 | 0.141 |
| 4 × 4 | 0.113 | 0.113 | 0.066 | 0.074 | 0.105 | ||
| 5 × 5 | 0.047 | 0.043 | 0.058 | 0.082 | 0.141 | ||
| 32 × 32 | 3 × 3 | 0.154 | 0.151 | 0.126 | 0.171 | 0.254 | |
| 4 × 4 | 0.165 | 0.159 | 0.146 | 0.191 | 0.281 | ||
| 5 × 5 | 0.198 | 0.200 | 0.208 | 0.226 | 0.297 | ||
| 48 × 48 | 3 × 3 | 0.227 | 0.228 | 0.208 | 0.213 | 0.239 | |
| 4 × 4 | 0.313 | 0.313 | 0.299 | 0.291 | 0.315 | ||
| 5 × 5 | 0.359 | 0.363 | 0.354 | 0.350 | 0.354 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zheng, S.; Lin, Y.; Song, H.; Xu, X.; Li, X.; Zheng, J.; Cao, Q.; Lin, X.; Tan, X. Low-Bit-Depth Detection for Phase Retrieval with Higher Efficiency in Holographic Data Storage. Photonics 2024, 11, 680. https://doi.org/10.3390/photonics11070680
Liu H, Zheng S, Lin Y, Song H, Xu X, Li X, Zheng J, Cao Q, Lin X, Tan X. Low-Bit-Depth Detection for Phase Retrieval with Higher Efficiency in Holographic Data Storage. Photonics. 2024; 11(7):680. https://doi.org/10.3390/photonics11070680
Chicago/Turabian StyleLiu, Hongjie, Shujun Zheng, Yongkun Lin, Haiyang Song, Xianmiao Xu, Xiong Li, Jihong Zheng, Qiang Cao, Xiao Lin, and Xiaodi Tan. 2024. "Low-Bit-Depth Detection for Phase Retrieval with Higher Efficiency in Holographic Data Storage" Photonics 11, no. 7: 680. https://doi.org/10.3390/photonics11070680
APA StyleLiu, H., Zheng, S., Lin, Y., Song, H., Xu, X., Li, X., Zheng, J., Cao, Q., Lin, X., & Tan, X. (2024). Low-Bit-Depth Detection for Phase Retrieval with Higher Efficiency in Holographic Data Storage. Photonics, 11(7), 680. https://doi.org/10.3390/photonics11070680





