A Reduction in the Rotational Velocity Measurement Deviation of the Vortex Beam Superposition State for Tilted Object
Abstract
1. Introduction
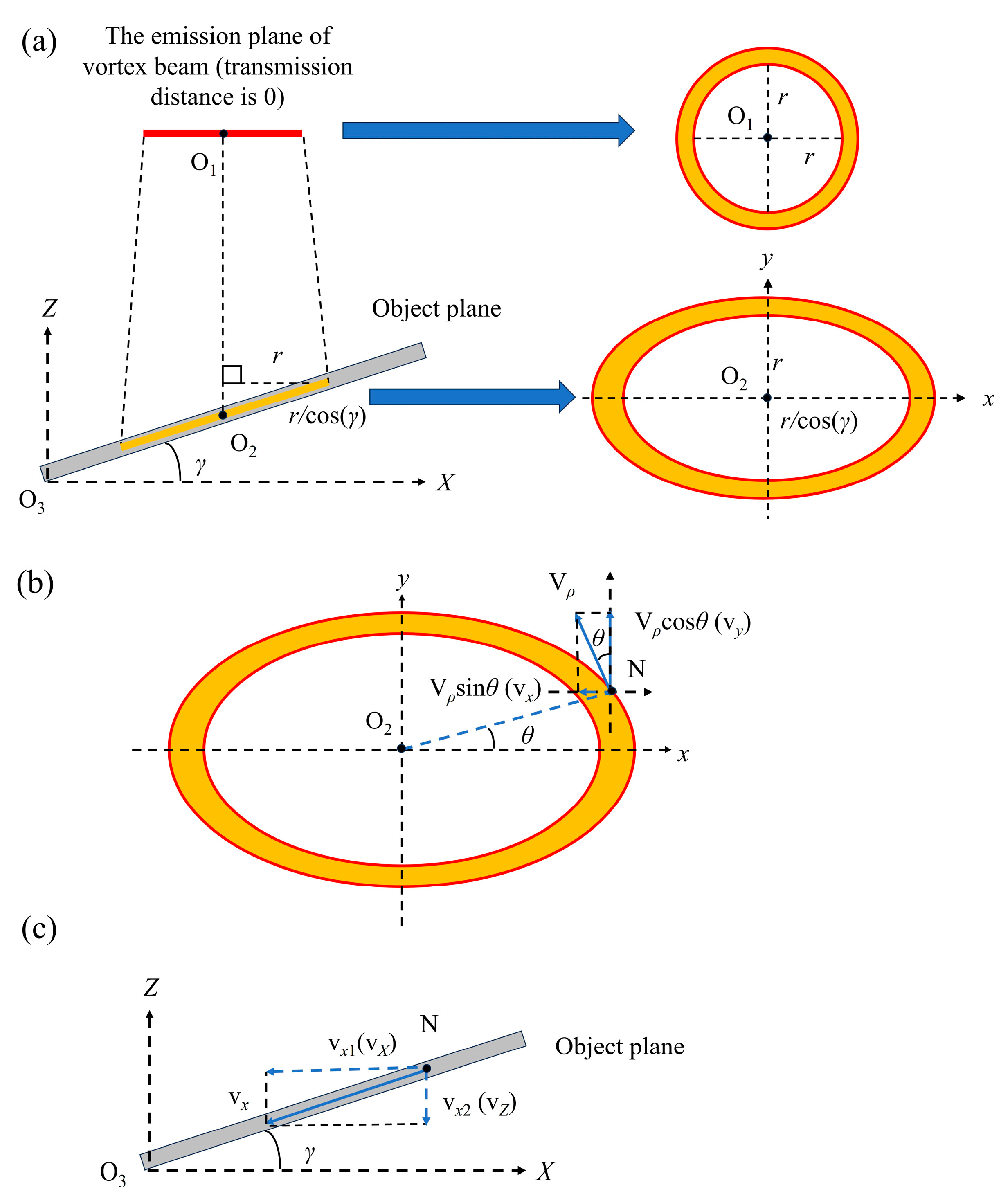
2. Principle and Theory
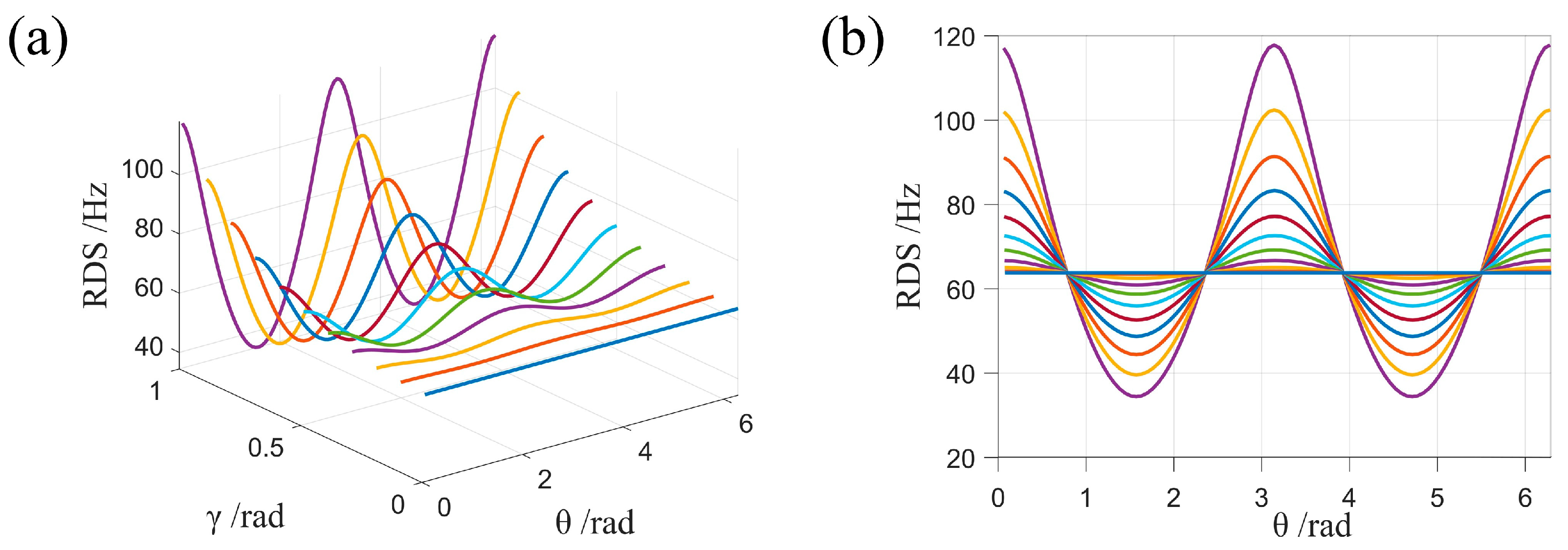
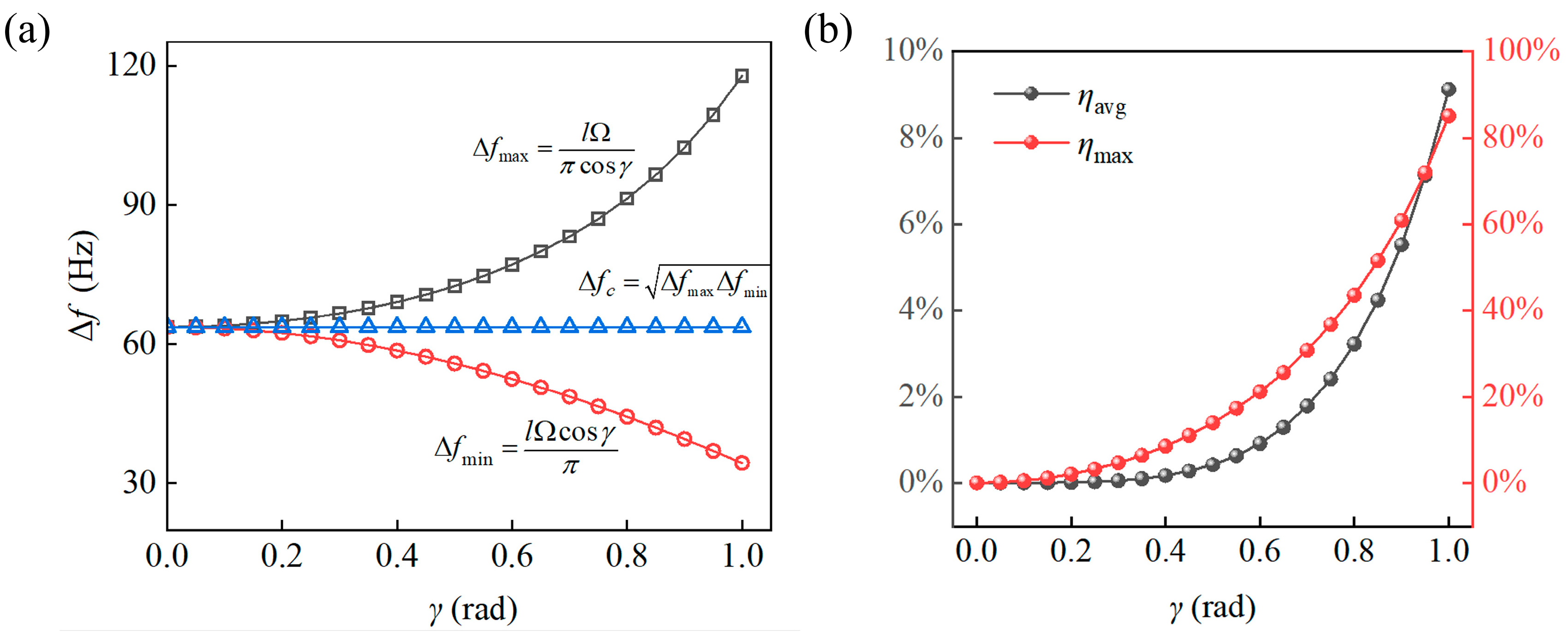
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Lavery, M.P.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Padgett, M.J.; Wang, J. Sharing a common origin between the rotational and linear Doppler effects. Laser Photonics Rev. 2017, 11, 1700183. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Hermosa, N.; Belmonte, A.; Torres, J.P. Measuring the translational and rotational velocities of particles in helical motion using structured light. Opt. Express 2014, 22, 16504–16509. [Google Scholar] [CrossRef]
- Lavery, M.P.; Barnett, S.M.; Speirits, F.C.; Padgett, M.J. Observation of the rotational Doppler shift of a white-light, orbital-angular-momentum-carrying beam backscattered from a rotating body. Optica 2014, 1, 1–4. [Google Scholar] [CrossRef]
- Neo, R.; Leon-Saval, S.; Bland-Hawthorn, J.; Molina-Terriza, G. OAM interferometry: The detection of the rotational Doppler shift. Opt. Express 2017, 25, 21159–21170. [Google Scholar] [CrossRef]
- Zhang, Z.; Cen, L.; Zhang, J.; Hu, J.; Wang, F.; Zhao, Y. Rotation velocity detection with orbital angular momentum light spot completely deviated out of the rotation center. Opt. Express 2020, 28, 6859–6867. [Google Scholar] [CrossRef]
- Deng, J.; Li, K.F.; Liu, W.; Li, G. Cascaded rotational Doppler effect. Opt. Lett. 2019, 44, 2346–2349. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Liu, T.; Ren, Y.; Li, Z.; Wang, C.; Shao, Q. Detection of spinning objects at oblique light incidence using the optical rotational Doppler effect. Opt. Express 2019, 27, 24781–24792. [Google Scholar] [CrossRef]
- Zhai, Y.; Fu, S.; Yin, C.; Zhou, H.; Gao, C. Detection of angular acceleration based on optical rotational Doppler effect. Opt. Express 2019, 27, 15518–15527. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Wang, Q.; Feng, R.; Zhao, Y. Enhanced Measurement of Vortex Beam Rotation Using Polarization-Assisted Particle Swarm Optimization for Phase Retrieval. Photonics 2023, 10, 1293. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, T.; Liu, Z.; Qiu, S.; Xu, L.; Ren, Y. Detection of a spinning object with circular procession using an optical vortex beam. Opt. Lett. 2022, 47, 2398–2401. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Ding, Y.; Liu, T.; Liu, Z.; Ren, Y. Rotational object detection at noncoaxial light incidence based on the rotational Doppler effect. Opt. Express 2022, 30, 20441–20450. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, Y.; Wang, F.; Zhao, Y. Measuring the rotational velocity and acceleration based on orbital angular momentum modulation and time–frequency analysis method. Opt. Commun. 2022, 502, 127414. [Google Scholar] [CrossRef]
- Zhao, M.; Gao, X.; Xie, M.; Zhai, W.; Xu, W.; Huang, S.; Gu, W. Measurement of the rotational Doppler frequency shift of a spinning object using a radio frequency orbital angular momentum beam. Opt. Lett. 2016, 41, 2549–2552. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Wang, T.; Zhang, Z.; Zhai, Y.; Gao, C. Non-diffractive Bessel-Gauss beams for the detection of rotating object free of obstructions. Opt. Express 2017, 25, 20098–20108. [Google Scholar] [CrossRef]
- Qiu, S.; Ren, Y.; Sha, Q.; Ding, Y.; Wang, C.; Li, Z.; Liu, T. Observation of the rotational Doppler shift of the ring Airy Gaussian vortex beam. Opt. Commun. 2021, 490, 126900. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Hermosa, N.; Belmonte, A.; Torres, J.P. Direction-sensitive transverse velocity measurement by phase-modulated structured light beams. Opt. Lett. 2014, 39, 5415–5418. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, T.; Ren, Y.; Qiu, S.; Wang, C.; Wang, H. Direction-sensitive detection of a spinning object using dual-frequency vortex light. Opt. Express 2021, 29, 7453–7463. [Google Scholar] [CrossRef]
- Guo, K.; Lei, S.; Lei, Y.; Zhou, H.; Guo, Z. Research on detecting targets’ accelerations based on vortex electromagnetic wave in non-line-of-sight scenario. IEEE Sens. J. 2023, 23, 4078–4084. [Google Scholar] [CrossRef]
- Guo, K.; Lei, S.; Lei, Y.; Zhou, H.-P.; Guo, Z.-Y. Detection accuracy of target accelerations based on vortex electromagnetic wave in keyhole space. Chin. Phys. B 2024, 33, 020603. [Google Scholar] [CrossRef]
- Fang, L.; Wan, Z.; Forbes, A.; Wang, J. Vectorial doppler metrology. Nat. Commun. 2021, 12, 4186. [Google Scholar] [CrossRef] [PubMed]
- Vasnetsov, M.; Pas’ Ko, V.; Soskin, M. Analysis of orbital angular momentum of a misaligned optical beam. New J. Phys. 2005, 7, 46. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K.; Allen, L.; Padgett, M. The production of multiringed Laguerre–Gaussian modes by computer-generated holograms. J. Mod. Opt. 1998, 45, 1231–1237. [Google Scholar] [CrossRef]
- Padgett, M.; Allen, L. The Poynting vector in Laguerre-Gaussian laser modes. Opt. Commun. 1995, 121, 36–40. [Google Scholar] [CrossRef]
- Belmonte, A.; Torres, J.P. Optical Doppler shift with structured light. Opt. Lett. 2011, 36, 4437–4439. [Google Scholar] [CrossRef]

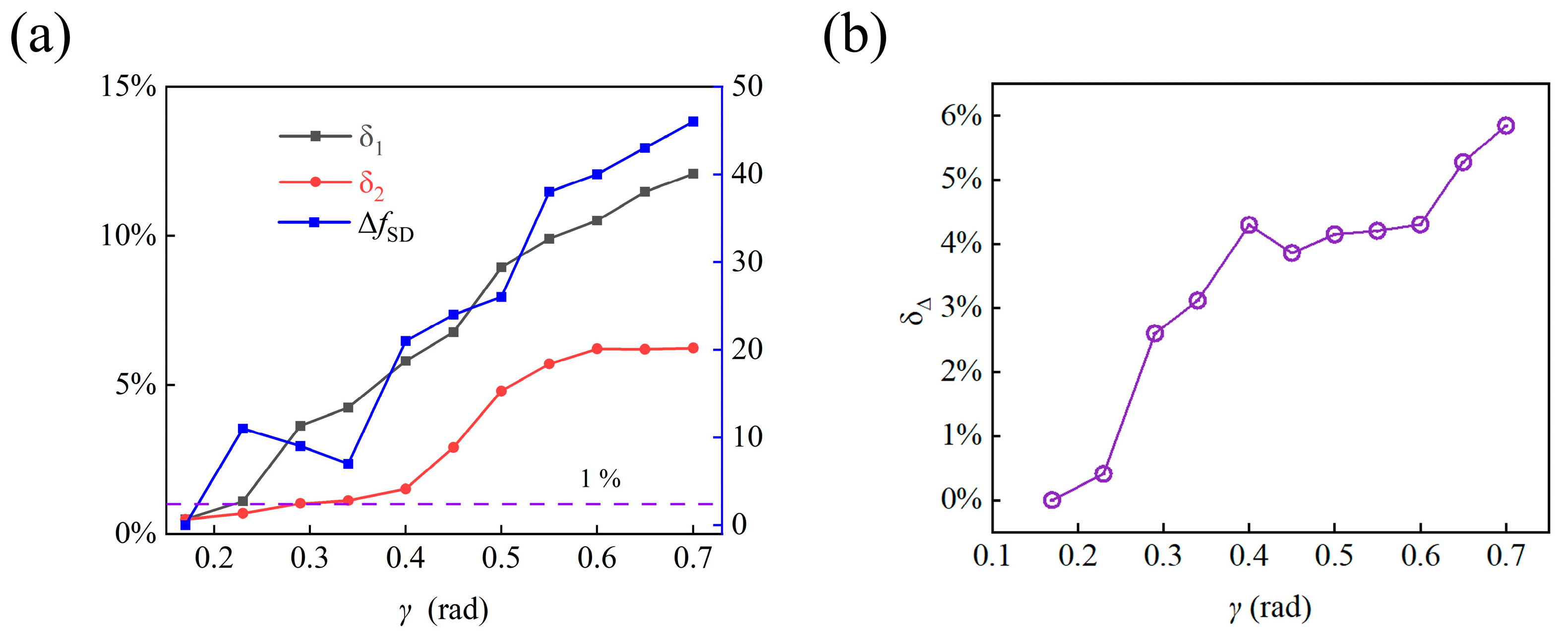
| γ | δ1 | δ2 | ||||
|---|---|---|---|---|---|---|
| 0.17 | 64 | 64 | 64 | 0.48% | 64 | 0.48% |
| 0.34 | 68 | 61 | 61 | 4.22% | 64.40 | 1.11% |
| 0.50 | 81 | 55 | 70 | 9.91% | 66.74 | 4.78% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yan, Y.; Zhang, Z.; Liu, H.; Lv, X.; Cui, C.; Yun, H.; Feng, R.; Zhao, Y. A Reduction in the Rotational Velocity Measurement Deviation of the Vortex Beam Superposition State for Tilted Object. Photonics 2024, 11, 679. https://doi.org/10.3390/photonics11070679
Wang H, Yan Y, Zhang Z, Liu H, Lv X, Cui C, Yun H, Feng R, Zhao Y. A Reduction in the Rotational Velocity Measurement Deviation of the Vortex Beam Superposition State for Tilted Object. Photonics. 2024; 11(7):679. https://doi.org/10.3390/photonics11070679
Chicago/Turabian StyleWang, Hongyang, Yinyin Yan, Zijing Zhang, Hao Liu, Xinran Lv, Chengshuai Cui, Hao Yun, Rui Feng, and Yuan Zhao. 2024. "A Reduction in the Rotational Velocity Measurement Deviation of the Vortex Beam Superposition State for Tilted Object" Photonics 11, no. 7: 679. https://doi.org/10.3390/photonics11070679
APA StyleWang, H., Yan, Y., Zhang, Z., Liu, H., Lv, X., Cui, C., Yun, H., Feng, R., & Zhao, Y. (2024). A Reduction in the Rotational Velocity Measurement Deviation of the Vortex Beam Superposition State for Tilted Object. Photonics, 11(7), 679. https://doi.org/10.3390/photonics11070679





