Computation Theory of Large-Scale Partially Coherent Imaging by the Modified Modal Expansion Method
Abstract
1. Introduction
2. Theory
2.1. A Review of the Theory of Partially Coherent Imaging with Coherent-Mode Representation
2.2. Computation Theory of Large-Scale Partial Coherent Imaging with Modified Modal Expansion
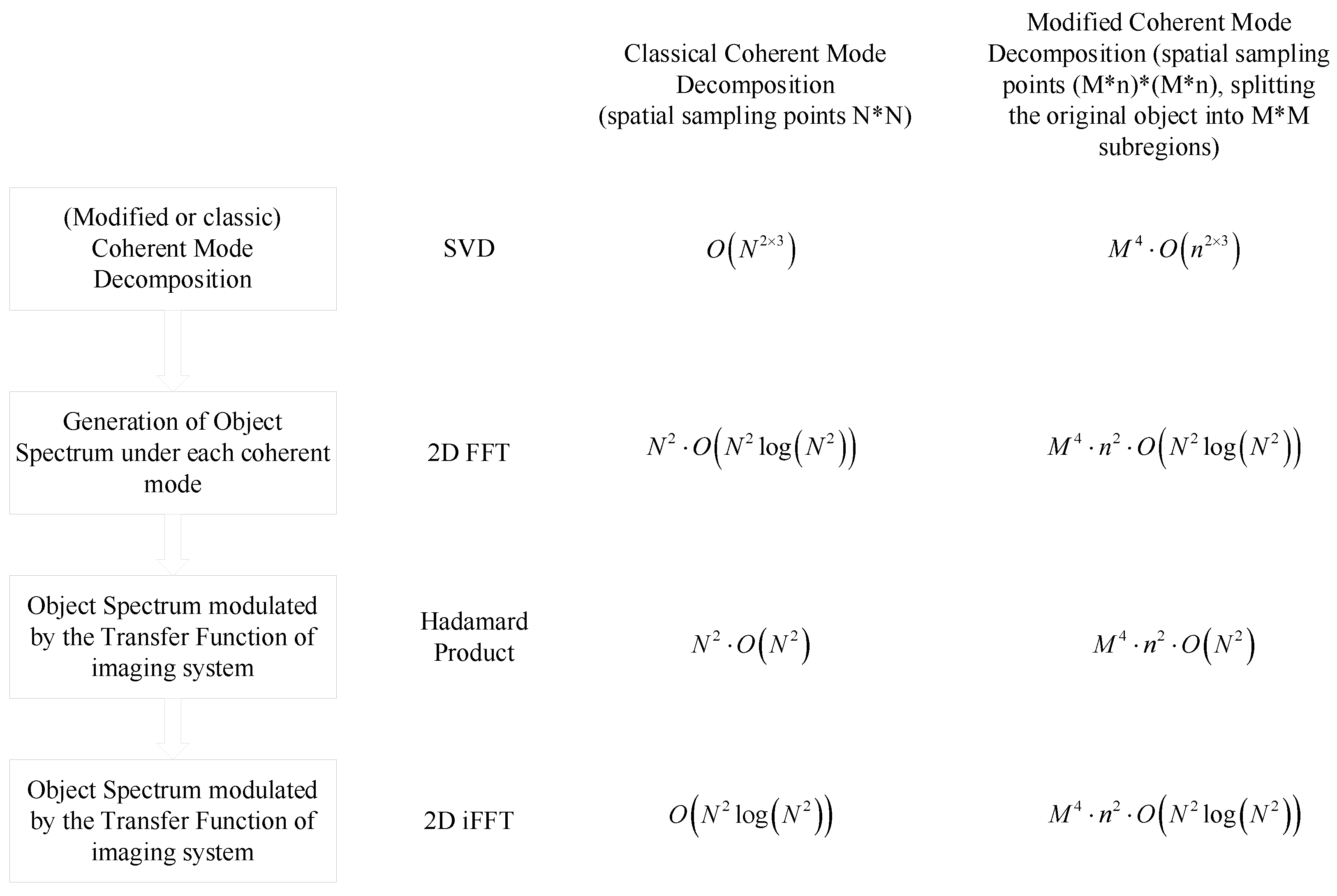
2.3. Summary of the Computation Procedure
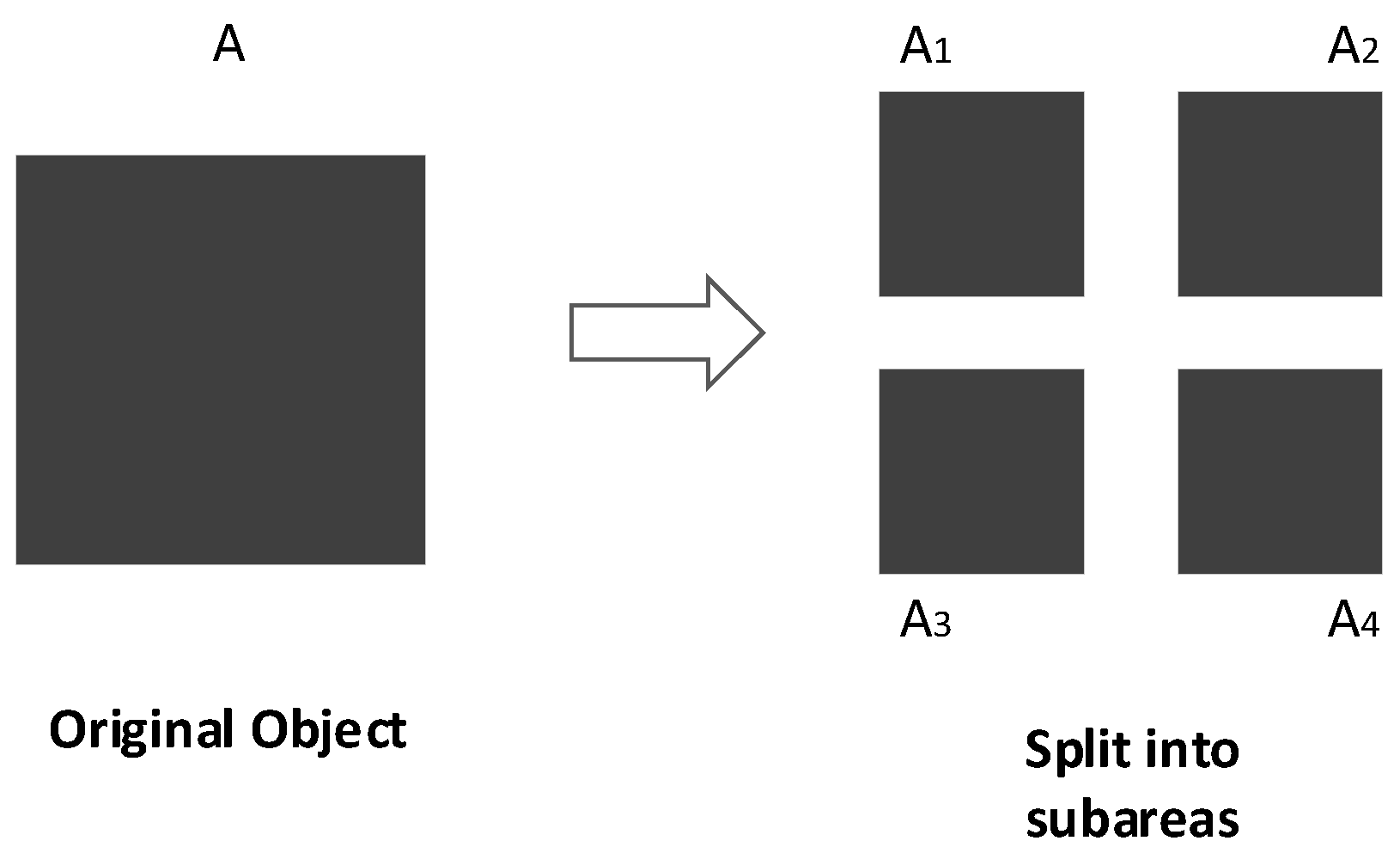
- Split the original partially coherent illuminated area into P subregions ~;
- Divide the original CSD matrix W into several sub-matrices according to the division of the lighting area as Equation (12). Through this step, we can obtain P diagonal sub-matrices representing the CSD of each subregion and sub-matrices representing the degree of coherence between different subregions;
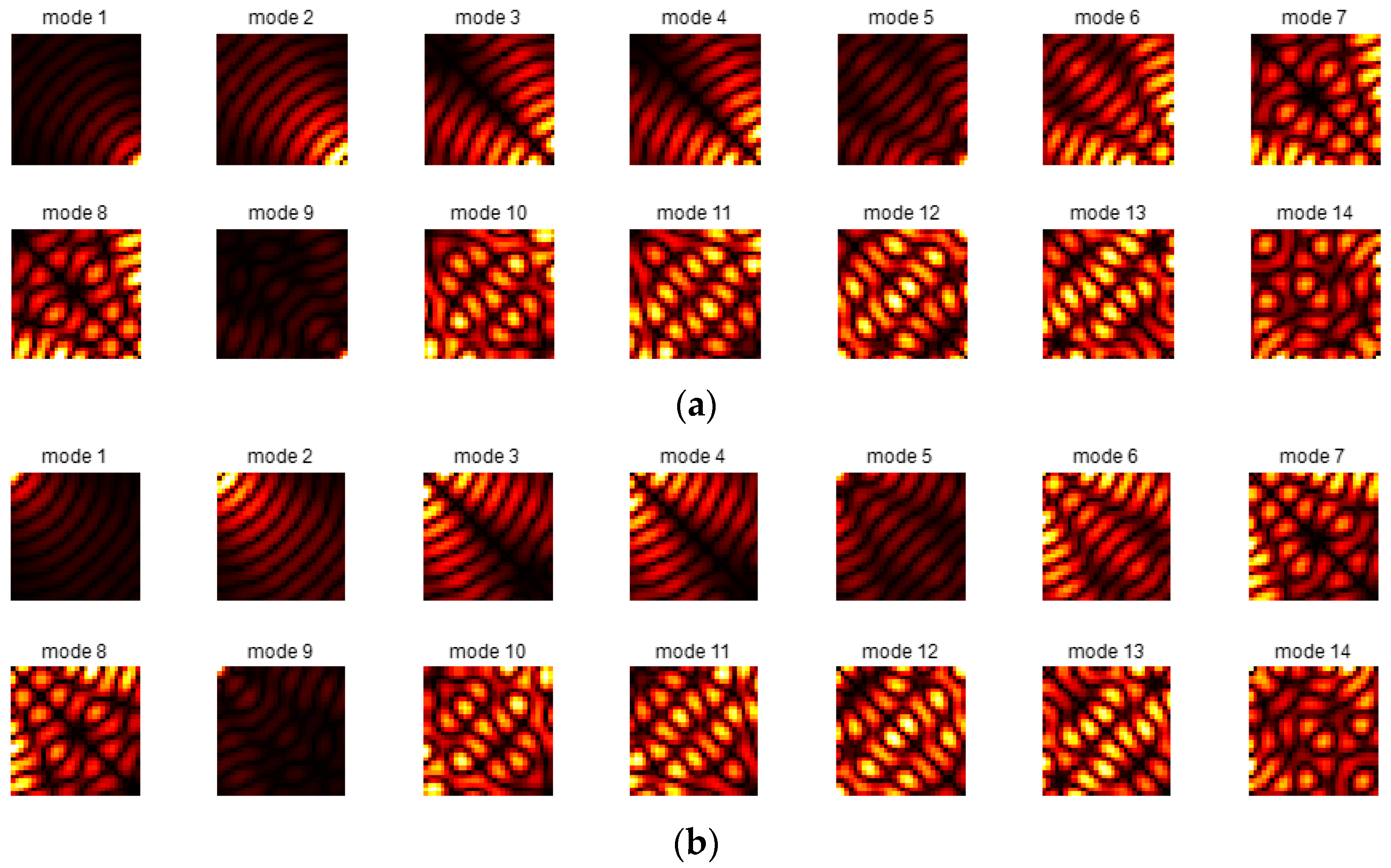
- Perform CMD decomposition on each diagonal sub-matrix and calculate the image plane intensity of each CSD sub-matrix propagated through the imaging system by following a similar procedure as Equations (5)−(8);
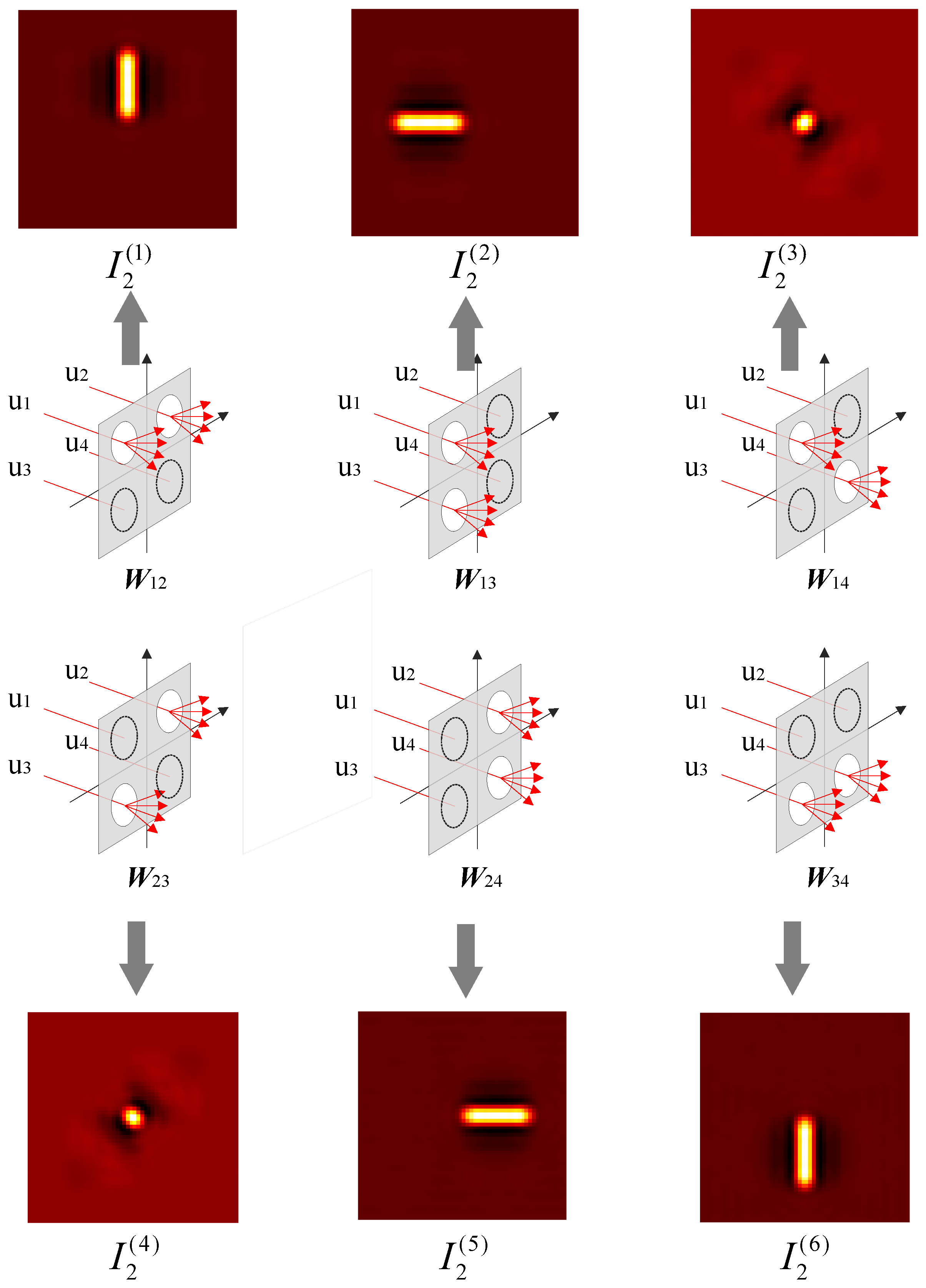
- Perform SVD decomposition on each off-diagonal submatrix , decomposing each submatrix into two sets of weighted spatially coherent light field modes and , by following Equation (14). Through this mathematical decomposition method, we can construct two partially coherent light fields in each pair of subregions, whose cross-correlation properties satisfy the mathematical description of the matrix;
- Propagate the weighted spatial coherent modes and to the imaging plane, obtaining the propagated light fields and on the entire image plane, by following Equations (16) and (17);
- Calculate the image plane intensity contributed by the mutual coherence between each pair of subregions, by following Equation (18);
- Calculate the total intensity in the image plane, by following Equation (9).
3. Simulation Results
3.1. A Tutorial of Simulation with the Proposed Method (2 × 2 Splitting Case)
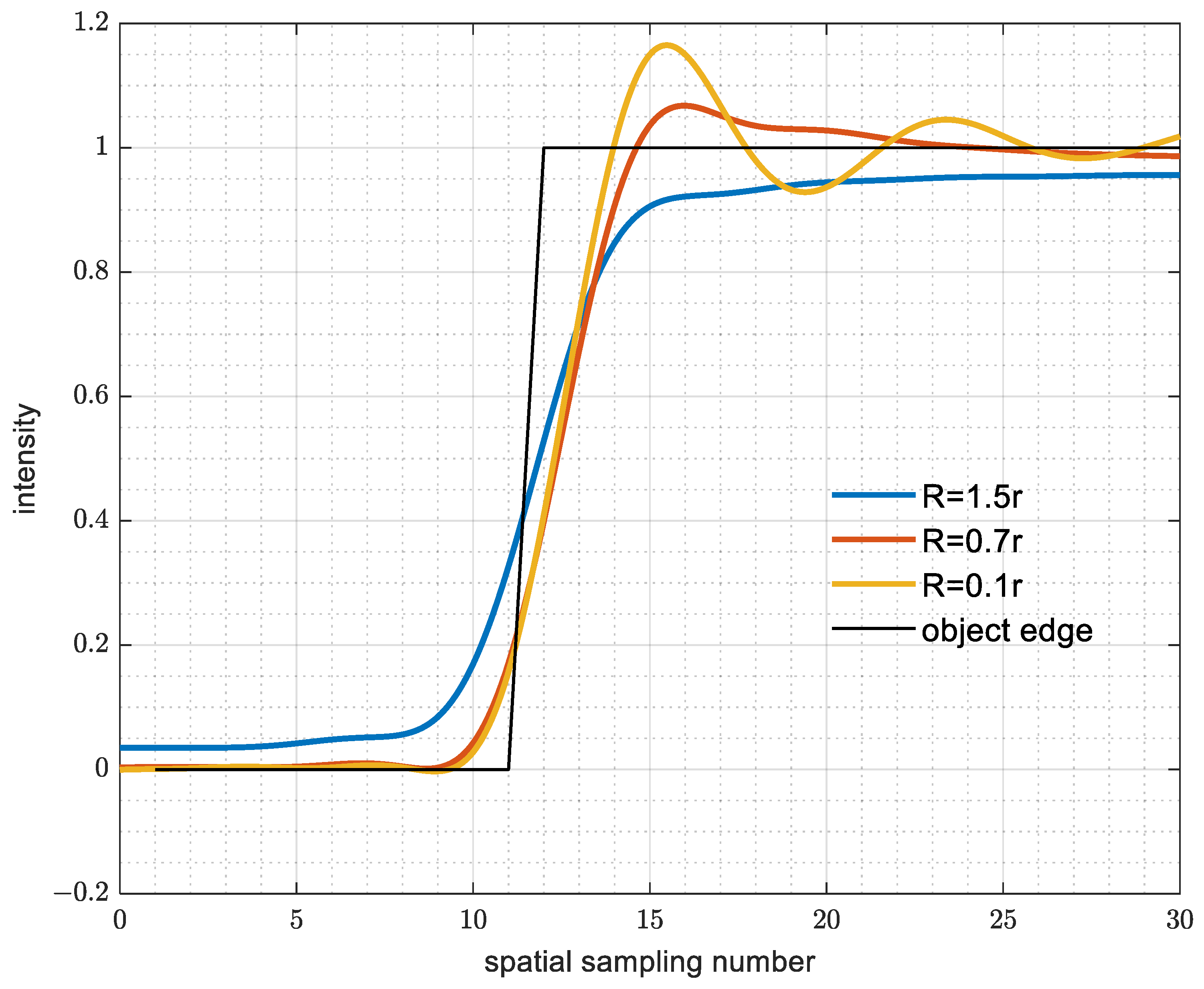
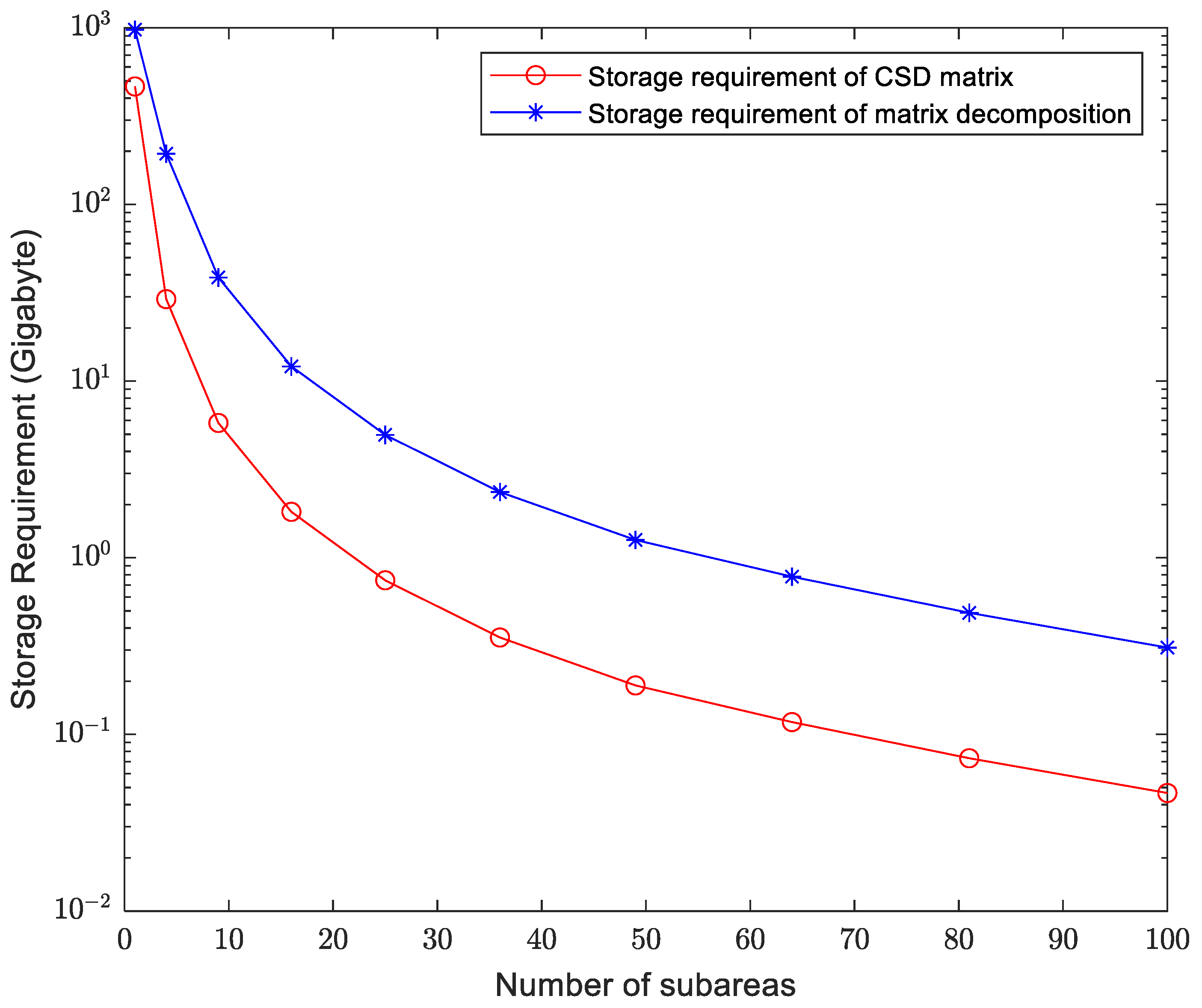
3.2. Performance in Comparison with Conventional Coherent Mode Decomposition Method
4. Further Discussion
4.1. Discussion on the Potential Limitations of the Modified Modal Expansion Method
4.2. Applicability on Anisoplanatic Imaging Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hopkins, H.H. On the Diffraction Theory of Optical Images. Proc. R. Soc. 1953, 217, 408–432. [Google Scholar]
- Smith, A.; Burvall, A.; Dainty, C. Numerical partially coherent imaging using elementaryfunctions. In Proceedings of the SPIE Conference on Optical Design and Engineering, Glasgow, UK, 27 September 2008. [Google Scholar]
- Yamazoe, K. Computation theory of partially coherent imaging by stacked pupil shift matrix. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2008, 25, 3111. [Google Scholar] [CrossRef] [PubMed]
- Yamazoe, K. Two models for partially coherent imaging. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2012, 29, 2591. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Lajunen, H.; Tervo, J.; Turunen, J. Imaging with partially coherent light: Elementary-field approach. Opt. Express 2015, 23, 28132–28140. [Google Scholar] [CrossRef] [PubMed]
- Mehta, S.B.; Sheppard, C.J.R. Phase-space representation of partially coherent imaging systems using the Cohen class distribution. Opt. Lett. 2010, 35, 348. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Statistical Optics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wolf, E. New theory of partial coherence in the space–frequency domain. Part I: Spectra and cross spectra of steady-state sources. J. Opt. Soc. Am. 1982, 72, 343–351. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Simon, R.; Piquero, G.; Borghi, R.; Guattari, G. Coherent-mode decomposition of partially polarized, partially coherent sources. J. Opt. Soc. Am. A 2003, 20, 78–84. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef] [PubMed]
- Ostrovsky, A.S. Coherent-Mode Representations in Optics; SPIE Press: Bellingham, WA, USA, 2006; Volume 164. [Google Scholar]
- Gbur, G.; Visser, T.D. Chapter 5—The Structure of Partially Coherent Fields. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; Volume 55, pp. 285–341. [Google Scholar]
- Saleh, B.E.; Rabbani, M. Simulation of partially coherent imagery in the space and frequency domains and by modal expansion. Appl. Opt. 1982, 21, 2770–2777. [Google Scholar] [CrossRef] [PubMed]
- Ozaktas, H.M.; Yuksel, S.; Kutay, M.A. Linear algebraic theory of partial coherence: Discrete fields and measures of partial coherence. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2002, 19, 1563–1571. [Google Scholar] [CrossRef] [PubMed]
- Davis, B.J.; Schoonover, R.W. Computationally efficient coherent-mode representations. Opt. Lett. 2009, 34, 923–925. [Google Scholar] [CrossRef] [PubMed]
- Magalhães, T.; Rebordão, J. Simulation of Partially Coherent Light Propagation Using Parallel Computing Devices; SPIE: Bellingham, WA, USA, 2017; Volume 10453. [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Wong, K.K. Optical Imaging in Projection Microlithography; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Ostrovsky, A.S.; Ramos-Romero, O.; Rodríguez-SOlís, M.V. Coherent-mode representation of partially coherent imagery. Opt. Rev. 1996, 3, 492–496. [Google Scholar] [CrossRef]
- Blomstedt, K.; Setälä, T.; Friberg, A.T. Effective degree of coherence: A second look. J. Opt. Soc. Am. A 2015, 32, 718–732. [Google Scholar] [CrossRef] [PubMed]
- Hyde, M.W. Simulating random optical fields: Tutorial. J. Opt. Soc. Am. A 2022, 39, 2383–2397. [Google Scholar] [CrossRef] [PubMed]
- Voipio, T.; Setälä, T.; Friberg, A.T. Coherent-mode representation of partially polarized pulsed electromagnetic beams. J. Opt. Soc. Am. A 2013, 30, 2433–2443. [Google Scholar] [CrossRef] [PubMed]





| Simulating Method | Wavelength (nm) | Numerical Aperture | Illumination Filling Factor | Object Scale (um) | Sampling Number of a Single Unit in the Space Domain | Sampling Number of a Single CSD Matrix | Number of Decomposed Coherent Modes |
|---|---|---|---|---|---|---|---|
| Conventional coherent mode decomposition | 1 | 0.75 | 1 | 2 × 2 | 6060 | 36003600 | 3600 |
| Modified method (22) | 3030 | 900900 | 14,400 | ||||
| Modified method (3 3) | 2020 | 400400 | 32,400 | ||||
| Modified method (44) | 1515 | 225225 | 57,600 | ||||
| Modified method (55) | 1212 | 144144 | 90,000 |
| Simulating Method | Memory Usage of Coherent Mode Decomposition (MB) | Computation Time of SVD (s) | Computation Time of Imaging (s) | Total Computation Time (s) | Precision (Proportion of Error in Comparison with the Conventional Result) |
|---|---|---|---|---|---|
| Conventional coherent mode decomposition | 648 | 46.47447 | 0.579663 | 47.05413 | 0 |
| 2) | 40.5 | 9.019392 | 6.084642 | 15.10403 | |
| 3) | 8 | 2.5074331 | 13.66546 | 16.1729 | |
| 4) | 2.53125 | 2.0448191 | 23.15931 | 25.20413 | |
| 5) | 1.0368 | 2.024232 | 39.94231 | 41.96654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yang, H. Computation Theory of Large-Scale Partially Coherent Imaging by the Modified Modal Expansion Method. Photonics 2024, 11, 668. https://doi.org/10.3390/photonics11070668
Li J, Yang H. Computation Theory of Large-Scale Partially Coherent Imaging by the Modified Modal Expansion Method. Photonics. 2024; 11(7):668. https://doi.org/10.3390/photonics11070668
Chicago/Turabian StyleLi, Jiaqi, and Huaijiang Yang. 2024. "Computation Theory of Large-Scale Partially Coherent Imaging by the Modified Modal Expansion Method" Photonics 11, no. 7: 668. https://doi.org/10.3390/photonics11070668
APA StyleLi, J., & Yang, H. (2024). Computation Theory of Large-Scale Partially Coherent Imaging by the Modified Modal Expansion Method. Photonics, 11(7), 668. https://doi.org/10.3390/photonics11070668




