Unraveling Electronic and Vibrational Coherences Following a Charge Transfer Process in a Photosystem II Reaction Center
Abstract
1. Introduction
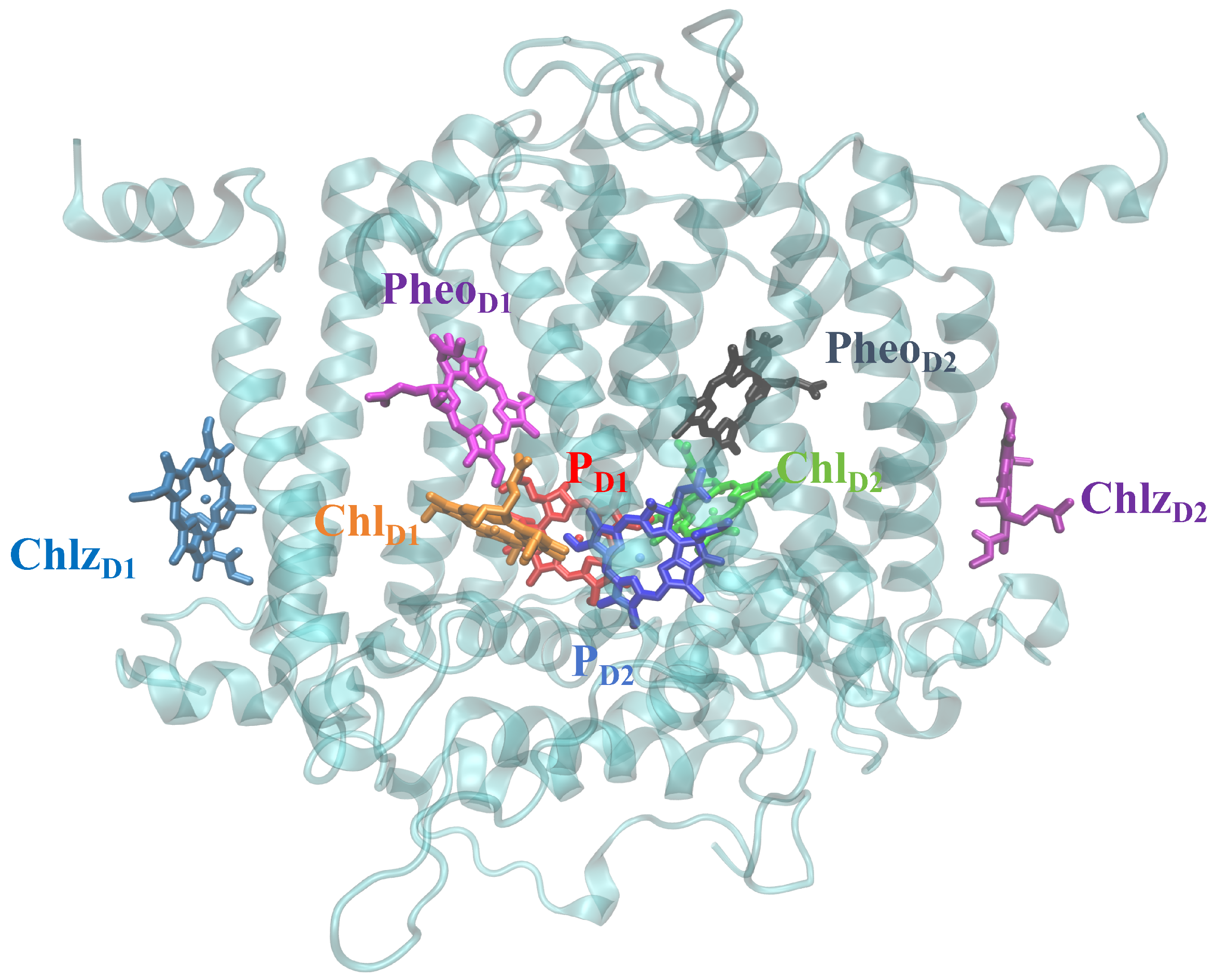
2. Modeling and Parameters
3. Results
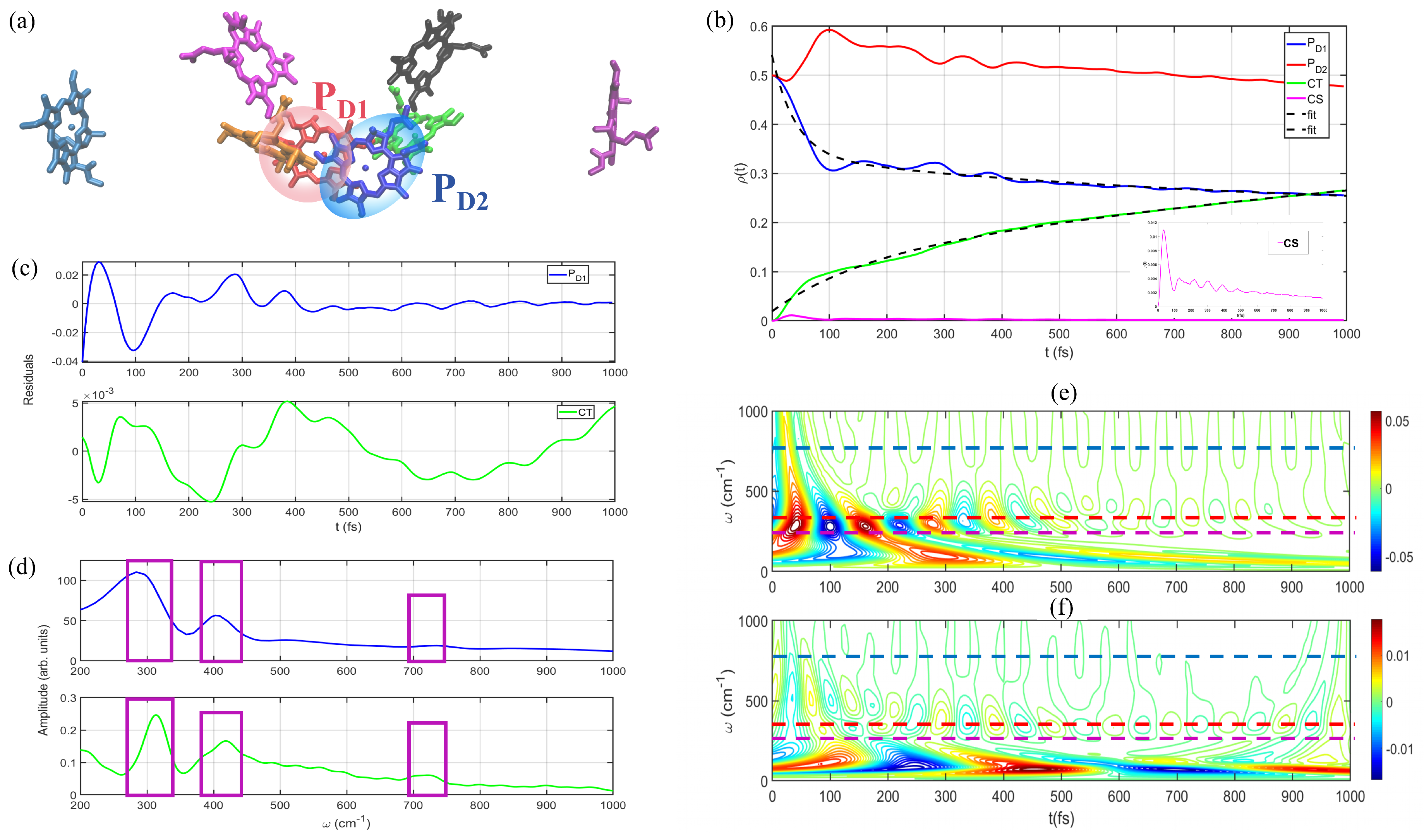
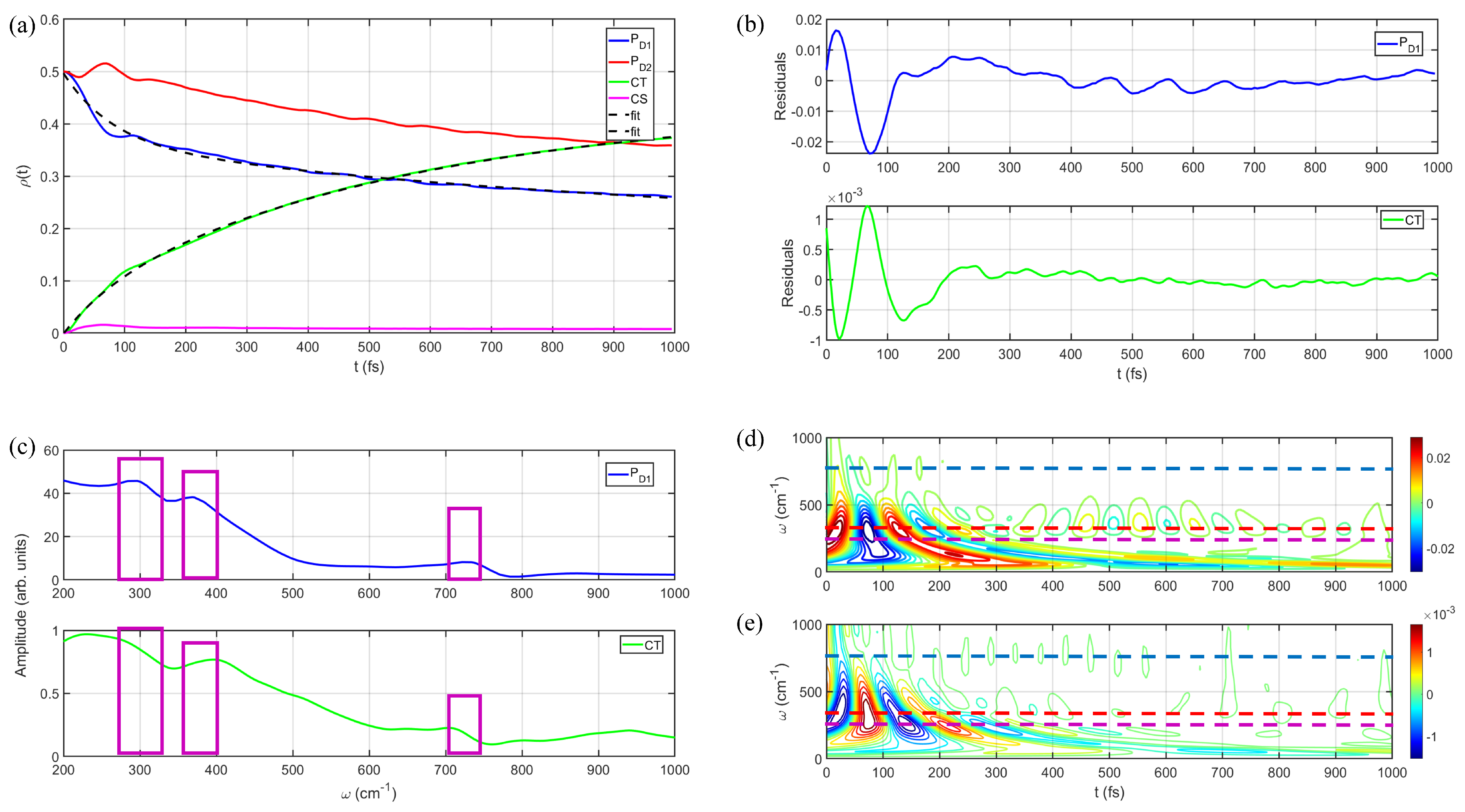
3.1. Energy and Charge Transfers between and
3.2. Population Dynamics of and
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Umena, Y.; Kawakami, K.; Shen, J.R.; Kamiya, N. Crystal structure of oxygen-evolving Photosystem II at a resolution of 1.9A. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Dods, R.; Båth, P.; Morozov, D.; Gagnér, V.A.; Arnlund, D.; Luk, H.L.; Kübel, J.; Maj, M.; Vallejos, A.; Wickstrand, C.; et al. Ultrafast structural changes within a photosynthetic reaction center. Nature 2020, 589, 310–314. [Google Scholar] [CrossRef]
- Suga, M.; Akita, F.; Hirata, K.; Ueno, G.; Murakami, H.; Nakajima, Y.; Shimizu, T.; Yamashita, K.; Yamamoto, M.; Ago, H.; et al. Native structure of photosystem II at 1.95 Å resolution viewed by femtosecond X-ray pulses. Nature 2015, 517, 99. [Google Scholar] [CrossRef]
- Diner, B.A.; Rappaport, F. Structure, dynamics, and energetics of the primary photochemistry of Photosystem II of oxygenic photosynthesis. Annu. Rev. Plant Biol. 2002, 53, 551–580. [Google Scholar] [CrossRef]
- Lewis, K.L.M.; Fuller, F.D.; Myers, J.A.; Yocum, C.F.; Mukamel, S.; Abramavicius, D.; Ogilvie, J. Simulation of the two-dimensional electronic spectroscopy of the photosystem II reaction center. J. Phys. Chem. A 2013, 117, 34–41. [Google Scholar] [CrossRef]
- Novoderezhkin, V.I.; Andrizhiyevskaya, E.G.; Dekker, J.P.; van Grondelle, R. Pathways and Timescales of Primary Charge Separation in the Photosystem II Reaction Center as Revealed by a Simultaneous Fit of Time-Resolved Fluorescence and Transient Absorption. Biophys. J. 2005, 89, 1464–1481. [Google Scholar] [CrossRef]
- Yoneda, Y.; Arsenault, E.A.; Yang, S.-J.; Orcutt, K.; Iwai, M.; Fleming, G.R. The initial charge separation step in oxygenic photosynthesis. Nat. Commun. 2022, 13, 2275. [Google Scholar] [CrossRef]
- Prokhorenko, V.I.; Holzwarth, A.R. Primary processes and structure of the Photosystem II reaction center: A photon echo study. J. Phys. Chem. B 2000, 104, 11563–11578. [Google Scholar] [CrossRef]
- Romero, E.; Van Stokkum, I.H.; Novoderezhkin, V.I.; Dekker, J.P.; Van Grondelle, R. Two different charge separation pathways in Photosystem, I.I. Biochemistry 2010, 49, 4300–4307. [Google Scholar] [CrossRef]
- Duan, H.G.; Prokhorenko, V.I.; Cogdell, R.J.; Ashraf, K.; Stevens, A.L.; Thorwart, M.; Miller, R.J.D. Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer. Proc. Natl. Acad. Sci. USA 2017, 114, 8493–8498. [Google Scholar] [CrossRef]
- Scholes, G.D.; Fleming, G.R.; Chen, L.X.; Aspuru-Guzik, A.; Buchleitner, A.; Coker, D.F.; Engel, G.; Van Grondelle, R.; Ishizaki, A.; Jonas, D.; et al. Using coherence to enhance function in chemical and biophysical systems. Nature 2017, 543, 647–656. [Google Scholar] [CrossRef] [PubMed]
- Thyrhaug, E.; Tempelaar, R.; Alcocer, M.J.P.; Žídek, K.; Bína, D.; Knoester, J.; Jansen, T.L.C.; Zigmantas, D. Identification and characterization of diverse coherences in the Fenna–Matthews–Olson complex. Nat. Chem. 2018, 10, 780–786. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.G.; Jha, A.; Chen, L.; Tiwari, V.; Cogdell, R.J.; Ashraf, K.; Prokhorenko, V.I.; Thorwart, M.; Miller, R.D. Quantum coherent energy transport in the Fenna–Matthews–Olson complex at low temperature. Proc. Natl. Acad. Sci. USA 2022, 119, e2212630119. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Allodi, M.A.; Engel, G.S. Quantum coherences reveal excited-state dynamics in biophysical systems. Nat. Rev. Chem. 2019, 3, 477–490. [Google Scholar] [CrossRef]
- Romero, E.; Novoderezhkin, V.I.; Grondelle van, R. Quantum design of photosynthesis for bio-inspired solar-energy conversion. Nature 2017, 543, 355–365. [Google Scholar] [CrossRef] [PubMed]
- Myers, J.A.; Lewis, K.L.; Fuller, F.D.; Tekavec, P.F.; Yocum, C.F.; Ogilvie, J.P. Two-dimensional electronic spectroscopy of the D1-D2-cyt b559 photosystem II reaction centre complex. J. Phys. Chem. Lett. 2010, 1, 2774–2780. [Google Scholar] [CrossRef]
- Fuller, F.D.; Pan, J.; Gelzinis, A.; Butkus, V.; Senlik, S.S.; Wilcox, D.E.; Yocum, C.F.; Valkunas, L.; Abramavicius, D.; Ogilvie, J.P. Vibronic coherence in oxygenic photosynthesis. Nat. Chem. 2014, 6, 706–711. [Google Scholar] [CrossRef]
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; Van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676–682. [Google Scholar] [CrossRef]
- Novoderezhkin, V.I.; Dekker, J.P.; van Grondelle, R. Mixing of Exciton and Charge-transfer states in Photosystem II Reaction centers: Modeling of Stark Spectra with Modified Redfield Theory. Biophys. J. 2007, 93, 1293–1311. [Google Scholar] [CrossRef]
- Novoderezhkin, V.I.; Romero, E.; Dekker, J.P.; van Grondelle, R. Multiple Charge-separation pathways in photosystem II: Modeling of transient absorption kinetics. Chem. Phys. Chem. 2011, 12, 681–688. [Google Scholar] [CrossRef]
- Gelzinis, A.; Valkunas, L.; Fuller, F.D.; Ogilvie, J.P.; Mukamel, S.; Abramavicius, D. Tight-binding model of the photosystem II reaction center: Application to two-dimensional electronic spectroscopy. New J. Phys. 2013, 15, 075013. [Google Scholar] [CrossRef]
- Jha, A.; Zhang, P.-P.; Tiwari, V.; Chen, L.; Thorwart, M.; Miller, R.J.D.; Duan, H.-G. Unraveling Quantum Coherences Mediating Primary Charge Transfer Processes in Photosystem II Reaction Center. Science Advances, accepted for publication. Sci. Adv. 2024, 10, eadk1312. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Sechrist, R.; Nguyen, H.H.; Johnson, W.; Abramavicius, D.; Redding, K.E.; Ogilvie, J.P. Excitonic structure and charge separation in the heliobacterial reaction center probed by multispectral multidimensional spectroscopy. Nat. Commun. 2021, 12, 2801. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenko, V.I. Global analysis of multi-dimensional experimental data. Eur. Photochem. Assoc. Newslett. 2012, 21–23. [Google Scholar]
- Duan, H.G.; Thorwart, M.; Miller, R.J. Does electronic coherence enhance anticorrelated pigment vibrations under realistic conditions? J. Chem. Phys. 2019, 151, 114115. [Google Scholar] [CrossRef] [PubMed]
- Girl, A.; Grisanti, L.; Masino, M.; Brillante, A.; Della Valle, R.G.; Venuti, E. Interaction of charge carriers with lattice and molecular phonons in crystalline pentacene. J. Chem. Phys. 2011, 135, 084701. [Google Scholar]
- Bakulin, A.A.; Morgan, S.E.; Kehoe, T.B.; Wilson, M.W.B.; Chin, A.W.; Zigmantas, D.; Egorova, D.; Rao, A. Real-time observation of multiexcitonic states in ultrafast singlet fission using coherent 2D electronic spectroscopy. Nat. Chem. 2016, 8, 16. [Google Scholar] [CrossRef] [PubMed]
- Miyata, K.; Kurashige, Y.; Watanabe, K.; Sugimoto, T.; Takahashi, S.; Tanaka, S.; Takeya, J.; Yanai, T.; Matsumoto, Y. Coherent singlet fission activated by symmetry breaking. Nature Chem. 2017, 9, 983. [Google Scholar] [CrossRef] [PubMed]
- Neef, A.; Beaulieu, S.; Hammer, S.; Dong, S.; Maklar, J.; Pincelli, T.; Xian, R.P.; Wolf, M.; Rettig, L.; Pflaum, J.; et al. Orbital-resolved observation of singlet fission. Nature 2023, 616, 275. [Google Scholar] [CrossRef]
- Duan, H.G.; Nalbach, P.; Miller, R.D.; Thorwart, M. Ultrafast Energy Transfer in Excitonically Coupled Molecules Induced by a Nonlocal Peierls Phonon. J. Phys. Chem. Lett. 2019, 10, 1206. [Google Scholar] [CrossRef]
- Duan, H.G.; Jha, A.; Li, X.; Tiwari, V.; Ye, H.; Nayak, P.K.; Zhu, X.L.; Li, Z.; Martinez, T.J.; Thorwart, M.; et al. Intermolecular vibrations mediate ultrafast singlet fission. Sci. Adv. 2020, 6, eabb0052. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zhang, X.; Tiwari, V.; Mei, C.; Jha, A.; Zhang, P.-P.; Duan, H.-G. Unraveling Electronic and Vibrational Coherences Following a Charge Transfer Process in a Photosystem II Reaction Center. Photonics 2024, 11, 519. https://doi.org/10.3390/photonics11060519
Zhou J, Zhang X, Tiwari V, Mei C, Jha A, Zhang P-P, Duan H-G. Unraveling Electronic and Vibrational Coherences Following a Charge Transfer Process in a Photosystem II Reaction Center. Photonics. 2024; 11(6):519. https://doi.org/10.3390/photonics11060519
Chicago/Turabian StyleZhou, Junhua, Xuanchao Zhang, Vandana Tiwari, Chao Mei, Ajay Jha, Pan-Pan Zhang, and Hong-Guang Duan. 2024. "Unraveling Electronic and Vibrational Coherences Following a Charge Transfer Process in a Photosystem II Reaction Center" Photonics 11, no. 6: 519. https://doi.org/10.3390/photonics11060519
APA StyleZhou, J., Zhang, X., Tiwari, V., Mei, C., Jha, A., Zhang, P.-P., & Duan, H.-G. (2024). Unraveling Electronic and Vibrational Coherences Following a Charge Transfer Process in a Photosystem II Reaction Center. Photonics, 11(6), 519. https://doi.org/10.3390/photonics11060519





