Abstract
This work proposes and experimentally demonstrates a high-performance polarization space parity-time (PT) symmetric fiber ring laser to achieve a low-noise, narrow-linewidth, and highly stable single-longitudinal-mode output. The gain/loss and coupling coefficients are regulated by adjusting a polarization controller (PC) and the pumping current of an erbium-doped fiber amplifier (EDFA) within the ring cavity. The results show that the single longitudinal mode oscillation of the laser can be implemented by PT symmetry breaking. The frequency noise spectral density and the linewidth characteristics of the laser are evaluated by the short-delay self-heterodyne method. The results reveal that excellent low-frequency noise (181 Hz2/Hz at a 10 kHz offset frequency) and narrow fundamental linewidth (68 Hz) can be achieved. Additionally, the laser exhibits outstanding stability with only 0.64 pm wavelength drift over 30 min. By tuning an optical tunable filter (OTF), the wavelength tunable range of the laser can cover the entire C-band. Furthermore, the impacts of different fiber length on the frequency noise spectral density and the filter bandwidth on stability are analyzed, offering guidance for component selection in such laser systems.
1. Introduction
Single longitudinal mode fiber ring lasers, renowned for their high coherence, compact structure, and excellent beam quality, have broad applications in fields such as laser ranging, optical communication, and microwave photon signal generation. In the optical fiber ring cavity, which is several tens of meters long, there exist free spectral ranges (FSRs) on the order of megahertz (MHz), while typical optical filters have bandwidths of the order of gigahertz (GHz). Consequently, by directly using conventional optical filters as wavelength selection elements for laser oscillators, it is challenging to achieve single-mode outputs. To overcome this challenge, common techniques for single-mode selection in fiber ring lasers include compound rings with Vernier effects [1,2,3,4,5], saturable absorbers [6,7,8,9], cascaded microfiber knots [10], whispering gallery mode resonator [11], phase-shifted fiber Bragg gratings [12], and dynamic gratings [13,14] to establish narrow linewidth filters. However, these methods often require complex cavity structures and fine parameter tuning.
In recent years, the concept of parity-time (PT) symmetry has emerged as a promising solution for achieving single-mode output in fiber ring lasers [15,16,17,18,19,20,21,22,23,24]. Typically, PT symmetric fiber ring systems utilize two subsystems with identical geometric length and balanced gain and loss to facilitate mode selection. When the gain coefficient exceeds the coupling coefficient, PT symmetry breaking occurs, significantly enhancing the gain difference between the principal mode and the side modes, thus enabling single-mode oscillation. One approach involves non-reciprocal loop-based PT symmetric fiber lasers [15,16,17,18] with two loops in the ring cavity. Gain and loss are balanced using optical isolators and polarization controllers (PCs) to establish PT symmetry and attain single-mode outputs. Another technique operates near exceptional points [19] by leveraging a tunable optical isolator to approach such points in the laser system, thereby achieving narrow linewidth single-mode outputs. Moreover, stimulated Brillouin scattering (SBS)-based PT symmetric schemes [20,21] have been investigated, combining adjustable gain and loss to construct PT symmetric cavities for mode selection and narrow linewidth single-mode generation. A dual-loop PT symmetric system [22] with two loops coupled at a rational length ratio has also been examined to achieve PT symmetry and single-mode outputs. Additionally, in fiber ring cavities, PT symmetry has been realized using polarization-dependent loss [23,24], as well as by employing a polarization-maintaining fiber Bragg grating [25], where adjusting the loss enables single-mode output generation upon PT symmetry breaking. These schemes offer advantages in mode selection, enabling single-mode outputs without high-quality (high-Q) filters, thereby simplifying system design and enhancing stability. However, challenges remain regarding system complexity, cost, and power conversion efficiency. Further optimization is necessary to realize more efficient, stable, and cost-effective single longitudinal mode fiber ring lasers.
In this work, we propose a structurally simple fiber ring laser based on polarization space PT symmetry breaking. By controlling the gain/loss and by coupling coefficients of two polarization states within a single fiber ring, the laser achieves a low-noise, narrow-linewidth, and highly stable single-mode optical output. By adjusting a PC and the pumping current of an erbium-doped fiber amplifier (EDFA) in the cavity, the gain/loss and coupling coefficients of the two polarization loops can be controlled. When the gain balances the loss and the gain coefficient exceeds the coupling coefficient, PT symmetry breaking occurs, significantly enhancing the gain difference between the principal mode and the side modes, thus enabling single-mode laser oscillation. The single-mode laser signal is analyzed using a short-delay self-heterodyne [26,27,28] method to obtain the frequency noise spectral density, fundamental linewidth, integral linewidth, and effective integral linewidth of the proposed PT symmetric fiber ring laser. The experimental results demonstrate that the laser is characterized by extremely low-frequency noise and linewidth, high stability, and a wide tuning range. Specifically, the frequency noise spectral density can be as low as approximately 181 Hz2/Hz at an offset frequency of 10 kHz, with a fundamental linewidth of approximately 68 Hz. Moreover, the laser exhibits excellent wavelength stability with only 0.64 pm drift over 30 min. By tuning an optical tunable filter (OTF), the single-mode output wavelength can cover the entire C-band. Additionally, the impacts of different fiber lengths on the frequency noise spectral density and the effects of various filter bandwidths on long-term stability are analyzed.
2. Experimental Setup and Operational Principle
Figure 1 illustrates the schematic diagram of the experimental setup for the proposed polarization space PT symmetric fiber ring laser, along with the setup for evaluating performance of the laser output signal. As shown in Figure 1a, the fiber ring cavity comprises two polarization loops within a single fiber loop. An erbium-doped fiber amplifier (EDFA) provides gain. An optical tunable filter (OTF) serves for coarse wavelength selection. A 70:30 optical coupler (OC1) serves to close the loop and output port. A polarization controller (PC1) and a polarization beam splitter (PBS) are the key elements realizing the polarization space PT symmetry. Here, the function of PBS is equivalent to that of a polarizer [23]. The total cavity length is 97.5 m, corresponding to 2.05 MHz of the FSR. The experimental setup for evaluating the laser output signal performance is shown in Figure 1b. The output is divided into two paths by a 10:90 optical coupler (OC2), where 10% is coupled with a high-precision optical spectrum analyzer (OSA, Aragon Photonics BOSA lite+, 20 MHz resolution bandwidth) for spectral analysis, while the remaining 90% enters a delayed self-heterodyne system for longitudinal mode and frequency noise analysis. In the delayed self-heterodyne system, the signal is split into upper and lower arms by a 3 dB optical coupler (OC3). The upper arm is delayed by a single-mode fiber (SMF), while the lower arm comprises a polarization controller (PC2) and an acousto-optic modulator (AOM, G-1550-80) with an 80 MHz frequency shift. The signals from the two arms are coupled by another 3 dB optical coupler (OC4) and detected by a photodetector (PD, XPDV2120R, 50 GHz bandwidth), generating a beat signal for spectral and phase noise analyzed by an electrical spectrum analyzer (ESA, R&S FSW, 67 GHz bandwidth). Noteworthy is the fact that a 40 km SMF is used to analyze the longitudinal mode and spectral line shape of the laser, while a 9.77 m SMF is employed to measure the frequency noise spectral density and linewidth of the laser in the delayed self-heterodyne system.
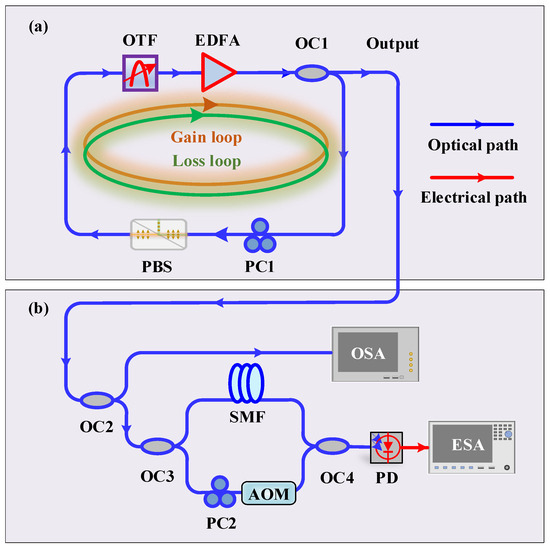
Figure 1.
(a) Schematic diagram of the experimental setup of the proposed polarization space PT symmetric fiber ring laser. (b) Schematic diagram of the experimental setup to evaluate the performance of the laser. OTF: optical tunable filter; EDFA: erbium-doped fiber amplifier; OC: optical coupler; PC: polarization controller; PBS: polarization beam splitter; OSA: optical spectrum analyzer; SMF: single-mode fiber; AOM: acoustic optical modulator; PD: photodetector; ESA: electrical spectrum analyzer.
In Figure 1a, the birefringence of PC1 induces two polarization components, Ex and Ey. The angle between the electric field vector Ex and the parallel polarization direction in the PBS, denoted as θ, can be controlled through PC1. Here, the PBS can be effectively regarded as a linear polarizer. The relations between the electric fields before and after passing through the concatenated combination of PC1 and PBS for one round trip inside the cavity, denoted as E0 and E1, can be expressed as [23,29]:
where the parameter G0 represents the round-trip gain when the electric field in the Ex or Ey direction is perfectly aligned with the parallel polarization direction of the PBS. Obviously, as the polarization components Ex and Ey circulate within the optical fiber loop, their relative angles with respect to the parallel polarization direction of the PBS lead to the round-trip gain coefficients as:
The round-trip coupling coefficient between the two loops can be expressed as:
Based on the definitions of gain and coupling per time unit coefficients, the gain and coupling coefficients can be expressed as [23,25]:
where T is the round-trip time of the light in the cavity.
When gain and loss are balanced, namely or , then:
Therefore, by adjusting PC1 to tune the angle θ or altering the pumping current of the EDFA to modify the gain parameter G0, the PT symmetric condition can be achieved.
Figure 2 illustrates the interrelationship among the round-trip gain/loss, coupling coefficients, angle θ, and gain parameter G0. Figure 2a,b show the variations in the round-trip gain/loss for both loops, the coupling coefficient, and the GxGy coefficient as functions of θ, for G0 = 2 and G0 = 4, respectively. As evident from Figure 2a, when G0 = 2, the PT symmetric condition (GxGy = 1) is satisfied only when θ = 45° and the system lies at the exceptional point (EP) with K = Gx. An EP is a branch point singularity in parameter space where two or more eigenvalues and their corresponding eigenvectors of a non-Hermitian system coalesce and become degenerate [30,31]. In comparison, Figure 2b shows that, when G0 = 4, the PT symmetric condition is satisfied for θ = 15° or θ = 75°. However, in this case, K is smaller than Gx or Gy, resulting in PT symmetry breaking. Figure 2c illustrates the values of θ corresponding to different G0 values under the fulfillment of the PT symmetric condition. When the value of θ satisfies Equation (8), it can be observed that, for θ < 45°, Ex-mode exhibits gain in the round-trip performance. Under this case, θ is recorded as θx. On the other hand, for θ > 45°, Ex-mode displays loss, while Ey-mode exhibits gain in the round-trip performance. Under this case, θ is recorded as θy. Finally, Figure 2d shows the round-trip gain and coupling coefficients for different G0 values under the fulfillment of the PT symmetric condition. Evidently, when G0 > 2 and θ = θx, K is smaller than Gx, leading to PT symmetry breaking.
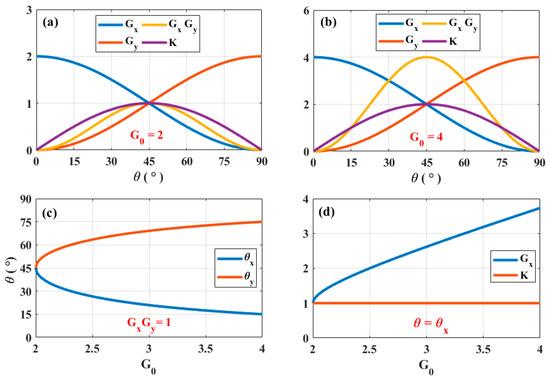
Figure 2.
Interrelationship among the round-trip gain/loss, coupling coefficients, θ, and G0 for the proposed laser. (a) Variations in round-trip gain/loss coefficients of the two polarization loops, coupling coefficient K, and product GxGy versus θ for G0 = 2. (b) Same as (a) but for G0 = 4. (c) Relationship between the values of G0 and θ to satisfy the PT symmetric condition GxGy = 1. (d) Round-trip gain coefficients Gx and coupling coefficient K versus G0 under the PT symmetric condition.
When converting the round-trip gain/loss and coupling coefficients into per unit time coefficients, the coupling equations of the proposed fiber ring laser can be expressed as [18,23]:
where denotes the frequency of the nth mode of the cavity. When + = 0, the PT symmetry condition of the system is satisfied, and the solutions for the eigenfrequencies of the coupled Equation (9) are obtained:
When the gain coefficient equals the coupling coefficient (|| = ), the eigenmodes become degenerate, reaching the so-called EP [17]. In contrast, when the gain coefficient is greater than the coupling coefficient (|| > ), complex solutions exist for the eigenfrequencies, leading to the spontaneous breaking of PT symmetry. In this case, two eigenmodes share the same frequency, yet the two coupled loops provide gain for one eigenmode while imparting an equivalent magnitude of loss to the other. Upon the occurrence of PT symmetry breaking, the eigenfrequencies exhibit a square root dependence on the gain, leading to an enhancement in the gain difference between the principal mode (highest longitudinal mode ) and the secondary mode (second highest gain longitudinal mode ). The enhancement factor for the gain difference is [16]:
where and represent the gain difference between the principal mode and the secondary mode in a system with PT symmetry and another system without PT configuration, respectively. In the PT symmetric non-Hermitian system, the gain difference increases by a factor of F, facilitating the achievement of a single-mode output without the high-Q optical filters.
In Figure 1b, the single-mode optical signal prior to entering the optical self-heterodyne system is characterized as:
where denotes the center frequency of the signal, represents the phase noise of the optical signal, and P signifies the power of the optical signal. Upon passing through OC3, one path is delayed by a SMF, while the other is frequency-shifted by with an AOM. Therefore, the optical signals of the two paths can be respectively delineated as:
Then, the beat signal obtained after the mutual superposition of the two via OC4 and detected by a PD with responsivity R is:
where:
which represents the phase noise in beat signal. The phase noise spectral density of the beat signal can be measured by the ESA. When the time delay is significantly smaller than the coherence time of the laser, the relationship between the phase noise spectral density of the beat signal and the frequency noise spectral density of the laser can be derived as:
Considering the zero point issue in Equation (17), the laser frequency noise spectral density at zero point needs further restorative measures [28].
3. Results and Discussion
An experiment was conducted using the setup shown in Figure 1. Initially, the transmittance spectrum of the OTF was measured by the ‘Component Analyzer’ module of the OSA, as indicated by the magenta trace in Figure 3 with a 3 dB bandwidth of 0.0446 nm. Next, the optical spectrum of a fiber ring laser without PT configuration was obtained by removing the PBS and PC1 from the system shown in Figure 1a, as indicated by the black trace in Figure 3. Then, the main experiment was performed with the pumping current fixed at 150 mA in the setup shown in Figure 1a. When PC1 was adjusted without PT symmetry, the optical spectrum of the laser appeared as the red trace in Figure 3. However, when adjusting PC1 to achieve gain–loss balance, with the gain coefficient exceeding the coupling coefficient, PT symmetry breaking occurred, resulting in the solitary spectral line shown by the blue trace in Figure 3.
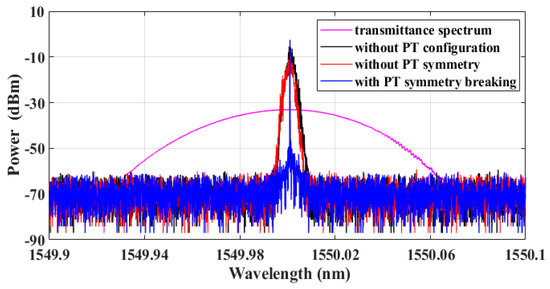
Figure 3.
Transmittance spectrum of the OTF (magenta trace) measured by the ‘Component Analyzer’ module of the OSA, and optical spectrum measured by the OSA for the laser without PT configuration (black trace), the laser without PT symmetry (red trace), and the laser with PT symmetry breaking (blue trace).
Given the 97.5 m length of the optical fiber ring cavity, the corresponding FSR was 2.051 MHz. However, the minimum resolution bandwidth (RBW) of the OSA was only 0.16 pm (20 MHz), which renders it challenging to definitively determine whether the output laser signal was single-longitudinal-mode. Hence, to assist in analyzing the oscillation modes of the laser signal, the output light was passed through an optical self-heterodyne system with a 40 km SMF length, followed by electric spectrum analysis of the beat signal obtained through the PD. The experimental setup shown in Figure 1b was utilized to observe the evolution of the output optical signal with variations in the EDFA pumping current (in 10 mA increments), while maintaining the state of PC1 fixed, as illustrated in Figure 4. Under different EDFA pumping currents, the spectral evolution of the output light is depicted in Figure 4a, with a span of 0.02 nm (25 GHz). Additionally, the spectral evolution of the beat signal is illustrated in Figure 4b, at a central frequency of 80.0 MHz, with a span of 100 MHz and an RBW of 10 kHz. As it can be seen from Figure 4 by observing the optical spectrum and electrical spectrum, under an EDFA pumping current of 80 mA, the output was noise. As the pumping current was increased to 90 mA, multiple peaks emerged in both spectra, suggesting a multimode output since the condition of PT symmetry breaking was unsatisfied. For the pumping current located at the range of 100~140 mA, only a peak with strong power was observed in the optical spectrum shown in Figure 4a, while some extra beating signals with weak power still appeared in the electrical spectrum shown in Figure 4b. With the increase in pump current, the extra beating signals gradually diminished, indicating that the system gradually approached the PT symmetry breaking state. Especially when the pumping current was increased to 150 mA, the side mode suppression ratio of the beat frequency signal attained its maximum of 55.2 dB. In this case, the PT symmetry breaking condition was well-satisfied, and the output exhibited single-mode behavior, corresponding to the principal mode. By further increasing the pump current to 220 mA, the condition of PT symmetry breaking deviated again, and the system presented the multimode output state. It should be pointed out that the results were obtained under fixed PC1. Our experimental results also show that, by adjusting PC1, the condition of PT symmetry breaking can also be well-satisfied under other pumping current conditions.
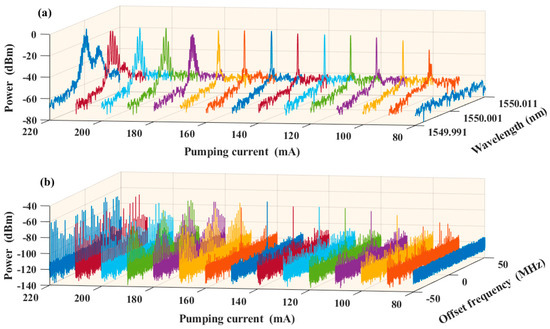
Figure 4.
(a) Evolution of the optical spectrum of the output of the fiber ring laser under different pumping currents of the EDFA with a span of 0.02 nm (25 GHz) and an RBW of 0.16 pm (20 MHz). (b) Evolution of the electrical spectrum of the beat signal under different pumping currents of the EDFA at a central frequency of 80.0 MHz with a span of 100 MHz and an RBW of 10 kHz.
Figure 5 specifically shows the electrical spectrum of the beat signals detected under the conditions of a pumping current equal to 200 mA without PT symmetry, and under the conditions of a pumping current equal to 150 mA with PT symmetry breaking at a central frequency of 80.0 MHz. The resolution bandwidth (RBW) was 10 kHz and the span was 100 MHz. In Figure 5a, it is evident from the spectrum that there were multimode signals with a mode spacing of 2.051 MHz, corresponding to a cavity length of 97.5 m. By adjusting the pumping current of the EDFA to 150 mA to achieve PT symmetry breaking, a single-mode laser output was realized. In Figure 5b, it can be observed that all side modes were suppressed, indicating the successful attainment of a single-longitudinal-mode laser operation. The inset in Figure 5b shows a zoomed-in view with a span of 4 MHz. From the inset, it can be observed that there are two wing-shaped spectral peaks caused by the relaxation oscillation of the laser at the center frequency of the beat signal.
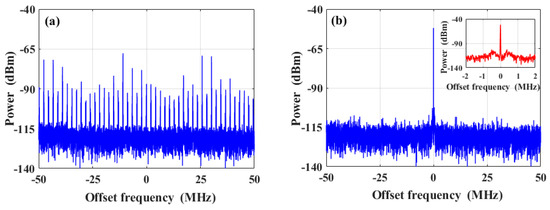
Figure 5.
Measured electrical spectrum of the beat signals (a) without PT symmetry and (b) with PT symmetry breaking and its zoomed-in view at a central frequency of 80.0 MHz.
When this fiber ring laser output a single-longitudinal-mode optical signal under the PT symmetry breaking phase, the linewidth and line shape of the laser were analyzed by the conventional long-delayed self-heterodyne method with a 40 km SMF, as shown in Figure 6. Figure 6a depicts the electrical spectrum of the beat signal. The measured 20 dB linewidth was determined to be 15.0 kHz, corresponding to a 3 dB Lorentzian linewidth of 750 Hz. Notably, upon power normalization of the measured spectra and subsequent fitting with Lorentzian and Voigt functions, as illustrated in Figure 6b, the Voigt fitting appeared to better conform to the experimental data. This observation indicates that 1/f noise predominated in the output optical signal. However, this linewidth estimation method has certain limitations. Utilizing the long-delayed self-heterodyne method requires determining the coherent delay length based on the linewidth, and the delay time must be approximately six times the coherence time of the laser [32]. Yet, excessively long fiber delay lines introduce unnecessary 1/f noise, rendering the long-delayed self-heterodyne method challenging for linewidth estimation. Therefore, the noise of the laser was analyzed using the short-delayed self-heterodyne method.
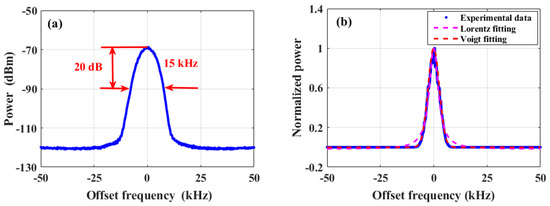
Figure 6.
Long-delayed heterodyne utilized for the assessment of the linewidth and line shape of a PT symmetric fiber ring laser. (a) Linewidth assessment and (b) line shape fitting with normalized power.
The frequency noise spectral density of the fiber ring laser was measured by a short-delay self-heterodyne system. A 9.77 m SMF was employed to ensure coherence between the optical signals in the two arms. The phase noise spectral density of the coherent beat signal obtained through the short-delay self-heterodyne system is illustrated in Figure 7a. According to the phase noise spectrum of the beat signal and to Equation (17), the frequency noise spectral density and the integral linewidth [33] of the laser can be obtained, as shown in Figure 7b. In Figure 7b, the blue spectrum line represents the frequency noise spectral density of the PT symmetric fiber ring laser, the red dashed line represents the β-separation line, and the gray area represents the region of high modulation index contributing to the integral linewidth over an observation time of 1 s. As shown in Figure 7b, the frequency noise decreased by approximately 109 times as the frequency offset increased from 1 Hz to 10 kHz, indicating that low-frequency noise dominated the optical signal noise. At an offset frequency of 10 kHz, the frequency noise spectral density could be reduced to approximately 181 Hz2/Hz. From an offset frequency ranging from 100 kHz to 1 MHz, the frequency noise initially increased and then decreased, possibly due to relaxation oscillations in the fiber laser. The side modes were suppressed below 47 Hz2/Hz. The fundamental linewidth [34] can be calculated from the white noise at high frequencies (much greater than 1 MHz) in the frequency noise spectral density, which is approximately 68 Hz. When starting from an offset frequency of 1 Hz (with an observation time of 1 s), the integral linewidth was calculated to be 456.224 kHz. The integral linewidth starting from different offset frequencies is shown in Figure 7c. From Figure 7c, it is evident that, as the starting offset frequency increased (corresponding to a short observation timescale), the integral linewidth gradually decreased. When the starting offset frequency was 2.11 kHz (with an observation time of 473.9 μs), the integral linewidth decreased to approximately 718 Hz. Furthermore, by utilizing the frequency noise spectral density of the laser, the effective integral linewidth [34,35] of the laser can be obtained, as illustrated in Figure 7d. By converting the frequency noise into phase noise of the laser and integrating the phase noise from high offset frequencies to a certain offset frequency such that its integrated value equals 1/π rad2, the corresponding offset frequency is defined as the effective integral linewidth. As depicted in Figure 7d, the effective integral linewidth of this laser was about 2.255 kHz.
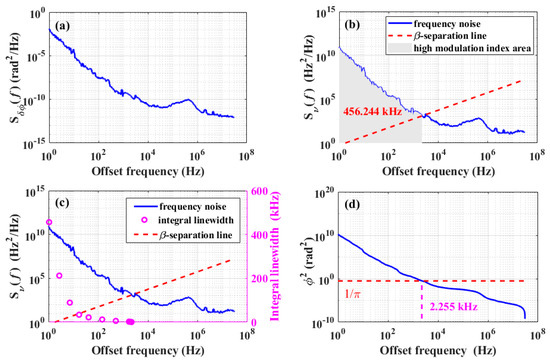
Figure 7.
(a) Phase noise spectral density of the coherent beat signal obtained by the PT symmetric fiber ring laser through the short-delay self-heterodyne system with a 9.77 m SMF. (b) Frequency noise spectral density and the integral linewidth of the laser for an observation time of 1 s. (c) Integral linewidth with different starting offset frequencies. (d) Effective integral linewidth of the laser.
The long-term stability of the laser was monitored during a 30 min period. As depicted in Figure 8, the optical spectrum of the generated laser signal exhibited a wavelength drift throughout the 30 min interval. The wavelength drift arose from internal noise within the laser device and interference induced by external environmental factors. The wavelength drift range of the PT symmetric fiber ring laser was approximately 0.64 pm.
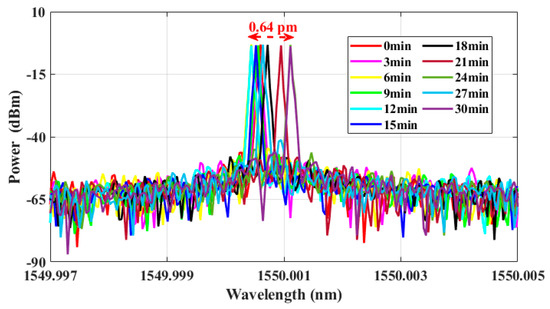
Figure 8.
Measurement of the wavelength drift in the PT symmetric fiber ring laser within a duration of 30 min.
By adjusting the OTF, wavelength tunability of the single-mode laser could be achieved, as illustrated in Figure 9. Figure 9a shows the optical spectra of the laser when the wavelength was finely tuned with a step of 20 pm from 1549.92 nm to 1550.08 nm, and Figure 9b shows the optical spectra of the laser when the wavelength was coarsely tuned with a step of 4 nm from 1529 nm to 1561 nm by tuning the OTF. The spectral range displayed in Figure 9b spanned from 1525 nm to 1565 nm, a limitation imposed by the measurement range of the OSA. Without the constraints of the measuring range of the instrument, the tuning range of this laser would likely be broader. It can be observed from Figure 9 that the tuning range of this laser covered the entirety of the C-band. It demonstrates that the polarization space PT symmetric fiber ring laser can effectively realize a wide wavelength tuning range.
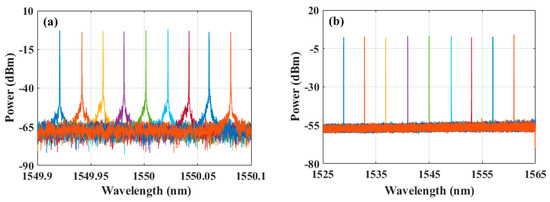
Figure 9.
Optical spectra of the tunability of the single mode of the PT symmetric fiber ring laser. (a) Fine-tuned with a step of 20 pm from 1549.92 nm to 1550.08 nm and (b) coarse-tuned with a step of 4 nm from 1529 nm to 1561 nm by tuning the OTF.
To investigate the influence of cavity length on the frequency noise of polarization space PT symmetric fiber ring lasers, the noise properties of single-mode optical signals generated by PT symmetry breaking in cavities with length of 46.2 m and 65.0 m were also examined, respectively. Figure 10 depicts the frequency noise spectral density of the PT fiber lasers with different cavity length and a high-performance tunable laser (TSL-570). The red spectrum line represents the frequency noise spectral density for a cavity length of 46.2 m. The magenta spectrum line corresponds to the frequency noise spectral density for a cavity length of 65.0 m. The blue spectrum line corresponds to the frequency noise spectral density for a cavity length of 97.5 m. The green spectrum line represents the frequency noise spectral density of the TSL-570. As it can be observed from Figure 10, within the offset frequency range of 102 Hz to 105 Hz, an increase in cavity length resulted in a notable suppression of the frequency noise of the output optical signal. Specifically, at an offset frequency of 10 kHz, the frequency noise spectral density was approximately 1.283 × 104 Hz2/Hz for a cavity length of 46.2 m, 1.657 × 103 Hz2/Hz for a cavity length of 65.0 m, and 181 Hz2/Hz for a cavity length of 97.5 m. Moreover, the frequency noise of the PT fiber lasers with the three different cavity length was lower than that of the TSL-570. In contrast, the PT symmetric fiber ring lasers demonstrated excellent low noise characteristics.
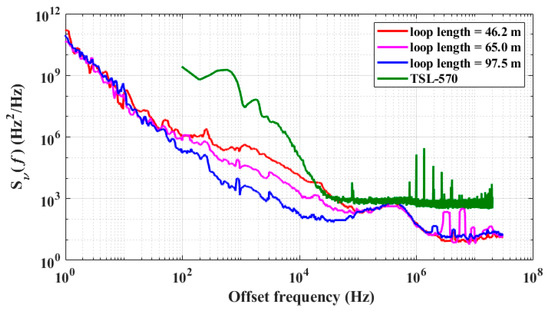
Figure 10.
Frequency noises spectral density of the PT symmetric fiber ring lasers with different cavity lengths and a high-performance tunable laser source (TSL-570).
The integral linewidth with various observation timescales of PT symmetric fiber ring lasers with different cavity length can be calculated by the frequency noise spectral density, as illustrated in Figure 11. The red circle represents the integral linewidth of the laser when the cavity length was 46.2 m, the magenta circle represents it at 65.0 m, and the blue circle represents it at 97.5 m. Specifically, at an observation time of 473.9 μs, the integral linewidth was approximately 46.47 kHz for a cavity length of 46.2 m, 16.25 kHz for a cavity length of 65.0 m, and 0.72 kHz for a cavity length of 97.5 m. When the observation time increased to 2.551 × 104 μs, the integral linewidth became approximately 86.97 kHz for a cavity length of 46.2 m, 44.32 kHz for a cavity length of 65.0 m, and 21.93 kHz for a cavity length of 97.5 m. Further increasing the observation time to 3.891 × 105 μs resulted in an integral linewidth of approximately 212.75 kHz for a cavity length of 46.2 m, 183.26 kHz for a cavity length of 65.0 m, and 212.27 kHz for a cavity length of 97.5 m. It is observable from Figure 11 that the integral linewidth widened with an increasing observation time. However, at smaller observation timescales, there was a significant discrepancy among the three different cavity lengths which diminished gradually as the observation time increased.
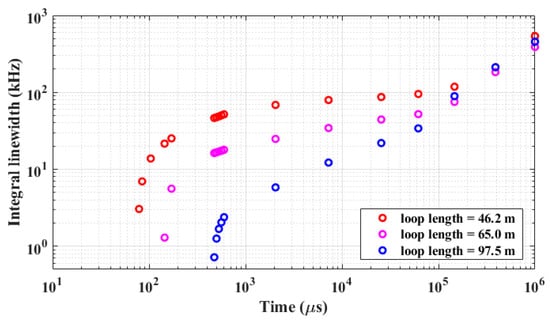
Figure 11.
Integral linewidth with various observation timescales of the PT symmetric fiber ring lasers with different cavity lengths.
The roll-off characteristics of the OTF can affect the gain difference between the principal mode and the side modes. A larger gain difference leads to a reduced influence of the wavelength drift from internal noise fluctuations and environmental interference within the laser. Therefore, the wavelength drift of the PT symmetric fiber ring laser over a period of 30 min is demonstrated with the different bandwidth of the OTF in Figure 12. Figure 12a shows the transmittance spectra of the OTF with different bandwidth measured by the OSA. Figure 12b illustrates the corresponding relationship between the bandwidth of the OTF and the wavelength drift range of the PT symmetric fiber ring laser during a 30 min period. As it can be observed from Figure 12b, an increase in the bandwidth of the OTF resulted in a deterioration of the long-term stability of the laser. Particularly, the wavelength drift range began to increase significantly when the bandwidth exceeded 0.5015 nm. The reason why may be due to two factors. One is that the flat-top part in the transmittance spectrum of the OTF significantly expanded, enhancing the variation range of the potential maximum gain position. The other originates from the disturbance of internal noise and the external environment. Consequently, the drift range of the principal mode wavelength selected by the PT symmetry breaking mechanism was much larger than the longitudinal mode spacing. Therefore, the selection of an optical filter with a large roll-off is helpful to improve the stability of the PT symmetric fiber ring laser.
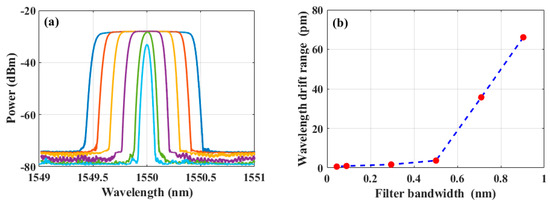
Figure 12.
(a) Transmission spectra and (b) wavelength drift range within a 30 min period for the PT symmetric fiber ring laser operating at different bandwidths of OTF.
4. Conclusions
In conclusion, we propose a high-performance fiber ring laser based on polarization space PT symmetry breaking. By adjusting a PC and the pumping current of an EDFA in the ring cavity, the gain/loss and coupling coefficients of the two polarization loops within a single fiber loop are controlled. When the gain of one polarization loop balances the losses of the other one and exceeds the coupling coefficient, the PT symmetry is broken, resulting in single-longitudinal-mode oscillations. Furthermore, the frequency noise spectral density and linewidth characteristics of the laser are tested by the short-delay self-heterodyne method, revealing excellent low noise with a frequency noise spectral density of approximately 181 Hz2/Hz at a 10 kHz offset frequency and a fundamental linewidth of about 68 Hz. Moreover, the laser exhibits outstanding wavelength stability, with a wavelength drift of only 0.64 pm during a 30 min period. Additionally, by tuning an OTF, the output single-longitudinal-mode signal can cover the entire C-band, providing a wide tuning range. We also analyze the impact of different fiber lengths on the frequency noise spectral density and filter bandwidth on the stability of the system, providing reference for component selection in such the lasers.
Author Contributions
Conceptualization, F.Z. and G.X.; methodology, F.Z.; validation, F.Z., G.X. and Z.W.; formal analysis, F.Z. and X.T.; investigation, F.Z.; resources, Z.W.; data curation, F.Z.; writing—original draft preparation, F.Z.; writing—review and editing, F.Z.; visualization, F.Z.; supervision, G.X.; project administration, Z.W.; funding acquisition, Z.W. and G.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (62335015, 61875167) and by the Chongqing Natural Science Foundation (CSTB2022NSCQ-MSX0313).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hsieh, S.-E.; Hsu, C.-H.; Yeh, C.-H.; Jiang, S.-Y.; Lai, Y.-T.; Chow, C.-W.; Liaw, S.-K. L-Band Wavelength-selectable erbium laser with stable single-frequency oscillation. Electronics 2022, 11, 2996. [Google Scholar] [CrossRef]
- Chen, L.-C.; Lai, Y.-T.; Yeh, C.-H.; Lin, W.-P.; Chow, C.-W.; Chen, J.-H. A stabilized single-longitudinal-mode and wide wavelength tunability erbium laser. Photonics 2022, 9, 336. [Google Scholar] [CrossRef]
- Yeh, C.-H.; Chen, J.-Y.; Chen, H.-Z.; Chen, J.-H.; Chow, C.-W. Stable and tunable single-longitudinal-mode erbium-doped fiber triple-ring laser with power-equalized output. IEEE Photonics J. 2016, 8, 1–6. [Google Scholar] [CrossRef]
- Yeh, C.-H.; Lai, Y.-T.; Liu, L.-H.; Ko, H.-S.; Lai, Y.-T.; Chen, Y.-C.; Chow, C.-W. Use of simple octa-ring configuration for tunable erbium laser with single-mode output. IEEE Access 2022, 10, 38750–38754. [Google Scholar] [CrossRef]
- Yeh, C.H.; Lin, W.-P.; Chang, Y.-J.; Xie, Y.-R.; Luo, C.-M.; Chow, C.-W. A selectable single-mode erbium laser with power-flattened output employing dual-sagnac-ring. IEEE Access 2019, 7, 92938–92942. [Google Scholar] [CrossRef]
- Yeh, C.-H.; Fan, K.-P.; Chi, S. Operation of saturable-absorber-based autotracking filter for a stabilized single-frequency erbium fiber laser. Jpn. J. Appl. Phys. 2005, 44, 4012. [Google Scholar] [CrossRef]
- Chien, H.-C.; Yeh, C.-H.; Lee, C.-C.; Chi, S. A tunable and single-frequency S-band erbium fiber laser with saturable-absorber-based autotracking filter. Opt. Commun. 2005, 250, 163–167. [Google Scholar] [CrossRef]
- Yeh, C.-H.; Chi, S. A broadband fiber ring laser technique with stable and tunable signal-frequency operation. Opt. Express 2005, 13, 2540–2544. [Google Scholar] [CrossRef]
- Hsieh, S.-E.; Chen, L.-Y.; Hsu, C.-H.; Lai, Y.-T.; Yeh, C.-H.; Jiang, S.-Y.; Liaw, S.-K.; Chow, C.-W. Selectable and stable single-frequency fiber laser with flattened power range and sub-kHz linewidth output. Phys. Scr. 2023, 98, 105513. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Q.; Xu, Z.; Luo, Y.; Liu, D. A single longitudinal mode fiber ring laser based on cascaded microfiber knots filter. IEEE Photonics Technol. Lett. 2016, 28, 2172–2175. [Google Scholar] [CrossRef]
- Chang, P.; Wang, C.; Han, H.; Gao, F.; Huang, L.; Wang, A. Tunable narrow-linewidth ring laser based on the polarization conversion in a tapered fiber-coupled whispering gallery mode resonator. Crystals 2021, 11, 1285. [Google Scholar] [CrossRef]
- Li, D.; Feng, T.; Guo, S.; Wu, S.; Yan, F.; Li, Q.; Yao, X.S. Wavelength-tunable single-longitudinal-mode narrow-linewidth thulium/holmium co-doped fiber laser with phase-shifted fiber Bragg grating and dual-coupler-ring filter. Photonics 2023, 10, 693. [Google Scholar] [CrossRef]
- Chen, X.; Xian, L.; Ogusu, K.; Li, H. Single-longitudinal-mode Brillouin fiber laser incorporating an unpumped erbium-doped fiber loop. Appl. Phys. B 2012, 107, 791–794. [Google Scholar] [CrossRef]
- Spirin, V.V.; López-Mercado, C.A.; Kinet, D.; Mégret, P.; Zolotovskiy, I.O.; Fotiadi, A.A. A single-longitudinal-mode Brillouin fiber laser passively stabilized at the pump resonance frequency with a dynamic population inversion grating. Laser Phys. Lett. 2013, 10, 015102. [Google Scholar] [CrossRef]
- Tao, L.; Wang, F.; Wu, Z.; Xia, G. Stable and tunable PT symmetric single-longitudinal-mode fiber laser using a nonreciprocal sagnac loop. IEEE Access 2023, 11, 23127–23135. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, W.; Qiu, Q.; Yao, J. Observation of PT-symmetry in a fiber ring laser. Opt. Lett. 2020, 45, 1027–1030. [Google Scholar] [CrossRef] [PubMed]
- Dai, Z.; Fan, Z.; Li, P.; Yao, J. Widely wavelength-tunable parity-time symmetric single-longitudinal-mode fiber ring laser with a single physical loop. J. Lightwave Technol. 2021, 39, 2151–2157. [Google Scholar] [CrossRef]
- Fan, Z.; Dai, Z.; Qiu, Q.; Yao, J. Parity-time symmetry in a single-loop photonic system. J. Lightwave Technol. 2020, 38, 3866–3873. [Google Scholar]
- Zhang, J.; Guo, J.; Wang, H.; Tang, D.; Shen, D. Single longitudinal mode lasing near the exceptional point in a fiber laser using a tunable isolator. Opt. Lett. 2022, 47, 2222–2225. [Google Scholar] [CrossRef]
- Deng, Z.; Li, L.; Zhang, J.; Yao, J. Single-mode narrow-linewidth fiber ring laser with SBS-assisted parity-time symmetry for mode selection. Opt. Express 2022, 30, 20809–20819. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Xu, X.; Jiang, K.; You, Y.; He, W.; Han, X.; Hou, J.; Chou, X. Narrow linewidth parity-time symmetric Brillouin fiber laser based on a dual-polarization cavity with a single micro-ring resonator. Opt. Express 2022, 30, 44545–44555. [Google Scholar] [CrossRef] [PubMed]
- Dai, Z.; Wang, Z.; Yao, J. Dual-loop parity-time symmetric system with a rational loop length ratio. Opt. Lett. 2023, 48, 143–146. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Cao, Y.; Zhi, Y.; Zhang, J.; Zou, Y.; Feng, X.; Guan, B.-O.; Yao, J. Polarimetric parity-time symmetry in a photonic system. Light Sci. Appl. 2020, 9, 109. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Zhou, H.; Huang, D.; Li, F.; Dong, J.; Zhang, X.; Wai, P.K.A. Suppression and revival of single-cavity lasing induced by polarization-dependent loss. Opt. Lett. 2021, 46, 3151–3154. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Yin, B.; Gao, M.; Liu, S.; Li, H.; Wang, M.; Wu, S. Polarimetric parity-time symmetry fiber laser with switchable and tunable orthogonal single-polarization narrow-linewidth output. Results Phys. 2023, 51, 106637. [Google Scholar] [CrossRef]
- Horak, P.; Loh, W.H. On the delayed self-heterodyne interferometric technique for determining the linewidth of fiber lasers. Opt. Express 2006, 14, 3923–3928. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Bai, Z.; Jin, D.; Qi, Y.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z.; Mildren, R.P. Narrow laser-linewidth measurement using short delay self-heterodyne interferometry. Opt. Express 2022, 30, 30600–30610. [Google Scholar] [CrossRef]
- Zhou, Q.; Qin, J.; Xie, W.; Liu, Z.; Tong, Y.; Dong, Y.; Hu, W. Dynamic frequency-noise spectrum measurement for a frequency-swept DFB laser with short-delayed self-heterodyne method. Opt. Express 2015, 23, 29245–29257. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Lin, X.; Wu, Z.; Xia, G. A symmetric parity-time coupled optoelectronic oscillator using a polarization-dependent spatial structure. Photonics 2023, 10, 1236. [Google Scholar] [CrossRef]
- Miri, M.A.; Alù, A. Exceptional points in optics and photonics. Science 2019, 363, eaar7709. [Google Scholar] [CrossRef]
- Mao, W.; Fu, Z.; Li, Y.; Li, F.; Yang, L. Exceptional-point-enhanced phase sensing. Sci. Adv. 2024, 10, eadl5037. [Google Scholar] [CrossRef] [PubMed]
- Richter, L.; Mandelberg, H.; Kruger, M.; McGrath, P. Linewidth determination from self-heterodyne measurements with subcoherence delay times. IEEE J. Quantum Electron. 1986, 22, 2070–2074. [Google Scholar] [CrossRef]
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple approach to the relation between laser frequency noise and laser line shape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef] [PubMed]
- Brodnik, G.M.; Harrington, M.W.; Dallyn, J.H.; Bose, D.; Zhang, W.; Stern, L.; Morton, P.A.; Behunin, R.O.; Papp, S.B.; Blumenthal, D.J. Optically synchronized fibre links using spectrally pure chip-scale lasers. Nat. Photonics 2021, 15, 588–593. [Google Scholar] [CrossRef]
- Liang, W.; Ilchenko, V.S.; Eliyahu, D.; Savchenkov, A.A.; Matsko, A.B.; Seidel, D.; Maleki, L. Ultralow noise miniature external cavity semiconductor laser. Nat. Commun. 2015, 6, 7371. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).