Sensing Characteristic Analysis of All-Dielectric Metasurfaces Based on Fano Resonance in Near-Infrared Regime
Abstract
1. Introduction
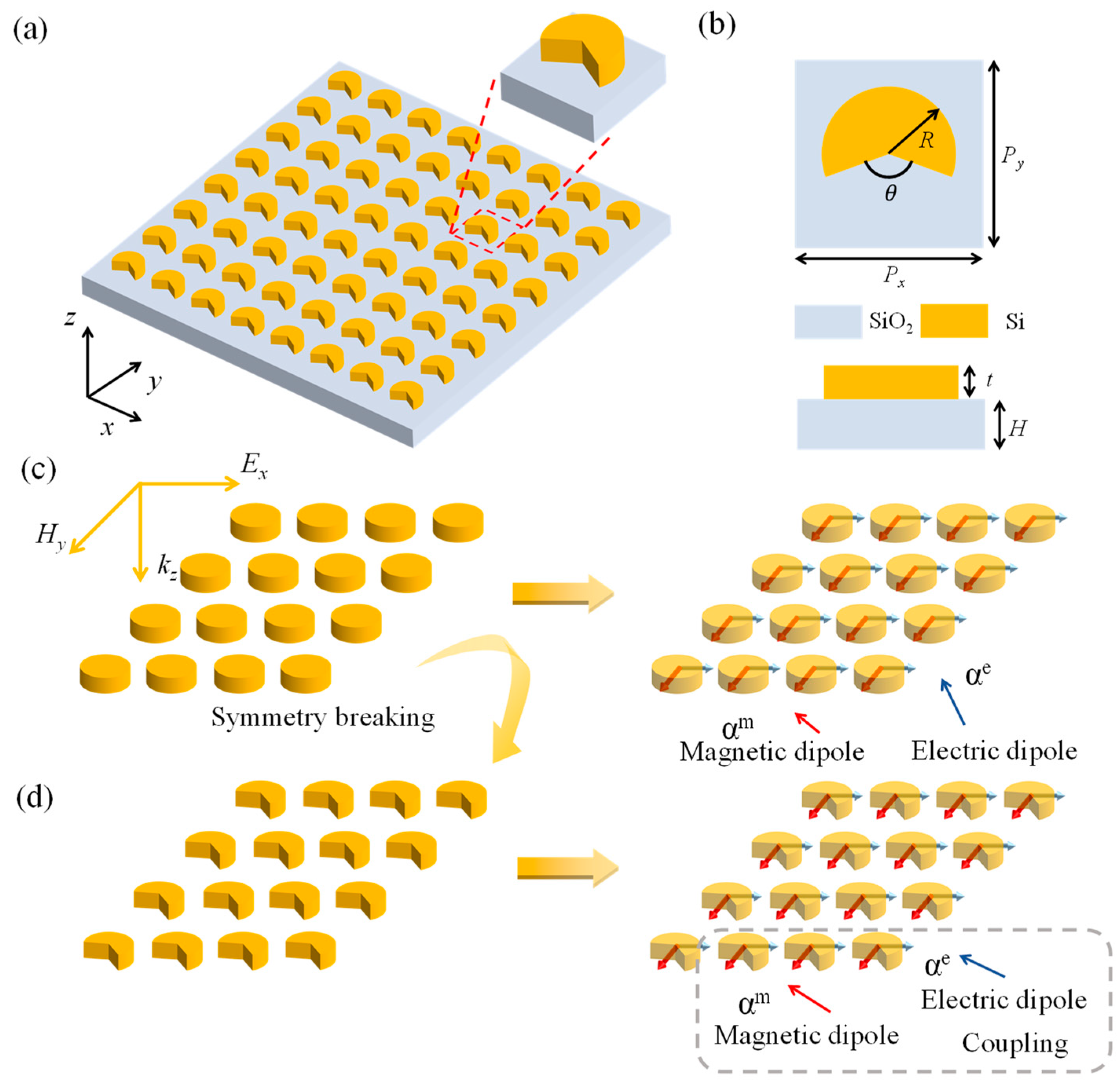
2. Design and Theoretical Analysis
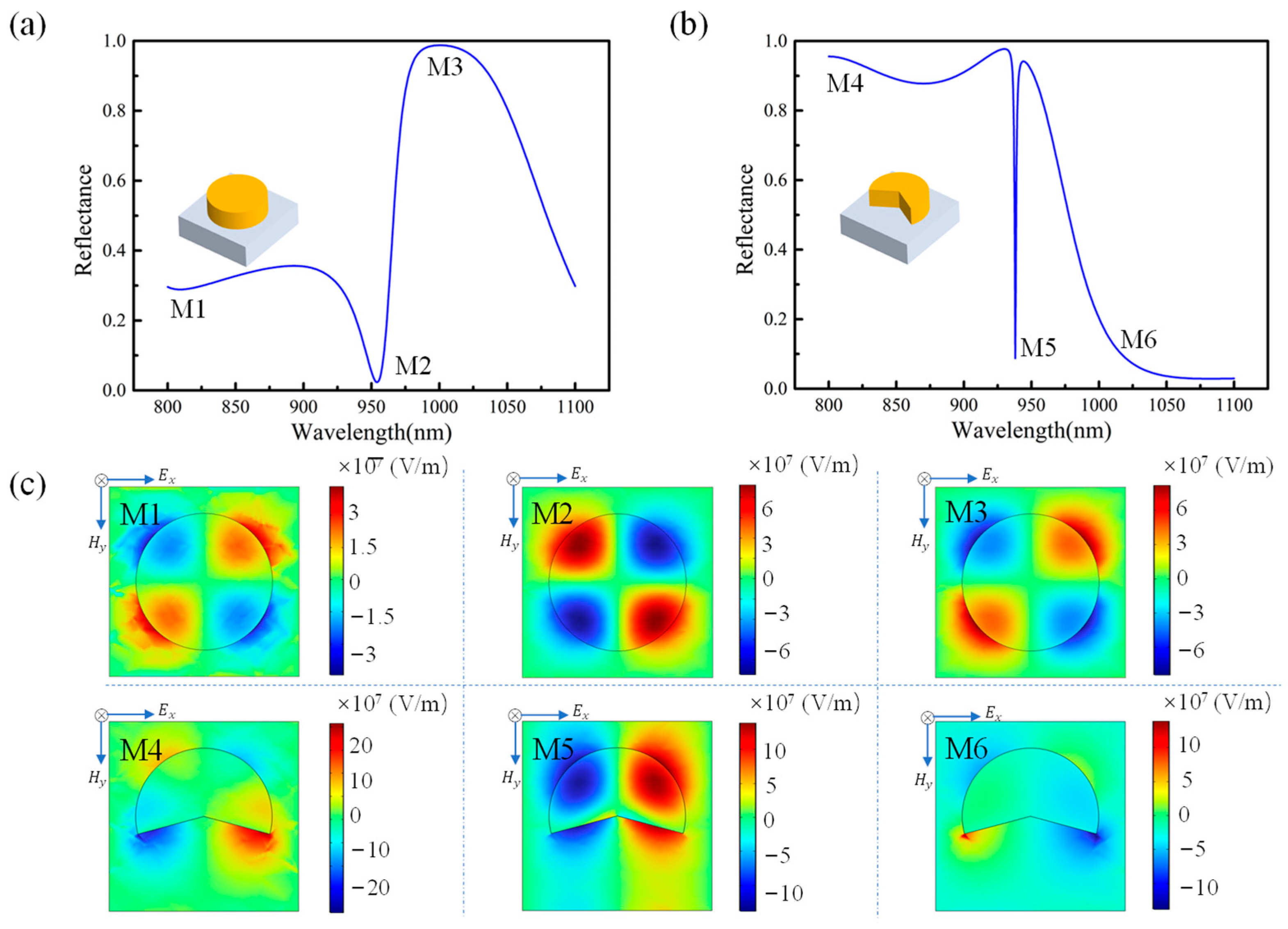
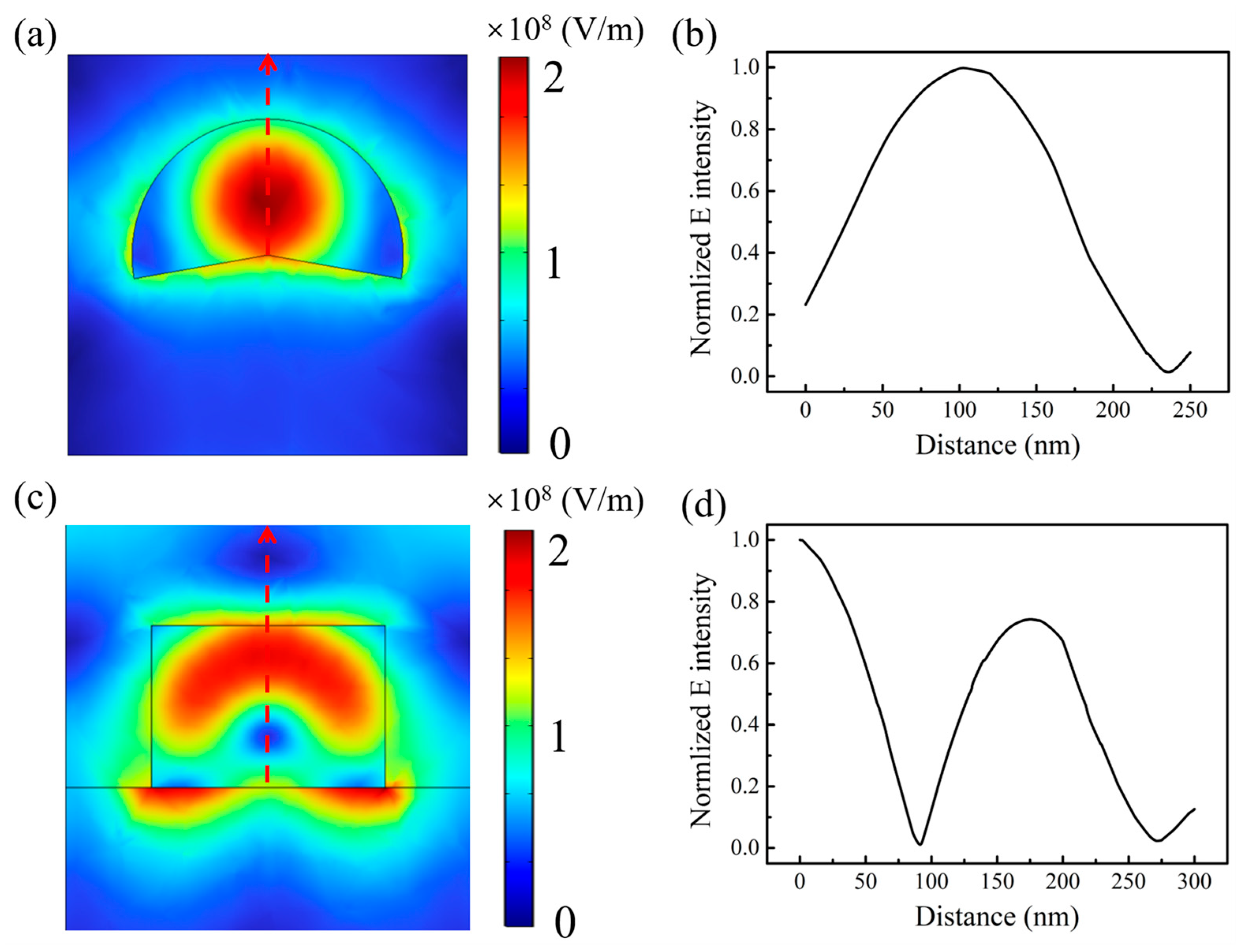
3. Results and Discussion
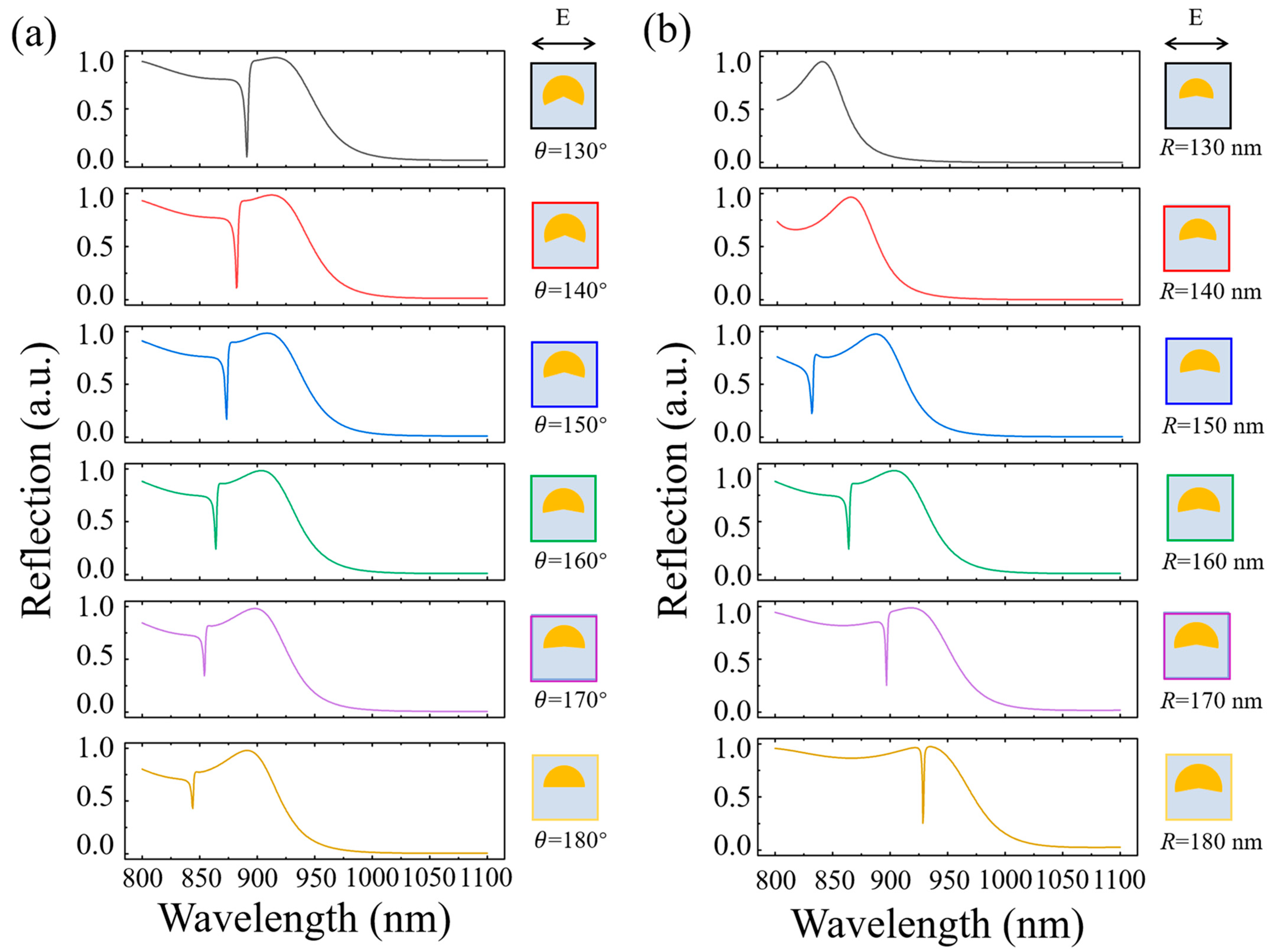
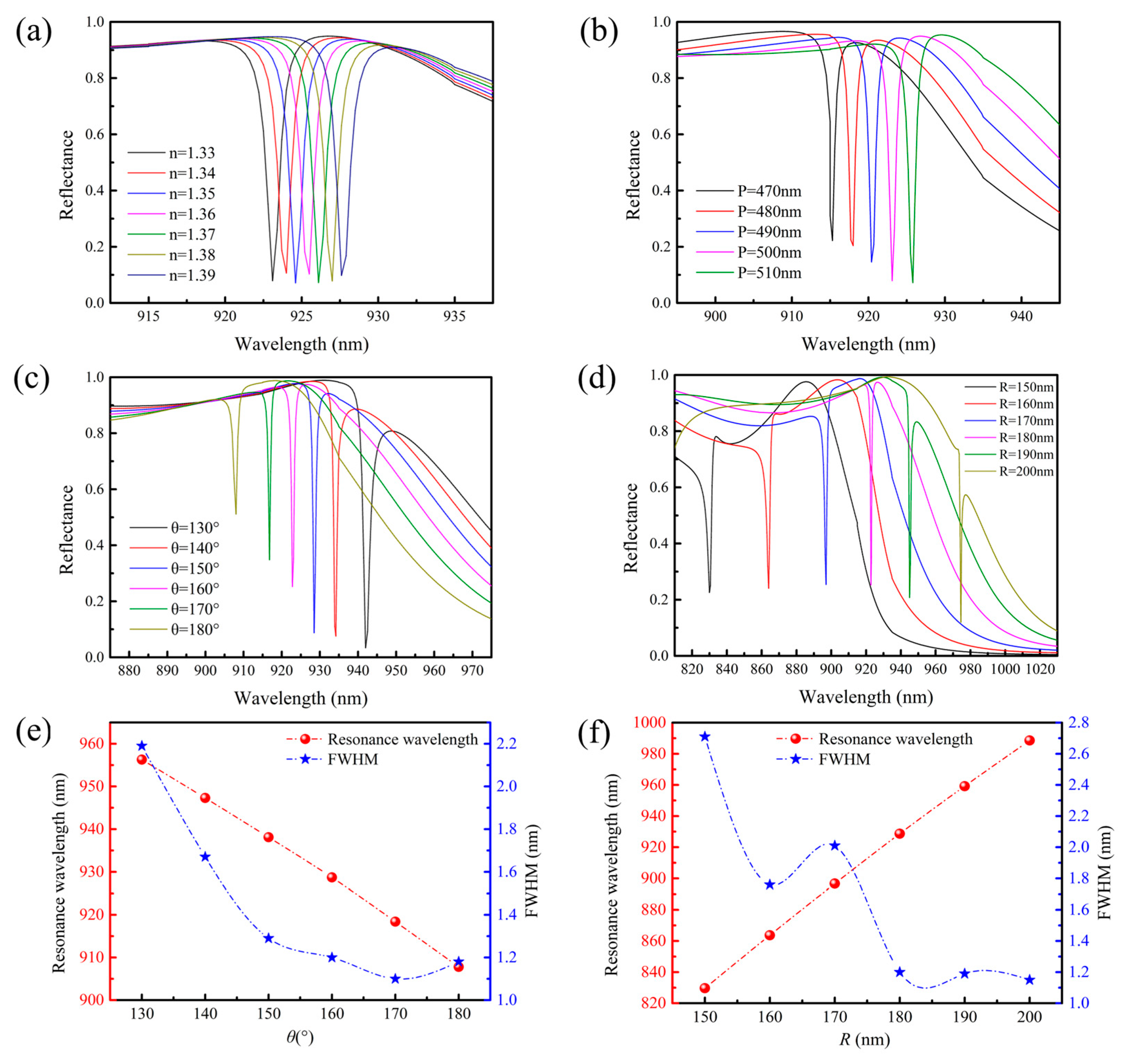
3.1. The Influence of Geometric Parameters
3.2. Sensing Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Principe, M.; Consales, M.; Castaldi, G.; Galdi, V.; Cusano, A. Evaluation of fiber-optic phase-gradient meta-tips for sensing applications. Nanomater. Nanotechnol. 2019, 9, 184798041983272. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wang, D.N.; Xu, B.; Wang, Z.K. Optical fiber tip interferometer gas pressure sensor based on anti-resonant reflecting guidance mechanism. Opt. Fiber Technol. 2018, 42, 11–17. [Google Scholar] [CrossRef]
- Pahlevaninezhad, H.; Khorasaninejad, M.; Huang, Y.-W.; Shi, Z.; Hariri, L.P.; Adams, D.C.; Ding, V.; Zhu, A.; Qiu, C.-W.; Capasso, F.; et al. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat. Photonics 2018, 12, 540–547. [Google Scholar] [CrossRef]
- Mao, R.Q.; Lin, Y.; Yang, K.; An, Q.; Fu, Y.Q. A High-Efficiency Fiber-Coupled Rydberg-Atom Integrated Probe and Its Imaging Applications. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 352–356. [Google Scholar] [CrossRef]
- Kasztelanic, R.; Filipkowski, A.; Anuszkiewicz, A.; Stafiej, P.; Stepniewski, G.; Pysz, D.; Krzyzak, K.; Stepien, R.; Klimczak, M.; Buczynski, R. Integrating Free-Form Nanostructured GRIN Microlenses with Single-Mode Fibers for Optofluidic Systems. Sci. Rep. 2018, 8, 5072. [Google Scholar] [CrossRef]
- Guggenheim, J.A.; Li, J.; Allen, T.J.; Colchester, R.J.; Noimark, S.; Ogunlade, O.; Parkin, I.P.; Papakonstantinou, I.; Desjardins, A.E.; Zhang, E.Z.; et al. Ultrasensitive plano-concave optical microresonators for ultrasound sensing. Nat. Photonics 2017, 11, 714–719. [Google Scholar] [CrossRef]
- Zhao, M.T.; Huang, Y.; Kang, J.U. Sapphire ball lens-based fiber probe for common-path optical coherence tomography and its applications in corneal and retinal imaging. Opt. Lett. 2012, 37, 4835–4837. [Google Scholar] [CrossRef]
- Mo, J.H.; Zheng, W.; Huang, Z.W. Fiber-optic Raman probe couples ball lens for depth-selected Raman measurements of epithelial tissue. Biomed. Opt. Express 2010, 1, 17–30. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 2011, 5, 523–530. [Google Scholar] [CrossRef]
- Sang, D.; Xu, M.F.; Pu, M.B.; Zhang, F.; Guo, Y.H.; Li, X.; Ma, X.L.; Fu, Y.Q.; Luo, X.G. Toward High-Efficiency Ultrahigh Numerical Aperture Freeform Metalens: From Vector Diffraction Theory to Topology Optimization. Laser Photonics Rev. 2022, 16, 2200265. [Google Scholar] [CrossRef]
- Zang, X.F.; Xu, W.W.; Gu, M.; Yao, B.S.; Chen, L.; Peng, Y.; Xie, J.Y.; Balakin, A.V.; Shkurinov, A.P.; Zhu, Y.M.; et al. Polarization-Insensitive Metalens with Extended Focal Depth and Longitudinal High-Tolerance Imaging. Adv. Opt. Mater. 2020, 8, 1901342. [Google Scholar] [CrossRef]
- Ahmed, H.; Kim, H.; Zhang, Y.B.; Intaravanne, Y.; Jang, J.; Rho, J.; Chen, S.Q.; Chen, X.Z. Optical metasurfaces for generating and manipulating optical vortex beams. Nanophotonics 2022, 11, 941–956. [Google Scholar] [CrossRef]
- Liu, B.Y.; Sain, B.; Reineke, B.; Zhao, R.Z.; Meier, C.; Huang, L.L.; Jiang, Y.Y.; Zentgraf, T. Nonlinear Wavefront Control by Geometric-Phase Dielectric Metasurfaces: Influence of Mode Field and Rotational Symmetry. Adv. Opt. Mater. 2020, 8, 1902050. [Google Scholar] [CrossRef]
- Zhao, Q.; Yuan, W.; Qu, J.; Cheng, Z.; Peng, G.-D.; Yu, C. Optical Fiber-Integrated Metasurfaces: An Emerging Platform for Multiple Optical Applications. Nanomaterials 2022, 12, 793. [Google Scholar] [CrossRef]
- Ding, F.; Chang, B.; Wei, Q.; Huang, L.; Guan, X.; Bozhevolnyi, S.I. Versatile Polarization Generation and Manipulation Using Dielectric Metasurfaces. Laser Photonics Rev. 2020, 14, 2000116. [Google Scholar] [CrossRef]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Lu, M.; Stein, A.; Zheng, C.X.; Yu, N.F. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light-Sci. Appl. 2019, 8, 92. [Google Scholar] [CrossRef]
- Lee, G.Y.; Yoon, G.; Lee, S.Y.; Yun, H.; Cho, J.; Lee, K.; Kim, H.; Rho, J.; Lee, B. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 2018, 10, 4237–4245. [Google Scholar] [CrossRef]
- Ren, H.; Jang, J.; Li, C.; Aigner, A.; Plidschun, M.; Kim, J.; Rho, J.; Schmidt, M.A.; Maier, S.A. An achromatic metafiber for focusing and imaging across the entire telecommunication range. Nat. Commun. 2022, 13, 4183. [Google Scholar] [CrossRef]
- Ren, X.B.; Ren, K.; Zhang, Y.; Ming, C.G.; Han, Q. Multiple Fano resonances with flexible tunablity based on symmetry-breaking resonators. Beilstein J. Nanotechnol. 2019, 10, 2459–2467. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Sun, J.B.; Tsukernik, A.; Pandey, A.; Nikolskiy, K.; Litchinitser, N.M. High-Efficiency All-Dielectric Metasurfaces for Ultracompact Beam Manipulation in Transmission Mode. Nano Lett. 2015, 15, 6261–6266. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, X.Q.; Xu, Q.; Plum, E.; Chen, K.; Xu, Y.H.; Liu, Y.C.; Zhang, H.F.; Chen, X.Y.; Ren, G.H.; et al. Dielectric Metasurfaces for Complete Control of Phase, Amplitude, and Polarization. Adv. Opt. Mater. 2022, 10, 2101223. [Google Scholar] [CrossRef]
- Liu, M.Z.; Zhu, W.Q.; Huo, P.C.; Feng, L.; Song, M.W.; Zhang, C.; Chen, L.; Lezec, H.J.; Lu, Y.Q.; Agrawal, A.; et al. Multifunctional metasurfaces enabled by simultaneous and independent control of phase and amplitude for orthogonal polarization states. Light-Sci. Appl. 2021, 10, 107. [Google Scholar] [CrossRef]
- Rahman, B.M.A.; Viphavakit, C.; Chitaree, R.; Ghosh, S.; Pathak, A.K.; Verma, S.; Sakda, N. Optical Fiber, Nanomaterial, and THz-Metasurface-Mediated Nano-Biosensors: A Review. Biosensors 2022, 12, 42. [Google Scholar] [CrossRef]
- Saleh, A.A.E.; Sheikhoelislami, S.; Gastelum, S.; Dionne, J.A. Grating-flanked plasmonic coaxial apertures for efficient fiber optical tweezers. Opt. Express 2016, 24, 20593–20603. [Google Scholar] [CrossRef]
- Liberale, C.; Minzioni, P.; Bragheri, F.; De Angelis, F.; Di Fabrizio, E.; Cristiani, I. Miniaturized all-fibre probe for three-dimensional optical trapping and manipulation. Nat. Photonics 2007, 1, 723–727. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, C.; Zheng, S.; Tao, X.; Liu, X.; Li, Y.; Wu, F.; Zheng, Z. Double-layer polarization-independent achromatic metasurface array for optical fiber bundle coupling in microendoscope. Sci. Rep. 2022, 12, 20476. [Google Scholar] [CrossRef]
- Xie, N.; Carson, M.D.; Froch, J.E.; Majumdar, A.; Seibel, E.J.; Bohringer, K.F. Large field-of-view short-wave infrared metalens for scanning fiber endoscopy. J. Biomed. Opt. 2023, 28, 094802. [Google Scholar] [CrossRef]
- Ghimire, I.; Yang, J.; Gurung, S.; Mishra, S.K.; Lee, H.W.H. Polarization-dependent photonic crystal fiber optical filters enabled by asymmetric metasurfaces. Nanophotonics 2022, 11, 2711–2717. [Google Scholar] [CrossRef]
- Li, J.; Li, R.; Xue, X.; Jiang, X.; Chen, X.; Chui, H.-C. Achromatic Flat Metasurface Fiber Couplers within Telecom Bands. Photonics 2022, 10, 28. [Google Scholar] [CrossRef]
- Mao, R.Q.; Lin, Y.; Fu, Y.Q.; Ma, Y.M.; Yang, K. Digital Beamforming and Receiving Array Research Based on Rydberg Field Probes. IEEE Trans. Antennas Propag. 2024, 72, 2025–2029. [Google Scholar] [CrossRef]
- Prajapati, N.; Rotunno, A.P.; Berweger, S.; Simons, M.T.; Artusio-Glimpse, A.B.; Voran, S.D.; Holloway, C.L. TV and video game streaming with a quantum receiver: A study on a Rydberg atom-based receiver’s bandwidth and reception clarity. AVS Quantum Sci. 2022, 4, 035001. [Google Scholar] [CrossRef]
- Lin, Y.; Wu, F.-C.; Mao, R.-Q.; Yao, J.-W.; Liu, Y.; An, Q.; Fu, Y.-Q. Development of three-port fiber-coupled vapor cell probe and its application in microwave digital communication. Acta Phys. Sin. 2022, 71, 170702. [Google Scholar] [CrossRef]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Fan, Z.B.; Shao, Z.K.; Xie, M.Y.; Pang, X.N.; Ruan, W.S.; Zhao, F.L.; Chen, Y.J.; Yu, S.Y.; Dong, J.W. Silicon Nitride Metalenses for Close-to-One Numerical Aperture and Wide-Angle Visible Imaging. Phys. Rev. Appl. 2018, 10, 014005. [Google Scholar] [CrossRef]
- Grann, E.B.; Moharam, M.G.; Pommet, D.A. Optimal design for antireflective tapered two-dimensional subwavelength grating structures. J. Opt. Soc. Am. A 1995, 12, 333–339. [Google Scholar] [CrossRef]
- Yoda, H.; Polynkin, P.; Mansuripur, M. Beam quality factor of higher order modes in a step-index fiber. J. Light. Technol. 2006, 24, 1350–1355. [Google Scholar] [CrossRef]
- Ye, H.; Sun, Q.; Guo, Z.; Hou, Y.; Wen, F.; Yuan, D.; Qin, F.; Zhou, G. Theoretical realization of single-mode fiber integrated metalens for beam collimating. Opt. Express 2021, 29, 27521–27529. [Google Scholar] [CrossRef]
- Marcuse. Gaussian approximation of the fundamental modes of graded-index fibers. J. Opt. Soc. Am. 1978, 68, 103–109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Geng, Q.; Liu, J.; Geng, Z. Sensing Characteristic Analysis of All-Dielectric Metasurfaces Based on Fano Resonance in Near-Infrared Regime. Photonics 2024, 11, 482. https://doi.org/10.3390/photonics11050482
Zhao Y, Geng Q, Liu J, Geng Z. Sensing Characteristic Analysis of All-Dielectric Metasurfaces Based on Fano Resonance in Near-Infrared Regime. Photonics. 2024; 11(5):482. https://doi.org/10.3390/photonics11050482
Chicago/Turabian StyleZhao, Yongpeng, Qingfubo Geng, Jian Liu, and Zhaoxin Geng. 2024. "Sensing Characteristic Analysis of All-Dielectric Metasurfaces Based on Fano Resonance in Near-Infrared Regime" Photonics 11, no. 5: 482. https://doi.org/10.3390/photonics11050482
APA StyleZhao, Y., Geng, Q., Liu, J., & Geng, Z. (2024). Sensing Characteristic Analysis of All-Dielectric Metasurfaces Based on Fano Resonance in Near-Infrared Regime. Photonics, 11(5), 482. https://doi.org/10.3390/photonics11050482




