Design and Analysis of a Narrow Linewidth Laser Based on a Triple Euler Gradient Resonant Ring
Abstract
1. Introduction
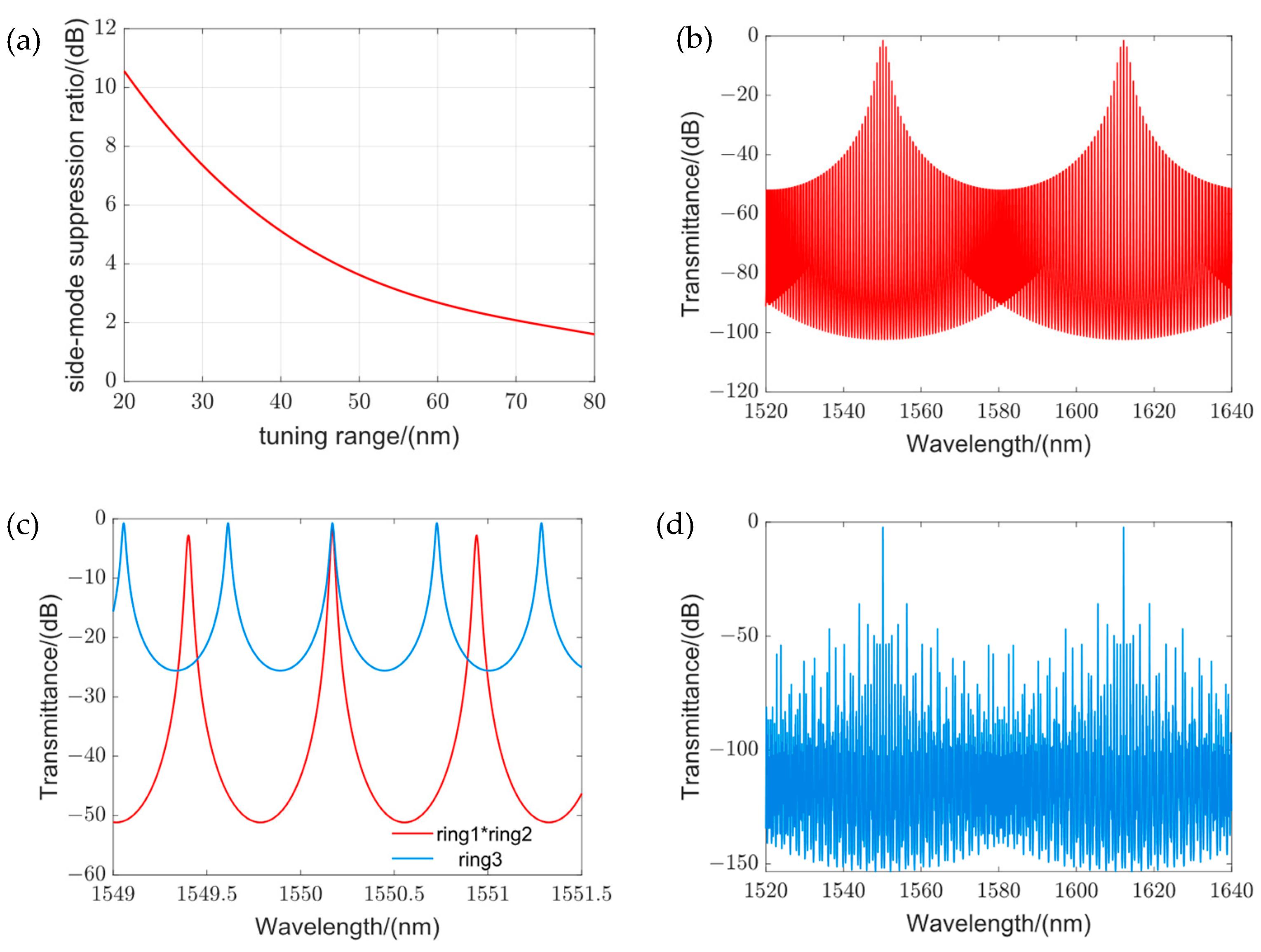
2. Tuning Range and Side-Mode Suppression Ratio
3. Laser Linewidth Theory
4. Laser Design
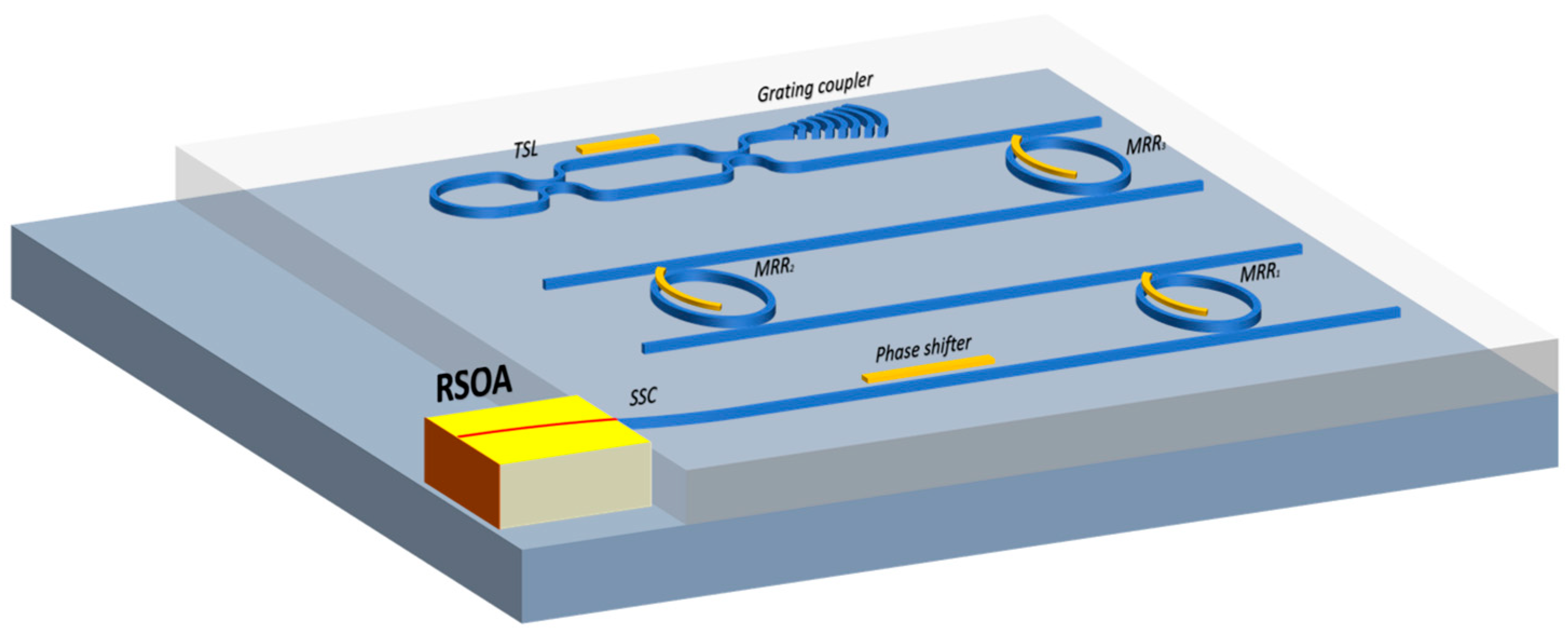
4.1. Laser Structure
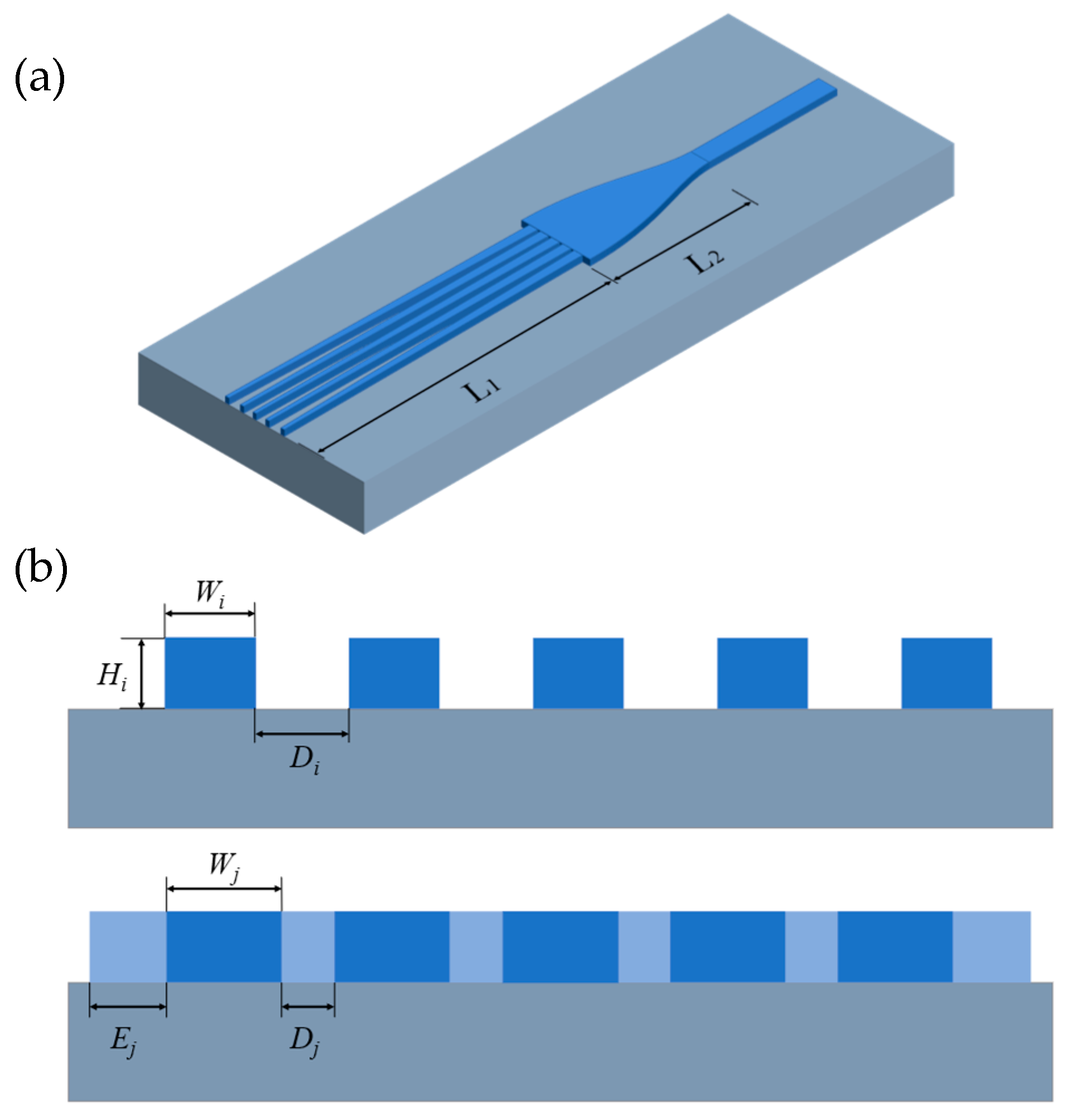
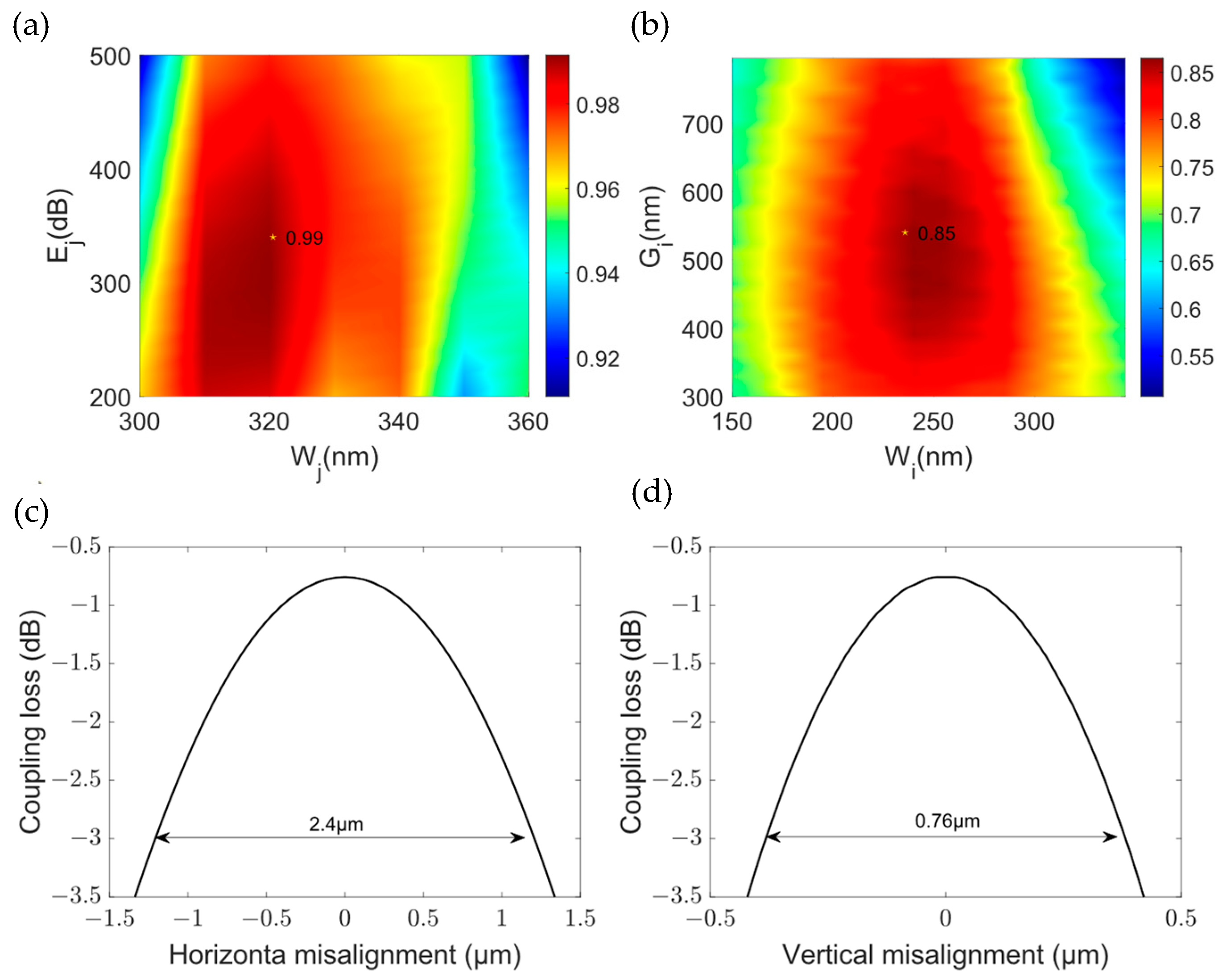
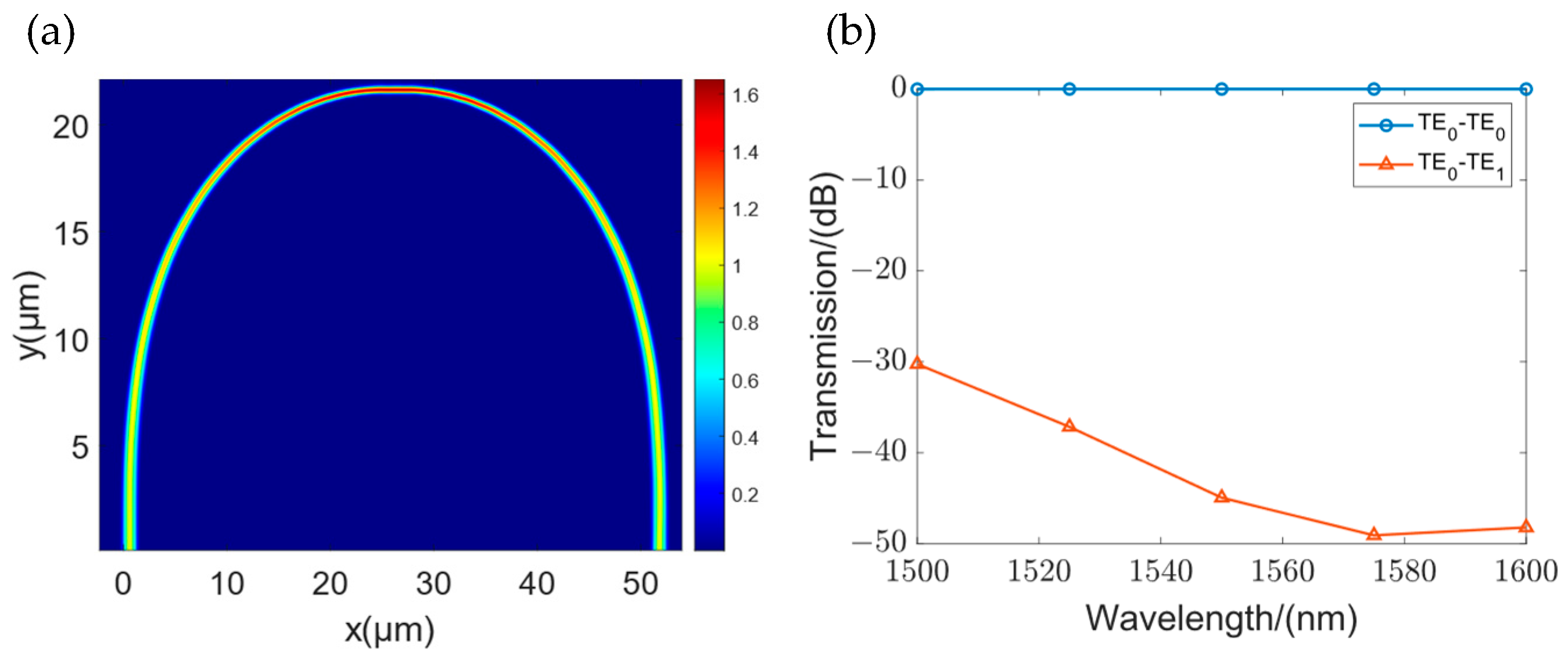
4.2. Edge Couplers
4.3. Euler Gradient Ring Design
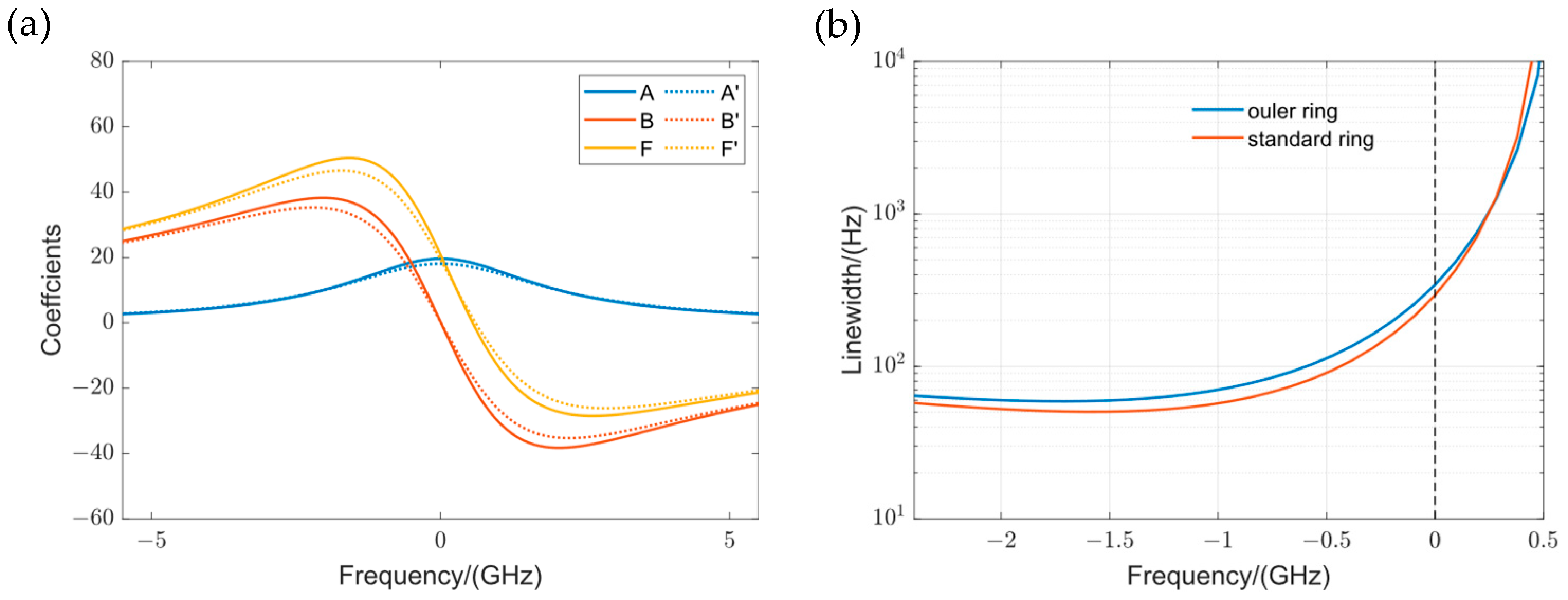
4.4. Theoretical Linewidth Calculation for Lasers
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seimetz, M. Laser linewidth limitations for optical systems with high-order modulation employing feed forward digital carrier phase estimation. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 February 2008; p. OTuM2. [Google Scholar]
- Kahn, J.M.; Ho, K. Spectral efficiency limits and modulation/detection techniques for DWDM systems. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 259–272. [Google Scholar] [CrossRef]
- Labaziewicz, J.; Richerme, P.; Brown, K.R.; Chuang, I.L.; Hayasaka, K. Compact, filtered diode laser system for precision spectroscopy. Opt. Lett. 2007, 32, 572–574. [Google Scholar] [CrossRef] [PubMed]
- Schioppo, M.; Brown, R.C.; McGrew, W.F.; Hinkley, N.; Fasano, R.J.; Beloy, K.; Yoon, T.H.; Milani, G.; Nicolodi, D.; Sherman, J.A. Ultrastable optical clock with two cold-atom ensembles. Nat. Photonics 2017, 11, 48–52. [Google Scholar] [CrossRef]
- Tang, L.; Jia, H.; Shao, S.; Yang, S.; Chen, H.; Chen, M. Hybrid integrated low-noise linear chirp frequency-modulated continuous-wave laser source based on self-injection to an external cavity. Photonics Res. 2021, 9, 1948–1957. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Pikovski, I.; Langellier, N.; Lukin, M.D.; Walsworth, R.L.; Ye, J. Gravitational wave detection with optical lattice atomic clocks. Phys. Rev. D 2016, 94, 124043. [Google Scholar] [CrossRef]
- Chu, T.; Fujioka, N.; Ishizaka, M. Compact, lower-power-consumption wavelength tunable laser fabricated with silicon photonic-wire waveguide micro-ring resonators. Opt. Express 2009, 17, 14063. [Google Scholar] [CrossRef] [PubMed]
- Oldenbeuving, R.M.; Klein, E.J.; Offerhaus, H.L.; Lee, C.J.; Song, H.; Boller, K. 25 kHz narrow spectral bandwidth of a wavelength tunable diode laser with a short waveguide-based external cavity. Laser Phys. Lett. 2012, 10, 15804. [Google Scholar] [CrossRef]
- Srinivasan, S.; Davenport, M.; Komljenovic, T.; Hulme, J.; Spencer, D.T.; Bowers, J.E. Coupled-Ring-Resonator-Mirror-Based Heterogeneous III–V Silicon Tunable Laser. IEEE Photonics J. 2015, 7, 2700908. [Google Scholar] [CrossRef]
- Lee, J.H.; Shubin, I.; Yao, J.; Bickford, J.; Luo, Y.; Lin, S.; Djordjevic, S.S.; Thacker, H.D.; Cunningham, J.E.; Raj, K.; et al. High power and widely tunable Si hybrid external-cavity laser for power efficient Si photonics WDM links. Opt. Express 2014, 22, 7678. [Google Scholar] [CrossRef]
- Hu, Y.; Cao, W.; Tang, X.; Ma, W.; Qiu, Y.; Li, S.; Yu, S. High power, high SMSR and wide tuning range silicon micro-ring tunable laser. Opt. Express 2017, 25, 8029. [Google Scholar] [CrossRef]
- Tran, M.A.; Huang, D.; Guo, J.; Komljenovic, T.; Morton, P.A.; Bowers, J.E. Ring-Resonator Based Widely-Tunable Narrow-Linewidth Si/InP Integrated Lasers. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1500514. [Google Scholar] [CrossRef]
- Liu, K.; Jin, N.; Cheng, H.; Chauhan, N.; Puckett, M.W.; Nelson, K.D.; Behunin, R.O.; Rakich, P.T.; Blumenthal, D.J. Ultralow 0.034 dB/m loss wafer-scale integrated photonics realizing 720 million Q and 380 μW threshold Brillouin lasing. Opt. Lett. 2022, 47, 1855–1858. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, G.; Dell, F.; Conteduca, D.; Armenise, M.N.; Ciminelli, C. Comprehensive mathematical modelling of ultra-high Q grating-assisted ring resonators. J. Opt. 2020, 22, 35802. [Google Scholar] [CrossRef]
- Lee, H.; Chen, T.; Li, J.; Yang, K.Y.; Jeon, S.; Painter, O.; Vahala, K.J. Chemically etched ultrahigh-Q wedge-resonator on a silicon chip. Nat. Photonics 2012, 6, 369–373. [Google Scholar] [CrossRef]
- Zhang, L.; Jie, L.; Zhang, M.; Wang, Y.; Xie, Y.; Shi, Y.; Dai, D. Ultrahigh-Q silicon racetrack resonators. Photonics Res. 2020, 8, 684. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, H.; Dai, D. Low-loss and low-crosstalk multimode waveguide bend on silicon. Opt. Express 2018, 26, 17680–17689. [Google Scholar] [CrossRef] [PubMed]
- Tsuchizawa, T.; Yamada, K.; Fukuda, H.; Watanabe, T.; Takahashi, J.; Takahashi, M.; Shoji, T.; Tamechika, E.; Itabashi, S.; Morita, H. Microphotonics devices based on silicon microfabrication technology. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 232–240. [Google Scholar] [CrossRef]
- Pu, M.; Liu, L.; Ou, H.; Yvind, K.; Hvam, J.M. Ultra-low-loss inverted taper coupler for silicon-on-insulator ridge waveguide. Opt. Commun. 2010, 283, 3678–3682. [Google Scholar] [CrossRef]
- Ku, K.; Lee, M.M. Wide-Band Optical Mode Converters for Coupling between Fibers and Silicon Photonic Wires with Large Misalignment Tolerance. J. Light. Technol. 2013, 31, 1616–1620. [Google Scholar] [CrossRef]
- Hatori, N.; Shimizu, T.; Okano, M.; Ishizaka, M.; Yamamoto, T.; Urino, Y.; Mori, M.; Nakamura, T.; Arakawa, Y. A novel spot size convertor for hybrid integrated light sources on photonics-electronics convergence system. In Proceedings of the 9th International Conference on Group IV Photonics, San Diego, CA, USA, 29–31 August 2012; pp. 171–173. [Google Scholar]
- Wang, J.; Xuan, Y.; Lee, C.; Niu, B.; Liu, L.; Liu, G.N.; Qi, M. Low-loss and misalignment-tolerant fiber-to-chip edge coupler based on double-tip inverse tapers. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–22 March 2016; pp. 1–3. [Google Scholar]
- Tu, X.; Dumais, P.; Li, M.; Goodwill, D.; Fu, H.; Geng, D.; Bernier, E. Low polarization-dependent-loss silicon photonic trident edge coupler fabricated by 248 nm optical lithography. In Proceedings of the Asia Communications and Photonics Conference, Hong Kong, China, 19–23 November 2015; p. AS4B. 3. [Google Scholar]
- Ren, G.; Chen, S.; Cheng, Y.; Zhai, Y. Study on inverse taper based mode transformer for low loss coupling between silicon wire waveguide and lensed fiber. Opt. Commun. 2011, 284, 4782–4788. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Zhai, W.; Peng, C.; Wang, Z.; Feng, J.; Guo, J. Reconfigurable spot size converter for the silicon photonics integrated circuit. Opt. Express 2021, 29, 37703. [Google Scholar] [CrossRef] [PubMed]
- Geuzebroek, D.H.; Klein, E.J.; Kelderman, H.; Tan, F.S.; Klunder, D.; Driessen, A. Thermally tuneable, wide FSR switch based on micro-ring resonators. In Proceedings of the 7th IEEE/LEOS Benelux Chapter Annual Symposium, Amsterdam, The Netherlands, 9 December 2002; pp. 155–158. [Google Scholar]
- Griffel, G. Vernier effect in asymmetrical ring resonator arrays. IEEE Photonics Technol. Lett. 2000, 12, 1642–1644. [Google Scholar] [CrossRef]
- Patzak, E.; Sugimura, A.; Saito, S.; Mukai, T.; Olesen, H. Semiconductor laser linewidth in optical feedback configurations. Electron. Lett. 1983, 24, 1026–1027. [Google Scholar] [CrossRef]
- Henry, C. Theory of the linewidth of semiconductor lasers. IEEE J. Quantum Electron. 1982, 18, 259–264. [Google Scholar] [CrossRef]
- Brunetti, G.; Heuvink, R.; Schreuder, E.; Armenise, M.N.; Ciminelli, C. Silicon Nitride Spot Size Converter with Very Low-Loss Over the C-Band. IEEE Photonics Technol. Lett. 2023, 35, 1215–1218. [Google Scholar] [CrossRef]
- Grillot, F.; Vivien, L.; Laval, S.; Pascal, D.; Cassan, E. Size influence on the propagation loss induced by sidewall roughness in ultrasmall SOI waveguides. IEEE Photonics Technol. Lett. 2004, 16, 1661–1663. [Google Scholar] [CrossRef]
- Dong, P.; Qian, W.; Liao, S.; Liang, H.; Kung, C.; Feng, N.; Shafiiha, R.; Fong, J.; Feng, D.; Krishnamoorthy, A.V. Low loss shallow-ridge silicon waveguides. Opt. Express 2010, 18, 14474–14479. [Google Scholar] [CrossRef]
- Mou, B.; Boxia, Y.; Yan, Q.; Yanwei, W.; Zhe, H.; Fan, Y.; Yu, W. Ultrahigh Q SOI ring resonator with a strip waveguide. Opt. Commun. 2022, 505, 127437. [Google Scholar] [CrossRef]
- Chrostowski, L.; Hochberg, M. (Eds.) Optical Materials and Waveguides; Cambridge University Press: Cambridge, UK, 2015; pp. 49–91. [Google Scholar]






| Coupling Scheme | Coupling Loss (dB) | Polarization | Length (µm) | Comments |
|---|---|---|---|---|
| A 3D waveguide structure [20] | 2.8 | TE | 850 | Three-dimensional (3D) SU-8 taper, silicon inverted nanotapers. |
| 4.1 | TM | |||
| Single inverted cone structure [30] | 0.2 | TE | 1000 | Low loss, broadband width, easy fabrication practical for mass production. |
| Subwavelength grating structure [25] | 0.63 | TE | 205 | Multiple grating combinations, integrated thermal phase modulators, phase compensation |
| Layered polymer waveguide structures [19] | 0.36 | TE | 300 | Thermal oxidation process, good TM mode support |
| 0.66 | TM | |||
| This work | 0.7 | TE | 90 | Compact, multi pointed, high coupling tolerance, low process requirements |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yan, B.; Zhou, M.; Sun, C.; Qi, Y.; Wang, Y.; Fan, Y.; Wang, Q. Design and Analysis of a Narrow Linewidth Laser Based on a Triple Euler Gradient Resonant Ring. Photonics 2024, 11, 412. https://doi.org/10.3390/photonics11050412
Wang Y, Yan B, Zhou M, Sun C, Qi Y, Wang Y, Fan Y, Wang Q. Design and Analysis of a Narrow Linewidth Laser Based on a Triple Euler Gradient Resonant Ring. Photonics. 2024; 11(5):412. https://doi.org/10.3390/photonics11050412
Chicago/Turabian StyleWang, Yikai, Boxia Yan, Mi Zhou, Chenxi Sun, Yan Qi, Yanwei Wang, Yuanyuan Fan, and Qian Wang. 2024. "Design and Analysis of a Narrow Linewidth Laser Based on a Triple Euler Gradient Resonant Ring" Photonics 11, no. 5: 412. https://doi.org/10.3390/photonics11050412
APA StyleWang, Y., Yan, B., Zhou, M., Sun, C., Qi, Y., Wang, Y., Fan, Y., & Wang, Q. (2024). Design and Analysis of a Narrow Linewidth Laser Based on a Triple Euler Gradient Resonant Ring. Photonics, 11(5), 412. https://doi.org/10.3390/photonics11050412





