Abstract
The transformation of the states of polarization of electromagnetic waves through their interaction with polarimetrically linear media can be represented by the associated Mueller matrices. A global measure of the ability of a linear medium to modify the states of polarization of incident waves, due to any combination of enpolarizing, depolarizing and retarding properties, is introduced as the distance from the Mueller matrix to the identity matrix. This new descriptor, called the polarizing power, is applicable to any Mueller matrix and can be expressed as a function of the degree of polarimetric purity and the trace of the Mueller matrix. The graphical representation of the feasible values of the polarizing power provides a general view of its main peculiarities and features. The values of the polarizing power for several typical devices are analyzed.
1. Introduction
There are certain well-known descriptors that can be derived from the Mueller matrix M and provide information on specific features related to enpolarizing (diattenuation and polarizance [1,2,3,4,5,6]), depolarizing [7,8,9,10,11,12,13,14,15,16,17,18,19], retarding [8,20,21] and other properties [22,23].
The definitions of such parameters (some of them summarized in Section 2) rely strongly on the algebraic characterization of Mueller matrices through the combination of two sets of inequalities, namely, the covariance conditions derived from the fact that any Mueller matrix can be considered as a convex sum, or ensemble average, of nondepolarizing Mueller matrices [24,25,26,27,28,29,30,31,32,33,34] and, on the other hand, the restrictions derived from the impossibility of amplifying the intensity of the interacting light through natural linear polarimetric transformations (passivity conditions) [33,35,36,37,38,39]. The covariance conditions can be formulated either through the nonnegativity of the eigenvalues of the Hermitian positive semidefinite coherency matrix associated with the Mueller matrix M [24,33,40] or equivalently by means of the eigenvalue analysis of the normal form of M [28,29,30,31,32]. Regarding the pair of passivity conditions, they are formulated in a very simple way as shown in Section 2.
Furthermore, several representations of Mueller matrices have been developed as products (serial decompositions) or convex sums (parallel decompositions) of simpler matrices [5,8,20,41,42,43], leading to the identification and definition of certain parameters that account for respective polarimetric properties of the medium or interaction represented by M.
Nevertheless, from the point of view of the analysis and exploitation of the information held by M, it still lacks the definition of a parameter giving an overall measure of the ability of the medium to transform the states of polarization of incident electromagnetic waves regardless of the origin and nature of the features involved (enpolarization, depolarization or retardation), which usually appear in a combined manner. Such an ability can be characterized through the distance from M to the 4 × 4 identity matrix I (which represents a completely neutral polarimetric effect).
Thus, the aim of this work is to introduce a properly defined measure of the polarizing power associated with M, which in no way replaces other known descriptors. The contents of this communication are organized as follows. Section 2 summarizes the theoretical concepts and notations necessary to describe the original results presented. Section 3 is devoted to the introduction of the concept of polarizing power associated with a given Mueller matrix, together with some related analyses and graphical representations. Section 4 deals with the invariance properties of the polarizing power with respect to certain polarimetric transformations. The results are illustrated in Section 5 through the inspection of the values taken by the polarizing power for typical polarization devices like diattenuators, retarders and intrinsic depolarizers.
2. Theoretical Background
Hereinafter we will use the term “light” for the sake of brevity; nevertheless, it can be understood as the more general “electromagnetic wave”.
The transformation of polarized light by the action of a linear medium (under fixed interaction conditions) can always be represented mathematically as , where s and are the Stokes vectors that represent the polarization states of the incident and emerging light beams, respectively, while M is the Mueller matrix associated with this kind of interaction and that can always be expressed as [8,26,44]
where is the mean intensity coefficient (MIC), i.e., the ratio between the intensity of the emerging light and the intensity of incident unpolarized light; is the normalized Mueller matrix; D and P are the diattenuation and polarizance vectors, with absolute values D (diattenuation) and P (polarizance); and vectors k, r, q, with respective absolute values k, r, and q, are constitutive of the normalized 3 × 3 submatrix m associated with M, which provides the complementary information on retardance and depolarization properties.
Mathematically, Mueller matrices are fully characterized by the so-called ensemble criterion [6], which involves two sets of inequalities, namely, the passivity, i.e., , with [33,39], together with the four covariance conditions constituted by the nonnegativity of the eigenvalues of the Hermitian coherency matrix C associated with M, whose explicit expression in terms of the elements of M is [24]
A measure of the ability of M to preserve the degree of polarization (DOP) of totally polarized incident light, is given by the degree of polarimetric purity of M (also called the depolarization index) [7], , which can be expressed as
where is the so-called degree of polarizance [45], or enpolarizance (a measure of the ability of M to increase the degree of polarization of light in either forward or reverse incidences),
and is the polarimetric dimension index (also called the degree of spherical purity), defined as [6,23,45]
Nondepolarizing media (i.e., media that do not decrease the degree of polarization of totally polarized incident light) exhibit the maximal degree of polarimetric purity, , so that the associated Mueller matrices are called nondepolarizing or pure. The minimal achievable value for , , is characteristic of perfect depolarizers, with associated Mueller matrix . The maximal value of , , entails with (nondepolarizing-nonenpolarizing media), which corresponds uniquely to retarders (regardless of the value of , i.e., regardless of whether they are transparent or exhibit a certain amount of isotropic attenuation), and the minimal polarimetric dimension index, , corresponds to Mueller matrices with . Maximal enpolarizance, , implies and corresponds to perfect polarizers, while the minimal, , is exhibited by nonenpolarizing interactions (either nondepolarizing or depolarizing) [15,45].
Regarding measures of the anisotropies involved in M, a set of anisotropy coefficients was defined in ref. [46], leading to an overall parameter called the degree of anisotropy, , which is obtained as a square average of linear and circular anisotropies due to enpolarizing and retarding properties, and can be expressed as follows (except for nondepolarizing diagonal Mueller matrices, i.e., , for which is undetermined) [46]
where superscript T indicates transpose. The values of are limited by .
As for the depolarizing properties of M, complete quantitative information is given by the corresponding indices of polarimetric purity (IPP), defined as follows in terms of the (nonnegative) eigenvalues of , labeled in nonincreasing order [5,13]:
Leaving aside systems exhibiting magneto-optic effects, the Mueller matrix that represents the same linear interaction as M, but with the incident and emergent directions of the light probe swapped, is given by [47,48]
Consequently, and , showing that D and P share a common nature related to the ability of the medium to enpolarize unpolarized light incoming in either forward or reverse directions [5,21].
3. Polarizing Power
Since a fully neutral polarimetric effect is characterized by , I being the 4 × 4 identity matrix, any enpolarizing, depolarizing or retarding effect implies that M takes a form different from I. Thus, the overall ability of M to change the incident state of polarization can be characterized by the polarizing power defined as the normalized distance between matrices M and I
where represents the Frobenius norm and g is a positive parameter that will be determined by imposing the limit .
By considering the partitioned form of M in Equation (1) together with Equations (3) and (5), and taking into account the relation
with tr representing the trace, we obtain
As expected, the lower limit for is zero and corresponds uniquely to , while the upper limit takes the value , which necessarily corresponds to a half-wave retarder (i.e., a retarder exhibiting retardance ), which satisfies and has the general form [6]
Thus, the choice is what matches the normalization criterion (and therefore ), so we define the polarizing power of M as
Since the physical meanings of the degree of polarimetric purity and the polarizing power are well established, the above definition provides an interpretation of the quantity as a sort of balance between the squared depolarization index and the squared polarizing power
or equivalently,
Note that , where the minimal achievable value corresponds necessarily to a half-wave retarder , while the maximum is reached uniquely when .
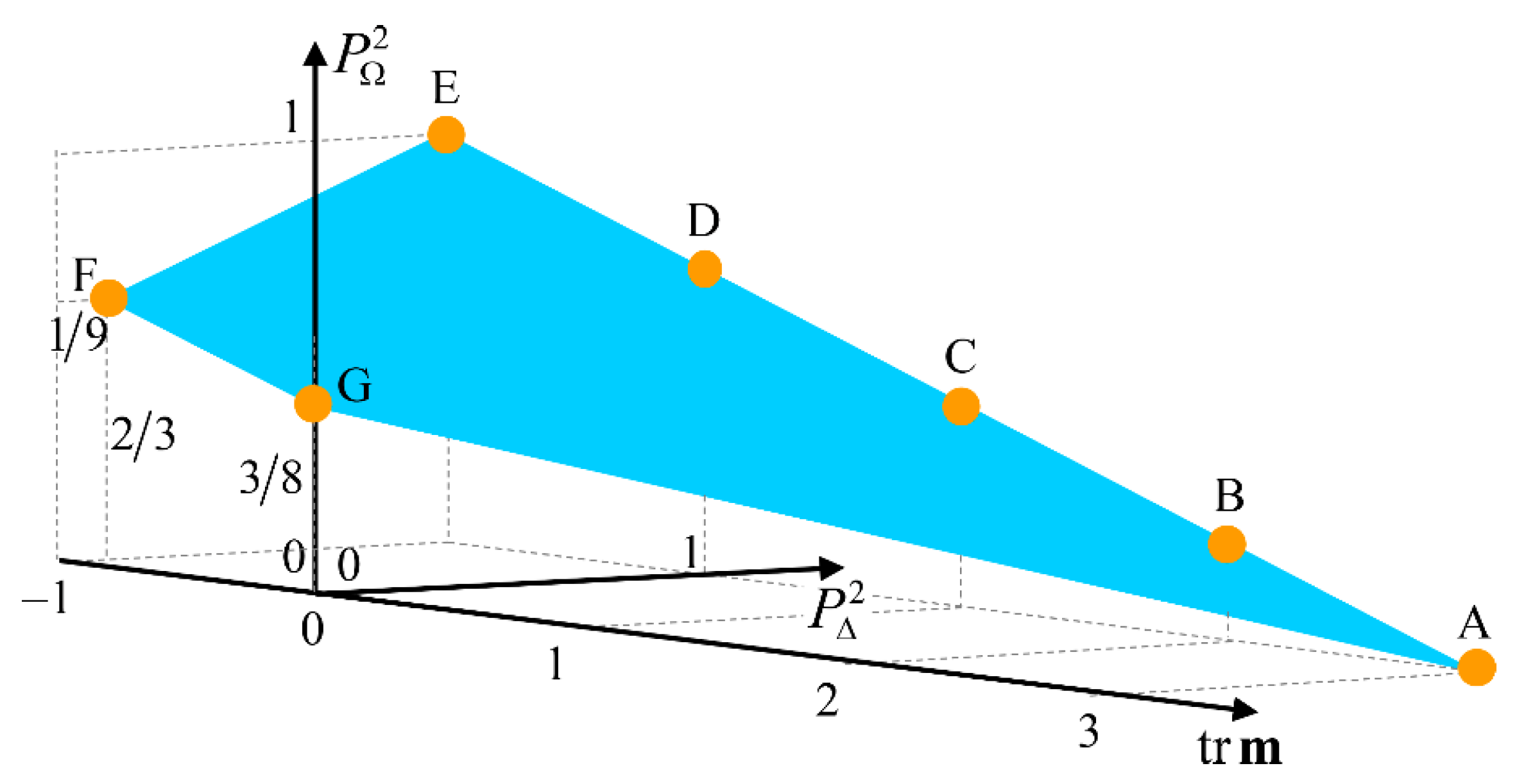
The feasible region for sets of values is shown in Figure 1. Achievable values are limited by the polygon with vertices AEFG. Edge AE corresponds uniquely to nondepolarizing Mueller matrices, with point A being genuine of , while as seen above, point E is reached exclusively by half-wave retarders. All physical situations for depolarizing Mueller matrices (i.e., ) have associated points in the polygon AEFGA, excluding edge AE. The values of the quantities for each of the points indicated in the figure are the following: , , , , , and .
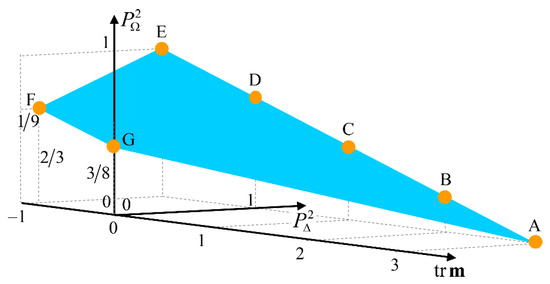
Figure 1.
The feasible values for are determined by the section of plane limited by edges AE, EF, FG and FA. The coordinates of the points shown in the figure are the following: , , , , , and . Points on edge AE are uniquely covered by nondepolarizing Mueller matrices ; vertex A corresponds uniquely to a neutral Mueller matrix ; vertex E is achieved uniquely by half-wave retarders; vertex F corresponds uniquely to isotropic depolarizers of the form ; and vertex G corresponds uniquely to perfect depolarizers .
Along edge AE , the values of increase from 0 up to 1 as decreases from (point A) down to −1 (point E).
The minimal feasible value for compatible with corresponds to diagonal Mueller matrices of the form (point F), so that along edge EF decreases from 1 (point E) down to (point F) as decreases from 1 down to .
Edge FG corresponds to isotropic Mueller matrices of the form , with , so that and decrease from , (point F, ) down to , (point G, ) as increases from up to , so point G corresponds uniquely to perfect depolarizers .
Edge GA corresponds to isotropic Mueller matrices of the form , with , so and evolve from , (point G), to , (point A), as increases from up to .
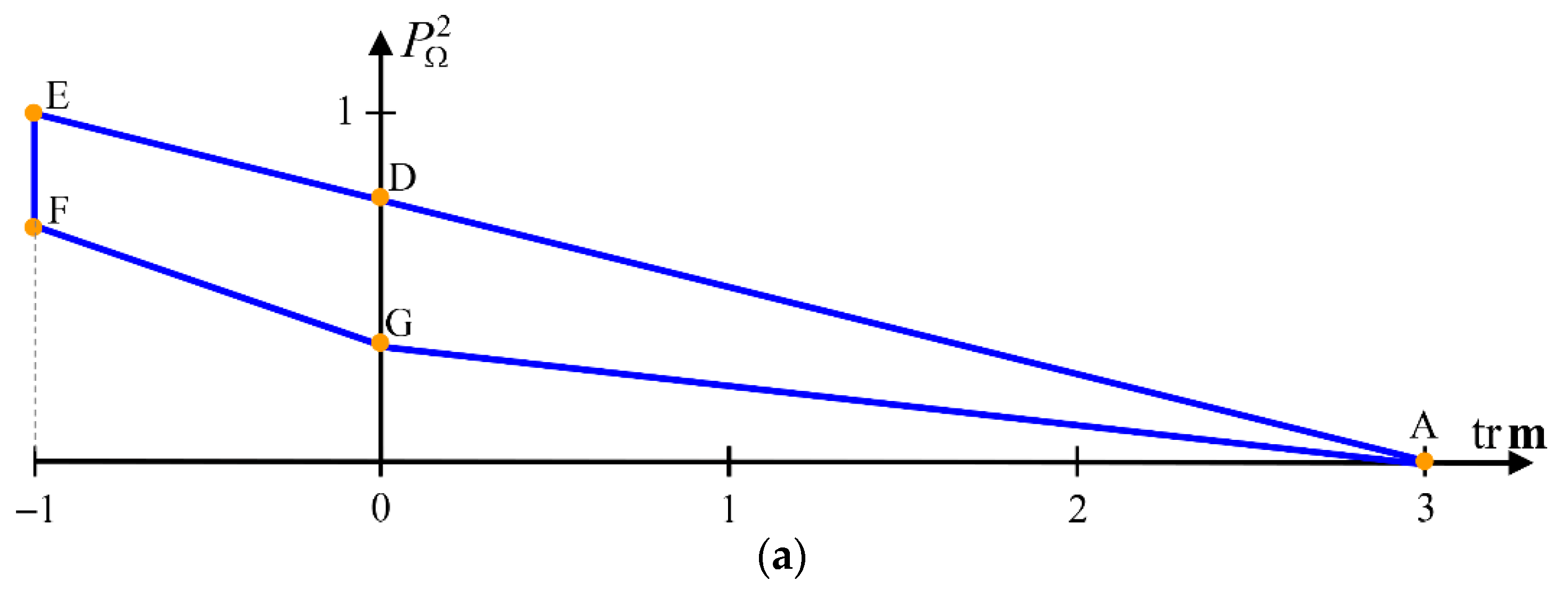
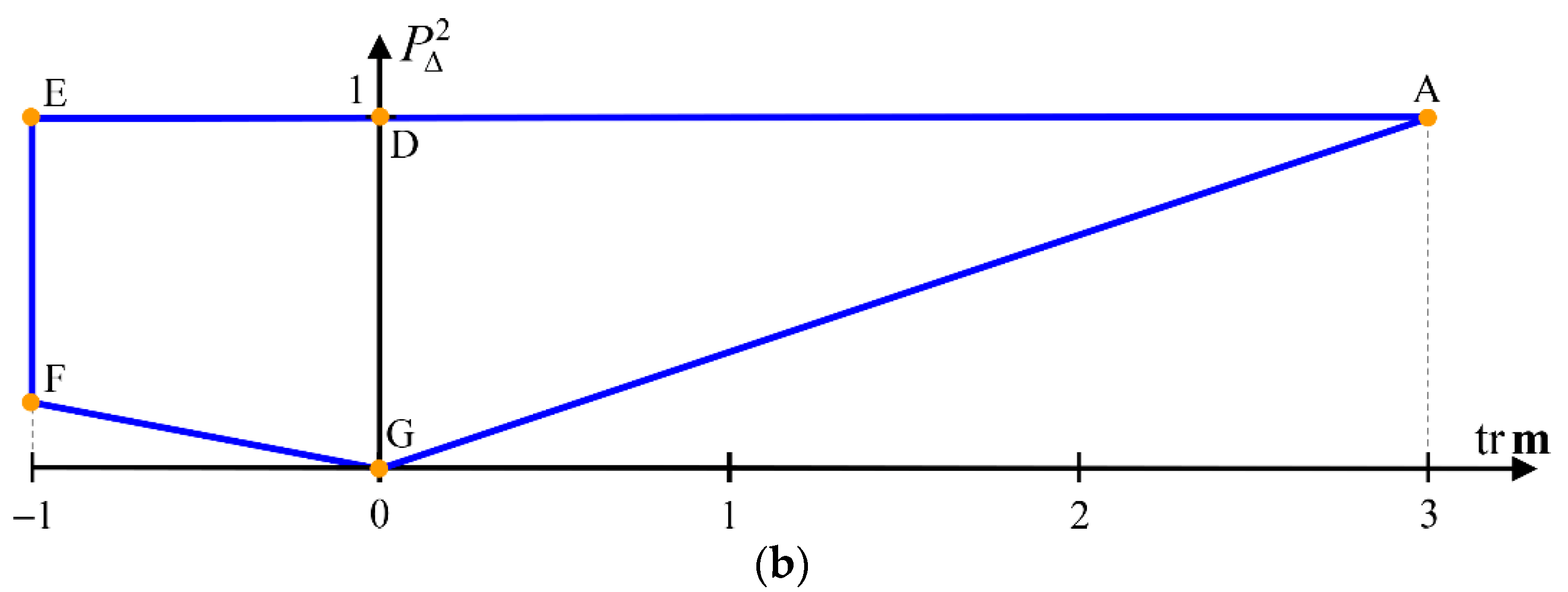
To make the interpretation of Figure 1 easier, respective projections of the feasible region on planes and are represented in Figure 2, while Figure 3 includes the feasible values for in the planes and .
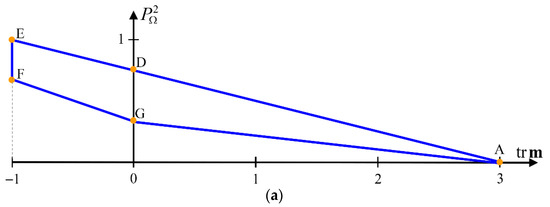
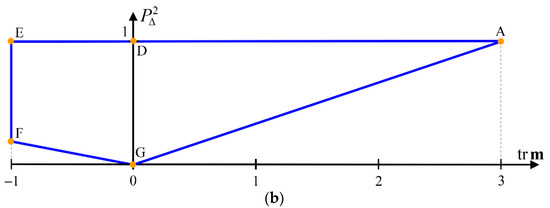
Figure 2.
Projection of the feasible region on the plane (a), and projection of the feasible region on the plane (b). Edge AE corresponds to nondepolarizing Mueller matrices , which exhibit maximal polarizing power for each given value of ; edge EF corresponds to Mueller matrices satisfying ; edge FG corresponds to isotropic intrinsic depolarizers of the form , with , which exhibit minimal polarizing power and minimal degree of polarimetric purity for each given negative value of ; and edge GA corresponds to Mueller matrices of intrinsic depolarizers of the form , with , which exhibit minimal polarizing power and minimal degree of polarimetric purity for each given positive value of .
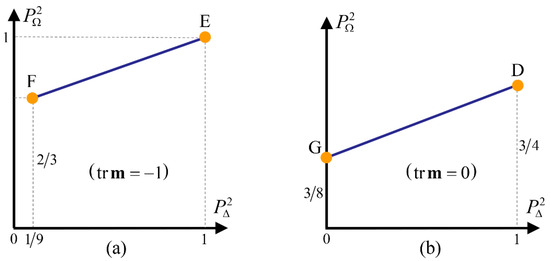
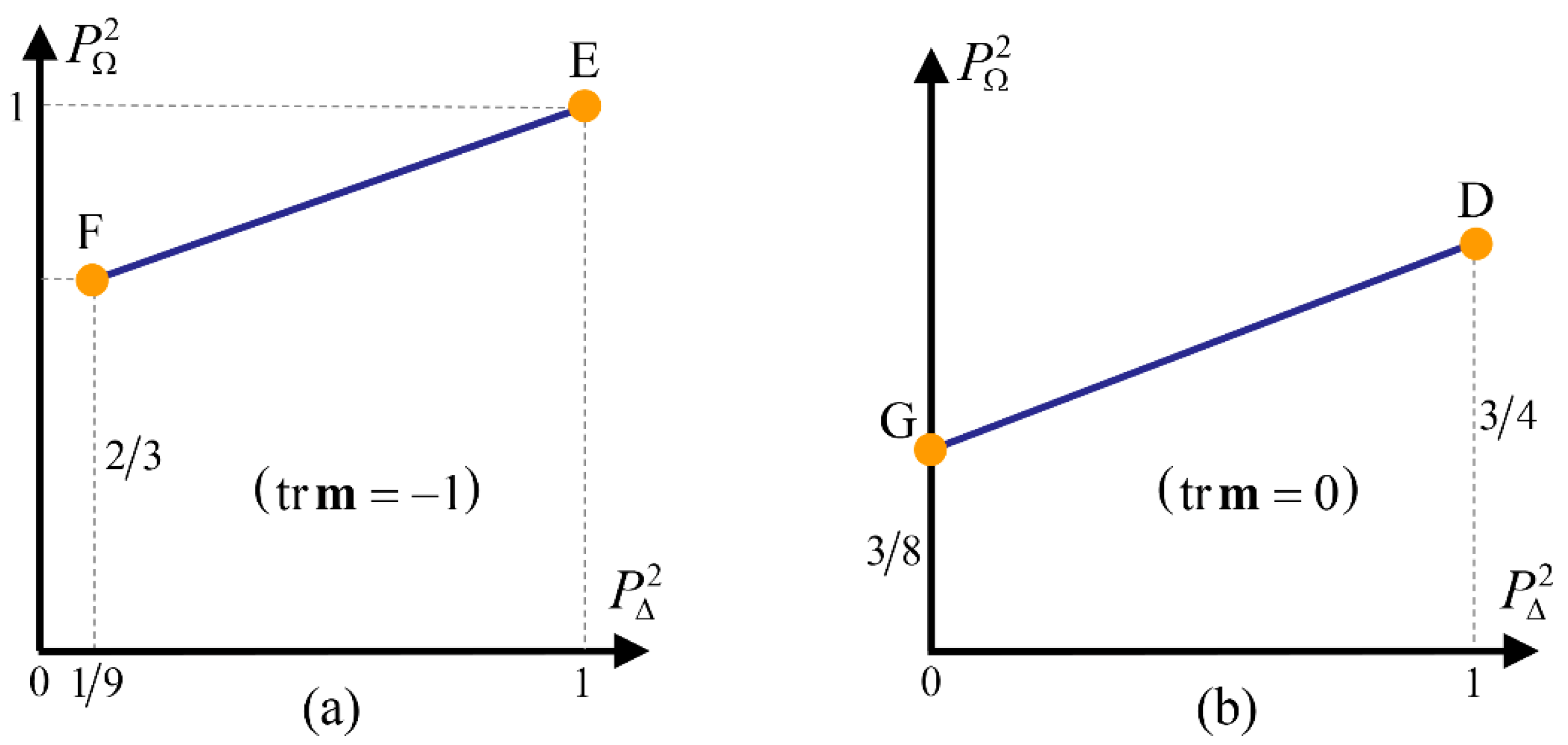
Figure 3.
The feasible values for the pair in the planes (a), and (b), are determined by the respective segments FE and GD.
4. Invariance
Given a Mueller matrix M, transformations , where is a proper orthogonal matrix (i.e., and ) and so represents a retarder, are called single retarder transformations [49] and play an important role in polarization theory. The general form of is
Since any given corresponds to a rotation of Stokes vectors in the Poincaré sphere [50,51], a single retarder transformation can be interpreted through the following consecutive steps: a Poincaré rotation of the incident Stokes vector s, and then the application of the inverse rotation to the Stokes vector after the action of M on , i.e., .
At this point it is worth recalling that a rotation (in the real space) of angle α about the direction of light propagation is mathematically represented through a matrix whose general form is [52]
and constitute a subclass of matrices that in fact are mathematically indistinguishable from those of circular retarders [6]. Consequently, a single retarder transformation invariance includes such a kind of rotation invariance.
Let us now observe that both quantities, and , appearing in the definition (13) of the polarizing power are invariant under single retarder transformations, which implies that is also invariant under such transformations.
Regarding the swapping of the incident and exit directions of light, which corresponds to the replacement of M (forward Mueller matrix) by (reverse Mueller matrix), it should be noted that, from its very definition, . Recall that both single retarder transformations and reciprocity invariances also hold for polarimetric quantities like , , , , , , , and .
5. Polarizing Power of Typical Devices
For a more detailed view of the peculiar features of the polarizing power, we next analyze its value for certain kinds devices typically found in polarimetry and polarization theory, like diattenuators, retarders and intrinsic depolarizers (also called diagonal depolarizers).
5.1. Diattenuators
Diattenuators constitute a subclass of nondepolarizing systems characterized by the fact that they produce differential intensity attenuation on their two polarization eigenstates. Diattenuators whose Mueller matrix is symmetric are called normal [53,54,55,56] or homogeneous [1].
The Mueller matrix of a normal diattenuator oriented at 0° has the generic form
where is the MIC, D is the diattenuation and K is called the counter diattenuation [51]. In the general case of an elliptical normal diattenuator with arbitrary orientation, its Mueller matrix, , can always be expressed though the single retarder transformation . Therefore, , and by applying definition (13), we obtain the following expression for the polarizing power of normal diattenuators
whose maximal value is achieved by perfect depolarizers, while decreases as D decreases down to .
For a given value D of diattenuation, the structure of the Mueller matrices of nonnormal diattenuators features more asymmetry than normal ones and consequently they exhibit larger values of . For instance, in the case of nonnormal perfect diattenuators with asymmetric Mueller matrices like
(together with arbitrary single retarder transformations of them), the polarizing power reaches the maximal achievable value among the diattenuators.
5.2. Retarders
Retarders constitute a subclass of nondepolarizing systems, characterized by the fact that they produce differential phase shifts on their two mutually orthogonal polarization eigenstates. The Mueller matrix of a retarder has the general form considered above and, as with normal diattenuators, is normal in the sense that its eigenstates are mutually orthogonal (represented by antipodal points in the Poincaré sphere [50,51]).
The Mueller matrix of a linear retarder, with retardance Δ and oriented at 0°, has the form
which allows the Mueller matrix of a general elliptical retarder to be expressed through a single retarder transformation (not in a unique manner), being the Mueller matrix of a retarder. Thus, the polarizing power of a retarder is given by
in such a manner that when and increases up to the maximal , which corresponds to (half-wave retarders [6]).
5.3. Intrinsic Depolarizers
The Mueller matrices associated with depolarizing systems can have very different forms. Among them, we consider here the so-called intrinsic depolarizers, which have the simple diagonal form [8,57].
The covariance conditions imply the following set of inequalities corresponding to the nonnegativity of the eigenvalues of the associated coherency matrix
Thus,
in such a manner that, as expected, the minimum corresponds to , while the maximum ( assumed to be nonnegative) is achieved for perfect depolarizers (recall that the covariance conditions imply ).
Interesting particular examples of intrinsic depolarizers are
together with alternative forms obtained by permuting the diagonal elements of their 3 × 3 submatrices m. The respective polarizing powers are
6. Conclusions
The parameter introduced as a measure of the overall polarizing power of a medium (or interaction) represented by any kind of Mueller matrix M, involves all polarimetric effects of M on the polarization states of incident electromagnetic waves, including enpolarizance, retardance and depolarization. From the natural definition of as the normalized distance from M to the identity matrix I, the different contributions to the polarizing power are combined in an unbiased and peculiar manner.
The polarizing power space, represented in Figure 1, Figure 2 and Figure 3, illustrates the main features and physically achievable values of . As occurs with other relevant polarimetric quantities, is fully determined from M, and it is invariant under single retarder transformations (including rotations of the Cartesian laboratory coordinate system) and under the replacement of M (forward Mueller matrix) by (reverse Mueller matrix). Thus, provides deeper insight in the interpretation of the information held by a measured Mueller matrix and also admits its application in imaging Mueller polarimetry to generate new images based on the representation of the point-to-point values of .
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Lu, S.-Y.; Chipman, R.A. Homogeneous and inhomogeneous Jones matrices. J. Opt. Soc. Am. A 1993, 11, 766–773. [Google Scholar] [CrossRef]
- Barakat, R. Polarization entropy transfer and relative polarization entropy. Opt. Commun. 1996, 123, 443–448. [Google Scholar] [CrossRef]
- Lu, S.-Y.; Chipman, R.A. Mueller matrices and the degree of polarization. Opt. Commun. 1998, 146, 11–14. [Google Scholar] [CrossRef]
- Tudor, T. On the enpolarization/depolarization effects of deterministic devices. Opt. Lett. 2018, 43, 5234–5237. [Google Scholar] [CrossRef]
- Gil, J.J. Polarimetric characterization of light and media. Physical quantities involved in polarimetric phenomena. Eur. Phys. J. Appl. Phys. 2007, 40, 1–47. [Google Scholar] [CrossRef]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Gil, J.J.; Bernabéu, E. Depolarization and polarization indices of an optical system. Opt. Acta 1986, 33, 185–189. [Google Scholar] [CrossRef]
- Lu, S.-Y.; Chipman, R.A. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Chipman, R.A. Depolarization index and the average degree of polarization. Appl. Opt. 2005, 44, 2490–2495. [Google Scholar] [CrossRef]
- Espinosa-Luna, R.; Bernabeu, E.; Atondo-Rubio, G. Q(M) and the depolarization index scalar metrics. Appl. Opt. 2008, 47, 1575–1580. [Google Scholar] [CrossRef] [PubMed]
- Ossikovski, R. Alternative depolarization criteria for Mueller matrices. J. Opt. Soc. Am. A 2010, 27, 808–814. [Google Scholar] [CrossRef] [PubMed]
- Espinosa-Luna, R.; Bernabeu, E.; Atondo-Rubio, G.; Hinojosa-Ruíz, S. A simple depolarization criterion for light. Optik 2011, 122, 407–410. [Google Scholar] [CrossRef]
- San José, I.; Gil, J.J. Invariant indices of polarimetric purity: Generalized indices of purity for n×n covariance matrices. Opt. Commun. 2011, 284, 38–47. [Google Scholar] [CrossRef]
- Cloude, S.R. Depolarization synthesis: Understanding the optics of Mueller matrix depolarization. J. Opt. Soc. Am. A 2013, 30, 691–700. [Google Scholar] [CrossRef]
- Gil, J.J. Structure of polarimetric purity of a Mueller matrix and sources of depolarization. Opt. Commun. 2016, 368, 165–173. [Google Scholar] [CrossRef]
- Hilfiker, J.N.; Hale, J.S.; Herzinger, C.M.; Tiwald, T.; Hong, N.; Schöche, S.; Arwin, H. Estimating Depolarization with the Jones Matrix Quality Factor. Appl. Surf. Sci. 2017, 421, 494–499. [Google Scholar] [CrossRef]
- Tariq, A.; Li, P.; Chen, D.; Lv, D.; Ma, H. Physically Realizable Space for the Purity-Depolarization Plane for Polarized Light Scattering Media. Phys. Rev. Lett. 2017, 119, 033202. [Google Scholar] [CrossRef]
- Ossikovski, R.; Vizet, J. Eigenvalue-based depolarization metric spaces for Mueller matrices. J. Opt. Soc. Am. A 2019, 36, 1173–1186. [Google Scholar] [CrossRef]
- Sheppard, C.J.R.; Bendandi, A.; Le Gratiet, A.; Diaspro, A. Characterization of the Mueller Matrix: Purity Space and Reflectance Imaging. Photonics 2022, 9, 88. [Google Scholar] [CrossRef]
- Ossikovski, R. Analysis of depolarizing Mueller matrices through a symmetric decomposition. J. Opt. Soc. Am. A 2009, 26, 1109–1118. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J. Transmittance constraints in serial decompositions of Mueller matrices. The arrow form of a Mueller matrix. J. Opt. Soc. Am. A 2013, 30, 701–707. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J.; Ossikovski, R.; San José, I. Physical Significance of the Determinant of a Mueller Matrix. Photonics 2022, 9, 246. [Google Scholar] [CrossRef]
- Gil, J.J. Thermodynamic Reversibility in Polarimetry. Photonics 2022, 9, 650. [Google Scholar] [CrossRef]
- Cloude, S.R. Group theory and polarization algebra. Optik 1986, 75, 26–36. [Google Scholar]
- Kim, K.; Mandel, L.; Wolf, E. Relationship between Jones and Mueller matrices for random media. J. Opt. Soc. Am. A 1987, 4, 433–437. [Google Scholar] [CrossRef]
- Xing, Z.-F. On the Deterministic and Non-deterministic Mueller Matrix. J. Mod. Opt. 1992, 39, 461–484. [Google Scholar] [CrossRef]
- Sridhar, R.; Simon, R. Normal form for Mueller Matrices in Polarization Optics. J. Mod. Opt. 1994, 41, 1903–1915. [Google Scholar] [CrossRef]
- van der Mee, C.V.M. An eigenvalue criterion for matrices. transforming Stokes parameters. J. Math. Phys. 1993, 34, 5072–5088. [Google Scholar] [CrossRef]
- Bolshakov, Y.; van der Mee, C.V.M.; Ran, A.C.M.; Reichstein, B.; Rodman, L. Polar decompositions in finite dimensional indefinite scalar product spaces: Special cases and applications. In Operator Theory: Advances and Applications; Gohberg, I., Ed.; Birkhäuser: Basel, Switzerland, 1996; Volume 87, pp. 61–94. [Google Scholar]
- Bolshakov, Y.; van der Mee, C.V.M.; Ran, A.C.M.; Reichstein, B.; Rodman, L. Errata for: Polar decompositions in finite di-mensional indefinite scalar product spaces: Special cases and applications. Integral Equ. Oper. Theory 1997, 27, 497–501. [Google Scholar] [CrossRef]
- Rao, A.V.G.; Mallesh, K.S.; Sudha. On the algebraic characterization of a Mueller matrix in polarization optics. I. Identifying a Mueller matrix from its N matrix. J. Mod. Opt. 1998, 45, 955–987. [Google Scholar] [CrossRef]
- Rao, A.V.G.; Mallesh, K.S.; Sudha. On the algebraic characterization of a Mueller matrix in polarization optics. II. Necessary and sufficient conditions for Jones derived Mueller matrices. J. Mod. Opt. 1998, 45, 989–999. [Google Scholar]
- Gil, J.J. Characteristic properties of Mueller matrices. J. Opt. Soc. Am. A 2000, 17, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Simon, B.N.; Simon, S.; Mukunda, N.; Gori, F.; Santarsiero, M.; Borghi, R.; Simon, R. A complete characterization of pre-Mueller and Mueller matrices in polarization optics. J. Opt. Soc. Am. A 2010, 27, 188–199. [Google Scholar] [CrossRef] [PubMed]
- Barakat, R. Conditions for the Physical Realizability of Polarization Matrices Characterizing Passive Systems. J. Mod. Opt. 1987, 34, 1535–1544. [Google Scholar] [CrossRef]
- Brosseau, C.; Barakat, R. Jones and Mueller polarization matrices for random media. Opt. Commun. 1991, 84, 127–132. [Google Scholar] [CrossRef]
- Kostinski, A.B.; Givens, R.C. On the gain of a passive linear depolarizing system. J. Mod. Opt. 1992, 39, 1947–1952. [Google Scholar] [CrossRef]
- Devlaminck, V.; Terrier, P. Non-singular Mueller matrices characterizing passive systems. Optik 2010, 121, 1994–1997. [Google Scholar] [CrossRef]
- San José, I.; Gil, J.J. Characterization of passivity in Mueller matrices. J. Opt. Soc. Am. A 2020, 37, 199–208. [Google Scholar] [CrossRef]
- Arnal, P.M. Modelo Matricial para el Estudio de Fenómenos de Polarización de la luz. Ph.D. Thesis, University of Zaragoza, Zaragoza, Spain, 1990. [Google Scholar]
- Savenkov, S.N.; Muttiah, R.S.; Sydoruk, O.I. Conditions for polarization elements to be dichroic and birefringent. J. Opt. Soc. Am. A 2005, 22, 1447–1452. [Google Scholar] [CrossRef]
- Savenkov, S.N.; Sydoruk, O.I.; Muttiah, R.S. Eigenanalysis of dichroic, birefringent, and degenerate polarization elements: A Jones-calculus study. Appl. Opt. 2007, 46, 6700–6709. [Google Scholar] [CrossRef]
- Ossikovski, R. Interpretation of nondepolarizing Mueller matrices based on singular-value decomposition. J. Opt. Soc. Am. A 2008, 25, 473–482. [Google Scholar] [CrossRef]
- Robson, B.A. The Theory of Polarization Phenomena; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Gil, J.J. Components of purity of a Mueller matrix. J. Opt. Soc. Am. A 2011, 28, 1578–1585. [Google Scholar] [CrossRef]
- Arteaga, O.; Garcia-Caurel, E.; Ossikovski, R. Anisotropy coefficients of a Mueller matrix. J. Opt. Soc. Am. A 2011, 28, 548–553. [Google Scholar] [CrossRef] [PubMed]
- Sekera, Z. Scattering Matrices and Reciprocity Relationships for Various Representations of the State of Polarization. J. Opt. Soc. Am. 1966, 56, 1732–1740. [Google Scholar] [CrossRef]
- Schönhofer, A.; Kuball, H.-G. Symmetry properties of the Mueller matrix. Chem. Phys. 1987, 115, 159–167. [Google Scholar] [CrossRef]
- Gil, J.J. Invariant quantities of a Mueller matrix under rotation and retarder transformations. J. Opt. Soc. Am. A 2016, 33, 52–58. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Gdoutos, E.E. Matrix Theory of Photoelasticity; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1979; ISBN 9780387215853. [Google Scholar]
- Gil, J.J.; San José, I. Two-vector representation of a nondepolarizing Mueller matrix. Opt. Commun. 2016, 374, 133–141. [Google Scholar] [CrossRef]
- Azzam, R.M.A.; Bashara, N.M. Ellipsometry and Polarized Light; North Holland: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Tudor, T. Operatorial form of the theory of polarization optical devices: I. Spectral theory of the basic devices. Optik 2003, 114, 539–547. [Google Scholar] [CrossRef]
- Tudor, T. Operatorial form of the theory of polarization optical devices: II. Spectral theory of composite devices. Optik 2004, 115, 173–180. [Google Scholar] [CrossRef]
- Tudor, T.; Gheondea, A. Pauli algebraic forms of normal and non-normal operators. J. Opt. Soc. Am. A 2007, 24, 204–210. [Google Scholar] [CrossRef]
- Tudor, T. Interaction of light with the polarization devices: A vectorial Pauli algebraic approach. J. Phys. A Math. Theor. 2008, 41, 415303. [Google Scholar] [CrossRef]
- Ossikovski, R. Canonical forms of depolarizing Mueller matrices. J. Opt. Soc. Am. A 2010, 27, 123–130. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).