Abstract
A novel inserting pilot scheme to generate and distribute a frequency 16-tupling millimeter wave (MMW) radio over fiber (ROF) system without the bit walk-off effect via Mach–Zehnder modulators (MZMs) is proposed. The operation principle is analyzed and the feasibility of our proposed scheme is verified by simulation test. The main part of our scheme is a ±8th-order sidebands generator (SG), which is constructed by four MZMs connected in parallel. In the back-to-back (BTB) transmission case, by properly adjusting the voltage and initial phase of the radio frequency (RF) drive signals of the MZMs, ±8th-order sidebands are generated by the SG. In the data transmission case, the data signal is first split into two beams, one of which modulates the RF drive signal with an electrical phase modulator (PM) while the other is amplified by an electrical gainer (EG), and then the two beams are combined into one and used as the composite RF drive signal of the MZMs. By adjusting the modulation index of the PM and the gain of the EG, the data signal can only be modulated to the +8th-order sideband of the output of the SG. The optical carrier from the continuous wave (CW) laser is split into two paths: one is sent into the SG, and the other is used as a pilot signal. The output signal of SG is combined with the pilot signal and is transmitted to the base station (BS) via optical fiber. At the BS, the pilot signal is filtered out by a fiber Bragg grating (FBG) and used as the carrier for the uplink for carrier reuse. After filtering out the pilot, the signal from the FBG, which is composed of ±8th-order sidebands, is injected into a photodetector, and a frequency 16-tupling MMW with downlink data is generated. The key parameters’ influence on the bit error rate (BER) and Q factor in the system is also analyzed. Our scheme can not only effectively overcome the bit walk-off effect caused by optical fiber chromatic dispersion and greatly increase the fiber transmission distance but can also effectively improve the performance and the tunability of system. Therefore, it has important application prospects in ROF systems.
1. Introduction
With the rapid development of wireless communication, such as wireless access networks, 5G, and 6G, ultrahigh-speed data can be realized by using high-frequency millimeter waves (MMWs). The radio over fiber (ROF) system is a key part of wireless communication [1,2,3,4]. In the ROF system, the generation of MMW signals beyond 100 GHz in electronic domains faces a serious challenge because of restrictions on the frequency responses of electronic modules and components [5].
This limitation can be overcome by generating MMWs in the optical domain [6]. The MMWs generated in the optical domain is referred to as optical MMWs. Optical MMWs consist of two coherent beams of light with a frequency interval of 30 GHz to 3000 GHz, with which the electrical MMW signal can be generated by beating these beams in a photodetector. It is important to note that the optical MMWs are different from electrical MMW signals; they comprise optical wave signals, which is a key technical term used in ROF systems.
The generation of optical MMWs is a key technique to realize low cost and high transmission performance in ROF systems [7]. Many schemes to generate optical MMW have been proposed, such as optical heterodyning methods [8], optoelectronic oscillator methods [9], mode-locked lasers methods [10], external modulator methods [11,12,13,14], and optical nonlinear effect methods [15,16]. Among the above methods, the external method with MZMs offers several advantages, such as a high frequency multiplication factor (FMF), a greater tunability, a higher reliability, a higher conversion efficiency, and receiver sensitivity. It is the most commonly used and proven method and has been widely exploited. The first proposal to utilize photonic frequency multiplication techniques for mm wave signal generation was made by O’Reilly J.J. [17]. The principle of photonic frequency multiplication techniques is as follows: firstly, the nonlinear property of an external modulator is utilized to generate multi-order sidebands, and the two sidebands, spaced at the desired millimeter wave, are extracted by various optical methods, which are called the optical millimeter wave. At the same time, it is necessary to suppress the other sidebands as much as possible. Then, these two extracted sidebands are injected into the photodetector for photo-electronic conversion to generate the desired millimeter-wave signals; in most cases, symmetrical ±nth-order sidebands are extracted and injected into the photodetector to generate the millimeter-wave with a frequency of 2n, where is the frequency of the RF driving signal loaded into the external modulator, and 2n is called the frequency multiplication factor (FMF). In order to obtain high-frequency millimeter-waves, either the FMF or the should be increased. Due to the limitations of the frequency of the RF driving signal and the frequency response of the external modulator, the general method to obtain high-frequency millimeter-waves is to increase the FMF. To improve the FMF, it is necessary to select the higher-order sidebands while suppressing the lower-order sidebands; this can be realized through cascading external modulators. External modulator methods, as well as frequency doubling [18,19], quadrupling [20], octupling [21], 12-tupling [22], and 16-tupling [23]. The highest FMF reached 24 [24,25] and 32 [26,27,28] in recent years. In general, the higher the FMF, the more complex the structure of the system.
The data modulation format is an important issue for ROF. It will greatly affect the transmission performance of the ROF system. The conventional data modulation formats for the optical MMW in an ROF are single-sideband (SSB) modulation, double-sideband (DSB) modulation, and optical carrier suppression (OCS) [29,30,31,32]. In the optical MMW, (a) when the optical carrier has two sidebands, it is regarded as the generalization DSB; (b) when there are two sidebands without an optical carrier, it is regarded as the generalization OCS; (c) when there is one sideband with the optical carrier, it is regarded as the generalization SSB. In the conventional modulation format of data in ROF, fiber chromatic dispersion causes not only the fading effect [33] but also the bit walk-off effect [34]. DSB modulation’s optical MMW suffers from both the periodical fading effect and the bit walk-off effect [35]. SSB and OCS modulation’s optical MMWs are immune to the fading effect [35], but there is the bit walk-off effect, which limits their transmission distance [36]. To avoid the bit walk-off effect, data signals have to be modulated on only one sideband of the optical MMW. Many schemes were proposed to modulate data signals onto only one of the two optical sidebands [37,38]. In the methods presented above, one of the optical sidebands was picked out with an optical filter first, and then the data signal was modulated on it [39,40]. The use of a filter will make the system very complicated, limit the frequency tuning speed, and lead to large insertion losses. Modulating data on one of two sidebands of the optical MMW without a filter has been the hot research issue in ROF in recent years. Two schemes were proposed with a dual parallel MZM (DPMZM) [41,42]. The structures of these schemes are complicated. To simplify the structure and increase the FMF, Z.H. Zhu. et al. proposed to generate optical MMW filterless schemes in which the data are modulated only on the −nth-order sidebands to overcome chromatic dispersion [43,44,45,46]. In their scheme, by properly adjusting the bias voltages of the MZM, as well as through the amplitudes and phases of the RF driving signal and the gain of the electrical gainer, the baseband data are only modulated on −nth-order sidebands. Their schemes can overcome the bit walk-off effect. However, the repetitive frequency of the optical MMW is only two times [43], four times [44], eight times [45], and twelve times [46] that of the RF signal. To influence the BER and Q factor, most parameters are related to the phase modulation index and the gain of the baseband signal. These were not considered in the literature.
To reduce the cost, the carrier reuse technique is often used in ROF systems at the BS. In the conventional frequency multiplication ROF system, one of the most common methods is that a part of the power of the idle sidebands is filtered out by an FBG for carrier reuse at BS [43,44]. One of the problems introduced by this method is that the center frequency of the FBG must be changed with the frequency of the idle sidebands. The frequency of the idle sidebands is changed with that of the RF driving signal. This limits the tunability of the system. There is another problem caused by this method. The carrier reuse is realized by reflecting part of the idle sidebands with the FBG. This method will cause a power imbalance between the two sidebands and reduce the performance of the downlink.
To reduce the frequency of the RF signal and the cost of the ROF system, it is necessary to increase the FMF of the optical MMW and the tunability of the system.
The problems to be solved in this paper are as follows: (1) the bit walk-off effect caused by fiber dispersion in a frequency 16-tupling MMW ROF system; (2) the performance degradation of the downlink of ROF caused by the conventional carrier reuse in ROF. The innovations of our proposed scheme are as follows: (1) the bit walk-off effect has been overcome in the frequency 16-tupling MMW ROF system, which greatly increases the transmission distance of the system; (2) the novel method of inserting guide frequency to realize carrier reuse can effectively improve the performance of the downlink of the system.
We also discuss the effect of the phase index of PM, the gain of the EG, and the extinction ratios of the MZM on the BER and Q factors of data transmission when they deviate from their theoretical or default values.
2. System Design
Figure 1 shows the schematic diagram of the inserted pilot signal frequency 16-tupling MMW ROF system without the bit walk-off effect caused by MZMs.
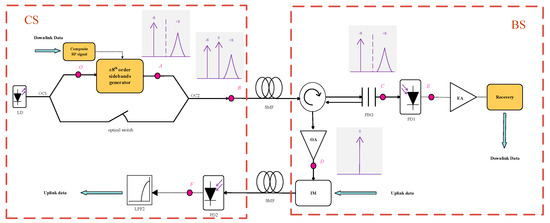
Figure 1.
Schematic diagram of the structure of the frequency 16-tupling MMW ROF system.
Figure 2 shows a schematic diagram of the three modules in Figure 1. These are the composite RF signal module, the ±8th-order sideband generator module, and the data recovery module, respectively.
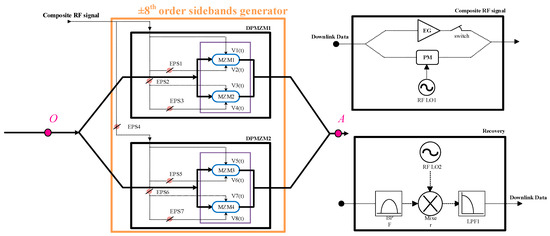
Figure 2.
Schematic diagram of the composite RF signal module, the ±8th-order sideband generator module, and the data recovery module.
The system is composed of two radio-frequency (RF) local oscillators (labeled LO1, LO2), electrical phase shifters (EPS) (labeled EPS1~EPS7), an electrical phase modulator (PM), an electrical gainer (EG), a continuous-wave (CW) laser, six 3 dB optical couplers(labeled OC1~OC6), a fiber Bragg grating (FBG), four MZMs (labeled MZM1~MZM4), an optical amplifier (OA) an electrical amplifier (EA), an intensity modulator (IM), a mixer (Mixer), a bandpass filter (BPF), two lowpass filters (labeled LPF1, LPF2), and two photodetectors (labeled PD1, PD2). The four MZMs are divided into two groups. Each group is constructed by two MZMs connected in parallel and is equivalent to a dual parallel MZM(DPMZM). The two DPMZMs are labeled as DPMZM1 (MZM1, MZM2), and DPMZM2 (MZM3, MZM4). When the initial values of EPS1~7 are set to 180°, 90°, 180°, 45°, 180°, 90°, and 180°, respectively, each MZM operates in maximum transmission point mode (MATP). The four MZMs that are connected in parallel can be regarded as a ±8th-order sideband generator (SG). The dashed line and solid line in Figure 1 indicate the electrical path and the optical path, respectively.
To compare our scheme with the conventional frequency 16-tupling MMW ROF system, we added an electrical switch to the module of the composite RF signal and an optical switch to the central station. When those switches are open, the system is the conventional frequency 16-tupling MMW ROF system.
3. Operation Principle
3.1. The Expression of the Output from MZMs
The optical carrier from CW laser is expressed as , where and are the amplitude and angular frequency of the optical carrier, respectively. The binary data signal is denoted as , where is the binary sequence, is the code form function, and is the code word duration.
The gain of EG is denoted as G and set as 6. The phase modulation constant of PM is denoted as P and set as 33.75° (). The half-wave voltage of the MZMs is set as . The RF drive signal of the MZMs is expressed as follows:
where and are the amplitude and angular frequency of the RF driving signal, .
The output signal of MZM1 can be expressed as follows:
where is the modulation index of MZM. In the process of the derivation of Equation (2), the Jacoby–Angell constant equation is applied, where is the nth-order Bessel function of the first kind.
When the initial phases of the RF driving signal of MZM1 and MZM2 are 0 and 90°, respectively, the output signal of DPMZM1 can be expressed as follows:
The structure of DPMZM2 is the same as that of DPMZM1. When the initial phase difference of the RF driving signals loaded into DPMZM2 is 45° compared to DPMZM1, the output signals of the SG are expressed as follows:
From Equation (4), we can see that the output of SG is the ±8n-order sideband signals.
3.2. Selection of the Modulation Index of MZM
From Equation (4), we can see that the amplitudes of the ±8n-order sidebands are proportional to . For the case of m = 5.5201, there are , , . It can be seen that the 0th-order sideband (the central optical carrier) is well suppressed and the ±8nth (n > 1)-order sidebands are too small to be neglected. When the sidebands are neglected except the ±8th-order sidebands, Equation (4) can be simplified as follows:
From Equation (5), we can see that the data are modulated only on the +8th sideband.
3.3. Output of the Central Station
The optical carrier from the CW laser is split into two beams: one is injected into the SG, and the other is used as the pilot signal. The output signal of the central station (CS) is the combined signals created by the output of the SG and the pilot signal with OC2, and can be expressed as follows:
3.4. Effect of Fiber Optic Dispersion on the Generated Frequency 16-Tupling MMW
In the base station (BS), after reflecting the 0th-order sideband via the FBG, the input optical signal is left only with the ±8th-order sidebands.
In the back-to-back (BTB) system, after beating the ±8th-order sidebands in the PD1, the frequency 16-tupling MMW is generated and can be expressed as follows:
where is the responsivity of the PD1.
In the optic fiber transmission system, the ±8th-order sidebands signals have different group velocities caused by fiber chromatic dispersion. After they transmit the distances of z, the output signal from the fiber can be expressed as follows:
where is the fiber loss coefficient, is the time delay of the binary code word, and is the propagation constant. Since the optical power is not very high, the nonlinearity of fiber is neglected here.
Comparing Equation (8) with Equation (6), we can see that the spectrum does not change after it transmits through the optical fiber. Injecting the output of fiber in the PD, the output electrical current from the PD can be expressed as follows:
Expanding in Equation (8) with the Taylor series, in the expanded form of the terms of are very small. Neglecting the terms of , the can be expressed as follows:
Substituting Equations (8) and (10) into Equation (9), the output current from the PD1 can be expressed as follows:
From Equation (11), it can be seen that the code words of the data signal do not undergo bit walk-off, except for the time delay.
4. Simulation Experiment
4.1. Simulation Parameter
According to Figure 1, a simulation system is designed using the Optisystem simulation tool. The parameters of the main devices in the simulation are listed in Table 1.

Table 1.
Parameter values of the main devices in the simulation system.
4.2. Results of the Simulation Experiment
Figure 3 is the optical spectrum of point A in Figure 1, from which we can see that all the sidebands are suppressed except the ±8th-order sidebands; the peak power of the +8th-order sideband is lower than that of the −8th-order; the data are only modulated into the +8th-order sideband.
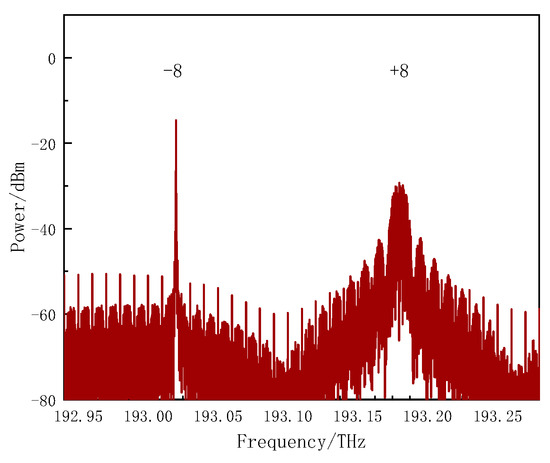
Figure 3.
Optical spectrum at the output of the 8th-order sideband generator (Point A) in Figure 1.
Figure 4 is the optical spectrum of point B in Figure 1. In Figure 1, the 0th-order sideband is the inserted pilot signal.
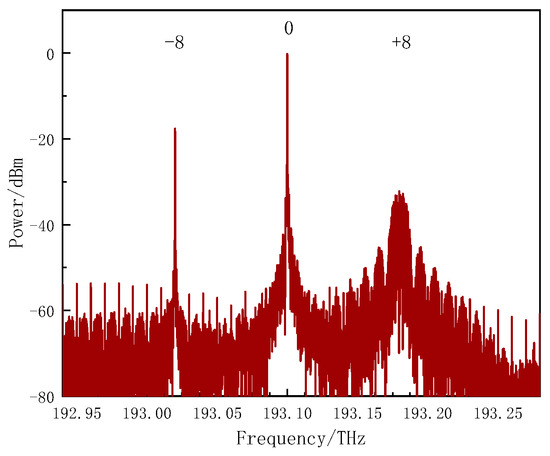
Figure 4.
Optical spectrum at the output of the CS (Point B) in Figure 1.
Figure 5 is the optical spectrum of point C in Figure 1, which is the optical spectrum obtained after filtering out the pilot signal. Figure 5 is similar to Figure 3.
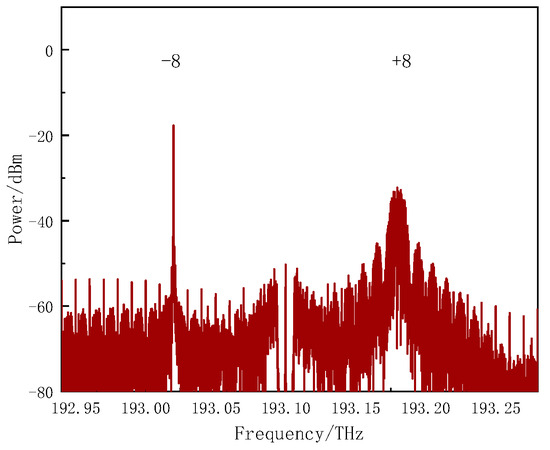
Figure 5.
Optical spectrum at the output of the FBG (Point C) in Figure 1.
Figure 6 is the optical spectrum of point D in Figure 1, from which we can see that the uplink data were modulated onto the pilot signal.
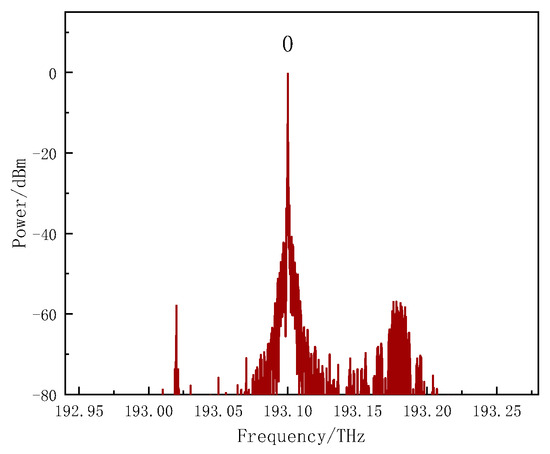
Figure 6.
Optical spectrum at the output of the OA (Point D) in Figure 1.
Figure 7 is the spectrum of point E in Figure 1. From Figure 7, we can see that the output of the PD contains the frequency 16-tupling MMW with the downlink data.
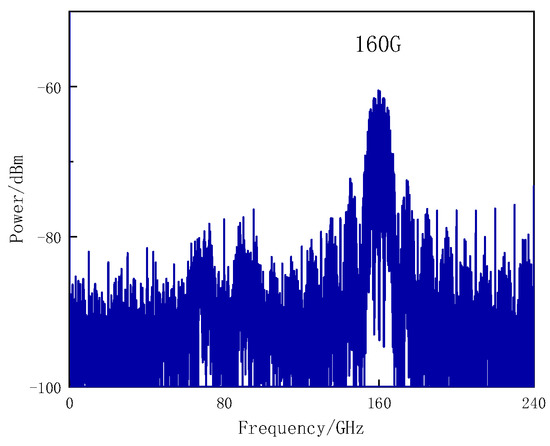
Figure 7.
Spectrum at the output of the PD1 (Point E) in Figure 1.
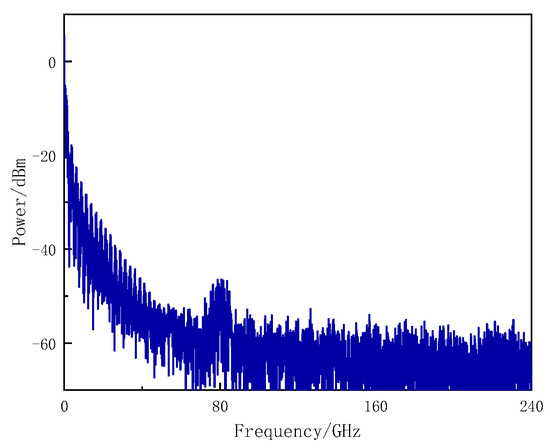
Figure 8.
Spectrum at the output of the PD2 (Point F) in Figure 1.
In Figure 9, the relation curve of the Q factor with the length of the transmission fiber is shown. The eye diagrams of the data signal at particular points of the curve at 0 km, 20 km, 40 km, and 60 km are inserted in Figure 9. From Figure 9, we can see that the distance of the transmission fiber can reach up to 60 km for a Q greater than 6.
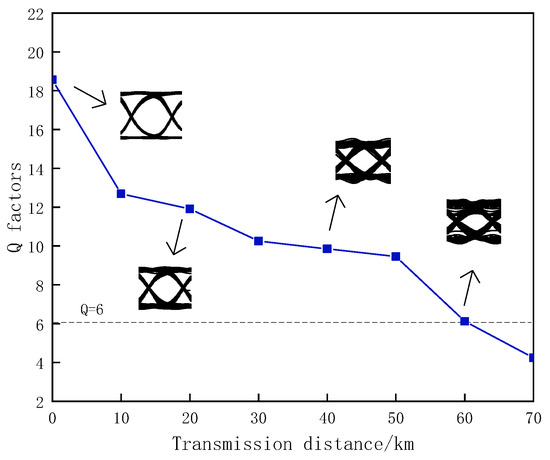
Figure 9.
The relationship of the Q factor with the transmission distance of the fiber.
Figure 10a,b show the relationship between the BER and the received power of the PD for the uplink and downlink, respectively. From Figure 10a, we can see that the power penalty in the downlink is 0.49 dB and 1.16 dB for transmission distances of 10 km and 20 km, respectively. From Figure 10b, we can see that the power penalties in the uplink are 0.48 dB and 0.99 dB for transmission distances of 10 km and 20 km, respectively.
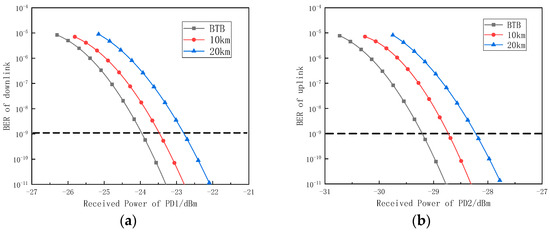
Figure 10.
The relationship between the BER and the received power of PD in the downlink and uplink: (a) downlink; (b) uplink.
4.3. Compare the Conventional Frequency 16-Tupling ROF System with Our Scheme
When the optical switch and electrical switch in Figure 1 are open, the system is the conventional frequency 16-tupling MMW ROF system. The downlink data are simultaneously modulated onto the ±8th-order sidebands.
The conventional ROF system reaches the maximum transmission distance when the eye diagram is fully closed. The maximum transmission distance satisfies the following equation [36]:
where is the duty cycle of the code word, is the code word period, is the dispersion constant of fiber, is the frequency of the RF driving signal, is the center wavelength of the optical carrier, respectively. When , , , , , according to Equation (12), the maximum transmission distance is 18.6 km.
The optical spectrum at point A is shown in Figure 11, from which we can see that the data are modulated on the ±8th-order sidebands.
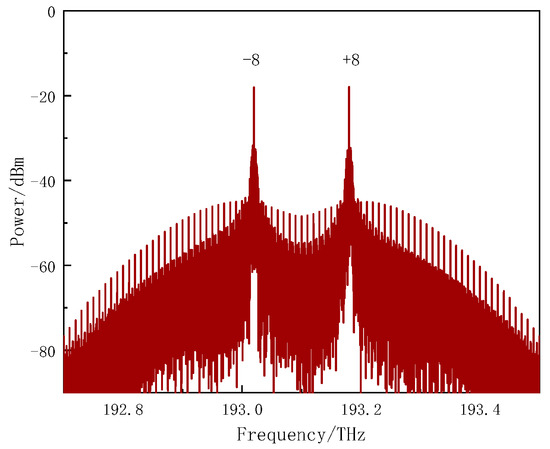
Figure 11.
Optical spectrum at the output of the 8th-order sideband generator (Point A) in Figure 1.
Figure 12 shows the spectrum of the generated frequency 16-tupling MMW. From Figure 12, we can see that the main component in the output signal from the PD is the frequency 16-tupling MMW, along with the data.
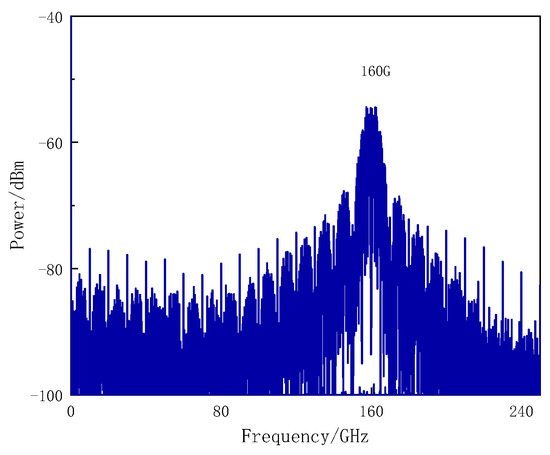
Figure 12.
Spectrum at the output of the PD1 (Point E) in Figure 1.
Figure 13 shows the eye diagram obtained at different transmission distances in the conventional frequency 16-tupling MMW ROF system. From Figure 13, we can see that the width of the code word becomes narrower and narrower as the transmission distance increases. The eye diagram is almost closed when the distance is 18.6 km; these results are in agreement with Equation (12).
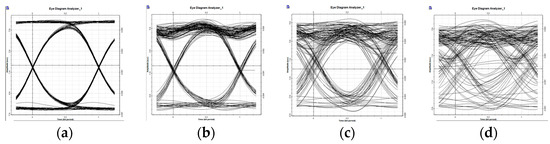
Figure 13.
Eye diagram at difference transmission distances: (a) BTB; (b) 6 km; (c) 12 km; (d) 18.6 km.
Figure 14 shows the eye diagrams obtained at different fiber transmission distances for our designed system. From Figure 14, we can see that the eye diagram is still open even though the transmission distance is 60 km.

Figure 14.
Eye diagrams at different transmission distances in our scheme: (a) BTB; (b) 20 km; (c) 40 km; (d) 60 km.
4.4. Compare the Conventional Carrier Reuse System with Our Scheme
When the optical switch in Figure 1 is on and the electrical switch is off, the system is the conventional carrier reuse system. In this case, the central frequency of the FBG in the BS is shifted to 193.02 THz from 193.1 THz, as shown in Figure 1.
Figure 15 shows the relationship between BER and the received power of the PDs in the conventional carrier reuse system and our scheme.
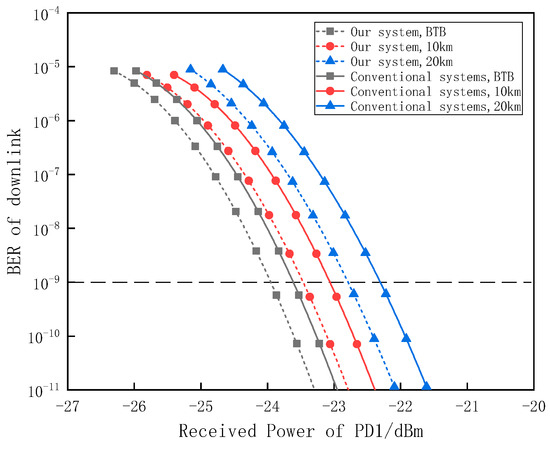
Figure 15.
The relationship of the BER of the downlink with the received power of PD1.
As the BER is less than 10−9, the improvements in the sensitivity of the receivers are listed in Table 2 for the transmission distances of 0 km,10 km, and 20 km, respectively.

Table 2.
The received power of the PD1 at BER = 10−9.
We can see that improvement in the sensitivity of receivers is increased with the increase in the fiber transmission distance.
5. Stability of System
The stability of a system is the range within which the main parameters in the system are allowed to deviate from their theoretical or default values, provided that specific requirements are met. In general, the wider the allowed range, the better the stability of the system.
The parameter values of the devices chosen in the simulation experiments are based on the theoretical analysis values and default values of the simulation tool. In practical applications, due to the variance in the environment and the limitations of the device fabrication process, those values often deviate from the theoretical values or default values; this will inevitably affect the Q factor of the system.
For the general requirements of digital communication systems, the BER is required to be lower than 10−9, or a Q factor greater than 6 is needed.
In practical systems, the factors that most affect the Q factor are the extinction ratios of the MZMs, the modulation index P of PM, and the gain G of the EG.
The larger the MZM extinction ratio, the more effective it is in suppressing the undesired sidebands. According to the theoretical analysis presented above, the P and G only directly affect the realization of modulating data on the +8th-order sideband.
5.1. Effect of Extinction Ratio of MZMs
Figure 16 shows the relationship between the extinction ratio of the MZM and the Q factor of the downlink. As seen in Figure 16, in the case of BTB and a 20 km transmission distance, the Q factor of the downlink remains unchanged when the extinction ratio is increased over 30 dB. In the case of a 40 km transmission distance, the Q factor of the downlink remains unchanged when the extinction ratio is increased over 40 dB.
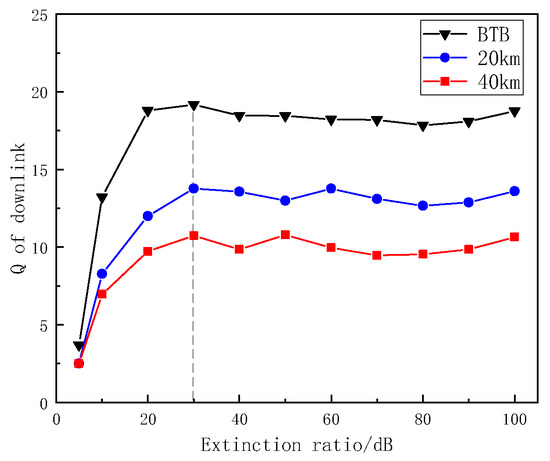
Figure 16.
Relation between the Q factor and extinction ratio.
5.2. Effect of the Phase Modulation Index P of the Phase Modulator PM
According to the previous analysis, the theoretical value P is 33.75°. When P varies in the range of 30.75°~36.75°, the relationship between the P and Q factors is shown in Figure 17. As seen in Figure 17, the Q factor rapidly decreases as P deviates from the theoretical value, and when P varies in the range of 32.26°~36.38°, Q > 6 is satisfied.
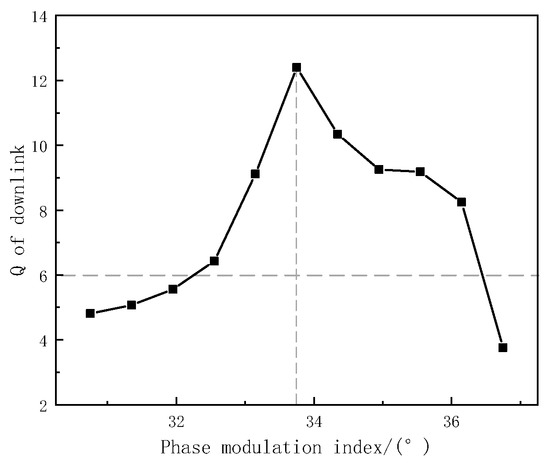
Figure 17.
Relation between the Q factor and phase modulation index.
5.3. Effect of the Amplification G of the Electrical EG
According to the previous analysis, the design value G is 6. When G varies in the range of 4.5 to 7.5, the relationship between G and the Q system is shown in Figure 18. As seen in Figure 18, the Q factor decreases rapidly as G deviates from the theoretical value; and when G varies in the range of 5.1 to 6.7, Q > 6 is satisfied.
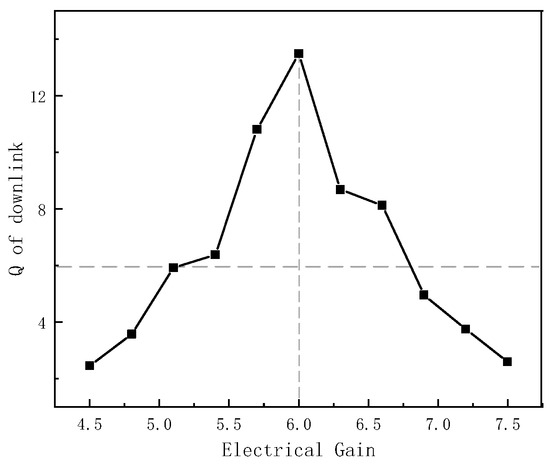
Figure 18.
Relation between the G of EG and system Q factor.
5.4. Effects of P and G
The effects on the Q factor when P and G deviate from the theoretical values are analyzed above, respectively. In practical applications, P and G often deviate from the theoretical values at the same time. Figure 19 shows the relationship of the Q factor with the P and G. In Figure 19, the blue marking line indicates a Q factor greater than 6, and the black marking point is the Q factor when G = 6 and P = 33.75°. It can be seen that when G = 6, and P = 33.75°, the Q factor reaches the peak value of 10.82.
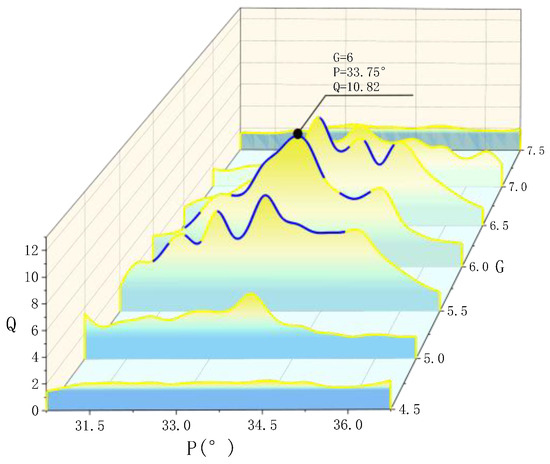
Figure 19.
Relation of the Q factor with the P and the G.
6. Discussion
(1) It is important to point out that our scheme is only applicable to cases which do not need to cancel the central optical carrier. If our designed mothed is adopted in a system that needs to cancel the central carrier, the data signal will be modulated onto the carrier component in addition to the +nth-order sidebands, and the center carrier that contains data cannot be completely cancelled out.
We proposed a method to solve this problem. A band-rejected filter is added before the PD to filter out the carrier with data. This method can ensure the data signal is modulated only on the +nth-order sidebands. Adopting a filter will increase the cost of the system and limit the tenability of the system.
(2) The method proposed in this paper can be suitable as a generic method to generate 2n frequency multiplication MMW, with the data carried only on the +nth-order sidebands.
According to the theoretical analyses, the key parameter for the realization of the data carried only on +nth-order sidebands is the selection of the P of PM and G of EG.
We suppose the RF drive signals loaded onto the MZMs can be expressed as follows:
The final output expression after multiple MZMs can be expressed as follows:
To make it possible to carry data only on the +nth-order sidebands, it is necessary to satisfy the following equation:
where the is the order of the sidebands and and are integers.
From Equation (15), we can obtain the following:
where and are integers.
Due to the limitation of the manuscript length, this paper did not discuss the issues presented above; they will be the subjects of our future research.
(3) The experiments in our manuscript are simulation experiments with “Optisystem 15.0” software. According to the literature available to us, due to the limitations of the experimental conditions in the schemes for generating high-frequency MMWs using MZMs, some schemes in which the frequency multiplication factor (FMF) is less than 12 were verified through experiments, and the innovation of most schemes in which the FMF is greater than 12 were generally verified by simulation. Due to the limitations to conditioning in our laboratory, it is still difficult to experimentally verify the method proposed in this paper. In the future, if the experimental conditions are available, we will continue with the related physical experiments.
7. Conclusions
A novel inserting pilot scheme to generate a 16-tupling frequency MMW ROF system with data modulated only on the +8th-order sideband is proposed. A ±8th-order sideband generator (SG) is constructed by connecting four MZMs in parallel. By adjusting the amplitude and initial phase of the RF drive signals of the MZMs, the output of the SG is ±8th-order sidebands. The data signal is first split into two beams: one first modulates the RF driving signal with the PM, another beam is gained by EG, and then the two beams are combined into one, which is used as the composite RF driving signal of the MZMs. By appropriately adjusting the P of the PM and the gain G of the EG, the data signal is modulated only to the +8th-order sideband.
We designed a conventional frequency 16-tupling MMW ROF system with the same structure and same parameters, except the part of the data that were modulated. For the transmission distance of 20 km with 2.5 Gpbs of data, under the condition that the Q factor is greater than 6, for our designed scheme, the power penalty of our designed scheme is 1.16 dB and the Q factor of the conventional ROF system is less than 6.
This paper also analyses the effects on the BER and Q factor when the extinction ratio of the MZM, the P of the PM, and the G of the EG deviate from their theoretical values. For the case of 40 km transmission distance with a data rate of 2.5 Gbps, the extinction ratio of the MZM is greater than 40 dB, the P varies in the range of 32.26°~36.38°, the G varies in the range of 5.1 to 6.7, and the Q factor is greater than 6.
The scheme designed in this paper can effectively solve the bit walk-off effect caused by fiber chromatic dispersion in the ROF system, greatly improve the fiber transmission distance, and has important application prospects in ROF.
Author Contributions
Conceptualization, X.C. (Xu Chen), X.C. (Xinqiao Chen), S.D., B.L. and L.W.; methodology, X.C. (Xu Chen) and S.D.; software, X.C. (Xu Chen); validation, X.C. (Xinqiao Chen) and B.L.; formal analysis, X.C. (Xu Chen) and S.D.; investigation, X.C. (Xu Chen); resources, X.C. (Xinqiao Chen) and L.W.; data curation, S.D.; writing—original draft preparation, X.C. (Xu Chen); writing—review and editing, X.C. (Xinqiao Chen); visualization, X.C. (Xu Chen); supervision, B.L. and L.W.; project administration, L.W.; funding acquisition, X.C. (Xinqiao Chen). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Project (2018YFB1404101).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xavier, N. Fernando, Radio over Fiber for Wireless Communications: From Fundamentals to Advanced Topics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Aljumaily, M.; Li, H. A Framework to Optimize the Frame Duration and the Beam Angle for Random Beamforming of mmWave Mobile Networks. In Proceedings of the International Conference of Information and Communication Technology, Baghdad, Iraq, 15–16 April 2019. [Google Scholar]
- Alavi, S.E.; Soltanian, M.R.K.; Amiri, I.S.; Khalily, M.; Supa’at, A.S.M.; Ahmad, H. Towards 5G: A photonic based millimeter wave signal generation for applying in 5G Access Fronthaul. Sci. Rep. 2016, 6, 19891. [Google Scholar] [CrossRef]
- Ranaweera, C.; Wong, E.; Nirmalathas, A.; Jayasundara, C.; Lim, C. 5G C-RAN with optical fronthaul: An analysis from a deployment perspective. J. Light. Technol. 2018, 36, 2059–2068. [Google Scholar] [CrossRef]
- Asha, D.S. A comprehensive review of millimeter wave based radio over fiber for 5G front haul transmissions. Indian J. Sci. Technol. 2020, 14, 86–100. [Google Scholar]
- Dar, A.; Ahmad, F.; Jha, R. Filterless 16 tupled optical millimeter wave generation using cascaded parallel Mach Zehnder modulator with extinction ratio tolerance. Prog. Electromagn. Res. Lett. 2020, 91, 129–135. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, A.; Shang, L. A full-duplex radio-over-fiber link with 12-tupling mm-wave generation and wavelength reuse for upstream signal. Opt. Laser Technol. 2011, 43, 1167–1171. [Google Scholar] [CrossRef]
- Ramos, R.T.; Seeds, A.J. Fast heterodyne optical phase-lock loop using double quantum well laser diodes. Electron. Lett. 1992, 28, 82–83. [Google Scholar] [CrossRef]
- Yao, X.S.; Davis, L.; Maleki, L. Coupled optoelectronic oscillators for generating both RF signal and optical pulses. IEEE/OSA J. Light. Technol. 2000, 18, 73–78. [Google Scholar] [CrossRef]
- Vawter, G.; Mar, A.; Hietala, V.; Zolper, J.; Hohimer, J. All optical millimeter-wave electrical signal generation using an integrated mode-locked semiconductor ring laser and photodiode. IEEE Photonics Technol. Lett. 1997, 9, 1634–1636. [Google Scholar] [CrossRef]
- Zhang, C.; Ning, T.; Li, J.; Pei, L.; Li, C.; Ma, S. A full-duplex WDM-RoF system based on tunable optical frequency comb generator. Opt. Commun. 2015, 344, 65–70. [Google Scholar] [CrossRef]
- Wu, P.; Ma, J. BPSK optical mm-wave signal generation by septupling frequency via a single optical phase modulator. Opt. Commun. 2016, 374, 69–74. [Google Scholar] [CrossRef]
- Zhou, W.; Qin, C. Simultaneous generation of 40, 80 and 120 GHz optical millimeter-wave from one Mach-Zehnder modulator and demonstration of millimeter wave transmission and down-conversion. Opt. Commun. 2017, 398, 101–106. [Google Scholar] [CrossRef]
- Mohamed, M.; Zhang, X.; Hraimel, B.; Wu, K. Frequency sixupler for millimeter-wave over fiber systems. Opt. Express 2008, 16, 10141–10151. [Google Scholar] [CrossRef] [PubMed]
- Baskaran, M.; Madhan, M.G. A novel approach for simultaneous millimeter wave generation and high bit rate data transmission for Radio over Fiber (RoF) systems. Optik 2014, 125, 6347. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, S.; Li, X.; Wang, W.; Tian, Z. Generation and transmission simulation of 60 G millimeter-wave by using semiconductor optical amplifiers for radio-over-fiber systems. Opt. Commun. 2009, 282, 4440. [Google Scholar] [CrossRef]
- O’Reilly, J.J.; Lane, P.M.; Heidemann, R.; Hofstetter, R. Optical generation of very narrow linewidth millimeter wave signals. Electron. Lett. 1992, 28, 2309–2311. [Google Scholar] [CrossRef]
- Shih, P.-T.; Chen, J.; Lin, C.-T.; Jiang, W.-J.; Huang, H.-S.; Peng, P.-C.; Chi, S. Optical millimeter-wave signal generation via frequency 12-tupling. IEEE/OSA J. Light. Technol. 2010, 28, 71–78. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; Xu, Y.; Chen, L.; Yu, J. Frequency-doubling photonic vector millimeter-wave signal generation from one DML. IEEE Photon. J. 2015, 7, 5501207. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; Yu, J. W-band vector millimeter-wave signal generation based on phase modulator with photonic frequency quadrupling and precoding. IEEE/OSA J. Light. Technol. 2017, 35, 2548–2558. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Xiao, J.; Zhang, Z.; Xu, Y.; Yu, J. W-band 8QAM vector signal generation by MZM-based photonic frequency octupling. IEEE Photonics Technol. Lett. 2015, 27, 1257–1260. [Google Scholar] [CrossRef]
- Wang, D.; Tang, X.; Fan, Y.; Zhang, X.; Xi, L.; Zhang, W. A new approach to generate the optical millimeter-wave signals using frequency 12-tupling without an optical filter. In Proceedings of the International Conference on Information Optics and Photonics, State Key Laboratory of Information Photonics and Optical Communications Beijing University of Posts and Telecommunications, Beijing, China, 8–11 July 2018. [Google Scholar]
- Wun, J.-M.; Liu, H.-Y.; Lai, C.-H.; Chen, Y.-S.; Yang, S.-D.; Pan, C.-L.; Bowers, J.E.; Huang, C.-B.; Shi, J.-W. Photonic high-power 160-GHz signal generation by using ultrafast photodiode and a high-repetition-rate femtosecond optical pulse train generator. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 3803507. [Google Scholar]
- Chen, X.G.; Xia, L.; Huang, D.X. A filterless 24-tupling optical millimeter wave generation and RoF distribution. Optik 2017, 147, 22–26. [Google Scholar] [CrossRef]
- Rani, A.; Kedia, D. Mathematical analysis of 24-tupled mm-wave generation using cascaded MZMs with polarization multiplexing for RoF transmission. Opt. Quantum Electron. 2024, 56, 193. [Google Scholar] [CrossRef]
- Chen, X.; Dai, S.; Li, Z.; Liu, X.; Chen, X.; Xiao, H. Filterless frequency 32-tupling millimeter-wave generation based on two cascaded dual-parallel Mach–Zehnder modulators. Front. Phys. 2023, 11, 1212482. [Google Scholar] [CrossRef]
- Chen, X.; Dai, S.; Li, Z.; Chen, X. Thirty-two-tupling frequency millimeter-wave generation based on eight Mach-Zehnder modulators connected in parallel. ETRI J. 2023, 46, 194–204. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.; Ren, L.; Zhang, H.; Wu, Z.; Li, W.; Zhang, F.; Wang, X. Photon Generation Scheme of 32-Fold Millimeter-Wave Signal Based on Mach-Zehnder Modulator. Ann. Phys. 2024, 536, 2300360. [Google Scholar] [CrossRef]
- Shang, Y.; Feng, Z.; Cao, C.; Huang, Z.; Wu, Z.; Xu, X.; Geng, J. A using remodulation filterless scheme of generating frequency 32-tupling millimeter-wave based on two DPMZMs. Opt. Laser Technol. 2022, 148, 107793. [Google Scholar] [CrossRef]
- Song, H.J.; Lee, J.S.; Song, J.I. Error-free simultaneous all-optical upconversion of WDM radio-over-fiber signals. IEEE Photonics Technol. Lett. 2005, 17, 1731–1733. [Google Scholar] [CrossRef]
- Yu, J.; Jia, Z.; Yi, L.; Su, Y.; Chang, G.K.; Wang, T. Optical millimeter-wave generation or up-conversion using external modulators. IEEE Photonics Technol. Lett. 2005, 18, 265–267. [Google Scholar]
- Griffin, R.A.; Salgado, H.M.; Lane, P.M.; O’Reilly, J.J. System capacity for millimeter-wave radio-over-fiber distribution employing an optically supported PLL. J. Light. Technol. 1999, 17, 2480. [Google Scholar] [CrossRef]
- Yu, J.; Jia, Z.; Chang, G.K. All-optical mixer based on cross-absorption modulation in electroabsorption modulator. IEEE Photonics Technol. Lett. 2005, 17, 2421–2423. [Google Scholar]
- Corral, J.L.; Marti, J.; Fuster, J.M. General expressions for IM/DD dispersive analog optical links with external modulation or optical up-conversion in a Mach-Zehnder electrooptical modulator. IEEE Trans. Microw. Theory Tech. 2001, 49, 1968–1976. [Google Scholar] [CrossRef]
- Ma, J.X.; Yu, C.X.; Zhou, Z.; Yu, J.J. Optical mm-wave generation by using external modulator based on optical carrier suppression. Opt. Commun. 2006, 268, 51–57. [Google Scholar] [CrossRef]
- Ma, J.X.; Yu, J.J.; Yu, C.; Xin, X.; Zeng, J.; Chen, L. Fiber dispersion influence on transmission of the optical millimeter-waves generated using LN-MZM intensity modulation. J. Light. Technol. 2007, 25, 3244–3256. [Google Scholar] [CrossRef]
- Ma, J.X.; Yu, J.J.; Yu, C.; Jia, Z.S.; Chang, G.K.; Sang, X.Z. The influence of fiber dispersion on the code form of the optical mm-wave signal generated by single sideband intensity-modulation. Opt. Commun. 2007, 271, 396–403. [Google Scholar] [CrossRef]
- Zhou, M.; Ma, J.X. The influence of fiber dispersion on the transmission performance of a quadruple-frequency optical millimeter wave with two signal modulation formats. Opt. Switch. Netw. 2012, 9, 343–350. [Google Scholar] [CrossRef]
- Chen, L.X.; Huang, C.; Chen, L. A modified scheme for optical millimeter-wave generation based on optical carrier suppression modulation. Laser Technol. 2008, 32, 659–662. [Google Scholar]
- Xie, J.L.; Huang, X.G.; Tao, J. A full-duplex radio-over-fiber system based on a novel double-sideband modulation and frequency quadrupling. Opt. Commun. 2010, 283, 874–878. [Google Scholar] [CrossRef]
- Liu, X.L.; Liu, Z.J.; Li, J.D.; Shang, T.; Zhao, J. Generation of optical carrier suppression millimeter-wave signal using one dual-parallel MZM to overcome chromatic dispersion. Opt. Commun. 2010, 283, 3129–3135. [Google Scholar] [CrossRef]
- Guo, D.F.; Zhang, Z.J.; Fang, X.K.; Shang, Y. Schemes to eliminate the time shift of code edges based on the optimal transmission point of DP-MZM. Appl. Opt. 2023, 62, 5652–5659. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Zhao, S.H.; Yao, Z.S.; Tan, Q.G.; Li, Y.J.; Chu, X.C.; Shi, L.; Hou, R. A novel OCS millimeter-wave generation scheme with data carried only by one sideband and wavelength reuse for uplink connection. Opt. Laser Technol. 2012, 44, 2366–2370. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Zhao, S.H.; Yao, Z.S.; Tan, Q.G.; Li, Y.J.; Chu, X.C.; Shi, L.; Zhang, X. Optical millimeter-wave signal generation by frequency quadrupling using one dual-drive Mach-Zehnder modulator to overcome chromatic dispersion. Opt. Commun. 2012, 285, 3021–3026. [Google Scholar] [CrossRef]
- Liang, D.; Jiang, W.; Tan, Q.G.; Zhu, Z.B.; Liu, F. A novel optical millimeter-wave signal generation approach to overcome chromatic dispersion. Opt. Commun. 2014, 320, 94–98. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, S.; Li, Y.; Chu, X.; Wang, X.; Zhao, G. A radio-over-fiber system with frequency 12-tupling optical millimeter-wave generation to overcome chromatic dispersion. IEEE J. Quantum Electron. 2013, 49, 919–922. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).