High-Efficiency and Large-Angle Homo-Metagratings for the Near-Infrared Region
Abstract
1. Introduction
2. Design of Si Metagrating
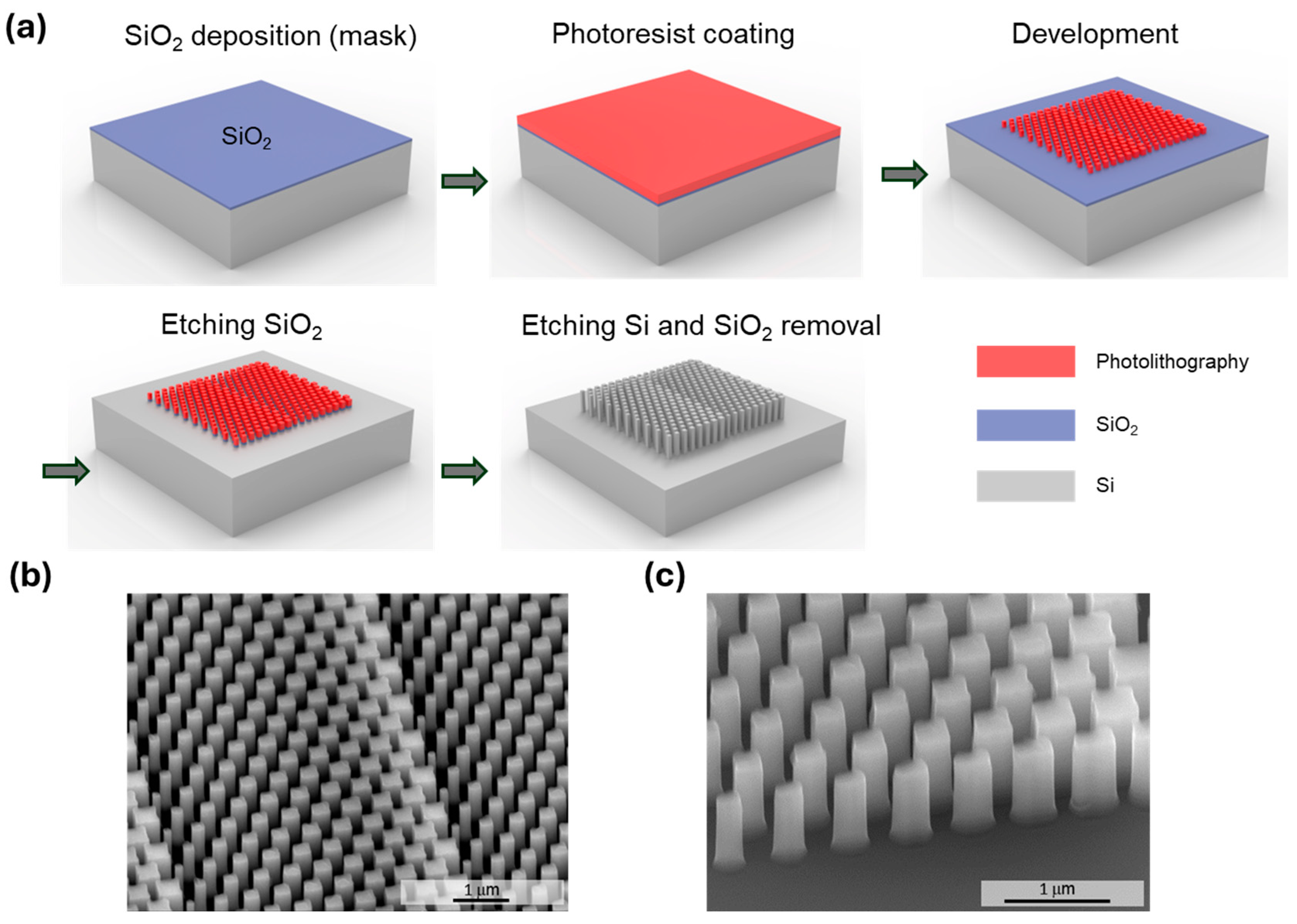
3. Fabrication of Metagratings
3.1. Fabrication Process of Si Metagratings Operating at a Wavelength of 1550 nm
3.2. Fabrication Process of GaAs Metagratings Operating at a Wavelength of 940 nm
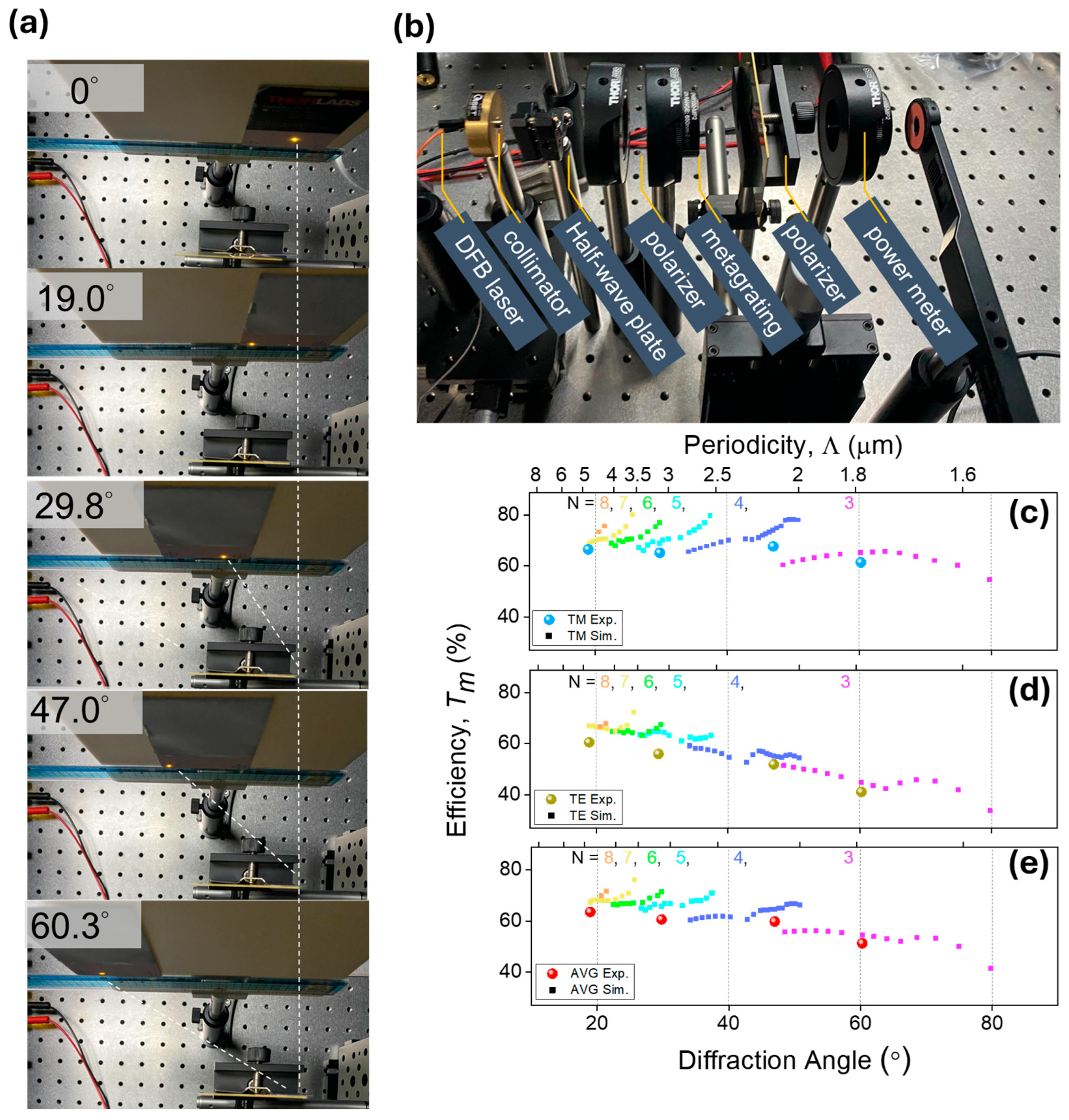
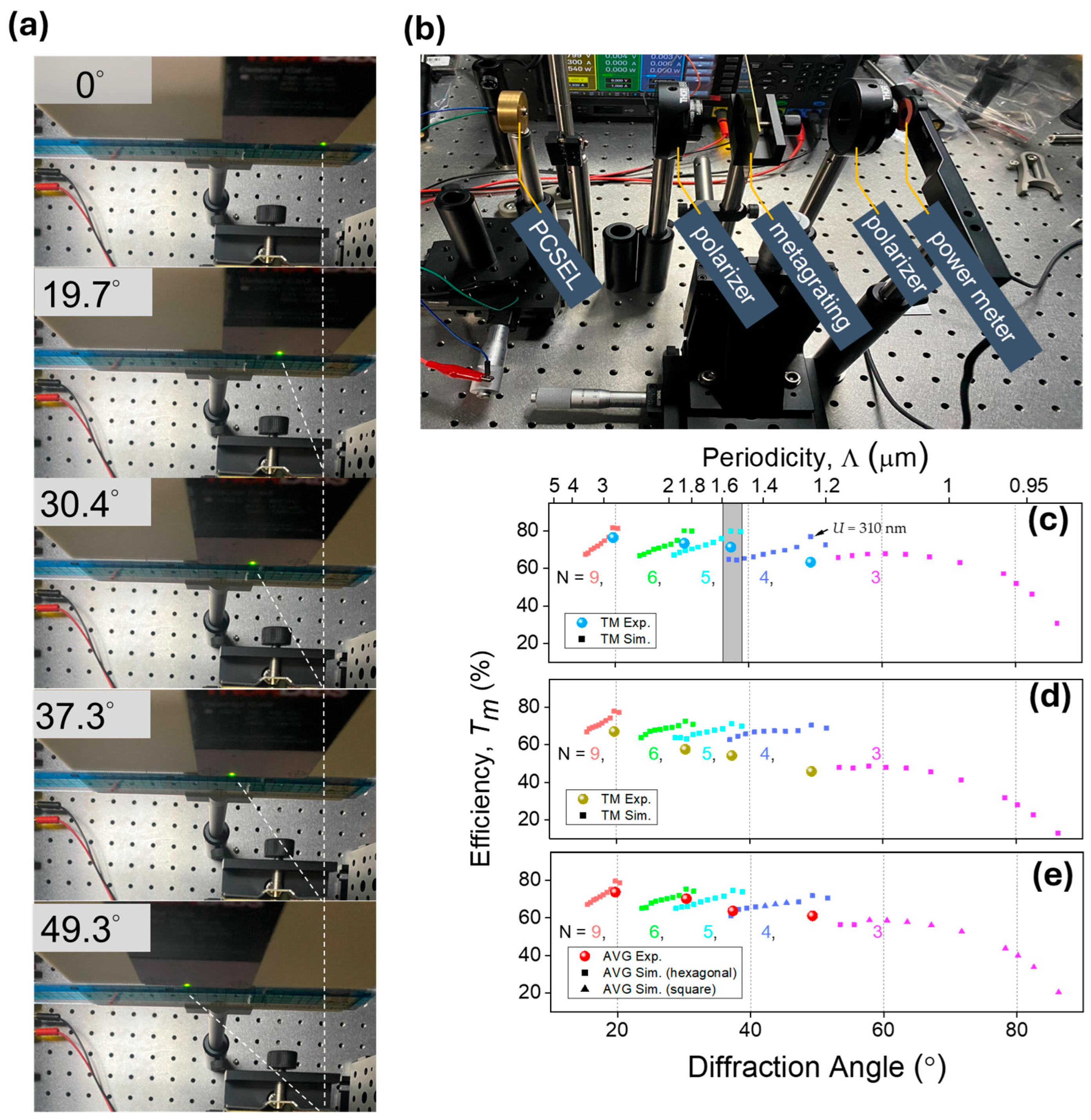
4. Efficiency Measurements
4.1. Measurement Setup and Results for Si Metagrating
4.2. Measurement Setup and Results for GaAs Metagrating
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, Y.-H.; Hsu, W.-C.; Tsai, W.-C.; Huang, Y.-W.; Chen, S.-C.; Kuo, H.-C. Ultracompact Nanophotonics: Light Emission and Manipulation with Metasurfaces. Nanoscale Res. Lett. 2022, 17, 41. [Google Scholar] [CrossRef]
- Hsiao, H.-H.; Chu, C.H.; Tsai, D.P. Fundamentals and Applications of Metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat Optics with Designer Metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Tseng, M.L.; Hsiao, H.-H.; Chu, C.H.; Chen, M.K.; Sun, G.; Liu, A.-Q.; Tsai, D.P. Metalenses: Advances and Applications. Adv. Opt. Mater. 2018, 6, 1800554. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M. Dielectric Gradient Metasurface Optical Elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A Broadband Achromatic Metalens for Focusing and Imaging in the Visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chen, M.-K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.-T.; Wang, J.-H.; et al. A Broadband Achromatic Metalens in the Visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Li, X.; Chen, C.; Guo, Y.; He, Q.; Zhang, R.; Pu, M.; Chen, X.; Jin, X.; Li, H.; Luo, X. Monolithic Spiral Metalens for Ultrahigh-Capacity and Single-Shot Sorting of Full Angular Momentum State. Adv. Funct. Mater. 2024, 34, 2311286. [Google Scholar] [CrossRef]
- Wen, D.; Meng, J.; Cadusch, J.J.; Crozier, K.B. VCSELs with On-Facet Metasurfaces for Polarization State Generation and Detection. Adv. Opt. Mater. 2021, 9, 2001780. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Chen, S.; Xie, Z.; Zheng, J.; Zhu, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; et al. All-Optical Controlled-NOT Logic Gate Achieving Directional Asymmetric Transmission Based on Metasurface Doublet. OEA 2023, 6, 220073–220079. [Google Scholar] [CrossRef]
- Tang, Z.; Li, L.; Zhang, H.; Yang, J.; Hu, J.; Lu, X.; Hu, Y.; Qi, S.; Liu, K.; Tian, M.; et al. Multifunctional Janus Metasurfaces Achieving Arbitrary Wavefront Manipulation at Dual Frequency. Mater. Des. 2022, 223, 111264. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface Holograms Reaching 80% Efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Lin, C.-H.; Huang, S.-H.; Lin, T.-H.; Wu, P.C. Metasurface-Empowered Snapshot Hyperspectral Imaging with Convex/Deep (CODE) Small-Data Learning Theory. Nat. Commun. 2023, 14, 6979. [Google Scholar] [CrossRef]
- Hsu, W.-C.; Chang, C.-H.; Hong, Y.-H.; Kuo, H.-C.; Huang, Y.-W. Metasurface- and PCSEL-Based Structured Light for Monocular Depth Perception and Facial Recognition. Nano Lett. 2024, 24, 1808–1815. [Google Scholar] [CrossRef]
- Wu, P.C.; Tsai, W.-Y.; Chen, W.T.; Huang, Y.-W.; Chen, T.-Y.; Chen, J.-W.; Liao, C.Y.; Chu, C.H.; Sun, G.; Tsai, D.P. Versatile Polarization Generation with an Aluminum Plasmonic Metasurface. Nano Lett. 2017, 17, 445–452. [Google Scholar] [CrossRef]
- Zhang, F.; Pu, M.; Li, X.; Ma, X.; Guo, Y.; Gao, P.; Yu, H.; Gu, M.; Luo, X. Extreme-Angle Silicon Infrared Optics Enabled by Streamlined Surfaces. Adv. Mater. 2021, 33, 2008157. [Google Scholar] [CrossRef]
- Shi, T.; Wang, Y.; Deng, Z.-L.; Ye, X.; Dai, Z.; Cao, Y.; Guan, B.-O.; Xiao, S.; Li, X. All-Dielectric Kissing-Dimer Metagratings for Asymmetric High Diffraction. Adv. Opt. Mater. 2019, 7, 1901389. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, J.; Su, R.; Yao, B.; Fang, H.; Li, K.; Zhou, L.; Liu, J.; Stellinga, D.; Reardon, C.P.; et al. Efficient Silicon Metasurfaces for Visible Light. ACS Photonics 2017, 4, 544–551. [Google Scholar] [CrossRef]
- Sell, D.; Yang, J.; Doshay, S.; Yang, R.; Fan, J.A. Large-Angle, Multifunctional Metagratings Based on Freeform Multimode Geometries. Nano Lett. 2017, 17, 3752–3757. [Google Scholar] [CrossRef]
- Ni, P.-N.; Fu, P.; Chen, P.-P.; Xu, C.; Xie, Y.-Y.; Genevet, P. Spin-Decoupling of Vertical Cavity Surface-Emitting Lasers with Complete Phase Modulation Using on-Chip Integrated Jones Matrix Metasurfaces. Nat. Commun. 2022, 13, 7795. [Google Scholar] [CrossRef]
- Fu, P.; Ni, P.-N.; Wu, B.; Pei, X.-Z.; Wang, Q.-H.; Chen, P.-P.; Xu, C.; Kan, Q.; Chu, W.-G.; Xie, Y.-Y. Metasurface Enabled On-Chip Generation and Manipulation of Vector Beams from Vertical Cavity Surface-Emitting Lasers. Adv. Mater. 2023, 35, 2204286. [Google Scholar] [CrossRef]
- Xie, Y.-Y.; Ni, P.-N.; Wang, Q.-H.; Kan, Q.; Briere, G.; Chen, P.-P.; Zhao, Z.-Z.; Delga, A.; Ren, H.-R.; Chen, H.-D.; et al. Metasurface-Integrated Vertical Cavity Surface-Emitting Lasers for Programmable Directional Lasing Emissions. Nat. Nanotechnol. 2020, 15, 125–130. [Google Scholar] [CrossRef]
- Wang, Q.-H.; Ni, P.-N.; Xie, Y.-Y.; Kan, Q.; Chen, P.-P.; Fu, P.; Deng, J.; Jin, T.-L.; Chen, H.-D.; Lee, H.W.H.; et al. On-Chip Generation of Structured Light Based on Metasurface Optoelectronic Integration. Laser Photonics Rev. 2021, 15, 2000385. [Google Scholar] [CrossRef]
- Tsai, W.-C.; Hong, Y.-H.; Kuo, H.-C.; Huang, Y.-W. Design of High-Efficiency and Large-Angle Homo-Metagratings for Light Source Integration. Opt. Express OE 2023, 31, 24404–24411. [Google Scholar] [CrossRef]
- Angelini, F.; Colao, F. Optimization of Laser Wavelength, Power and Pulse Duration for Eye-Safe Raman Spectroscopy. J. Eur. Opt. Soc. Rapid Publ. 2019, 15, 2. [Google Scholar] [CrossRef]
- Cheng, J.-X. New “HOPE” Laser for Photoacoustic Imaging of Water. Light. Sci. Appl. 2022, 11, 107. [Google Scholar] [CrossRef]
- Hugonin, J.P.; Lalanne, P. RETICOLO Software for Grating Analysis. arXiv 2023, arXiv:2101.00901v3. [Google Scholar]
- Kim, I.; Martins, R.J.; Jang, J.; Badloe, T.; Khadir, S.; Jung, H.-Y.; Kim, H.; Kim, J.; Genevet, P.; Rho, J. Nanophotonics for Light Detection and Ranging Technology. Nat. Nanotechnol. 2021, 16, 508–524. [Google Scholar] [CrossRef]
- Wang, D.; Watkins, C.; Xie, H. MEMS Mirrors for LiDAR: A Review. Micromachines 2020, 11, 456. [Google Scholar] [CrossRef]
- Li, Z.; Lin, P.; Huang, Y.-W.; Park, J.-S.; Chen, W.T.; Shi, Z.; Qiu, C.-W.; Cheng, J.-X.; Capasso, F. Meta-Optics Achieves RGB-Achromatic Focusing for Virtual Reality. Sci. Adv. 2021, 7, eabe4458. [Google Scholar] [CrossRef]
- Li, Z.; Pestourie, R.; Park, J.-S.; Huang, Y.-W.; Johnson, S.G.; Capasso, F. Inverse Design Enables Large-Scale High-Performance Meta-Optics Reshaping Virtual Reality. Nat. Commun. 2022, 13, 2409. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, W.-C.; Chang, C.-H.; Yu, T.-C.; Huang, Y.-H.; Chow, C.-W.; Hong, Y.-H.; Kuo, H.-C.; Huang, Y.-W. High-Efficiency and Large-Angle Homo-Metagratings for the Near-Infrared Region. Photonics 2024, 11, 392. https://doi.org/10.3390/photonics11050392
Tsai W-C, Chang C-H, Yu T-C, Huang Y-H, Chow C-W, Hong Y-H, Kuo H-C, Huang Y-W. High-Efficiency and Large-Angle Homo-Metagratings for the Near-Infrared Region. Photonics. 2024; 11(5):392. https://doi.org/10.3390/photonics11050392
Chicago/Turabian StyleTsai, Wei-Cheng, Chia-Hsun Chang, Tai-Cherng Yu, Yi-Hsuan Huang, Chi-Wai Chow, Yu-Heng Hong, Hao-Chung Kuo, and Yao-Wei Huang. 2024. "High-Efficiency and Large-Angle Homo-Metagratings for the Near-Infrared Region" Photonics 11, no. 5: 392. https://doi.org/10.3390/photonics11050392
APA StyleTsai, W.-C., Chang, C.-H., Yu, T.-C., Huang, Y.-H., Chow, C.-W., Hong, Y.-H., Kuo, H.-C., & Huang, Y.-W. (2024). High-Efficiency and Large-Angle Homo-Metagratings for the Near-Infrared Region. Photonics, 11(5), 392. https://doi.org/10.3390/photonics11050392








