Abstract
The structural, electronic, mechanical, and optical properties of pseudo-cubic CH3NH3PbI3 perovskite have been studied within the framework of density functional theory, in line with solar cell applications. The computed values of lattice and elastic constants concurred with the available theoretical and experimental data. This compound has a semi-conducting behavior, with a direct band gap of about 1.49 eV. Note that the solar radiation spectrum has a maximum energy intensity value of approximately 1.50 eV. Thus, semiconductors with such gaps are preferred for photovoltaic applications. Its elastic parameters reveal that it is a ductile material that is mechanically stable. Optical descriptors such as refractive index, reflectivity, extinction, energy loss, and absorption have been explored with the aim of establishing the optical features of the material. Our findings demonstrate that this perovskite is suitable for solar cell applications based on the size and nature of the band gap, as also supported by the obtained upper limit value of simulated power conversion efficiency via the spectroscopic limited maximum efficiency mathematical model.
1. Introduction
Solar energy plays a crucial role in solving the pressing environmental challenges and meeting ever increasing energy demands. Solar cells are often classified depending on the absorber layer available, so those that use a perovskite material as their absorber layer are called perovskite solar cells. Perovskites are potential candidates for substitution of the crystalline silicon in fabricating solar cells that are thinner, lighter, and cheaper. Contrary to silicon solar cells, which can only absorb the visible light spectrum, the perovskite solar cell has the optical and electrical property of absorbing not only the visible light spectrum but also the near-infrared. Simply defined, solar energy refers to the portion of energy in which the form of sunlight can be converted via photovoltaics into electricity by the solar cell.
Generally, a solar cell has six major components, but for decades, the scientific community has been focusing mainly on the determination of a better photoactive material, keeping the other five components intact. This is achieved by tuning the efficiency of a photovoltaic device through identification of a material that has a better ability to absorb more photons based on its power conversion efficiency as provided herein [1,2,3]. As stated above, a typical perovskite solar cell consists of six main layers of different materials: a glass layer, a thin layer of fluorine-doped tin oxide substrate (FTO), an electron transport layer of TiO2, a perovskite layer known as methylammonium lead iodide (CH3NH3PbI3), a hole transport layer of Spiro-OMeTAD, and a gold (Au) electrode [4]. According to Zhang et al. [5], an ideal solar absorber should provide high absorption, be ultra wideband, and be insensitive to polarization and incident angles that pose challenges to research. Kaulachs et al. [6] have indicated that physical properties such as high charge carrier mobility, very low recombination rates, large carrier lifetime and diffusion length, large absorption coefficients, and very weak exciton binding energies are defining the high power conversion efficiency of methylammonium lead trihalide solar cells. From a study conducted by Mangrulkar et al. [7], the MAPbI3 absorber layer provides one of the highest open-circuit voltages (Voc), low Voc loss/deficit, and low exciton binding energy, resulting in better charge transport with decent charge carrier mobilities and long diffusion lengths of charge carriers, making it a suitable candidate for photovoltaic applications. Wu et al. [8] developed an additive engineering strategy to realize a facile and convenient fabrication method of large-area uniform perovskite films composed of large crystal sizes and a low density of defects.
Suitability of the material can be gauged using the spectroscopic limited maximum efficiency (SLME) approach [9]. This technique provides a better model for predicting the upper limit of solar cell efficiency as compared to the conventional Shockley–Quisser (S–Q) efficiency approach [10], since it considers the non-radiative recombination losses that are omitted in the latter approach. The S–Q technique only utilizes the information about the band gap, black body radiation, and solar spectrum to estimate an upper limit for the solar efficiency. Developed from the S–Q, the SLME method of determining theoretical efficiency of a solar cell device takes photon absorptivity into account.
The energy conversion efficiency of perovskite-based solar cells has risen quickly over the years from 3.8% [11] to about 20% [12]. According to various literature such as Poglitsch et al. [13], Lu et al. [14], and Kawamura et al. [15], temperature variation stimulates phase transition in CH3NH3PbI3, whereby it transforms at 327.4 K from a high temperature phase that is cubic with high symmetry (space group Pmm) to a tetragonal phase (space group I4/mcm). Subsequently, it changes to an orthorhombic phase of low symmetry (space group Pnma) at 162.2 K.
This phenomenon of thermally induced phase transition in methylammonium lead iodide has been extensively explored experimentally using various techniques such as single crystal X-ray diffraction and infrared spectroscopy [15,16]. Moreover, Wu et al. [17] recently explored the phase transition kinetics of MAPbI3 for the tetragonal-to-orthorhombic evolution using the nudged elastic band method from the theoretical point of view to provide a basis for understanding the crystal-phase dependent stability and the low-temperature efficiency of hybrid organic–inorganic perovskites. Yun et al. [18] have assessed the current understanding of structural and electronic properties, defects, ionic diffusion, and shift current for CH3NH3PbI3 perovskite, as well as the effect of ionic transport on the hysteresis of current–voltage curves in perovskite solar cells based on first-principles calculations. Jiang et al. [19] have found a feasible and effective post-treatment method that is cheap, valid, and essential for fabrication of high-efficiency perovskite solar cells. According to Faghihnasiri et al. [20], electron-hole diffusion length as long as 1 micron, low effective mass, high charge mobility, high optical absorbance coefficient, narrow optical absorbance edge, large dielectric constant, proper optical band gap in the visible range, and strong dipole moments are some of the features that make MAPbI3 one of the most promising materials to use as an absorbance layer in solar cells.
Basically, there are numerous techniques of fabricating perovskite-based solar cells. The most widely applied approach is a single-step deposition technique that is often preferred due to its simplicity and cost effectiveness. In this method, the precursor solution is spin-coated over the TiO2 scaffold where the organic and inorganic solutes are mixed together in an aprotic polar solvent, resulting in a precursor solution that is then annealed at a temperature of 80 °C to 150 °C [21,22]. Another approach is a two-step sequential deposition technique that was designed to overcome the shortcomings of the former approach. In this technique, the film is first deposited over nanoporous TiO2 layer by spin-coating the solution of a polar solvent like dimethylformamide at 70 °C and subsequently transforming it into perovskite by exposing it to a solution of CH3NH3I [23]. Besides the two stated techniques of fabricating perovskite solar cells, other methods exist, such as rapid deposition crystallization [24], the Lewis base adduct method [25], vapor-assisted solution processing [26], and thermal evaporation [27], among others.
Recently, Terada et al. [28] have investigated the effects of the addition of potassium iodide (KI) and ethylammonium bromide (EABr) on the microstructures of the perovskite layers. From their findings, co-addition of KI and EABr to MAPbI3 by using the air-blowing method and inserting a decaphenylcyclopentasilane layer is an effective method of fabricating photovoltaic devices with improved properties and efficiency. Hedayati and Olyalee [29] proposed that, by using n-type and p-type homojunction perovskite connections instead of the usual connection of p-i-n and n-i-p perovskite, the transfer and separation of charge carriers can be done by an internal electric field. Thus, the discharge area will be reduced, the recombination of carriers will be increased, and the light losses will be reduced, thereby boosting the light absorption and consequently improving the efficiency of the cell. Likewise, Semchenko et al. [30] have investigated the photocurrent and spectral sensitivity of Si/SrTiO3:xNb/perovskite structures and found that, at various configurations of the applied voltage between silicon, SrTiO3, and CH3NH3PbI3−xClx, the structures are photosensitive, which could be applicable in designing photodetectors.
This work provide insights into the structural and mechanical properties of the pseudo-cubic phase of methylammonium lead iodide, thus contributing to a better understanding of its physical properties that are critically important for its applications in photovoltaic technology. Additionally, we present an in-depth analysis of its optoelectronic properties upon interacting with light. This is crucial for a better understanding of its photovoltaic-related properties such as power conversion efficiency. Although its structural and mechanical properties have been widely explored from both the theoretical and experimental points of view, scanty information exists on its optical features, which creates a gap that this study intends to fill. Hence, we attempt to bridge the information gap and open a window for fine-tuning its optoelectronic properties, such as through doping, based on our findings that lead (Pb) and iodine (I) states dominate its electronic and optical properties. Moreover, to the best of the authors’ knowledge, there is no report on the melting temperature of pseudo-cubic CH3NH3PbI3 perovskite prior to this study. Additionally, determination of the upper limit value of the simulated power conversion efficiency of this material via the spectroscopic limited maximum efficiency mathematical model has not been extensively reported for this material; thus, this study provides some contributions.
2. Computational Details
This study is based on density functional theory as implemented in the Vienna Ab initio Simulation Package (VASP) [31]. The plane wave basis energy cut-off was set to 500 eV as guided by our convergence data, all atoms in the structure were allowed to relax to less than 10−6 eV per atom, and the residual forces converged to 10−2 eV/Å. The Brillouin zone integrations were computed using Γ-centered grids with 10 × 10 × 10 mesh for the structural and electronic calculations. Pseudo-potential that treats the semicore states (5d) of lead (Pb) as valence electrons was used in our simulation because the valence d electrons are of prominent chemical importance in transition-metal compounds [32], considering that the chemical and physical properties of any system are determined by the inter-atomic interactions.
The exchange correlation energy of electrons was described using the generalized gradient approximation (GGA) as parameterized by Perdew–Burke–Ernzerhof (PBE) [33] and PBEsol [34]. The latter is a flavor of PBE that is specifically written to describe the behavior of solids with good accuracy, as it minimizes their reliance on error cancellation between the exchange part and the correlation part. For optical study, a k-point mesh of 6 × 6 × 6 was applied, the plane wave cut-off energy was adjusted to 300 eV as a trade-off, and ground-state wave functions were used as input for GW0 and BSE calculations. The absorptivity data obtained upon calculating the optical properties of our material at the Bethe–Salpeter level of approximation were used as ingredients together with the computed value of the optical gap to estimate the upper limit of solar conversion efficiency, based on the SLME mathematical model as applied by Choudhary et al. [35].
3. Results and Discussion
3.1. Structural Parameters
The structural data for the pseudo-cubic methylammonium lead iodide layer is provided in Table 1, and the resultant unit cell of the crystal structure is provided in Figure 1 (left) as visualized using the XCrySDen tool [36] in ball-and-stick format. Its 3 × 2 × 3 supercell is provided in Figure 1 (right) as viewed using VESTA software [37], represented in polyhedral format in order to obtain a pictorial representation of the perovskite structure, where the PbI6 octahedra are shaded gray. Our compound of study shows a slight variation from the ideal unit cell of a cubic structure in that the -value deviates from 90° by a small margin of less than 2° for both the PBE and PBEsol functionals considered. This gives rise to a pseudo-cubic structure of CH3NH3PbI3 perovskite, where the lattice constants in the x-, y-, and z-axes vary by a small margin. The deviation from an ideal cubic structure is thought to arise from the presence of the organic cations that break the ideal lattice symmetry [38]. This has been reported by various researchers as well [20,39,40].

Table 1.
The optimized structural parameters for pseudo-cubic CH3NH3PbI3, alongside other published results.
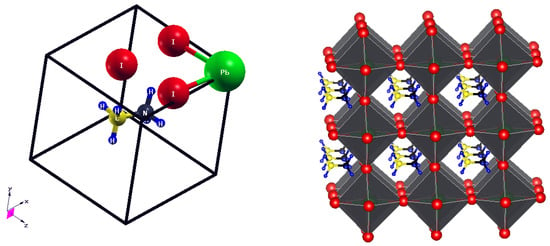
Figure 1.
Crystal structure of pseudo-cubic CH3NH3PbI3 alongside the polyhedral format of the structure (color online).
Figure 2 shows the total energy per formula unit as a function of the lattice constant of pseudo-cubic CH3NH3PbI3. This indicates how the optimized values of the equilibrium lattice constant a were obtained using PBE and PBEsol functionals. Note that the dots and stars indicate the data obtained from the calculations whereas the lines indicates the linear fits. Consequently, for the pseudo-cubic structure, when the lattice constant a changes, b and c also change. The optimized ground state lattice constants in x-, y-, and z-axes, together with the obtained volume (V) and density (), are listed in Table 1 alongside other existing reports.
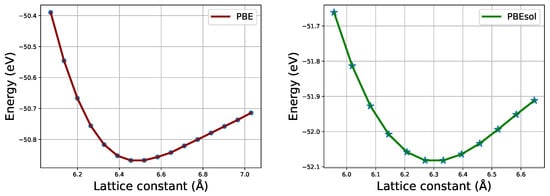
Figure 2.
Optimization of lattice constant a using PBE and PBEsol functionals.
Upon comparing our obtained values of lattice constants, we note that they are in agreement with previously reported theoretical values as provided. They are also within the limit of the existing experimental data, whose reported lattice constant values range from 6.27 Å to 6.391 Å as relayed in previous studies [13,41,42,43]. The units of the structural parameters listed in Table 1 are as follows: lattice constants (Å), angles (°), volume (Å3), and density (g/cm3). From Table 1, we observe that the optimized values of the lattice constants obtained using the PBEsol functional mimic better the ground state structure of our material of interest compared to experimental findings, relative to PBE. This is crucial since the first-principles calculations can be applied to compute various physical properties of a material based on the crystal structural information. Thus, our subsequent calculations of other properties of interest were only done using the PBEsol functional.
3.2. Mechanical Parameters
Upon undertaking the elastic constant calculation of our perovskite compound, we obtained a 6 × 6 elastic tensor consisting of elastic constants. These were then applied in computing other mechanical descriptive parameters such as the bulk, shear, and Young’s modulus by using Equations (1) and (2) alongside other existing theoretical and experimental reports on its mechanical properties as provided in Table 2, where we observe an adequate correlation. The bulk modulus, independent elastic coefficients, shear modulus, Young’s modulus, and Poisson’s ratio are denoted by B, , G, E, and , respectively. Note that, in this study, we adopted Hill’s averaging scheme, which frequently gives the mean of the Voight and Reuss values. The Voight scheme often overestimates numerical data, as it assumes a uniform strain, whereas the Reuss method underestimates numerical data, since it presumes a uniform stress [44].

Table 2.
The calculated mechanical parameters for pseudo-cubic CH3NH3PbI3 in comparison with previously published results.
The shear modulus obtained when Hill’s averaging scheme was applied is denoted GH, whereas GV and GR denote the values of the shear modulus obtained using the Voight and Reuss averaging schemes, respectively.
The agreement between our predicted mechanical features of the pseudo-cubic MAPbI3 and other existing reports is good, with the shear modulus and Poisson’s ratio being well-reproduced when compared with the experimental data taken along 100 faces of cubic MAPbI3 [46]. The computed values of the independent elastic coefficients provided in Table 2 conform to Born mechanical stability criteria for cubic systems [47] when substituted into Equation (3), which affirms that the pseudo-cubic CH3NH3PbI3 is a mechanically stable material.
Thereafter, we utilized the values of the computed density (), the bulk modulus (B), and the shear modulus (G) provided in Table 1 and Table 2 to predict the values of sound velocities as well as Debye and melting temperatures as provided in Table 3, where Equations (4) and (5) were applied. Thermal properties of a material are related to the Debye temperature (), as indicated in Equation (4), where is the Boltzmann constant, h is the Plank constant, n is the number of atoms in its chemical formula, is the Avogadro constant, is the density of the material, and M is the molecular weight.

Table 3.
Calculated sound velocities as well as Debye and melting temperatures for pseudo-cubic CH3NH3PbI3, together with other published results.
The units of the sound velocities and both Debye and melting temperatures are in meters per second (m/s) and Kelvin (K), respectively. The longitudinal, transverse, and average sound velocities are denoted by , , and , respectively, as indicated in Equation (4).
Melting temperature denoted by was estimated using Equation (5).
3.3. Electronic Band Structure and Density of States for Pseudo-Cubic CH3NH3PbI3
From the electronic band structure plot, the pseudo-cubic phase of CH3NH3PbI3 possesses a direct band gap that is located at the E/M1 wave vector in the irreducible Brillouin zone. The electronic band gap obtained was 1.49 eV, which represents the energy required to promote an electron within the electronic structure of the material from the top of the valence band to the bottom of the conduction band. Our computed electronic band gap is similar to that reported by Qian et al. [48] and is in accordance with previously reported experimental values ranging from 1.50 eV to 1.57 eV [49,50,51,52]. The agreement between our computed value of the band gap obtained using the PBEsol functional and the existing experimental data is discernible, and the same applies to the findings obtained by Umari et al. [53].
Partial density of states (PDOS) provide insights to the role of each atomic orbital in the electronic properties of the system under study. From the partial and total density of states plot provided in Figure 3, hybridization of lead and iodine components occur at the top (bottom) of the valence (conduction) band near the Fermi level. The methylammonium component (that is, carbon, nitrogen, and hydrogen) contributes only at energy levels that are far from the Fermi level, hence having minimal impact on the electronic behavior of the pseudo-cubic phase of methylammonium lead iodide. Its direct band gap greatly promotes radiative recombination of electron-hole pairs, thus resulting in more photons being emitted. For an indirect band gap material, radiative recombination is less likely to occur because phonons are required in the process.
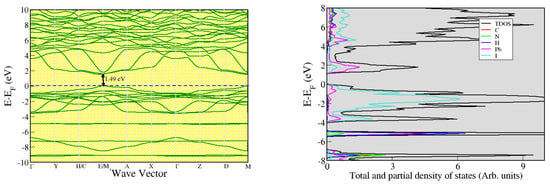
Figure 3.
Electronic band structure alongside the total and partial density of states.
3.4. Optical Properties
Optical properties provide crucial information about how a given material tends to respond to the incident radiation. Thus, the incoming photons can be absorbed, conducted, dispersed, refracted, reflected, or transmitted at various degrees. Although the primary optical property of interest is the absorption coefficient in reference to its efficiency in generating electricity, other properties will be examined as well so as to obtain a wider scope, since they are interrelated. For instance, the lower the photon reflectivity index of a material, the higher the degree of absorption of the solar radiation. We derived its optical features, such as reflectivity R(), absorption , refractive index n(), energy loss L(), and the extinction coefficient k() with respect to photon energy (), from the real part and imaginary part of the dielectric function as per the Krammer–Kronig relations [54,55] provided in Equations (6) and (7).
Optical examination acts as a probe into the photo-physics of CH3NH3PbI3 as the absorber layer in a single junction solar cell. The extinction coefficient is a measure of the damping of the electromagnetic wave as it passes through a medium. It indicates the rate of transmitted light via scattering and absorption for a medium. The visible regime of the electromagnetic spectra ranges from 1.65 to 3.3 eV (translating to a wavelength of between 390 to 770 nm) and is very crucial for getting insights about the optical features of any material [56]. Moreover, light is poorly absorbed in materials with a low absorption coefficient. The static values of the dielectric constant (), the refractive index (n), and the extinction coefficient (k) were obtained to be 3.8, 1.95, and 1.38, respectively, as provided in Figure 4. A large static dielectric constant is essential for obtaining an efficient active layer in classic solar cells for better control of the electron-hole recombination process [57]. The real part () and imaginary part () of the dielectric constant represent charge polarization and dissipation, respectively. The highest value of reflectivity is attained when the energy of the incoming photons is about 2.7 eV. At this energy value, approximately 30% of the incoming solar radiation is reflected, as indicated by the blue dotted line in Figure 5.
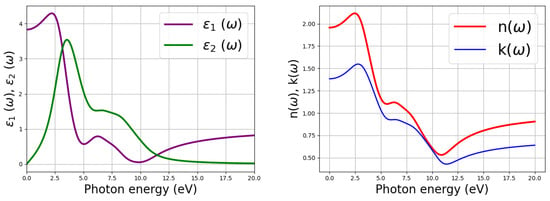
Figure 4.
Real and imaginary parts of the dielectric constant alongside the refractive index and extinction coefficient (color online).
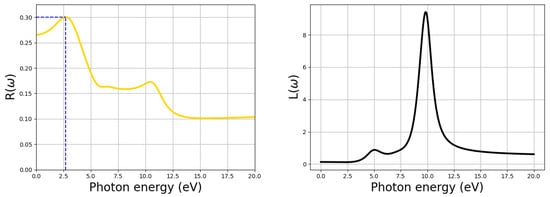
Figure 5.
Reflectivity alongside the energy loss function.
As revealed in the optical data plot provided in Figure 6, the pseudo-cubic MAPbI3 has a high value of absorption coefficient of about 2.1 × 105 cm−1 at a photon energy of 4 eV, where the first absorption peak is located. This compound has a high optical absorption in a wide spectral range as shown, with an optical absorption coefficient on the order 105 cm−1, which contributes to the effective utilization of solar radiation. Moreover, such an order of magnitude for the optical absorption coefficient has been reported by various scholars as well [40,58,59]. If a material has a high absorption coefficient, it signifies that it absorbs more photons that excite electrons from the valence band to the conduction band.
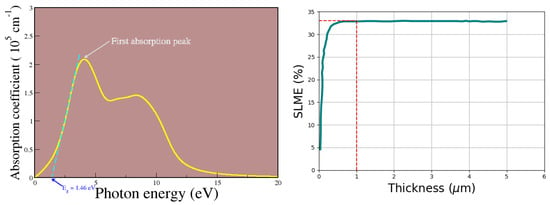
Figure 6.
Absorption coefficient alongside the simulated power conversion efficiency via the SLME approach.
The highest value of energy loss occurs outside the visible region, and the optical gap of the material was obtained to be 1.46 eV that was extracted upon drawing a tangent at the onset of the first absorption peak, and the magnitude of the obtained optical gap affirms the suitability of this material in photovoltaic applications when the light-absorbing material is perovskite. Our obtained value for the optical band gap of our material as well as its absorption coefficient deduced from Figure 6 were utilized in computing the simulated SLME value at room temperature using the Jarvis tools [60]. SLME takes into account the band gap, the shape of the absorption spectra, and the material-dependent non-radiative recombination losses. The theoretical value of the SLME upper value of about 33% (indicated by the red dotted lines in Figure 6), obtained from simulation when thin film thickness is 1 μm, suggests that this material is suitable for solar cell applications. Our simulated value for the SLME is comparable to that reported by Qian et al. [48] of 31%.
4. Conclusions
We have investigated the structural, mechanical, electronic, and optical properties of the pseudo-cubic phase of methylammonium lead iodide using the first principles approach. From our electronic dispersion analysis, this material has a direct band gap. Moreover, lead (Pb) and iodine (I) ions play an important role in the material’s electronic properties, whereas methylammonium (MA) forms its structural framework. Electronic band structure analysis revealed that the origin of the energy gap in the pseudo-cubic CH3NH3PbI3 compound lies in the states of the inorganic component (PbI3), since the organic component (CH3NH3) does not contribute to the bands near the Fermi level. Our computed values of elastic properties confirm that this compound is ductile and mechanically stable. Additionally, we have simulated the upper theoretical value of its power conversion efficiency while also providing a comprehensive probe into its optical properties such as reflectivity, absorption, extinction, energy loss, and refractivity.
Author Contributions
All authors participated in conceptualization, review, and editing. E.K.R., a postdoctoral fellow, performed all the calculations, analyzed the reported data, and wrote the manuscript under the project supervision of N.E.M. and co-supervision of R.R.M., R.E.M. and J.K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by University of Stellenbosch National Institute for Theoretical and Computational Science, grant number SEA/21/PHY/08 and the APC was funded by University of Venda.
Data Availability Statement
Data associated with this article, such as crystal structure information, averaged values of the real and imaginary parts of the complex dielectric function, and absorptivity data used to theoretically predict the upper limit of solar efficiency, is openly available at a github pseudo-cubic repository (https://github.com/elkana35/MAPbI3_pseudo-cubic.git (accessed on 3 May 2023)).
Acknowledgments
We wish to thank the University of Venda for the support infrastructure to carry out this research and the Centre for High Performance Computing for the computational resources. E. K. Rugut is grateful to Daniel Joubert for facilitation of VASP software and to Thokozane Mlotshwa for proofreading the article.
Conflicts of Interest
The authors declare no conflicts of interest regarding this work.
References
- Liu, C.; Li, W.; Zhang, C.; Ma, Y.; Fan, J.; Mai, Y. All-inorganic CsPbI2Br perovskite solar cells with high efficiency exceeding 13%. J. Am. Chem. Soc. 2018, 140, 3825–3828. [Google Scholar] [CrossRef]
- Ullah, S.; Liu, P.; Wang, J.; Yang, P.; Liu, L.; Yang, S.; Guo, H.; Xia, T.; Chen, Y. Optimizing the working mechanism of the CsPbBr3-based inorganic perovskite solar cells for enhanced efficiency. Sol. Energy 2020, 209, 79–84. [Google Scholar] [CrossRef]
- Alsalloum, A.; Turedi, B.; Zheng, X.; Mitra, S.; Zhumekenov, A.; Lee, K.; Maity, P.; Gereige, I.; AlSaggaf, A.; Roqan, I. Low-temperature crystallization enables 21.9% efficient single-crystal MAPbI3 inverted perovskite solar cells. ACS Energy Lett. 2020, 5, 657–662. [Google Scholar] [CrossRef]
- Husainat, A.; Ali, W.; Cofie, P.; Attia, J.; Fuller, J. Simulation and analysis of methylammonium lead iodide (CH3NH3PbI3) perovskite solar cell with Au contact using SCAPS 1D simulator. Am. J. Opt. Photon 2019, 7, 33. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, Y.; Li, W.; Liang, S.; Ma, J.; Cheng, S.; Yang, W.; Yi, Y. High Absorptivity and Ultra-Wideband Solar Absorber Based on Ti-Al2O3 Cross Elliptical Disk Arrays. Coatings 2023, 13, 531. [Google Scholar] [CrossRef]
- Kaulachs, I.; Ivanova, A.; Tokmakov, A.; Roze, M.; Mihailovs, I.; Rutkis, M. Perovskite CHNHPbICl Solar Cells and their Degradation (Part 1: A Short Review). Latv. J. Phys. Tech. Sci. 2021, 58, 44–52. [Google Scholar] [CrossRef]
- Mangrulkar, M.; Stevenson, K. The progress of additive engineering for CH3NH3PbI3 photo-active layer in the context of perovskite solar cells. Crystals 2021, 11, 814. [Google Scholar] [CrossRef]
- Wu, Y.; Xie, F.; Chen, H.; Yang, X.; Su, H.; Cai, M.; Zhou, Z.; Noda, T.; Han, L. Thermally stable MAPbI3 perovskite solar cells with efficiency of 19.19% and area over 1 cm2 achieved by additive engineering. Adv. Mater. 2017, 29, 1701073. [Google Scholar] [CrossRef]
- Yu, L.; Zunger, A. Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys. Rev. Lett. 2012, 108, 068701. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H. Detailed balance limit of efficiency of p-n junction solar cells. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Yang, W.; Noh, J.; Jeon, N.; Kim, Y.; Ryu, S.; Seo, J.; Seok, S. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 2015, 348, 1234–1237. [Google Scholar] [CrossRef]
- Poglitsch, A.; Weber, D. Dynamic disorder in methylammoniumtrihalogenoplumbates (II) observed by millimeter-wave spectroscopy. J. Chem. Phys. 1987, 87, 6373–6378. [Google Scholar] [CrossRef]
- Lu, R.; Liu, Y.; Zhang, J.; Zhao, D.; Guo, X.; Li, C. Highly efficient (200) oriented MAPbI3 perovskite solar cells. Chem. Eng. J. 2022, 433, 133845. [Google Scholar] [CrossRef]
- Kawamura, Y.; Mashiyama, H.; Hasebe, K. Structural study on cubic-tetragonal transition of CH3NH3PbI3. J. Phys. Soc. Jpn. 2002, 71, 1694–1697. [Google Scholar] [CrossRef]
- Onoda-Yamamuro, N.; Matsuo, T.; Suga, H. Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II). J. Phys. Chem. Solids 1990, 51, 1383–1395. [Google Scholar] [CrossRef]
- Wu, J.; Chen, J.; Wang, H. Phase Transition Kinetics of MAPbI3 for Tetragonal-to-Orthorhombic Evolution. JACS Au 2023, 3, 1205–1212. [Google Scholar] [CrossRef]
- Yun, S.; Zhou, X.; Even, J.; Hagfeldt, A. Theoretical treatment of CH3NH3PbI3 perovskite solar cells. Angew. Chem. Int. Ed. 2017, 56, 15806–15817. [Google Scholar] [CrossRef]
- Jiang, Y.; Tu, L.; Li, H.; Li, S.; Yang, S.; Chen, Y. A feasible and effective post-treatment method for high-quality CH3NH3PbI3 films and high-efficiency perovskite solar cells. Crystals 2018, 8, 44. [Google Scholar] [CrossRef]
- Faghihnasiri, M.; Izadifard, M.; Ghazi, M. DFT study of mechanical properties and stability of cubic methylammonium lead halide perovskites (CH3NH3PbI3, X = I, Br, Cl). J. Phys. Chem. C 2017, 121, 27059–27070. [Google Scholar] [CrossRef]
- Roy, P.; Sinha, N.; Tiwari, S.; Khare, A. A review on perovskite solar cells: Evolution of architecture, fabrication techniques, commercialization issues and status. Sol. Energy 2020, 198, 665–688. [Google Scholar] [CrossRef]
- Shen, D.; Yu, X.; Cai, X.; Peng, M.; Ma, Y.; Su, X.; Xiao, L.; Zou, D. Understanding the solvent-assisted crystallization mechanism inherent in efficient organic–inorganic halide perovskite solar cells. J. Mater. Chem. A 2014, 2, 20454–20461. [Google Scholar] [CrossRef]
- Burschka, J.; Pellet, N.; Moon, S.; Humphry-Baker, R.; Gao, P.; Nazeeruddin, M.; Grätzel, M. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 2013, 499, 316–319. [Google Scholar] [CrossRef]
- Xiao, M.; Huang, F.; Huang, W.; Dkhissi, Y.; Zhu, Y.; Etheridge, J.; Gray-Weale, A.; Bach, U.; Cheng, Y.B.; Spiccia, L. A fast deposition-crystallization procedure for highly efficient lead iodide perovskite thin-film solar cells. Angew. Chem. Int. Ed. 2014, 53, 9898–9903. [Google Scholar] [CrossRef]
- Ahn, N.; Son, D.; Jang, I.; Kang, S.; Choi, M.; Park, N. Highly reproducible perovskite solar cells with average efficiency of 18.3% and best efficiency of 19.7% fabricated via Lewis base adduct of lead (II) iodide. J. Am. Chem. Soc. 2015, 137, 8696–8699. [Google Scholar] [CrossRef]
- Chen, Q.; Zhou, H.; Hong, Z.; Luo, S.; Duan, H.; Wang, H.; Liu, Y.; Li, G.; Yang, Y. Planar heterojunction perovskite solar cells via vapor-assisted solution process. J. Am. Chem. Soc. 2014, 136, 622–625. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Johnston, M.; Snaith, H. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef]
- Terada, S.; Oku, T.; Suzuki, A.; Okita, M.; Fukunishi, S.; Tachikawa, T.; Hasegawa, T. Ethylammonium bromide-and potassium-added CH3NH3PbI3 perovskite solar cells. Photonics 2022, 9, 791. [Google Scholar] [CrossRef]
- Hedayati, M.; Olyaee, S. High-efficiency pn homojunction perovskite and CIGS tandem solar cell. Crystals 2022, 12, 703. [Google Scholar] [CrossRef]
- Semchenko, A.; Ayvazyan, G.Y.; Malyutina-Bronskaya, V.V.; Khakhomov, S.A.; Kovalenko, D.L.; Boiko, A.A.; Sidski, V.V.; Nestsiaronak, A.V.; Mayevsky, A.A.; Danilchenko, K.D.; et al. Photoactive properties of transport sol-gel layers based on strontium titanate for perovskite solar cells. Photonics 2023, 10, 845. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Scrocco, M. X-ray photoemission spectra of Pb (II) halides: A study of the satellites on the core and valence bands. Phys. Rev. B 1982, 25, 1535. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Perdew, J.; Ruzsinszky, A.; Csonka, G.; Vydrov, O.; Scuseria, G.; Constantin, L.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Choudhary, K.; Garrity, K.; Reid, A.; DeCost, B.; Biacchi, A.; Hight, W.; Trautt, Z.; Hattrick-Simpers, J.; Kusne, A.; Centrone, A. The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design. npj Comput. Mater. 2020, 6, 173. [Google Scholar] [CrossRef]
- Kokalj, A. XCrySDen-a new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 1999, 17, 176–179. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Brivio, F.; Frost, J.; Skelton, J.; Jackson, A.; Weber, O.; Weller, M.; Goni, A.; Leguy, A.; Barnes, P.; Walsh, A. Lattice dynamics and vibrational spectra of the orthorhombic, tetragonal, and cubic phases of methylammonium lead iodide. Phys. Rev. B 2015, 92, 144308. [Google Scholar] [CrossRef]
- Batool, R.; Mahmood, T. A comparative study of cubic methylammonium lead iodide (CH3NH3PbI3) perovskite by using density functional theory. Mater. Today Commun. 2023, 35, 105814. [Google Scholar] [CrossRef]
- Kipkwarkwar, T.; Nyawere, P.; Maghanga, C. First-principles calculations to investigate the mechanical structure and optical properties of lead halide perovskite. Adv. Condens. Matter Phys. 2022, 2022, 1565268. [Google Scholar] [CrossRef]
- Luan, M.; Song, J.; Wei, X.; Chen, F.; Liu, J. Controllable growth of bulk cubic-phase CH3NH3PbI3 single crystal with exciting room-temperature stability. CrystEngComm 2016, 18, 5257–5261. [Google Scholar] [CrossRef]
- Weber, D. CH3NH3PbI3 a Pb (II)-system with cubic perovskite structure. Z. Naturforschung B 1978, 33, 1443–1445. [Google Scholar] [CrossRef]
- Oku, T. Crystal structures of CH3NH3PbI3 and related perovskite compounds used for solar cells. Sol.-Cells-New Approaches Rev. 2015, 1, 77–92. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Feng, J. Mechanical properties of hybrid organic-inorganic CH3NH3BX3 (B = Sn, Pb; X = Br, I) perovskites for solar cell absorbers. APL Mater. 2014, 2, 081801. [Google Scholar] [CrossRef]
- Rakita, Y.; Cohen, S.; Kedem, N.; Hodes, G.; Cahen, D. Mechanical properties of APbX3 (A = Cs or CH3NH3; X = I or Br) perovskite single crystals. MRS Commun. 2015, 5, 623–629. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Qian, J.; Bin, T. A comprehensive theoretical study of halide perovskites ABX3. Org. Electron. 2016, 37, 61–73. [Google Scholar] [CrossRef]
- Noh, J.; Im, S.; Heo, J.; Mandal, T.; Seok, S. Chemical management for colorful, efficient and stable inorganic–organic hybrid nanostructured solar cells. Nano Lett. 2013, 13, 1764–1769. [Google Scholar] [CrossRef]
- Stoumpos, C.; Malliakas, C.; Kanatzidis, M. Semiconducting tin and lead iodide perovskites with organic cations: Phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 2013, 52, 9019–9038. [Google Scholar] [CrossRef]
- Eperon, G.; Stranks, S.; Menelaou, C.; Johnston, M.; Herz, L.; Snaith, H. Formamidinium lead trihalide: A broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 2014, 7, 982–988. [Google Scholar] [CrossRef]
- Qiu, J.; Qiu, Y.; Yan, K.; Zhong, M.; Mu, C.; Yan, H.; Yang, S. All-solid-state hybrid solar cells based on a new organometal halide perovskite sensitizer and one-dimensional TiO2 nanowire arrays. Nanoscale 2013, 5, 3245–3248. [Google Scholar] [CrossRef]
- Umari, P.; Mosconi, E.; Angelis, F.D. Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 perovskites for solar cell applications. Sci. Rep. 2014, 4, 4467. [Google Scholar] [CrossRef]
- Lucarini, V.; Saarinen, J.; Peiponen, K.; Vartiainen, E. Kramers-Kronig Relations in Optical Materials Research; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 110. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; He, J.; Tian, Y. Ab initio investigations of optical properties of the high-pressure phases of ZnO. Phys. Rev. B 2005, 71, 125132. [Google Scholar] [CrossRef]
- Saleh, G. Opto-electronic properties of organic-inorganic Tin-based perovskite: A theoretical investigations. World J. Adv. Res. Rev. 2023, 17, 836–845. [Google Scholar] [CrossRef]
- Farhadi, B.; Zabihi, F.; Lugoloobi, I.; Liu, A. A hypothesis on optoelectronic behaviour of CH3NH3SnIxBr3−x perovskite: Density functional theory approach. Sol. Energy 2022, 233, 11–17. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Zhang, P.; Zhang, W. High intrinsic carrier mobility and photon absorption in the perovskite CH3NH3PbI3. Phys. Chem. Chem. Phys. 2015, 17, 11516–11520. [Google Scholar] [CrossRef]
- Kesavan, A.; Rao, A.; Ramamurthy, P. Tailoring optoelectronic properties of CH3NH3PbI3 perovskite photovoltaics using al nanoparticle modified PC61BM layer. Sol. Energy 2020, 201, 621–627. [Google Scholar] [CrossRef]
- Choudhary, K.; Bercx, M.; Jiang, J.; Pachter, R.; Lamoen, D.; Tavazza, F. Accelerated discovery of efficient solar cell materials using quantum and machine-learning methods. Chem. Mater. 2019, 31, 5900–5908. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).