Abstract
Due to the fundamental differences between the quantum world and the classical world, some phenomena, such as entanglement and wave–particle duality, only exist in the quantum realm. These peculiar phenomena cannot be demonstrated by classical means: Quantum networks, quantum cryptography, and quantum precision measurements all require quantum sources. Photons are particularly well-suited as quantum sources owing to their minimal interaction with the environment, high flight speed, and ease of interaction with current typical quantum systems. Single-photon sources include pulsed excitation of quantum dots, spontaneous parametric down-conversion, and photon blockade. Herein, we propose that the anti-Jaynes–Cummings model can induce a pronounced photon antibunching effect when subjected to intense cavity dissipation. Similar to the photon blockade caused by strong photon–photon interaction, this antibunching effect is referred to as ’dissipation-induced blockade’. Our findings indicate that the minimum decay rate of a qubit, coupled with a high decay rate for photons, is conducive to achieving strong antibunching within the system. Notably, , a characteristic of photon antibunching, is only valid under the optimal condition . Conversely, is satisfied across all parameters, indicating that is not a prerequisite for antibunching in the anti-Jaynes–Cummings model. Moreover, under the optimal conditions of the antibunching effect, the average photon number attains its peak value. Consequently, the current anti-Jaynes–Cummings model is promising for developing single-photon sources characterized by excellent purity and average photon number.
1. Introduction
The generation of nonclassical light is pivotal for advancing quantum optics and quantum information science [1,2,3,4,5]. Single-photon sources are integral to quantum information technology as prominent sources of nonclassical radiation. Consequently, they have been studied extensively over the past four decades. In fields such as quantum cryptography [6], quantum communication [7], quantum measurement [8], and quantum computing [9], numerous single-photon sources have been proposed. A single-photon source emits individual photons and, therefore, exhibits behavior that aligns with the antibunching effect, represented by . Several methods have been proposed to generate single photons, including the pulsed excitation of a two-level quantum emitter [10] and the photon blockade effect.
The Cavity QED system stands as the predominant quantum optical platform and facilitates the exploration of numerous intriguing nonlinear optical phenomena. These include but are not limited to photonic Josephson effects [11,12,13] and photon blockade. In quantum optical systems characterized by strong nonlinearity, intense light-matter interactions can lead to a nonuniform splitting of the energy spectrum. When an external driving field resonantly excites a single-photon state, the detuning between the two-photon transition frequencies and driving field increases, which, in turn, significantly suppresses the number of two-photon states. Consequently, only a single photon is permitted in the system. This behavior is called conventional or nonlinear dispersion-induced photon blockade [14]. Carmichael first proposed a photon blockade (photon antibunching) in atom-cavity systems [15]. Other platforms, such as quantum-dot cavity systems [16,17,18,19], or , nonlinearities [20,21,22], superconducting qubit systems [23,24,25], and optomechanical systems [26,27,28], have demonstrated conventional photon blockades. In quantum systems with weak nonlinearity, an unconventional photon blockade arises due to quantum interference among distinct quantum transition pathways. This type of photon blockade has been studied in various contexts, including weakly nonlinear photonic molecules [29,30], quantum-dot cavity systems [31,32], and weakly coupled nonlinear cavities via or nonlinearities [33,34]. The first experimental investigation demonstrated that photon blockade can be conducted in a trapped atom system within optical cavities [35]. Recently, photon blockade was observed in quantum-dot cavity systems [36,37]. Unconventional photon blockade has also been experimentally verified in a quantum-dot cavity [38] and superconducting resonators [39]. Moreover, other mechanisms contribute to photon antibunching, including nonlinear dissipation-induced photon [40,41,42] and quantum Zeno blockades [43].
The Jaynes–Cummings (JC) model integrates a two-level emitter with a single-mode light field and has been extensively utilized to investigate the quantum entanglement [44] and photon antibunching effect [45,46]. This model has also been employed to produce large average photon numbers and high-purity, single-photon sources by exploiting the photon blockade effect [34]. Conversely, by modulating the transition frequency of a two-level system, the anti-JC terms can be improved [47,48,49]. Here, a photon can be generated while an atom is simultaneously excited in a vacuum. Of course, due to the conservation of energy, such phenomena do not exist in the JC model. Considering the interactions between a system and its environment, the average number of photons in a cavity increases gradually, which leads to super-Poissonian quantum statistics of the field [50]. However, for a special initial state, the anti-JC model exhibits the photon antibunching effect, eliminating atomic decay and cavity leakage [51]. From an application perspective, cavity decays must be considered to enable the emission of intracavity photons for the development of a genuine single-photon source based on the anti-JC model.
This study aims to explore the quantum statistics of the light field within an anti-JC model under the consideration of atomic decay and cavity leakage. The physical configuration for the anti-JC model considered in this study can be a nanomechanical resonator coupled to a spin [52] or transmission line resonator that is connected to superconducting qubits [53]. In cases involving a bad cavity limit [54], the light field of the system exhibits a photon antibunching effect. This finding contradicts those of a previous study [50], where large dissipation of the cavity mode had a significant effect on photon blockade. In this context, it is imperative to underscore that the photon blockade phenomenon observed in the anti-JC model is primarily attributed to linear dissipation rather than nonlinear dissipation [40,41,42]. Specifically, , indicating that the light field can function as a true single-photon source. Moreover, under optimal conditions for maximum photon antibunching, a resonant enhancement in the average photon number can be observed. In summary, the blockade effect observed in this work is a novel type of unconventional photon blockade effect. In contrast to the conventional photon blockade effect, which is typically induced by strong photon–photon interaction, the anti-JC model requires only weak nonlinearity for effective photon blockade.
This paper is structured as follows: Section 2 presents the model of the system and a theoretical analysis of the quantum statistics of the cavity field based on the master equation for the steady-state density matrix. In Section 3, the statistical characteristics of the anti-JC model are investigated through numerical simulations using the second-order correlation function. Section 4 concludes the paper.
2. Model and Theoretical Analysis
As illustrated in Figure 1a, the physical model considered in this study comprises a superconducting qubit that interacts with the fundamental mode confined to the transmission line resonator [53]. The corresponding Hamiltonian can be expressed as
where is the superconducting qubit transition frequency, represents the increasing (decreasing) operator of the superconducting qubit, denotes the generation (annihilation) operators for the fundamental mode of a transmission line resonator with a frequency of , and is the coupling strength between the superconducting qubit and fundamental mode of the transmission line resonator. In the current model, the coupling strength g can be modulated over time by controlling the change in the magnetic flux [55], assuming and . Using the rotational wave approximation (with respect to the reference frequency and assuming that the counter-rotating term in the Rabi interaction becomes resonant), the Hamiltonian of the anti-JC model can be obtained from the interaction image.
where is the detuning between the transition frequency of the superconducting qubit and the frequency of the fundamental mode of the transmission line resonator, and . The Hamiltonian Equation (2) is the starting point of this study.
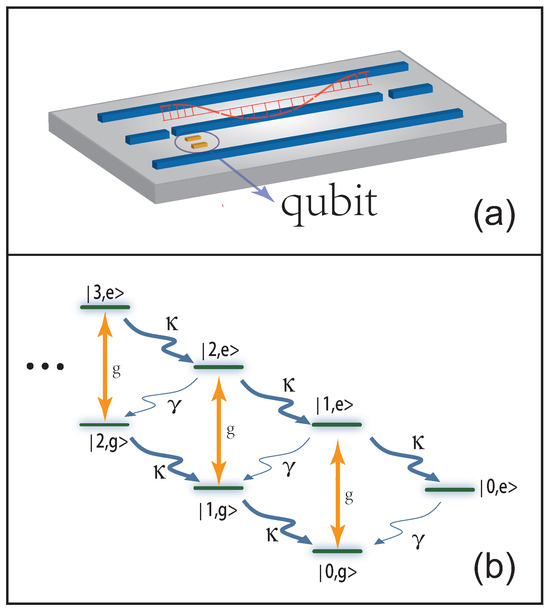
Figure 1.
(a) Schematic of a superconducting qubit interacting with the fundamental mode electromagnetic field confined within a transmission line resonator. (b) Energy level structure of the system.
In quantum optics, a zero-time-delay second-order correlation function is typically employed to characterize the photon-number distribution statistics. The state with () indicates sub-Poissonian super-Poissonian) statistics, whereas a coherent state () suggests Poissonian statistics. Conversely, the two-time, second-order correlation function can be utilized to determine whether a light field is bunched () or antibunched (). While sub-Poissonian statistics and photon antibunching represent distinct features of nonclassical light, they often coexist. As reported in reference [56], while equality is frequently accompanied by , this does not guarantee an antibunching effect. Consequently, we must evaluate the inequality rather than to determine the antibunching effect of photons.
To elucidate the quantum statistics of a light field within a transmission line resonator, the two-time second-order correlation function must be computed and examined when the system reaches a steady state. For a dissipation system with weak modulation regime [57,58], system dynamics can be simulated using the master equation for the density matrix , where the superoperator is defined as with the Lindblad operator . Herein, and are the spontaneous decay rates of the transmission line resonator and the superconducting qubit, respectively.
The zero-time delay second-order correlation function is typically expressed as . As the system reaches a steady state, this function can also be expressed as TrTr, where represents the steady state density matrix, which is determined using the master equation for the density matrix . In scenarios with weak coupling and large dissipation, the population of high-photon-number states can be neglected. Consequently, the Hilbert space can be truncated into a finite photon-number state such that . The base state vectors can then be defined as . Based on this assumption, the zero-time-delay second-order correlation function is expressed as follows:
In the bad cavity limit, , we obtain the following density matrix elements after lengthy calculations (please refer to the detailed derivation process in the Appendix A):
with . Substituting the density matrix elements [Equations (4)–(7)] into the equation for the zero-time-delay second-order delay correlation function [Equation (3)], we obtain an analytical expression for the zero-time-delay second-order correlation function,
We also obtained the average photon number as follows,
Given that is considerably smaller than , it is implied that . Consequently, the zero-time delay second-order correlation function [Equation (8)] is considerably less than one. Specifically, . This shows that under bad cavity and weak-coupling limit conditions, remains substantially less than one. When , attains its minimum value of . Therefore, the optimal sub-Poissonian distribution can be achieved using the anti-JC model with as the optimal parameter condition. As discussed in the subsequent section, this condition corresponds to the optimal parameter for strong photon antibunching. Furthermore, Equation (9) shows that the average photon number approaches the maximum value when . This suggests that a quantum light source with high purity and a large average photon number can be realized under optimal parameter conditions in the anti-JC model.
We succinctly explain the strong photon antibunching effect at in the system as illustrated by the energy level transition diagram [see Figure 1b] under bad cavity and weak modulation strength conditions. When the coupling strength is modulated by , as discussed in [49], the counter-rotating term experiences resonance enhancement. Under these conditions, one photon originates from the vacuum, and the qubit transitions from its ground state to the excited state because of the energy supplied by the external modulation of the coupling strength. In the absence of dissipation, the system oscillates between the states and , as highlighted in [48,49]. However, the dissipation alters this scenario. Cavity leakage causes photons to exit the cavity, transitioning the system from to . Additionally, the decay of the qubit triggers the transition , as depicted in Figure 1b. The modulation of the coupling excites the system from the states to , causing higher-photon states to be excited [50]. Given that , the transition probability from state to state significantly surpasses that of state , which results in a population reduction in two-/multi-photon-number states owing to the high-photon decay rate of the resonator. This forms the physical mechanism responsible for the photon antibunching or blockade observed in the anti-JC model. Because of its weak modulation strength, the average photon number is also small; this phenomenon is termed dissipation-induced photon blockade. We also observe that the average photon number approaches the maximum value at the optimal condition. Hence, it represents a conventional photon blockade in the current anti-JC model. We stress that, contrary to previous work, the conventional photon blockage is induced by the large cavity leakage, rather than the anharmonic eigen-every level structure of the system stemming from strong photon–photon interactions. This result denotes the main findings of the study.
3. Quantum Statistical Properties in the Model
In this section, we numerically evaluate the statistical properties of photons in a resonator in the anti-JC model under the assumption of a steady state. We numerically solve the homogeneous linear equation for elements of the density matrix under the normalized condition . To streamline our analysis, we rescaled the parameters to align them with the decay rate of the resonator. The numerical results are shown in Figure 2, wherein we illustrate the zero-time-delay correlation function and the average photon number as a function of detuning , using and . Figure 2a clearly shows that within the specified parameter region is accompanied by a dip around . The second-order correlation function exhibits the lowest value at . Because approaches infinity, the zero-time-delay second-order correlation function converges to a constant value of . Our findings suggest that the resonator mode exhibits a pronounced sub-Poissonian distribution across a substantial part of the parameter region. To delve deeper into the antibunching characteristics of the photons, we computed the time-delayed second-order correlation function using the quantum regression theorem [59]. Figure 2c,d show the time-delayed second-order correlation function with various detunings. At the resonant point (i.e., ), escalates consistently with an increase in the delay. However, condition is not invariably met as is not the minimum value within the specified time delay region for . From these observations, we can infer that the photons display antibunching and a sub-Poissonian distribution at . When the detuning is nonzero, the photons continue to exhibit sub-Poissonian distribution but lack antibunching. This result indicates that antibunching of the light field cannot be solely indicated by , but must rather be indicated by . Notably, we observed that at , suggesting that the proposed model functions as a true single-photon source when it operates at the optimal point. Additionally, Figure 2b shows that the average photon number resonantly attains the peak value at , as anticipated from the analytical expression determined in the previous section. The juxtaposed numerical results (solid line) of and and analytical results (denoted by a circle) in Figure 2 reveal a strong congruence, which validates the analytical results based on the assumptions of a bad cavity and weak-coupling limits.
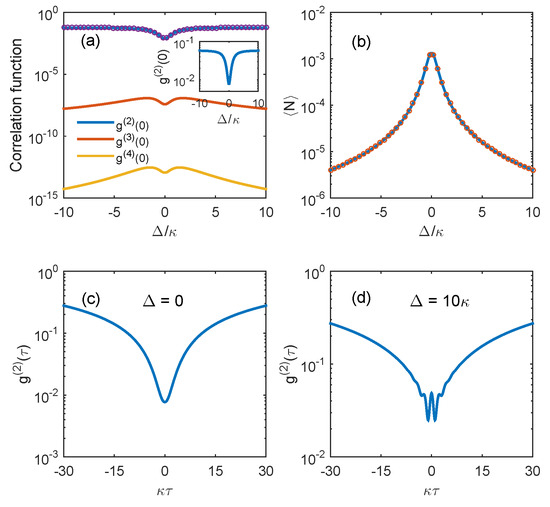
Figure 2.
(a) Zero-time delay correlation functions and (b) average photon number as a function of the resonator detuning . The other parameters are taken as , and . The solid lines represent the numerical results, and the symbols “o” denote the analytical results [based on Equations (8) and (9)]. The inset is the zero-time-delay second-order correlation function . The time-dependent second correlation function with the resonator detunings (c) and (d) .
Figure 3 shows the zero-time-delay second-order correlation function and the average photon number as functions of g for evaluating the influence of the coupling strength of the quantum light statistics. We set the detuning to its optimal value, , and the qubit decay rate at . Figure 3a shows three distinct regions characteristic of the behavior of the zero-time-delay second-order correlation function. Region (I) is characterized by where the zero-time-delay second-order correlation function remains constant at , signifying a pronounced antibunching of the light field. Region (II) spans , during which the second-order correlation function exhibits an upward trend before stabilizing with increasing g, thus suggesting a diminishing antibunching effect. Finally, region (III) corresponds to , where the zero-time-delay second-order correlation function reaches approximately , indicating that only a mild antibunching effect was observed. These observations imply that a minimal coupling strength is essential for achieving a strong antibunching effect or enhanced pure single-photon source. These analytical findings are consistent with the numerical values derived from the zero-time-delay second-order correlation function Equation (8), revealing that in the weak-coupling limit, ; by contrast, in the strong coupling limit, . On the other hand, the trajectory of the average photon number diverges from that of the second-order correlation function with varying coupling strength. As depicted in Figure 3b, the logarithmic average photon number of the light field increases linearly at , whereas the variation in the average photon number at tends toward stability. Comparing Figure 3a,b, we can conclude that the average photon number is relatively low in regions where the photon antibunching is strong. However, when , represented by the turning point of region (i) and region (ii) in Figure 3a, the average photon number can reach a maximum value while the photon antibunching is maintained at its optimal value.
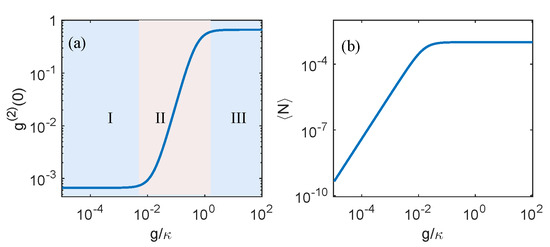
Figure 3.
(a) Zero-time delay second-order correlation and (b) average photon number as a function of the coupling strength g. I, II and III denote the different regions of zero-time delay second-order correlation. The other parameters are: , and .
Using Figure 4, we delve deeper into the correlation between the zero-time-delay second-order correlation function and average photon number in relation to the qubit decay rate under optimal detuning conditions. As depicted in Figure 4, an apparent increase in is observed with an increase in the qubit decay rate . Notably, for modest coupling strengths, such as , exhibits a nearly linear dependence on the qubit decay rate within the weak atomic decay regime. This observation aligns with the analytical prediction . However, when larger coupling strengths are considered, the zero-time-delay second-order correlation function deviates from the linear relationship with the qubit decay rate . Consequently, a low coupling strength and qubit decay rate contribute to enhanced photon antibunching. This behavior can be elucidated by considering that a small value can suppress the spontaneous decay of single-photon states , causing additional reduction in the population at higher-photon-number states. By contrast, for larger coupling strengths, the average photon number consistently increases with the qubit decay rate . Evidently, the combination of lower coupling strengths and moderate qubit decay rates is advantageous for producing high-purity and bright single-photon sources.
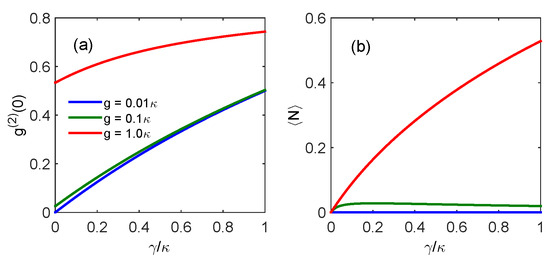
Figure 4.
(a) Zero-time delay second-order correlation and (b) average photon number as a function of the spontaneous decay rate of the superconducting qubit for , and . The other parameters are set to and .
Finally, we explore the relationship between the resonator decay rate and the zero-time-delay second-order correlation function and average photon number. As shown in Figure 5a, for a weak-coupling strength (), the second-order correlation function diminishes as the resonator decay rate increases, indicative of a transitioning from bunching to antibunching in a light field. When the resonator decay rate surpasses that of the qubit, the light field exhibits pronounced antibunching. Notably, for strong coupling strengths, such as , the small resonator decay rate results in a coherent light field distribution, as indicated by . Conversely, the average photon number decreases consistently with an increase in the resonator decay rates across all coupling strengths. This trend can be elucidated by analyzing the energy level diagram (Figure 1b). The likelihood of state decaying to increases with the resonator decay rate, thus leading to an increased propensity for multiphoton states (). Consequently, both the zero-time-delay second-order correlation function and the average photon number are amplified with reduced resonator decay rates.
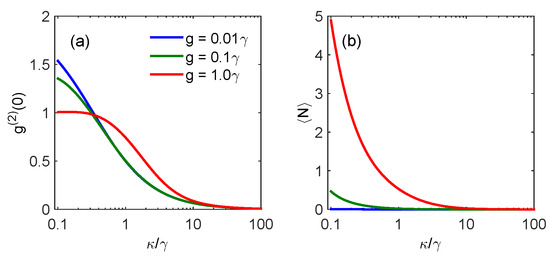
Figure 5.
(a) Zero-time delay second-order correlation function and (b) average photon number as a function of the cavity decay rate at different coupling strengths , and . The other parameters are and .
4. Conclusions
In this study, we explored the photon antibunching effect within the context of the anti-JC model. Assuming a poor cavity and weak-coupling modulation, we analytically derived both the zero-time-delay second-order correlation function and the average photon number of the light field by evaluating the master equation of the density matrix. Subsequently, we established optimal parameters to achieve pronounced photon antibunching and offered a physical interpretation of this phenomenon grounded in the energy level diagram of the system. In contrast to the conventional photon blockade induced by an anharmonic eigen-energy level structure of systems in a strong nonlinear quantum optics system, the large linear dissipation of the cavity mode contributes to the photon blockade in this work. Our results indicate that both the minimal coupling strength coupled with the qubit decay rate and the extensive decay rate of the resonators can facilitate enhanced photon antibunching. Notably, when the system operated under optimal parameter conditions, it exhibited maximal antibunching and peak average photon numbers. Based on these findings, we believe that the photon blockade effect appearing in this work is a new type of traditional photon blockade effect, named dissipation-induced photon blockade. Since the implementation of the photon blockade effect in the anti-JC model does not require strong coupling and the generated photon flux has a large average photon number and good purity, it is superior to the general scheme for preparing single-photon sources based on conventional/unconventional photon blocking effect.
Author Contributions
Conceptualization, Z.D. and B.F.; methodology, Z.D.; investigation, B.H. and C.L.; writing—original draft preparation, B.H.; writing—review and editing, Z.D. and B.F.; project administration, Z.D.; funding acquisition, Z.D. and B.F. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (grant numbers 12364046, and 12364047), and by the Major Discipline Academic and Technical Leaders Training Program in Jiangxi Province (grant number 20204BCJ23026).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data can be accessed upon request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
In this section, we derive the Hamiltonian of the anti-JC model. The Hamiltonian of the system is ,
With the unitary transformation, , we can obtain the Hamiltonian,
That is given by
where .
We assume that the coupling strength is modulated over time, and Equation (A3) is
Assuming that , we maintain the counter-rotational term
In the truncated photon-number Hilbert space (), the base vectors are , . The Hamiltonian of the system can be expressed as
The corresponding density matrix is expressed as
By substituting the Hamiltonian [Equation (A1)] and density matrix [Equation (A2)] into the steady-state master equation for the density matrix , we obtain a coupled equation set of matrix elements as follows,
From the expression for the second-order correlation function
We only need to calculate the diagonal elements to evaluate the second-order correlation functions. Based on the bad cavity and weak-coupling limit assumption, the diagonal elements obey the following relation, , , , . Finally, we obtain the approximate expression for the diagonal elements iteratively, as follows,
where . If we assume that the decay rate of the spin is smaller than that of the resonator, then .
Appendix B
In this section, we will present the numerical method to solve the homogeneous linear equations for the elements of the density matrix . with the normalized condition for the density matrix, i.e., . Since is in matrix form in the equation, it needs to be vectorized into column vector form before solving this homogeneous linear system. According to the ref. Assuming is density matrix, the vectorization procedure for the density matrix can be performed as follows:
where denotes the transpose of the matrix O. Here, we employ the relation , the Lindblad superoperator in matrix form can be rewritten as
where I is the identity matrix, ⊗ denotes the Kronecker product, and A is matrices and represents the operators for a and . According to these relations, the whole Lindblad superoperator L can be written in a linear matrix form .
To build the matrix corresponding to L acting on a truncated Fock-state space, we write the annihilation operator a as a matrix with -dimension.
and the decreasing operator of the superconducting qubit with 2-dimension
where is the maximal photon number and .
To directly operate on the -dimensional vector space, the operator matrices for the light field and atom are constructed as
where and are the and identity matrices. This definition allows the Hamiltonian to be calculated using simple matrix multiplications instead of as the Kronecker product on the truncated Fock-state space.
References
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dusek, M.; Lutkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46. [Google Scholar] [CrossRef] [PubMed]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Rao, V.S.C.M.; Hughes, S. On chip single photon sources using planar photonic crystals and single quantum dots. Laser Photon. Rev. 2009, 4, 499. [Google Scholar] [CrossRef]
- Pironio, S.; Acín, A.; Brunner, N.; Gisin, N.; Massar, S.; Scarani, V. Device-independent quantum key distribution secure against collective attacks. New J. Phys. 2009, 11, 045021. [Google Scholar] [CrossRef]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef]
- Pezze, L.; Smerzi, A. Mach-Zehnder interferometry at the Heisenberg limit with coherent and squeezed-vacuum light. Phys. Rev. Lett. 2008, 100, 073601. [Google Scholar] [CrossRef] [PubMed]
- Bennerr, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar]
- Ding, X.; He, Y.; Duan, Z.-C.; Gregersen, N.; Chen, M.-C.; Unsleber, S.; Maier, S.; Schneider, C.; Kamp, M.; Hofling, S.; et al. On-demand single photons with high extraction efficiency and near-unity indistinguishability from a resonantly driven quantum dot in a micropillar. Phys. Rev. Lett. 2016, 116, 020401. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Yu, X.-L.; Li, Z.B.; Liu, W.M. Non-Abelian Josephson Effect between Two F = 2 Spinor Bose-Einstein Condensates in Double Optical Traps. Phys. Rev. Lett. 2009, 102, 185301. [Google Scholar] [CrossRef] [PubMed]
- Ji, A.-C.; Sun, Q.; Xie, X.C.; Liu, W.M. Josephson Effect for Photons in Two Weakly Linked Microcavities. Phys. Rev. Lett. 2009, 102, 023602. [Google Scholar] [CrossRef] [PubMed]
- Ji, A.-C.; Xie, X.C.; Liu, W.M. Quantum Magnetic Dynamics of Polarized Light in Arrays of Microcavities. Phys. Rev. Lett. 2007, 99, 183602. [Google Scholar] [CrossRef] [PubMed]
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299. [Google Scholar] [CrossRef]
- Carmichael, H.J. Photon antibunching and squeezing for a single atom in a resonant cavity. Phys. Rev. Lett. 1985, 55, 2790. [Google Scholar] [CrossRef] [PubMed]
- Faraon, A.; Fushman, I.; Englund, D.; Stoltz, N.; Petroff, P.; Vuckovic, J. Coherent generation of non-classical light on a chip via photon-induced tunnelling and blockade. Nat. Phys. 2008, 4, 859. [Google Scholar] [CrossRef]
- Tang, J.; Geng, W.D.; Xu, X.L. Quantum interference induced photon blockade in a coupled single quantum dot-cavity system. Sci. Rep. 2015, 5, 9252. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, A.; Bajcsy, M.; Rundquist, A.; Vuvckovic, J. Loss-enabled sub-Poissonian light generation in a bimodal nanocavity. Phys. Rev. Lett. 2012, 108, 183601. [Google Scholar] [CrossRef] [PubMed]
- Verger, A.; Ciuti, C.; Carusotto, I. Polariton quantum blockade in a photonic dot. Phys. Rev. B 2006, 73, 193306. [Google Scholar] [CrossRef]
- Majumdar, A.; Gerace, D. Single-photon blockade in doubly resonant nanocavities with second-order nonlinearity. Phys. Rev. B 2013, 87, 235319. [Google Scholar] [CrossRef]
- Ferretti, S.; Gerace, D. Single-photon nonlinear optics with Kerr-type nanostructured materials. Phys. Rev. B 2012, 85, 033303. [Google Scholar] [CrossRef]
- Imamoglu, A.; Schmidt, H.; Woods, G.; Deutsch, M. Strongly interacting photons in a nonlinear cavity. Phys. Rev. Lett. 1997, 79, 1467. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Srinivasan, S.J.; Schmidt, S.; Spietz, L.; Aumentado, J.; Tureci, H.E.; Houck, A.A. Dispersive photon blockade in a superconducting circuit. Phys. Rev. Lett. 2011, 107, 053602. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Xu, X.W.; Miranowicz, A.; Nori, F. From blockade to transparency: Controllable photon transmission through a circuit-QED system. Phys. Rev. A 2014, 89, 043818. [Google Scholar] [CrossRef]
- Miranowicz, A.; Bajer, J.; Paprzycka, M.; Liu, Y.X.; Zagoskin, A.M.; Nori, F. State-dependent photon blockade via quantum-reservoir engineering. Phys. Rev. A 2014, 90, 033831. [Google Scholar] [CrossRef]
- Xu, X.W.; Li, Y.J.; Liu, Y.X. Photon-induced tunneling in optomechanical systems. Phys. Rev. A 2013, 87, 025803. [Google Scholar] [CrossRef]
- Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 2011, 107, 063601. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.Q.; Nori, F. Photon blockade in quadratically coupled optomechanical systems. Phys. Rev. A 2013, 88, 023853. [Google Scholar] [CrossRef]
- Bamba, M.; Imamoglu, A.; Carusotto, I.; Ciuti, C. Origin of strong photon antibunching in weakly nonlinear photonic molecules. Phys. Rev. A 2011, 83, 021802. [Google Scholar] [CrossRef]
- Flayac, H.; Savona, V. Unconventional photon blockade. Phys. Rev. A. 2017, 96, 053810. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.Y.; Liu, Y.M.; Peng, Y.W. Optimal photon antibunching in a quantum-dotCbimodal-cavity system. Phys. Rev. A 2014, 89, 043832. [Google Scholar] [CrossRef]
- Liang, X.Y.; Duan, Z.L.; Guo, Q.; Liu, C.J.; Guan, S.G.; Ren, Y. Antibunching effect of photons in a two-level emitter-cavity system. Phys. Rev. A 2019, 100, 063834. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Shen, H.Z.; Yi, X.X. Unconventional photon blockade with second-order nonlinearity. Phys. Rev. A 2015, 92, 023838. [Google Scholar] [CrossRef]
- Sarma, B.; Sarma, A.K. Quantum-interference-assisted photon blockade in a cavity via parametric interactions. Phys. Rev. A 2017, 96, 053827. [Google Scholar] [CrossRef]
- Birnbaum, K.M.; Boca, A.; Miller, R.; Boozer, A.D.; Northup, T.E.; Kimble, H.J. Photon blockade in an optical cavity with one trapped atom. Nature 2005, 436, 87. [Google Scholar] [CrossRef] [PubMed]
- Reinhard, A.; Volz, T.; Winger, M.; Badolato, A.; Hennessy, K.J.; Hu, E.L.; Imamoglu, A. Strongly correlated photons on a chip. Nat. Photonics 2012, 6, 93–96. [Google Scholar] [CrossRef]
- Volz, T.; Reinhard, A.; Winger, M.; Badolato, A.; Hennessy, K.J.; Hu, E.L.; Imamoglu, A. Ultrafast all-optical switching by single photons. Nat. Photonics 2012, 6, 605–609. [Google Scholar] [CrossRef]
- Snijders, H.J.; Frey, J.A.; Norman, J.; Flayac, H.; Savona, V.; Gossard, A.C.; Bowers, J.E.; van Exter, M.P.; Bouwmeester, D.; Lofler, W. Observation of the unconventional photon blockade. Phys. Rev. Lett. 2018, 121, 043601. [Google Scholar] [CrossRef] [PubMed]
- Vaneph, C.; Morvan, A.; Aiello, G.; Fechant, M.; Aprili, M.; Gabelli, J.; Esteve, J. Observation of the unconventional photon blockade in the microwave domain. Phys. Rev. Lett. 2018, 121, 043602. [Google Scholar] [CrossRef]
- Zhang, H.L.; Duan, Z.-L. Photon blockade in the Jaynes-Cummings model with two-photon dissipation. Opt. Express 2023, 31, 22580–22593. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Tang, J.-S.; Xia, K.Y. Nonlinear dissipation-induced photon blockade. Phys. Rev. A 2022, 106, 063707. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Kumar, P. Antibunched emission of photon pairs via quantum zeno blockade. Phys. Rev. Lett. 2012, 108, 030502. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.-Z.; Huang, Y.-P.; Kumar, P. Photonic nonlinearities via quantum zeno blockade. Phys. Rev. Lett. 2013, 110, 223901. [Google Scholar] [CrossRef] [PubMed]
- Qiang, W.-C.; Sun, G.-H.; Dong, Q.; Camacho-Nieto, O.; Dong, S.-H. Concurrence of three JaynesCCummings systems. Quantum Inf. Process 2018, 17, 90. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89. [Google Scholar] [CrossRef]
- Del Valle, E.; Laussy, F.P.; Tejedor, C. Luminescence spectra of quantum dots in microcavities. II. Fermions. Phys. Rev. B 2009, 79, 235326. [Google Scholar] [CrossRef]
- Huang, J.-F.; Liao, J.-Q.; Tian, L.; Kuang, L.-M. Manipulating counter-rotating interactions in the quantum Rabi model via modulation of the transition frequency of the two-level system. Phys. Rev. A 2017, 96, 043849. [Google Scholar] [CrossRef]
- Dodonov, A.V. Photon creation from vacuum and interactions engineering in nonstationary circuit QED. J. Phys. Conf. Ser. 2009, 161, 012029. [Google Scholar] [CrossRef]
- Liberato, S.D.; Gerace, D.; Carusotto, I.; Ciuti, C. Extracavity quantum vacuum radiation from a single qubit. Phys. Rev. A 2009, 80, 053810. [Google Scholar] [CrossRef]
- Werlang, T.; Dodonov, A.V.; Duzzioni, E.I.; Villas-Boas, C.J. Rabi model beyond the rotating-wave approximation: Generation of photons from vacuum through decoherence. Phys. Rev. A 2008, 78, 053805. [Google Scholar] [CrossRef]
- Mayero, C. Photon statistics and quantum field entropy in the anti-jaynes-cummings model: A comparison with the jaynes-cummings interaction. Quantum Inf. Process. 2023, 22, 182. [Google Scholar] [CrossRef]
- Xue, F.; Zhong, L.; Li, Y.; Sun, C.P. Analogue of cavity quantum electrodynamics for coupling between spin and a nanomechanical resonator: Dynamic squeezing and coherent manipulations. Phys. Rev. B 2007, 75, 033407. [Google Scholar] [CrossRef]
- Felicetti, S.; Sabin, C.; Fuentes, I.; Lamata, L.; Romero, G.; Solano, E. Relativistic motion with superconducting qubits. Phys. Rev. B 2015, 92, 064501. [Google Scholar] [CrossRef]
- Tian, L. Circuit QED and sudden phase switching in a superconducting qubit array. Phys. Rev. Lett. 2010, 105, 167001. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Chen, Y.; Sank, D.; O’Malley, P.J.J.; White, T.C.; Barends, R.; Kelly, J.; Lucero, E.; Mariantoni, M.; Megrant, A.; et al. Catch and release of microwave photon states. Phys. Rev. Lett. 2013, 110, 107001. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.T.; Mandel, L. Photon-antibunching and sub-Poissonian photon statistics. Phys. Rev. A 1990, 41, 475. [Google Scholar] [CrossRef] [PubMed]
- Veloso, D.S.; Dodonov, A.V. Prospects for observing dynamical and anti-dynamical Casimir effects in circuit QED due to fast modulation of qubit parameters. J. Phys. B 2015, 48, 165503. [Google Scholar] [CrossRef]
- Dodonov, A.V.; Valente, D.; Werlang, T. Antidynamical Casimir effect as a resource for work extraction. Phys. Rev. A 2017, 96, 012501. [Google Scholar] [CrossRef]
- Gardiner, C.; Zoller, P. Quantum Noise; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).