Mode Shift of a Thin-Film F-P Cavity Grown with ICPCVD
Abstract
1. Introduction
2. Basic Theory and Experiment
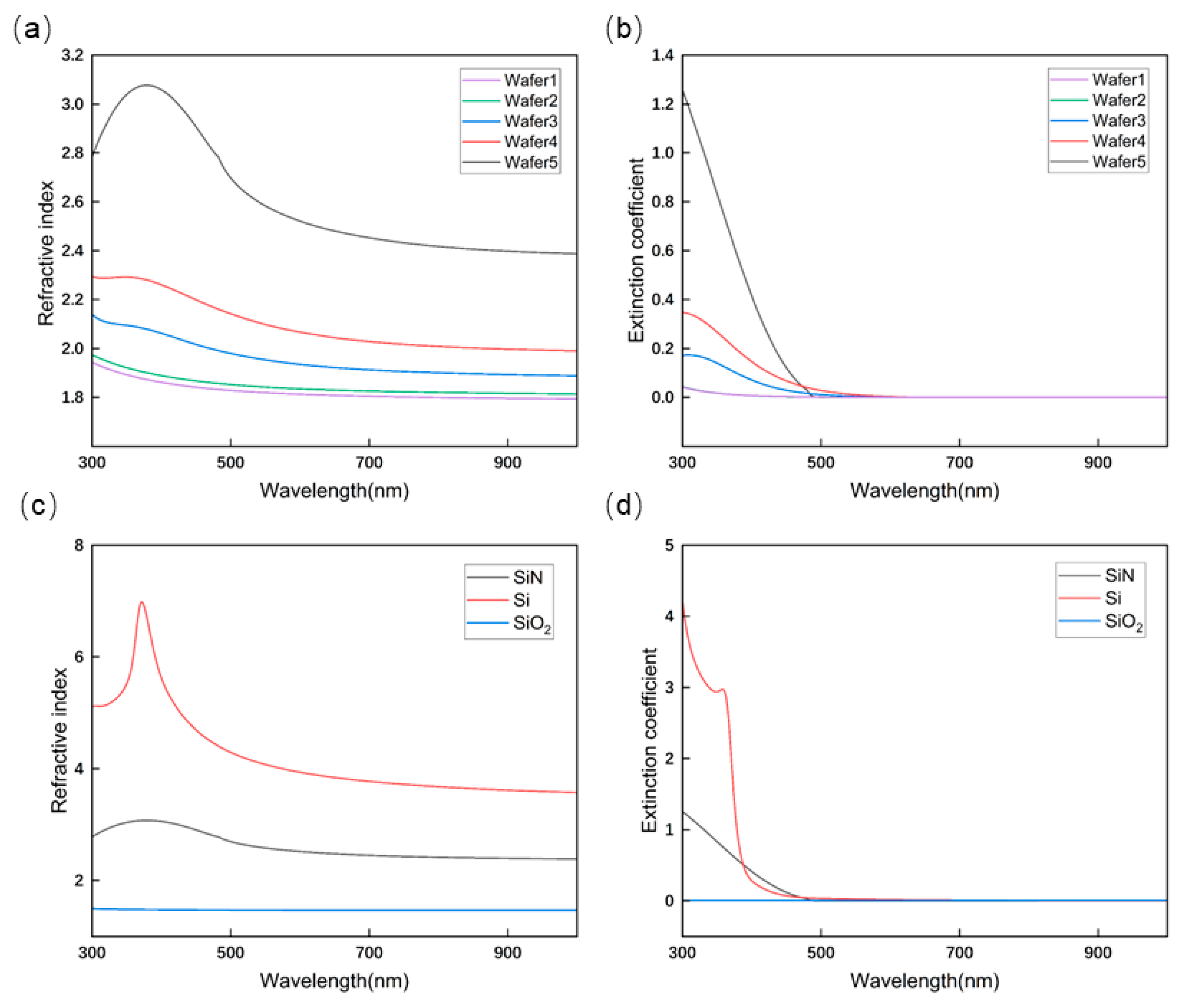
2.1. Analysis of Film Thickness
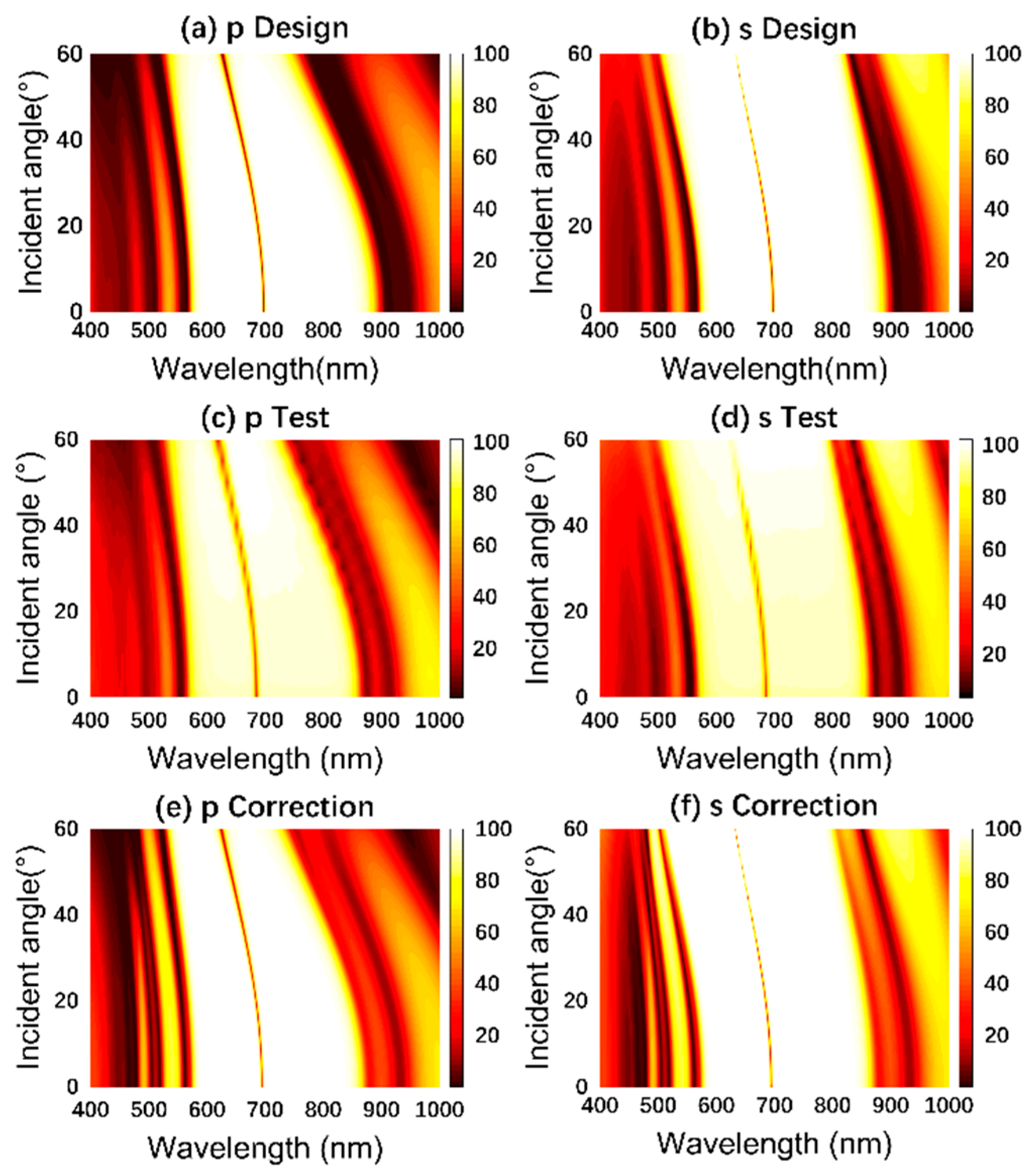
2.2. Oblique Incidence on Dielectric Film Surface
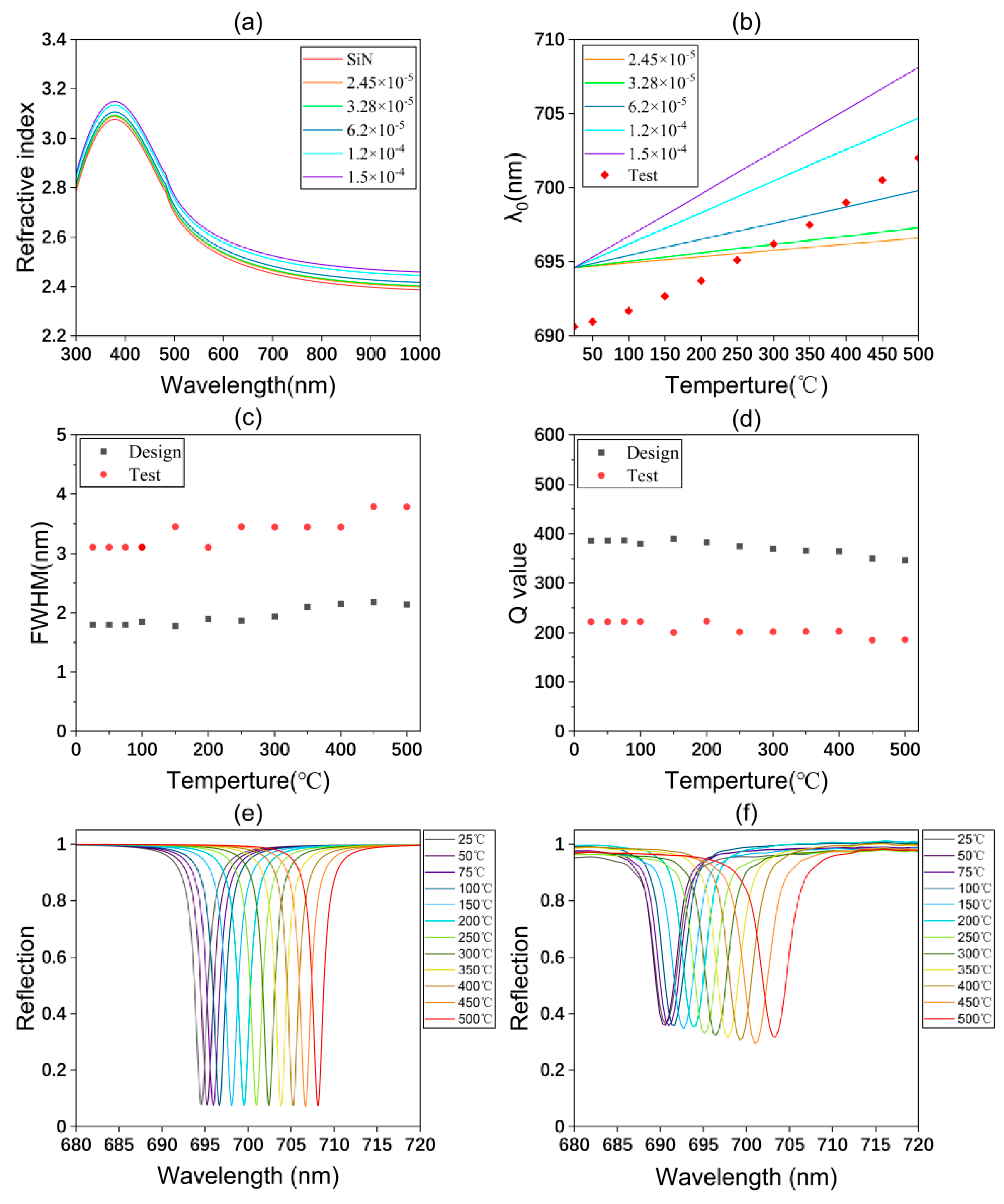
2.3. Temperature Coefficient of Refractive Index
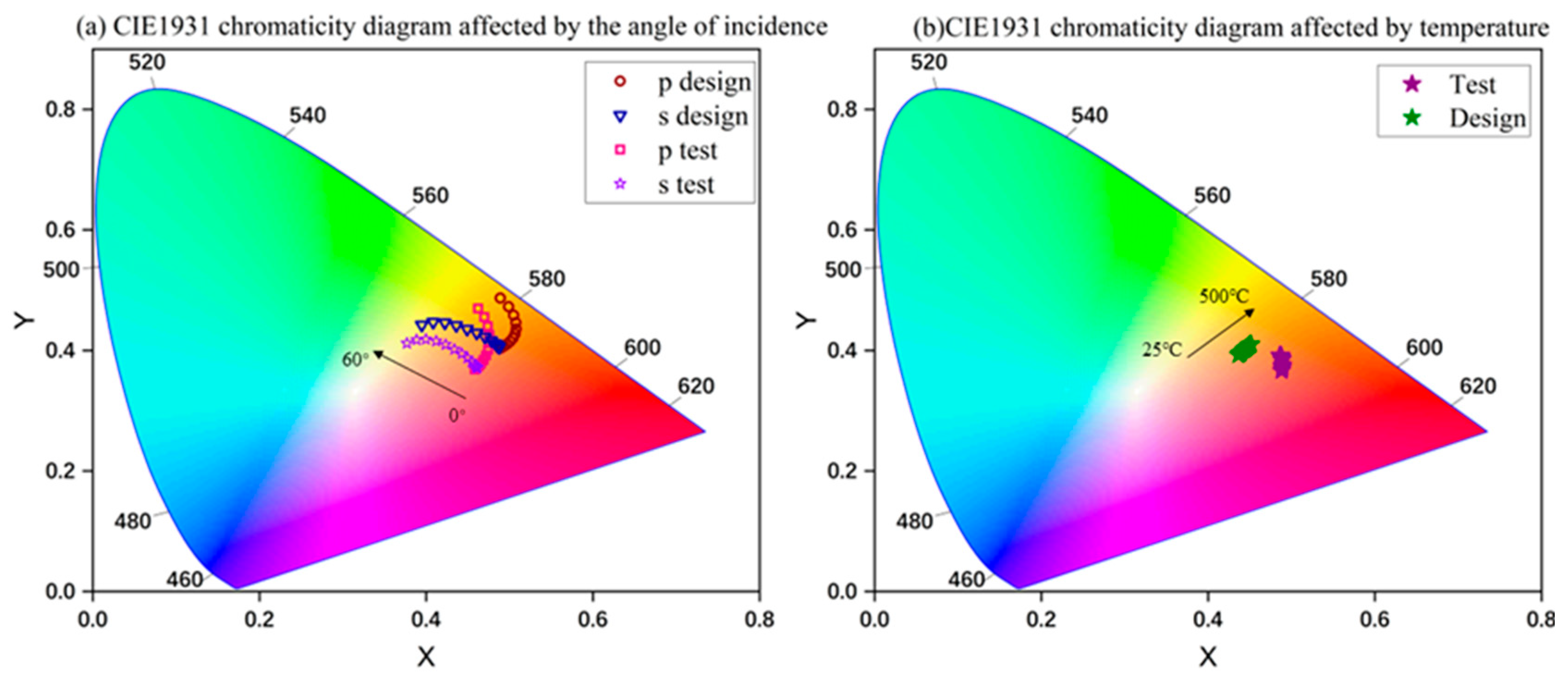
2.4. Colorimetry
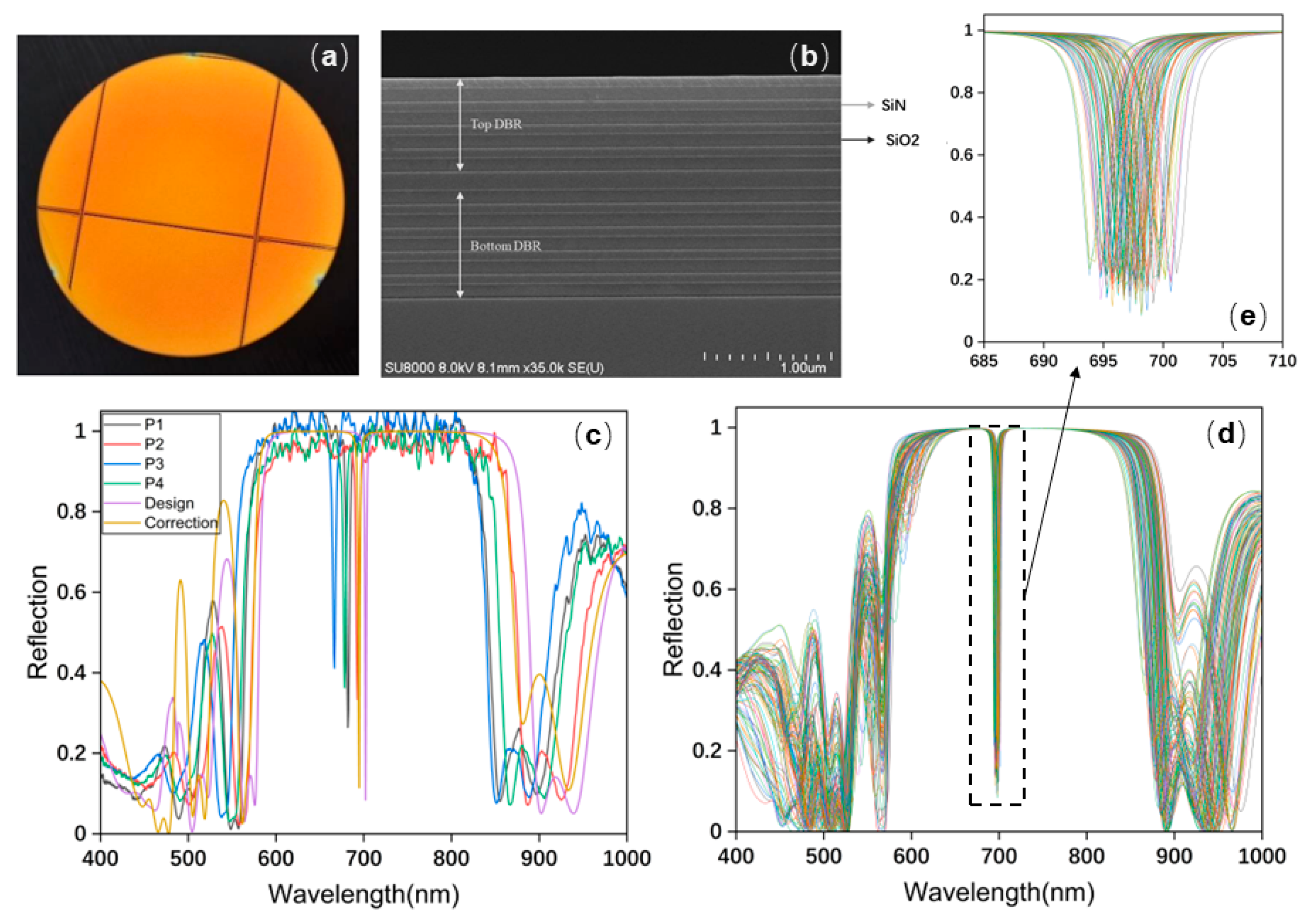
2.5. Experiment
3. Result and Discussion
3.1. Film Thickness Analysis
3.2. The Influence of Incident Angle Changes
3.3. The Influence of Temperature Changes
3.4. Chromatic Spatial Characterisation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Han, J.H.; Kim, D.Y.; Kim, D.; Choi, K.C. Highly Conductive and Flexible Color Filter Electrode Using Multilayer Film Structure. Sci. Rep. 2016, 6, 7. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.Y.; Butun, S.; Aydin, K. Large-Area, Lithography-Free Super Absorbers and Color Filters at Visible Frequencies Using Ultrathin Metallic Films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- Lin, Y.S.; Ho, C.P.; Koh, K.H.; Lee, C. Fabry-Perot Filter Using Grating Structures. Opt. Lett. 2013, 38, 902–904. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhai, L.Y.; Xu, J.; Wu, Y.M. Design and Fabrication of Independent-Cavity Fp Tunable Filter. Opt. Commun. 2013, 297, 154–164. [Google Scholar] [CrossRef]
- Meng, F.; Yu, H.; Zhou, X.; Wang, M.; Zhang, Y.; Yang, W.; Pan, J. Low Fabrication Cost Wavelength Tunable Wg-Fp Hybrid-Cavity Laser Working over 1.7 Μ M; IOP Publishing Ltd.: Bristol, UK, 2022. [Google Scholar]
- Yin, D.; Yu, S.; Fang, Z.; Huang, Q.; Gao, L.; Wang, Z.; Liu, J.; Huang, T.; Zhang, H.; Wang, M.; et al. On-Chip Electro-Optically Tunable Fabry-Perot Cavity Laser on Erbium Doped Thin Film Lithium Niobate. Opt. Mater. Express 2023, 13, 2644–2650. [Google Scholar] [CrossRef]
- Chowdhury, H.R.; Han, M. Fiber Optic Temperature Sensor System Using Air-Filled Fabry–Pérot Cavity with Variable Pressure. Sensors 2023, 23, 3302. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Chen, Y.; Zhang, Q.; Tang, Q.; Zhu, Y.; Yu, Y.; Du, C.; Ruan, S. High-Sensitivity Temperature Sensor Based on Fiber Fabry-Pérot Interferometer with UV Glue-Filled Hollow Capillary Fiber. Sensors 2023, 23, 7687. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Zou, M.; Zhao, C.; Jiang, Y.; Chen, R.; Xu, Z.; Yang, C.; Wang, X.; Dong, B.; Wang, Y.; et al. Fabry-Perot Interferometer Based on a Fiber-Tip Fixed-Supported Bridge for Fast Glucose Concentration Measurement. Biosensors 2022, 12, 391. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Gao, W.; Liu, B.; Cao, X.; Tao, T.; Xie, Z.; Zhao, H.; Chen, D.; Ping, H.; Zhang, R. Design and Fabrication of UV Band-Pass Filters Based on SiO2/Si3N4 Dielectric Distributed Bragg Reflectors. Appl. Surf. Sci. 2016, 364, 886–891. [Google Scholar] [CrossRef]
- Ailing, Z.; Heliang, L.; Demokan, M.S.; Tam, H.Y. Stable and Broad Bandwidth Multiwavelength Fiber Ring Laser Incorporating a Highly Nonlinear Photonic Crystal Fiber. IEEE Photonics Technol. Lett. 2005, 17, 2535–2537. [Google Scholar] [CrossRef][Green Version]
- Chen, H.; Liang, Y. Analysis of the Tunable Asymmetric Fiber F-P Cavity for Fiber Strain Sensor Edge-Filter Demodulation. Photonic Sens. 2014, 4, 338–343. [Google Scholar] [CrossRef]
- Lee, J.W.; Mackenzie, K.D.; Johnson, D.; Sasserath, J.N.; Pearton, S.J.; Ren, F. Low Temperature Silicon Nitride and Silicon Dioxide Film Processing by Inductively Coupled Plasma Chemical Vapor Deposition. J. Electrochem. Soc. 2000, 147, 1481–1486. [Google Scholar] [CrossRef]
- Shi, M.; Shao, X.M.; Tang, H.J.; Li, T.; Wang, Y.J.; Li, X.; Gong, H.M. Inductively Coupled Plasma Chemical Vapor Deposition Silicon Nitride for Passivation of In0.83Ga0.17As Photodiodes. Infrared Phys. Technol. 2014, 67, 197–201. [Google Scholar] [CrossRef]
- Macleod, H.A. Thin-Film Optical Filters; Institute of Physics Pub.: Bristol, UK, 2001. [Google Scholar]
- Habermehl, S. Coefficient of Thermal Expansion and Biaxial Young’s Modulus in Si-Rich Silicon Nitride Thin Films. J. Vac. Sci. Technol. A 2018, 36, 8. [Google Scholar] [CrossRef]
- Hu, D.; Huang, Q.a.; Li, W. Structure for Electrical Measurement of the Thermal Expansion Coefficient of Polysilicon Thin Films. Chin. J. Semicond. 2008, 29, 2018–2022. [Google Scholar]
- Tada, H.; Kumpel, A.E.; Lathrop, R.E.; Slanina, J.B.; Nieva, P.; Zavracky, P.; Miaoulis, I.N.; Wong, P.Y. Thermal Expansion Coefficient of Polycrystalline Silicon and Silicon Dioxide Thin Films at High Temperatures. J. Appl. Phys. 2000, 87, 4189–4193. [Google Scholar] [CrossRef]
- Arbabi, A.; Goddard, L.L. Measurements of the Refractive Indices and Thermo-Optic Coefficients of Si3N4 and SiOx Using Microring Resonances. Opt. Lett. 2013, 38, 3878–3881. [Google Scholar] [CrossRef]
- Li, B.; Zhang, S.; Xie, P.; Zhang, L.; Liu, D.; Zhang, F. Improving Low-Temperature Performance of Infrared Thin-Film Interference Filters Utilizing Temperature Dependence of Refractive Index of Pb1−xGexTe. In Proceedings of the Conference on Infrared Components and Their Applications, Beijing, China, 8–11 November 2004. [Google Scholar]
- Yang, X.Y.; Li, H.; You, L.X.; Zhang, W.J.; Zhang, L.; Wang, Z.; Xie, X.M. Temperature Dependence of an Optical Narrow-Bandpass Filter at 1.5 μm. Appl. Opt. 2015, 54, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Palik, E.D. (Ed.) Chapter 3—Thermo-Optic Coefficients. In Handbook of Optical Constants of Solids; Academic Press: Burlington, MA, USA, 1997; pp. 115–261. [Google Scholar]
- Mondal, P.; Venkatachalam, P.; Singh, R.; Shelwade, S.; Sushma, G.; Selvaraja, S.K. Linear and Nonlinear Characterization of a Broadband Integrated Si-Rich Silicon Nitride Racetrack Ring Resonator for on-Chip Applications. Appl. Opt. 2023, 62, 3703–3709. [Google Scholar] [CrossRef]
- Zanatta, A.R.; Gallo, I.B. The Thermo Optic Coefficient of Amorphous SiN Films in the near-Infrared and Visible Regions and Its Experimental Determination. Appl. Phys. Express 2013, 6, 4. [Google Scholar] [CrossRef]
- Pruiti, N.G.; Klitis, C.; Gough, C.; May, S.; Sorel, M. Thermo-Optic Coefficient of PECVD Silicon-Rich Silicon Nitride. Opt. Lett. 2020, 45, 6242–6245. [Google Scholar] [CrossRef] [PubMed]
- Broadbent, A.D. A Critical Review of the Development of the CIE1931 RGB Color-Matching Functions. Color Res. Appl. 2004, 29, 267–272. [Google Scholar] [CrossRef]
- Smith, T.; Guild, J. The CIE Colorimetric Standards and Their Use. Trans. Opt. Soc. 1931, 33, 73. [Google Scholar] [CrossRef]
- Price, J.; Hung, P.Y.; Rhoad, T.; Foran, B.; Diebold, A.C. Spectroscopic Ellipsometry Characterization of HfxSiyOz Films Using the Cody-Lorentz Parameterized Model. Appl. Phys. Lett. 2004, 85, 1701–1703. [Google Scholar] [CrossRef]
- Zhang, P.; Li, C.; Zhang, M.; Chen, T.; Wang, D.S. Optical Constants of Thin Films of Silicon Oxycarbide Using the Transmission Spectrum. Spectr. Lett. 2015, 48, 367–370. [Google Scholar]
| Deposition Material | SiN | SiO2 |
|---|---|---|
| SiH4 gas flow/cm3 min−1 | 55 | 20 |
| N2 gas flow/cm3 min−1 | 30 | 0 |
| N2O gas flow/cm3 min−1 | 0 | 40 |
| Ar gas flow/cm3 min−1 | 200 | 200 |
| Reaction pressure/mTorr | 16 | 16 |
| Reaction temperature/°C | 80 | 80 |
| RF power/W | 300 | 300 |
| No. of Layers | Materials (from Top to Bottom) | Simulation Thickness (nm) | Fabrication Thickness (nm) | Percentage Deviation |
|---|---|---|---|---|
| 1 | SiN/SiO2 | 70/118 | 81/102 | +15.7%/−13.6% |
| 2 | SiN/SiO2 | 70/118 | 81/109 | +15.7%/−7.6% |
| 3 | SiN/SiO2 | 70/1181 | 78/106 | +11.4%/−10.2% |
| 4 | SiN/SiO2 | 70/118 | 78/107 | +11.4%/−9.3% |
| 5 | SiN/SiO2 | 140/118 | 148/107 | +5.7%/−9.3% |
| 6 | SiN/SiO2 | 70/118 | 77/101 | +10%/−14.4% |
| 7 | SiN/SiO2 | 70/118 | 79/102 | +12.8%/−13.6% |
| 8 | SiN/SiO2 | 70/118 | 78/108 | +11.4%/−8.4% |
| 9 | SiN/SiO2 | 70/118 | 78/104 | +11.4%/−11.8% |
| Reflection Spectra | Polarization | (nm) | Transmission Peak | ||
|---|---|---|---|---|---|
| 0° | 40° | 0° | 40° | ||
| Measured spectra | p | 685 | 650 | 70.6% | 62.4% |
| s | 685 | 652 | 70.6% | 61.7% | |
| Simulated spectra of the designed structure | p | 698 | 665 | 93.1% | 91% |
| s | 698 | 664 | 93.1% | 90.3% | |
| Simulated spectra with actual thickness | p | 690 | 665 | 89.1% | 73.1% |
| s | 690 | 658 | 89.1% | 71.4% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Gao, Z.; Duan, J.; Li, W.; Liu, B.; Chen, C. Mode Shift of a Thin-Film F-P Cavity Grown with ICPCVD. Photonics 2024, 11, 329. https://doi.org/10.3390/photonics11040329
Zhang Y, Gao Z, Duan J, Li W, Liu B, Chen C. Mode Shift of a Thin-Film F-P Cavity Grown with ICPCVD. Photonics. 2024; 11(4):329. https://doi.org/10.3390/photonics11040329
Chicago/Turabian StyleZhang, Yuheng, Zhuo Gao, Jian Duan, Wenbing Li, Bo Liu, and Chang Chen. 2024. "Mode Shift of a Thin-Film F-P Cavity Grown with ICPCVD" Photonics 11, no. 4: 329. https://doi.org/10.3390/photonics11040329
APA StyleZhang, Y., Gao, Z., Duan, J., Li, W., Liu, B., & Chen, C. (2024). Mode Shift of a Thin-Film F-P Cavity Grown with ICPCVD. Photonics, 11(4), 329. https://doi.org/10.3390/photonics11040329





