OLED-Pumped Organic Laser Diode
Abstract
1. Introduction
2. Model Description
2.1. OLED Model
2.2. Laser Model
3. Results
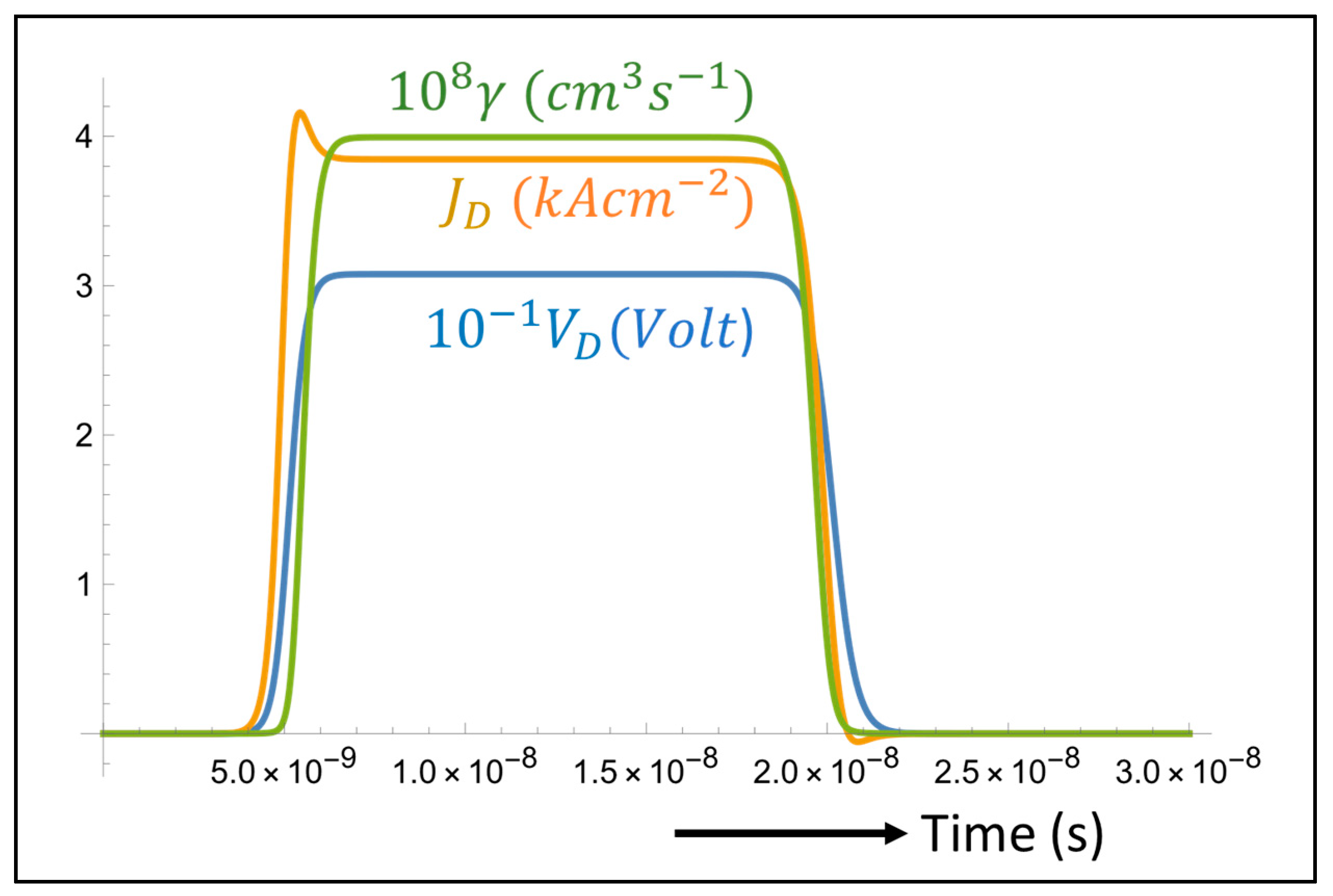
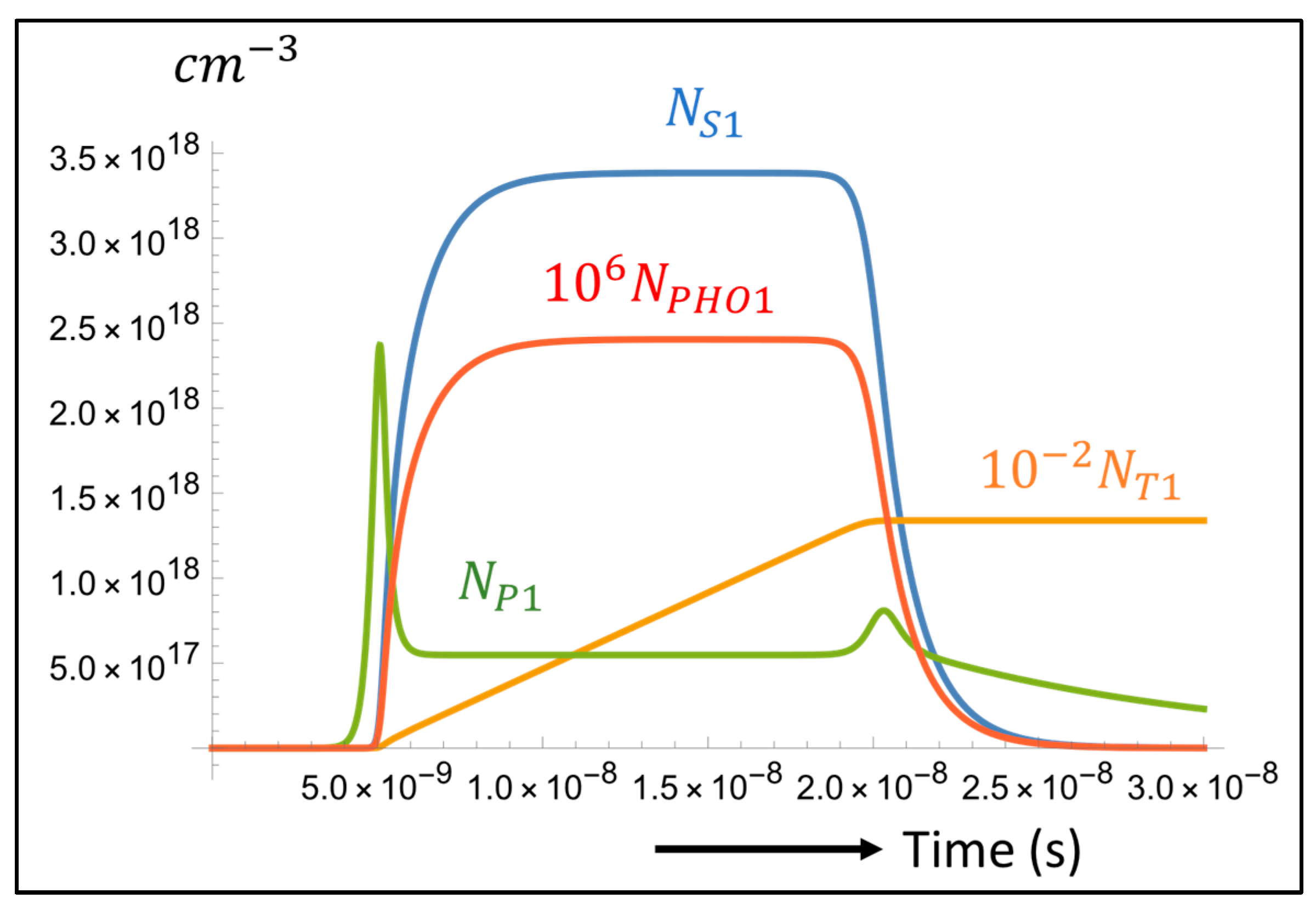
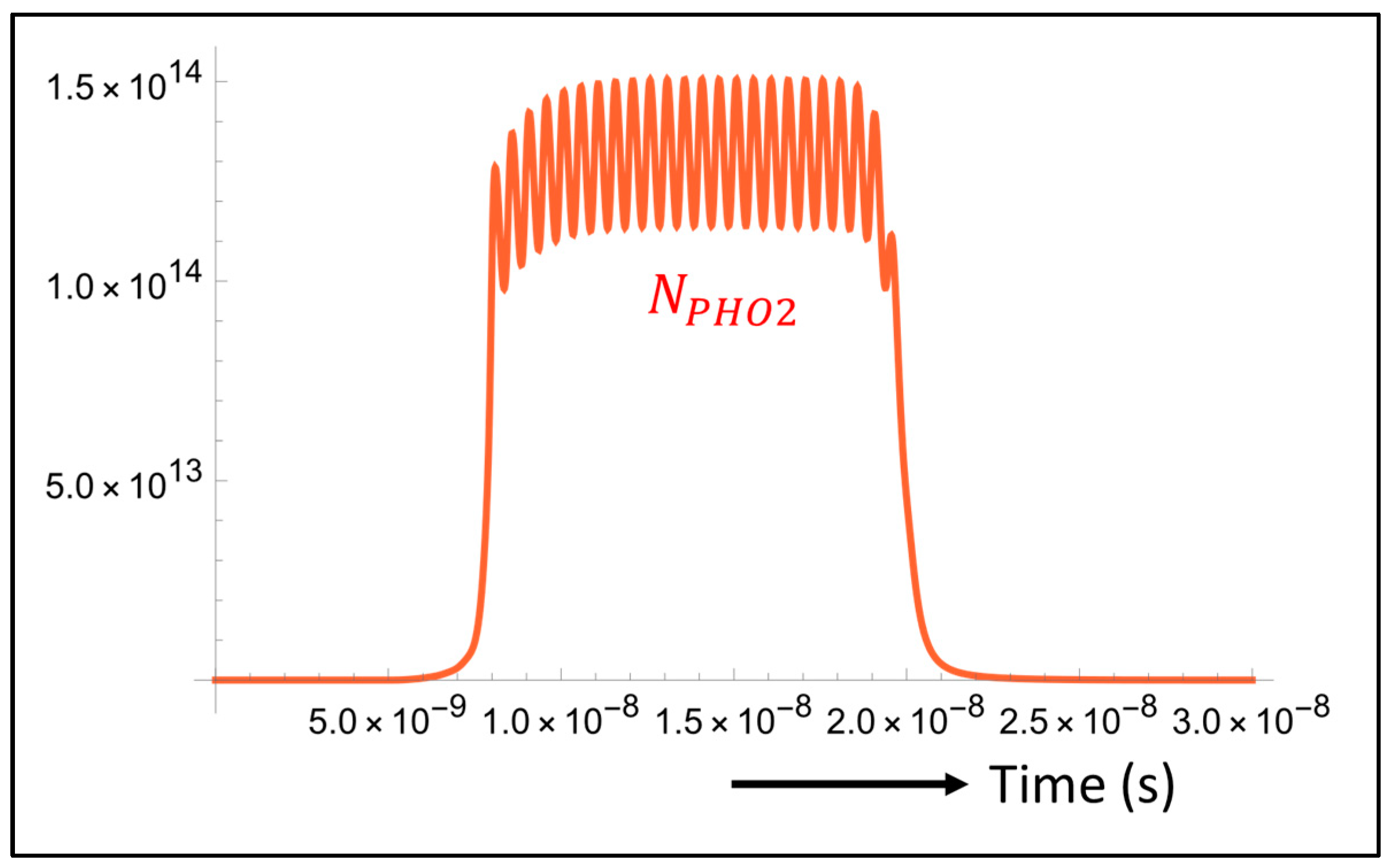
3.1. OLED Performance
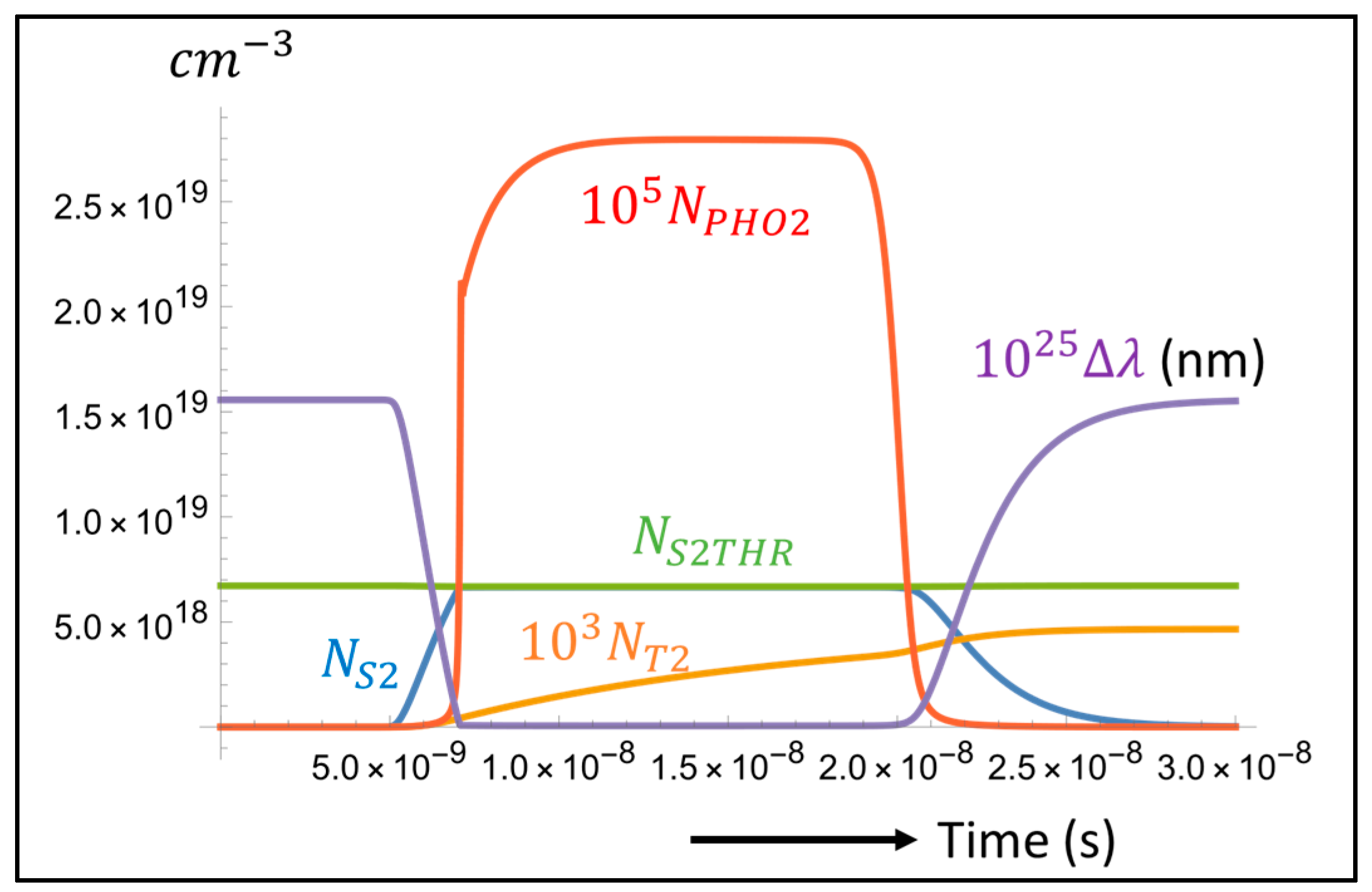
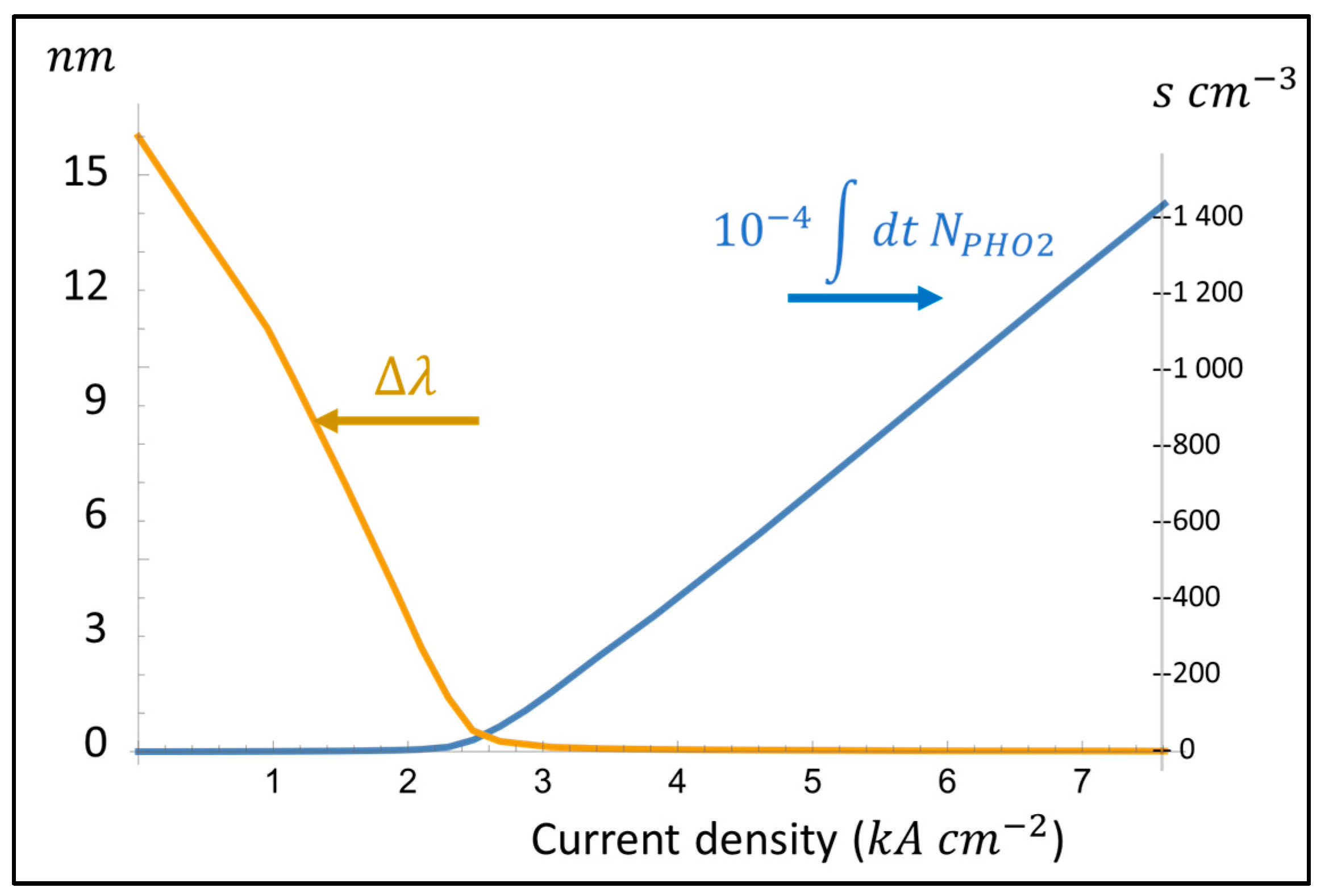
3.2. Laser Performance
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kasemann, D.; Brückner, R.; Fröb, H.; Leo, K. Organic light-emitting diodes under high currents explored by transient electroluminescence on the nanosecond scale. Phys. Rev. B 2011, 84, 115208. [Google Scholar] [CrossRef]
- Sandanayaka, A.S.D.; Matsushima, T.; Bencheikh, F.; Terakawa, S.; Potscavage, W.J.P., Jr.; Qin, C.; Fujihara, T.; Goushi, K.; Ribierre, J.-C.; Adachi, C. Indication of current-injection lasing from an organic semiconductor. Appl. Phys. Express 2019, 12, 061010. [Google Scholar] [CrossRef]
- Samuel, I.D.W.; Turnbull, G.A. Organic semiconductor lasers. Chem. Rev. 2007, 107, 1272–1295. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Gong, J.; Kanibolotsky, A.L.; Skabara, P.J.; Turnbull, G.A.; Samuel, I.D. Electrically driven organic laser using integrated OLED pumping. Nature 2023, 621, 746–752. [Google Scholar] [CrossRef] [PubMed]
- Giebink, N.C.; Forrest, S.R. Temporal response of optically pumped organic semiconductor lasers and its implication for reaching threshold under electrical excitation. Phys. Rev. B 2009, 79, 073302. [Google Scholar] [CrossRef]
- Ouirimi, A.; Chime, A.C.; Loganathan, N.; Chakaroun, M.; Fischer, A.P.; Lenstra, D. Threshold estimation of an organic laser diode using a rate-equation model validated experimentally with a microcavity OLED submitted to nanosecond electrical pulses. Org. Electron. 2021, 97, 106190. [Google Scholar] [CrossRef]
- Lenstra, D.; Fischer, A.P.; Ouirimi, A.; Chime, A.C.; Loganathan, N.; Chakaroun, M. Organic Diode Laser Dynamics: Rate-Equation Model, Reabsorption, Validation and Threshold Predictions. Photonics 2021, 8, 279. [Google Scholar] [CrossRef]
- Gärtner, C. Organic Laser Diodes: Modelling and Simulation. Ph.D. Thesis, Universität Karlsruhe, Karlsruhe, Germany, 2008. [Google Scholar]
- Murgatroyd, P.N. Theory of space-charge-limited current enhanced by Frenkel effect. J. Phys. D Appl. Phys. 1970, 3, 151. [Google Scholar] [CrossRef]
- Gispert, J.R. Coordination Chemistry; Wiley-VCH: Hoboken, NJ, USA, 2008; p. 483. ISBN 3-527-31802-X. [Google Scholar] [CrossRef]
- Ahmad, V.; Sobus, J.; Greenberg, M.; Shukla, A.; Philippa, B.; Pivrikas, A.; Vamvounis, G.; White, R.; Lo, S.-C.; Namdas, E.B. Charge and exciton dynamics of OLEDs under high voltage nanosecond pulse: Towards injection lasing. Nat. Commun. 2020, 11, 4310. [Google Scholar] [CrossRef] [PubMed]
- Kao, K.C. Dielectric Phenomena in Solids; Elsevier Academic Press: San Diego, CA, USA, 2004; ISBN 9780123965615. [Google Scholar]
- Lenstra, D.; A Fischer, A.P.; Ouirimi, A.; Chime, A.C.; Loganathan, N.; Chakaroun, M. Ultra-short optical pulse generation in micro OLEDs and the perspective of lasing. J. Opt. 2022, 24, 034007. [Google Scholar] [CrossRef]
- Lenstra, D.; Fischer, A.; Ouirimi, A.; Loganathan, N.; Chakaroun, M. OLED-pumped Organic Laser. Proc. SPIE Photonics Eur. 2024; submitted. [Google Scholar]
- Gartner, C.; Karnutsch, C.; Pflumm, C.; Lemmer, U. Numerical Device Simulation of Double-Heterostructure Organic Laser Diodes Including Current-Induced Absorption Processes. IEEE J. Quantum Electron. 2007, 43, 1006–1017. [Google Scholar] [CrossRef]
- Ou, Q.; Peng, Q.; Shuai, Z. Computational screen-out strategy for electrically pumped organic laser materials. Nat. Commun. 2020, 11, 4485. [Google Scholar] [CrossRef] [PubMed]

| Symbol | Name | Value | Ref. |
|---|---|---|---|
| OLED series resistance | Choice | ||
| OLED layer resistance | Choice | ||
| OLED diode capacitance | Estimate | ||
| d | OLED active layer thickness | 20 nm | [4] |
| OLED active area | Choice | ||
| elementary charge | - | ||
| Molecular density (TSBF) | 1.0 × 1021 cm−3 | Estimate | |
| Zero-field Langevin recombination rate | 6.2 ×10−12 cm3 s−1 | [15] | |
| Polaron decay rate | Choice | ||
| Singlet-exciton decay rate | 7.7 × 108 s−1 | [16] | |
| Singlet-exciton radiative decay rate | 7.1 × 108 s−1 | [16] | |
| Triplet decay rate | 1 × 103 s−1 | [16] | |
| Inter-system crossing rate | 2.7 × 105 s−1 | [16] | |
| Singlet-polaron annihilation (SPA) rate | 1 × 10−10 s−1 | [8] | |
| Γ | Confinement factor | 0.29 | [6,13] |
| Stimulated emission gain coefficient | 5.7 × 10−6 cm3 s−1 | [16] | |
| Reabsorption coefficient | 1.5 × 10−8 cm3 s−1 | [16] | |
| Triplet absorption (TA) coefficient | 3.5 × 10−8 cm3 s−1 | [16] | |
| Polaron absorption (PA) coefficient | 1.15 × 10−6 cm3 s−1 | [16] | |
| Spontaneous emission factor | 0.504 | Estimate | |
| Activation voltage (Poole-Frenkel) | 0.4 Volt | [13] | |
| Peak luminescence wavelength | 440 nm | [4] | |
| Peak absorption wavelength | 370 nm | [16] | |
| Duration of current switch-on | 0.2 ns | Choice | |
| Duration of current switch-off | 0.3 ns | Choice |
| Symbol | Name | Value | Ref. |
|---|---|---|---|
| Molecular density (BsB-Cz) | 1.0 × 1021 cm−3 | Estimate | |
| Photon transmission OLEDlaser | 0.75 | [4] | |
| Singlet-exciton decay rate | 8.0 × 108 s−1 | [16] | |
| Triplet decay rate | 9.1 × 103 s−1 | [16] | |
| Inter-system crossing rate | 6.6 × 104 s−1 | [16] | |
| Stimulated emission gain coefficient | 9.4 × 10−6 cm3 s−1 | [16] | |
| Reabsorption coefficient | 4.4 × 10−7 cm3 s−1 | [16] | |
| Peak absorption coefficient | 5.3 × 10−6 cm3 s−1 | [16] | |
| Triplet absorption (TA) coefficient | 3.3 × 10−7 cm3 s−1 | [16] | |
| Cavity photon decay rate | - | ||
| Spontaneous emission factor | Estimate | ||
| Peak luminescence wavelength | 505 nm | [16] | |
| Peak absorption wavelength | 440 nm | [16] | |
| Cavity refractive index | 1.7 | Estimate | |
| Vacuum light velocity | - | ||
| Cavity quality factor | 500 | Estimate |
| Exciting pulse duration | |
| Excitation pulse repetition rate | |
| Laser threshold current | |
| Laser pulse duration | |
| Laser linewidth | |
| Threshold optical pump intensity | |
| Optical data transmission speed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenstra, D.; Fischer, A. OLED-Pumped Organic Laser Diode. Photonics 2024, 11, 327. https://doi.org/10.3390/photonics11040327
Lenstra D, Fischer A. OLED-Pumped Organic Laser Diode. Photonics. 2024; 11(4):327. https://doi.org/10.3390/photonics11040327
Chicago/Turabian StyleLenstra, Daan, and Alexis Fischer. 2024. "OLED-Pumped Organic Laser Diode" Photonics 11, no. 4: 327. https://doi.org/10.3390/photonics11040327
APA StyleLenstra, D., & Fischer, A. (2024). OLED-Pumped Organic Laser Diode. Photonics, 11(4), 327. https://doi.org/10.3390/photonics11040327






