1. Introduction
Laser sources based on the parametric oscillation of counterpropagating waves, also known as a backwards optical parametric oscillator (BOPO), are an attractive means to generate high power, narrow linewidth mid-infrared (mid-IR) light emission [
1,
2,
3,
4]. When compared to a common optical parametric oscillator (OPO), BOPOs exhibit unique advantages including removing the need for external mirrors to confine the generated light and the narrow linewidth counterpropagating wave [
1,
2,
3,
4]. These traits make BOPOs an ideal source of mid-IR light generation compared to standard OPOs.
Despite these advantages, the development of BOPOs has been limited by difficulties in phase matching caused by the counterpropagating wave [
1,
3]. Due to the counterpropagating wave, the momentum mismatch between the three waves is much larger than in the co-propagating case [
1,
2,
3,
4]. The most promising method to compensate for this momentum mismatch is the quasi-phase matching (QPM) technique, which periodically inverts the sign of the nonlinear coefficient to satisfy the phase matching condition. However, the large momentum mismatch calls for a sub-micron period with a high-quality duty cycle, which is difficult to achieve in most nonlinear materials. To date, sub-micron poling in bulk materials, with a high-quality duty cycle, has only been demonstrated in periodically poled potassium titanyl phosphate (PPKTP) [
2,
3]. While achieving sub-micron poling in PPKTP is possible, it has only been demonstrated with short crystal lengths (sub 1 cm), which limits the operation of these BOPOs to the pulsed mode only [
2,
3].
One option to overcome the need for a short period is to use higher order QPM, where the period is multiplied by an odd integer [
5]. While this does reduce the effective nonlinear coefficient of the material, it removes the need to achieve submicron poling, allowing for the use of materials with higher nonlinear coefficients than KTP such as lithium niobate (LN), as well as the use of longer crystals [
5]. Due to the reduced nonlinear coefficient, and hence the reduced conversion efficiency, extensive optimization is needed to ensure that not only can the threshold of the BOPO be reached but that output powers are high enough to be useful for the desired applications. As such, systematic studies are needed to optimize the laser cavity design. However, due to the prohibitive cost of PPLN, experimental system studies have not been performed. In 2017, a systematic theoretical study on a PPLN BOPO with 5th order QPM in a single pass configuration aiming to find the optimum pulse parameters to achieve maximum output power was reported [
5]. The authors found that it was possible to reach the BOPO threshold with a 700 ps and pulse energy of 70 μJ in a single pass configuration. In 2022, a theoretical study was performed on the threshold and linewidth of single pass CW BOPOs but, due to the single pass configuration, the threshold to reach CW operation was too high, even when using 1st order QPM [
6]. Another structure which can be used to realize a CW BOPO is an intracavity structure, which would reduce the device threshold and allow for operation with a low power pump source. We recently showed it was possible to reach the BOPO threshold for CW operation using 5th order QPM in PPLN with a low pump power [
7].
In this paper, we report a systematic study of a CW intracavity BOPO based on 5th order QPM in PPLN to determine the optimum operating configuration. We study the effects of changing various cavity parameters including PPLN length, laser cavity length, pump laser diode power, pump laser diode spot size, and output coupler (OC) radius, while also accounting for various physical phenomena such as nonlinear loss due to the nonlinear conversion process, the thermal lens effect, and mode overlap between the three waves.
2. Theoretical Background and Model
Figure 1 shows a diagram of a singly resonant IC-BOPO-based mid-IR laser structure. The pump laser is an 808 nm laser diode. In this study, we assume the max output power from the 808 nm LD to be 10 W, which pumps the Nd:YVO
4 crystal to achieve 1064 nm emission. The nonlinear crystal used is PPLN, which is placed inside of the pump cavity. The input facet of the Nd:YVO
4 (coating #1) is high reflection (HR) coated at the BOPO pump wavelength (1064 nm) and high transmission (HT) coated at 808 nm. The output facet of the Nd:YVO
4 crystal (coating #2) is antireflection (AR) coated at the BOPO pump wavelength (1064 nm). The input facet of the PPLN (coating #3) is HR coated at the BOPO signal wavelength (1590 nm) and AR coated at the BOPO pump wavelength 1064 nm. The output facet of the PPLN (coating #4) is AR coated at the BOPO signal, pump, and idler (3.2 μm) wavelengths. The optical coupler (OC) is HR coated (coating #5) at both the signal and pump wavelength of BOPO, and AR coated at the BOPO idler wavelength (3210 nm). The pump cavity is formed by coatings #1 and #5. The signal cavity is formed by coatings #3 and #5.
To analyze the laser depicted in
Figure 1, we have used a model developed within our group and reported previously [
7]. Since the intracavity structure used results in both forwards and backwards propagating waves, forward propagating waves are assumed to travel in the +z direction and backward propagating waves are assumed to travel in the -z direction. The first order coupled wave equations for the forward propagating waves can be written as [
5]
where
As,
Ai, and
Ap are the slowly varying signal, idler, and pump amplitudes, respectively. P(
z) is a periodic function which accounts for the effect of the poling in the
LN, taking a value of ±1, depending on if the region has a positive or negative nonlinear coefficient. Δ
k is the momentum mismatch given by Δ
k =
kp −
ks +
ki.
αs,
αi, and
αp are the material loss values for PPLN at the signal, idler, and pump wavelengths, respectively. The substitution
is made to enable to the use a single coupling constant
κ, where
where
dPPLN is the second order nonlinear coefficient
d33 of
PPLN,
c is the vacuum speed of light,
ω is the angular frequency of the respective wave, and
n is the refractive index of the respective wave in
PPLN. Millers rule was used to scale the nonlinear coefficient to the wavelengths used in this study [
8]. Additionally, another factor was added to the nonlinear coupling part of Equations (1)–(3),
β, which is used to account for the overlap between the respective fields in each coupled wave equation. The term has a value which ranges from 0 to 1, where 0 represents no overlap and 1 represents perfect overlap. Since the plane wave assumption assumes perfect overlap between the fields, this term serves as a correction factor and reduces the efficiency of the nonlinear interaction if the fields’ spatial overlap is poor, which is used to improve the accuracy of the model. The overlap of two fields, in this case the signal and idler, can be evaluated as
where
Ei is the spatial distribution of the idler electric field and
Es is the spatial distribution of the signal electric field. The remaining two overlap parameters can be calculated using the above equation with the corresponding fields. In order to properly evaluate Equation (5), the spatial distribution of the fields inside of the nonlinear crystal is needed. An ABCD matric method was used to determine the beam waists inside of the cavity.
The initial conditions for the signal and idler wave are determined by calculating the flux of a single photon [
5,
9,
10]. The initial condition for the pump wave can be found by calculating the circulating 1064 nm optical power.
To calculate the circulating 1064 nm optical power, a previously reported model for an intracavity laser was used [
11]. The calculated 1064 nm power was then used as the initial condition for the pump field in the coupled wave equations which were then solved using a Lax–Wendroff method [
12]. However, due to the inclusion of the nonlinear crystal, an additional loss term, which results from the conversion of the pump beam to the signal and idler in the nonlinear process, must be considered. This nonlinear loss term is added to the linear loss term, which includes material loss due to absorption, reflection of components involved in the cavity, and imperfect mirrors. The nonlinear loss term is the total loss of the 1064 nm beam that occurs from travelling through the nonlinear crystal due to the nonlinear conversion process. This nonlinear loss term can be calculated as
where
αnl is the nonlinear loss term,
Ni is the number of idler photons generated in the forwards and backwards direction, and
Np is the number of pump photons incident on the nonlinear crystal. This term can be added to the other loss sources to determine the total loss at the BOPO pump wavelength as
where
αtot is the total loss,
αcav is the cavity loss,
αPPLN is the loss in
PPLN due to scattering and absorption, and
αOC is the loss due to imperfect mirrors. The new value of the 1064 nm circulating power which was calculated by including the nonlinear loss term was then used as the input to the coupled wave equations, resulting in new signal and idler powers and a new nonlinear loss term. This process was repeated until all output values converged, at which point the steady state signal, idler, and intracavity pump powers were found.
In order to properly model the intracavity laser power, the thermal lens effect in the Nd:YVO
4 crystal must be considered. The thermal lens effect can be modeled as [
13]
where ζ is the fractional thermal loading,
Pabs is the absorbed pump power, κ
c is the thermal conductivity,
α is the absorption coefficient at the pump wavelength, l is the crystal length,
dn/
dT is the thermos-optic coefficient, α
T is the thermal expansion coefficient, and
ωp is the 808 nm LD pump size in the laser crystal. Thermal effects within the PPLN crystal have not been considered due to the low absorption coefficient of PPLN at the wavelengths of interest resulting in negligible heating. Precise temperature control of the PPLN can be achieved with standard methods, such as ovens and thermoelectric coolers, which can maintain temperature control to 0.1 °C.
To allow for step sizes greater than the poling period to be used, an effective nonlinear coefficient was calculated by integrating the poling function, P(z), the phase mismatch term, , and the nonlinear coefficient over length of the crystal and then dividing this value by the length of the crystal. The period of the poling function is chosen to equal the momentum mismatch at the desired signal and idler wavelengths.
Due to the intracavity structure used, the fields within the cavity must be broken into forwards and backwards components. In our model, we assume forward to refer to fields travelling from left to right (coating #1 to the OC in the context of
Figure 1) and backwards to refer to fields travelling from right to left (from the OC to coating #1 in the context of
Figure 1). Since both the pump and signal wave are confined, each will have a forwards and backwards component. Since there are both forwards and backwards travelling signal and pump waves, there must also be a forward and backwards travelling idler wave. When considering a BOPO, the phase matching convention assumes that the pump and signal wave co-propagate and generate a counterpropagating idler wave, as opposed to a regular IC-OPO where the copropagating pump and signal field will result in a copropagating idler field. This means that the forward travelling signal and pump will generate a backwards travelling idler wave and vice versa in the case of an IC-BOPO.
A list of the parameters used in the simulations is provided in
Table 1.
3. Results and Discussion
3.1. Dependence on PPLN and Cavity Length
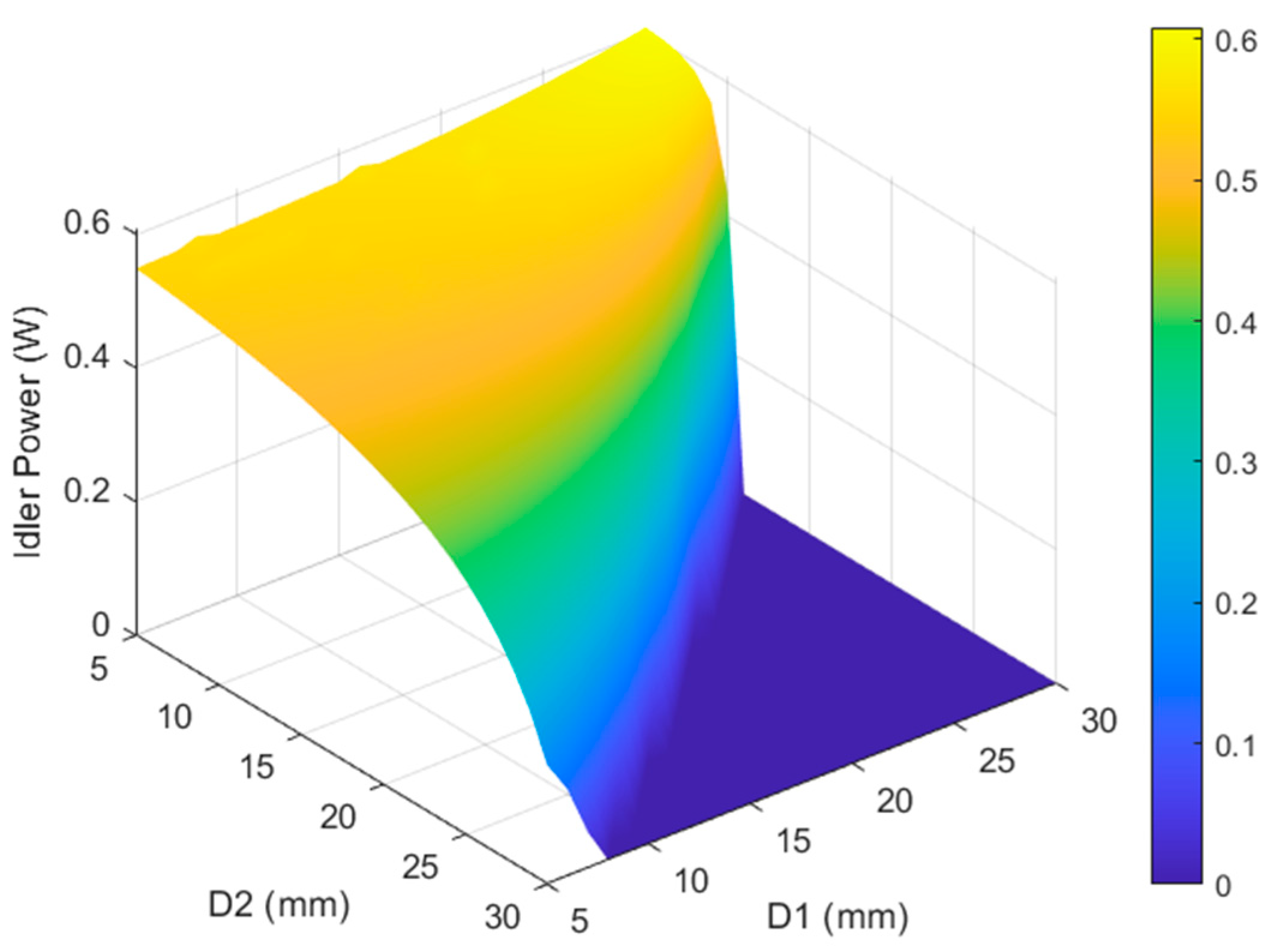
Figure 2 shows the idler power for a 5 cm PPLN with various cavity sizes. The power from the 808 nm LD was 10 W and was focused to a radius of 165 μm in the Nd:YVO
4 crystal. The radius of the OC used was 100 mm. The x- and y- axis are the spacing between the Nd:YVO
4 crystal and PPLN (D1) and the spacing between the PPLN and OC (D2), respectively. A number of observations can be made from the data in
Figure 2. The first observation is that an idler output power of 600 mW is achievable with a 10 W pump source by using the proposed intracavity structure corresponding to an idler conversion efficiency of 6%. This conversion efficiency is comparable to the theoretical report from 2017 [
5]. However, here the device is operated in CW mode instead of pulsed. Second, the idler output power increases slightly with increasing D1 within the range of the simulation (i.e., D1 < 30 mm), as long as the D2 value is small. Third, the idler output power decreases with increasing D2 for all D1 values. Last, the geometric stability of the cavity shows a greater dependence on the D2 value than the D1 value.
These effects can be explained as follows. Due to the thermal lens effect in the Nd:YVO
4 crystal, the shape of the 1064 nm beam waist within the cavity resembles an asymmetric parabola. As a result, it is necessary to place the PPLN in a location within the cavity such that the average beam waist inside of the PPLN is minimized. Increasing D1, while D2 is kept small (<10 mm), results in the average 1064 beam radius decreasing within the PPLN, resulting in higher conversion efficiencies. The improvement in output power is small though as decreasing the 1064 nm beam in the PPLN also reduces the overlap between the signal and pump as the signal beam size is unaffected by the D1 value. When increasing D2, it was found that the average 1064 nm beam radius always increased, regardless of the D1 value which resulted in the decrease in output power with increasing D2. It was also found that increasing either D1 or D2 above a certain value resulted in a rapid increase in the average 1064 nm beam radius in the PPLN, leading to a rapid decrease in output power. This rapid decrease in output power occurs as the cavity approaches geometric instability. As can be seen in
Figure 2, the D1 and D2 values at which this occurs vary depending on the overall cavity size. However, this drop occurs at lower D2 values than D1 values, indicating that the geometric stability of the cavity is affected more by the D2 value than the D1 value.
An important point which must be considered is that the optimum cavity setup will largely depend on the focal length of the thermal lens inside the Nd:YVO4 crystal. Changing the focal length will then affect the optimum D1 and D2 value. As stated earlier, the maximum output power configuration occurs right before a rapid drop in output power if either D1 or D2 is increased further. As such, if the cavity is set up in the optimum configuration, small thermal fluctuations in the Nd:YVO4 crystal can drastically reduce the output power. However, this can be accounted for in the cavity by using values of D1 and D2 slightly below the optimum values to allow more room for thermal fluctuations.
Based on the above observation, two conclusions can be made. First, optimizing the D1 value is important to achieve the highest output power. The output power can be improved by as much as 10% from the most compact cavity configuration (540 mW vs. 600 mW) by employing an optimized D1 value. Second, the D2 value should be kept as small as possible so that the cavity remains stable while maximum output power is achieved.
Figure 3 shows the threshold of the laser with the same cavity configuration as was used for
Figure 2. Additionally, the same simulation parameters were used, as indicated in
Table 1. Minimizing the IC-BOPO threshold is necessary to enable the use of a low power pump source. Additionally, due to the use of 5th order QPM, the effective nonlinear coefficient is reduced, resulting in the need for increased cavity optimization so the threshold can be reached with a low power source. From
Figure 3, we can see that the laser threshold was lowest, approximately 5.4 W, when the cavity was in the most compact configuration (D1 = D2 = 5 mm). The threshold was found to increase with increasing D1 and D2 values. The threshold value was also found to be more sensitive to a change in D1 than D2, although the difference was small. The decrease in threshold when the cavity size is reduced is due to the change in the 1064 nm cavity mode. At low input powers, the position of the minimum beam waist is shifted nearer to the Nd:YVO
4 crystal. This results in the 1064 nm beam waist being shifted towards the Nd:YVO
4 crystal due to the larger thermal lens focal length. As a result, the PPLN, in order to achieve the smallest average 1064 nm beam waist, must be placed as close to the Nd:YVO
4 crystal as possible.
From
Figure 2 and
Figure 3, it is clear that there is a trade-off between achieving high output power and achieving a low threshold. According to
Figure 2, the maximum idler output power occurs when D1 = 30 mm and D2 = 5 mm. However, as previously mentioned, the minimum threshold is achieved when D1 = D2 = 5 mm. As such, increasing the maximum power would also result in an increased threshold and vice versa.
Figure 4 shows the variation in idler output power with a 10 W pump for different PPLN sizes when D1 and D2 value are kept constant. Both D1 and D2 were set to 5 mm for all PPLN lengths. D1 and D2 were set to 5 mm for all crystal lengths to ensure that the cavity remained geometrically stable for all crystal lengths at all input powers.
Figure 4 shows an increased maximum idler power for longer crystals, with a significant increase in output power occurring by increasing the length from 3 cm to 4 cm (300 mW to 460 mW), while the increase in output power due to using a 5 cm PPLN instead of 4 cm is not as substantial (460 mW to 540 mW).
Figure 4 suggests that there are diminishing returns when increasing the PPLN length in terms of the maximum achievable output idler power. As previously mentioned, increasing the PPLN length from 3 to 4 cm resulted in an increased output power of roughly 50%, while the PPLN length was increased by only 30%. Comparing this to the 20% increase in output power when increasing the PPLN length from 4 cm to 5 cm, it is clear that increasing the PPLN length does not have a linear effect on output power. This can be explained as follows: while the conversion efficiency is dependent on the length of the PPLN, increasing the PPLN length also increases the size of all three beams within the cavity, reducing the intensity. Additionally, as the conversion efficiency increases with increased PPLN length, so does the nonlinear loss term present in Equation (7), which reduces the intracavity 1064 nm power. The diminishing returns in output power when increasing PPLN length is important to consider as a longer PPLN will increase the device footprint, as well as increase the cost. Furthermore, maintaining a high quality duty cycle over a longer crystal is an additional challenge which could further reduce device performance.
3.2. Dependence on 808 nm LD Laser Beam Waist
Figure 5 shows the beam radius of the 1064 nm beam in the PPLN crystal for various D1 values and various 808 nm beam spot sizes. For all data points shown in
Figure 5, D2 was set to 5 mm and the PPLN length was 5 cm. From
Figure 5, two observations can be made. The first is the importance of choosing an optimum 808 nm beam waist to achieve the minimum 1064 nm beam radius in the PPLN crystal for a given cavity configuration. The second is that the smaller the 808 nm beam waist, the smaller the cavity must be to remain geometrically stable.
From
Figure 5, it is clear that there exists an optimum 808 nm beam waist at which the 1064 nm beam will have a minimum radius within the PPLN. As can be seen by the result in
Figure 5, this optimum beam waist depends on the spatial configuration of the cavity. For the 145 μm 808 nm LD beam waist, we see that the minimum PPLN beam waist is achieved at a D1 value of approximately 15 mm. The change in beam waist was small when decreasing D1 below 15 mm, reaching a value of approximately 105 μm at a D1 value of 5 mm. However, the rate of change in the beam waist was rapid when increasing D1 past 15 mm, with the cavity becoming geometrically unstable at D1 values larger than 20 mm. Choosing the correct D1 value ensures that the 1064 intracavity beam waist is approximately in the center of the PPLN, minimizing the average beam waist in the PPLN. For the other 808 nm beam waists, a similar trend was observed, although not as pronounced as the 145 μm case. This result is due to the thermal lens focal length being dependent on the 808 nm beam waist, with a smaller beam waist producing a smaller focal length and hence a greater focusing power. As a consequence of smaller 808 nm beam waists producing a thermal lens with a smaller focal length, the maximum cavity size must be limited in order to ensure it remains geometrically stable.
This shows the importance of achieving excellent thermal stability to keep the focal length of the thermal lens constant in the Nd:YVO4 crystal. If the focal length decreases due to heating, then the D1 value that results in the minimum beam waist will also decrease, resulting in a much larger beam waist which will lead to a substantial drop in laser performance. As expected, use of a larger 808 nm LD beam waist resulted in a decreased sensitivity to either a change in the temperature stability of the Nd:YVO4 crystal or a change in the spatial configuration of the cavity. If thermal control/stability is expected to be an issue, then the use of a larger 808 nm LD beam waist is recommended.
Figure 6 shows the calculated idler power at each of the data points shown in
Figure 5. For both the 185 μm and 145 μm beam waist, we see that the idler power decreases roughly linearly with the pump beam radius. For the 165 μm beam waist, only part of the data points follow this trend. The explanation for this is as follows: for the three data points with the lowest output powers, the change in beam waist between the three data points is small, only about 1% between each of the data points. At the same time, the change in the overlap integral between the pump and signal increases by about 2% as the 1064 nm beam waist increases due to the large radius of the signal beam in the PPLN, which offsets the reduced intensity. As the beam radius continues to decrease, the change in increased intensity eventually overcomes the loss due to the reduced overlap integral, which resulted in a higher output power. Due to the beams being concentric within the PPLN crystal, the overlap integral value generally remains quite high, >80%, and does not change much when the radius of any of the beams change. As a result of this, we found that it is better to design the cavity to minimize the beam waist in the PPLN crystal than to focus on increasing the overlap integral.
3.3. Dependence on OC Radius
Figure 7 shows the output idler power calculated for different OC radii with a 5 cm PPLN and having D1 and D2 set to 5 mm. The 808 nm LD beam waist in the Nd:YVO
4 crystal was set to 165 μm. The output power for both the 100 mm radius and 50 mm radius was nearly identical at all input powers. The reasons for this are as follows. Reducing the radius of the OC to 50 mm resulted in a reduced 1064 nm beam radius within the PPLN, which should result in a higher output power. However, the radius of the 1064 nm beam is also reduced inside of the Nd:YVO
4 crystal, resulting in it being smaller than the 808 nm LD beam waist. As stated in the original paper by Risk [
10], it is ideal to have the 808 nm pump waist smaller than the 1064 nm waist in the Nd:YVO
4 crystal to achieve a high slope efficiency. The ratio of the 808 nm LD spot size to the 1064 nm spot size is approximately 1.7 at 10 W when using the 50 mm OC, resulting in a reduced slope efficiency which greatly reduces the circulating 1064 nm power inside of the laser cavity. The ratio when using the 100 mm OC was calculated to be 1.3, which resulted in a higher slope efficiency. When using the 100 mm OC, the 1064 nm power in the forward direction is calculated to be 102 W, compared to the 50 mm OC which resulted in a forward 1064 nm power of 90 W. The slope efficiency was shown to rapidly decrease as the ratio between the two beams was increased above 1, which explains the large reduction in circulating 1064 nm power in our simulations.
As mentioned earlier, the signal beam waist inside of the PPLN crystal is much larger than the pump beam waist, which reduces the overlap integral. An advantage of the 50 mm OC is that it reduced the signal beam waist in the PPLN from 160 μm (when using the 100 mm OC) to 130 μm, which improved the overlap between the pump and signal beam, increasing the conversion efficiency. The change in the overlap integral, combined with the reduced beam waist, was enough to mitigate the reduced 1064 nm power, resulting in both OCs having the same output idler power.
Figure 8 shows a comparison of the idler output power using a 3 cm PPLN for both a 50 and 100 mm OC radius. The 808 nm LD beam waist was set to 165 μm. D1 and D2 were both set to 5 mm. From
Figure 8, a substantial increase in output power can be seen when using a 50 mm OC as opposed to a 100 mm OC. The output power increased from 300 mW, when using the 100 mm OC, to 370 mW when using the 50 mm OC. In addition to the increase in output power, the threshold of the laser is also reduced when using the 3 cm PPLN, from 7.5 W to 6.5 W.
While switching to a 50 mm radius OC does result in a worse 808 nm to 1064 nm beam waist ratio for the 3 cm PPLN (1.46 with the 100 mm OC vs. 1.74 with the 50 mm OC), the change is not as significant as with the 5 cm PPLN (1.28 with the 100 mm OC vs. 1.69 with the 50 mm OC). As a result, the reduction in the slope efficiency and circulating 1064 nm power is not as significant when using the 3 cm PPLN. In addition to this, the pump beam waist in the 3 cm PPLN has a greater decrease when using the 50 mm OC than when using the 5 cm PPLN, resulting in a greater 1064 nm intensity increase when using the shorter PPLN. The increased 1064 nm intensity results in an increased idler conversion efficiency. There is also a slight increase in the mode overlap between the signal and pump when using the 3 cm PPLN, which further increases the output power.
One option to improve the performance of the laser when using a 50 mm OC would be to decrease the thermal lens focal length, which will, in turn, increase the divergence of the 1064 nm beam in the laser cavity, increasing its beam waist in the Nd:YVO
4 crystal and thus increasing the slope efficiency.
Figure 9 shows the calculated idler output power when using a 50 mm OC for different 808 nm LD beam waists. A roughly linear increase in output power is observed with a decrease in the 808 nm LD beam waist. As predicted, the main reason for the improvement in performance is due to the improved 808 nm LD to 1064 nm beam waist ratio. When the beam waist was set to 115 μm, a drop in power was observed when the input power was increased from 8 to 9 W, which is due to the 1064 nm beam waist rapidly increasing in the PPLN. At 10 W, the cavity was no longer geometrically stable when an 808 nm LD beam waist of 115 μm was used.
Figure 10 shows the output power for various PPLN lengths using different 808 nm LD beam waists for a 50 mm OC. Both D1 and D2 were set to 5 mm. As was discussed previously,
Figure 10 shows that reducing the OC radius has a greater effect on the performance of the laser when using a shorter PPLN. This allows for the use of shorter PPLN crystals while still achieving high output powers.
For the 5 cm PPLN, the output power increased from 550 mW to 710 mW when the 808 nm LD beam waist was decreased from 165 μm to 125 μm, compared to the 3 cm PPLN which increases in power from 380 mW to 600 mW when changing the 808 nm LD beam waist from 165 μm to 110 μm. Similar to previous results, the maximum power point is followed by a rapid drop in output power before the cavity becomes geometrically unstable. For both the 4 and 5 cm PPLN, decreasing the 808 nm beam waist from 125 μm to 115 μm resulted in the cavity no longer being geometrically stable.
From
Figure 10, we can see that if an appropriate 808 nm LD beam waist is chosen, the difference in power between a 4 and 5 cm PPLN is almost negligible. Furthermore, the 3 cm PPLN maximum output power is only 60 mW less than that of the 4 and 5 cm PPLN. From this, we can see that it is possible to achieve a higher output power with a 3 cm PPLN using a 50 mm OC than when using a 5 cm PPLN and 100 mm OC. Another interesting result is that if a 50 mm OC is used, it is possible to reach the threshold with a 2 cm PPLN, although the requirements for reaching the threshold and maintaining cavity stability are extremely strict. Only a small range of 808 nm LD beam waists allow the laser to reach the threshold before the cavity becomes unstable. From the results, it is clear that higher performance can be achieved when using a smaller radius OC compared to a larger radius OC. Improved output power can be achieved with shorter PPLNs, allowing for more compact laser designs, but this comes at the cost of increased temperature control requirements.
3.4. Dependence on Cavity Loss
Figure 11 shows the idler output power as a function of both the signal and pump cavity loss values. The loss values displayed on the x- and y-axis do not include material loss and the loss due to mirrors, but these sources of loss were considered when calculating the output power. D1 and D2 were set to 5 mm, and the input power was set to 10 W. From
Figure 11, we see that optimizing the cavity to minimize the pump loss results in improved performance. Looking at the extremes of
Figure 11, when the pump loss is set to 1% and the signal loss is set to 0% or vice versa, we see that the performance is approximately 15% better in the case of the 0% pump cavity loss configuration. Additionally, the threshold is also minimized by minimizing the pump cavity loss as opposed to minimizing the signal loss. As such, it is found that when optimizing the cavity, reducing the loss at the pump wavelength should be the primary focus.
Due to the forward idler beam being dependent on the backwards travelling pump, it is expected that the forwards travelling idler wave will have a lower intensity than the backwards travelling idler, due to pump depletion from the nonlinear process. A worthwhile consideration is whether or not the use of an intracavity dichroic mirror, placed between the Nd:YVO
4 crystal and the PPLN, to extract the backwards travelling idler will result in improved performance despite the additional source of cavity loss.
Figure 12 shows the output power of the backwards travelling idler for four different dichroic mirror loss values and the forwards travelling idler when no dichroic mirror is present in the cavity for a range of different cavity loss values. The cavity was set to the configuration which achieved the highest idler output power. The OC radius was 50 mm, PPLN length was set to 5 cm, D1 was set to 30 mm, D2 was set to 20 mm, and the 808 nm LD beam waist was set to 165 μm. It is important to note that for the data in
Figure 12, the loss due to material absorption and due to imperfect mirrors was still considered for both the signal and pump.
As expected, when the loss of both the dichroic mirror and laser cavity is low enough, the backwards travelling idler power is larger than the forwards travelling idler, indicating that it is advantageous to use the dichroic mirror to extract the backwards travelling wave. However, the gain in output power is small. When both the pump and signal cavity have a loss value of 0%, and the loss introduced by the dichroic mirror to the pump wave is set to 0.1%, the backwards travelling idler wave has an output power roughly 6% higher than the forwards travelling idler with no dichroic mirror present in the cavity. As the loss values of the dichroic mirror and signal cavity loss are increased to more realistic values, we see that the output powers of the different cases become smaller until the loss due to the dichroic mirror causes the forwards travelling idler to perform better. While theoretically it is possible to improve the performance with the dichroic mirror and extract the backwards travelling, low enough loss values would be extremely difficult, if not impossible, to result in a performance improvement.
3.5. BOPO Linewidth
One of the key characteristics of a BOPO is that the generated counterpropagating wave is expected to have a linewidth much narrower than the generated copropagating wave or the pump wave. This allows for the BOPO to be used as a source for narrow linewidth, high power, mid-ir emission. The linewidth can be estimated by expanding the BOPO phase matching condition as first order Taylor series, as long as the BOPO is operated away from the degeneracy point. Assuming the pump spectrum to be a delta function and expanding the phase matching conditions gives
where Δω is the angular frequency bandwidth of the signal or idler wave,
νg,i is the idler group velocity,
νg,s is the signal group velocity, and L is the crystal length. Using Equation (9), an idler bandwidth of 0.02 nm is calculated for a 5 cm PPLN. Comparing this to a standard OPO where all waves co-propagate, an idler linewidth of 2 nm is found. This difference is due to the counterpropagating nature of the BOPO, which results in the additional of the group velocities in the denominator of Equation (9), different from the conventional OPO where the difference in the group velocities appears in the denominator. Another unique aspect of the BOPO is that the wavelength tuning rate of the counterpropagating wave with respect to the pump is orders of magnitude smaller than the tuning rate of the copropagating wave with respect to the pump. The counterpropagating idler tuning rate is calculated to be 0.006 with respect to the pump, while the copropagating signal tuning rate is calculated to be 1.006 with respect to the pump [
2]. Intracavity 1064 nm lasers generally have a linewidth of a few nm [
17], so the idler bandwidth increase due to the pump bandwidth is expected to be approximately 0.02 nm.