Modal Phase Modulators Based on Liquid Crystals with 3D-Printed Polymer Microstructures: Increasing Size and Complexity

Abstract

We present extended capabilities in simple liquid crystal-based devices that are applicable to adaptive optics and other related fields requiring wavefront manipulation. The laser-written devices can provide complex phase profiles, but are extremely simple to operate, requiring only a single electrode pair tuned between 0 and 10 V RMS. Furthermore, the devices operate in the transmissive mode for easy integration into the optical path. We present here as examples three such devices: the first device reproduces the defocus Zernike polynomial; the second device reproduces a seventh-order Zernike polynomial, tertiary coma; and the last example is of a primary spherical aberration. All devices offer wavelength-scale wavefront manipulation up to more than $2\pi$ radians peak-to-peak phase at a wavelength of 660 nm. The coma correction device is significantly more complex, reproducing a mode two orders higher than previous demonstrations, while the spherical device is nearly a full order of magnitude larger, measuring 2 mm in diameter.

1. Introduction

Adaptive optics is widely used in imaging fields as diverse as microscopy and astronomy for the correction of aberrations. In microscopy, these aberrations can be introduced from a variety of sources, ranging from changes in the refractive index within the sample, to flaws in the imaging apparatus. These aberrations are often characterized by a series of modes, with the most common choice being the Zernike polynomials, whose orthogonality and correspondence to common optical aberrations make them well suited to adaptive optics applications [1]. Generally, these modes are used as the basis for aberration correction, which can be implemented by deformable mirrors, spatial light modulators (SLMs), or deformable phase plates. While these devices can offer high-resolution modal correction, they are bulky and often prohibitively expensive for compact, low-cost optical applications, especially when only a few modes need to be corrected.

One of the most common modes for which modulation is required is defocus, which corresponds to a change of axial focal position of the imaging system. Non-mechanical alternatives to defocus adjustment offer significant advantages in systems where electronic tuning is desirable or where mechanical elements are unfeasible, and thus have seen widespread adoption, for example in miniaturization [2]. A widely employed technique for non-mechanical correction is via the application of an electrowetting lens [3]. These lenses consist of a well filled with water, with a small droplet of non-polar liquid deposited at the bottom of the well. By applying a high voltage across the bottom of the well, the shape of the fluid boundary can be distorted, creating the desired tunable defocus shape. While this technique is useful for a wide range of applications, it is limited to the generation of the defocus mode or other simple monotonically varying radially symmetric modes. Furthermore, it requires relatively high voltages to achieve this degree of tunability. These challenges mean that for higher order modes there are no suitable technologies that serve as a low-cost alternative to SLMs or deformable mirrors. While deformable phase plates have become available recently as a third alternative technology [4], these devices are still physically complex, and suffer from many of the drawbacks of their predecessors.

Nematic liquid crystals (LCs), which are a key element in SLM technologies, are a class of birefringent material whereby the molecules can align, on average, along the same direction. By reorienting the LC bulk with an applied electric field, the refractive index that light experiences on passing through the LC layer can be similarly adjusted. The local orientation of the LC is thus defined by a spatially varying pseudo-unit vector known as the director, $\overrightarrow{n}$. This continuously tunable nature of a nematic LC has already been explored for the creation of defocus lenses. For example, some of the earliest experiments on LC-based defocus lenses come from Sato et al. [5]. In these early attempts, a nematic LC was capillary filled between two curved substrates, creating a tunable lens. Other attempts to create these devices have involved patterning the electrodes within the device. By doing so, a laterally nonuniform electric field could be applied across the LC bulk, providing the desired lens shape. While these complex electrode patterns do increase the overall manufacturing cost of the device, these attempts have been encouragingly successful, employing both the use of spiral [6] and branching resistive electrodes [7]. Recent innovations with this technique have expanded even further, and are able to replicate many different commonly used lenses, such as a cylindrical, spheric, and defocus lenses [8]. However, these developments often need to employ the use of multiple AC signals each with their own adjustable amplitude, frequency, and phase, adding to the required electrical bulk needed to operate the device.

Photopolymerization of the LC also offers a potential alternative to these techniques wherein the nematic LC is dispersed with a reactive mesogen and photoinitiator. By exposing the resulting LC mixture to a wavelength of light that overlaps with the absorption spectrum of the photoinitiator, the alignment of the LC director field can be preserved as a result of the formation of a polymer network. This enables the director to be fixed regardless of subsequent changes to the amplitude of the applied electric field. Initial explorations of this technique were first carried out by using photomasks or beam-shaped lasers [9,10,11]. However, these techniques do not readily enable the production of higher resolution devices as well as modes that are more complex than a simple defocus. Encouragingly, the rise of direct laser writing (DLW) offers us an alternative.

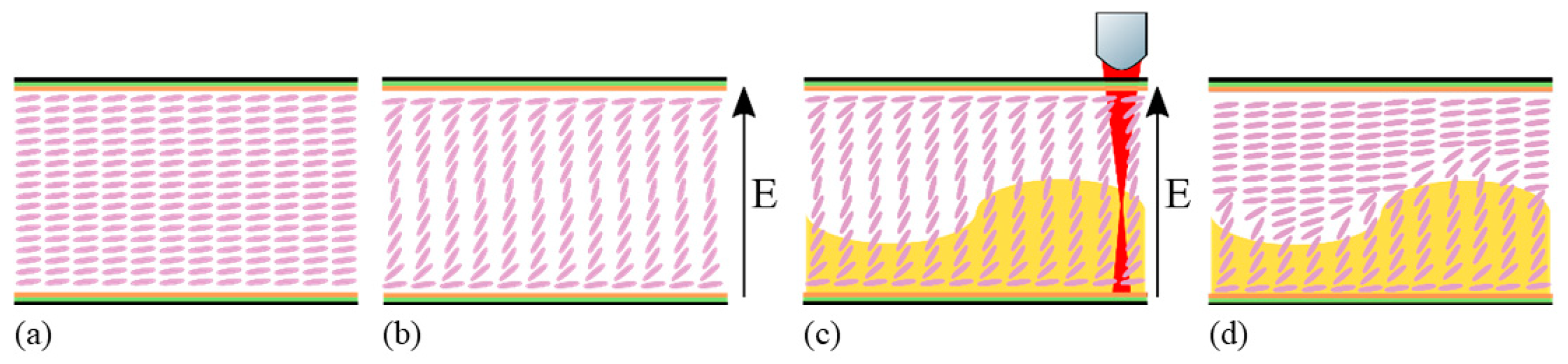
While DLW in photoresists laid the foundation [12], the manufacturing process can be significantly streamlined and enhanced by writing structures directly into the polymerizable LC. Here, the LC mixture is directly polymerized using a femtosecond pulsed laser. By varying the height of the polymerized LC structure across the device, we can selectively fix the average refractive index, thereby creating new refractive index profiles. Combining two-photon polymerization and a 3D translation stage, we can polymerize the LC bulk with high spatial resolution, allowing for the replication of many Zernike modes. The principle behind this approach is illustrated in Figure 1. Recently, in Xu et al. [13], we demonstrated the versatility of such an approach, replicating one Zernike mode from each of the first five non-trivial orders of Zernike modes, with our tilt device demonstrating a root mean square (RMS) phase error of no more than 0.27 rad for all amplitudes.

In this study, we present new LC devices that demonstrate important extensions to the versatility of this approach. First, we use DLW to demonstrate an LC device that generates the defocus mode $\left(Z_2^0\right)$ before presenting results for a seventh-order Zernike polynomial coma $\left(Z_7^1\right)$, matching the modal complexity delivered by liquid phase plates [4]. Finally, we further demonstrate that this technology may soon allow us to manufacture low-cost devices that are compatible with commercial optics, by demonstrating a 2 mm-wide spherical aberration correction device—64 times larger in area than those presented in Xu et al. [13]. Each device functions in transmission mode and is electrically simple to operate, requiring only a single electrode pair tuned between 0 and 10 volts. The devices are able to deliver wavelength-scale aberration correction up to a total phase magnitude of more than $2\pi$ rad. The coma device is also significantly larger in diameter than previous attempts, measuring $400$ μm across, while the demonstrator defocus lens measures $250$ μm. These sizes were chosen for ease of fabrication, although we expect that the manufacturing process could be readily scaled up to provide much larger millimeter-scale diameters if desired.

2. Materials and Methods

2.1. Design and Simulation

Our design methodology for these devices followed the approach described in detail in Xu et al. [13]. The devices were manufactured in glass cells with a gap (corresponding to the thickness of the LC layer) of $20$ μm. The devices were treated with antiparallel rubbing to allow for a planar alignment of the LC molecules at 0 V.

To determine the average refractive index of the LC at various voltages, we employed a one-constant approximation of the elastic constant, $K$, with a variable electric field. Noting that for the birefringent LC, the dielectric permittivity for an electric field applied perpendicular to the substrate of the device is described as

$${\mathsf{ϵ}}_{zz}\left(x,y,z\right)={\mathsf{ϵ}}_{\perp }\cos \left(\theta \left(x,y,z\right)\right)+{\mathsf{ϵ}}_{\left|\right|}\sin \left(\theta \left(x,y,z\right)\right),$$

(1)

where $\theta$ is the angle of the local director $\overrightarrow{n}$ relative to the glass substrate of the device [14]. With the permittivity for the polymerized sections being fixed at high voltage and approximated as ${\mathsf{ϵ}}_{zz}\left(x,y,z\right)={\mathsf{ϵ}}_{\left|\right|}$, we noted that we could therefore assume a constant dielectric displacement $D=\mathsf{ϵ}E$, which implied that the spatially varying electric field $E_{zz}\left(z\right)$ could be approximated as

$$E_z\left(z\right)=\frac{V}{{\mathsf{ϵ}}_{zz}\left(z\right)}{\left({{\displaystyle \int }}_0^{d_{tot}}\frac{1}{{\mathsf{ϵ}}_{zz}\left(z\right)}dz\right)}^{-1},$$

(2)

Since the total voltage $V={{\displaystyle \int }}_0^{d_{tot}}E\left(z\right)dz$ across the device was known, the spatially varying electric field could easily be calculated. This allowed us to easily solve the relevant one elastic constant approximation of the LC Euler Lagrange equation of motion [14]

$$\frac{d\mathsf{\theta }\left(x,y,z\right)}{dt}=K\frac{d^2\mathsf{\theta }}{d{z}^2}+\mathsf{\Gamma }\left(x,y,z\right)\sin \left(\theta \left(x,y,z\right)\right)\cos \left(\theta \left(x,y,z\right)\right),$$

(3)

where $\mathsf{\Gamma }\left(x,y,z\right)$ is the drive term $\mathsf{\Gamma }\left(x,y,z\right)=\Delta \mathsf{ϵ}{\mathsf{ϵ}}_0{E}_z{\left(x,y,z\right)}^2$. For the nematic LC E7, we approximated the elastic constant $K$ as 1.4 × 10⁻¹¹ N [15]. The spatially varying local refractive index $n\left(z\right)$ of the LC is related to the director field through the relation

$$n\left(z\right)=\frac{n_e{n}_0}{{\left(n_e^2{\cos }^2\theta \left(z\right)+n_0^2{\sin }^2\theta \left(z\right)\right)}^{1/2}},$$

(4)

where $n_e$ and $n_o$ are the extraordinary and ordinary refractive indices, respectively [14]. This allowed us to calculate the relevant retardance,

$$\Delta \mathsf{\varphi }={{\displaystyle \int }}_0^{d_{unpol}}n\left(z\right)kdz+n_{o}k{d}_{pol}$$

(5)

where $d_{pol}$ is the thickness of the polymerized area, and $d_{nonpol}$ is the thickness of the non-polymerized area. As the LC was polymerized in the presence of a large applied voltage, when the LC was held completely in a homeotropic alignment, the refractive index of the polymerized section was approximated to be the ordinary refractive index $n_o$. To determine the average refractive index $n_{avg}$ of these devices, we could finally scale the retardance by dividing it by the wavenumber and device thickness,

$$n_{avg}=\Delta \mathsf{\varphi }/\left(k{d}_{\mathrm{tot}}\right),$$

(6)

where $d_{tot}$ is the total bulk thickness, which is of course $d_{tot}=d_{pol}+d_{nonpol}$. The average refractive index for a device with a $20$ μm-thick LC layer at various voltages is shown in Figure 2a. By also simulating the varying average refractive index of the device at other voltages, we could predict the expected response and tunability of the manufactured device.

We were then able to solve for the ideal polymerized region of the defocus and coma devices using the relation

$$Z\left(x,y\right)=\left(n_{avg}\left(x,y,d_{pol}\right)-n_o\right)k{d}_{tot}+c_{1}x+c_{2}y+c_3{x}^2+c_4{y}^2+c_{5}xy,$$

(7)

where $Z\left(x,y\right)$ is the arbitrary wavefront desired, such as a Zernike mode, and the terms $c_n$ are used to correct the tilt and curvature of the stage, as well as a change in voxel size introduced by the surrounding polymer LC bulk. The ideal polymer thickness maps for the defocus $(Z_2^0)$, high-order coma $(Z_7^1)$, and spherical $(Z_4^0)$ are shown in Figure 2b, Figure 2c, and Figure 2d, respectively, assuming no corrections $c_n$ are necessary. We found that we could switch from 0 to $2\pi$ phase spatially in a minimum distance of $20 \mathsf{\mu }\mathrm{m},$ approximately the total thickness of the LC cell. A maximum phase amplitude of $2\pi$ rad was chosen to prevent the thickness of the polymerized LC regions from exceeding $8$ μm, the maximum polymerization height that could be achieved by the DLW system in a single pass of the laser. As the devices were polymerized at a high voltage, a greater polymerization height generally corresponded to a lower phase shift as the refractive index of the polymer bulk is nearly uniformly $n_o$.

2.2. Experiment

Each laser-written mode was manufactured in an Instec LC2-20 glass cell with 20 μm glass spacer beads. The inner surfaces of the glass substrates were coated with Indium Tin Oxide (ITO) electrodes and an antiparallel rubbed polyimide alignment layer. These cells were then capillary filled with an LC mixture consisting of 79 wt.% E7 (Synthon Chemicals Ltd., Bitterfeld-Wolfen, Germany), with 1.0 wt.% Irgacure 819 (Ciba-Geigy, Basel, Switzerland) photoinitiator and 20 wt.% RM257 (1,4-Bis-[4-(3-acryloyloxypropyloxy) benzoyloxy]-2-methylbenzene (Synthon Chemicals Ltd., Bitterfeld-Wolfen, Germany) reactive mesogen. This mixture was chosen because it exhibits a nematic LC phase at room temperature and the dielectric, optical, and elastic properties have been characterized extensively, though it is sensitive to 1-photon polymerization for wavelengths shorter than 460 nm. Two wires were soldered to the two ITO electrode surfaces to allow the application of the electric field.

The devices were then manufactured using the two-photon DLW system described in Xu et al. [13] Each LC device was mounted onto a 3D translation stage composed of an Aerotech ANT95XY 2D translation stage with an ANT95v vertical translation stage and polymerized using a Spectra Physics Mai-Tai Titanium-Sapphire laser (λ = 780 nm) providing 100 fs pulses at an 80 MHz repetition rate, focused through a 0.45 NA lens at 20 × magnification. Exposure to the laser was performed while an AC square wave signal of 100 V RMS was applied to the devices using a Tektronix AFG3021 signal generator and an FLC F10AD voltage amplifier, ensuring a homeotropic alignment of the director for the polymerized LC bulk. Each device was created by writing in a raster pattern, with a continuously adjusted height as determined by Equation (7). This pattern was written with a pixel size of approximately 0.5 µm and a nominal writing speed of 1.25 mm/sec.

Next, the devices were imaged using polarizing optical microscopy (POM). Every modal corrector underwent imaging while positioned between crossed polarizers. This imaging process utilized an Olympus BX51 polarizing optical microscope paired with a QImaging R6 Retiga Camera. The magnification was set to 20× using an Olympus LMPLFLN20x objective lens. To maintain specific imaging conditions—preventing additional polymerization and ensuring the observation of a narrow band retardance—a narrowband Thorlabs FB660-10 filter was incorporated into the illumination path. To facilitate imaging, the setup involved connecting the devices to a Multicomp MP750510 AC square wave signal generator operating at a frequency of 1 kHz. The imaging was performed across a range of RMS Voltages, varying from 0 V to 10 V.

3. Results

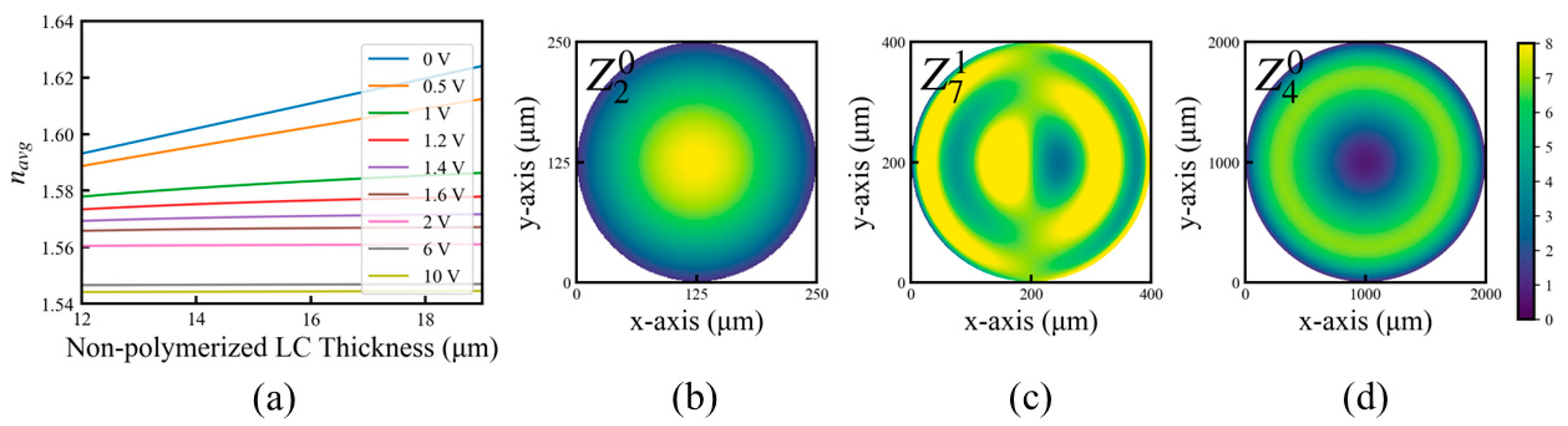
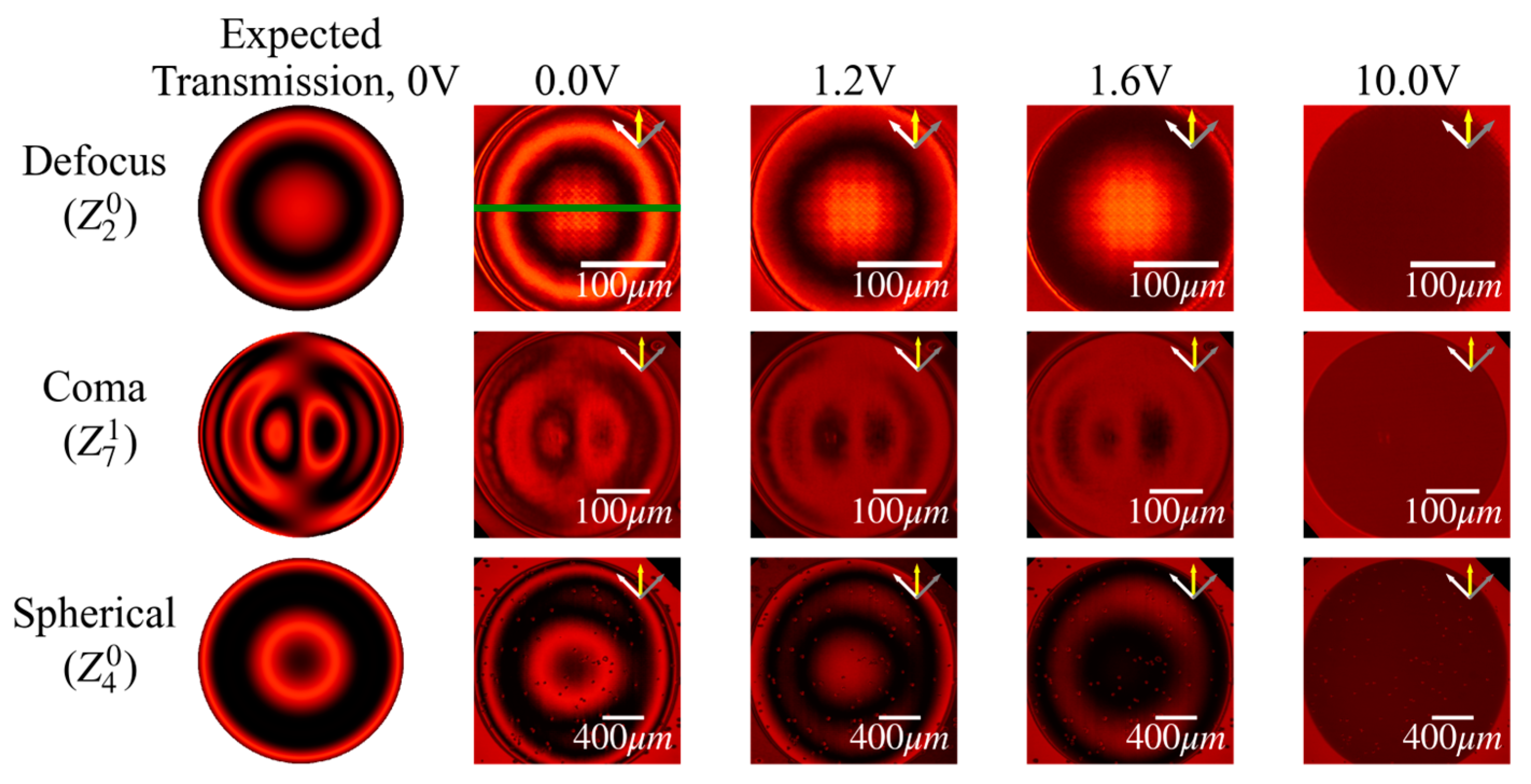
Figure 3 shows the POM images of the manufactured correction devices with a 1 kHz AC voltage varying from 0 to 10 V RMS, compared with the idealized transmission values at 0 V for the defocus and coma respectively. The rise time of the device was measured to be of the order of 10 ms, while the fall time was measured to be of the order of 100 ms. We found the rise and fall times, along with the maximum voltage necessary, to be relatively stable over long-term operation. As shown in the figure, we saw that the device displayed its maximum phase amplitude with no voltage applied. As the voltage was increased, the amplitude of the phase decreased, becoming fully transparent around 10 V. These figures demonstrate good agreement between the actual measured and ideal modes at 0 V. We noted that the spherical device was significantly larger than the devices in our previous report in Ref. [13], measuring 2 mm in diameter compared to the previously achieved 250 μm with an area that was 64 times larger, while the coma device presented in this figure was significantly more complex, presenting a Zernike profile two orders higher, demonstrating the versatility and scalability of this manufacturing technique.

In Xu et al. [13], we were able to demonstrate that this laser writing technique could reliably manufacture polymerization structures to the desired specifications with sufficient precision. As such, we also estimated the retardance in the defocus device. For a device placed at 45° located between two crossed polarizers, the imaged intensity of the device $I$ is proportional to the retardance via $I={\sin }^2\left(\Delta \mathsf{\varphi }/2\right)$. While this does mean that multiple retardances can produce the same intensities, we can be generally confident that the maximum polymer thickness, and therefore the minimum retardance, occurred at the center of the defocus device. Thus, we expected the retardance of the lens to increase roughly monotonically as the position moved towards the edge of the device. By defining $\mathsf{\varphi }=2\arcsin \left(\sqrt{I}\right)$, we noted that all phase amplitudes of the form $2\pi m+{\left(-1\right)}^n\mathsf{\varphi }$, where $n,m$ are integers, were set to produce the same amplitude. As such, we could increment the appropriate index $n,m$ as we measured the intensity further from the center of the device to estimate the correct phase. The process was then repeated, moving outwards from the center of the correction device until the dataset was exhausted.

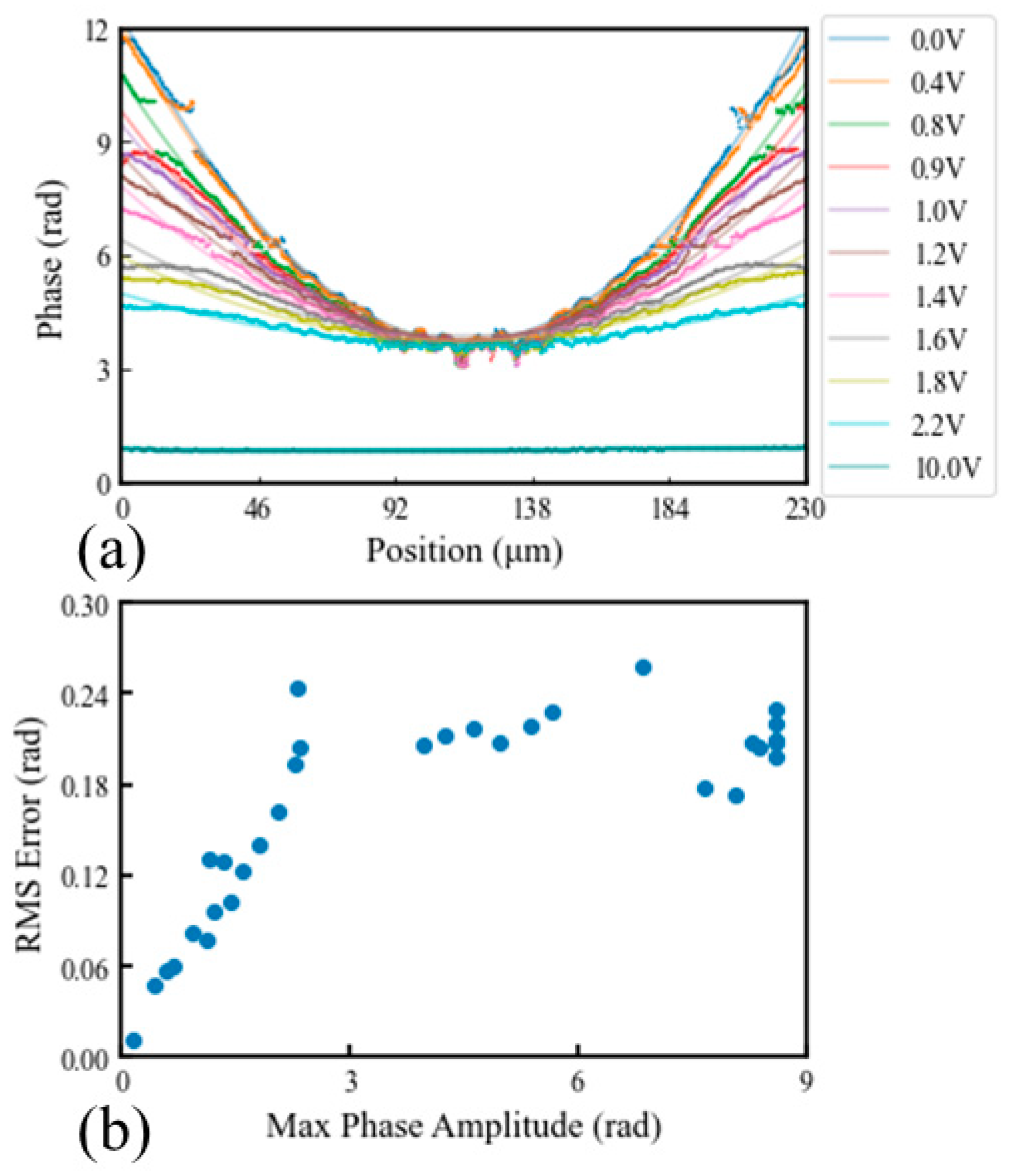
These estimates for the defocus lens, extracted along the green line shown in Figure 4, as well as the ideal parabolic phase shape at each voltage, are shown in Figure 4a. While the device measured $250$ μm across, for these estimates we only considered the central $230$ μm to be the aperture of the device for the purpose of phase measurements. These measurements were then compared to the ideal profile at each voltage, with the ideal phase at each voltage shown with a solid line of the same color, and the RMS difference between the two shown in Figure 4b. The total RMS error is defined as

$$Error={{\displaystyle \sum }}_{x=0}^{nx}{\left(\Delta \mathsf{\varphi }\left(x\right)-{\mathsf{\varphi }}_{ideal}\left(x\right)\right)}^2$$

(8)

where $\Delta \mathsf{\varphi }\left(x\right)$ is the estimated phase across the lens calculated with this method, and ${\mathsf{\varphi }}_{ideal}\left(x\right)$ is the closest parabolic fit calculated with a least square fitting method. As demonstrated in this figure, the RMS error was below 0.27 rad for all voltages. This value corresponds to an effective Strehl ratio of $0.93$, demonstrating high precision. The largest deviations were seen in the intermediate voltages, around 1.6 V. These deviations were likely introduced by non-linearities in the LC response, as this voltage was close to the expected Fréedericksz threshold voltage of the nematic LC used in this work. At this voltage, extreme gradients in polymer height can force the reorientation of the director field at a lower voltage than otherwise predicted by the one elastic constant approximation used during simulation.

4. Discussion

We have used two-photon polymerization direct laser writing to address one of the most often tackled problems in adaptive optics, the creation of a tunable defocus lens. The devices are simple to operate, offering single electrode pair wavelength scale tuning in the transparent mode, to a total phase amplitude of more than $2\pi$ rad with no necessary electrode patterning. These devices showed accurate phase reproduction, with the defocus device demonstrating an RMS error no greater than 0.27 rad. We further expanded on this work by creating a novel seventh-order Zernike polynomial device, corresponding to the third order coma ($Z_7^1$). The device was both larger than previous attempts, measuring $400$ μm across compared to the previous $250$ μm devices reported in Ref. [13], allowing for easier integration into the imaging path, as well as two orders of polynomial higher in complexity than any previous attempt, again demonstrating versatility of this correction method. Finally, we presented a 2 mm-wide spherical aberration correction device. This device is significantly larger than previous attempts and is large enough to be integrated into standard optical components with no additional beam shaping required.

These results show that the fabrication method has potential to create correction devices for arbitrary higher-order modes. Both the vertical and lateral resolutions are limited only by the physical properties of the LC, and are able to perform a full $2\pi$ rad phase ramp in 10 s of microns. We have demonstrated here that by creating larger devices, increasingly complex phase patterns can be generated. For millimeter-sized devices that are easily combined with commercial off-the-shelf optics components, this feature is more than sufficient for the generation of Zernike polynomials on the same order as those generated by deformable mirrors. For applications where the correction of only a few modes is necessary, we expect that these devices will offer a versatile, cost-effective alternative to more traditional adaptive optics elements and have the potential for major impact by allowing the inclusion of adaptive optics technology in a wider range of applications than previously possible.