Abstract
Driven by life-science applications, a mega-electron-volt Scanning Transmission Electron Microscope (MeV-STEM) has been proposed here to image thick frozen biological samples as a conventional Transmission Electron Microscope (TEM) may not be suitable to image samples thicker than 300–500 nm and various volume electron microscopy (EM) techniques either suffering from low resolution, or low speed. The high penetration of inelastic scattering signals of MeV electrons could make the MeV-STEM an appropriate microscope for biological samples as thick as 10 m or more with a nanoscale resolution, considering the effect of electron energy, beam broadening, and low-dose limit on resolution. The best resolution is inversely related to the sample thickness and changes from 6 nm to 24 nm when the sample thickness increases from 1 μm to 10 μm. To achieve such a resolution in STEM, the imaging electrons must be focused on the specimen with a nm size and an mrad semi-convergence angle. This requires an electron beam emittance of a few picometers, which is ~1000 times smaller than the presently achieved nm emittance, in conjunction with less than 10−4 energy spread and 1 nA current. We numerically simulated two different approaches that are potentially applicable to build a compact MeV-STEM instrument: (1) DC (Direct Current) gun, aperture, superconducting radio-frequency (SRF) cavities, and STEM column; (2) SRF gun, aperture, SRF cavities, and STEM column. Beam dynamic simulations show promising results, which meet the needs of an MeV-STEM, a few-picometer emittance, less than 10−4 energy spread, and 0.1–1 nA current from both options. Also, we designed a compact STEM column based on permanent quadrupole quintuplet, not only to demagnify the beam size from 1 m at the source point to 2 nm at the specimen but also to provide the freedom of changing the magnifications at the specimen and a scanning system to raster the electron beam across the sample with a step size of 2 nm and the repetition rate of 1 MHz. This makes it possible to build a compact MeV-STEM and use it to study thick, large-volume samples in cell biology.
1. Introduction
Predictive power on living organisms requires a deep knowledge of cellular structure, which includes both the hierarchical organization and the interaction of components. These insights are essential for predicting and controlling biological function in support of the Department of Energy (DOE) research missions and life-science applications. One appealing method to provide such knowledge with nanometer resolution is cryo-Electron Tomography (cryo-ET), where biological samples are fast-frozen to preserve their native hydrated states, then imaged at liquid nitrogen temperature to reduce radiation damage during the measurement. Cryo-ET has been successfully employed to resolve subcellular structures, with the capability of achieving nanometer resolution for the entire sample as well as atomic resolution for abundant molecular components through averaging those structures [1,2,3,4,5,6,7].
Due to the low electron dose required by biological samples to reduce the radiation damage and the short electron elastic mean free path at 100–300 keV, cryo-ET limits the sample thickness to 300–500 nm [8,9,10,11]. To visualize large/thick frozen biological samples (e.g., cells and tissues), various volume electron microscopy (EM) techniques have been developed [12,13]. In array tomography, sections prepared by microtome, cryo-microtome, or ultramicrotome are imaged using scanning electron microscopes (SEMs) or TEMs. The resolution is limited by the section thickness ). Alternatively, the top surface is imaged after cutting with an ultramicrotome in serial block face SEM (SBF-SEM) or with a focused ion beam (FIB) in FIB-SEM. In both SBF-SEM and FIB-SEM, the resolution is limited by the slice thickness (around ). Moreover, to ensure that biological samples are as close as possible to their native state, cryo-FIB-SEM has been developed [14,15,16,17,18]. Resolution in depth can be as high as a few nanometers. However, depending on the imaging parameters, the imaging process often takes 15–25 s, and the milling process takes 7–36 s [15]. A total of 15–20 h is required to image a 10 μm thick sample with a slice thickness of 8 nm and an area of 3 × 2 μm2 (8 nm pixel size) [18]. In addition, there are charging artifacts due to positively charged lipid deposits, curtaining artifacts due to density and content changes, and linear artifacts due to the milling process [14,16]. Thus, being able to study thick samples rapidly and efficiently while maintaining nanoscale resolution is highly desirable, as it will significantly increase the rate of structural observations and determinations.
In cryo-EM or cryo-ET, with the assumption of “Weak Phase Object Approximation” (WPOA), the one-to-one mapping between the exit electron wave function and the projected potential of the specimen can be established. The image is mainly formed by coherent interference (i.e., elastic scattering) among the electron waves (i.e., the phase contrast, which strongly depends on defocus, spherical aberration, objective aperture size, and illumination conditions). The elastically scattered electrons contribute to the signal, while inelastically scattered electrons contribute to the background noise, thus decreasing the signal-to-noise ratio (SNR). As shown by M. Du et al. [19], when the ice is thicker than 1.7 μm in a TEM, there are essentially no elastically scattered electrons within the detectable angular range at 300 keV. Thus, conventional cryo-EM and cryo-ET are not suitable to study thick samples using WPOA.
As shown [20,21,22,23], STEM has been employed to study frozen biological samples up to 1000 nm thick, as opposed to 300 nm thick biological samples imaged by cryo-EM and cryo-ET using 200–300 keV TEMs [22]. In STEM, the electron beam is focused on the plane of the specimen, and there is no image-magnifying lens behind the specimen. The image is formed by mapping detector counts point by point to scan positions. The bright-field (BF), annular dark-field (ADF), and high-angle annular DF (HAADF) images are formed by collecting electrons within small (e.g., ), medium (e.g., ), and high (e.g., ) angles, respectively [24,25,26]. For cryo-samples, objects with higher concentrations of heavy atoms will be preferentially detected by HAADF, forming the so-called “Z-contrast” (Z is the atomic number); in addition, Bragg-scattered electrons will be collected by ADF, forming the so-called “Diffraction-contrast” [27]. The mass density variations in different parts of the sample are detected by BF imaging.
As the allowable sample thickness depends on the electron energy and image formation mechanism, we propose to implement a mega-electron-volt Scanning Transmission Electron microscope (MeV-STEM) mainly based on amplitude contrast instead of phase contrast. In a TEM for structural biology, an objective lens focuses the transmitted electrons to form an image based on phase contrast. In a STEM, a focused electron beam scans across the sample in a raster pattern, and the transmitted electrons are collected to form a mainly amplitude-contrast image. In a STEM, any severe energy loss due to multiple inelastic scattering and large angle deviation that occurred during the electron thick-sample interaction will not affect a STEM image in a similar way regarding a TEM image since there exists no lens between the sample and the detector; in a TEM, those effects would make the image resolution much worse via chromatic and spherical aberrations. Thus, STEM is not limited to the sample being ultra-thin, enabling the study of thicker samples or 3D materials. However, a full understanding of electron scattering and attainable spatial resolution in biological samples that are a few micron thick or more represents a highly intricate undertaking, necessitating substantial dedication and resources. It is important to note that delving into these intricacies is beyond the scope of this paper. This will be our future studies.
As we will discuss in the STEM imaging below, at 300 keV, the unscattered, single elastic scattered and multiple (named plural) elastic scattered electrons emerging from the sample drop to less than 1%, while the inelastic scattered electrons stay at 31% after a 1 μm thick ice layer. Furthermore, the inelastic scattered electrons are still above 1% after passing through a 4 μm thick ice layer. If the electron energy is increased to 3 MeV, the inelastically scattered electrons will remain at 63% after passing through a 10 μm thick ice layer and 40% after passing through a 20 μm thick ice layer. Thus, compared to conventional TEM, STEM can image much thicker samples (). This makes MeV-STEM extremely appealing to life-science applications: MeV-STEM could be used to study intact cells with a sample thickness of 10 µm or more. For the first time, such a system will be able to image large biological samples rapidly and efficiently (subcellular structures, biomolecular components, and bio-reactions in cells) while maintaining nanometer resolution ().
With conventional round lenses and DC accelerating technology, the 3 MeV electron microscope needs to be more than 10 m tall, and the lens has usually 1 m in diameter [28]. Instead, we designed a generic MeV-electron superconducting radio-frequency (SRF) Linac and a STEM column based on the novel quadrupole quintuplets pioneered at Brookhaven National Laboratory for MeV electron microscopes [29]. With the permanent quadrupole quintuplet, the lens diameter is only around a centimeter, and the microscope can fit in a small laboratory. Such an MeV-STEM column will not only demagnify the beam size but also have the freedom of changing the beam size at the specimen, together with an adjustable aperture, in a broad range from 2 nm to 16 μm.
2. Results
2.1. Design Parameters of Achieving 6–24 nm Resolution for a 1–10 μm Thick Bio-Sample
2.1.1. Model Electron Cross-Section Formulae
The angular distribution of scattering from a target atom can be described by the differential scattering cross section. For elastic scattering, the differential cross section follows the Rutherford formula for the screened Coulomb potential of the nuclear charge. In the Wentzel approximation, the differential cross section for elastic scattering in first-order Born approximation becomes [22]:
where σel is the elastic scattering cross section, Ω is the solid angle, Z is the atomic number, E is the electron energy, E0 is the rest energy of the electron, aH is the Bohr radius (0.0529 nm), θ is the scattering angle, θ0 is the characteristic scattering angle below which 50% of the electrons are scattered into, and λ is the electron wavelength. The characteristic scattering angle for oxygen is 15 mrad for 200 keV electrons. Integrating Equation (1) yields the total cross section [22]:
The angular dependence and the cross section of inelastic scattering can be approximated with a Bethe model [22,26]:
where σinel is the inelastic scattering cross section, θE is the characteristic angle that is responsible for the decay of the inelastic scattering, and DE is the mean energy loss from a single inelastic scattering event (e.g., 39.3 eV for amorphous ice [19]). An inelastic scattering is concentrated within much smaller angles than elastic scattering. The characteristic angle θE is typically of the order of 0.1 mrad for 200 keV electrons.
The total cross section for scattering from amorphous ice is [30]
where and are the scattering cross sections of oxygen and hydrogen atoms in amorphous ice. As pointed out by Jacobsen et al. [31], the inelastic scattering of hydrogen was not accurate. Thus, the approximation proposed by Jacobsen et al. was followed.
The chance of an electron undergoing event i (e.g., elastic scattering, inelastic scattering) within a sample thickness dt is given by
where is the cross section for event i, is the sample density, and is the scattering coefficient.
After interacting with the sample, the electron would fall into the following five categories [19,31], depending on the respective scattering coefficients (Equation (7)):
- Inoscat designates electrons undergoing no scattering;
- I1el designates electrons being elastically scattered once, remaining within the detector collection angles;
- Iel,plural designates electrons undergoing multiple elastic scatterings without any inelastic scatterings and remaining within the detector collection angles;
- Iinel designates electrons undergoing at least one inelastic scattering and remaining within the detector collection angles;
- Iout designates electrons being scattered outside the detector collection angles.
The sum of these five types of electrons is equal to the incident electron beam intensity I0:
and the corresponding scattering coefficients are:
where KI,in is the scattering coefficients for category I (“el” including single to multiple elastic scattering, and “inel” includes at least one inelastic scattering) within the detector collection angles and can be estimated by numerically integrating Equations (1) and (3) then multiplying the sample density (Equation (5)), and KI can be estimated by numerically integrating Equations (1) and (3) over all possible angles. The cross sections of oxygen in amorphous ice are calculated using Equations (1)–(3) and listed in Table 1. For detector collection angles from 0 to 10 mrad, the scattering coefficients for oxygen in amorphous ice are calculated using Equation (7), and the results are listed in Table 2.
Inoscat + I1el + Iel,plural + Iinel + Iout = I0

Table 1.
Electron scattering cross section for oxygen from 100 keV to 3 MeV. θ0 and θE are the characteristic scattering angles for elastic and inelastic scattering.

Table 2.
Scattering coefficients for electrons to be scattered from 100 keV to 3 MeV with a collection angle from 0 to 10 mrad (nm−1).
How the electron intensity changes while traveling through the specimen is described in the Appendix A in detail. A plot of the electron distributions in the five categories is shown in Figure 1. As shown in Figure 1a, the single elastic scattered electrons (blue dashed line) and plural (multiple) elastic scattered electrons (black dashed line) emerging from the sample drop to less than 1% after a 1 μm thick ice layer, and the inelastic scattered electrons (red dashed line) drop below 1% after a 4 μm thick ice layer at 300 keV. However, if the electron energy increases to 3 MeV, the single elastic scattered electrons (blue solid line) drop below 1% after a 2 μm thick ice layer (sample thickness doubled), while the plural scattered electrons (black solid line) drop below 1% after a 3.5 μm thick ice layer. The inelastically scattered electrons still stay at 63% after a 10 μm thick ice layer and 40% after a 20 μm thick ice layer, shown as the red solid line curve. In addition, Figure 1c clearly indicates the benefit of increasing the electron beam energy—the characteristic angle of elastic scattering (θ0) decreases from 22.3 mrad to 2.1 mrad (a factor of 10) with the increase in beam energy from 100 keV to 3 MeV; hence, a detector with fixed angles (e.g., 0–10 mrad) collects much more multiple scattering events as signals in the 3 MeV case compared to low-energy cases. Such difference increases with the increase in sample thickness (see Figure 1b). Therefore, an MeV-STEM is capable of imaging much thicker samples (10 μm or thicker) than a conventional TEM, with a compromised resolution depending on the sample thickness.
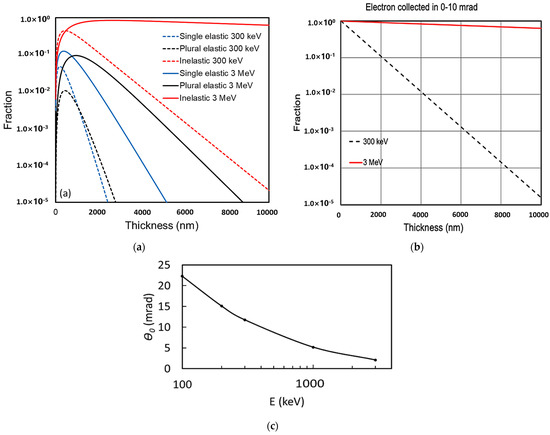
Figure 1.
(a) Electrons scattered in ice as a function of thickness at incident electron energies of 300 keV (dashed lines) and 3 MeV (solid lines) including single elastic (blue), plural elastic (black), and inelastic scattering (red). (b) Total electrons collected within 0–10 mrad (the sum of all electrons shown in panel (b) decreases as the sample thickness increases). Black dash line: 300 keV electrons; red solid line: 3 MeV electrons. (c) Characteristic angle of elastic scattering (θ0) as a function of the beam energy.
2.1.2. Image Contrast and Resolution
To improve the resolution in a STEM, the probe size should be focused as small as possible onto a specimen (e.g., no more than 2 nm in diameter for the targeted resolution). As the electron probe rasters over the specimen point by point, the accuracy of the steering coil to shift the electron probe (scanning accuracy) should be no more than half of the probe size, 1 nm. When the sample is thick (more than 1000 nm), the angular distribution of scattered electrons produces a spatial distribution that broadens the incident electron probe normal to the beam direction (Figure 2a [22]). The broadening of the probe in thick biological samples is, to first approximation, governed by the probe semi-convergence angle and the scattering of electrons in the sample. When a point electron probe is focused on the center of the specimen, the minimal geometrical broadening of the exiting electron probe dbottom is
where t is the sample thickness, and is the beam semi-convergence angle (in the range of ). As shown in Figure 2, the larger the semi-convergence angle, the larger the exiting beam size.
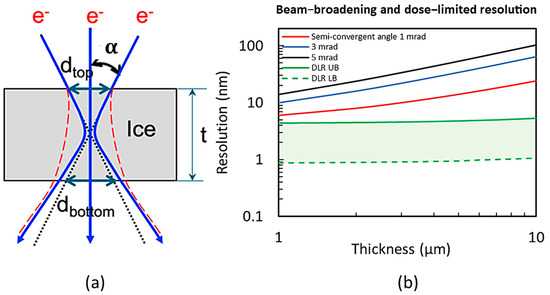
Figure 2.
(a) Schematic of electron beam broadening. This represents the vacuum case with the assumption of the electron probe being focused on the center of the specimen (blue curves). The red dashed curves show the estimated broadening of the beam in amorphous ice [22]. (b) The resolution (in diameter), considering the electron beam broadening in the sample as the limiting factor, is shown as a function of the sample thickness for three different semi-convergent angles, 1 mrad (red), 3 mrad (blue), and 5 mrad (black), respectively. Also, the dose-limited resolution (DLR) is plotted as a function of the sample thickness for DLR UB (see details later) with the image contrast C = 0.1 (green solid) and DLR LB with C = 0.4 (green dash), respectively. Here, the image contrast C is defined as the density difference between the features and the background over the density of the background.
The broadening of the probe due to electron scattering can be estimated based on a wave optical multislice algorithm [32,33]. The plural elastic scattering of electrons at 200 keV in vacuum and amorphous ice has been estimated by Wolf et al. [22]. When multiple scattering is included, the broadening of the probe is expected to be worse. Based on their estimation, a schematic beam broadening for 3 MeV is sketched in Figure 2a. Assuming the probe size of 2 nm in focus, the smallest beam size exiting the sample is estimated to be from 3 to 12 nm for a 1-to-10 μm thick sample. The corresponding resolution will be mainly limited by the electron beam broadening, ranging from 6 to 24 nm. (The absolute resolution of a sensor is determined by its Nyquist limit, which is twice that of the pixel size).
A dose-limited resolution (DLR) imposed by radiation damage of imaging electrons can be estimated using a standard formula [25,34]:
where , , , and are the signal-to-noise ratio, contrast, detective quantum efficiency of the detector, fraction of electrons that reached the detector (see Figure 1b), and characteristic electron fluence, respectively. In STEM mode, SNR (dose efficiency) is much smaller compared to the TEM case. To be able to resolve a feature in an image, needs to be minimum 3 or higher according to the Rose criterion [35], and we take in our estimation. The average electron dose limited by radiation damage is about 2 e−/Å2 in each image of a cryo-ET tilting series, typically consisting of 40–60 images collected at different tilt angles as measured for frozen-hydrated samples [22,23]. For a modern detector, such as a direct electron detector, is routinely achievable [34].
In thick frozen biological specimens, the density of different organelles and cells can exhibit significant variations. For example, the average protein density is 1.3–1.4 g/mL [36], the density of mitochondria is 1.19 g/mL [37], and the average density of bacteria E Coli is 1.1 g/mL [38,39]. As one of the goals of MeV-STEM is to image an intact frozen cell without cutting it into thin slices, the contrast of the frozen cell needs to be calculated for the estimation of the DLR. In a frozen cell, the most noticeable and thickest organelle is the nucleus. The nucleus is a dense fibrillar network of DNA, RNA, and proteins, normally around 5–10 μm in diameter in many multicellular organisms. Its density is about 1.4 g/mL [40]. Taking the observation of the minimal presence of ice layers above the top surface and below the bottom surface of a frozen cell in standard cryo-ET studies, the contrast of biological sample vs. amorphous ice can be estimated to be 0.4 (determined as the DLR lower bound, named DLR LB) and 0.1 (determined as the DLR upper bound, named DLR UB) for the nucleus and cell. The DLR for a 10 μm thick frozen biological sample is 1.1 nm for the nucleus. For other parts of a cell with a contrast of 0.1, the DLR for a 10 μm thick frozen biological sample is 5.3 nm.
The DLR is estimated as a function of the sample thickness for the upper bound with contrast (green solid in Figure 2b) and the lower bound with (green dash), whereas the fraction of electrons received by the detector is obtained from Figure 1b. Over the targeted sample thickness (<10 μm), the DLR is smaller than the resolution limited by the beam broadening (red curve in Figure 2b), and it likely will not limit the ultimate resolution of an MeV-STEM. Thus, the resolution in MeV-STEM is mainly limited by the beam semi-convergence angle and the beam size. To achieve higher resolution, the beam semi-convergence angle and beam size need to be as small as possible (e.g., 1 mrad, 2 nm in diameter).
2.1.3. Electron Beam Parameters for 6–24 nm Resolution with 1–10 μm Thick Bio-Sample
Biological samples are sensitive to radiation damage. The commonly used electron dose for cryo-ET is 100–120 e−/Å2 distributed among 40–60 images collected at different tilt angles. The average electron dose is about 2 e−/Å2 in each image. The allowable dose of electrons per beam position varies from 800 electrons to 5000 electrons when the beam size changes from 2 nm to 5 nm (Table 3). To form a 1024 1024-pixel STEM image at each tilt angle, it will take 1 s with 1 µs dwelling time for each scanning point, which is comparable to current 300 kV STEMs. Thus, the fourth design parameter is the beam flux: 800–5000 e−/µs, which converts to the current of 0.13 to 0.8 nA.

Table 3.
Allowable electron dose per spot across varying beam size to mitigate potential harm to the frozen biological sample.
The energy spread is determined by the criteria that the amount of the probe beam size blurring on the sample caused by the energy spread () of incident electrons and chromatic aberration () should be much smaller than the probe size on the specimen required by MeV STEM (see Equation (10)).
Here, is the aperture angle. We must design an optimal STEM column (see Beamline Optics section in detail) and constrain the electron beam energy spread [29]; thus, the ultimate probe size on the specimen is mainly determined by the electron beam emittance (the product of transverse size and semi-convergence angle at the beam waist).
In summary, to achieve nanometer spatial resolution for up to 10 μm thick frozen biological samples using MeV-STEM, there are important parameters to consider (see Table 4): (1) electron beam size (dsam): 2 nm; (2) semi-convergence angle (α): 1 mrad; (3) flux (I): 0.1–1 nA; (4) energy spread (∆E/E): <10−4 (see later section in detail); and (5) scanning accuracy (∆xcen): 1 nm.

Table 4.
Electron beam parameters for nanometer-resolution MeV-STEM.
2.2. Conceptual Design of MeV-STEM
Here, we will illustrate the possible design and implementation of MeV-STEM, based on a photocathode gun followed by accelerating section, an aperture, a STEM column, which includes three condenser lenses, an objective lens and scanning coils, a sample stage, and a detector. However, to meet the nm beam size and mrad semi-convergence angle on the specimen, the MeV-STEM requires an emittance of a few picometers (e.g., at the focal point, the product of a nanometer transverse beam size and an mrad semi-convergence angle being 1000 times smaller than currently achievable nanometer emittance), along with all other parameters listed in Table 4 being met simultaneously. We will show that the combination of an ultralow emittance electron source with the additional emittance reduction achieved using an optimized aperture can achieve these challenging parameters. This research will pave the way to construct a novel MeV-STEM, which has the potential of transforming our bioimaging capability in support of fundamental research in biological systems.
For the design of an MeV-STEM achieving a few-nanometer spatial resolution, we foresee the following major challenges:
- Obtaining a 2 nm sized electron beam with 1 mrad semi-convergence angle at the specimen in the pulse mode. The choice of the pulse mode is mainly due to its compatibility with the L-band (1–2 GHz) SRF Linac, which is applied to boost the electron energy up to a few MeV with RF frequency of 1.3 GHz (see detailed explanation in Section 2.3.2).
- Demonstrating the generation of an electron beam with ultralow emittance and energy spread (see Table 4), and low spatial-pointing jitter (a few angstrom on the sample) using a photocathode-based SRF gun or DC gun.
- Delivering the electron beam current at the specimen: 0.1–1.0 nA.
- Scanning the probe beam with the accuracy of half of the beam size at the specimen: 1 nm.
We focused on the design of three critical components required for the construction of the nanometer-resolution MeV-STEM instrument:
- MeV class electron source: a photocathode gun and optimized aperture can potentially deliver the electron beam with the required parameters in terms of emittance, energy spread, and average current. The reason why we choose a photoelectron gun will be explained in Section 2.3.2.
- STEM column: not only demagnify the electron beam from a micron size at the aperture to 2 nm on the specimen plane but also provide the flexibility to adjust magnification over a wide range.
- Electron beam scanning system capable of achieving a nanometer precision at the specimen.
We have performed electron beam transport simulations exploring two different approaches of the electron source for the MeV-STEM instrument: (1) DC gun, aperture, SRF cavities, and STEM column; (2) SRF gun, aperture, SRF cavities, and STEM column. Beam dynamic simulations show very promising results as they show that the condition exists for which the MeV-STEM requirements (see Table 4) can be met with both options. Also, we illustrate the design of a novel STEM column capable of demagnifying the beam size from 1 µm at the aperture to 2 nm at the specimen and varying such beam size from 2 nm to 16 µm, and a steering coil to scan the electron beam across the sample with 2 nm step size and 1 MHz repetition rate.
2.3. Critial Components
2.3.1. Photocathode Electron Source
The forementioned specifications imply a required transverse normalized emittance , which is presently beyond the state of the art that has been demonstrated in a photoinjector system but is not outside the bounds of feasibility, as we will show below. The emittance we mentioned earlier is the geometric emittance, which is , the Lorentz factor) times smaller than the normalized emittance . Here, and are the total energy and kinematic energy of the electron beam, respectively. A single electron per bunch at the gigahertz (GHz) repetition rate is sufficient to provide average current. This implies that the space charge effects will not be a factor in the dynamics, provided the source directly generates emittance. To minimize the source emittance, we naturally seek to minimize both source size and intrinsic mean transverse energy (MTE). High quantum efficiency (QE) and low-emittance electron beams provided by multi-alkali photocathodes make them of great interest for next-generation high-brightness photoinjectors. When operated with photon energy close to their workfunction, these photocathodes can provide electron beams suitable for ultrafast electron diffraction (UED) and/or ultrafast electron microscopy (UEM) by having a lower emittance and higher QEs compared to those of metals [41,42].
Even with a state-of-the art photoemission MTE of as demonstrated in alkali antimonide photocathodes [41,42], normalized source emittance requires an RMS emission size of . However, due to the proximity of the optical diffraction limit, generating laser spots of even a few microns is a non-trivial task: photocathodes in most photoinjectors are typically operated in reflection mode in high electric fields of high-voltage DC or RF guns, and the final lens of the optical imaging system for the laser to the photocathode surface cannot be located closer than tens of centimeters from the cathode surface itself, which typically yields photoemission source sizes in RMS. However, a multi-alkali photocathode grown onto a glass substrate allows the photocathode to be operated in the transmission mode [43,44]. A photocathode plug based on the INFN/DESY geometry equipped with a short focal lens sitting right behind the photocathode (left panel in Figure 3) was successfully tested in an inverted-geometry DC gun [44]. Initial laser spot sizes smaller than (right panel in Figure 3) have been obtained by focusing the laser light via a lens with very short focal length placed in the ultrahigh-vacuum (UHV) environment of the gun, which is a few millimeters away from the back surface of the photocathode [43]. While nanopatterning of the photocathode either via work function spatial modulation or plasmonic enhancement [45] are viable routes to achieving emission sizes well below the optical diffraction limit of the drive laser, their compatibility with the low MTE photoemission conditions is not clear at present. As such, we opt for a simpler option: one would photoemit a dense bunch of electrons at the photocathode with the achievable minimum spot size (here we assume this to be μm) and use an aperture just downstream of the gun to clip down to 10 pm emittance and 1 electron/pulse. Space charge effects are significant in the dynamics up to the pinhole, and we ignore them downstream of the pinhole. Thanks to the large correlated divergence from space charge repulsion and intrinsic gun defocusing (called lateral position and energy chirp), in all simulations below the required pinhole diameters are in the order of tens of microns, for which sufficiently thick apertures can be manufactured via laser machining.

Figure 3.
A modified INFN/DESY cathode plug allows microscale spot size in transmission mode with a short focal lens. (Left panel): cross-section view of plug concept. (Center panel): Machined prototype. (Right panel): knife edge beam size measurement yielding RMS spot size at photocathode surface of .
We chose to explore two options for the photoelectron gun: a DC (constant voltage) source and an SRF gun. The DC photogun option is to be viewed as lower risk and cost but potentially lower performance. Several DC gun designs may be applicable here, including both traditional insulator [46] and compact inverted insulator [47] designs. DC guns delivering kinetic energy with photocathode electric field of are capable of reliable operation for many years. The DC gun we used in this study is the Cornell ERL photoinjector DC source, operated at 300 keV.
SRF guns promise much higher output kinetic energy and higher photocathode source field, and are compatible with low-emittance semiconductor photocathodes, and thus higher brightness performance is expected. Aside from the DC gun, efforts are in place to design and demonstrate the operation of photocathode in transmission mode in SRF guns [48]. However, interfacing replaceable photocathodes with some geometries of SRF guns is a complex engineering challenge; optimizing this interface is an active area of research [48,49]. The SRF gun we chose for this study is the 1.3 GHz, 1.5 cell SRF photogun under development by Euclid [49], with output kinetic energy of ) at 20 MV/m at the cathode, ultimately reaching 47 MV/m during experiment in liquid helium. Progress on the SRF technology based on Nb3Sn resulted in the development of accelerating cavities that may in the near future be operated without the need of a cryoplant for the production of liquid helium [50]. Nb3Sn has a critical temperature of 18 K, which makes them compatible with commercially available cryostats, e.g., the SRF gun built by Euclid [51]. However, the limited cooling power provided by cryostats may complicate the use of removable photocathode plugs coated with alkali antimonide, as the stalk will likely provide yet another channel of thermal losses. But for the main purpose of our study, we will assume from here forward that similar performances from the photocathode (minimum laser spot size and photoemission MTE) can be achieved in both injector configurations.
Thanks to the tightly focused laser spot size of a few microns when the photocathode operated in transmission mode, the spatial pointing stability of the electron source should be better than a few percent of the laser spot size (<100 nm) [52]; due to the factor of or larger demagnification, the stability of the probe beam on the specimen will be in the level of a few angstroms.
2.3.2. Photoinjector Layout and Optimization
For the general photoinjector design, we take inspiration from the Cornell ERL photoinjector, which was recently considered as a source for ultrafast electron diffraction [53], and further develop it into a generic MeV-electron SRF Linac. The photoelectron gun (either DC or SRF) is followed by a transversely focusing solenoid, a normal conducting 1.3 GHz bunching cavity, a second transversely focusing solenoid, and two 1.3 GHz SRF accelerating cavities. The maximum accelerating voltages that a DC gun and an SRF gun [50] can deliver are 400 kV and 1.6 MeV, respectively. Hence, following a photoelectron gun, the Linac, which comprises two SRF cavities, is generically designed to boost the electron energy up to 3 MeV despite different options of photoelectron guns and simultaneously mitigate the energy spread caused by the random jitter of cavity phase and amplitude. Moreover, to statically image a frozen large, thick biological sample, the critical parameter in the longitudinal phase space is the energy spread since the chromatic aberration of the STEM column could ultimately limit the minimum probe size on the specimen. Instead, there is no special requirement on the pulse duration of an electron bunch, which happens about 1 ps resulting from optimizing of the energy spread. In the manuscript, we did not consider the use of the most proven high-brightness electron sources: the field emission guns (FEGs) and the cold FEGs (CFEGs) in particular, which are widely used by high-resolution TEMs. The reason is because for an MeV-STEM, the electron energy needs to be as high as 3 MeV, instead of 300 keV or less for most of the high-resolution TEMs. To boost the electron beam energy up to a few MeV, the choice of the accelerating technology could strongly favor L-band SRF cavities (e.g., 1.3 GHz), whereas the fabrication process is matured and the SRF cavities are widely used in both linear and circular accelerators [52]. Moreover, if the DC accelerating technology is applied to boost the electron beam energy up to a few MeV, as an example, the 3 MeV microscope built by Osaka university [28], the microscope is more than 10 m tall and a few meters in diameter, which has difficulty in fitting into any laboratory with the standard size.
As a result, we pursued two photoelectron gun options, DC and SRF. The electron pulses, which are generated by photoemission of the drive laser pulses, can be fully captured by and synchronized to the standing RF waveform of the SRF cavity with the precision of tens of fs. Compared to the DC gun, the SRF gun is far more complicated to operate and yet needs to be proven. However, if the approach of SRF gun succeeds, the payoff could be profound and significant. As an example, the kinetic energy of 1.6 MeV boosted by an SRF gun could be sufficiently high for most of the UED/UEM applications; thus, the rest of the Linac can be eliminated. The MeV-STEM could be much more compact and cost-effective ($2 million less with the cost of $1 million per SRF cavity). In the manuscript, we present the SRF gun as a feasible option and compare its potential performance with the DC gun case. It is numerically evident that the SRF gun case could outperform the DC gun option regarding the minimum energy spread and transverse emittance (see details later in Section 2.3.2), which are crucial for the nanoscale resolution.
This layout is shown in Figure 4a. The label “photogun” represents both DC and SRF photoelectron guns. We utilize multiobjective genetic optimization of space charge simulations carried out in General Particle Tracer [54,55]. We seek to simultaneously optimize emittance and energy spread from the injector downstream of the SRF cavities. Our simulations begin with an initial bunch charge of 12,500 electrons/pulse similar for both DC and SR gun cases, and ultimately an aperture located within the first solenoid lens will reduce the bunch charge down to 1 electron/pulse on average. To alleviate long computation times, we first optimize with a larger pinhole which is tuned on a case-by-case basis to transmit 600 electrons/pulse (). We will later select from the Pareto optimal front individual cases to rerun with a larger number of macroparticles to enable heavier aperture clipping. In cases where we clip down to on average 1 electron per pulse, we ignore Coulomb interaction effects after the pinhole. In reality, Poisson statistics will dictate that the number of electrons in a bunch will vary, and this fluctuating small number of electrons will interact via the bare Coulomb potential; this stochasticity is beyond the scope of this work and is left for future study.
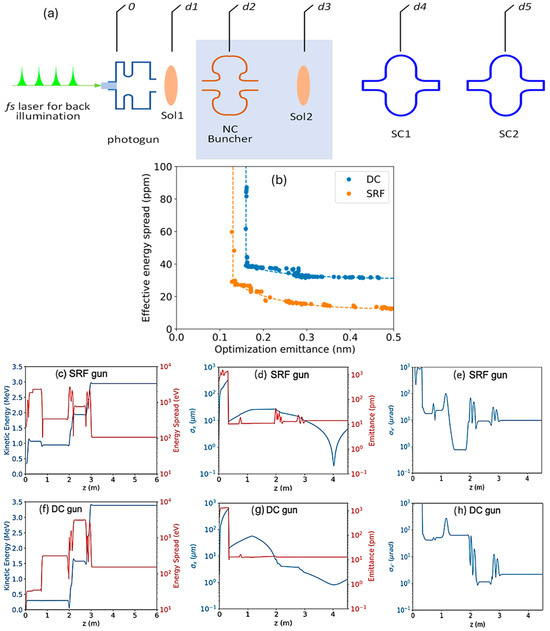
Figure 4.
(a) Beamline layout showing the longitudinal positions of the photoelectron gun (either DC or SRF) and the common section after the gun: transverse focusing solenoids, a normal conducting 1.3 GHz buncher cavity, and two 1.3 GHz SRF cavities. An aperture within the first solenoid is used to reduce emittance down to about 10 pm. The blue colored area highlights that in the SRF gun case, the section from the exit of the first solenoid to the exit of the second solenoid can be eliminated without any degradation of the electron source properties; in the DC gun case, this section is still needed to keep similarly minimized emittances and energy spread. Here, d1 = 0.35 m, d2 = 0.75 m, d3 = 1.15 m, d4 = 2.10 m, and d5 = 2.85 m are the longitudinal positions of solenoid 1, buncher cavity, solenoid 2, SRF accelerating cavities 1 and 2, respectively. (b) Pareto optimal performance of effective energy spread and transverse emittance for a transmitted charge of 100 aC, for both DC (blue) and SRF (orange) guns. Dotted lines guide the eye. Individual solutions from these sets are chosen and rerun with clipping down to the level of one electron per pulse on average. (c–e) Energy, energy spread, transverse size, transverse emittance, and transverse divergence for the SRF gun case. (f–h) Same but for the DC gun case. Transverse emittance remains constant after . The final energy spreads shown in (c,f) are uncorrelated energy spreads.
The optimizer is permitted to modify the laser duration (constrained to be ), and the RMS transverse laser size (m), where the longitudinal distribution is assumed to be uniform and the transverse distribution is assumed to be fully Gaussian. The photoemission MTE is set to be 35 meV. The optimizer has the freedom to change the amplitudes and phases of all fields within practical bounds. As was carried out for temporal resolution in a previous work [53], our figure of merit for energy spread includes both the energy spread of the bunch and effects of energy jitter. Using previously characterized values for amplitude and phase stability of the accelerating elements, we compute multiple simulations per machine setpoint within the bounds of this jitter to determine the RMS energy jitter value . The effective energy spread ( we compute is the quadrature sum of the bunch energy spread and the RMS energy jitter . The total kinetic energy of the bunch after acceleration is constrained to lie within 2.5 and 3.5 MeV.
The Pareto optimal frontier of energy spread and emittance with a final charge of 100 aC/pulse is shown in Figure 4b. For either the DC gun (blue) or the SRF gun (orange), the sharp slope in the vertical direction corresponds to emittance reduction induced by the pinhole located inside the first solenoid lens; still, a few points with different energy spreads fluctuate within the slope. The SRF gun is capable of outperforming the DC gun in both emittance and effective energy spread. The emittance improvement we attribute to the use of a higher photocathode field, which permits higher charge densities on the cathode, and relativistic energies which suppresses the space charge interaction force. The energy spread improvement is primarily due to less energy jitter, as amplitude and phase changes in the gun lead to smaller arrival time differences at the downstream cavities since the bunch velocity at the gun exit is nearly saturated at c (speed of light). In Figure 4c–h, we have selected optimal solutions for both DC and SRF guns and have rerun them for the case of clipping down to one electron per pulse on average. Emittance values in both cases are very near , with total effective energy spread on the scale of , which suggests that both beamline designs are appropriate sources for MeV-STEM.
2.3.3. Beamline Optics: STEM Column
We adopted a similar design based on permanent quadrupole (PMQ) quintuplets pioneered at Brookhaven National Laboratory for MeV electron microscopes [29] to construct the MeV-STEM column, since the electron optics of a STEM column are similar to those of a TEM column based on reciprocity [56]. Quadrupoles are known to have very strong focusing capability, especially for high-energy (3 MeV) electron beams due to their focusing strength being inversely proportional to the momentum [57]. In comparison, the focusing power of a round magnetic lens is inversely proportional to the momentum squared [58]. Therefore, the focusing system based on quadrupoles can be made much more compact and lower cost. To overcome the property of a quadrupole focusing in one direction while defocusing in the other, at least two quadrupoles with opposite polarities are necessary to form a lens that focuses the beam on both transverse directions. A multiplet of quadrupoles, including quadruplet and quintuplet, can form a lens with more desirable properties, such as rotational symmetry of the paraxial rays and widely tunable focal length.
The STEM column is used not only to focus the electron beam onto the sample with the size of a few nanometers but also to provide the beam with various sizes at the specimen to enable scanning at different magnifications. We used four lenses in the STEM column, with one objective lens and three condenser lenses (see Appendix A and Figure 5a for details). To keep the minimum aberrations, the objective lens must be much stronger than the condenser lenses. As a result, the pole tip radius of the objective lens is half of the value of the condenser lenses and ultimately limits the maximum probe size that can be achieved on the sample. The design strategies are: (1) the strength of each lens can be adjusted to vary the probe size 1400 and 5360 times for the SRF and DC gun cases; (2) the aperture in solenoid 1 provides the additional freedom of changing the electron beam size at the exit of the electron source up to 10 and 2.5 times for the SRF and DC gun case, respectively (see Figure 4d,g for the aperture at ); hence, the ultimate probe size at the specimen can be varied from 2 nm to 16 . The variation in the aperture can greatly mitigate the required change in the magnetic field of those lenses to ±8.2 T/m and ±10.8 T/m for the SRF and the DC gun cases, respectively. For a 1 mm pole tip radius, ±8.2 T/m and ±10.8 T/m correspond to ±3.3 Ampere turn and ±4.3 Ampere turn, respectively. This entails that it is feasible to add coils to the PMQs to adjust their field strengths to achieve the required change in probe size.
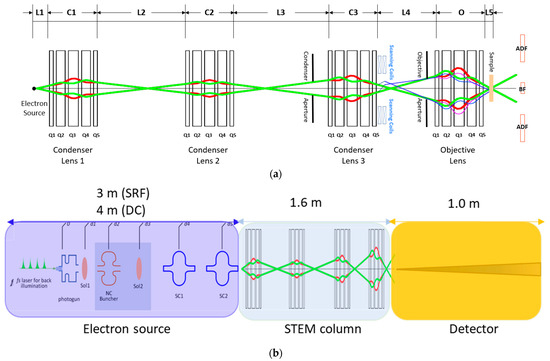
Figure 5.
(a) Layout of the STEM column based on the quadrupole quintuplet lenses. The red and green ray diagrams are the calculated beam path in the x–z and y–z directions, respectively. (b) Layout with dimensions of the MeV-STEM instrument.
From Figure 4d,g, we learn that the RMS size of the electron beam (z = 4 m) for the cases of the SRF gun and the DC gun are 0.2 μm and 0.8 μm, respectively. The normalized emittances for the cases of the SRF gun and the DC gun are 13.9 pm and 13.1 pm, respectively. The kinetic energies of the electrons at the end of SRF and the DC source are 3.0 MeV and 3.4 MeV, respectively. Lastly, the opening angles at the sample are 10.0 μrad and 2.2 μrad, respectively. Because the beam sizes at the exit of the two sources differ by a factor of four, the necessary demagnification of the columns also differs by a factor of four. The precise values of the demagnifications will be determined below, minimizing the beam size at the sample based on the aberrations of the objective lens. In order to minimize the aberrations, the focal length of the objective lens is minimized through reducing the pole tip radius (allowing for higher gradient), the lengths of the magnets, and the spacing between them. The results are listed in Table A1 in the Appendix A (see Figure 6a for magnetic field profile). Since the aberrations of the condenser lens do not affect the resolution significantly, the focal length can be larger, which greatly relaxes the design requirement of the condenser lens (in Appendix A, see Table A2 for condenser lenses 1 and 2 and Table A3 for condenser lens 3). The layout of the STEM column is shown in Table 5. The aberrations of the objective lens parameters are shown in Table 6.
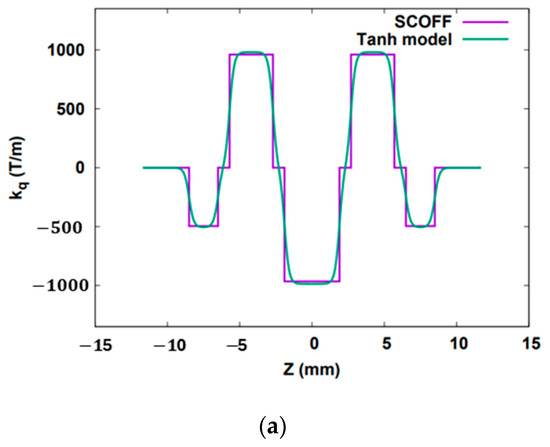
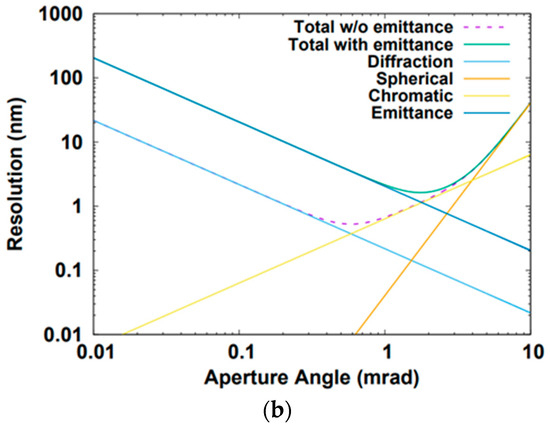
Figure 6.
(a) Magnetic field profile of the objective lens. (b) RMS resolution for the SRF gun. (That for the DC gun is not shown since it looks rather similar.) The “Total w/o emittance” is the resolution defined in Equation (12). The “Total with emittance” is the resolution defined in Equation (11).

Table 5.
Layout of the STEM column ().

Table 6.
Objective lens parameters including the focal length and main aberrations (obtained using the hyper-tangent fringe-field model).
In order to obtain the final probe size, the effect of the aberrations of the objective lens has to be included, which are shown in Table 6. From Figure 4c,f, energy spreads for SRF and DC sources are roughly 107 eV and 155 eV, respectively. The relative energy spreads are and , respectively. Since at the downstream of an aperture within the first solenoid that is used to reduce emittance down to about 10 pm, optimal solutions for the cases of clipping down to one electron per pulse on average have been chosen and rerun in the simulation for the rest of the beamline, space charge effects do not play any role. As a result, the final probe beam size in RMS can be estimated by Equation (11):
where , , taking into account the disk of least confusion, and , and Parameters , , , , , and are the wavelength, the aperture angle on the sample, the spherical aberration, the chromatic aberration, the relative energy spread and the geometrical transverse emittance, respectively. The wavelengths for the SRF and the DC sources are 0.36 pm and 0.32 pm, respectively. The theoretically minimum resolution can be obtained by
The result is shown in Figure 6b. Unlike conventional STEM, the resolution of this instrument is limited by chromatic aberration due to its larger energy spread. The theoretically minimum resolutions for the SRF (aperture angle mrad) and the DC (aperture angle mrad) sources are 0.53 nm and 0.57 nm, respectively. If the current is of no concern, the best theoretical resolution of the instrument can always be reached through increasing demagnification, resulting in a small probe size. Yet in this design, at roughly 13 to 14 p.m. normalized emittance, there is on average only 1 electron per pulse, which entails that the maximum current is around 200 pA. Thus, the emittance of the electron beam cannot be much further reduced. The effect of the emittance on the resolution is shown in Figure 6b. The minimum resolution values for the SRF and the DC cases are 1.63 nm and 1.69 nm, respectively, with aperture angles of 1.75 mrad and 1.44 mrad, respectively. The resulted demagnifications for the SRF and the DC cases are 175 and 670, respectively. The demagnification of the objective lens is chosen to be 20 for both cases. The demagnifications of the condenser lens for the SRF and the DC cases are 8.75 and 33.5, respectively.
2.3.4. Scanning Coils
To demonstrate the feasibility of rastering a nm-sized probe beam across the specimen with a sub-nm precision, we numerically study the critical component—scanning, or steering coils. Based on the preliminary design of the MeV-STEM instrument, simulation is carried out in GPT. To cover the sample with 2000 2000 pixels at the step size of 2 nm, scanning coils need to be positioned right after the last condenser lens. A numerical study indicates that the entire range of the steering should cover ±0.32 mrad with a step size of 160 nrad. The 0.2 nm scanning accuracy (10% beam size) requires a power supply with a precision better than 25 ppm, which is achievable based on the currently demonstrated performance of power supplies.
A schematic layout of the MeV-STEM instument is shown in Figure 5b. Despite the two options based on either a DC gun or an SRF gun, the common section of the MeV-STEM instrument starts from the aperture and ends with the detector. Also, the same drive laser system can be applied to both the DC and SRF guns. The photocathode drive laser can be a turnkey femtosecond laser with a 1-to-10 GHz repetition rate, delivering more than 1 W of average power in pulses as short as 50 fs, from Novanta Photonics [59]. The pulse energy of 1 nJ can generate the charge >2 fC per pulse with the multi-alkali photocathode, whereas only 2 fC/pulse is needed.
3. Discussion
As the allowable sample thickness without radiation damage depends on the electron energy and image formation mechanism, we propose to develop an MeV-STEM. The remarkable ability of MeV-STEM to penetrate deeply into samples, even as thick as 10 μm or more, while still achieving nanoscale resolution, positions it as an excellent choice for biological specimen analysis. The impact of electron energy, beam broadening, and low-dose constraints on resolution has been examined. Notably, the finest achievable resolution exhibits an inverse relationship with sample thickness, shifting from 6 nm for 1 μm thick samples to 24 nm for 10 μm thick ones. These make MeV-STEM capable of imaging large and thick frozen biological samples (up to 10 μm in thickness). However, achieving MeV-STEM capabilities necessitates electron beam emittance that goes beyond the state of the art (a few-pm emittance, better than 10−4 energy spread and 0.1–1 nA current).
Our preliminary simulation study as well as our MeV-UEM hardware research and development suggest that building such an MeV-STEM is possible. A photocathode gun based on the ERL injector at Cornell University can produce electron beams with a few-picometer emittance, better than 10−4 energy spread, and nA beam current. Since all the critical components (ultralow-emittance DC gun, SRF accelerating cavity and momentum aperture) already have been demonstrated and reliably operated, the MeV-STEM source can be realized based on this design. Alternatively, a compact SRF gun similar to the one built by Euclid Techlabs may provide even better performance for an MeV-STEM instrument. In the last case, several significant challenges related to the cathode insertion mechanism and its operation in transmission mode have yet to be addressed before the last solution can be adopted. So far, it has been numerically confirmed that in the SRF gun case, one can eliminate the section including the buncher cavity and second solenoid while keeping similarly minimized emittance and energy spread. The MeV-STEM instrument can be built within a total length of less than 6 m.
Furthermore, the numerically demonstrated ultralow-emittance (ϵgeo = 2 pm) MeV electron source can deliver a quasi-monochromatic pencil beam. Such an MeV electron source could help in experimentally answering some long-standing challenging problems as well as easily be reconfigured into single-shot MeV-UED/UEM operational mode without any hardware change, which is highly desired for solving challenges in probing matter at ultrafast-temporal ultrasmall-spatial scales.
Author Contributions
L.W. (Liguo Wang) introduced the concept of MeV-STEM for imaging thick bio-samples, conducted calculations of the intensity change in electrons in various categories while traveling through thick samples, estimated the contrast in biological samples, and analyzed the effect of beam broadening and low-dose limit on resolution. X.Y. proposed a technical solution for MeV electron sources, specifically the DC and SRF photoguns, to meet the requirement of nanometer-resolution MeV-STEM, formulated the ultimate resolution including source emittance, and provided critical suggestions on extending the adjustable magnification of the STEM column. W.W. was responsible for the design of the STEM column, especially for finding the optimal solution of STEM column with the minimum aberration and maximum tuning range. J.M., A.C.B. and M.K. performed beam dynamic simulations and optimized the performance of the electron source. C.J. and R.K. provided the field map of the SRF photocathode gun. L.C. contributed to the design of the photocathode. Y.Z. provided critical views on the complexity of electron scattering in thick samples and its impact on resolution and offered guidance and expertise on the design of STEM column. L.W. (Lijun Wu) contributed to discussions and dynamic calculations of elastic scattering for thick samples. S.M. provided advice on the design of MeV-STEM. T.S. and V.S. provided advice on design issues of the instrument and overall structure of the paper. All authors actively participated in figure preparation and collectively contributed to the writing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the U.S. Department of Energy under grants DE-SC0012704 and BNL LDRD 22-029. The SRF photogun presented in the article is funded by SBIR Grant DE-SC0018621.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated and analyzed during the current study are not publicly available, due to the reason that we want to know who has an interest in our datasets, but are available from the corresponding author upon reasonable request.
Acknowledgments
We would like to thank Sharon Wolf for her valuable insights and discussions on using STEM for imaging biological samples, Ming Du, and Chris J Jacobsen for their enlightening discussions on electron scattering in specimens, and Ray Egerton for discussion of image resolutions.
Conflicts of Interest
Authors Chunguang Jing and Roman Kostin were employed by the company Euclid Techlabs LLC. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
Appendix A.1. Electron Intensity Change while Traveling through the Specimen
The intensity change in electrons in each category after passing through a sample slice of thickness dt is
- Unscattered:
- 2.
- Detected single elastic scattered electrons:
- 3.
- Detected multiple elastically scattered electrons:
- 4.
- Detected inelastic scattered electrons:
- 5.
- Undetected electrons:
Although these expressions possess limitations in capturing certain nuances of plural scattering (e.g., the probability that scattered-out electrons might be scattered back and fall within the detector collection angles, the direction change in scattered electrons after passing through the sample), they serve as a valuable initial approximation.
Appendix A.2. Layout and Gradients of the Objective and Condenser Lenses

Table A1.
Layout and gradients of the objective lens. The pole tip radius is 0.5 mm. The focal length is 1.00 cm for both the cases of the SRF and the DC guns.
Table A1.
Layout and gradients of the objective lens. The pole tip radius is 0.5 mm. The focal length is 1.00 cm for both the cases of the SRF and the DC guns.
| L (mm) | Gradient (SRF, T/m) | Gradient (DC, T/m) | |
|---|---|---|---|
| Quadrupole | 2.0 | −504.1 | −562.7 |
| Drift | 0.8 | ||
| Quadrupole | 3.0 | 981.3 | 1095.4 |
| Drift | 0.8 | ||
| Quadrupole | 3.8 | −986.2 | −1100.9 |
| Drift | 0.8 | ||
| Quadrupole | 3.0 | 981.3 | 1095.4 |
| Drift | 0.8 | ||
| Quadrupole | 2.0 | −504.1 | −562.7 |

Table A2.
Layout and gradients of the condenser lenses 1 and 2. The pole tip radius is 1 mm.
Table A2.
Layout and gradients of the condenser lenses 1 and 2. The pole tip radius is 1 mm.
| L (mm) | Gradient (SRF, T/m) | Gradient (DC, T/m) | |
|---|---|---|---|
| Quadrupole | 6 | −36.2–−30.6 | −55.8–−34.2 |
| Drift | 5 | ||
| Quadrupole | 14 | 43.0–37.3 | 61.8–41.7 |
| Drift | 5 | ||
| Quadrupole | 16 | −46.6–−41.3 | −63.5–−46.1 |
| Drift | 5 | ||
| Quadrupole | 14 | 43.0–37.3 | 61.8–41.7 |
| Drift | 5 | ||
| Quadrupole | 6 | −36.2–−30.6 | −55.8–−34.2 |

Table A3.
Layout and gradients of the condenser lenses 3. The pole tip radius is 1 mm.
Table A3.
Layout and gradients of the condenser lenses 3. The pole tip radius is 1 mm.
| L (mm) | Gradient (SRF, T/m) | Gradient (DC, T/m) | |
|---|---|---|---|
| Quadrupole | 6 | −16.9–−30.7 | −18.7–−34.3 |
| Drift | 5 | ||
| Quadrupole | 14 | 21.6–37.4 | 23.9–41.7 |
| Drift | 5 | ||
| Quadrupole | 16 | −24.9–−41.3 | −27.6–−46.1 |
| Drift | 5 | ||
| Quadrupole | 14 | 21.6–37.4 | 23.9–41.7 |
| Drift | 5 | ||
| Quadrupole | 6 | −16.9–−30.7 | −18.7–−34.3 |
References
- Tegunov, D.; Xue, L.; Dienemann, C.; Cramer, P.; Mahamid, J. Multi-particle cryo-EM refinement with M visualizes ribosome-antibiotic complex at 3.5 Å in cells. Nat. Methods 2021, 18, 186–193. [Google Scholar] [CrossRef]
- Nicastro, D.; Schwartz, C.; Pierson, J.; Gaudette, R.; Porter, M.E.; McIntosh, J.R. The molecular architecture of axonemes revealed by cryoelectron tomography. Science 2006, 313, 944–948. [Google Scholar] [CrossRef] [PubMed]
- Dobro, M.J.; Oikonomou, C.M.; Piper, A.; Cohen, J.; Guo, K.; Jensen, T.; Tadayon, J.; Donermeyer, J.; Park, Y.; Solis, B.A.; et al. Uncharacterized Bacterial Structures Revealed by Electron Cryotomography. J. Bacteriol. 2017, 199, 10–1128. [Google Scholar] [CrossRef] [PubMed]
- Li, X. Cryo-electron tomography: Observing the cell at the atomic level. Nat. Methods 2021, 18, 440–441. [Google Scholar] [CrossRef] [PubMed]
- Brocard, L.; Immel, F.; Coulon, D.; Esnay, N.; Tuphile, K.; Pascal, S.; Claverol, S.; Fouillen, L.; Bessoule, J.J.; Bréhélin, C. Proteomic Analysis of Lipid Droplets from Arabidopsis Aging Leaves Brings New Insight into Their Biogenesis and Functions. Front. Plant Sci. 2017, 8, 894. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Jiang, Z.; Zhang, K.; Wang, P.; Cao, X.; Yue, N.; Wang, X.; Zhang, X.; Li, Y.; Li, D.; et al. Three-Dimensional Analysis of Chloroplast Structures Associated with Virus Infection. Plant Physiol. 2018, 176, 282–294. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.W.; Rettberg, L.; Treuner-Lange, A.; Iwasa, J.; Søgaard-Andersen, L.; Jensen, G. Architecture of the type IVa pilus machine. Biophys. J. 2016, 351, 1165. [Google Scholar] [CrossRef]
- Weiner, E.; Pinskey, J.M.; Nicastro, D.; Otegui, M.S. Electron microscopy for imaging organelles in plants and algae. Plant Physiol. 2022, 188, 713–725. [Google Scholar] [CrossRef]
- Böhning, J.; Bharat, T.A.M. Towards high-throughput in situ structural biology using electron cryotomography. Prog. Biophys. Mol. Biol. 2021, 160, 97–103. [Google Scholar] [CrossRef]
- Oikonomou, C.M.; Jensen, G.J. Cellular Electron Cryotomography: Toward Structural Biology In Situ. Annu. Rev. Biochem. 2017, 86, 873–896. [Google Scholar] [CrossRef]
- Otegui, M.S.; Pennington, J.G. Electron tomography in plant cell biology. Microscopy 2019, 68, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Cooper, C.; Thompson, R.C.A.; Clode, P.L. Investigating parasites in three dimensions: Trends in volume microscopy. Trends Parasitol. 2023, 39, 668–681. [Google Scholar] [CrossRef] [PubMed]
- Collinson, L.M.; Bosch, C.; Bullen, A.; Burden, J.J.; Carzaniga, R.; Cheng, C.; Darrow, M.C.; Fletcher, G.; Johnson, E.; Narayan, K.; et al. Volume EM: A quiet revolution takes shape. Nat. Methods 2023, 20, 777–782. [Google Scholar] [CrossRef]
- Capua-Shenkar, J.; Varsano, N.; Itzhak, N.R.; Kaplan-Ashiri, I.; Rechav, K.; Jin, X.; Niimi, M.; Fan, J.; Kruth, H.S.; Addadi, L. Examining atherosclerotic lesions in three dimensions at the nanometer scale with cryo-FIB-SEM. Proc. Natl. Acad. Sci. USA 2022, 119, e2205475119. [Google Scholar] [CrossRef] [PubMed]
- Schertel, A.; Snaidero, N.; Han, H.-M.; Ruhwedel, T.; Laue, M.; Grabenbauer, M.; Möbius, W. Cryo FIB-SEM: Volume imaging of cellular ultrastructure in native frozen specimens. J. Struct. Biol. 2013, 184, 355–360. [Google Scholar] [CrossRef] [PubMed]
- Spehner, D.; Steyer, A.M.; Bertinetti, L.; Orlov, I.; Benoit, L.; Pernet-Gallay, K.; Schertel, A.; Schultz, P. Cryo-FIB-SEM as a promising tool for localizing proteins in 3D. J. Struct. Biol. 2020, 211, 107528. [Google Scholar] [CrossRef]
- Vidavsky, N.; Akiva, A.; Kaplan-Ashiri, I.; Rechav, K.; Addadi, L.; Weiner, S.; Schertel, A. Cryo-FIB-SEM serial milling and block face imaging: Large volume structural analysis of biological tissues preserved close to their native state. J. Struct. Biol. 2016, 196, 487–495. [Google Scholar] [CrossRef]
- Raguin, E.; Weinkamer, R.; Schmitt, C.; Curcuraci, L.; Fratzl, P. Logistics of Bone Mineralization in the Chick Embryo Studied by 3D Cryo FIB-SEM Imaging. Adv. Sci. 2023, 10, e2301231. [Google Scholar] [CrossRef]
- Du, M.; Jacobsen, C. Relative merits and limiting factors for x-ray and electron microscopy of thick, hydrated organic materials. Ultramicroscopy 2018, 184, 293–309. [Google Scholar] [CrossRef]
- Wolf, S.G.; Elbaum, M. CryoSTEM tomography in biology. Methods Cell Biol. 2019, 152, 197–215. [Google Scholar] [CrossRef]
- Hohmann-Marriott, M.F.; Sousa, A.A.; Azari, A.A.; Glushakova, S.; Zhang, G.; Zimmerberg, J.; Leapman, R.D. Nanoscale 3D cellular imaging by axial scanning transmission electron tomography. Nat. Methods 2009, 6, 729–731. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.G.; Shimoni, E.; Elbaum, M.; Houben, L. STEM Tomography in Biology. In Cellular Imaging: Electron Tomography and Related Techniques; Hanssen, E., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 33–60. [Google Scholar]
- Wolf, S.G.; Houben, L.; Elbaum, M. Cryo-scanning transmission electron tomography of vitrified cells. Nat. Methods 2014, 11, 423–428. [Google Scholar] [CrossRef] [PubMed]
- Hawkes, P.W. (Ed.) Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2009; Volume 159. [Google Scholar]
- Reimer, L.; Kohl, H. Transmission Electron Microscopy: Physics of Image Formation, 5th ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Tanaka, N. Electron Nano-Imaging, 1st ed.; Springer: Tokyo, Japan, 2017. [Google Scholar]
- Gammer, C.; Ozdol, V.B.; Liebscher, C.H.; Minor, A.M. Diffraction contrast imaging using virtual apertures. Ultramicroscopy 2015, 155, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Dupouy, G. Performance and applications of the Toulouse 3 million volt electron microscope. J. Microsc. 1973, 97, 3–28. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Chen, F.R.; Zhu, Y. Design of compact ultrafast microscopes for single- and multi-shot imaging with MeV electrons. Ultramicroscopy 2018, 194, 143–153. [Google Scholar] [CrossRef]
- Williams, D.B.; Carter, C.B. Transmission Electron Microscopy; Springer: New York, NY, USA, 2009. [Google Scholar]
- Jacobsen, C.; Medenwaldt, R.; Williams, S. A Perspective on Biological X-Ray and Electron Microscopy. In X-ray Microscopy and Spectromicroscopy: Status Report from the Fifth International Conference, Würzburg, 19–23 August 1996; Thieme, J., Schmahl, G., Rudolph, D., Umbach, E., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 197–206. [Google Scholar]
- Wu, L.; Zhu, Y.; Vogt, T.; Su, H.; Davenport, J.W.; Tafto, J. Valence-electron distribution inMgB2by accurate diffraction measurements and first-principles calculations. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 064501. [Google Scholar] [CrossRef]
- Li, J.; Yin, W.-G.; Wu, L.; Zhu, P.; Konstantinova, T.; Tao, J.; Yang, J.; Cheong, S.-W.; Carbone, F.; Misewich, J.A.; et al. Dichotomy in ultrafast atomic dynamics as direct evidence of polaron formation in manganites. NPJ Quantum Mater. 2016, 1, 16026. [Google Scholar] [CrossRef]
- Egerton, R.F. Choice of operating voltage for a transmission electron microscope. Ultra-Microsc. 2014, 145, 85–93. [Google Scholar] [CrossRef]
- Rose, H. Effect of Coulomb Interactions on Resolution in Ultrafast Electron Microscopy. Microsc. Microanal. 2006, 12, 1424–1425. [Google Scholar] [CrossRef][Green Version]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer Associates, Inc.: Sunderland, MA, USA, 2001. [Google Scholar]
- Rickwood, D.; Chambers JA, A.; Barat, M. Isolation and preliminary characterisation of DNA-protein complexes from the mitochondria of Saccharomyces cerevisiae. Exp. Cell Res. 1981, 133, 1–13. [Google Scholar] [CrossRef]
- Baldwin, W.W.; Myer, R.; Powell, N.; Anderson, E.; Koch, A.L. Buoyant density of Escherichia coli is determined solely by the osmolarity of the culture medium. Arch. Microbiol. 1995, 164, 155–157. [Google Scholar] [CrossRef] [PubMed]
- Loferer-Krössbacher, M.; Klima, J.; Psenner, R. Determination of bacterial cell dry mass by transmission electron microscopy and densitometric image analysis. Appl. Environ. Microbiol. 1998, 64, 688–694. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.S. Cell Fractionation Based on Density Gradient. 2023. Available online: https://user.eng.umd.edu/~nsw/ench485/lab10.htm (accessed on 12 August 2023).
- Li, W.H.; Duncan, C.J.R.; Andorf, M.B.; Bartnik, A.C.; Bianco, E.; Cultrera, L.; Galdi, A.; Gordon, M.; Kaemingk, M.; Pennington, C.A.; et al. A kiloelectron-volt ultrafast electron micro-diffraction apparatus using low emittance semiconductor photocathodes. Struct. Dyn. 2022, 9, 024302. [Google Scholar] [CrossRef]
- Gordon, M.; Li, W.H.; Andorf, M.B.; Bartnik, A.C.; Duncan, C.J.R.; Kaemingk, M.; Pennington, C.A.; Bazarov, I.V.; Kim, Y.K.; Maxson, J.M. Four-dimensional emittance measurements of ultrafast electron diffraction optics corrected up to sextupole order. Phys. Rev. Accel. Beams 2022, 25, 084001. [Google Scholar] [CrossRef]
- Lee, H.; Cultrera, L.; Bazarov, I. Intrinsic emittance reduction in transmission mode photocathodes. Appl. Phys. Lett. 2016, 108, 124105. [Google Scholar] [CrossRef]
- Lee, H.; Liu, X.; Cultrera, L.; Dunham, B.; Kostroun, V.O.; Bazarov, I.V. A cryogenically cooled high voltage DC photoemission electron source. Rev. Sci. Instrum. 2018, 89, 083303. [Google Scholar] [CrossRef] [PubMed]
- Pierce, C.M.; Durham, D.B.; Riminucci, F.; Dhuey, S.; Bazarov, I.; Maxson, J.; Minor, A.M.; Filippetto, D. Experimental Characterization of Photoemission from Plasmonic Nanogroove Arrays. Phys. Rev. Appl. 2023, 19, 034034. [Google Scholar] [CrossRef]
- Maxson, J.; Bazarov, I.; Dunham, B.; Dobbins, J.; Liu, X.; Smolenski, K. Design, conditioning, and performance of a high voltage, high brightness dc photoelectron gun with variable gap. Rev. Sci. Instrum. 2014, 85, 093306. [Google Scholar] [CrossRef]
- Hernandez-Garcia, C.; Adderley, P.; Bullard, B.; Benesch, J.; Grames, J.; Gubeli, J.; Hannon, F.; Hansknecht, J.; Jordan, J.; Kazimi, R.; et al. Compact −300 kV dc inverted insulator photogun with biased anode and alkali-antimonide photocathode. Phys. Rev. Accel. Beams 2019, 22, 113401. [Google Scholar] [CrossRef]
- Konomi, T.; Honda, Y.; Kako, E.; Kobayashi, Y.; Michizono, S.; Miyajma, T.; Sakai, H.; Umemori, K.; Yamaguchi, S.; Yamamoto, M. Development of srf gun applying new cathode idea using a transparent superconducting layer. In Proceedings of the 59th ICFA Advanced Beam Dynamics Workshop on Energy Recovery Linacs (ERL17), Geneva, Switzerland, 18–23 June 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Kostin, R.; Jing, C.; Posen, S.; Khabiboulline, T.; Bice, D. Nb3Sn SRF Photogun High Power Test at Cryogenic Temperatures. J. Latex Cl. Files 2021, 14, 1–5. [Google Scholar]
- Posen, S.; Lee, J.; Seidman, D.N.; Romanenko, A.; Tennis, B.; Melnychuk, O.S.; Sergatskov, D.A. Advances in Nb3Sn superconducting radiofrequency cavities towards first practical accelerator applications. Supercond. Sci. Technol. 2021, 34, 025007. [Google Scholar] [CrossRef]
- Kostin, R.; Jing, C.; Posen, S.; Khabiboulline, T.; Bice, D. First high-gradient results of UED/UEM srf gun at cryogenic temperatures. In Proceedings of the 5th North American Particle Accelerator Conference, Albuquerque, NM, USA, 7–12 August 2022; pp. 607–610. [Google Scholar]
- Vicario, C.; Ganter, R.; Hauri, C.; Hunziker, S.; Le Pimpec, F.; Ruchert, C.; Trisorio, A. Photocathode drive laser for swissfel. In Proceedings of the FEL2010, Malmö, Sweden, 23–27 August 2010; pp. 425–428. [Google Scholar]
- Bartnik, A.; Gulliford, C.; Hoffstaetter, G.H.; Maxson, J. Ultimate bunch length and emittance performance of an MeV ultrafast electron diffraction apparatus with a dc gun and a multicavity superconducting rf linac. Phys. Rev. Accel. Beams 2022, 25, 093401. [Google Scholar] [CrossRef]
- Pulsar. Pulsar Physics and the General Particle Tracer (GPT) Code. Available online: https://www.pulsar.nl/gpt/ (accessed on 1 January 2022).
- van der Geer, S.B.; Luiten, O.J.; de Loos, M.J.; Poplau, G.; van Rienen, U. 3D space-charge model for GPT simulations of high-brightness electron bunches. Inst. Phys. Conf. Ser. 2005, 175, 101–110. [Google Scholar]
- Zuo, J.M.; Spence, J.C.H. Advanced Transmission Electron Microscopy; Springer: New York, NY, USA, 2017; ISBN 978-1-4939-6605-9. [Google Scholar]
- Lim, J.K.; Frigola, P.; Travish, G.; Rosenzweig, J.B.; Anderson, S.G.; Brown, W.J.; Jacob, J.S.; Robbins, C.L.; Tremaine, A.M. Adjustable, short focal length permanent-magnet quadrupole based electron beam final focus system. Phys. Rev. Spec. Top. -Accel. Beams 2005, 8, 072401. [Google Scholar] [CrossRef]
- Xiang, D.; Fu, F.; Zhang, J.; Huang, X.; Wang, L.; Wang, X.; Wan, W. Accelerator-based single-shot ultrafast transmission electron microscope with picosecond temporal resolution and nanometer spatial resolution. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2014, 759, 74–82. [Google Scholar] [CrossRef]
- Photonics, N. Taccor—Ultrafast Femtosecond Lasers. Available online: https://novantaphotonics.com/product/taccor-ultrafast-femtosecond-lasers/ (accessed on 10 August 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).