Scattering over Varying Amplification Grating

Abstract

The scattering pattern from a narrow absorbing/amplifying grating is investigated. A simple model of a narrow amplifying grating is solved exactly numerically and approximately analytically for the regime where the beam’s wavelength is much shorter than the grating’s wavelength. The main result is that the incident angle divides the scattering pattern into two regimes: below and above the incident angles. The former regime has a weak dependence on the incident angle but has a strong dependence on the scattering one. In this regime, a new grating formula is derived. The opposite occurs in the latter regime, which is very sensitive to the incident angle but has only weak dependence on the scattering angle. Consequently, at certain incident angles, all of the scattering is concentrated in the first regime, i.e., all scattering angles are lower than the incident angle.

1. Introduction

The periodicity of crystals and gratings exhibits universal scattering patterns, which are manifested by the well-known grating formula and grating’s spectral resolution [1].

In general, the grating’s scattering is much more complicated, and it depends on the grating’s material, profile, and grooving method [1,2,3]. In particular, plasmon excitations in the metal grating are responsible for anomalous scattering [4,5,6]. Moreover, it was found that even dielectric gratings exhibit anomalous scattering behavior [7,8]. These results were in clear contrast to the traditional belief that narrow dielectric gratings can have only a small effect on the incident light beam [9]. It was shown that even when the dielectric grating has weak modulation, the reflection coefficient can be very high [10,11]. The modulation can be either in the refraction index [12] or in the grating’s grooves [7]. These results show that, in principle, the reflectance at specific incident angles can be arbitrarily close to 100%. It should be stressed that these angles (with 100% reflectance) have nothing to do with the grating formula.

This anomalous conduct is related to a specific case of Fano resonances [8,13,14,15]. Recently, it was shown that in theory perfect reflection (zero transmission) can occur for an arbitrarily narrow dielectric grating layer [16]. The layer thickness can be arbitrarily narrow and the grating modulation amplitude can be arbitrarily low and still, the effect of 100% reflectance occurs.

This conduct resembles a similar effect in quantum mechanics, where the transmission via an oscillating barrier can be suppressed completely at certain incoming particles’ energies. Even though the quantum phenomenon was discovered after its optical equivalent, it was thoroughly investigated for both scattering scenarios [17,18,19,20,21,22,23] as well as for transition between adjacent quantum wells [24,25,26].

This effect occurs when the particle’s energy approximately equals the oscillations’ quanta. However, this is a relatively simple quantum system. When the system becomes more complex, the dynamics are much less intuitive. In particular, it has been shown that if the oscillating potential is a well, which is located in an opaque barrier, then this system exhibits complex behavior. The current is extremely sensitive to the system’s parameters, it can either increase substantially (activation and elevation) or almost vanish (complete suppression) [27,28,29,30].

When the barrier is absent, this complex behavior vanishes. The reason is that the system’s behavior is determined by the ratio between the oscillating potential’s amplitude and the wavenumber in its vicinity. If this ratio is imaginary, no complex behavior appears.

The barrier’s presence makes sure that the wavenumber is approximately real, and since the potential amplitude is real, then the ratio is approximately real as well.

However, if the barrier is absent, then the ratio can still be real, provided the potential amplitude is imaginary. In that case, some of this complex behavior reappears.

While the physical application of an imaginary barrier is not entirely clear, the optical counterparts, i.e., imaginary wavenumber and imaginary refractive index, are very common.

These conclusions can be applied to optical equivalent systems where the wavefunction is replaced with the electromagnetic field, and the oscillating potential is replaced with a spatial dielectric (grating as in Ref. [16] but for the complex dielectric coefficient).

Then, similarly, the complex structure’s dynamics can reappear by either putting the grating in a low index of refraction environment or by replacing the dielectric grating with an amplifying/absorbing one. In what follows, we will focus on the latter: the scattering pattern of an amplifying/absorbing grating is going to be investigated.

Modulated amplification can be carried out by gradually changing the pumping over the grating, causing a gradual change in the population inversion.

However, it is much simpler to create a uniform amplifying layer and attach to it a modulated absorber. If both layers are considerably narrower than the wavelength, then the two-layer system can be regarded as a single layer with modulated amplification/absorption.

Using this model, the scattering problem is reduced to a set of linear difference equations, which can easily be solved numerically. Moreover, an approximate analytical solution can be derived as well. The main novelty of these solutions is that, for specific incident angles, the scattered angles cannot exceed the incident angle. That is, while for most incident angles $\mathsf{\theta }$, the e-m field is scattered in all directions, for specific incident fields ($\mathsf{\theta }={\mathsf{\theta }}_m$), the scattered angles obey ${\mathsf{\theta }}_{out}\le \mathsf{\theta }$.

2. The System under Study

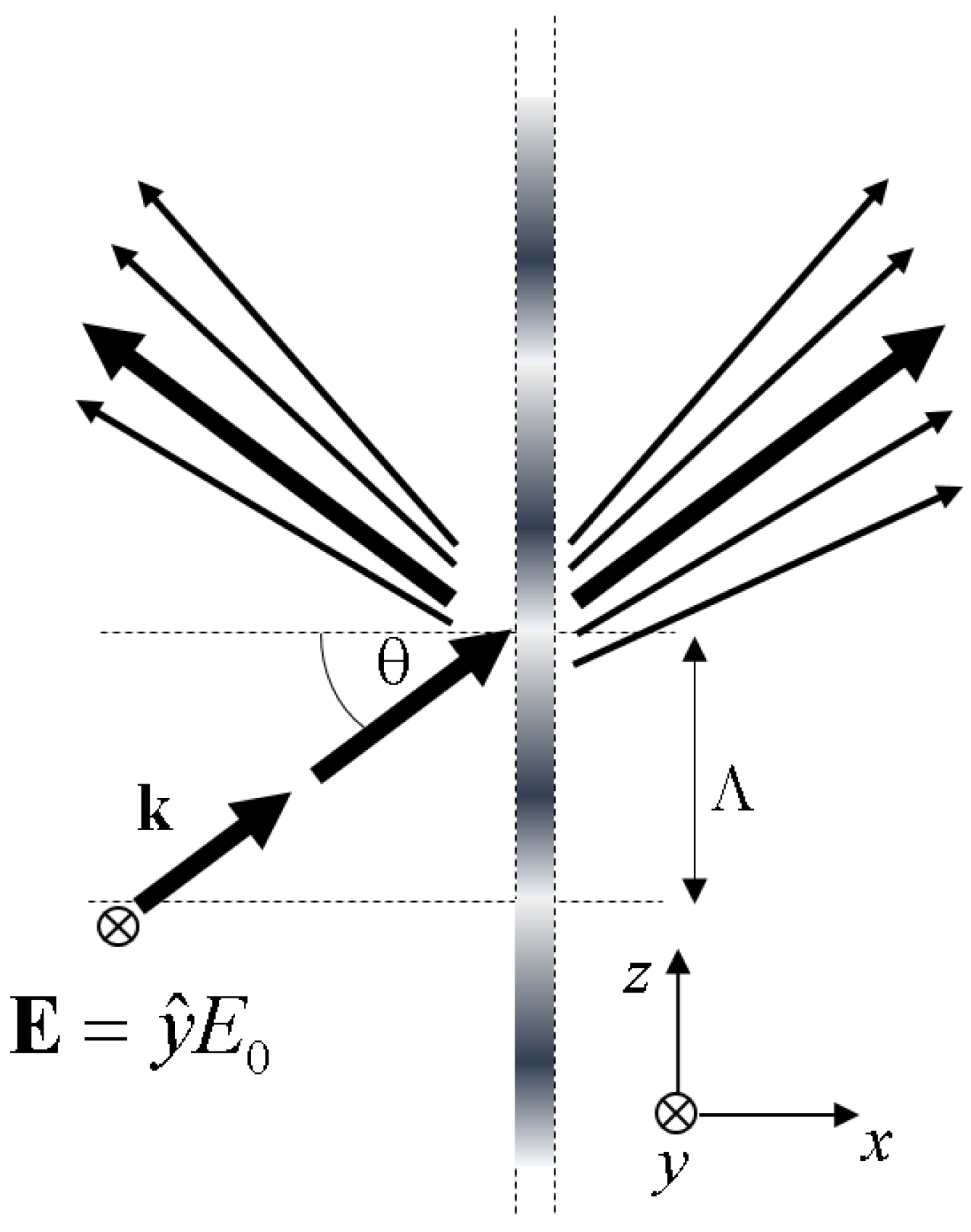
The system under study is a plane wave’s scattering from a grating. This scenario is presented in Figure 1. A TE-polarized plane-wave beam hits an active grating at an incident angle $\mathsf{\theta }$. The grating is located on the x = 0 plane. The gratings variations occur in the z-direction, in which case the electromagnetic Maxwell’s wave equation can be written as:

$$\frac{{\partial }^2}{\partial x^2}E+\frac{{\partial }^2}{\partial z^2}E+k^2\left(x,z\right)E=0$$

(1)

where the electric field is polarized in the y-direction (TE polarization) $E=\widehat{y}E\left(x,z\right)$, and $k^2\left(x,z\right)$ satisfies

$$k^2\left(x,z\right)=k_0^2\left\{1+i\delta \left(x\right)d\left[{\epsilon }^{″}+\delta {\epsilon }^{″}\cos \left(Kz\right)\right]\right\}$$

(2)

where the grating’s frequency is the reciprocal of the groove spacing $\Lambda$ (the pitch), i.e.,

$$K\equiv 2\pi /\Lambda .$$

(3)

In (2), we followed Ref. [16] and chose a delta function to represent the narrow grating’s layer. In this reference, it was shown that a very narrow dielectric grating can reflect 100% of the incident light at specific incident angles, no matter how narrow the grating layer is and how weak its modulation depth is.

As was explained in [16] (and references therein), a delta function is an excellent approximation for layers, which are shorter than the electromagnetic field’s wavelength. To be more specific, a dielectric with the following properties, $\mathsf{\epsilon }\left(x,y\right)=\left\{\begin{array}{cc}{\mathsf{\epsilon }}_0\left(x,y\right)& 0<x<d\\ 0& else\end{array}\right.$ where $d$ is the narrow layer’s thickness and can be approximated with great accuracy by $\mathsf{\delta }\left(x\right){\displaystyle {\int }_0^d{\mathsf{\epsilon }}_0\left(x^{\prime }\right)d{x}^{\prime }}$. Since in what follows we focus on the limit of extremely narrow layers, this is an excellent approximation. Moreover, the validity of this approximation is improved when the incident angle increases since the x-component of the beam’s wavenumber decreases. We will see that it is easier to measure the effect in the large incident angle domain. When the incident angle approaches π/2, the approximation is accurate.

3. Exact Numerical Solution

Let $\mathsf{\theta }$ be the incident angle; therefore, the wavenumber is $k=k_0\left(\widehat{x}\cos \mathsf{\theta }+\widehat{z}\sin \mathsf{\theta }\right)$ (see Figure 1), and the electromagnetic field can be written in all space as:

$$E\left(x,z\right)/E_0=\left\{\begin{array}{cc}\exp \left[i{k}_0\left(x\cos \mathsf{\theta }+z\sin \mathsf{\theta }\right)\right]+{\displaystyle \sum _n{r}_n\exp \left(-i{q}_{n}x+i{p}_{n}z\right)}& x<0\\ {\displaystyle \sum _n{t}_n\exp \left(i{q}_{n}x+i{p}_{n}z\right)}& x>0\end{array}\right.$$

(4)

where $p_n\equiv k_0\sin \mathsf{\theta }+Kn$ and $q_n\equiv \sqrt{k_0^2-p_n^2}=k_0\sqrt{1-{\left(\sin \mathsf{\theta }+\lambda n/\Lambda \right)}^2}$, i.e., $q_0=k_0\cos \mathsf{\theta }$ and $q_0=k_0\cos \mathsf{\theta }$. The boundary conditions on the grating requires

$$\begin{array}{l}E\left(x=+0,z\right)=E\left(x=-0,z\right) \mathrm{and}\\ {\left.\frac{\partial }{\partial x}E\left(x,z\right)\right|}_{x=+0}-{\left.\frac{\partial }{\partial x}E\left(x,z\right)\right|}_{x=-0}=-id{k}_0^2\left[{\mathsf{\epsilon }}^{″}+\mathsf{\delta }{\mathsf{\epsilon }}^{″}\cos \left(Kz\right)\right]E\left(x=0,z\right)\end{array}$$

(5)

and using the dimensionless parameters

$$s\equiv \lambda /\Lambda , P_n\equiv p_n/k_0=\sin \mathsf{\theta }+ns{Q}_n\equiv q_n/k_0=\sqrt{1-{\left(\sin \mathsf{\theta }+ns\right)}^2}, \mathsf{\alpha }\equiv \frac{1}{2}d{k}_0{\mathsf{\epsilon }}^{″}, \mathrm{and} \mathsf{\beta }=d{k}_0\frac{1}{4}\mathsf{\delta }{\mathsf{\epsilon }}^{″}$$

(6)

the problem reduces to the following difference equation

$$\left(Q_n+\mathsf{\alpha }\right)t_n+\mathsf{\beta }\left(t_{n+1}+t_{n-1}\right)=Q_0\mathsf{\delta }\left(n\right)$$

(7)

which can be rewritten in a more compact matrix form

$$M_0\cdot t=v$$

(8)

where

$$M_0\equiv \left(\begin{array}{ccccc}\ddots & \ddots & & & \\ \ddots & Q_{-1}+\mathsf{\alpha }& \mathsf{\beta }& & \\ & \mathsf{\beta }& Q_0+\mathsf{\alpha }& \mathsf{\beta }& \\ & & \mathsf{\beta }& Q_1+\mathsf{\alpha }& \ddots \\ & & & \ddots & \ddots \end{array}\right)t\equiv \left(\begin{array}{c}⋮\\ t_{-1}\\ t_0\\ t_1\\ ⋮\end{array}\right), \mathrm{and} v\equiv \left(\begin{array}{c}⋮\\ 0\\ Q_0\\ 0\\ ⋮\end{array}\right).$$

(9)

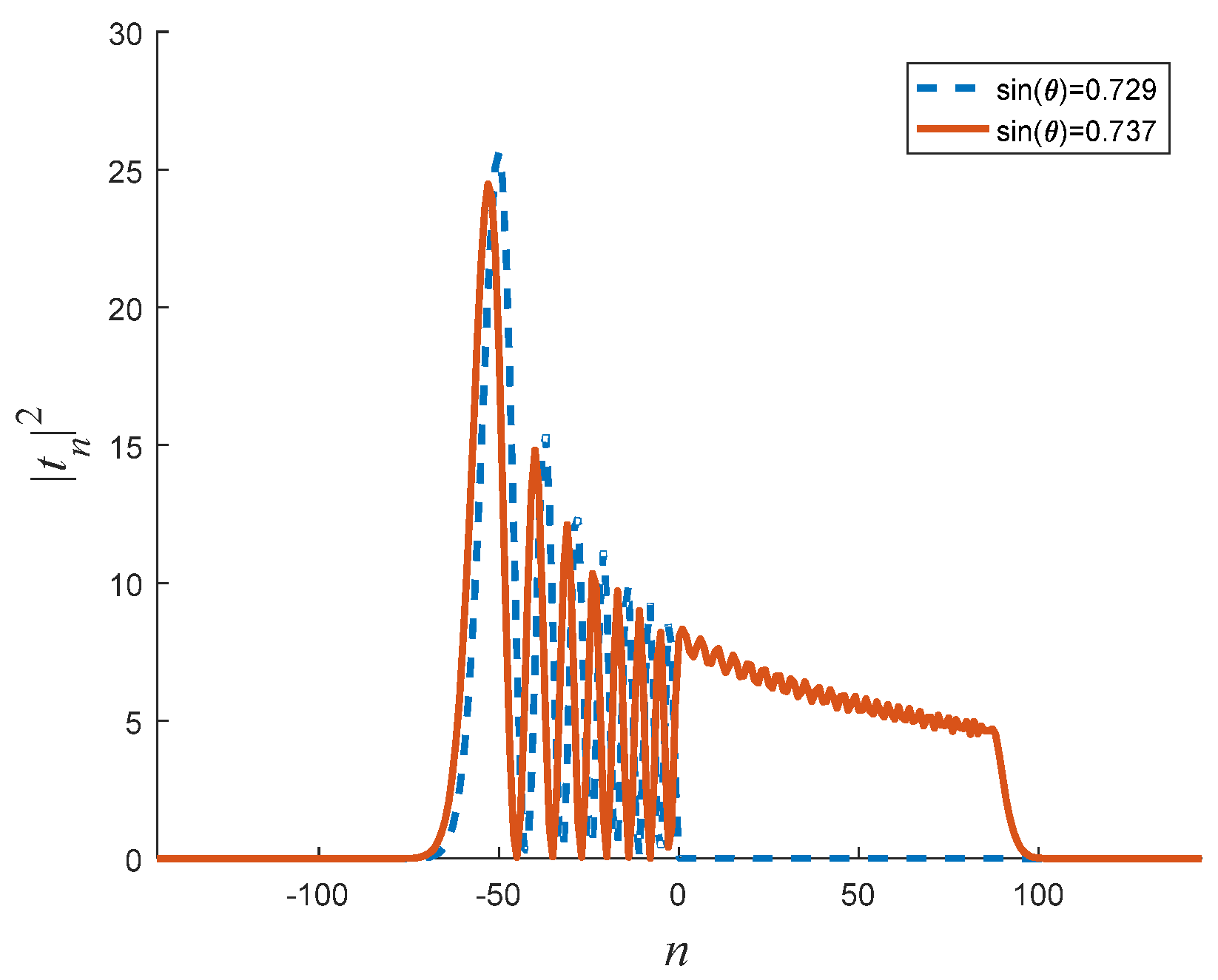
The numerical solution of this set of equations is presented, for two specific cases, in Figure 2.

Equation (7) illustrates the fact, which was mentioned in the introduction, that the dynamics is governed by the ratio between oscillations amplitude $\mathsf{\beta }$ and $Q_n$. When this ratio is imaginary (note that $\mathsf{\beta }$ is the imaginary part of the oscillations’ amplitude), the spectrum cannot have a complex structure.

As can be seen from this figure, there are incident angles in which the transmission coefficient of the non-negative, i.e., $n\ge 0$, modes vanish. A small change in the incoming angle reduces the positive modes’ transmission probability from the maximum value to zero. This behavior is demonstrated in Figure 2, where a small change of only ~1.4% in the incident angle suppresses the positive modes completely. On the other hand, the incoming angle has a small effect on the negative modes (see Figure 2). Unlike the positive modes regime, where the differences between the mode’s amplitudes are small, on the negative regime, the spectrum consists of ridges and valleys. This spectrum structure and behavior is similar to the quantum system of Ref. [29].

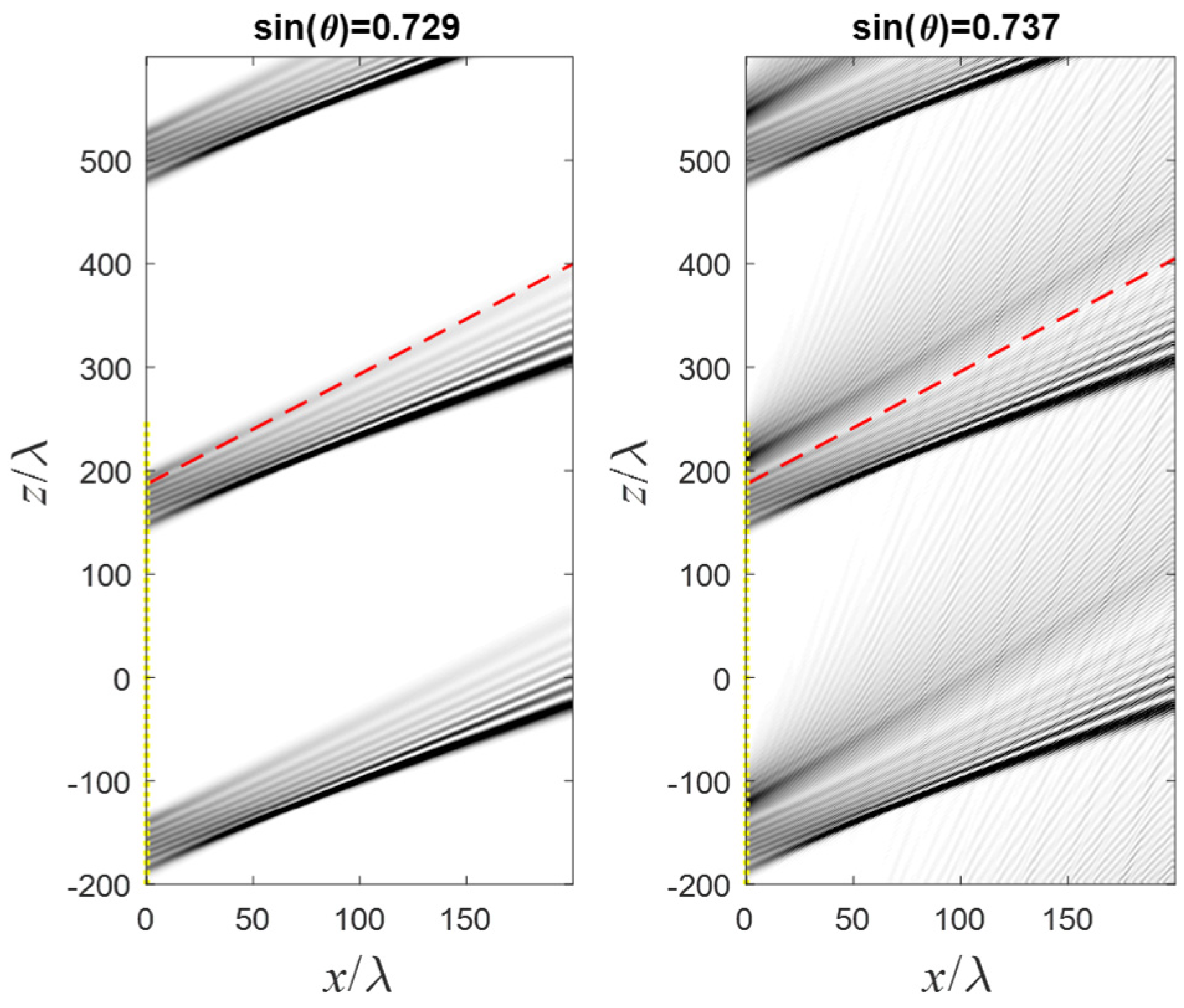
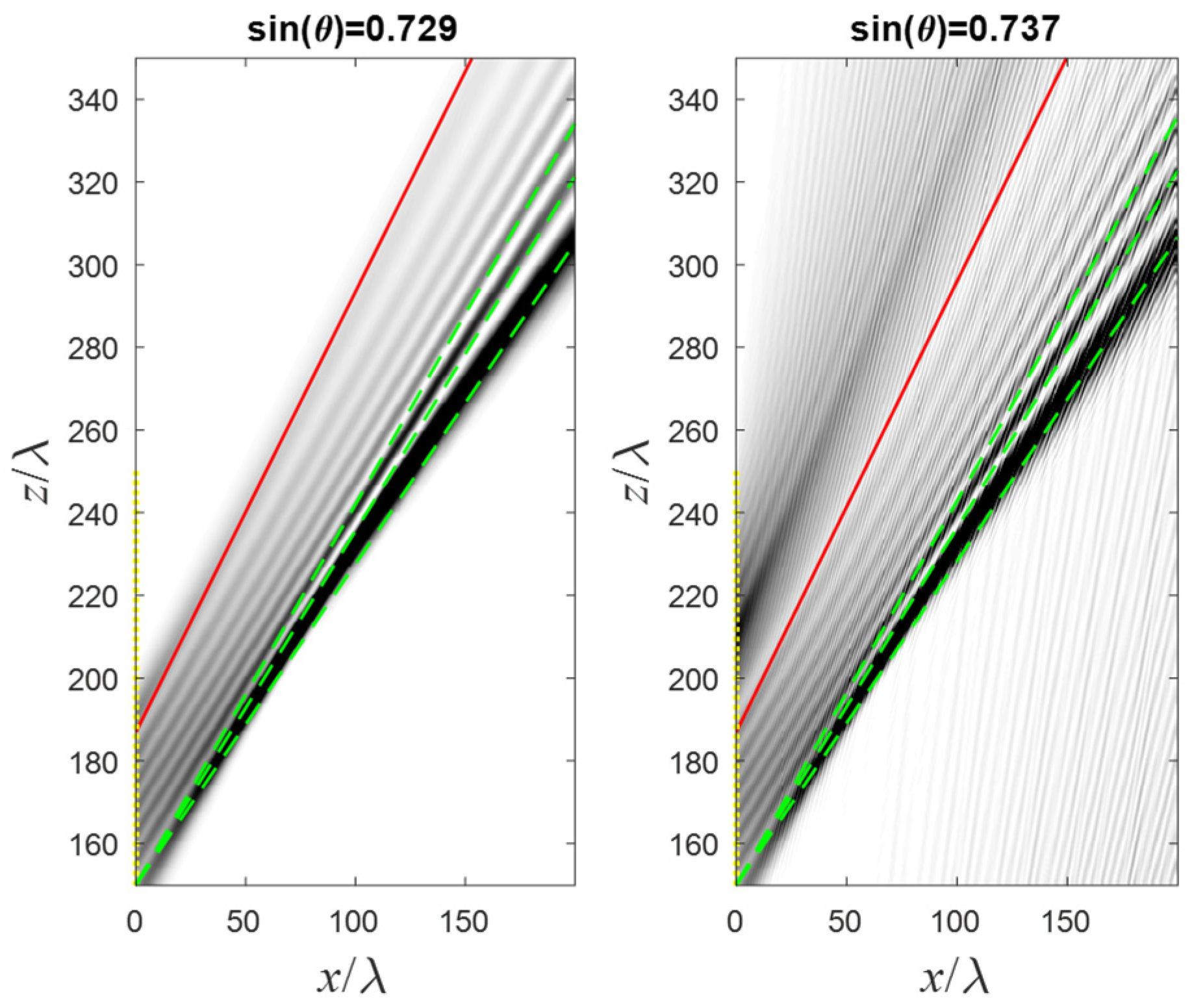
In Figure 3, the grating’s scattering pattern is presented for these two incident angles. The darker the color, the higher the light intensity ${\left|E\left(x,z\right)\right|}^2$. When the incident angle is $\sin \mathsf{\theta }=0.729$ (an example of a suppression scenario), then the e-m field is scattered only in the $\sin {\mathsf{\theta }}_{sc}<0.729$ angles. Nothing is scattered at angles, which exceed the incident angle $\sin {\mathsf{\theta }}_{sc}>0.729$. Below the incident angle, the e-m field is scattered at only specific angles.

On the other hand, when the incident angle is $\sin \mathsf{\theta }=0.737$ (an example of a non-suppression scenario), the e-m is scattered at all angles even beyond the incident angle $\sin {\mathsf{\theta }}_{sc}>0.737$. Below the incident angle, the scattering pattern is similar—in this regime, the e-m field is scattered at only specific angles.

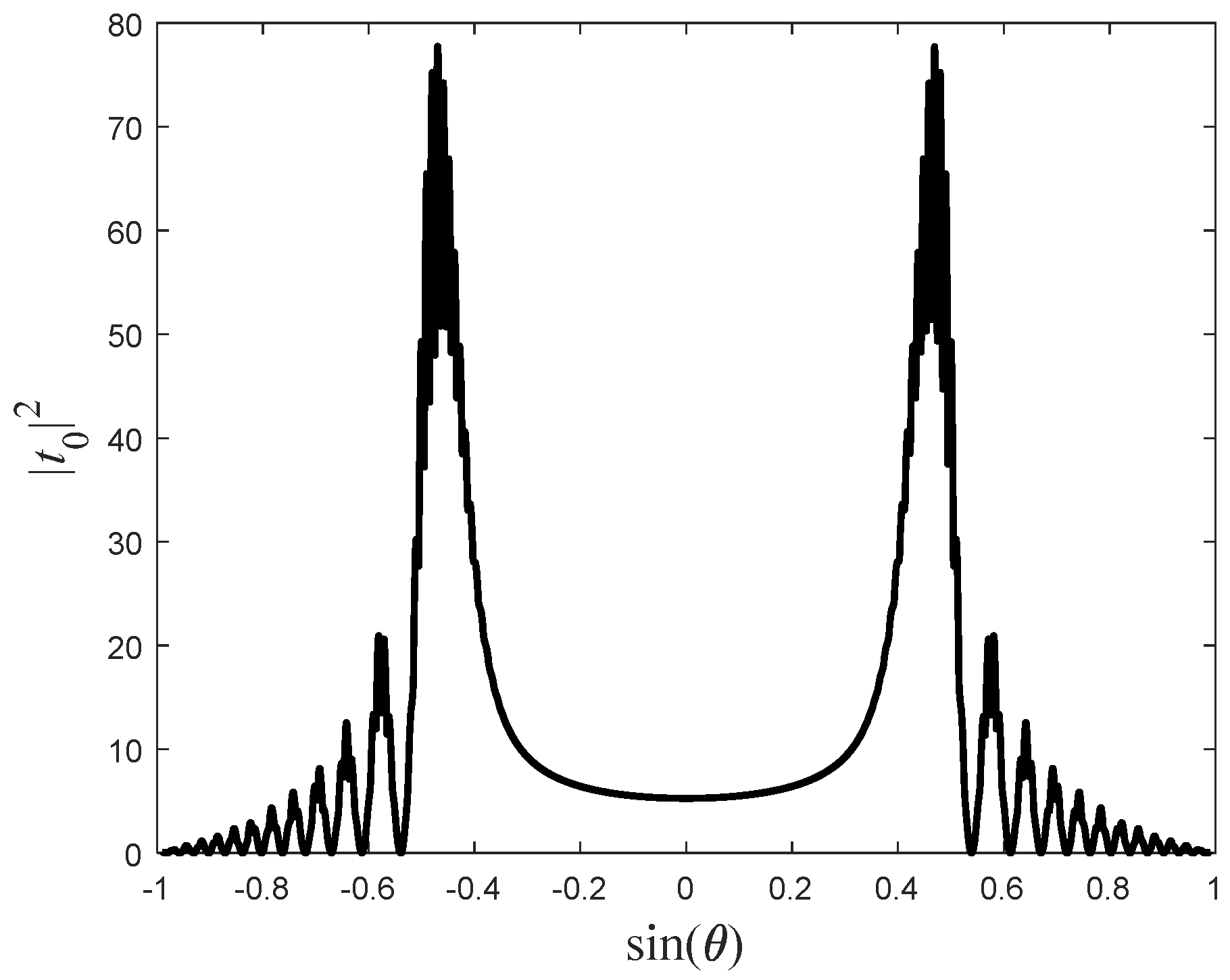
Since all the $n\ge 0$ modes vanish simultaneously, one can focus on the central mode $n=0$. In Figure 4, the amplitude of the central mode is presented as a function of the incident angle. As can be seen, beyond a certain angle, the transmission coefficient vanishes for several angles.

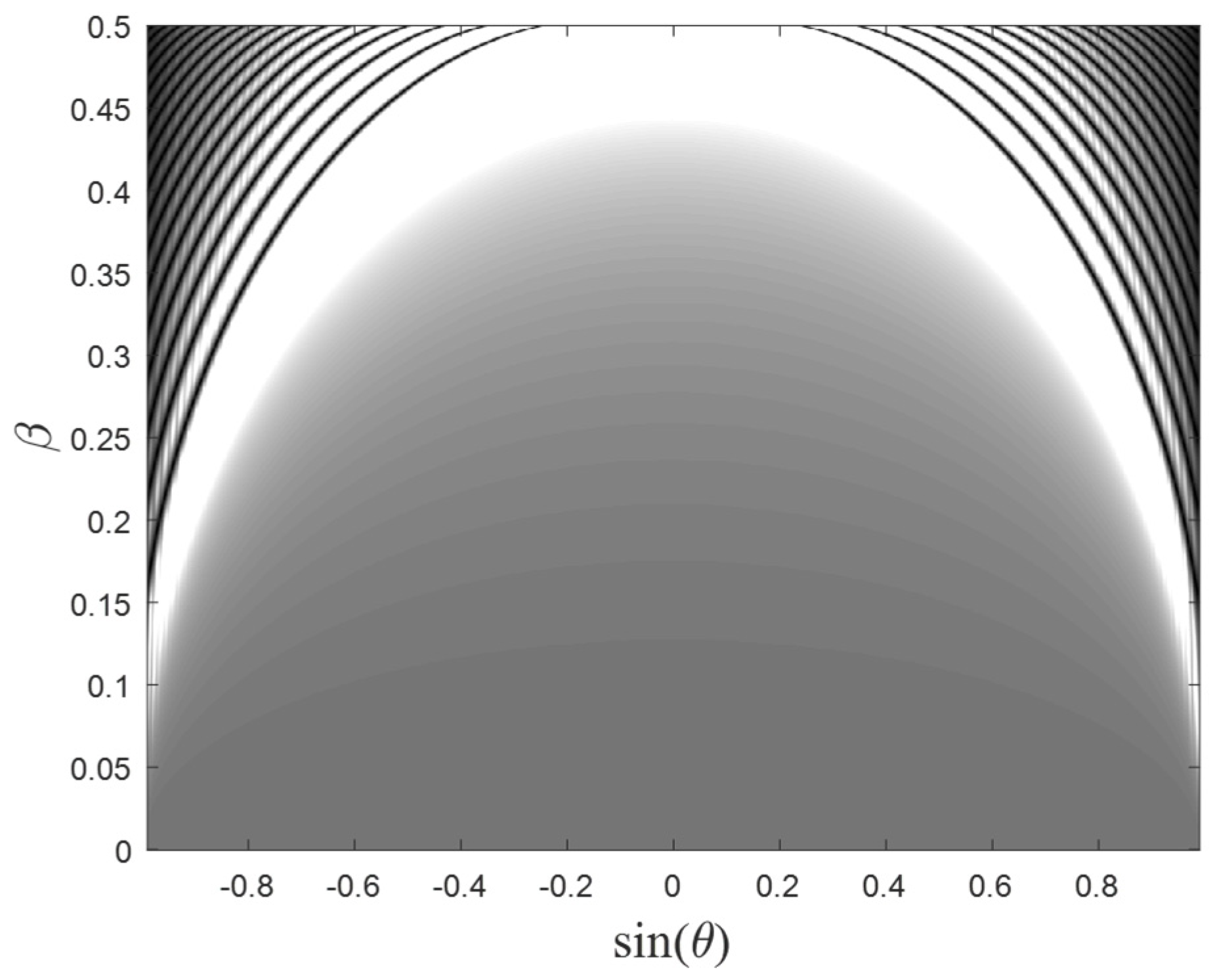
When the modulation depth $\mathsf{\beta }$ varies, so does the number of incident angles, in which the non-negative modes vanish. As can be seen in Figure 5, the larger the modulation depth (high $\mathsf{\beta }$), the larger the number of incident angles, in which the non-negative modes vanish. This fact is manifested by the multiple black curves, which represent zero transmission.

4. Approximate Analytical Derivation

The numerical studies show that this effect occurs when the grating constant is considerably larger than the incident beam’s wavelength. In this regime, Equation (7) can be simplified to allow for analytical derivation. In this regime,

$$Q_n\equiv q_n/k_0\cong \cos \mathsf{\theta }-ns\tan \mathsf{\theta }$$

(10)

which follows that Equation (7) can be simplified to

$$\left(\frac{\left(\cos \mathsf{\theta }+\mathsf{\alpha }\right)}{\mathsf{\beta }}-n\frac{s}{\mathsf{\beta }}\tan \mathsf{\theta }\right)t_n+\left(t_{n+1}+t_{n-1}\right)=\frac{Q_0}{\mathsf{\beta }}\mathsf{\delta }\left(n\right)$$

(11)

This difference equation can be solved with Bessel functions. Using Equation (9.1.27) of Ref. [31], $F_{\mathsf{\nu }-1}\left(x\right)+F_{\mathsf{\nu }+1}\left(x\right)=\frac{2\mathsf{\nu }}{x}{F}_{\mathsf{\nu }}\left(x\right)$ the solution of (11) can be written as

$$t_n=\left\{\begin{array}{cc}A{J}_{-n+n_0}\left(u\right)& n<0\\ C{J}_{n-n_0}\left(u\right)& n>0\end{array}\right.$$

(12)

where $n_0\equiv \frac{\left(\cos \mathsf{\theta }+\mathsf{\alpha }\right)}{s\tan \mathsf{\theta }}$, $u\equiv \frac{2\mathsf{\beta }}{s\tan \mathsf{\theta }}$, $J_n\left(u\right)$ are the Bessel functions of the first kind [31] and the coefficients A and C can be calculated by matching the solution and substituting the solution in (12), i.e.,

$A{J}_{n_0}\left(u\right)=C{J}_{-n_0}\left(u\right)$, and $\frac{s}{\mathsf{\beta }}\tan \mathsf{\theta }\left(n_0\right)C{J}_{-n_0}\left(u\right)+\left(C{J}_{1-n_0}\left(u\right)+A{J}_{1+n_0}\left(u\right)\right)=\frac{Q_0}{\mathsf{\beta }}$.

The solution therefore reads

$$A=\frac{\frac{Q_0}{\mathsf{\beta }}{J}_{-n_0}\left(u\right)}{\frac{s}{\mathsf{\beta }}\tan \mathsf{\theta }\left(n_0\right)J_{-n_0}\left(u\right)J_{n_0}\left(u\right)+\left(J_{n_0}\left(u\right)J_{1-n_0}\left(u\right)+J_{-n_0}\left(u\right)J_{1+n_0}\left(u\right)\right)}$$

(13)

$$C=\frac{\frac{Q_0}{\mathsf{\beta }}{J}_{n_0}\left(u\right)}{\frac{s}{\mathsf{\beta }}\tan \mathsf{\theta }\left(n_0\right)J_{-n_0}\left(u\right)J_{n_0}\left(u\right)+\left(J_{n_0}\left(u\right)J_{1-n_0}\left(u\right)+J_{-n_0}\left(u\right)J_{1+n_0}\left(u\right)\right)}$$

(14)

Now, we have an approximate solution of the entire spatial spectrum, from which two main results can be derived: (A) the incident angles in which the scattered e-m is bounded to lower angles and (B) the grating formula.

5. Calculating the Incident Angles for Which Scattering Is Bounded

From (12) and (14), it follows that suppression of high-angle scattering occurs for $C=0$, i.e., for

$$J_{n_0}\left(u\right)=0$$

(15)

and in which case, all the $n\ge 0$ modes vanish as well.

Since this approximation was derived for the limit of $s<<1$, then both relations $\frac{2\mathsf{\beta }}{s\tan \mathsf{\theta }}>>1$ and $n_0>>1$ hold. Therefore, using Equation (9.3.3) of Ref. [31],

$$J_{\mathsf{\nu }}\left(\mathsf{\nu }\sec B\right)\cong \sqrt{\frac{2}{\pi \mathsf{\nu }\tan B}}\cos \left[\mathsf{\nu }\left(\tan B-B\right)-\pi /4\right]$$

(16)

where in this case,

$$B\equiv \arccos \left(\frac{\cos \mathsf{\theta }+\mathsf{\alpha }}{2\mathsf{\beta }}\right) \mathrm{and} \mathsf{\nu }\equiv n_0$$

(17)

For a solution, in which the argument of the cosine function of (16) is small whilst still $s<<1$, the parameter $B$ must be accordingly small. Therefore, we seek a solution around

$$\cos \mathsf{\theta }\cong 2\mathsf{\beta }-\mathsf{\alpha },$$

(18)

in which case, (15) and (16) yield

$$n_0{B}^3/3=\left(m+\frac{3}{4}\right)\pi$$

(19)

Solving (19) for $\mathsf{\beta }$, we finally obtain the condition for high-angle suppression

$$\mathsf{\beta }\cong \frac{\left(\cos \mathsf{\theta }+\mathsf{\alpha }\right)}{2}\left[1+\frac{1}{2}{\left[3\frac{s\tan \mathsf{\theta }}{\left(\cos \mathsf{\theta }+\mathsf{\alpha }\right)}\left(m+\frac{3}{4}\right)\pi \right]}^{2/3}\right]$$

(20)

or equivalently, one can find the incident angles ${\mathsf{\theta }}_m$ for which high-angle scattering does not occur

$$\cos {\mathsf{\theta }}_m\cong 2\mathsf{\beta }{\left[1+\frac{1}{2}{\left[3\frac{s}{2\mathsf{\beta }}\sqrt{{\left(2\mathsf{\beta }-\mathsf{\alpha }\right)}^{-2}-1}\left(m+\frac{3}{4}\right)\pi \right]}^{2/3}\right]}^{-1}-\mathsf{\alpha }$$

(21)

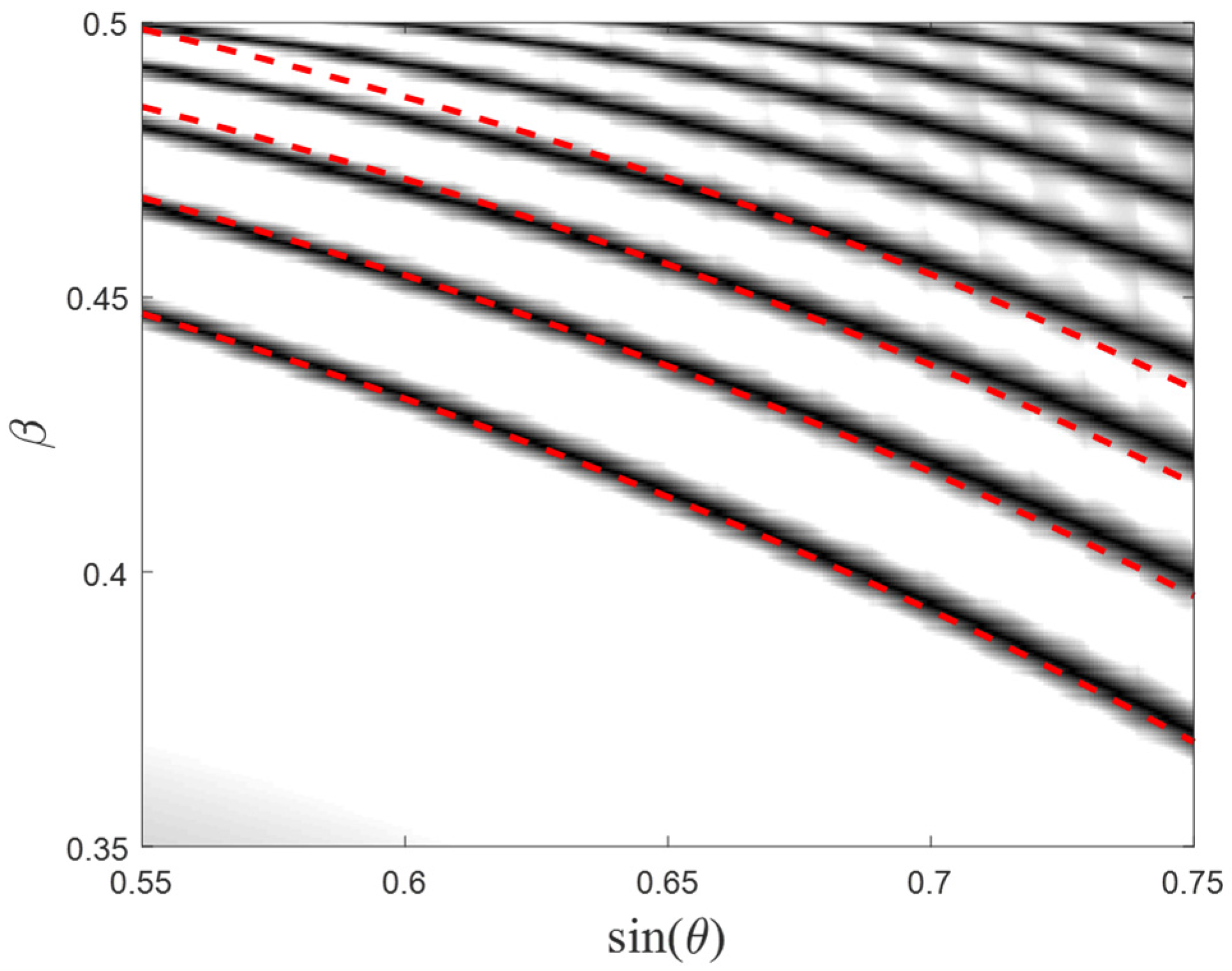
In Figure 6, the approximation (20) is plotted on top of the exact numerical simulation (Figure 5). As can be seen, this approximation shows high agreement with the numerical results.

6. Scattering Angles

The scattered beam takes the following form:

$$\begin{array}{l}E\left(x,z\right)/E_0={\displaystyle \sum _n{t}_n\exp \left(i{q}_{n}x+i{p}_{n}z\right)}=\\ {\displaystyle \sum _{n}A{J}_{-n+n_0}\left(\frac{2\mathsf{\beta }}{s\tan \mathsf{\theta }}\right)\exp \left(i{k}_0\left(\sqrt{1-{\left(\sin \mathsf{\theta }+ns\right)}^2}x+\left(\sin \mathsf{\theta }+ns\right)z\right)\right)}\end{array}$$

(22)

where A is the constant (13).

To calculate the scattering angles, one can use the fact that $s<<1$. In this case, the summation can be approximated by an integral

$$E\left(x,z\right)/E_0\cong s^{-1}A{\displaystyle \int d\mathsf{\eta }}{J}_{\left({\mathsf{\eta }}_0-\mathsf{\eta }\right)/s}\left(\frac{2\mathsf{\beta }}{s\tan \mathsf{\theta }}\right)\exp \left(i{k}_0\left(\sqrt{1-{\left(\sin \mathsf{\theta }+\mathsf{\eta }\right)}^2}x+\left(\sin \mathsf{\theta }+\mathsf{\eta }\right)z\right)\right)$$

(23)

Using the method of stationary phase approximation, this integral can be evaluated at

$$\sin {\mathsf{\theta }}_{sc}-\sin \mathsf{\theta }=\mathsf{\eta }$$

(24)

Note that (24) is the classical grating formula.

Therefore, the scattering amplitude at the scattering angle ${\mathsf{\theta }}_{sc}$ is approximately

$${\left|A{J}_{\left({\mathsf{\eta }}_0-\left(\sin {\mathsf{\theta }}_{sc}-\sin \mathsf{\theta }\right)\right)/s}\left(\frac{2\mathsf{\beta }}{s\tan \mathsf{\theta }}\right)\right|}^2$$

(25)

Again, since $s<<1$, one can use Equation (9.3.3) of Ref. [31], in which case

$$B\cong \sqrt{2\left(1-\frac{\left(\cos \mathsf{\theta }+\mathsf{\alpha }\right)-ns\tan \mathsf{\theta }}{2\mathsf{\beta }}\right)}$$

(26)

the angles which yield the maximum value of (25) must satisfy

$$n_0{B}^3/3-\pi /4=\left(m\pi \right)$$

(27)

Substituting (26) into (27) and solving the angle, while keeping in mind that $\sin {\mathsf{\theta }}_{out}-\sin \mathsf{\theta }=\mathsf{\eta }$, one finally obtain the grating formula

$$\left(\sin {\mathsf{\theta }}_{out}^m-\sin \mathsf{\theta }\right)\cong \left[\mathsf{\beta }\left\{{\left[\frac{3\pi }{n_0}\left(m+\frac{1}{4}\right)\right]}^{2/3}-2\right\}+\left(\cos \mathsf{\theta }+\mathsf{\alpha }\right)\right]\cot \mathsf{\theta }$$

(28)

As can be seen in Figure 7, the scattered angles ${\mathsf{\theta }}_{out}^m$ for $m=0,1$ and $2$ show high agreement with the approximation (28). It should be stressed that the grating Formula (28) appears on top of the classical one (24).

7. Physical Realization

The realization of this grating requires simultaneous changes in both the real and imaginary components of the refractive index; however, they do not change in the same manner.

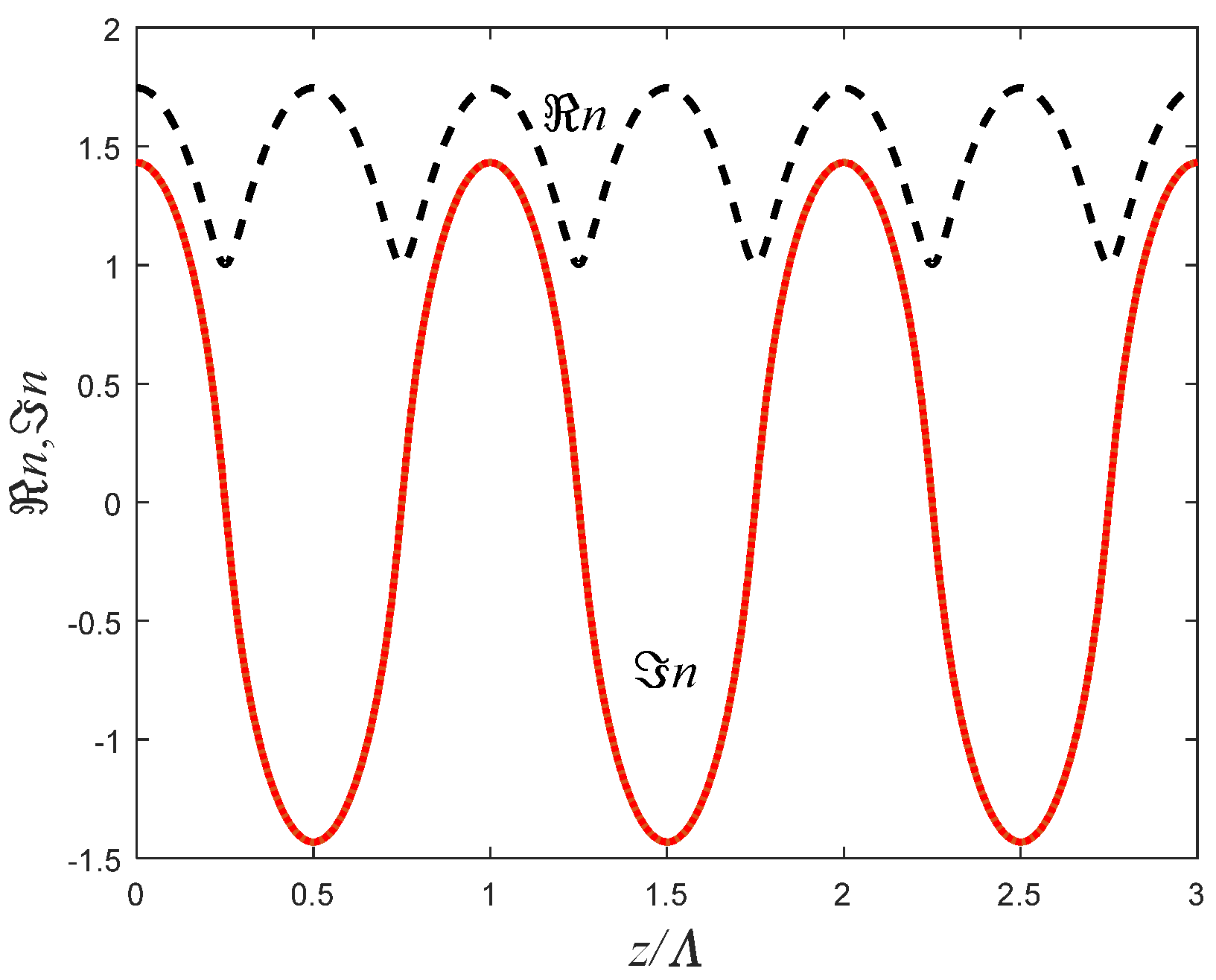
To simplify the model, the harmonic change occurs in the imaginary component of the dielectric constant $\mathsf{\delta }{\mathsf{\epsilon }}^{″}\cos \left(Kz\right)$. Therefore, the real and imaginary parts of the refraction index are

$$\Im n=2^{-1/2}\mathsf{\delta }{\mathsf{\epsilon }}^{″}\cos \left(Kz\right)/\sqrt{1+\sqrt{1+{\left(\mathsf{\delta }{\mathsf{\epsilon }}^{″}\cos \left(Kz\right)\right)}^2}}$$

(29)

$$\Re n=2^{-1/2}\sqrt{1+\sqrt{1+{\left(\mathsf{\delta }{\mathsf{\epsilon }}^{″}\cos \left(Kz\right)\right)}^2}}$$

(30)

These components are plotted in Figure 8 for $\mathsf{\delta }{\mathsf{\epsilon }}^{″}=5$. As can be seen, for this value, the real part of the refractive index changes between 1 and 1.7, while the imaginary part varies between −1.5 to +1.5. Then, if the layer thickness is $d/\lambda \cong 0.03$, then $\mathsf{\beta }=d{k}_0\frac{1}{4}\mathsf{\delta }{\mathsf{\epsilon }}^{″}\cong 0.24$, which is sufficient to measure several angles which shows this effect (according to Figure 5). It should be noted that if we seek the effect at high, i.e., grazing, angles, the layers width can be increased substantially, while keeping the narrow layer approximation still. In this case, multiple angles should be detected. Moreover, most of this work concentrated, for simplicity, on the $\mathsf{\alpha }=0$ scenario; however, by varying $\mathsf{\alpha }$, the effect will appear even for very weak $\mathsf{\beta }$, in which case, it will be easier to measure the effect. Nevertheless, a full study of this effect for different values of $\mathsf{\alpha }$ and different modulations is beyond the scope of this paper.

8. Summary

The scattering from an active grating layer was analyzed. In this model, the imaginary component of the dielectric coefficient varies harmonically. The grating’s layer width is shorter than the optical beam wavelength, while the grating’s wavelength is longer than the beam’s wavelength. A new grating formula is formulated, which is the profile on top of the classical grating formula. An approximate analytical expression for this formula was derived. Besides the scattering orders, a special scattering pattern appears for certain incident angles.

It was found that in some cases, the scattering angles ${\mathsf{\theta }}_{out}$ cannot exceed the incident angle $\mathsf{\theta }$, i.e., for specific $\mathsf{\theta }={\mathsf{\theta }}_m$, the scattered angles obey ${\mathsf{\theta }}_{out}\le \mathsf{\theta }$.