Abstract
Optical phased arrays (OPAs) are renowned for their exceptional ability to manipulate and direct light beams, positioning them as an ideal choice for solid-state light detection and ranging (LiDAR) technologies. This review provides a comprehensive examination of the current research landscape for photonic integrated circuit (PIC)-based OPAs. It begins by addressing the critical design elements at the component level necessary for optimal functionality. This review then delves into phase calibration techniques and the overarching architecture of OPAs. It concludes by emphasizing the innovative 3-D OPA design, which stands out for its enhanced optical efficiency.
1. Introduction
Since the early 1980s, the exploration of photonic devices for information processing and communication has led to significant advances, notably the development of the photonic integrated circuit (PIC). This circuit offers a host of benefits over their electronic counterparts, such as increased speed and reduced power consumption, thanks to the inherent properties of photons. Their application spans a variety of sectors, including telecommunications, data center connectivity, biomedical imaging, and sensing technologies. As the demand for swift data transmission and sophisticated processing escalates, PICs are playing a pivotal role in shaping the future of communication and computing infrastructures.
In parallel, the optical phased array (OPA) emerges as a transformative technology, manipulating light wave phases to tailor beam propagation characteristics without the need for mechanical adjustments. This capability is realized through a meticulously arranged array of optical emitters, allowing for precise control over the beam’s direction, shape, and pattern. The OPAs’ versatility allows for utility in LiDAR, wireless communications, and optical imaging, boasting advantages, such as rapid responsiveness, enhanced precision, and energy efficiency, over the conventional beam-steering mechanisms. As optical systems demand greater speed and accuracy, OPAs are becoming increasingly integral to a myriad of applications.
OPAs featuring micron-scale emitters are achievable through various means, including liquid crystal, metasurface, and solid-state PICs. Among these, PIC-based OPAs have garnered substantial research interest due to their quick response times and compatibility with CMOS manufacturing processes. Numerous reviews have been published, offering diverse perspectives on OPA and LiDAR technologies [1,2,3,4,5,6]. This paper aims to present a current and focused review of OPA technology, with special attention given to design considerations at the component level and advancements at the system level. We recognize the challenge of encapsulating the breadth of such a rapidly advancing field and extend our apologies for any inadvertent omissions of researchers’ or institutions’ contributions.
2. Basic Configuration of PIC-OPA
A typical configuration of a PIC-OPA consists of four basic blocks: a light source, a light distribution network, a phase modulation array, and an emitter array. This is shown in Figure 1.
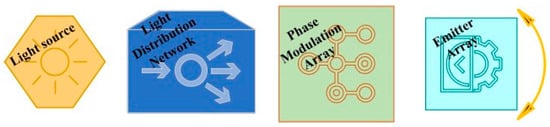
Figure 1.
Basic configuration of PIC-OPA.
In most studies, researchers typically use either an external tunable laser or an on-chip active laser as the light source. Once the light is generated, it is distributed across multiple channels using one of three common light distribution networks: MMI/Y-splitter trees, star-couplers, or cascaded directional coupler arrays. The advantages and disadvantages of each type will be discussed in the later sections. Once the light is distributed, the phase of the light mode in each channel must be modulated to determine the phase profile when the light is emitted. This modulation allows for the phase profile to be tailored to the specific application. For example, beam steering is a commonly studied application for OPAs, and the phase profile is designed to vary linearly with the emitter position. This approach enables the formation of a flat equal-phase plane in free space, generating a beam with the best spatial convergence perpendicular to the equal-phase plane. Additionally, if the emitting phase profile can be accurately controlled, the beam’s propagation direction can be adjusted without the need for any mechanical moving parts.
3. Component-Level Designing Concerns
A high-performance PIC requires careful optimization of every component, including the coupler, waveguide bending, power splitters, and any other necessary elements. An OPA is one of the most complex PICs currently known; thorough optimization of every component is necessary for optimal performance. In this section, the authors review the component-level innovations from published articles, including unique designs in emitter arrays, phase shifters, and on-chip light sources.
3.1. Emitter Array
The emitter array plays a crucial role in an OPA as it determines the intensity and phase profile of the emitting plane, ultimately affecting the interference of light in free space. The accurate control of light interference is essential for the excellent performance and versatile functionality of PIC-OPAs. Therefore, the emitter array is considered the most significant component of an OPA.
3.1.1. Emitter Type
There are three typical configurations of emitter arrays, an end-fire emitter array, a waveguide grating array, and a nano-antenna array. Figure 2 illustrates the three types, with examples from published papers.
- End-Fire Array
The simplest design for an emitter array is the end-fire configuration [7,8,9,10]. In this setup, the light is divided into multiple channels with precisely controlled phases, and then each channel waveguide terminates with an air interface that serves as a basic edge coupler toward the free space. With the end-fire configuration, the light emission does not depend on diffraction, which allows for achieving high efficiency across a broad spectrum. Fabrication is also simplified as the waveguide layer in an end-fire OPA can be defined in just one lithography step, unlike the other two types that require at least two lithograph steps for the waveguide layer. However, there is a downside to this design. Since most PICs use a single-waveguide-layer setup, the end-fire array can only provide a 1 × N array that produces a beam that converges horizontally, but diverges vertically, resulting in a fan beam, as shown in Figure 2a,b.
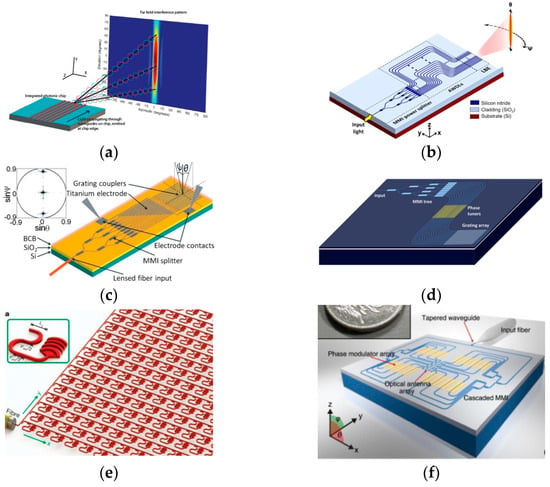
Figure 2.
Three types of emitter array. (a,b) End-fire array [9,10]. (c,d) Waveguide grating array [11,12]. (e,f) Nano-antenna array [13,14].
- Waveguide Grating Array
The most commonly investigated configuration is waveguide grating [11,12,15,16,17], as shown in Figure 2c,d. This configuration operates in a manner similar to the end-fire array, where light is also divided into 1 × N channels. However, instead of terminating the waveguides towards free space, this configuration features a grating coupler region. In this region, waveguide gratings of a certain length are situated along each waveguide. Once the light reaches the grating region, it undergoes diffraction and is emitted in a certain direction. When the grating period is determined, the diffracted light will constructively interfere to converge in a specific direction, providing beam convergence in that direction. In an OPA with a waveguide grating array, the diffraction gratings converge the emitted light beam in the waveguide direction (usually labeled as θ in the related publications), and the waveguide array converges the beam through interference in the perpendicular direction (usually labeled as ψ in the related publications). With a configuration that is only slightly more complex than an end-fire OPA, the waveguide grating array OPA can emit a 2-D converged beam, making it highly desirable for LiDAR applications.
However, the waveguide grating array has a downside, which is the limited emitting efficiency. This is due to the fact that the grating coupler emits light through diffraction, resulting in the emission of an upward beam as well as a downward leakage beam into the silicon substrate. This symmetric diffraction causes about half of the light power to be wasted. On the other hand, in this configuration, beam steering in the waveguide direction (θ) is achieved through wavelength tuning. However, when this type of OPA is used in an FMCW (frequency-modulated continuous wave) LiDAR system, the resolution in one direction (typically the vertical direction) cannot be maximized due to the wavelength dependency of the emitting angle. This results in the resolution being limited to the steering angle within the frequency modulation range.
- Nano-antenna Array
End-fire arrays and waveguide grating arrays both have 1 × N channels, which implies that their phase profiles can be controlled in only one direction. However, in the other direction, an end-fire array has no convergence, while a waveguide grating array has a predetermined phase profile that cannot be modulated. The proposed solution for having the ability to define the 2-D phase profile arbitrarily is to use a nano-antenna array OPA [13,14,18]. This setup distributes light into the M X N channels, with each channel ending at a nano-antenna that emits light with a broad field of view. The light emitted from these antennas can then interfere in both directions (θ and ψ) in free space, allowing for the creation of a customizable 2-D phase profile. Compared to the waveguide grating array OPA, the nano-antenna array OPA has additional capabilities beyond beam convergence. For instance, a 64 × 64 antenna array OPA can produce complex patterns, such as an “MIT” pattern [13] or a multi-beam pattern [18], in the far field. This is due to the fact that the nano-antenna array OPA allows for more precise control over the phase profile of the emitted light than the waveguide grating array OPA.
On the flip side, it should be noted that implementing a nano-antenna array OPA is a more challenging task than using the other two configurations due to its more complex layout. An M × N emitter array necessitates a larger space for the phase shifters and routing waveguides, making the layout more complicated than a 1 × N array. Additionally, the larger size of the nano-antennas compared to the typical waveguide dimensions results in a wider separation between the emitters than that in the 1 × N configuration, which leads to a stronger aliasing effect. Furthermore, the design of nano-antennas is based on diffraction from the waveguide gratings, which also results in a roughly 50% power loss.
3.1.2. Emitter Envelope Function
OPAs utilize phase manipulation to determine the direction of constructive interference and shape a beam. However, their ability to steer a beam is limited to the range of the single emitter, and the intensity of the beam in a particular direction depends on the emitter’s envelope function. Typically, the envelope function is a Gaussian profile, which can result in a significantly higher intensity in the normal direction compared to that in the other directions. To address this issue, it is preferable to design emitters with a relatively broader envelope function by reducing the emitter size to promote more divergent emissions. Additionally, in the end-fire configuration, a low-index cavity such as a silica cavity can be added to broaden the center part of the envelope function [19], resulting in a plateau envelope, as depicted in Figure 3b.
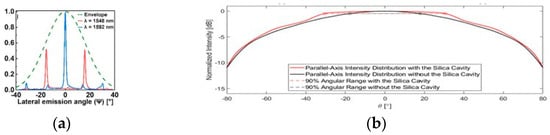
Figure 3.
Emitter envelope function. (a) In a normal emitter envelope function [10], the beam in the normal direction has the greatest intensity (blue curve), whereas the beam a certain degree away exhibits a considerably lower intensity (red curve) [10]. (b) A relatively flat envelope function can make the beam has a similar intensity in a much broader range [19].
3.1.3. Emitter Arrangement
OPA research begins with the arrangement of emitters at specific intervals, creating a periodic layout. In PIC-OPAs, waveguides are used to direct light to the emitters. However, if the waveguide array is too dense, it can cause crosstalk between the different channels, resulting in a distorted emitting phase profile. Therefore, the emitting pitch in a typical OPA design must be larger than roughly one wavelength. One consequence of having a large pitch is the occurrence of the aliasing effect, as shown in Figure 4a. When a target periodic signal (represented by the red curve) is sampled by periodic dots (represented by the blue dots) with a pitch that is too large (greater than half of the signal periodicity), the dots can form a signal with a different periodicity (represented by the blue curve). This is similar to what happens in periodic OPAs, where the distance between emitters is greater than half of the light wavelength. This causes grating lobes to appear in addition to the main lobe in the far field, and the sparser the emitters are, the denser the grating lobes are. This phenomenon ultimately restricts the effective range over which the beam can be steered, thereby limiting the application of such OPAs in LiDAR systems.
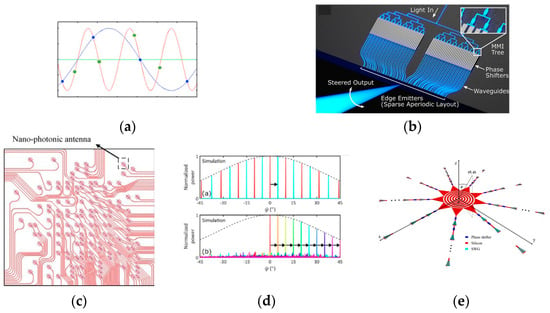
Figure 4.
Aliasing effect and aperiodic OPAs. (a) Illustration of aliasing effect. Blue dots: periodic sampling; green dots: aperiodic sampling. (b) Aperiodic end-fire array OPA [20]. (c) The suppression of the aliasing effect by aperiodic arrangement [21]. (d) Aperiodic nano-antenna array OPA [22]. (e) Circular OPA [23].
- Aperiodic Arrangement
A method used to mitigate the issue of aliasing without challenging the half-wavelength limit is to utilize an aperiodic emitter arrangement. In Figure 4a, the periodic blue dots represent samples along the target red curve, creating an aliasing blue curve; if one is using the green dots located at various positions, the target red curve can still be achieved, and the aliasing blue curve is no longer needed. In the illustrated situation in Figure 4a, it is possible that the green dots may support another aliasing curve. However, it is theoretically feasible to create an aperiodic design where no more than two emitting dots support the same aliasing curve; therefore, the aliasing effect can be well suppressed.
This idea has been applied and extensively studied in PIC-OPA devices [20,21,22,24,25,26,27,28,29,30,31]. The design of aperiodic arrangements for OPA devices is highly dependent on factors such as the emitter count, spacing, and total aperture requirements, making it a case-sensitive process. Currently, there is no analytical solution available that can guide the design of every aperiodic arrangement. The design of these arrangements can be based on either regular aperiodic patterns or purely irregular patterns [24]. In cases where an OPA needs to cover a larger emitting aperture with fewer emitters, the average spacing between the emitters must be increased. In such cases, regular aperiodic patterns may not be effective [24], and the design process typically relies on optimization algorithms, like particle sweep optimization, genetic optimization, etc. [25,26,27].
In a 1 × N channel OPA, aperiodic arrangement effectively mitigates the aliasing effect in one direction (ψ), while the far field performance in the other direction (θ) depends on the OPA configuration, whether it is an end-fire array or waveguide grating array [20,21,28,29]. Figure 4b depicts an end-fire array OPA, where this figure showcases the aperiodic arrangement of the emitter [20]. In Figure 4c, the simulation result of an aperiodic waveguide grating array OPA is shown [21]. The top figure displays a reference periodic OPA, which exhibits a strong aliasing effect, whereas the bottom figure shows a single main lobe in the field of view, even when the beam is steered from 0° to 45°. Applying a 2-D aperiodic layout in a nano-antenna array OPA may enhance the system’s complexity and design difficulty (as depicted in Figure 4d), but it has the potential to mitigate the aliasing effect in both the θ and ψ directions [22,30,31].
However, it is important to note that this aperiodic arrangement is not flawless. Its main purpose is to prevent the emitters from supporting the same aliasing function, thereby minimizing the appearance of grating lobes in the far field. However, rather than eliminating the grating lobes, this method aims to flatten them out. Consequently, the noise level, commonly referred to as the “side lobe level” in many publications, is higher in the far field, as illustrated in Figure 4c. Furthermore, the power of light that was originally concentrated in the grating lobes in a periodic OPA is merely evenly distributed in the far field in an aperiodic OPA, but does not converge into the main lobe. Therefore, the aperiodic arrangement simply makes the main lobe the only noticeable beam, rather than enhancing the beam power.
The design of a 2-D aperiodic nano-antenna array OPA typically relies on an optimization method. All such methods can be categorized as improved exhaustive methods. However, a common challenge with these methods is that while the grating lobe level can be effectively suppressed for a specific beam direction during optimization; this may dramatically increase when the beam direction changes. This is attributable to the absence of circular symmetry in the rectangular OPAs. Circularly arranged OPAs have been proposed as a solution to this problem [23,32,33,34,35]. In addition to solving the issue of the grating lobe level increasing when the beam direction changes, circular OPAs offer another advantage. Light can be fed into them using a grating coupler situated at the center of the circle, which greatly simplifies the layout of the OPA, as illustrated in Figure 4e.
- Challenge the Half-Wavelength Pitch Criteria (Table 1)

Table 1.
Crosstalk and SLL between arrays according to number, pitch, and width of waveguides.
Table 1.
Crosstalk and SLL between arrays according to number, pitch, and width of waveguides.
| Reference | Number of Waveguides | Pitch | Width | Crosstalk | SLL |
|---|---|---|---|---|---|
| [36] | 24 | 1.3 µm | 280 nm | −12 dB | - |
| [37] | 64 | 775 nm | 300/400/350 nm | −17 dB | −11.4 dB |
| [38] | 16 | 695 nm | 500 nm | −26 dB | - |
| [39] | 8 | 695 nm | 50 nm | −25 dB | - |
| [40] | 16 | 695 nm | 500 nm | −19 dB | −10.9 dB |
| [41] | 64 | 1.2 µm/775 nm | 560/400/580/380 nm | −13 dB | −19 dB |
| [42] | 16 | 4 µm | 290 nm | No crosstalk | −5 to −10 dB |
| [31] | 9 × 9 | 20 µm | - | −6 dB | |
| [33] | 1 × 64 | 87.5 µm | 1.5 µm | No crosstalk | −20 dB |
| [35] | 820 | 9 µm | - | - | −10 dB |
| [43] | 1024 | 4 µm | 1.5 µm | - | −10 dB |
| [44] | 8 × 8 | - | 0.4 µm | - | −25 dB |
Although the aperiodic arrangement of emitters can effectively reduce the distortion caused by aliasing, resulting in only the main lobe being noticeable in the far field, it does not enhance the power of the beam. Careful optimization of the waveguide geometry can push the emitting pitch to 1.3 µm in the SOI (silicon on insulator) platform [36], which can suppress aliasing much better. However, to completely eliminate aliasing, it is necessary to use a half-wavelength pitch, but this can be challenging due to the crosstalk between waveguides that are positioned too closely. Different methods have been proposed to mitigate crosstalk, such as using highly confined waveguide modes and minimizing the propagation length when the waveguides are at the half-wavelength pitch [9]. However, this approach is not easily scalable and is not appropriate for the waveguide grating array configuration since there is insufficient space to include a long grating coupler region, as crosstalk suppression relies on a propagation length as short as 10 µm.
Several methods have been proposed to reduce crosstalk over a more extended propagation distance. Firstly, the use of waveguides with different geometries having different mode indexes can help suppress crosstalk by inducing index mismatching when such waveguides are placed close to each other [37,38,39,40,45,46], as shown in Figure 5a. Secondly, using a sinusoidal-shaped waveguide array can break the symmetry along the centerline of the array, thereby keeping the difference between the super-mode propagation constants of closely spaced waveguides at zero [38,39,40], as shown in Figure 5b. Thirdly, the use of extreme skin depth (e-skid) waveguides can significantly reduce the evanescent depth by employing high-index gratings at the waveguide spacings [45], as shown in Figure 5c. All these three designs can effectively suppress crosstalk between closely spaced waveguides and approximately achieve a half-wavelength emitting pitch.
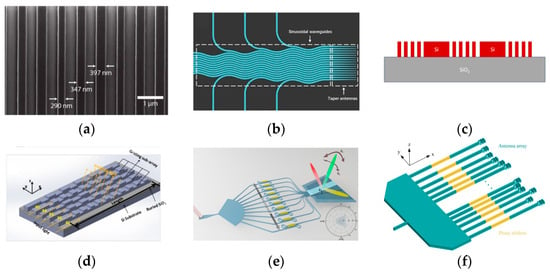
Figure 5.
PIC designs to achieve half-wavelength emitting pitch. (a) Different waveguide widths to suppress crosstalk [37]. (b) Sinusoidal waveguide array [40]. (c) Extreme skin depth (e-skid) waveguide [45]. (d) Grating array superlattice [46]. (e) Slab grating region [41]. (f) Effective half-wavelength at projection [47].
However, these methods rely on unique designs to suppress waveguide crosstalk, which significantly increases the complexity of the overall OPA device. In the first method, the emitting array comprises waveguides with varying widths, making it easy to achieve the end-fire array [37,46], but challenging to apply to the waveguide grating coupler array configuration; thus, it is difficult to obtain a 2-D converged beam. This is because that the different widths between the waveguides effectively suppress crosstalk, but also cause the propagation constant of the waveguide modes to differ, making it unsuitable to apply the same waveguide grating across the array. To make this work, the periodicity of the waveguide grating must be adjusted to the waveguide width so that the emitting angle from each waveguide remains the same [46], as shown in Figure 5d. However, designing such a grating superlattice is not as challenging as its fabrication, where strict accuracy is required. A more practical approach is to use a slab grating region [41]. As shown in Figure 5e, instead of emitting the light from different waveguides and interfering with the free space, a slab grating region allows the light from various channels to interfere first in the slab waveguide region, and then emit the interference light from the grating region across the whole slab waveguide. On the other hand, in the second method, the sinusoidal waveguide array results in the light propagation direction varying at each position, making it unsuitable for the waveguide grating array configuration [38,39,40]. The third method uses high-index gratings to reduce the evanescent depth, which requires an almost 10-times-higher lithography resolution (with a feature size as small as 36 nm in the design [45]), significantly increasing the fabrication difficulty.
The three methods mentioned can produce an emitting pitch close to a half-wavelength in a 1 × N configuration, which is suitable for end-fire or waveguide grating array OPAs. However, in an M × N configuration for a nano-antenna array OPA, it is hard to achieve a true 2-D half-wavelength emitting pitch due to the limited footprint of state-of-the-art nano-antennas. Nevertheless, an effective half-wavelength emitting pitch can be obtained in this configuration [47]. By arranging the nano-antennas back and forth, their projection in the x-direction can be spaced a half-wavelength apart, while their projection in the y-direction forms a large-aperture aperiodic arrangement. Together, they create a 2-D converged beam with a true aliasing-free performance in the x-direction and an aliasing-suppressed performance in the y-direction, as shown in Figure 5f.
3.1.4. Emitting Aperture and Intensity Profile
Although the term “optical phased array” suggests that the phase is the critical factor in an OPA device because it determines how light interferes with free space, other factors such as the total emitting aperture and intensity profile also play crucial roles in light interference. Generally, a larger emitting aperture is preferred in an OPA device as it determines the maximum beam divergence that can be achieved [21,43,48]. This is often accomplished using a plane phase profile that emits a Gaussian beam, and the resulting beam divergence is described as θ = (4λ)/(πD), where θ is the beam divergence in radian, λ is the wavelength of light, and D is the total emitting aperture [2]. As a result, the design of OPAs usually aim for a smaller emitting aperture for individual emitters to achieve a broader envelope function. At the same time, they aim for a larger total emitting aperture to minimize beam divergence. LiDAR is considered to be the most widely used application for OPAs. This typically requires a horizontal resolution of 0.1°, which is based on the size of a human at the braking distance of a car [2]. To have this level of resolution, an emitting aperture of over 1mm is required when the light beam is emitted in the normal direction. In addition, to maintain the same 0.1° horizontal resolution across the entire field of view, an even larger physical emitting aperture is necessary as the effective emitting aperture becomes smaller when the light beam is steered in other directions.
For an OPA device with a 1 × N configuration, it is typically easier to achieve a larger emitting aperture in the direction across N channels (ψ), while the emitting aperture in the other direction (θ) is often constrained by the effective emitting length of the waveguide grating coupler. In Section 3.1.5, designs that address this issue are described in detail. In addition to the phase, the intensity profile is also a crucial factor in light interference. While a uniform intensity profile is commonly used in most publications, it can lead to a common issue in phased array technology-side lobes; this occurs due to higher-order interference. To mitigate this issue, an apodized intensity profile has been proposed as a solution in [18,44]. This technique involves applying a Gaussian distribution to the emitted light intensity profile, which enhances the main lobe and reduces the occurrence of side lobes in the resulting interference pattern. However, this approach comes with a trade-off; it reduces the effective emitting aperture, which leads to a more beam divergence. The impact of both the suppressed side lobes and the increased divergence can be observed in the comparison between Figure 6b,d. Obtaining the desired intensity profile necessitates precise control over the power splitting of light. One way to achieve this in a 1 × N channel OPA is to use a star coupler [21]. Alternatively, a directional coupler array can be utilized to achieve this in M × N channel OPAs [44].
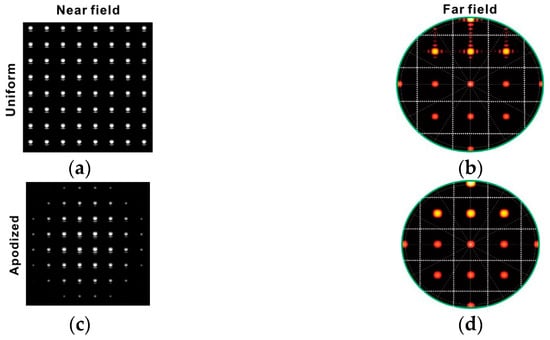
Figure 6.
Simulation results of apodized intensity profile for OPA [44]. (a) Nearfield of uniform intensity profile. (b) Far field of uniform intensity profile. (c) Nearfield of apodized intensity profile. (d) Far field of apodized intensity profile.
3.1.5. Waveguide Grating Coupler Design
In the waveguide grating array configuration of OPAs, light is manipulated and directed by waveguide grating couplers in the θ direction. A typical waveguide grating coupler has gratings with a constant periodicity and duty cycle, which are fabricated using an additional lithography process or along with a waveguide patterning step [42]. The gratings cause the waveguide mode to fluctuate and generate a series of harmonic waves. One of these harmonic waves has a propagation constant that matches the wavenumber of the radiation mode in a particular direction, allowing the light beam to be emitted in that direction. Coupling between the harmonic wave and the radiation mode can be described by the following equation.
where Λ is the periodicity of the gratings; θ is the emitting angle; k0 is the free space wavenumber; β0 is the propagation constant of the waveguide mode in the grating area; and m is the diffraction order, which in most cases is −1.
k0 sin θ = β0 + m(2π/Λ)
Unique designs have been proposed to improve the performance of waveguide grating couplers, including the beam steering range, beam convergence, emitting efficiency, etc.
Steering Range
Equation (1) can be derived as follows:
sin θ = neff + m(λ/Λ),
The emitting angle θ can be adjusted by wavelength tuning. Although there is some dispersion of neff, the primary factor affecting the direction of the beam is the term m(λ/Λ). To ensure that sin θ ∈ $(−1, 1), a suitable value of Λ must be chosen. This means that the amount by which the angle θ changes in response to a change in wavelength λ, denoted as dθ/dλ, is constrained by neff, while the value of neff is determined by the material platform used. The SOI platform is one of the most extensively researched platforms for OPAs. This platform is characterized by a large index contrast between the waveguide and cladding, with indices of approximately 3.47 for Si and 1.46 for SiO2 at a wavelength of around 1550 nm. For this platform, the value of dθ/dλ is limited to approximately 15° per 100 nm wavelength range around 1550 nm [11]. On other platforms with a lower-index contrast, such as SiN waveguides with SiO cladding, the value of dθ/dλ is typically lower, approximately 7.4° per 100 nm wavelength as described in reference [49]. This limitation significantly restricts the field of view (FoV) of an OPA system.
Various designs have been proposed to overcome this limitation, as described in these references [50,51,52,53,54,55,56,57]. These designs can be divided into two categories. The first category involves ensuring that the grating coupler functions effectively as multiple normal grating couplers, which have a uniform periodicity and duty cycle [50,51,52,53]. By spatially combining two normal grating couplers, a compound period grating coupler can be formed, which can generate two emitting beams, resulting in a steering range of approximately 26° over a 100 nm wavelength range, which is roughly double the original steering capability [50]. The multibeam concept can be further developed to generate nine beams from a single grating coupler, although this is more about detecting nine points simultaneously rather than enlarging the steering range [51]. By utilizing three different modes and designing nano-gratings that create spatial fluctuation specifically for each mode, the steering range can be roughly tripled to approximately 40° [52]. Additionally, by incorporating a switch and two polarization rotators before the grating coupler, both directions (forward and backward) and both polarizations (TE and TM) can be selected, resulting in a steering range that is roughly four times greater, reaching 54.5° over a 100 nm wavelength range [53]. The second category of attempts to mitigate the restriction of the steering range involves manipulating the effective index (neff) by incorporating a photonic crystal waveguide [54,55,56,57]. In this type of waveguide, neff can be substantially increased at the spectral boundary of the photonic bandgap, resulting in a significantly greater dθ/dλ despite a limited wavelength range defined by the photonic band spectrum. This approach can achieve a steering range of 23° over a 29 nm wavelength range [55]. All these designs are illustrated in Figure 7.
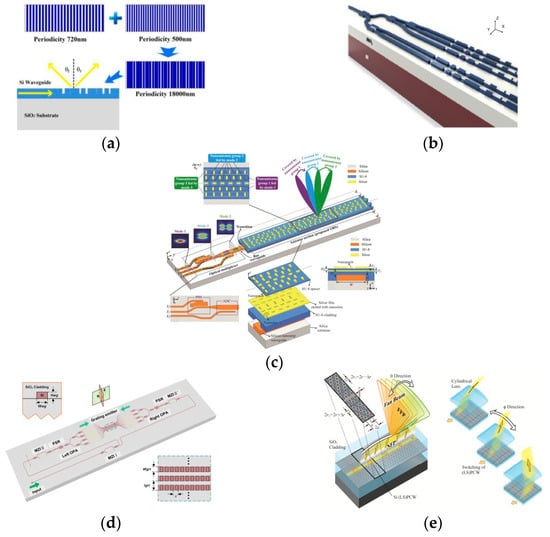
Figure 7.
Designs of waveguide grating coupler to increase the beam steering range. (a) Compound period grating coupler [50]. (b) Multi-beam grating coupler [51]. (c) Polarization division and spatial division grating coupler [52]. (d) Dual polarization and bi-directional grating coupler [53]. (e) Photonic crystal slow light grating coupler [54].
Effective Aperture
In a typical waveguide grating coupler, the periodicity and duty cycle of the gratings are identical, causing each grating to emit an equal proportion of the rest of the light in the waveguide. As a result, the emitting intensity profile decays, and the effective emitting aperture is limited, which ultimately leads to poorer interference conditions in this direction. According to reference [11], the emitting power declines to 1/e2 after passing through 35 gratings, resulting in an effective emitting aperture of only about 20 microns, even though 50 gratings were fabricated.
One effective way to address this issue is to perform shallow etching of the grating, which can reduce the portion of light emitted per grating. Research has shown that even with an identical periodicity and duty cycle, shallow etched gratings as thin as 16 nm can achieve a 0.14° FWHM using a waveguide grating over a 1 mm distance [21]. Another approach involves using gratings with gradually adjusted duty cycles, which can produce a uniform emitting intensity profile from a decaying waveguide mode. This method has been demonstrated to achieve a 3.3° FWHM with a small aperture of 32 µm, as depicted in Figure 8a [58]. However, while the silicon-on-insulator (SOI) platform offers a relatively better beam steering capability, it also limits the effective emitting aperture due to the excellent mode confinement of silicon waveguides, which results in a greater amount of mode power being emitted per grating. On the other hand, silicon nitride (SiN) waveguides are better suited as effective emitting aperture, but their beam steering capability is limited. A combination of silicon waveguides and SiN gratings can provide the advantages of both. As shown in Figure 8b,c, by placing SiN gratings with gradually adjusted duty cycles above the silicon waveguide, waveguide grating couplers with a uniform emitting pattern, large emitting aperture, and good beam steering capability (comparable to 15°/100 nm, which is the typical value for SOI-OPAs) can be achieved [59,60,61]. The beam convergence (FWHM) has been proved to be approximately 0.089° for 1mm long waveguide gratings [59,60] and approximately 0.0435° for 3 mm long waveguide gratings [61].
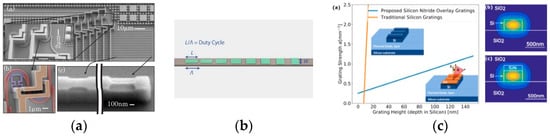
Figure 8.
Designs of waveguide grating coupler to increase effective emitting aperture size. (a) Gradually adjusted grating coupler for uniform emission [58] (b) Uniform emission grating coupler with SiN gratings on Si waveguides [59]. (c) Comparison between Si gratings and SiN gratings [60].
Emitting Directionality
Waveguide gratings have the ability to emit light through diffraction, but this process also reduces their efficiency, typically resulting in less than 50% of the light being emitted upwards due to symmetrical downward emission. As a result, a significant portion of the light energy is lost to the substrate [50]. In LiDAR applications, this low optical efficiency limits the detection range, creating a major obstacle to achieving a complete product at the industry level.
To tackle this problem, two methods have been proposed [62,63,64,65,66]. The first approach involves using reflections at the interfaces between the waveguide layer and the top/bottom claddings [62,63,64], as shown in Figure 9a–c. With this method, detached gratings are fabricated on another layer above the waveguide, allowing the downward emission to be reflected on the top and bottom surfaces of the waveguide and the bottom surface of the buried oxide layer. By carefully adjusting the layer thickness, it is possible to optimize the efficiency of upward emission. The detached gratings can be fabricated on a low-index SiO2 layer on top of the waveguide to achieve an upward emitting efficiency of over 70% within a 100 nm wavelength range and a steering angle of 15° [62]. Alternatively, the gratings can be fabricated on a high-index layer above the top cladding, where the waveguide mode is first coupled to the top grating layer, and then emitted [63,64]. By fabricating high-index gratings on an amorphous silicon layer, an efficiency of over 50% can be achieved within a broad wavelength range from 1480 nm to 1620 nm, along with a steering angle of 20.2° (comparable to 15° per 100 nm wavelength range) [63]. However, this approach has a lower efficiency due to the angular dependence of light reflection. To optimize directionality, the gratings can be fabricated on the top Si3N4 layer, limiting the beam steering to 8.6° per 100 nm wavelength range, while achieving a directionality of over 86% within the wavelength range [64].
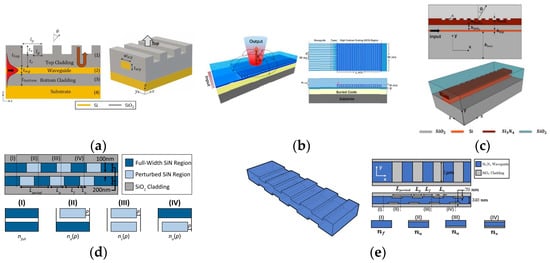
Figure 9.
Designs of waveguide grating coupler to increase emitting directionality. (a) Detached low-index SiO2 gratings [62]. (b) Detached high-index a − Si gratings [63]. (c) Detached high-index Si3N4 gratings [64]. (d) Dual gratings using dual-layer SiN [65]. (e) Dual gratings with top and bottom trenches on SiN waveguide [66].
The second method involves creating two different spatial fluctuations with a slight offset, which are dual gratings in the waveguide mode [65,66]. These dual gratings generate separate upward and downward beams, with a careful design to ensure that the two upward beams interfere constructively, and the two downward beams interfere destructively, resulting in high directionality. Dual gratings can be achieved through a dual-layer Si3N4 waveguide configuration [65] or by making different trenches on both the top and bottom surfaces of a silicon waveguide [66]. Both configurations can achieve an emitting efficiency of over 90% at the design wavelength (1550 nm), although their broadband performance and beam steering capability have not been reported.
3.2. Phase Shifters
Typically, in OPA devices, a phase shifter is needed for each channel to regulate the emitting phase profile and control the far field pattern. Thermo-optic and electro–optic effects are the two common options, as they both are effective using silicon [67]. An optimal phase shifter for OPAs should meet several criteria, such as being small enough to not require a larger phase shifter array for a certain sized emitter array, responding rapidly to enable a high beam steering speed, being to prevent affecting light power during phase tuning, being adequately isolated to avoid interference with the adjacent channels, consuming less power to keep the total power for the entire OPA within reasonable limits, and being easily fabricable. It should also be capable of tuning the phase across the full 2π range, although phase shifters with an insufficient tuning range can also be used [68]. Designing phase shifters that meet all the criteria is critical, but perhaps not possible.
- Thermo-Optic Phase Shifter.
The thermo-optic effect is present in nearly all materials, with a greater intensity typically observed in semiconductors compared to that in insulators. Silicon, in particular, exhibits a substantial thermo-optic coefficient. Additionally, the fabrication process for a thermo-optic phase shifter is relatively straightforward, as it does not require any doping or heterogeneous integration. Consequently, TO phase shifters are commonly utilized in OPA systems. Typically, a conventional TO phase shifter is constructed using a conductor pad located a few microns above the waveguide. This allows the pad to heat the waveguide material without affecting with the waveguide mode. However, this type of phase shifter has some limitations, such as a relatively slow response time (up to around 100 kHz) and a higher power consumption (approximately 10–20 mW/π), as it relies on heat conduction through the insulating cladding layer for heating and cooling [2]. To address these limitations, a potential solution is to explore more efficient heat transfer mechanisms, despite that this also leads to a more complex fabrication process in most cases. One approach is to use designs such as a contacted waveguide heater, which directly heat the waveguide without affecting the propagation mode by leveraging the mode profile during waveguide bending [13] (as shown in Figure 10a). Alternatively, graphene heaters with an air trench [69] (as shown in Figure 10b) or polymer heaters [70] can also be employed to achieve improved heat transfer. Another possible approach to enhance the efficiency of TO phase shifters is to increase the effective light path at the heater region. This can be achieved through the use of a resonance cavity [71] (as illustrated in Figure 10c) or a mode multiplexing system [72] (as shown in Figure 10d). However, it should be noted that this approach is usually wavelength-dependent and could potentially affect the mode intensity during the phase tuning process, as either the resonator or mode coupling is sensitive to the wavelength.
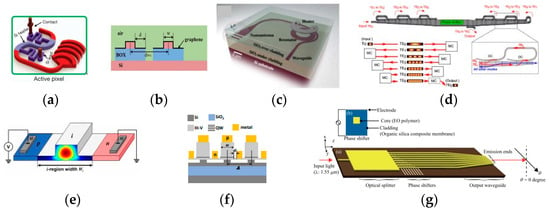
Figure 10.
TO phase shifter designs for OPAs. (a) Contacted waveguide heater [13]. (b) Graphene heater with air trench [69]. (c) Tunable ring-resonator phase shifter [71]. (d) Heater with mode multiplexing [72] EO phase shifter designs for OPAs. (e) PIN free carrier plasma dispersion phase shifter [73]. (f) Heterogeneous integrated III–V phase shifter [74]. (g) EO polymer phase shifter [75].
- Electric–Optic Phase Shifter.
Although there are various distinctive designs available to improve the efficiency of a TO phase shifter, it remains a relatively slow method due to the slower heat transfer mechanism. In contrast, the electro–optic (EO) effect is faster, and therefore, an EO phase shifter is typically over 10 times faster than a TO phase shifter. However, silicon lacks a good electro–optic effect, and to construct a silicon-based EO phase shifter, a PIN diode (as shown in Figure 10e, [73]) or PN diode must be built. Then, it can utilize the diode to adjust the free carrier density in the waveguide area. Nevertheless, both carrier depletion and carrier injection cause significant optical loss in the waveguide and are at least one order of magnitude larger than their thermo-optic counterpart in regard to their footprint. Moreover, building such EO phase shifters entails a doping process, which substantially increases the fabrication complexity. Despite all the disadvantages mentioned above, an OPA driven by EO phase shifters is several orders of magnitude faster than TO-OPAs. Therefore, it remains the preferred choice for applications that require a high scanning rate, such as LiDAR. In addition, there are alternative options available for EO phase shifters, such as heterogeneous integrated III-V phase shifters (illustrated in Figure 10f, [74]) or EO polymers (illustrated in Figure 10g, [75]), which can be utilized if CMOS compatibility is not a critical requirement.
- Reducing the Required Number of Phase Shifters (Table 2)
 Table 2. Performance of surveyed OPAs regarding TO and EO phase shifters. Wavelength tuning is denoted by WT.
Table 2. Performance of surveyed OPAs regarding TO and EO phase shifters. Wavelength tuning is denoted by WT.
Current Efforts and Strategies. OPAs generally require an individual phase shifter for each emitter. While having more emitters in an OPA typically improves its performance, increasing the number of individual phase shifters may not always have only a positive effect. Using too many individual phase shifters can result in excessive power consumption, as well as increased complexity in the driven circuit, and it may take a longer time for the phase calibration process. Despite the ongoing attempts to obtain more individual phase shifters [76], the need to balance the number of emitters and individual phase shifters in an OPA has motivated significant research into developing configurations that enable the control of multiple emitters with fewer individual phase shifters, while maintaining a consistent phase across all emitters.
To achieve this goal, two methods are employed. The first approach involves grouping multiple phase shifters into one drive. By using a triangular heater to proportionally heat multiple waveguides, the phase change across different channels can be made linear, as shown in Figure 11a [11,77]. Additionally, by using one drive to heat up the phase shifters in one line, 2-D beam steering can be achieved using column and row phase shifters together, as long as the initial phase is able to converge the beam, as illustrated in Figure 11b [13,18]. The cascaded or group cascaded shifters offer the same phase shifting to all the channels, and along with passive phase shifting from the waveguide length and power splitter, the phases at multiple emitters can align to form and steer the beam, as shown in Figure 11c,d [58,78,79]. The other method involves leveraging the interference of waveguide modes. By combining two modes with the same propagation constant but different phases, a single mode can be formed with the same propagation constant and an average phase. Using this approach, an M × N OPA with N2 emitters can be controlled by 2N phase shifters (Figure 11e, [80]), and a 1 × N OPA with N emitters can be controlled by (N + 1)/2 phase shifters (Figure 11f, [81]). Nonetheless, these designs are susceptible to phase errors because they assume that the same passive waveguide path will always result in the same phase change, which may not hold true in real samples due to imperfections in the fabrication process. Consequently, it is imperative to develop designs and materials with better fabrication tolerances for these approaches [79].
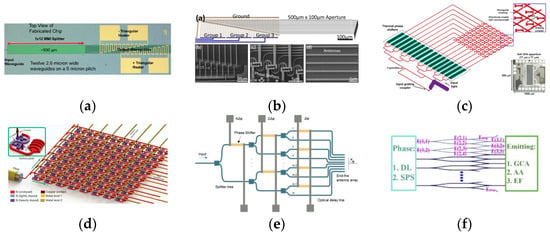
Figure 11.
Configurations to control multiple emitters with fewer individual phase shifters. (a) Triangular heaters [77]. (b) Column phase shifters [13]. (c) Cascaded phase shifters [78]. (d) Grouped cascaded phase shifters [79]. (e) Interference-based configuration for M × N OPAs [80]. (f) Interference-based configuration for 1 × N OPAs [81].
3.3. On-Chip Light Source
While applying an on-chip light source can improve the performance of OPAs [82,83,84,85,86,87,88,89], its advantages over other types of PICs, such as optical transceivers or sensors, are not significant. The challenges in installing an on-chip light source on an OPA are the same as those involved in developing a light source on a silicon platform, which is primarily due to the indirect bandgap of silicon. Nonetheless, researchers have reported the successful use of heterogeneous integrated InP light sources [83,84,85,86,88] and Erbium-doped light sources [87] for PIC-OPAs. Integrating an on-chip light source can significantly reduce the size and complexity of the OPA system, eliminating the need for an external laser. This, in turn, has the potential to reduce the cost of OPA-LiDAR.
4. Phase Calibration and On-Chip Emitting Monitoring
Fabrication imperfection is a prevalent problem in PICs, caused by roughness and errors during the layer deposition and lithography processes. This can lead to propagation loss and phase errors in the passive waveguides. Additionally, in OPAs, a fabrication imperfection can cause practical issues where the initial emitting phase profile is often irregular, regardless of the intended design for a regular phase profile. When faced with such scenarios, OPAs that possess an equal quantity of emitters and phase shifters can depend on their phase shifters to correct any passive phase errors. On the other hand, OPAs with fewer phase shifters must utilize designs and materials that allow for fabrication tolerance in order to compensate for such errors. Nevertheless, optimizing the phase compensation process that involves multiple variables can be a time-consuming task, even though the desired phase profile may vary according to the application, such as a linear phase profile for beam steering or a customized phase profile to generate an arbitrary pattern [18,90]. Despite the fact that it is also feasible to conduct phase calibration at the wafer level [91], this procedure typically occurs at the chip level.
Numerous algorithms have been successfully utilized for the phase calibration of OPAs, such as the particle swarm optimization (PSO) [84], the deterministic stochastic gradient descent (DSGD) method [92], the chaotic stochastic parallel gradient descent (CSPGD) method [93], the rotating element vector (REV) method [94] or modified REV method [95], the radix-p method [96], the adjacent sampling principal component analysis (AS-PCA) method [97], and the random phase modulation method [98]. Although these algorithms are much more effective than the exhaustive method, they are still numerical optimization algorithms because they are unable to detect the phase difference directly between each pair of emitters. While it is indeed achievable by calculating the interference pattern [99], which can significantly reduce the time required for phase calibration.
Typically, a calibrated OPA includes an internal database that contains multiple sets of voltage values. Each of these sets is specifically calibrated to be applied to phase shifters and is effective at a particular angle. However, the OPAs are normally sensitive to environmental changes such as temperature [100]. An on-chip monitor can be applied to OPAs to track the emitting far field pattern [84,85,86,101]. The reported on-chip monitors are all based on the 1 × N channel waveguide grating array OPAs. The fundamental concept involves allowing the waveguide gratings to leave a small portion of light power, and then couple all the channels directly into a slab waveguide area. The light from multiple channels will interfere in the slab waveguide in the same manner as it does in free space. By capturing the interference pattern in the slab area using a multi-output photodiode array, the far field emitting pattern can be monitored at the cost of a lower-emitting efficiency.
5. System-Level OPA Designs
OPAs have a versatile configuration, which makes them suitable for various applications. However, designing OPAs for different situations requires careful consideration of the entire system to ensure that they meet the practical needs. Therefore, this section provides an overview of OPAs as a whole system, which aims to provide a more comprehensive understanding of OPA studies.
5.1. Passive OPAs
OPAs utilize control of the emitter phase profile across the emitter array to achieve functions such as beam shaping and steering. This usually involves the use of multiple phase shifters to attain the desired phase profile. However, as highlighted in Section 3.2, employing a large number of phase shifters can result in practical challenges, such as high power consumption, operational difficulty, and a time-intensive phase calibration process. Consequently, efforts have been made to develop purely passive OPAs to mitigate these issues [102]. Unlike waveguide grating array OPAs, which are semi-passive and rely on wavelength tuning and electrical tuning to achieve steering in different directions (θ and ψ), purely passive OPAs have only one degree of freedom for wavelength tuning. Passive OPAs require the pre-coding of the emitting phase profile in the design, typically through the use of components such as waveguide length and symmetric power splitter networks. However, due to that active phase shifters no longer exist, this approach is much more susceptible to phase errors resulting from fabrication imperfections. To improve fabrication tolerance and mitigate the impact of phase errors, low-index materials, like silicon nitride and silica, are commonly employed as waveguide materials in passive OPAs [10,103].
Achieving 2-D beam steering with only one degree of freedom is a significant challenge in passive OPAs. However, this issue can be addressed by leveraging the interference that can occur in multiple orders [48,104,105,106]. This solution involves implementing relatively slower beam steering in one direction (θ), which can be achieved using waveguide grating couplers [48,104,105] or short delay lines across channels [106]. In contrast, much faster beam steering must be implemented in the other direction (ψ), which can be achieved using longer delay lines across the channels. As a result, the beam can be steered in θ across the entire wavelength range (Table 3) and steered in ψ at multiple smaller wavelength ranges, with each smaller range corresponding to a different angle in θ. This is illustrated in Figure 12.

Table 3.
Beam steering based on wavelength tuning (WT).
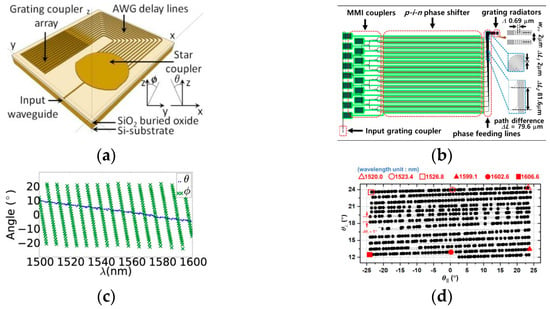
Figure 12.
Configuration designs to achieve 2-D beam steering with only wavelength tuning. (a,c) Ref [104]. (b,d) Ref [105].
5.2. Distance Detection for LiDAR Application
The intense interest in OPA research is driven by the demand for solid-state LiDAR, which is considered a key component in autonomous driving technology. This interest is not limited to the OPA itself, as system-level OPA-LiDAR is also being studied. Several successful distance detection methods have been reported [78,107,108,109,110] for OPA-LiDAR. Regardless of the number of degrees of freedom (depending on the number of individual phase shifters) an OPA uses for 2-D beam steering, an additional degree of freedom is required for distance detection.
A straightforward approach involves adjusting the light power to measure the distance, as depicted in Figure 13a. This technique entails emitting a light pulse towards the target, followed by detecting a reflection pulse at a later time. The time interval between the two pulses can be used to compute the distance by measuring the time of flight (ToF) [107]. Nonetheless, this approach is prone to interference from ambient light. To ensure adequate differentiation of the reflection light, a relatively higher light intensity is required, leading to increased power consumption during LiDAR and raising concerns about eye safety.
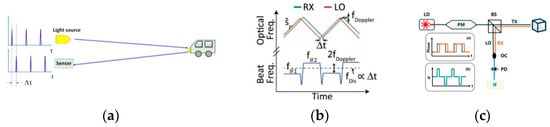
Figure 13.
Distance detection methods. (a) Time of flight (ToF) [107]. (b) Frequency-modulated continuous wave (FMCW) [78]. (c) Phase-modulated continuous wave (PhMCW) [110].
The frequency-modulated continuous wave (FMCW) is proposed as an improved LiDAR approach [78,107,108,109], as illustrated in Figure 13b. This method employs a continuous wave with periodic variations in frequency to compute the distance by measuring the phase difference between the emitted and reflected light. Moreover, FMCW LiDAR is less susceptible to ambient light as a small fraction of emitted light is directed towards the receiving end and oscillates with reflected light (known as the local oscillator) to form a beat frequency, making it easier to distinguish reflected light. Another advantage of FMCW over ToF is its ability to detect the object’s velocity, thanks to the Doppler effect, which induces a frequency shift in reflected light. This frequency shift is also easily distinguished due to local oscillation. In contrast to 3-D mapping achieved by ToF-LiDAR, FMCW-LiDAR involves performing 4-D mapping, which includes 3-D mapping and velocity. Nonetheless, the resolution of the FMCW technique for detection is somewhat restricted in OPA-LiDAR if the OPA utilizes frequency as a degree of freedom for beam steering. This is because the beam is not stationary in one direction during frequency modulation. As an alternative, a phase-modulated continuous wave (PhMCW) method, as illustrated in Figure 13c, is proposed [110]. With this approach, the phase of the emitting beam is utilized as the degree of freedom for distance detection instead of frequency.
5.3. Other Material Platforms
Most of the PIC-OPAs are on silicon platforms, such as SOI (silicon on insulator) or amorphous silicon [111]. In addition, OPAs on other material platforms are also studied for various purposes.
- Silicon Nitride (SiN) and Germanium–Silicon (Ge-Si)
Silicon is a material that is well suited for OPAs used in telecommunication wavelengths, but there is also a growing interest in researching OPAs for shorter wavelengths, including the visible range. This is due to the potential applications in fields such as virtual reality displays, biomedical sensing, stimulation, etc. Silicon loses its effective- ness as a material for wavelengths shorter than 1.1 µm, but there is a viable alternative in silicon nitride (SiN). SiN is a good option due to its transparency in the visible and near-infrared spectra, which is ideal for OPAs that require a wide range of operating wavelengths [112,113,114]. Moreover, SiN is CMOS-compatible, which offers a possible cost-effective production method for SiN-OPAs. On the other hand, SiN also has certain limitations that need to be taken into account. One of the main issues is its low refractive index, which results in a low-confinement mode in the SiN waveguides, making it challenging to build a dense SiN waveguide array. Consequently, SiN-OPAs may suffer from a strong aliasing effect [43] or require the use of an aperiodic arrangement [20], which increases the complexity of the system. In addition, SiN is an insulator lacking an effective electro–optic effect, and its heat transfer coefficient and thermosoptic coefficient are both about one order of magnitude lower than those of Si. As a result, thermal tuning is relatively ineffective. While switching light between multiple OPAs with different passive targets may mitigate this issue, it can make the entire OPA device overly complex [115].
The limitations of SiN include its low refractive index and its properties as an insulator. However, these limitations can also offer advantages in other aspects. The low refractive index of SiN results in a low-confinement mode, which can be advantageous in terms of tolerance to fabrication imperfections. In lower-index waveguides, a certain sidewall roughness takes up less of the waveguide mode area, so the fabrication errors result in fewer phase errors in such modes. Thus, SiN is preferred for passive OPAs [10]. In addition, OPAs have been reported that use SiN for passive components, such as input couplers, power splitters, and waveguide bends, and use Si for the phase shifters [116,117,118,119]. This allows them to take advantage of SiN in passive components and also the effective modulation of Si at the same time. On the other hand, the fact that SiN is an insulator also means that it is free of two-photon absorption, which is a limitation when using Si to propagate high-power light. SiN-OPAs can therefore handle high-power light, making them desirable for achieving a longer detection range in LiDAR [119].
SiN is considered suitable for lower-wavelength OPAs, whereas Germanium (Ge) is preferred for higher-wavelength OPAs [120]. Ge has a wide transparent window that ranges from 2 µm to 14 µm. Ge’s refractive index is higher than that of Si, which enables the direct fabrication of Ge waveguides on a Si substrate, without the need for a buried oxide layer. Moreover, the high refractive index of Ge facilitates the achievement of the half-wavelength criteria in a Ge-Si OPA.
- III–IV materials
Ge-Si is not the sole choice for optical parametric amplifiers (OPAs) operating at wavelengths greater than 1550nm. III-V semiconductor materials can also be utilized for OPAs, including the GaAs/AlGaAs platform [7,15] and InP platform [92,121]. In comparison to Ge-Si, InP offers additional benefits, aside from having a relatively wider transparent window [121]. InP is a direct bandgap semiconductor, which enables the availability of a widely tunable on-chip light source with this platform. Furthermore, it is possible to integrate semiconductor optical amplifiers (SOA) into InP-OPAs to boost the optical power output, allowing for the emission of high-power beams. Additionally, InP-based phase shifters can employ the current injection electro–optic effect, which provides a fast tuning speed of just a few nanoseconds [92].
5.4. Other Applications
Research on OPAs has gained momentum due to the emergence of autonomous driving technology, which requires solid-state LiDAR. However, OPAs can have multiple applications beyond autonomous driving, given their ability to precisely control the phase profile by using a sufficient number of phase shifters. These applications include emitting various types of beams, such as orbital beams [122], quasi-Bessel beams [123], and focusing beams [124], as well as imaging by combining multiple scanning points [125,126,127]. OPAs can also function as receivers by detecting the emitting angle of an incoming beam [128], allowing for the creation of directional reflectors [129] and OPA cameras [130]. By combining the receiving and emitting capabilities of OPAs, optical transceivers can be developed [131,132,133], enabling wireless communication with directional links [77,134,135,136,137,138] and also underwater wireless communication [139,140]. Additionally, OPAs have potential in bio-applications, where a neural stimulation OPA [141] and a neural probe [142] have been developed.
6. Three-Dimensional OPAs
The prevalent approach in optical phased array (OPA) research has largely centered around a single-waveguide-layer architecture, mirroring the foundational framework of CMOS electronic integrated circuits. This conventional platform, while established for photonic integrated circuits (PICs), introduces notable challenges, such as significant insertion loss primarily stemming from fiber-to-chip coupling and diffraction-based emitters crucial for 2-D beam convergence. Given the pivotal role of optical efficiency in applications like solid-state LiDAR—where it directly influences the detection range and power efficiency—enhancing light utilization is paramount [11,13,18,58,62,63,64,65,66,76,77,78,79,80,81,82]. Although various strategies have been proposed to mitigate optical efficiency and power consumption issues, extending the detection range remains a critical hurdle for OPA-LiDAR integration, especially in autonomous vehicle applications.
The advent of 3-D OPA technology (Figure 14) presents a promising avenue to address these challenges [139,143,144,145,146,147,148]. Unlike traditional 2-D OPAs, which are limited to emitting 1-D converged beams, 3-D OPAs can emit 2-D converged beams through an end-fire array mechanism, offering highly efficient broadband. This advancement necessitates the adoption of a multilayer waveguide structure at the emitter’s end, diverging from the single-layer norm and adding to the fabrication complexity. A notable attempt to bridge this gap involves using ultrafast laser inscription (ULI) to craft hybrid 2-D/3-D OPAs, facilitating the seamless transition between 1 × 16 2-D arrays and 4 × 4 3-D arrays. However, this method’s compatibility with CMOS technology remains a challenge, and the lower-index waveguides it produces demand significant separation to mitigate the aliasing effects. An alternative, CMOS-compatible, active 3-D OPA design proposes leveraging multiple waveguide layers with integrated phase shifters, enabling the active adjustment of the light beam’s phase profile upon emission. This approach outlines a potential fabrication pathway that could harmonize with the existing CMOS processes, marking a significant step forward in the practical application of 3-D OPAs.
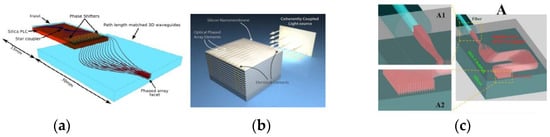
Figure 14.
Three-dimensional OPAs. (a) Hybrid 2-D/3-D OPA [143]. (b) Proposed active 3-D OPA [144]. (c) Passive 3-D OPA with proof of concept [147].
Moreover, the exploration of passive 3-D OPAs offers a simplified fabrication route, while maintaining CMOS compatibility. By employing a multi-waveguide-layer design, these OPAs can produce 2-D converged beams via end-fire emission and enhanced fiber-to-chip coupling efficiency [139,146,147,148]. Innovations such as the shaped region for wavelength-tuned beam steering and aperiodic arrangements to suppress aliasing underscore the potential of passive 3-D OPAs in reducing the manufacturing complexity without necessitating phase shifters on each layer. Yangzhou Qunfa Photonics Co., Ltd. officially initiated a solid-state OPA LiDAR chip project in 2019 with the University of Michigan, aiming to develop and commercialize 3-D OPA technology. Over four years, QunFa has developed silicon photonic chips at renowned MEMS platforms, such as the Suzhou Institute of Nano-tech and Nano-bionics (SINANO), CAS, and the Shanghai Institute of Microsystem and Information Technology (SIMIT), CAS. The company’s wafer runs on these platform lines, with technical personnel mastering the entire process and accumulating a complete set of OPA silicon photonic chip fabrication processes. The development of 3-D OPA silicon photonic chips requires further increased demands for waveguide loss and fabrication precision. With strong collaboration with the UM, this company aims to build the country’s first silicon photonics pilot line that is entirely focused on silicon photonic chip research and production [30,148].
In summary, the transition towards 3-D OPAs signifies a pivotal shift in overcoming the limitations of the current OPA-LiDAR technologies, especially for long-range detection applications. By addressing the dual challenges of optical efficiency and fabrication complexity, 3-D OPAs pave the way for more efficient, compact, and versatile optical systems, promising to extend the operational range and reliability of LiDAR systems in critical applications [139,146,147,148].
7. Summary
The aim of this paper is to provide a comprehensive overview of the latest developments in photonic integrated circuit-based optical phased array (PIC-OPA) technologies. This article starts by thoroughly exploring the design factors essential for maximizing performance, including enhanced steering capabilities, minimal aliasing, and superior optical efficiency. It proceeds to discuss the intricacies of the phase calibration process and outlines a wide range of system-level applications for OPAs. Lastly, this paper showcases a newly validated 3-D OPA configuration, which presents a significant breakthrough in overcoming a major challenge of employing OPA-LiDAR in autonomous vehicles through achieving a high optical efficiency.
Author Contributions
D.W. and Y.Y. wrote the review, B.Y., V.K., Y.Z. and A.K. helped with suggestions. All authors have read and agreed to the published version of the manuscript.
Funding
This review received no external funding.
Conflicts of Interest
Author Yating Zhuang was employed by the company QunFa Photonics Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Heck, M.J. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, L.; Zhang, Q.; Zhang, W. Si Photonics for Practical LiDAR Solutions. Appl. Sci. 2019, 9, 4225. [Google Scholar] [CrossRef]
- Hashemi, H. A Review of Semiconductor-Based Monolithic Optical Phased Array Architectures. IEEE Open J. Solid-State Circuits Soc. 2021, 1, 222–234. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, Y.; Li, C.; Zhang, H.; Zhou, X.; Zhang, L. Integrated Optical Phased Arrays for Beam Forming and Steering. Appl. Sci. 2021, 11, 4017. [Google Scholar] [CrossRef]
- Kim, I.; Martins, R.J.; Jang, J.; Badloe, T.; Khadir, S.; Jung, H.Y.; Kim, H.; Kim, J.; Genevet, P.; Rho, J. Nanophotonics for light detection and ranging technology. Nat. Nanotechnol. 2021, 16, 508–524. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Yiu, G.Z.; Chang, Y.C. Free-Space Applications of Silicon Photonics: A Review. Micromachines 2022, 13, 990. [Google Scholar] [CrossRef]
- Wight, D.R.; Heaton, J.M.; Hughes, B.T.; Birbeck, J.C.H.; Hilton, K.P.; Taylor, D.J. Novel phased array optical scanning device implemented using GaAs/AlGaAs technology. Appl. Phys. Lett. 1991, 59, 899–901. [Google Scholar] [CrossRef]
- Qin, C.; Shang, K.; Feng, S.; Liu, G.; Liu, G.; Pathak, S.; Yoo, S.J.B. 1 × 256 Multi-layer, low-loss, Si3N4 waveguide optical phased arrays with 0.050° Instantaneous-Field-of-View. In Proceedings of the Conference on Lasers and Electro-Optics, Munich, Germany, 25–29 June 2017; Optica Publishing Group: Washington, DC, USA, 2017; p. STh1M.2. [Google Scholar] [CrossRef]
- Kossey, M.R.; Rizk, C.; Foster, A.C. End-fire silicon optical phased array with half-wavelength spacing. APL Photonics 2017, 3, 011301. [Google Scholar] [CrossRef]
- Bhandari, B.; Wang, C.; Gwon, J.Y.; Heo, J.M.; Ko, S.Y.; Oh, M.C.; Lee, S.S. Dispersive silicon–nitride optical phased array incorporating arrayed waveguide delay lines for passive line beam scanning. Sci. Rep. 2022, 12, 18759. [Google Scholar] [CrossRef]
- Acoleyen, K.V.; Bogaerts, W.; Jágerská, J.; Thomas, N.L.; Houdré, R.; Baets, R. Off-chip beam steering with a one-dimensional optical phased array on silicon-on-insulator. Opt. Lett. 2009, 34, 1477–1479. [Google Scholar] [CrossRef]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Coldren, L.A.; Bowers, J.E. Two-dimensional free-space beam steering with an optical phased array on silicon-on-insulator. Opt. Express 2011, 19, 21595–21604. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Lv, J.; Peng, C.; Hu, W. Fast beam steering enabled by a chip-scale optical phased array with 8 × 8 elements. Opt. Commun. 2020, 461, 125267. [Google Scholar] [CrossRef]
- Vasey, F.; Reinhart, F.K.; Houdré, R.; Stauffer, J.M. Spatial optical beam steering with an AlGaAs integrated phased array. Appl. Opt. 1993, 32, 3220–3232. [Google Scholar] [CrossRef]
- Acoleyen, K.V.; Komorowska, K.; Bogaerts, W.; Baets, R. One-Dimensional Off-Chip Beam Steering and Shaping Using Optical Phased Arrays on Silicon-on-Insulator. J. Light. Technol. 2011, 29, 3500–3505. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Covey, J.; Zhang, Y.; Xu, X.; Subbaraman, H.; Chen, R.T. On-chip silicon optical phased array for two-dimensional beam steering. Opt. Lett. 2014, 39, 941–944. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Su, Z.; Hosseini, E.S.; Cole, D.B.; Watts, M.R. Large-Scale Silicon Photonic Circuits for Optical Phased Arrays. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 264–278. [Google Scholar] [CrossRef]
- Xu, W.; Zhou, L.; Lu, L.; Chen, J. Aliasing-free optical phased array beam-steering with a plateau envelope. Opt. Express 2019, 27, 3354–3368. [Google Scholar] [CrossRef]
- Shin, M.C.; Mohanty, A.; Watson, K.; Bhatt, G.R.; Phare, C.T.; Miller, S.A.; Zadka, M.; Lee, B.S.; Ji, X.; Datta, I.; et al. Chip-scale blue light phased array. Opt. Lett. 2020, 45, 1934–1937. [Google Scholar] [CrossRef]
- Hutchison, D.N.; Sun, J.; Doylend, J.K.; Kumar, R.; Heck, J.; Kim, W.; Phare, C.T.; Feshali, A.; Rong, H. High-resolution aliasing-free optical beam steering. Optica 2016, 3, 887–890. [Google Scholar] [CrossRef]
- Fatemi, R.; Khachaturian, A.; Hajimiri, A. A nonuniform sparse 2-D large-FOV optical phased array with a low-power PWM drive. IEEE J. Solid-State Circuits 2019, 54, 1200–1215. [Google Scholar] [CrossRef]
- Liu, Q.; Benedikovic, D.; Smy, T.; Atieh, A.; Cheben, P.; Ye, W.N. Circular Optical Phased Arrays with Radial Nano-Antennas. Nanomaterials 2022, 12, 1938. [Google Scholar] [CrossRef]
- Komljenovic, T.; Helkey, R.; Coldren, L.; Bowers, J.E. Sparse aperiodic arrays for optical beam forming and LIDAR. Opt. Express 2017, 25, 2511–2528. [Google Scholar] [CrossRef]
- Zhuang, D.; Zhagn, L.; Han, X.; Li, Y.; Li, Y.; Liu, X.; Gao, F.; Song, J. Omnidirectional beam steering using aperiodic optical phased array with high error margin. Opt. Express 2018, 26, 19154–19170. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Chen, H.; Yang, S.; Chen, M. An improved aperiodic OPA design based on large antenna spacing. Opt. Commun. 2020, 475, 125852. [Google Scholar] [CrossRef]
- Du, K.; Wang, R.; Guo, J.; Jiang, R.; Kan, D.; Zhang, Y. Design of a sparse array for a one-dimensional non-uniform optical phased array. J. Opt. Soc. Am. B 2022, 39, 1141–1146. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Zhang, Y.; Chen, R.T. 1 × 12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane. Appl. Phys. Lett. 2011, 99, 051104. [Google Scholar] [CrossRef]
- Shin, D.; Lee, J.; Hwang, I.; Otsuka, T.; Lee, C.; Shim, D.; Lee, E.; Ha, K.; Ryu, H.Y.; Choo, H.; et al. Aperiodic optical phased array based on number theory. Optica, 2023; preprint. [Google Scholar] [CrossRef]
- Kazemian, A.; Wang, P.; Zhuang, Y.; Yi, Y. Optimization of the silicon-based aperiodic optical phased array antenna. Opt. Lett. 2021, 46, 801–804. [Google Scholar] [CrossRef]
- Xue, Y.; Zhang, Q.; Ren, Y.; Lei, Y.; Sun, X.; Zhang, L. Two-dimensional single-lobe Si photonic optical phased array with minimal antennas using a non-uniform large spacing array design. Appl. Opt. 2022, 61, 7158–7162. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, D.; Pan, S. Fast and wide-range optical beam steering with ultralow side lobes by applying an optimized multi-circular optical phased array. Appl. Opt. 2018, 57, 4977–4984. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Luo, G.; Li, Y.; Wang, M.; Meng, F.; Yang, W.; Yu, H.; Zhou, X.; Zhang, Y.; Pan, J. Two-dimensional large-angle scanning optical phased array with single wavelength beam. In Proceedings of the CLEO: Applications and Technology, San Jose, CA, USA, 13–18 May 2018; Optica Publishing Group: Washington, DC, USA, 2019; p. JTh2A–72. [Google Scholar]
- Liu, X.; Xiong, B.; Sun, C.; Hao, Z.; Wang, L.; Wang, J.; Han, Y.; Li, H.; Luo, Y. Circular optical phased array for 360 constant amplitude scanning. In Proceedings of the 10th International Conference on Information Optics and Photonics, San Diego, CA, USA, 27 September 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10964, pp. 1044–1048. [Google Scholar]
- Benedikovič, D.; Liu, Q.; Sánchez-Postigo, A.; Atieh, A.; Smy, T.; Cheben, P.; Ye, W.N. Circular optical phased array with large steering range and high resolution. Sensors 2022, 22, 6135. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ling, Y.C.; Zhang, K.; Gentry, C.; Sadighi, D.; Whaley, G.; Colosimo, J.; Suni, P.; Yoo, S.B. Sub-wavelength-pitch silicon-photonic optical phased array for large field-of-regard coherent optical beam steering. Opt. Express 2019, 27, 1929–1940. [Google Scholar] [CrossRef] [PubMed]
- Phare, C.T.; Shin, M.C.; Sharma, J.; Ahasan, S.; Krishnaswamy, H.; Lipson, M. Silicon optical phased array with grating lobe-free beam formation over 180 degree field of view. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 13–18 May 2018; Optica Publishing Group: Washington, DC, USA, 2018; p. SM3I-2. [Google Scholar]
- Yi, X.; Zeng, H.; Gao, S.; Qiu, C. Design of an ultra-compact low-crosstalk sinusoidal silicon waveguide array for optical phased array. Opt. Express 2020, 28, 37505–37513. [Google Scholar] [CrossRef]
- Yi, X.; Zhang, Y.; Zeng, H.; Gao, S.; Guo, S.; Qiu, C. Demonstration of an Ultra-compact 8-channel sinusoidal silicon waveguide array for optical phased array. Opt. Lett. 2022, 47, 226–229. [Google Scholar] [CrossRef] [PubMed]
- Liang, D.; Li, W.; Wang, X.; Zhao, X.; Guo, Z.; Han, X.; Chen, J.; Dai, D.; Shi, Y. Grating lobe-free silicon optical phased array with periodically bending modulation of dense antennas. Opt. Express 2023, 31, 11423–11430. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, H. Silicon optical phased array with a 180-degree field of view for 2D optical beam steering. Optica 2022, 9, 903–907. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Covey, J.; Xu, X.; Zhang, Y.; Chakravarty, S.; Chen, R.T. Corrugated waveguide-based optical phased array with crosstalk suppression. IEEE Photonics Technol. Lett. 2014, 26, 991–994. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Raval, M.; Su, Z.; Li, N.; Timurdogan, E.; Coolbaugh, D.; Vermeulen, D.; Watts, M.R. Large-scale silicon nitride nanophotonic phased arrays at infrared and visible wavelengths. Opt. Lett. 2017, 42, 21–24. [Google Scholar] [CrossRef]
- Sun, J.; Shah Hosseini, E.; Yaacobi, A.; Cole, D.B.; Leake, G.; Coolbaugh, D.; Watts, M.R. Two-dimensional apodized silicon photonic phased arrays. Opt. Lett. 2014, 39, 367–370. [Google Scholar] [CrossRef]
- Kong, Z. Design and Characterization of Optical Phased Array with Half-Wavelength Spacing. Ph.D. Thesis, Purdue University Graduate School, West Lafayette, IN, USA, 2021. [Google Scholar]
- Wu, Z.; Jiang, W.; Xia, J.; Huang, Q. Optical phased array antenna with wide steering range using grating array superlattices. In Proceedings of the 6th International Conference on Optical and Photonic Engineering (icOPEN 2018), Shanghai, China, 8–11 May 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10827, pp. 645–650. [Google Scholar]
- Lei, Y.; Zhang, L.; Xue, Y.; Ren, Y.; Zhang, Q.; Zhang, W.; Sun, X. Effective half-wavelength pitch optical phased array design for aliasing-free 2D beam steering. Appl. Opt. 2022, 61, 9423–9428. [Google Scholar] [CrossRef]
- Dostart, N.; Zhang, B.; Khilo, A.; Brand, M.; Al Qubaisi, K.; Onural, D.; Feldkhun, D.; Wagner, K.H.; Popovic, M.A. Serpentine optical phased arrays for scalable integrated photonic lidar beam steering. Optica 2020, 7, 726–733. [Google Scholar] [CrossRef]
- Im, C.S.; Bhandari, B.; Lee, K.P.; Kim, S.M.; Oh, M.C.; Lee, S.S. Silicon nitride optical phased array based on a grating antenna enabling wavelength-tuned beam steering. Opt. Express 2020, 28, 3270–3279. [Google Scholar] [CrossRef]
- Wu, D.; Guo, W.; Yi, Y. Compound period grating coupler for double beam generation and steering. Appl. Opt. 2019, 58, 361–367. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, Z.; Wang, L.; Xiong, B.; Sun, C.; Wang, J.; Li, H.; Han, Y.; Luo, Y. A single-chip multi-beam steering optical phased array: Design rules and simulations. Opt. Express 2021, 29, 7049–7059. [Google Scholar] [CrossRef]
- Zeng, Y.; Qu, S.; Wu, J. Polarization-division and spatial-division shared-aperture nanopatch antenna arrays for wide-angle optical beam scanning. Opt. Express 2020, 28, 12805–12826. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, J.; Shi, Y. Dual polarization and bi-directional silicon-photonic optical phased array with large scanning range. IEEE Photonics J. 2022, 14, 6620905. [Google Scholar] [CrossRef]
- Abe, H.; Takeuchi, M.; Takeuchi, G.; Ito, H.; Yokokawa, T.; Kondo, K.; Furukado, Y.; Baba, T. Two-dimensional beam-steering device using a doubly periodic Si photonic-crystal waveguide. Opt. Express 2018, 26, 9389–9397. [Google Scholar] [CrossRef] [PubMed]
- Kondo, K.; Tatebe, T.; Hachuda, S.; Abe, H.; Koyama, F.; Baba, T. Fan-beam steering device using a photonic crystal slow-light waveguide with surface diffraction grating. Opt. Lett. 2017, 42, 4990–4993. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, G.; Terada, Y.; Takeuchi, M.; Abe, H.; Ito, H.; Baba, T. Thermally controlled Si photonic crystal slow light waveguide beam steering device. Opt. Express 2018, 26, 11529–11537. [Google Scholar] [CrossRef] [PubMed]
- Gondo, J.; Ito, H.; Tamanuki, T.; Baba, T. Space-time-domain observation of high-speed optical beam scanning in a thermo-optic Si photonic crystal slow-light beam scanner. Opt. Lett. 2021, 46, 3600–3603. [Google Scholar] [CrossRef] [PubMed]
- Yaacobi, A.; Sun, J.; Moresco, M.; Leake, G.; Coolbaugh, D.; Watts, M.R. Integrated phased array for wide-angle beam steering. Opt. Lett. 2014, 39, 4575–4578. [Google Scholar] [CrossRef]
- Shang, K.; Qin, C.; Zhang, Y.; Liu, G.; Xiao, X.; Feng, S.; Yoo, S. Uniform emission, constant wavevector silicon grating surface emitter for beam steering with ultra-sharp instantaneous field-of-view. Opt. Express 2017, 25, 19655–19661. [Google Scholar] [CrossRef] [PubMed]
- Zadka, M.; Chang, Y.C.; Mohanty, A.; Phare, C.T.; Roberts, S.P.; Lipson, M. On-chip platform for a phased array with minimal beam divergence and wide field-of-view. Opt. Express 2018, 26, 2528–2534. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, H.; Chen, B.; Xia, P.; Zhou, Z.; Huang, Q.; Dai, T.; Wang, Y.; Yang, J. A Tri-Layer SiN-on-Si Optical Phased Array With High Angular Resolution. IEEE Photonics Technol. Lett. 2022, 34, 1108–1111. [Google Scholar] [CrossRef]
- Han, K.; Yurlov, V.; Yu, N.E. Highly directional waveguide grating antenna for optical phased array. Curr. Appl. Phys. 2018, 18, 824–828. [Google Scholar] [CrossRef]
- Wang, P.; Luo, G.; Yu, H.; Li, Y.; Wang, M.; Zhou, X.; Chen, W.; Zhang, Y.; Pan, J. Improving the performance of optical antenna for optical phased arrays through high-contrast grating structure on SOI substrate. Opt. Express 2019, 27, 2703–2712. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Zeng, Y.; Wang, W.; Cai, Y.; Tu, Z.; Yue, W.; Wang, X.; Fang, Q.; Yu, M. Dual-layer waveguide grating antenna with high directionality for optical phased arrays. Appl. Opt. 2019, 58, 5807–5811. [Google Scholar] [CrossRef]
- Raval, M.; Poulton, C.V.; Watts, M.R. Unidirectional waveguide grating antennas with uniform emission for optical phased arrays. Opt. Lett. 2017, 42, 2563–2566. [Google Scholar] [CrossRef]
- Chen, B.; Li, Y.; Zhang, L.; Li, Y.; Liu, X.; Tao, M.; Hou, Y.; Tang, H.; Zhi, Z.; Gao, F.; et al. Unidirectional large-scale waveguide grating with uniform radiation for optical phased array. Opt. Express 2021, 29, 20995–21010. [Google Scholar] [CrossRef]
- Kim, S.H.; You, J.B.; Ha, Y.G.; Kang, G.; Lee, D.S.; Yoon, H.; Yoo, D.E.; Lee, D.W.; Yu, K.; Youn, C.H.; et al. Thermo-optic control of the longitudinal radiation angle in a silicon-based optical phased array. Opt. Lett. 2019, 44, 411–414. [Google Scholar] [CrossRef]
- Yang, B.; Chen, H.; Yang, S.; Chen, M. A design method of optical phased array with insufficient phase tuning range. IEEE Photonics J. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, L.; Chen, Y.; Jia, P.; Qin, L.; Liu, Y.; Ning, Y.; Wang, L. Improved performance of optical phased arrays assisted by transparent graphene nanoheaters and air trenches. RSC Adv. 2018, 8, 8442–8449. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.M.; Park, T.H.; Im, C.S.; Lee, S.S.; Kim, T.; Oh, M.C. Temporal response of polymer waveguide beam scanner with thermo-optic phase-modulator array. Opt. Express 2020, 28, 3768–3778. [Google Scholar] [CrossRef] [PubMed]
- Larocque, H.; Ranzani, L.; Leatham, J.; Tate, J.; Niechayev, A.; Yengst, T.; Komljenovic, T.; Fodran, C.; Smith, D.; Soltani, M. Beam steering with ultracompact and low-power silicon resonator phase shifters. Opt. Express 2019, 27, 34639–34654. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.A.; Chang, Y.C.; Phare, C.T.; Shin, M.C.; Zadka, M.; Roberts, S.P.; Stern, B.; Ji, X.; Mohanty, A.; Gordillo, O.A.J.; et al. Large-scale optical phased array using a low-power multi-pass silicon photonic platform. Optica 2020, 7, 3–6. [Google Scholar] [CrossRef]
- Kang, G.; Kim, S.H.; You, J.B.; Lee, D.S.; Yoon, H.; Ha, Y.G.; Kim, J.H.; Yoo, D.E.; Lee, D.W.; Youn, C.H.; et al. Silicon-Based Optical Phased Array Using Electro-Optic p-i-n Phase Shifters. IEEE Photonics Technol. Lett. 2019, 31, 1685–1688. [Google Scholar] [CrossRef]
- Xie, W.; Bowers, J. High-performance III-V/Si Phase Shifter Arrays for Beam Steering. In Proceedings of the 2019 IEEE Photonics Society Summer Topical Meeting Series (SUM), Lauderdale, FL, USA, 8–10 July 2019; pp. 1–2. [Google Scholar]
- Hirano, Y.; Miyamoto, Y.; Miura, M.; Motoyama, Y.; Machida, K.; Yamada, T.; Otomo, A.; Kikuchi, H. High-speed optical-beam scanning by an optical phased array using electro-optic polymer waveguides. IEEE Photonics J. 2020, 12, 6600807. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Moss, B.; Shatrovoy, O.; Khandaker, M.; Watts, M.R. Coherent LiDAR with an 8,192-element optical phased array and driving laser. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 6100508. [Google Scholar] [CrossRef]
- Rabinovich, W.S.; Goetz, P.G.; Pruessner, M.; Mahon, R.; Ferraro, M.S.; Park, D.; Fleet, E.; DePrenger, M.J. Free space optical communication link using a silicon photonic optical phased array. In Proceedings of the Free-Space Laser Communication and Atmospheric Propagation XXVII, San Francisco, CA, USA, 16 March 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9354, pp. 96–101. [Google Scholar]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef]
- Li, W.; Chen, J.; Liang, D.; Dai, D.; Shi, Y. Silicon optical phased array with calibration-free phase shifters. Opt. Express 2022, 30, 44029–44038. [Google Scholar] [CrossRef]
- Ashtiani, F.; Aflatouni, F. N×N optical phased array with 2N phase shifters. Opt. Express 2019, 27, 27183–27190. [Google Scholar] [CrossRef]
- Wu, D.; Yu, B.; Yi, Y. Phase-combining unit for aliasing suppression in an optical phased array. Opt. Lett. 2022, 47, 1996–1999. [Google Scholar] [CrossRef]
- Han, Y.; Park, H.; Bowers, J.; Lau, K. Recent advances in light sources on silicon. Adv. Opt. Pho. 2022, 14, 404–453. [Google Scholar] [CrossRef]
- Doylend, J.; Heck, M.; Bovington, J.; Peters, J.; Davenport, M.; Coldren, L.; Bowers, J. Hybrid III/V silicon photonic source with integrated 1D free-space beam steering. Opt. Lett. 2012, 37, 4257–4259. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Binetti, P.R.; Althouse, C.; Mašanovic´, M.L.; Ambrosius, H.P.; Johansson, L.A.; Coldren, L.A. Two-dimensional optical beam steering with InP-based photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 6100212. [Google Scholar] [CrossRef]
- Hulme, J.; Doylend, J.; Heck, M.; Peters, J.; Davenport, M.; Bovington, J.; Coldren, L.; Bowers, J. Fully integrated hybrid silicon free-space beam steering source with 32-channel phased array. In Proceedings of the Smart Photonic and Optoelectronic Integrated Circuits XVI, San Francisco, CA, USA, 2–5 February 2019; SPIE: Bellingham, WA, USA, 2014; Volume 8989, pp. 18–32. [Google Scholar]
- Hulme, J.; Doylend, J.; Heck, M.; Peters, J.; Davenport, M.; Bovington, J.; Coldren, L.; Bowers, J. Fully integrated hybrid silicon two dimensional beam scanner. Opt. Express 2015, 23, 5861–5874. [Google Scholar] [CrossRef]
- Notaros, J.; Li, N.; Poulton, C.V.; Su, Z.; Byrd, M.J.; Magden, E.S.; Timurdogan, E.; Baiocco, C.; Fahrenkopf, N.M.; Watts, M.R. CMOS-compatible optical phased array powered by a monolithically-integrated erbium laser. J. Light. Technol. 2019, 37, 5982–5987. [Google Scholar] [CrossRef]
- Yue, J.; Cui, A.; Wang, F.; Han, L.; Dai, J.; Sun, X.; Lin, H.; Wang, C.; Chen, C.; Zhang, D. Design of Monolithic 2D Optical Phased Arrays Heterogeneously Integrated with On-Chip Laser Arrays Based on SOI Photonic Platform. Micromachines 2022, 13, 2117. [Google Scholar] [CrossRef] [PubMed]
- Misugi, Y.; Okayama, H.; Kita, T. Compact and Low Power-Consumption Solid-State Two-Dimensional Beam Scanner Integrating a Passive Optical Phased Array and Hybrid Wavelength-Tunable Laser Diode. J. Light. Technol. 2023, 41, 3505–3512. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, J.; Yaacobi, A.; Poulton, C.V.; Watts, M.R. Design of 3D hologram emitting optical phased arrays. In Proceedings of the Integrated Photonics Research, Silicon and Nanophotonics, Boston, MA, USA, 27 June–1 July 2015; Optica Publishing Group: Washington, DC, USA, 2015; p. IT4A-7. [Google Scholar]
- Guerber, S.; Fowler, D.; Faugier-Tovar, J.; Carim, K.A.; Delplanque, B.; Szelag, B. Wafer-level calibration of large-scale integrated optical phased arrays. Opt. Express 2022, 30, 35246–35255. [Google Scholar] [CrossRef] [PubMed]
- Komljenovic, T.; Pintus, P. On-chip calibration and control of optical phased arrays. Opt. Express 2018, 26, 3199–3210. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, L.; Chen, W. A chaotic stochastic parallel gradient descent algorithm for fast phase correction of optical phased array. In Proceedings of the 11th International Conference on Information Optics and Photonics (CIOP 2019), Xi’an, China, 6–9 August 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11209, pp. 1277–1289. [Google Scholar]
- Jin, J.; Lee, E.S.; Chun, K.W.; Lee, S.S.; Oh, M.C. Fast-running beamforming algorithm for optical phased array beam scanners comprised of polymeric waveguide devices. Opt. Express 2022, 30, 768–779. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zhang, L.; Li, Z.; Wu, W.; Wang, G.; Sun, X.; Zhang, W. An antenna array initial condition calibration method for integrated optical phased array. arXiv 2019, arXiv:1902.06203. [Google Scholar]
- Sung, J.Y.; Lee, S.L. Fast phase error calibration through radix-p optimization processing. Opt. Express 2021, 29, 41776–41787. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, K.; Yan, Q.; Wang, Y.; Wang, X.; Liu, H.; Feng, J.; Zhang, F.; Feng, Z.; Siviloglou, G.A. Universal dimension reduced phase compensation algorithm for an optical phased array. Opt. Lett. 2022, 47, 2871–2874. [Google Scholar] [CrossRef]
- Li, L.J.; Chen, W.; Zhao, X.Y.; Sun, M.J. Fast optical phased array calibration technique for random phase modulation LiDAR. IEEE Photonics J. 2018, 11, 6900410. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Peng, C.; Hu, W. Phase calibration of on-chip optical phased arrays via interference technique. IEEE Photonics J. 2020, 12, 6600210. [Google Scholar] [CrossRef]
- Yepez, P.A.K.; Scholz, U.; Zimmermann, A. Temperature dependence of the steering angles of a silicon photonic optical phased array. IEEE Photonics J. 2020, 12, 6800813. [Google Scholar] [CrossRef]
- Shim, J.; You, J.B.; Rhee, H.W.; Yoon, H.; Kim, S.H.; Yu, K.; Park, H.H. On-chip monitoring of far-field patterns using a planar diffractor in a silicon-based optical phased array. Opt. Lett. 2020, 45, 6058–6061. [Google Scholar] [CrossRef]
- Xiao, F.; Hu, W.; Xu, A. Optical phased-array beam steering controlled by wavelength. Appl. Opt. 2005, 44, 5429–5433. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Y.; Yoon, J.; Kim, J.; Kwon, N.H.; Rhee, H.W.; Baek, M.; Lee, Y.; Park, H.H.; Yoon, H. Demonstration of beam steering using a passive silica optical phased array with wavelength tuning. Opt. Lett. 2022, 47, 4857–4860. [Google Scholar] [CrossRef] [PubMed]
- Van Acoleyen, K.; Bogaerts, W.; Baets, R. Two-dimensional dispersive off-chip beam scanner fabricated on silicon-on-insulator. IEEE Photonics Technol. Lett. 2011, 23, 1270–1272. [Google Scholar] [CrossRef]
- Yoon, H.; Rhee, H.W.; Kwon, N.H.; Kim, J.Y.; Kim, J.; Yoon, J.; Park, H.H. Demonstration of Two-Dimensional Beam Steering through Wavelength Tuning with One-Dimensional Silicon Optical Phased Array. Photonics. 2022, 9, 812. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Rogier, H.; Baets, R. Two-dimensional optical phased array antenna on silicon-on-insulator. Opt. Express 2010, 18, 13655–13660. [Google Scholar] [CrossRef]
- Martin, A.; Dodane, D.; Leviandier, L.; Dolfi, D.; Naughton, A.; O’Brien, P.; Spuessens, T.; Baets, R.; Lepage, G.; Verheyen, P.; et al. Photonic integrated circuit-based FMCW coherent LiDAR. J. Light. Technol. 2018, 36, 4640–4645. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Chen, B.; Wang, Y.; Li, H.; Hou, Y.; Tao, M.; Li, Y.; Zhi, Z.; Liu, X.; et al. Two-dimensional multi-layered SiN-on-SOI optical phased array with wide-scanning and long-distance ranging. Opt. Express 2022, 30, 5008–5018. [Google Scholar] [CrossRef]
- Suyama, S.; Ito, H.; Kurahashi, R.; Abe, H.; Baba, T. Doppler velocimeter and vibrometer FMCW LiDAR with Si photonic crystal beam scanner. Opt. Express 2021, 29, 30727–30734. [Google Scholar] [CrossRef]
- Mingshi, Z.; Yubing, W.; Lanxuan, Z.; Qian, H.; Shuhua, Z.; Lei, L.; Yongyi, C.; Li, Q.; Junfeng, S.; Lijun, W. Phase-modulated continuous-wave coherent ranging method for optical phased array lidar. Opt. Express 2023, 31, 6514–6528. [Google Scholar] [CrossRef]
- Fantoni, A.; Lourenço, P.; Costa, J.; Vieira, M. Amorphous silicon photonic optical phased array for beam steering. In Proceedings of the Physics and Simulation of Optoelectronic Devices XXXI, San Francisco, CA, USA, 31 January–2 February 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12415, pp. 90–98. [Google Scholar]
- Sabouri, S.; Jamshidi, K. Design considerations of silicon nitride optical phased array for visible light communications. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 8300707. [Google Scholar] [CrossRef]
- Zhu, S.; Hu, T.; Li, Y.; Xu, Z.; Zhong, Q.; Dong, Y.; Singh, N. CMOS-compatible integrated silicon nitride optical phase array for electrically tunable off-chip laser beam steering. In Proceedings of the 2019 Electron Devices Technology and Manufacturing Conference (EDTM), Singapore, 12–15 March 2019; pp. 228–230. [Google Scholar]
- Sun, C.; Li, B.; Shi, W.; Lin, J.; Ding, N.; Tsang, H.K.; Zhang, A. Large-Scale and Broadband Silicon Nitride Optical Phased Arrays. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 8200710. [Google Scholar] [CrossRef]
- Tyler, N.A.; Fowler, D.; Malhouitre, S.; Garcia, S.; Grosse, P.; Rabaud, W.; Szelag, B. SiN integrated optical phased arrays for two-dimensional beam steering at a single near-infrared wavelength. Opt. Express 2019, 27, 5851–5858. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Luo, G.; Xu, Y.; Li, Y.; Su, Y.; Ma, J.; Wang, R.; Yang, Z.; Zhou, X.; Zhang, Y.; et al. Design and fabrication of a SiN-Si dual-layer optical phased array chip. Photonics Res. 2020, 8, 912–919. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Jia, L.; Cai, Y.; Yue, W.; Yu, M. Silicon nitride assisted 1× 64 optical phased array based on a SOI platform. Opt. Express 2021, 29, 10509–10517. [Google Scholar] [CrossRef]
- Li, Y.; Chen, B.; Na, Q.; Xie, Q.; Tao, M.; Zhang, L.; Zhi, Z.; Li, Y.; Liu, X.; Luo, X.; et al. Wide-steering-angle high-resolution optical phased array. Photonics Res. 2021, 9, 2511–2518. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Hou, Y.; Wang, Y.; Tao, M.; Chen, B.; Na, Q.; Li, Y.; Zhi, Z.; Liu, X.; et al. Investigation and demonstration of a high-power handling and large-range steering optical phased array chip. Opt. Express 2021, 29, 29755–29765. [Google Scholar] [CrossRef] [PubMed]
- Prost, M.; Ling, Y.C.; Cakmakyapan, S.; Zhang, Y.; Zhang, K.; Hu, J.; Zhang, Y.; Yoo, S.B. Solid-state MWIR beam steering using optical phased array on germanium-silicon photonic platform. IEEE Photonics J. 2019, 11, 6603909. [Google Scholar] [CrossRef]
- Midkiff, J.; Yoo, K.M.; Shin, J.D.; Dalir, H.; Teimourpour, M.; Chen, R.T. Optical phased array beam steering in the mid-infrared on an InP-based platform. Optica 2020, 7, 1544–1547. [Google Scholar] [CrossRef]
- Sun, J.; Moresco, M.; Leake, G.; Coolbaugh, D.; Watts, M.R. Generating and identifying optical orbital angular momentum with silicon photonic circuits. Opt. Lett. 2014, 39, 5977–5980. [Google Scholar] [CrossRef]
- Notaros, J.; Poulton, C.V.; Byrd, M.J.; Raval, M.; Watts, M.R. Integrated optical phased arrays for quasi-Bessel-beam generation. Opt. Lett. 2017, 42, 3510–3513. [Google Scholar] [CrossRef]
- Notaros, J.; Poulton, C.V.; Raval, M.; Watts, M.R. Near-field-focusing integrated optical phased arrays. J. Light. Technol. 2018, 36, 5912–5920. [Google Scholar] [CrossRef]
- Raval, M.; Yaacobi, A.; Watts, M.R. Integrated visible light phased array system for autostereoscopic image projection. Opt. Lett. 2018, 43, 3678–3681. [Google Scholar] [CrossRef]
- Kohno, Y.; Komatsu, K.; Tang, R.; Ozeki, Y.; Nakano, Y.; Tanemura, T. Ghost imaging using a large-scale silicon photonic phased array chip. Opt. Express 2019, 27, 3817–3823. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Liao, J.; Wang, C.; Cao, R.; JIn, L.; Cao, C. High-resolution dynamic imaging system based on a 2D optical phased array. Opt. Express 2021, 29, 39342–39351. [Google Scholar] [CrossRef]
- Fatemi, R.; Abiri, B.; Khachaturian, A.; Hajimiri, A. High sensitivity active flat optics optical phased array receiver with a two-dimensional aperture. Opt. Express 2018, 26, 29983–29999. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; O’Brien, D.; Payne, F.; Bogaerts, W.; Baets, R. Optical retroreflective marker fabricated on silicon-on-insulator. IEEE Photonics J. 2011, 3, 789–798. [Google Scholar] [CrossRef]
- Abiri, B.; Fatemi, R.; Hajimiri, A. A 1-D heterodyne lens-free optical phased array camera with reference phase shifting. IEEE Photonics J. 2018, 10, 6601712. [Google Scholar] [CrossRef]
- Abediasl, H.; Hashemi, H. Monolithic optical phased-array transceiver in a standard SOI CMOS process. Opt. Express 2015, 23, 6509–6519. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, R.; Wei, M. Two-Dimensional High-Efficiency Transceiver Integrated Optical Phased Array with Dual-Port Antenna. IEEE Photonics J. 2022, 14, 5047605. [Google Scholar] [CrossRef]
- Dostart, N.; Zhang, B.; Brand, M.; Al Qubaisi, K.; Onural, D.; Feldkhun, D.; Popović, M.; Wagner, K. Vernier optical phased array lidar transceivers. Opt. Express 2022, 30, 24589–24601. [Google Scholar] [CrossRef] [PubMed]
- Poulton, C.V.; Vermeulen, D.; Hosseini, E.; Timurdogan, E.; Su, Z.; Moss, B.; Watts, M.R. Lens-free chip-to-chip free-space laser communication link with a silicon photonics optical phased array. In Proceedings of the Frontiers in Optics, Washington, DC, USA, 18–21 September 2017; Optica Publishing Group: Washington, DC, USA, 2017; p. FW5A-3. [Google Scholar]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-range LiDAR and free-space 1025 data communication with high-performance optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 7700108. [Google Scholar] [CrossRef]
- Foster, A.C.; Kossey, M.; MacFarlane, N.; Rizk, C.; Kott, T.; Osiander, R.; Mosavi, N. Chip-scale optical phased arrays for inter-spacecraft communications. In Proceedings of the Micro-and Nanotechnology Sensors, Systems, and Applications XI, Orlando, FL, USA, 13 May 2019; SPIE: Bellingham, WA, USA, 2019; Volume 10982, pp. 54–61. [Google Scholar]
- Rhee, H.W.; You, J.B.; Yoon, H.; Han, K.; Kim, M.; Lee, B.G.; Kim, S.C.; Park, H.H. 32 Gbps data transmission with 2D beam-steering using a silicon optical phased array. IEEE Photonics Technol. Lett. 2020, 32, 803–806. [Google Scholar] [CrossRef]
- Chow, C.W.; Chang, Y.C.; Kuo, S.I.; Kuo, P.C.; Wang, J.W.; Jian, Y.H.; Ahmad, Z.; Fu, P.H.; Shi, J.W.; Huang, D.W.; et al. Actively controllable beam steering optical wireless communication (OWC) using integrated optical phased array (OPA). J. Light. Technol. 2022, 41, 1122–1128. [Google Scholar] [CrossRef]
- Wu, D.; Owen, K.; Yu, B.; Yi, Y. Fabrication of a self-aligned multi-waveguide-layer passive Si3N4/SiO2 photonic integrated circuit for a 3-D optical phased array device. Opt. Mater. Express 2024, 14, 13–21. [Google Scholar] [CrossRef]
- Derakhshandeh, A.; Pachnicke, S.; Hoeher, P.A. Underwater Wireless Laser-Based Communications Using Optical Phased Array Antennas. IEEE Photonics J. 2023, 15, 7304309. [Google Scholar] [CrossRef]
- Kossey, M.R.; Alt, S.; Rizk, C.; Foster, A.C. Integrated photonic arrays as a platform for infrared neural stimulation. In Proceedings of the Bio-Optics: Design and Application, San Diego, CA, USA, 2–5 April 2017; Optica Publishing Group: Washington, DC, USA, 2017; p. BoS2A-8. [Google Scholar]
- Sacher, W.D.; Liu, X.; Chen, F.D.; Moradi-Chameh, H.; Almog, I.F.; Lordello, T.; Chang, M.; Naderian, A.; Fowler, T.M.; Segev, E.; et al. Beam-steering nanophotonic phased-array neural probes. In Proceedings of the CLEO: Applications and Technology, San Jose, CA, USA, 5–10 May 2019; Optica Publishing Group: Washington, DC, USA, 2019; p. ATh4I-4. [Google Scholar]
- Guan, B.; Qin, C.; Scott, R.P.; Ercan, B.; Fontaine, N.K.; Su, T.; Yoo, S. Hybrid 3D photonic integrated circuit for optical phased array beam steering. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 15 May 2015; Optica Publishing Group: Washington, DC, USA, 2015; p. STu2F-1. [Google Scholar]
- Hosseini, A.; Kwong, D.; Zhao, Y.; Chen, Y.S.; Crnogorac, F.; Pease, R.F.W.; Chen, R.T. Unequally spaced waveguide arrays for silicon nanomembrane-based efficient large angle optical beam steering. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1439–1446. [Google Scholar] [CrossRef]
- Hosseini, A.; Kwong, D.; Zhang, Y.; Chandorkar, S.A.; Crnogorac, F.; Carlson, A.; Fallah, B.; Bank, S.; Tutuc, E.; Rogers, J.; et al. On the fabrication of three-dimensional silicon-on-insulator based optical phased array for agile and large angle laser beam steering systems. J. Vac. Sci. Technol. B 2010, 28, C6O1–C6O7. [Google Scholar] [CrossRef]
- Wu, D.; Yi, Y.; Zhang, Y. High-efficiency end-fire 3D optical phased array based on a multi-layer Si3N4/SiO2 platform. Appl. Opt. 2020, 59, 2489–2497. [Google Scholar] [CrossRef]
- Wu, D.; Yu, B.; Kakdarvishi, V.; Yi, Y. Photonic integrated circuit with multiple waveguide layers for broadband high-efficient 3D OPA. Opt. Lett. 2023, 48, 968–971. [Google Scholar] [CrossRef]
- Wang, P.; Kazemian, A.; Zeng, X.; Zhuang, Y.; Yi, Y. Optimization of aperiodic 3D optical phased arrays based on multilayer Si3N4/SiO2 platforms. Appl. Opt. 2021, 60, 484–491. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).