1. Introduction
Spatial division multiplexing (SDM) is the latest—and possibly final—fertile territory for exploration in the quest to extend information transmission capacity in optical systems [
1]. It follows developments in the multiplexing of wavelength, polarisation, amplitude, time and phase. All such multiplexing is possible in single-mode fibre (SMF) [
2]—but SDM requires multimode fibres. These allow for orthogonal spatial amplitude distributions to be utilised as independent channels. However, this adds additional complexities, such as additional channel-dependent amplification requirements and issues with modal crosstalk. Embracing the challenge of SDM is becoming necessary to address the impending “capacity crunch” in optical fibre systems [
3]. Free-space optics (FSO) is a natural area of development for delivering high-capacity data connections where no infrastructure exists, where the installation of optical fibres is excessively expensive and where radio frequency-based systems do not have the capacity [
4]. It is a logical progression to take fibre-based optical communication technology and transition to free-space optical systems, releasing light into free space and then capturing and reintroducing it into a fibre-based receiver. This inevitably results in significant loss due to divergence and the wavefront-degrading properties of atmospheric turbulence, which prevent light from being efficiently focussed into a single-mode fibre [
5,
6,
7]. This loss takes the form of a large signal fade, and forward-error correction-encoding schemes are inefficient here because the length of the signal drop (1 mS) is long compared to the bit length (<1 nS) [
8,
9]. Adaptive bit rates have been applied to account for atmospheric effects [
10]. Adaptive optics systems which correct wavefront distortion are effective at restoring lost power [
11], but acquiring and counteracting the distortion information introduces additional complexity.
Multimode fibre (MMF) would be more efficient [
12] but would require a method of distinguishing or reintegrating numerous modes. Using orthogonal spatial modes as independent channels is an effective way of increasing channel capacity and has been demonstrated using orbital angular momentum (OAM) modes [
13,
14], Hermite–Gaussian (HG) and Laguerre–Gaussian modes [
15].
Clearly, the method of collection and modal discrimination is a key factor in the SDM system. One approach has been to use photonic lanterns [
16] that consist of a bundle of SMFs which are drawn together into a MMF output. These devices are good for a small number of modes (~10) but are not scalable to larger numbers of modes in a practical manner [
17]. In this work, we have made use of multi-plane light converters (MPLC) which use progressive diffraction from -phase plates to map different input modes to specific output locations [
17,
18], where an array of single-mode fibres is located, mapping specific modes to individual fibres. These work in both directions—to separate incoming modes within a wavefront, or to combine inputs to produce a multimodal output wavefront. The MPLCs were acquired from Cailabs (Tilba units with 21 modes), with one used as transmitter to produce selectable individual HG mode outputs and another used as receiver again with selectable input mode. The effect of atmospheric turbulence would be to transfer power from the transmitted mode to other modes. In single-mode systems, this power would be lost unless wavefront correction is established using adaptive optics, which requires information feedback between the transmitter and receiver. The ability to capture the additional modes increases the captured power and enables the reconstruction of the transmitted signal. Emulating the effects of atmospheric turbulence was achieved using a digital micromirror device (DMD) in line with our previous work [
12]. This enabled different strengths of turbulence, represented through the refractive index structure function (Cn
2) from weak (C
n2 = 1 × 10
−16 m
2/3) to strong (C
n2 = 1 × 10
−13 m
2/3), to be created so that the induced crosstalk between modes can be observed.
The capability of selecting, affecting and discriminating many distinct spatial modes enables operational benefits in terms of capacity and resilience. Capacity gain comes from the use of multiple input multiple output (MIMO) processing where crosstalk between modes requires significant digital signal processing to disentangle the signals. In this work, we have observed how the intensity of a CW laser in a single mode is distributed across multiple modes as a result of emulated turbulence. This is repeated for different transmission modes to emulate what would be experienced by a MIMO system; although we have not performed MIMO processing, we have seen how different transmission channels interact differently to the same turbulence.
Having observed the received powers across all channels from all transmitted channels, a subset of 6 channels—common for transmitter and receiver—was used to examine the behaviour of data transfer through DMD-induced turbulence and compare the effects of fixed single-channel performance with multiple receiver channels. Here, we have demonstrated how single input multiple output (SIMO) processing can help improve the resilience of FSO communications in the presence of turbulence.
The work presented here is, to our knowledge, the first example of the use of 2 MPLC devices to emulate a FSO comms connection with incorporated turbulence. This approach would naturally lead to a full duplex system with no additional optical enhancements required beyond those needed for one-way communication. However, we concentrate on presenting observations of modal crosstalk.
2. Materials and Methods
2.1. Theory of Modal Overlap
The MPLC devices operate by producing or dispersing a set of HG modes. The atmospheric turbulence effects can be described in terms of a set of Zernike modes (ZM) which manipulate the phase of the HG mode wavefront between the transmitter and receiver. We can represent the scale of the received signal as an overlap integral of the transmission and receive modes incorporating the phase-distorting effects of the Zernike modes. The expression for the relevant HG and ZMs in Cartesian coordinates is given in
Table 1. We make the simplistic assumption that magnification of the system is unity at the location of the MPLC receiver’s input beam waist. This allows us to ignore the travelling wave nature of the HG modes and define them in terms of their stationary amplitude and phase:
where
Hi is the Hermite polynomial,
m and
n are the mode indices in the
x and
y directions and
is the beam waist size. The overlap between the transmitted and received mode is then:
where the prime represents indices in the receiver space, and
is the
jth order Zernike mode. This enables us to examine the effects of specific atmospheric modes upon the receiver by examining the overlap function with neighbouring modes for specific ZM contribution, where we would see that tip (j = 1) and tilt (j = 2) modes have the most impact upon the overlap function. In the emulated turbulence, the wavefront disturbance is implemented as a set of ZMs with amplitudes related to C
n2 (and aperture) [
15]. We can, thus, estimate the effects of a controlled level of atmospheric turbulence from such a set of Zernike modes by summing the modal phase effects as follows:
2.2. Phase 1—Intensity Measurements of Induced Crosstalk
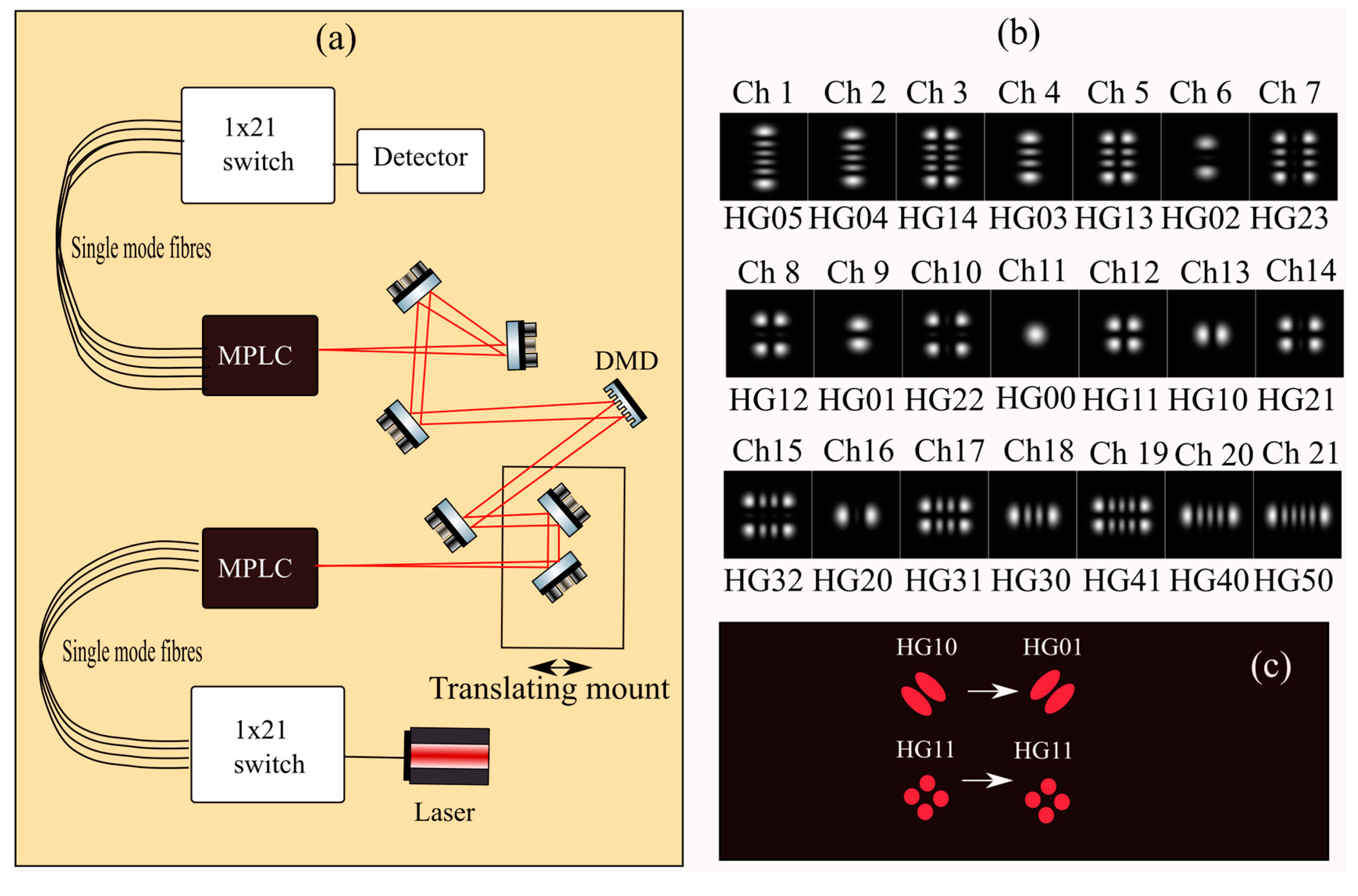
A system to select, transmit and receive specific HG modes was constructed using 2 MPLCs to provide mode selection and discrimination. Output from a single narrow linewidth laser at a wavelength of 1545 nm is sent to a 21-way switch connected to the 21 fibre channels of an MPLC. Light in the selected output mode is directed to a DMD which produces an emulated turbulent wavefront through diffraction. This light is then directed into the second MPLC where another 21-way switch is used to sample the power in each channel sequentially—see
Figure 1a. The turbulence emulation is performed by preparing a contiguous sequence of frames where the amount of wavefront distortion is related to a chosen value of the refractive index structure function (C
n2) along a defined path length. The emulated turbulence was for an equivalent path length of 1 km and an equivalent capture aperture of 10 cm. The distortion is represented as a set of orthogonal Zernike mode functions whose amplitudes are selected from a random distribution and whose widths are statistically related to the values of C
n2 [
19]. Smooth transitions between frames are created by interpolating between values [
20]. Thus, a smoothly varying sequence of frames can represent changing wavefront distortions of a chosen turbulence strength, and this sequence can be repeated to provide a consistent comparison of the effects across all possible channels (modes) at a frame rate that is completely controllable; up to 10 kHz, if required. This approach of using a DMD to emulate turbulence in a controllable, reproducible way is presented in more detail in ref [
8]. More sophisticated turbulence emulations operate with multiple planes to better represent turbulence effects spread along the entire path [
21,
22]. The loss associated with the DMD makes this infeasible, but it is sufficient to explore the effects arising from large-scale intensity variations. This arrangement forms the kernel of experiments aimed at observing the turbulence-induced modal channel mixing across all channels, measuring just the intensity, and across a selected subset of channels across a communications link.
The 21 channels of the MPLC relate to the HG modes shown in
Figure 1b. The diagram in
Figure 1a shows a diverging output beam from the first MPLC, but the second MPLC must receive a beam that is well-matched in both divergence and beam waist size. To achieve this, the DMD must also focus the beam with unit magnification. This is achieved by adding to the distortion frames a controlled amount of the Zernike focus mode (Z
3). The result is that the light is distributed into a first-order diffraction focus, a zero-order undiffracted beam and a negative first-order defocussed beam. This results in less than 10% efficiency of the collected power, but only the first-order focus is effectively received by the MPLC. Unity magnification is found by adjusting the length of the input path to the DMD, adjusting the position of a pair of fold mirrors on a translation stage.
One further stage is required. The DMD has tilting mirrors that reflect light away from the optical axis which adds aberrations—most notably astigmatism—to the diffracted wavefront. These additional aberrations can be at least partially corrected using the same Zernike mode structures as the ones used for distorting the wavefront in accordance with [
23]. Thus, a set of fixed correcting Zernike modes is added to the fixed focussing and the varying turbulence distortion to produce the final sequence of turbulence emulation frames. One final point is that the effect of the single-lens function performed by the DMD is to invert the image of the mode at the receiver. This is because the orthogonal mode directions are at 45 degrees to the plane of the experiment (see
Figure 1c). Thus, rotationally symmetrical modes (
) are received in the corresponding modes of the receiver, but asymmetric modes swap mode indices e.g.,
.
2.3. Phase 2—Coherent Data Measurements of Induced Crosstalk
A second stage to this experiment involves using the DMD turbulence emulator within a SDM communications setup, shown in
Figure 2. Phase 1 shows us how turbulence can affect the distribution of optical power across all the receiver modes. Understanding what this means for the use of FSO-based SDM for communications requires a further implementation of comms across this same setup. This involved using a polarization multiplexed coherent QPSK signal generated using a Ciena Wavelogic 3 transponder with a 6-digit on-board arbitrary waveform generator (AWG) with a sampling rate of 39.385 GSa/s. The signal was shaped by a root-raised-cosine (RRC) filter with a roll-off factor of 0.1. It has a frame structure of 20,000 symbols with a 560-symbol training sequence and a pilot for every 9 data symbols. The carrier wavelength was 1550.12 nm, and the output was directed to the transmitting MPLC via a 21-way switch, selecting the HG mode of transmission. As this is a different wavelength from the setup in phase 1, it requires a separate turbulence sequence to be created with different focussing mode amplitudes.
The system has the capacity to process light from 6 received modes. A subset of 6 receiver channels was selected based on the most efficient mode coupling to principal transmission modes observed without turbulence. These same modes were also selected for independent transmission. The receiver channels were temporally multiplexed with unique fibre delays, separating the channels in time and allowing data capture with a single coherent receiver similar to our previous work [
24,
25]. In this case, the DMD takes on a third role, that of data–frame synchronisation, where the turbulence frame is active for 20 µs and disabled for a further 140 µs before the next frame. In previous work, this role was performed by an acousto-optic modulator which introduced a 5 dB loss, and its removal helped to compensate for the additional loss created by the DMD. Collecting signals in multiple channels enables an increase in the signal-to-noise ratio (SNR) through the use of digital signal processing.
2.4. SIMO Processing
At the receiver side, the 6 modes were delayed by 25, 20, 15, 10, 5, and 0 km fibre delay lines (FDLs), generating a signal delay of ~24.5 μs between adjacent channels. The delay was slightly longer than the signal burst generated by the DMD to enable the time-division multiplexing (TDM) receiver structure. After being combined by a fibre coupler and amplified by an EDFA, the TDM signals were received by one single coherent receiver with a 23 GHz, 50 GSa/s oscilloscope, and demodulated by offline SIMO Digital Signal Processing, for which the stages are shown in
Table 2.
The core module of the offline SIMO DSP is a pilot-aided 3-dimensional LMS equaliser, which mitigates the inter-symbol interference (ISI), the polarization mixing, and performs a maximum-likelihood combination of the SIMO signals [
26]. To obtain the optimum performance, standard pre-compensation algorithms for IQ imbalance, chromatic dispersion (CD), timing error, and frequency error were also included in the DSP, with a matched RRC filter and a standard frame synchronization module [
27].
Using a sequence of aberrating turbulence frames enables an examination of the effect of turbulence upon different transmission modes under the same turbulence conditions. This allows for a direct comparison to be made regarding performance and resilience. However, in this preliminary experiment of data transmission, it was not possible to sustain data capture across multiple frames, and so, specific frames were selected representing a ‘frozen’ turbulence.
3. Results
3.1. Phase 1
The first stage in creating turbulence sequences is to ensure the efficient coupling of transmission mode and receive mode is achieved by systematically varying the Zernike mode (ZM) amplitudes to maximise the received intensity. This involves finding the correct focus amplitude needed to overcome the divergence of the transmission mode and refocus into the receiver. Scanning of the amplitudes for other ZM parameters is used to locate and fix the best values, accounting for the significant effects of astigmatism, in particular. Once these ZM amplitude values are found, they are used as a fixed base in each frame upon which the varying turbulence amplitudes are added. A sequence of 400 frames was produced to represent strong turbulence effects with Cn2 = 1 × 10−13 m2/3.
The turbulence sequence is loaded to the DMD, the transmission mode selected, and the received intensity for the turbulence sequence recorded for each receiver mode individually. This process is repeated for the next transmission mode, and so on.
Figure 3 shows separate plots for 20 transmission modes showing the received intensity for all receive modes (horizontal axis of each plot) for each frame of the sequence (vertical axis). The inverting image effect of the DMD-focussing “lens” means that the transmitted modes HG
m,
n are received as HG
n,m; thus, only where m = n is the receive channel, the same as the transmit channel (in this case channels 10, 11 and 12).
In each plot, the receiver channel/mode that should correspond to the transmission channel/mode are referred to as the principal channels—transmitter ch11(
HG00) matches to receiver ch11(
HG00) and transmitter ch6(
HG02) matches to receiver ch16(
HG20). We can observe many frames where the principal channel is strongly attenuated and the received power increases in other neighbouring channels, thus demonstrating the modal redistribution effect of the turbulence. Thus,
capturing multiple modes reduces the loss inflicted upon a single mode system by turbulence [
28].
For selected principal channels, the received intensity variation for the sequence is shown in
Figure 4c—a vertical profile through transmission channel plot, as seen in
Figure 3. We can see that
HG00 is the best coupled principal channel, and that coupling efficiency reduces as mode order increases. On some occasions, where the
HG00 channel is strongly attenuated, other principal channels show a larger intensity—for example, frame 248. Different modes, therefore, respond differently to the same turbulence.
Figure 4b shows plots of the horizontal profile through the plot—equivalent to the total received power—varying with frame number for the given transmission mode. This clearly shows that even with a large modal space, significant power is lost to the receiver and, yet again, that different modes will interact differently withthe same turbulence. The plot in
Figure 4d shows the fractional change in average intensity across the whole sequence, with red showing positive change and blue negative change. The channels have been ordered to account for the mode inversion effects and place the principal channels on the main diagonal. Here, we can see the net loss in the principal channels and redistribution to other channels.
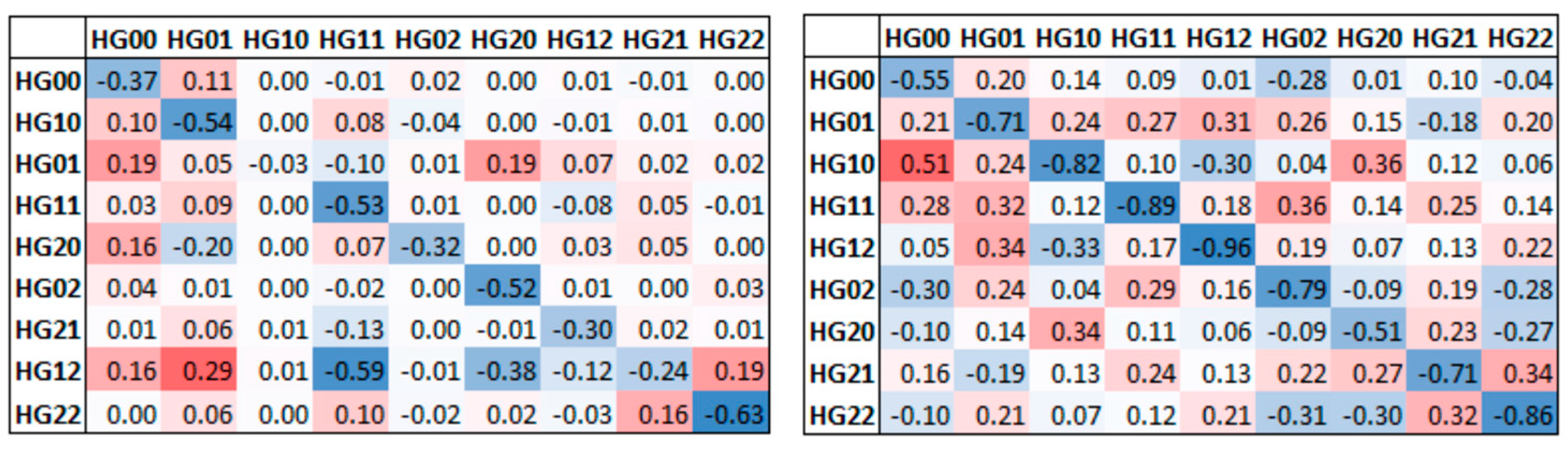
Coupling with higher order modes is quite inefficient, so we concentrate on the lower order modes. We calculate the average change in the received intensity, determined as the average value of the difference between the intensity at each frame and the maximum intensity within the sequence. This allows us to see in which direction the received power is changing for each channel because of the turbulence. This is shown in
Figure 5 where the left-hand matrix shows the lowest order channels
HG00 to
HG22, with a clear reduction for all the principal channels and increases in neighbouring channels. The right-hand matrix is the result of calculated values of the difference in modal overlap given the expected parameters for ZMs with a C
n2 = 1 × 10
−13 m
2/3. The calculation is simplistic; it does not include the effects of mode-related divergence changes, but it is enough to give an understanding of expectations and show similarities with the measured data. With the predominant ZMs being tip and tilt [
19,
29], we can see, in terms of measurement and calculation, how these beam-steering modes will, for example, direct power from
HG00 to
HG10 and
HG01. Intuitively, we can understand this as translating the central node of
HG00 to an offset node such as
HG10.
3.2. Phase 2
To examine the effects upon a free-space optical communication system, a coherent QPSK modulation format, as described earlier, was introduced to the transmitter switch. A new turbulence sequence for 1550 nm was constructed and intensity measurements for the relevant channels were made. The subset of 6 of the strongest-coupled channels were connected directly from the receiver MPLC through a set of delay lines to a coherent receiver. In creating a sequence of aberrating frames, we were able to specifically understand the effect of each frame upon the incident beam by measuring the intensity variation, as in phase 1, and this sequence is shown in
Figure 6a. We could, thus, select representative frames from within the statistical set of turbulence frames, reducing the need to examine many frames to cover all eventualities. A set of 5 specific frames from the turbulence sequence was selected for individual use with the comms setup. These frames were chosen to represent instances of both strong turbulence attenuation (frames 48 and 274) and weak attenuation (frames 110 and 249), plus an intermediate level (frame 229), as seen in the intensity variation of the HG
00 principal channel.
The subset of 6 Tx-Rx channels were
HG00(ch11),
HG01(ch9),
HG10(ch13),
HG11(ch12),
HG02(ch6) and
HG20(ch16)—this set allows for consistency and reciprocity for the mode index swapping that occurs between transmitter and receiver.
Figure 6 shows matrix plots for the subset of channels taken for each of the chosen frames, with the plots of
Figure 6b showing the intensity in the receive channel (horizontal axis) for different transmitter channels (vertical axis). The plots of
Figure 6c display the phase 2 SNR of the coherent signals in the same manner, with SNR converted from the calculated Error Vector Magnitude to give linear comparisons with the plots of
Figure 6b. Frames 110 and 249 represent positions of little turbulence within the sequence and we can see—particularly for ch11—that this is the strongest channel seen in both the intensity and coherent data plots. Frames of strong turbulence effect (48 and 229) reduce the SNR and see the input power distributed around other channels.
The plots of
Figure 6d show a comparison of the SNR calculated from SIMO compared to the SNR of the strongest individual channels for each transmitted channel. This value is always higher than for a single channel, with SIMO processing giving an average improvement of 1.5 dB (±0.33), thus demonstrating the potential for improved signal recovery within a strong turbulence environment. This SIMO gain will be limited by saturation effects because the system was set up with optimal power without turbulence. There is, then, limited gain to be achieved, with a maximum expected SIMO gain of 4 dB. Lower transmission power (or stronger turbulence) could result in gain beyond 1.5 dB. However, the issue here is the improvement in resilience of the FSO communication rather than the improvement in signal gain. This aligns with previous measurements of mode diversity coherent receipt, which show limited gain but a reduction in fluctuations [
26]. There are inherent crosstalk effects caused by the DMD, which are not completely corrected using ZMs. However, SIMO processing is also correcting these imperfections.
4. Discussion
Establishing an SDM setup with emulated turbulence effects has led to several useful and usable observations that will relate to future implementations of FSO communications systems. Firstly, the viability of using MPLCs to generate and disperse numerous spatial modes seems obvious when there are advantages that arise from their use. Capturing multiple modes is equivalent to using a larger effective aperture—one that surpasses the use of a fixed physical aperture collecting light into a single-mode fibre. This is akin to the use of a multimode fibre. As well as capturing more of the collected light entering the physical aperture, modal dispersal is actually a characterization of the atmospheric conditions and, to some extent, obviates the need for adaptive optics to manipulate an incoming wavefront for better coupling into an SMF. As we have shown here, the use of digital signal processing with multiple channels can improve the resultant SNR. Moreover, removing an AO system simplifies an optical system and removes the need for feedback from receiver to transmitter and additional laser sources to measure atmospheric distortion.
For emulating the turbulence within an SDM system, the DMD-based approach has some benefits. The use of a repeatable sequence of turbulence frames is especially useful when the behaviour of multiple channels needs to be assessed, as it allows for the multiplexing of receiver equipment. The DMD performs multiple functions in this work—producing turbulence, focusing into the receiver and rapidly switching to enable SIMO multiplexing. However, this comes at the cost of lossy diffraction and significant wavefront distortions due to the off-axis nature of the DMD reflections, which shows up as asymmetry in modal redistribution and limited coupling efficiency.
One important observation from this is that different spatial mode transmissions behave subtly differently in the same turbulence conditions. The isoplanatic angle is the angle at which turbulence-induced variation will correlate, corresponding to a lateral physical extent of atmosphere seen by different incoming rays [
27]. In our case, all transmitted modes experience the same frame and amplitudes of ZM turbulence contributions (although, larger beams experience a physically larger area of the DMD). We might, therefore, expect all principal modes to experience the same effects. Whilst they broadly follow the same variation, there are instances where some modes are less attenuated than others. For instance, around frame 370, modes
HG01 and
HG10 have a higher intensity than the HG00 mode, despite this one being much more efficiently coupled. The implication is that the same turbulence has had less effect on the coupling of
HG10 than on
HG00. Higher-order aberration modes correlate less well through turbulence, resulting in a mode-dependent isoplanatic angle [
30], so it is reasonable to assume that higher-order transmission modes will also respond differently to the same turbulent atmosphere.
The suggestion from this work is that even strong turbulence redistributes power locally, i.e., within a limited range of (m, n) values around the transmission mode. It so happens that these are neighbouring physical channels within the MPLC, and distribution appears in channels around the principal channel. Coupling between modes is related to the modal overlap function which involves both the spatial intensity distribution and the modal divergence. The predominant ZMs induced by turbulence are tip and tilt which result in beam steering. A HG00 Gaussian beam is laterally translated by tip/tilt and, thus, increases the overlap with HG01 and HG10 modes. A strong coupling of power out of HG00(ch11) and into HG01(ch9) and HG10(ch13) can be observed in the data. This tells us that power redistribution is not random and that judicious choice of receive channels is beneficial. Indeed, utilizing many modes would require more hardware and could be a limiting factor. Thus, the use of a subset of receiver channels, as was shown in Phase 2, is a sensible compromise. This enables the use of an adaptive SIMO approach where the choice of receiver channels could be actively controlled depending on the observed turbulence conditions.
5. Conclusions
We have demonstrated that turbulence-like effects upon a modal transmitter beam will transfer power out of the transmission (Hermite–Gaussian) mode and into neighbouring modes, with consequences for FSO communications. The capability of MPLC devices to deconstruct a received wavefront into constituent modes reduces lost power in comparison to single-mode systems and can improve the resilience against turbulence in FSO communications through the use of SIMO processing. MPLC devices are well-suited to this task, being compact devices that map specific modes into single-mode fibres, making them easy to integrate with conventional fibre-based communications equipment. In addition, they offer the capability of producing a large number—potentially hundreds—of modes and can reduce the requirements for adaptive optics systems to ensure efficient power capture. Indeed, in this work, we have shown that modes can interact differently with strong turbulence, and adaptive optics would fail to compensate for this. We have highlighted that, in certain situations, modes other than the main transmitted modes can be received more efficiently, leading to advantages for adaptive mode control by the transmitter. A further advantage of MPLC-based FSO communication could be that the MPLC devices are capable of operating as transmitters and receivers simultaneously through a judicious choice of modes. This may simplify the engineering requirements involved in producing a full duplex FSO communication system.
In this work, we have also shown that the DMD micromirror array has performed multiple roles simultaneously—focusing, turbulence emulation and frame synchronization—showing how the device is, indeed, a versatile photonic tool that will continue to find varied applications.
Author Contributions
Conceptualization, D.B.; Methodology, D.B. and A.E.; Software, D.B. and Y.L.; Validation, D.B. and Y.L.; Formal analysis, Y.L.; Investigation, D.B. and Y.L.; Resources, A.E. and A.B.; Data curation, D.B.; Writing—original draft preparation, D.B.; Writing—review and editing, A.E. and A.B.; Visualization, D.B.; Supervision, A.E.; Project administration, A.E.; Funding acquisition, A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by Engineering and Physical Sciences Research Council (EP/T009047/1 and EP/S016171/1) and by H2020 Marie Skłodowska-Curie Actions (713694).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available upon reasonable request.
Acknowledgments
We thank Ciena and Charles Laperle for kindly providing the WaveLogic 3 transponder for our experiments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Winzer, P.J. Making spatial multiplexing a reality. Nat. Photonics 2014, 8, 345–348. [Google Scholar] [CrossRef]
- Ellis, A.D.; Suibhne, N.M.; Saad, D.; Payne, D.N. Communication networks beyond the capacity crunch. Philos. Trans. R. Soc. A 2016, 374, 20150191. [Google Scholar] [CrossRef] [PubMed]
- Trichili, A.; Cox, M.A.; Ooi, B.S.; Alouini, M.S. Roadmap to free space optics. JOSA B 2020, 37, A184–A201. [Google Scholar] [CrossRef]
- Bian, Y.; Li, Y.; Chen, E.; Li, W.; Hong, X.; Qiu, J.; Wu, J. Free-space to single-mode fiber coupling efficiency with optical system aberration and fiber positioning error under atmospheric turbulence. J. Opt. 2022, 24, 025703. [Google Scholar] [CrossRef]
- Dikmelik, Y.; Davidson, F.M. Fiber-coupling efficiency for free-space optical communication through atmospheric turbulence. Appl. Opt. 2005, 44, 4946–4952. [Google Scholar] [CrossRef]
- Toyoshima, M. Maximum fiber coupling efficiency and optimum beam size in the presence of random angular jitter for free-space laser systems and their applications. J. Opt. Soc. Am. A 2006, 23, 2246. [Google Scholar] [CrossRef]
- Goyal, P.; Kumar, A.; Nath, V. Mitigation of atmospheric turbulence in free space optics: A review. In Proceedings of the 2015 Fifth International Conference on Advanced Computing & Communication Technologies, Rohtak, India, 21–22 February 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 634–640. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Free space optical communication: Challenges and mitigation techniques. arXiv 2015, arXiv:1506.04836. [Google Scholar]
- García-Zambrana, A.; Castillo-Vázquez, C.; Castillo-Vázquez, B. Rate-adaptive FSO links over atmospheric turbulence channels by jointly using repetition coding and silence periods. Opt. Express 2010, 18, 25422–25440. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, H.; Li, D.; Wang, R.; Jin, C.; Yin, X.; Gao, S.; Mu, Q.; Xuan, L.; Cao, Z. Performance analysis of an adaptive optics system for free-space optics communication through atmospheric turbulence. Sci. Rep. 2018, 8, 1124. [Google Scholar] [CrossRef] [PubMed]
- Benton, D.M.; Ellis, A.D.; Li, Y.; Hu, Z. Emulating atmospheric turbulence effects on a micro-mirror array: Assessing the DMD for use with free-space-to-fibre optical connections. Eng. Res. Express 2022, 4, 045004. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Z.; Liao, P.; Li, L.; Xie, G.; Huang, H.; Zhao, Z.; Yan, Y.; Ahmed, N.; Willner, A.; et al. Experimental characterization of a 400 Gbit/s orbital angular momentum multiplexed free-space optical link over 120 m. Opt. Lett. 2016, 41, 622–625. [Google Scholar] [CrossRef] [PubMed]
- Pang, K.; Song, H.; Zhao, Z.; Zhang, R.; Song, H.; Xie, G.; Li, L.; Liu, C.; Du, J.; Molisch, A.F.; et al. 400-Gbit/s QPSK free-space optical communication link based on four-fold multiplexing of Hermite–Gaussian or Laguerre–Gaussian modes by varying both modal indices. Opt. Lett. 2018, 43, 3889. [Google Scholar] [CrossRef]
- Velázquez-Benítez, A.M.; Antonio-López, J.E.; Alvarado-Zacarías, J.C.; Fontaine, N.K.; Ryf, R.; Chen, H.; Hernández-Cordero, J.; Sillard, P.; Okonkwo, C.; Leon-Saval, S.G.; et al. Scaling photonic lanterns for space-division multiplexing. Sci. Rep. 2018, 8, 8897. [Google Scholar] [CrossRef]
- Fontaine, N.K.; Carpenter, J.; Gross, S.; Leon-Saval, S.; Jung, Y.; Richardson, D.J.; Amezcua-Correa, R. Photonic Lanterns, 3-D Waveguides, Multiplane Light Conversion, and Other Components That Enable Space-Division Multiplexing. Proc. IEEE 2022, 110, 1821–1834. [Google Scholar] [CrossRef]
- Fontaine, N.K.; Ryf, R.; Zhang, Y.; Alvarado-Zacarias, J.C.; van der Heide, S.; Mazur, M.; Huang, H.; Chen, H.; Amezcua-Correa, R.; Li, G.; et al. Digital turbulence compensation of free space optical link with multimode optical amplifier. In Proceedings of the 45th European Conference on Optical Communication (ECOC 2019), Dublin, Ireland, 22–26 September 2019; Institution of Engineering and Technology: Stevenage, UK, 2019; p. 281. [Google Scholar] [CrossRef]
- Noll, R.J. Zernike Polynomials and Atmospheric Turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Wilcox, C.C.; Santiago, F.; Martinez, T.; Andrews, J.R.; Restaino, S.R.; Corley, M.; Teare, S.W.; Agrawal, B.N. A method of generating atmospheric turbulence with a liquid crystal spatial light modulator. In Advanced Wavefront Control: Methods, Devices, and Applications VIII; International Society for Optics and Photonics: Bellingham, DC, USA, 2010; Volume 7816, p. 78160E. [Google Scholar]
- Li, Y.; Chen, Z.; Benton, D.M.; Patel, M.; Lavery, M.P.J.; Ellis, A.D. Single-wavelength polarization- and mode-division multiplexing free-space optical communication at 689 Gbit/s in strong turbulent channels. Opt. Lett. 2023, 48, 3575–3578. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, DC, USA, 2005. [Google Scholar]
- Zandi, M.; Benton, D.; Sugden, K. Laser beam wavelength determination algorithm using a digital micromirror device. Opt. Eng. 2023, 62, 064101. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Z.; Benton, D.M.; Ali, A.; Patel, M.; Ellis, A.D. Demonstration of 10-channel mode- and polarization-division multiplexed free-space optical transmission with successive interference cancellation DSP. Opt. Lett. 2022, 47, 2742. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Y.; Benton, D.M.; Ali, A.A.; Patel, M.; Ellis, A.D. Single-wavelength transmission at 1.1-Tbit/s net data rate over a multi-modal free-space optical link using commercial devices. Opt. Lett. 2022, 47, 3495. [Google Scholar] [CrossRef]
- Winters, J.H. Optimum combining in digital mobile radio with cochannel interference. IEEE Trans. Veh. Technol. 1984, 33, 144–155. [Google Scholar] [CrossRef]
- Faruk, M.S.; Savory, S.J. Digital signal processing for coherent transceivers employing multilevel formats. J. Light. Technol. 2017, 35, 1125–1141. [Google Scholar] [CrossRef]
- Zheng, D.; Li, Y.; Zhou, H.; Bian, Y.; Yang, C.; Li, W.; Qiu, J.; Guo, H.; Hong, X.; Zuo, Y.; et al. Performance enhancement of free-space optical communications under atmospheric turbulence using modes diversity coherent receipt. Opt. Express 2018, 26, 28879–28890. [Google Scholar] [CrossRef]
- Andrews, L.C. Field Guide to Atmospheric Optics; SPIE: Bellingham, WA, USA, 2019. [Google Scholar]
- Bolbasova, L.; Lukin, V.P. Isoplanatic Requirements for Adaptive-Optics Systems; SPIE: Bellingham, WA, USA, 2009; Volume 21. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).