Analysis of Faceted Gratings Using C-Method and Polynomial Expansion
Abstract
1. Introduction
2. Statement of the Problem
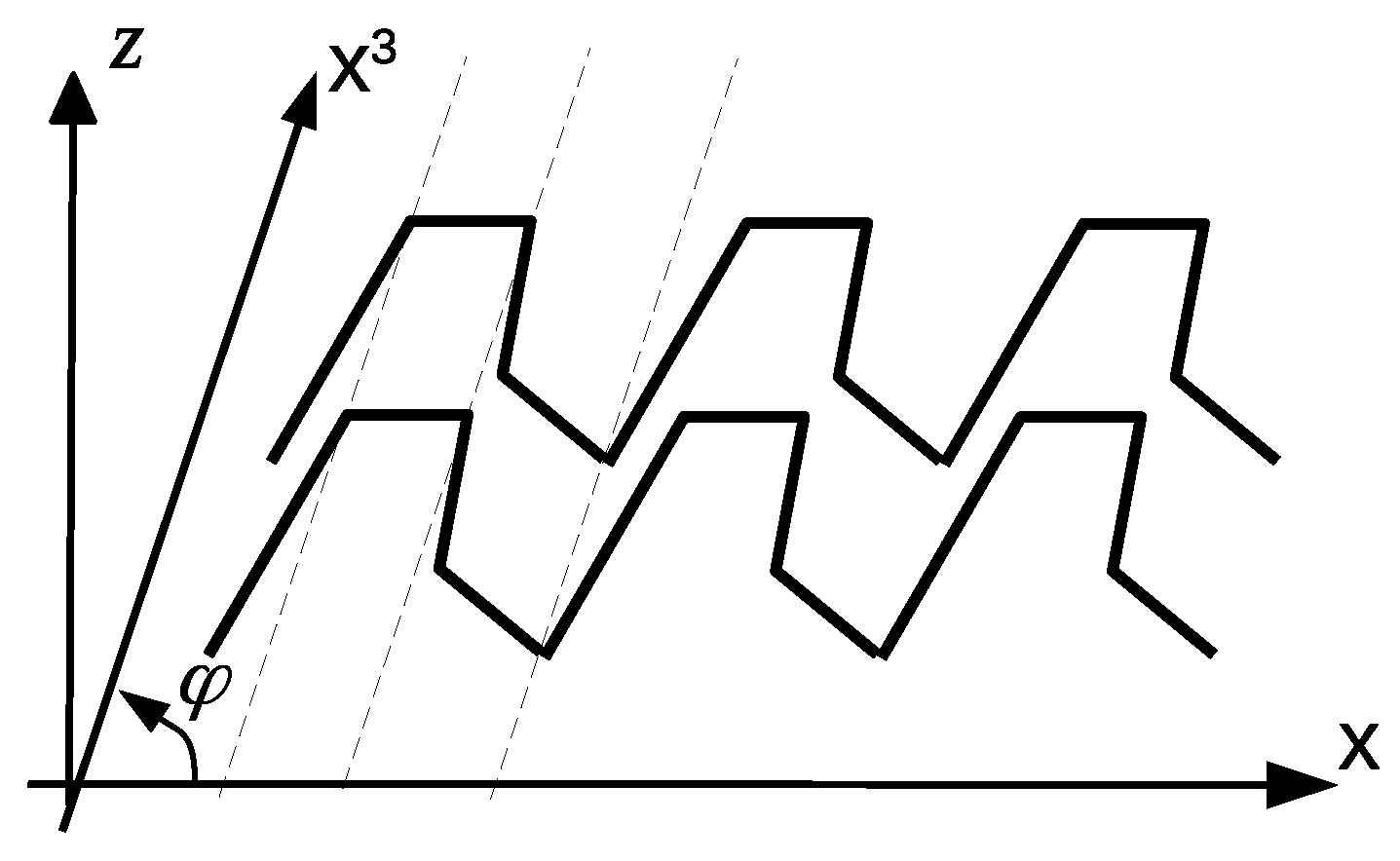
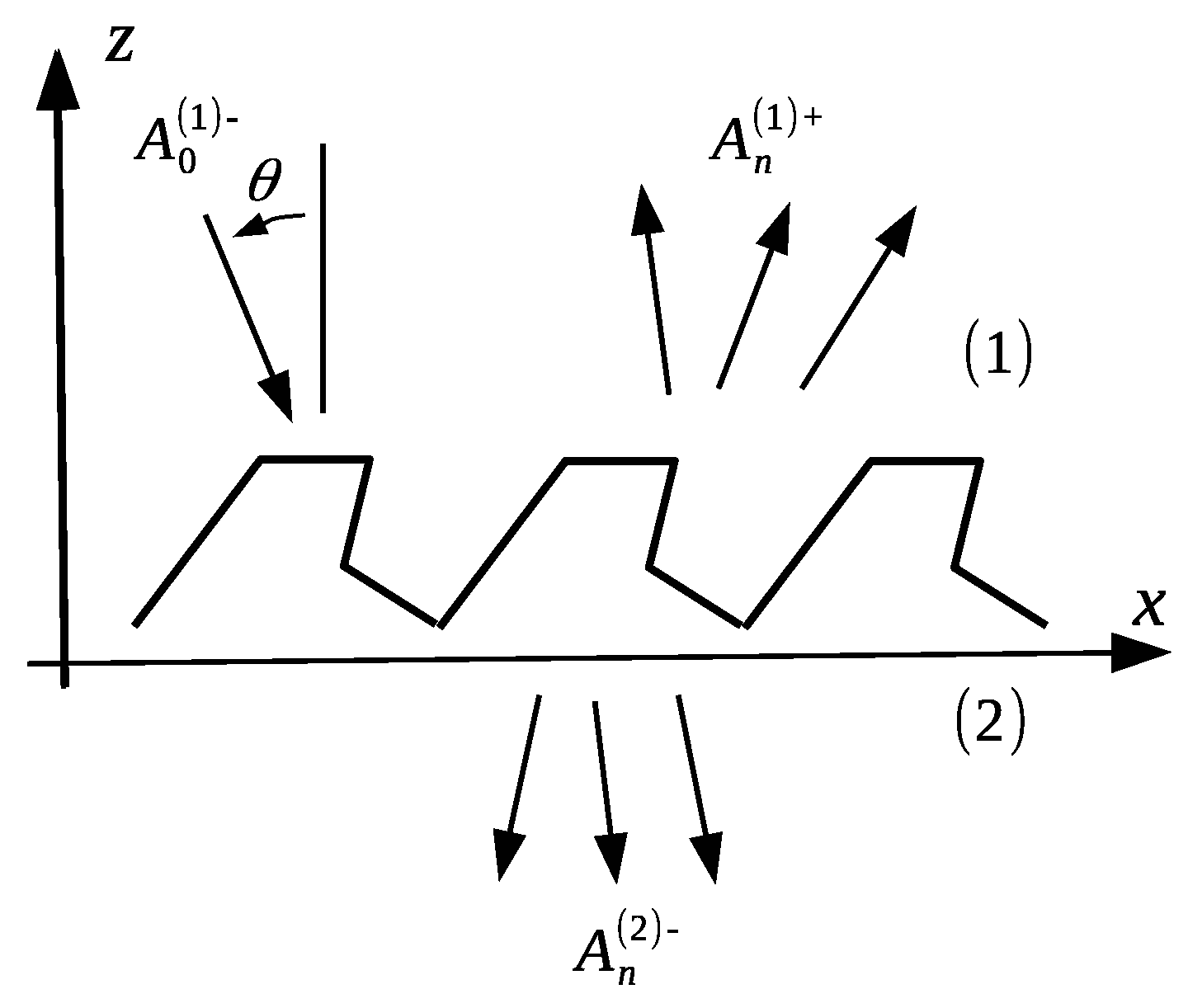
2.1. Geometry of the Profile
2.2. Overview of C-Method
3. Spectral Formulation of the Problem with C-Method
3.1. Maxwell’s Equations under the Covariant Form
3.2. 2D Operator
4. Numerical Solution
4.1. Method of Moments
4.2. Polynomial Basis
4.2.1. Legendre Polynomials
4.2.2. Expansion Basis and Test Basis
Properties of the New Basis
- It has to be emphasized that the test functions are orthogonal to themselves but also to the . Indeed we have:
- The relation (16) between the Legendre polynomials and their derivative may be generalized to the new basis. The inner product generates the following matrix:where the exponent t is for transposition and where is a bloc diagonal matrix constituted of the matrices the dimensions of which are
4.3. Algebraic Eigenequation
4.4. Application to Diffraction Gratings
5. Results
5.1. Validation by Comparison with Published Data
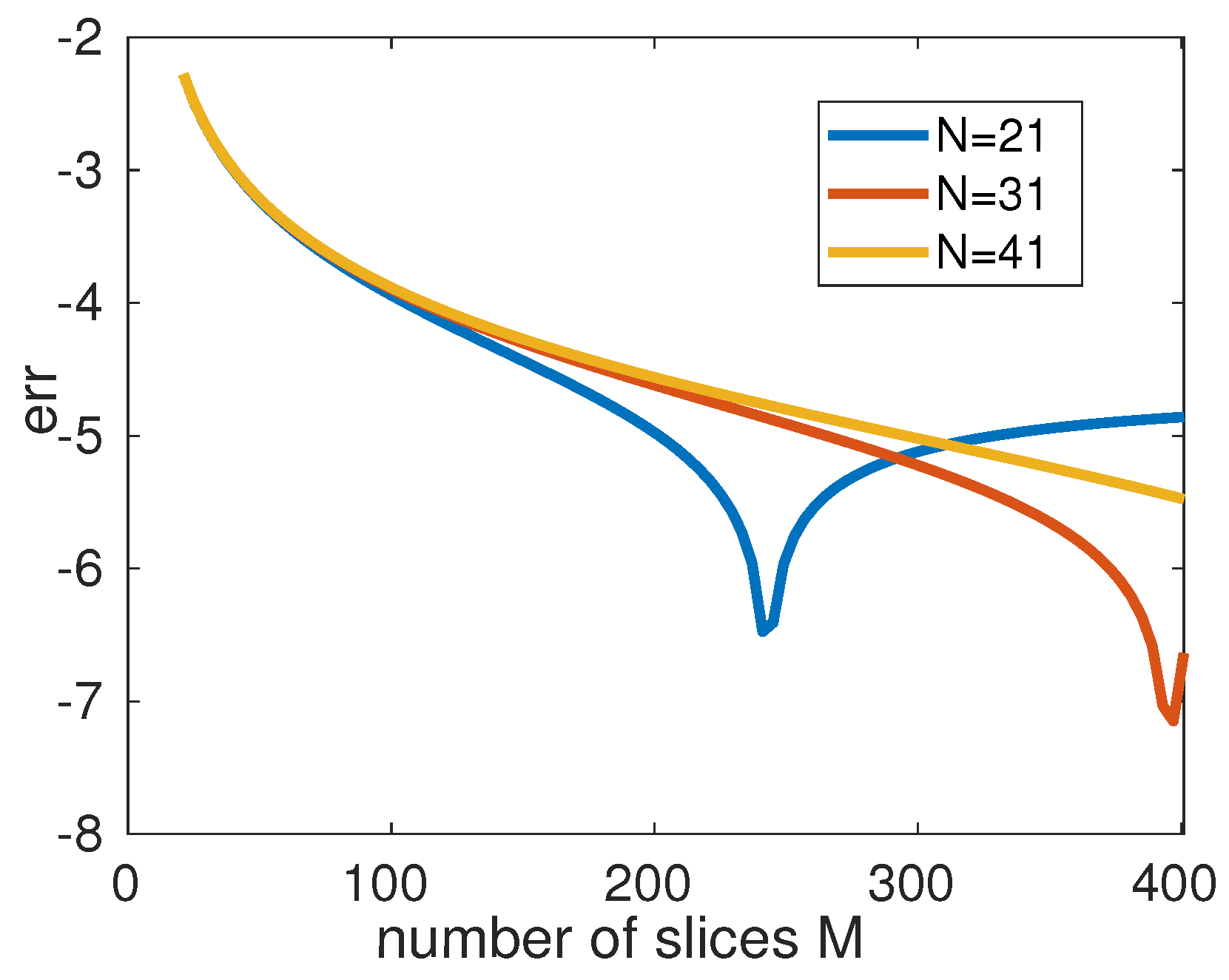
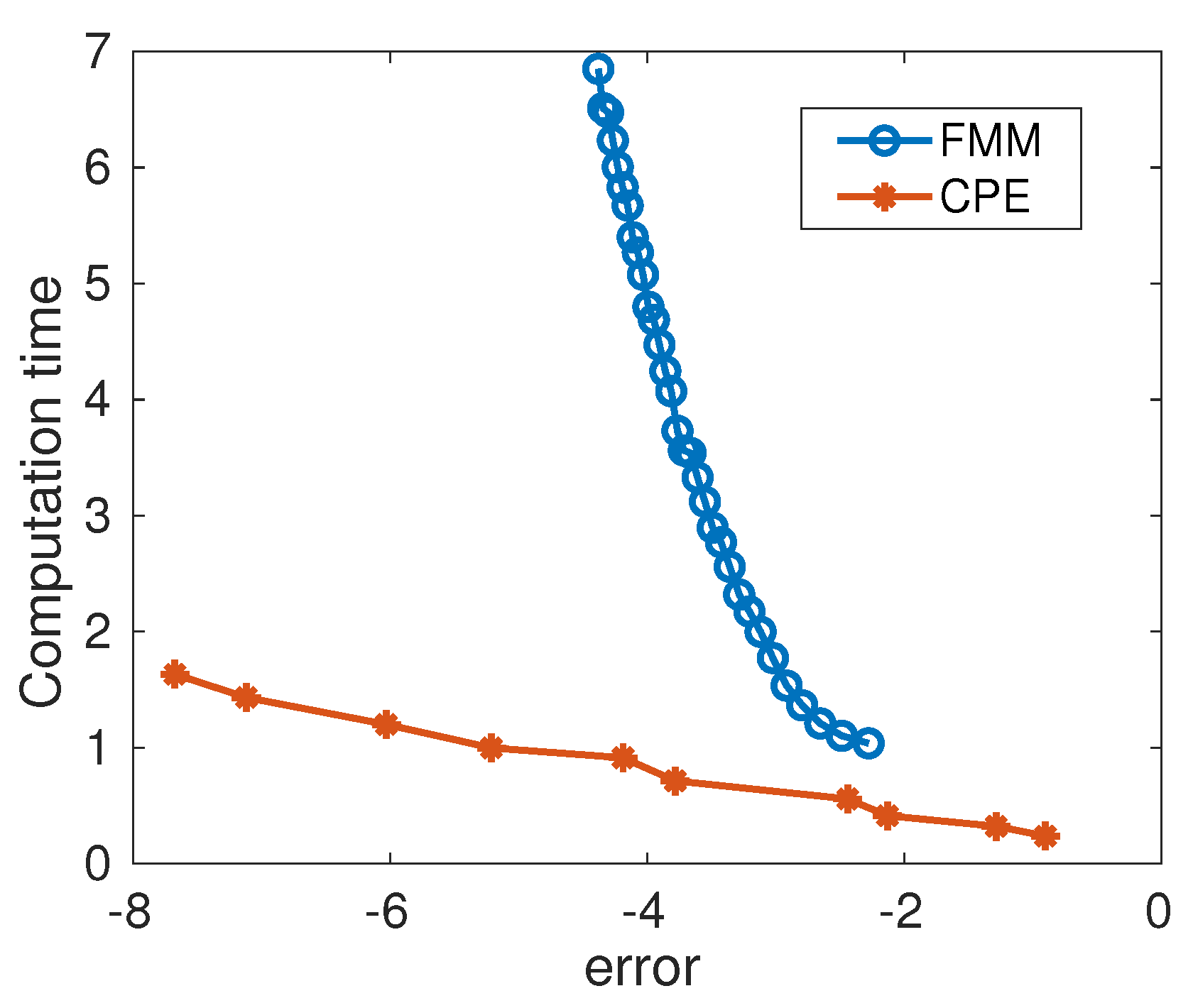
5.2. Comparison of Convergence between FMM and CPE
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Song, Q.; Pigeon, Y.E.; Heggarty, K. Faceted gratings for an optical security feature. Appl. Opt. 2020, 59, 910–917. [Google Scholar] [CrossRef]
- Song, J.; Ding, J.F. Echelle diffraction grating demultiplexers with a single diffraction passband. Opt. Commun. 2010, 283, 537–541. [Google Scholar] [CrossRef]
- Miller, J.M.; de Beaucoudrey, N.; Chavel, P.; Turunen, J.; Cambril, E. Design and fabrication of binary slanted surface-relief gratings for a planar optical interconnection. Appl. Opt. 1997, 36, 5717–5727. [Google Scholar] [CrossRef] [PubMed]
- Mattelin, M.A.; Radosavljevic, A.; Missinne, J.; Cuypers, D.; Steenberge, G.V. Design and fabrication of blazed gratings for a waveguide-type head mounted display. Opt. Express 2020, 28, 11175–11190. [Google Scholar] [CrossRef] [PubMed]
- Popov, E. (Ed.) Gratings: Theory and Numeric Applications, 2nd ed.; AMU, CNRS, Institut Fresnel: Marseille, France, 2014. [Google Scholar]
- Bernd, H.; Kleemann, A.M.; Wyrowski, F. Integral equation method with parametrization of grating profile theory and experiments. J. Mod. Opt. 1996, 43, 1323–1349. [Google Scholar] [CrossRef]
- Chandezon, J.; Raoult, G.; Maystre, D. A new theoretical method for diffraction gratings and its numerical application. J. Opt. 1980, 11, 235. [Google Scholar] [CrossRef]
- Chandezon, J.; Dupuis, M.T.; Cornet, G.; Maystre, D. Multicoated gratings: A differential formalism applicable in the entire optical region. J. Opt. Soc. Am. 1982, 72, 839–846. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of metallic surface-relief gratings. J. Opt. Soc. Am. A 1986, 3, 1780–1787. [Google Scholar] [CrossRef]
- Moharam, M.G.; Grann, E.B.; Pommet, D.A.; Gaylord, T.K. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Lalanne, P.; Morris, G.M. Highly improved convergence of the coupled-wave method for TM polarization. J. Opt. Soc. Am. A 1996, 13, 779–784. [Google Scholar] [CrossRef]
- Granet, G.; Guizal, B. Efficient implementation of the coupled-wave method for metallic lamellar gratings in TM polarization. J. Opt. Soc. Am. A 1996, 13, 1019–1023. [Google Scholar] [CrossRef]
- Li, L. Use of Fourier series in the analysis of discontinuous periodic structures. J. Opt. Soc. Am. A 1996, 13, 1870–1876. [Google Scholar] [CrossRef]
- Li, L.; Chandezon, J. Improvement of the coordinate transformation method for surface-relief gratings with sharp edges. J. Opt. Soc. Am. A 1996, 13, 2247–2255. [Google Scholar] [CrossRef]
- Morf, R.H. Exponentially convergent and numerically efficient solution of Maxwell’s equations for lamellar gratings. J. Opt. Soc. Am. A 1995, 12, 1043–1056. [Google Scholar] [CrossRef]
- Edee, K.; Fenniche, I.; Granet, G.; Guizal, B. Modal method based on subsectional Gegenbauer polynomial expansion for lamellar gratings: Weighting function, convergence and stability. Prog. Electromagn. Res. 2013, 133, 13–35. [Google Scholar] [CrossRef]
- Granet, G.; Randriamihaja, M.H.; Raniriharinosy, K. Polynomial modal analysis of slanted lamellar gratings. J. Opt. Soc. Am. A 2017, 34, 975–982. [Google Scholar] [CrossRef]
- Edee, K.; Plumey, J.P. Numerical scheme for the modal method based on subsectional Gegenbauer polynomial expansion: Application to biperiodic binary grating. J. Opt. Soc. Am. A 2015, 32, 402–410. [Google Scholar] [CrossRef]
- Plumey, J.P.; Guizal, B.; Chandezon, J. Coordinate transformation method as applied to asymmetric gratings with vertical facets. J. Opt. Soc. Am. A 1997, 14, 610–617. [Google Scholar] [CrossRef]
- Preist, T.W.; Harris, J.B.; Wanstall, N.P.; Sambles, J.R. Optical response of blazed and overhanging gratings using oblique chandezon transformations. J. Mod. Opt. 1997, 44, 1073–1080. [Google Scholar] [CrossRef]
- Li, L. Oblique-coordinate-system-based Chandezon method for modeling one-dimensionally periodic, multilayer, inhomogeneous, anisotropic gratings. J. Opt. Soc. Am. A 1999, 16, 2521–2531. [Google Scholar] [CrossRef]
- Ming, X.; Sun, L. Simple reformulation of the coordinate transformation method for gratings with a vertical facet or overhanging profile. Appl. Opt. 2021, 60, 4305–4314. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Chandezon, J.; Granet, G.; Plumey, J.P. Rigorous and efficient grating-analysis method made easy for optical engineers. Appl. Opt. 1999, 38, 304–313. [Google Scholar] [CrossRef] [PubMed]
- Plumey, J.P.; Granet, G. Generalization of the coordinate transformation method with application to surface-relief gratings. J. Opt. Soc. Am. A 1999, 16, 508–516. [Google Scholar] [CrossRef]
- Harrington, R.; Antennas, I.; Society, P. Field Computation by Moment Methods; IEEE Press Series on Electromagnetic Waves; IEEE: New York, NY, USA, 1996. [Google Scholar]



| Orders | C-Method (a) | FMM (a) | CPE | |||
|---|---|---|---|---|---|---|
| D | LD | D | LD | D | LD | |
| TE polarization | ||||||
| 0.04506 | 0.23791 | 0.04502 | 0.23602 | 0.45071 | 0.23869 | |
| 0.00316 | 0.31502 | 0.00315 | 0.30576 | 0.00316 | 0.31410 | |
| 0.00019 | 0.10992 | 0.00019 | 0.10593 | 0.00020 | 0.10922 | |
| 0.35193 | 0.35197 | 0.35199 | ||||
| 0.02459 | 0.02459 | 0.02459 | ||||
| 0.5659 | 0.56594 | 0.56591 | ||||
| 0.00913 | 0.00912 | 0.00913 | ||||
| TM polarization | ||||||
| 0.03438 | 0.45797 | 0.03418 | 0.42275 | 0.03445 | 0.45382 | |
| 0.00114 | 0.14879 | 0.00111 | 0.14854 | 0.00115 | 0.15215 | |
| 0.00004 | 0.00841 | 0.00004 | 0.00322 | 0.00005 | 0.00616 | |
| 0.11085 | 0.11061 | 0.11087 | ||||
| 0.16566 | 0.16515 | 0.16569 | ||||
| 0.68405 | 0.68501 | 0.68396 | ||||
| 0.00384 | 0.00389 | 0.00386 | ||||
| Orders | C-Method (a) | CPE |
|---|---|---|
| TE polarization | ||
| 0.1156 (−1) | 0.01162 | |
| 0.3981 (−2) | 0.00397 | |
| 0.2673 (−3) | 0.00270 | |
| 0.9877 (−1) | 0.98399 | |
| 0.4771 | 0.47659 | |
| 0.9975 (−1) | 0.09944 | |
| 0.2685 | 0.26885 | |
| 0.3831 (−1) | 0.03428 | |
| TM polarization | ||
| 0.5258 (−2) | 0.00523 | |
| 0.3197 (−2) | 0.00320 | |
| 0.5832 (−3) | 0.00058 | |
| 0.3419 (−1) | 0.03405 | |
| 0.7470 | 0.74813 | |
| 0.4760 (−1) | 0.04749 | |
| 0.1502 | 0.15022 | |
| 0.1240 (−1) | 0.01239 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Granet, G.; Edee, K. Analysis of Faceted Gratings Using C-Method and Polynomial Expansion. Photonics 2024, 11, 215. https://doi.org/10.3390/photonics11030215
Granet G, Edee K. Analysis of Faceted Gratings Using C-Method and Polynomial Expansion. Photonics. 2024; 11(3):215. https://doi.org/10.3390/photonics11030215
Chicago/Turabian StyleGranet, Gérard, and Kofi Edee. 2024. "Analysis of Faceted Gratings Using C-Method and Polynomial Expansion" Photonics 11, no. 3: 215. https://doi.org/10.3390/photonics11030215
APA StyleGranet, G., & Edee, K. (2024). Analysis of Faceted Gratings Using C-Method and Polynomial Expansion. Photonics, 11(3), 215. https://doi.org/10.3390/photonics11030215





