Quantum Dynamics of Cavity–Bose–Einstein Condensates in a Gravitational Field
Abstract
1. Introduction
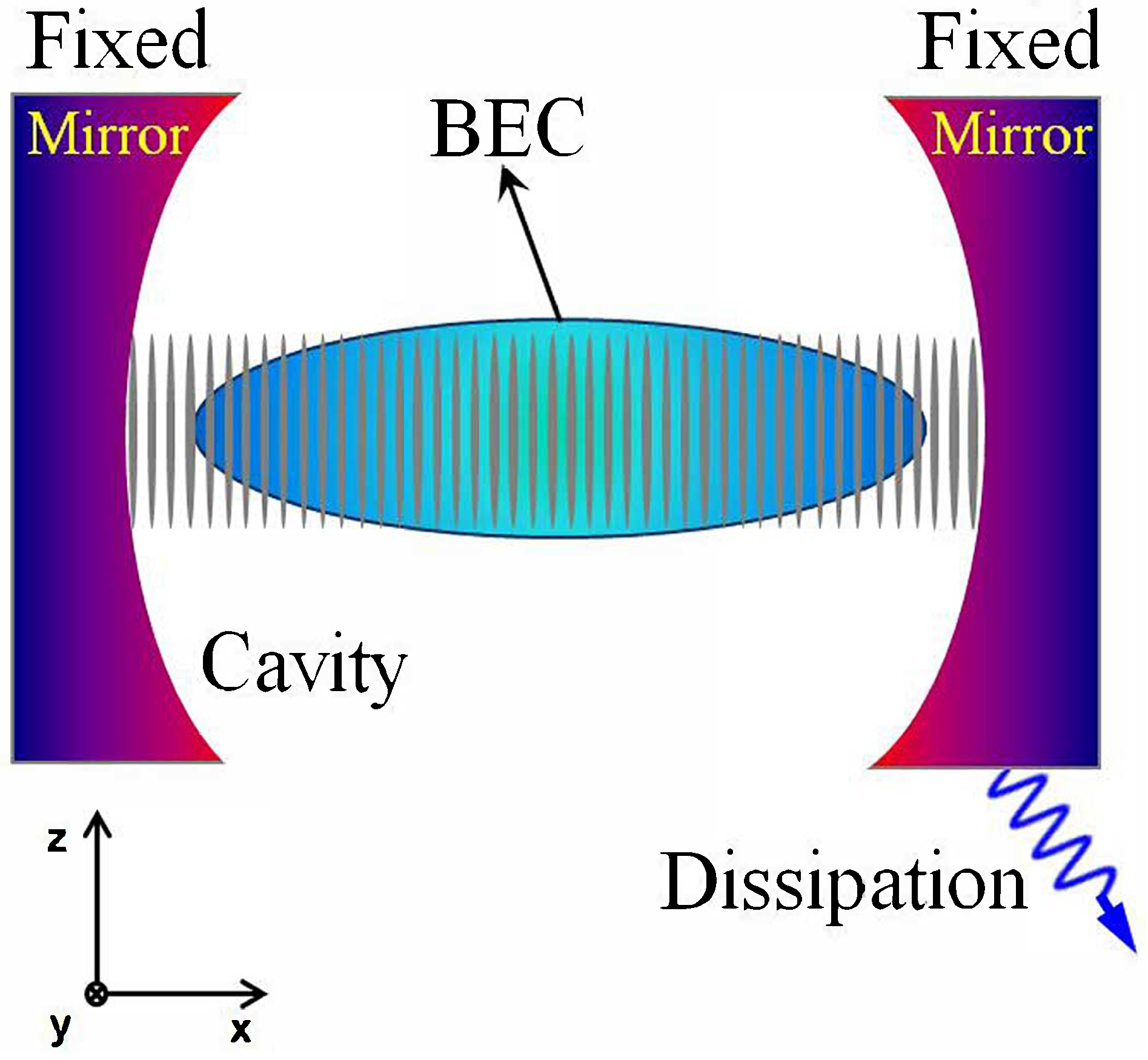
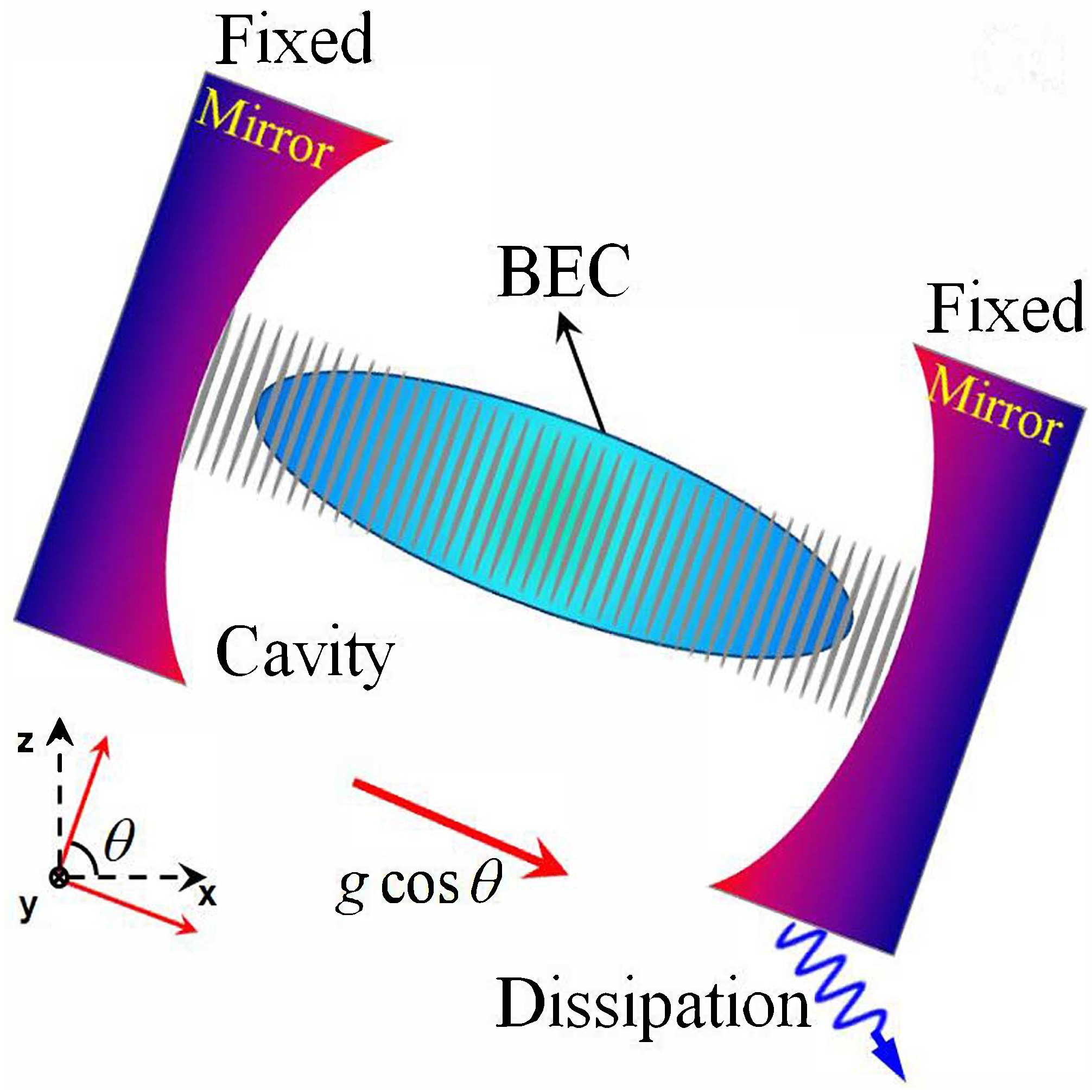
2. Physical Model and Solution
2.1. System Hamiltonian
2.2. The Eigenvalues and Eigenstates of the System
3. Dynamical Characteristics of the System
3.1. State Vector Dynamics
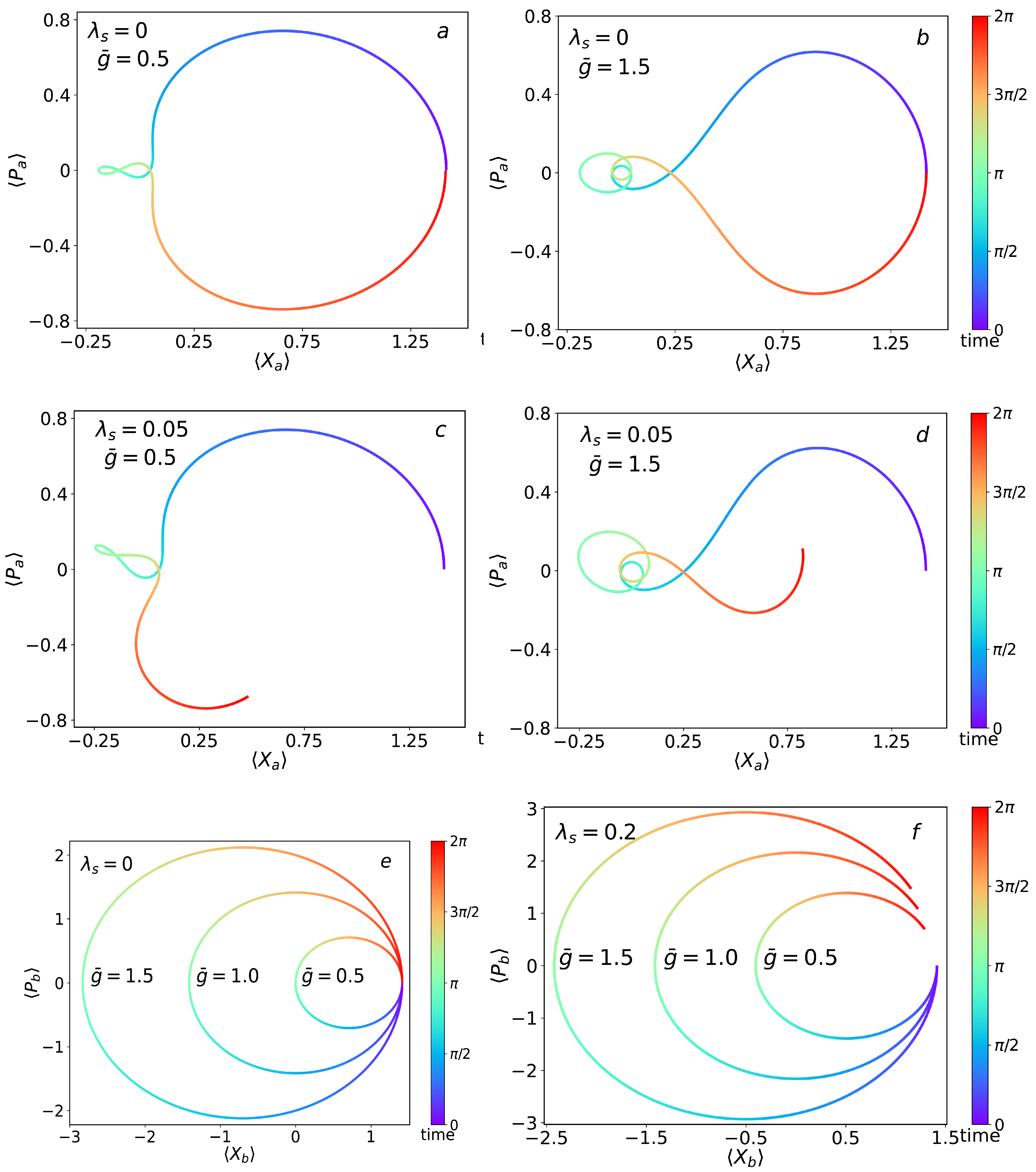
3.2. Time Trajectories in Phase Space
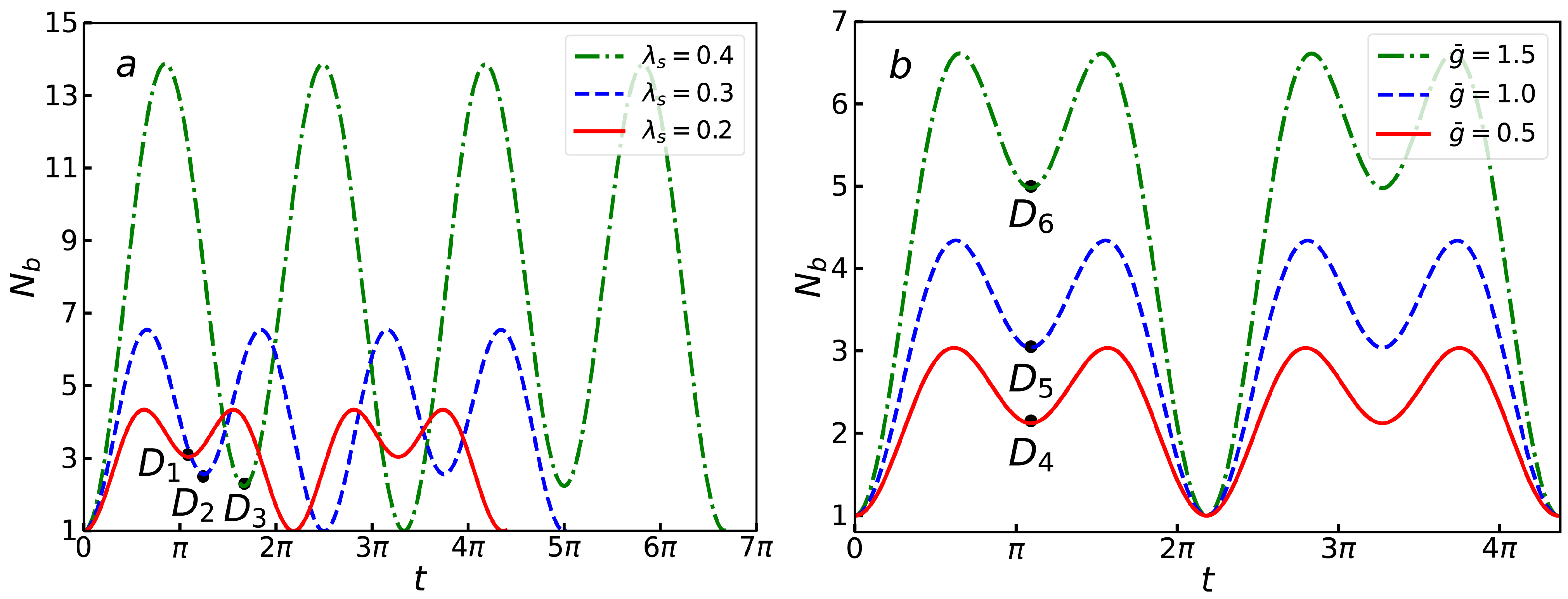
3.3. Excitation Number Dynamics
3.4. Transient Cat States
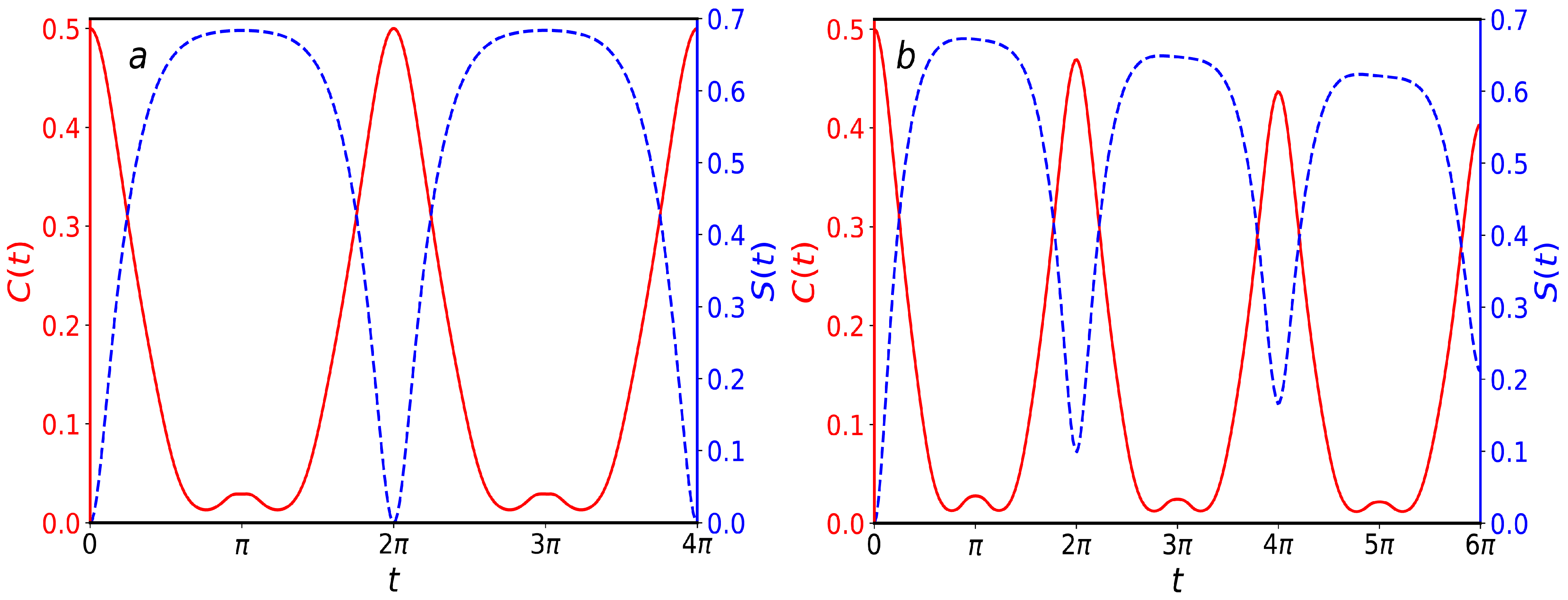
4. Quantum Resource Dynamics
4.1. Quantum Entanglement Dynamics
4.2. Quantum Coherence Dynamics
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Diagonalization of the Hamiltonian Htot
Appendix A.1. The First Step of Diagonalization
Appendix A.2. The Second Step of Diagonalization
References
- Hillenbr, R.; Taubner, T.; Keilmann, F. Phonon-enhanced light–matter interaction at the nanometre scale. Nature 2002, 418, 159–162. [Google Scholar] [CrossRef]
- Rivera, N.; Kaminer, I. Light–matter interactions with photonic quasiparticles. Nat. Rev. Phys. 2020, 2, 538–561. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005. [Google Scholar] [CrossRef]
- Brennecke, F.; Ritter, S.; Donner, T.; Esslinger, T. Cavity optomechanics with a Bose-Einstein condensate. Science 2008, 322, 235–238. [Google Scholar] [CrossRef]
- Robb, G.R.M.; Tesio, E.; Oppo, G.L.; Firth, W.J.; Ackemann, T.; Bonifacio, R. Quantum threshold for optomechanical self-structuring in a Bose-Einstein condensate. Phys. Rev. Lett. 2015, 114, 173903. [Google Scholar]
- Murch, K.W.; Moore, K.L.; Gupta, S.; Stamper-Kurn, D.M. Observation of quantum-measurement backaction with an ultracold atomic gas. Nat. Phys. 2008, 4, 561–564. [Google Scholar] [CrossRef]
- Chauhan, A.K.; Biswas, A. Motion-induced enhancement of Rabi coupling between atomic ensembles in cavity optomechanics. Phys. Rev. A 2017, 95, 023813. [Google Scholar]
- Gong, Z.R.; Ian, H.; Liu, Y.X.; Sun, C.P.; Nori, F. Effective Hamiltonian approach to the Kerr nonlinearity in an optomechanical system. Phys. Rev. A 2009, 80, 065801. [Google Scholar] [CrossRef]
- Mancini, S.; Tombesi, P. Quantum noise reduction by radiation pressure. Phys. Rev. A 1994, 49, 4055. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H. Intrinsic cross-Kerr nonlinearity in an optical cavity containing an interacting Bose-Einstein condensate. Phys. Rev. A 2017, 95, 043601. [Google Scholar] [CrossRef]
- Pirkkalainen, J.M.; Cho, S.U.; Massel, F.; Tuorila, J.; Heikkilä, T.T.; Hakonen, P.J.; Sillanpää, M.A. Cavity optomechanics mediated by a quantum two-level system. Nat. Commun. 2015, 6, 6981. [Google Scholar] [CrossRef]
- Huang, S.; Agarwal, G.S. Normal-mode splitting in a coupled system of a nanomechanical oscillator and a parametric amplifier cavity. Phys. Rev. A 2009, 80, 033807. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H.; Soltanolkotabi, M.; Barzanjeh, S. Nonlinear effects of atomic collisions on the optomechanical properties of a Bose-Einstein condensate in an optical cavity. Phys. Rev. A 2013, 87, 013417. [Google Scholar] [CrossRef]
- Kazemi, S.H.; Ghanbari, S.; Mahmoudi, M. Controllable optical bistability in a cavity optomechanical system with a Bose–Einstein condensate. Laser Phys. 2016, 26, 055502. [Google Scholar] [CrossRef]
- Gothe, H.; Valenzuela, T.; Cristiani, M.; Eschner, J. Optical bistability and nonlinear dynamics by saturation of cold Yb atoms in a cavity. Phys. Rev. A 2019, 99, 013849. [Google Scholar] [CrossRef]
- Li, Z.; Lu, W. Antibunching Effects in the Hybrid Cavity–Bose–Einstein Condensates System. Photonics 2023, 10, 123. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H. Controlling steady-state bipartite entanglement and quadrature squeezing in a membrane-in-the-middle optomechanical system with two Bose-Einstein condensates. Phys. Rev. A 2017, 96, 033631. [Google Scholar] [CrossRef]
- Motazedifard, A.; Dalafi, A.; Naderi, M.H.; Roknizadeh, R. Strong quadrature squeezing and quantum amplification in a coupled Bose–Einstein condensate—optomechanical cavity based on parametric modulation. Ann. Phys. 2019, 405, 202–219. [Google Scholar] [CrossRef]
- Yasir, K.A.; Zhuang, L.; Liu, W.M. Spin-orbit-coupling-induced backaction cooling in cavity optomechanics with a Bose-Einstein condensate. Phys. Rev. A 2017, 95, 013810. [Google Scholar] [CrossRef]
- Jiang, C.; Cui, Y.; Zhai, Z.; Yu, H.; Li, X.; Chen, G. Tunable slow and fast light in parity-time-symmetric optomechanical systems with phonon pump. Opt. Express 2018, 26, 28834–28847. [Google Scholar] [CrossRef]
- Bochmann, J.; Vainsencher, A.; Awschalom, D.D.; Clel, A.N. Nanomechanical coupling between microwave and optical photons. Nat. Phys. 2013, 9, 712–716. [Google Scholar] [CrossRef]
- Sohn, D.B.; Kim, S.; Bahl, G. Time-reversal symmetry breaking with acoustic pumping of nanophotonic circuits. Nat. Photonics 2018, 12, 91–97. [Google Scholar] [CrossRef]
- Morsch, O.; Oberthaler, M. Dynamics of Bose-Einstein condensates in optical lattices. Rev. Mod. Phys. 2006, 78, 179. [Google Scholar] [CrossRef]
- Maschler, C.; Ritsch, H. Quantum motion of laser-driven atoms in a cavity field. Opt. Commun. 2004, 243, 145–155. [Google Scholar] [CrossRef]
- Motazedifard, A.; Dalafi, A.; Bemani, F.; Naderi, M.H. Force sensing in hybrid Bose-Einstein-condensate optomechanics based on parametric amplification. Phys. Rev. A 2019, 100, 023815. [Google Scholar] [CrossRef]
- Timmermans, E.; Tommasini, P.; Hussein, M.; Kerman, A. Feshbach resonances in atomic Bose–Einstein condensates. Phys. Rep. 1999, 315, 199–230. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Maschler, C.; Ritsch, H. Cold atom dynamics in a quantum optical lattice potential. Phys. Rev. Lett. 2005, 95, 260401. [Google Scholar] [CrossRef]
- Nagy, D.; Domokos, P.; Vukics, A.; Ritsch, H. Nonlinear quantum dynamics of two BEC modes dispersively coupled by an optical cavity. Eur. Phys. J. D 2009, 55, 659–668. [Google Scholar] [CrossRef]
- Scala, M.; Kim, M.S.; Morley, G.W.; Barker, P.F.; Bose, S. Matter-wave interferometry of a levitated thermal nano-oscillator induced and probed by a spin. Phys. Rev. Lett. 2013, 111, 180403. [Google Scholar] [CrossRef]
- Qvarfort, S.; Serafini, A.; Barker, P.F.; Bose, S. Gravimetry through nonlinear optomechanics. Nat. Commun. 2018, 9, 3690. [Google Scholar] [CrossRef]
- Qvarfort, S.; Plato, A.D.; Bruschi, D.E.; Schneiter, F.; Braun, D.; Serafini, A.; Rätzel, D. Optimal estimation of time-dependent gravitational fields with quantum optomechanical systems. Phys. Rev. Res. 2021, 3, 013159. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13. [Google Scholar] [CrossRef]
- Liao, J.Q.; Tian, L. Macroscopic quantum superposition in cavity optomechanics. Phys. Rev. Lett. 2016, 116, 163602. [Google Scholar] [CrossRef]
- Lee, K.S.; Kim, M.S.; Bŭzek, V. Amplification of multicomponent superpositions of coherent states of light with quantum amplifiers. JOSA B 1994, 11, 1118–1129. [Google Scholar] [CrossRef]
- Huang, Y.; Tan, Q.S.; Fu, L.B.; Wang, X. Coherence dynamics of a two-mode Bose-Einstein condensate coupled with the environment. Phys. Rev. A 2013, 88, 063642. [Google Scholar] [CrossRef]
- Li, Z.; Kuang, L.M. Controlling quantum coherence of a two-component Bose–Einstein condensate via an impurity atom. Quantum Inf. Process. 2020, 19, 188. [Google Scholar] [CrossRef]
- Chitambar, E.; Gour, G. Quantum resource theories. Rev. Mod. Phys. 2019, 91, 025001. [Google Scholar] [CrossRef]
- Hu, M.L.; Hu, X.; Wang, J.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762, 1–100. [Google Scholar] [CrossRef]
- Jack, M.W. Effect of atom loss on collapse and revivals of phase coherence in small atomic samples. Phys. Rev. A 2003, 67, 043612. [Google Scholar] [CrossRef]
- Jack, M.W. Decoherence due to three-body loss and its effect on the state of a Bose-Einstein condensate. Phys. Rev. Lett. 2002, 89, 140402. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Fu, L.B.; Yi, X.X. Effect of decoherence on the dynamics of Bose-Einstein condensates in a double-well potential. Phys. Rev. A 2007, 75, 045601. [Google Scholar] [CrossRef]
- Johansson, J.R.; Nation, P.D.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760–1772. [Google Scholar] [CrossRef]
- Johansson, J.R.; Nation, P.D.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H.; Motazedifard, A. Effects of quadratic coupling and squeezed vacuum injection in an optomechanical cavity assisted with a Bose-Einstein condensate. Phys. Rev. A 2018, 97, 043619. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H. Dispersive interaction of a Bose-Einstein condensate with a movable mirror of an optomechanical cavity in the presence of laser phase noise. Phys. Rev. A 2016, 94, 063636. [Google Scholar] [CrossRef]
- Murakami, Y.; Tsuji, N.; Eckstein, M.; Werner, P. Nonequilibrium steady states and transient dynamics of conventional superconductors under phonon driving. Phys. Rev. B 2017, 96, 045125. [Google Scholar] [CrossRef]
- Levitan, B.A.; Metelmann, A.; Clerk, A.A. Optomechanics with two-phonon driving. New J. Phys. 2016, 18, 093014. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lu, W.-J.; Jiao, Y.-F. Quantum Dynamics of Cavity–Bose–Einstein Condensates in a Gravitational Field. Photonics 2024, 11, 205. https://doi.org/10.3390/photonics11030205
Li Z, Lu W-J, Jiao Y-F. Quantum Dynamics of Cavity–Bose–Einstein Condensates in a Gravitational Field. Photonics. 2024; 11(3):205. https://doi.org/10.3390/photonics11030205
Chicago/Turabian StyleLi, Zhen, Wang-Jun Lu, and Ya-Feng Jiao. 2024. "Quantum Dynamics of Cavity–Bose–Einstein Condensates in a Gravitational Field" Photonics 11, no. 3: 205. https://doi.org/10.3390/photonics11030205
APA StyleLi, Z., Lu, W.-J., & Jiao, Y.-F. (2024). Quantum Dynamics of Cavity–Bose–Einstein Condensates in a Gravitational Field. Photonics, 11(3), 205. https://doi.org/10.3390/photonics11030205




