Design Optimization of Silicon-Based Optically Excited Terahertz Wave Modulation
Abstract
1. Introduction
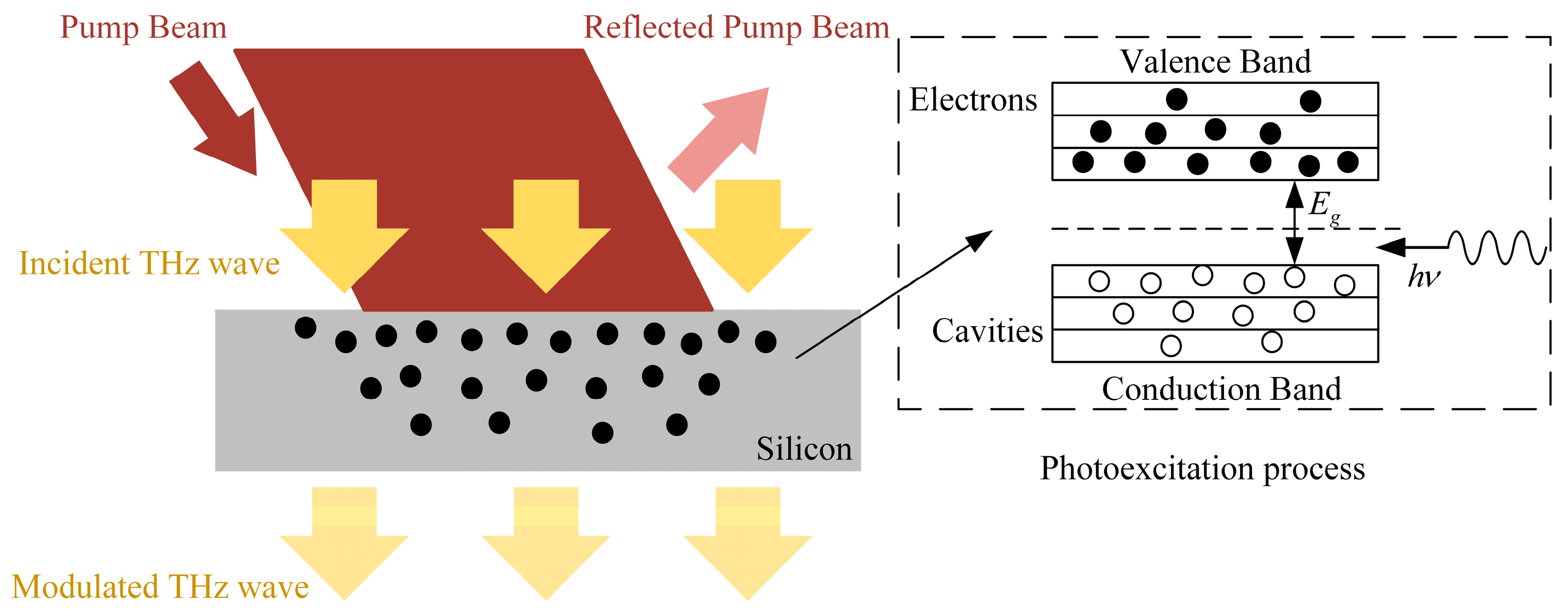
2. Principle of Silicon-Based Optically Excited THz Modulator
2.1. The Drude Model
2.2. The Complex Refractive Index of Excited High-Resistance Silicon
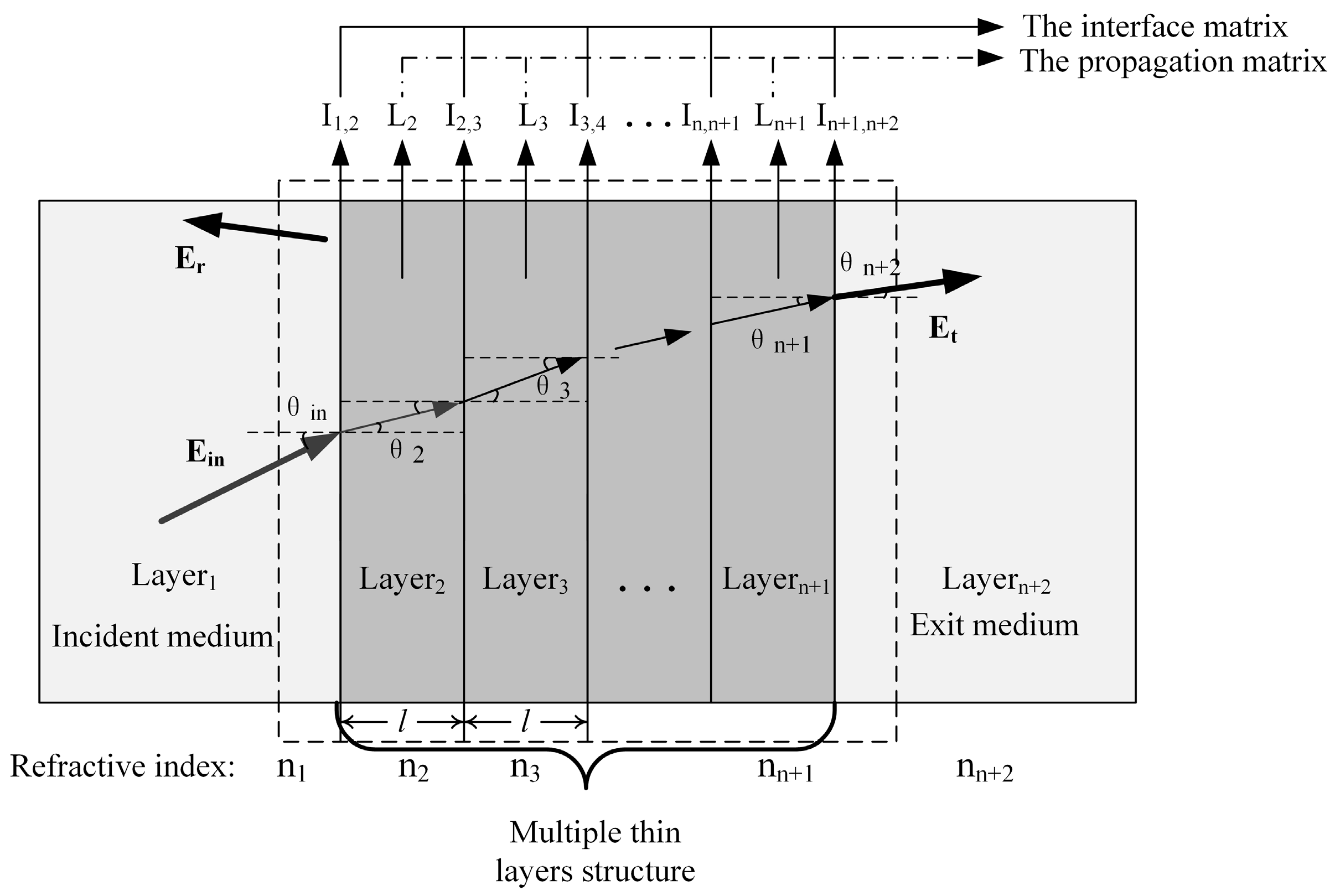
2.3. The Transmittance and Reflectance of THz Waves
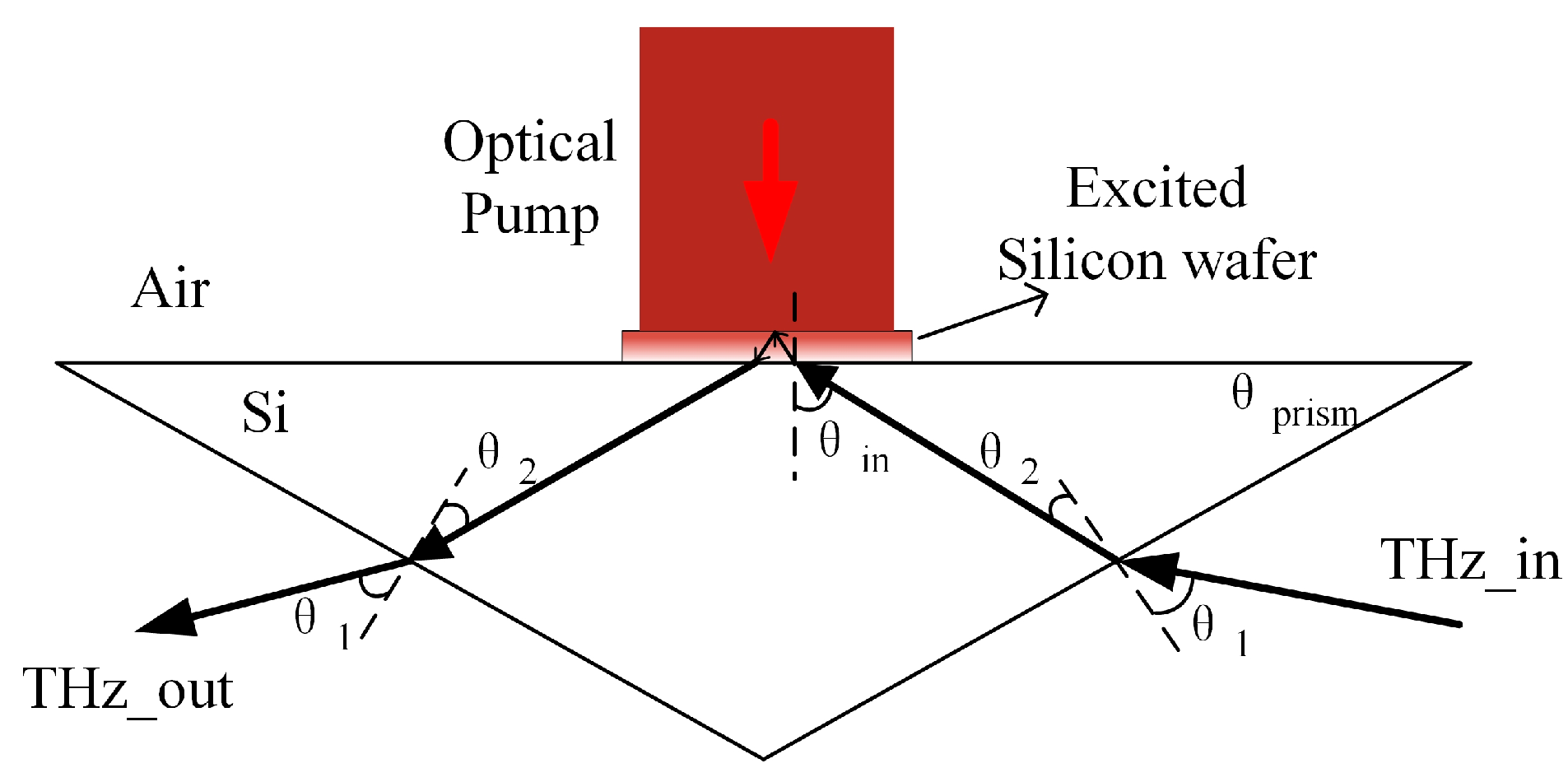
3. Simulation of a Silicon-Based Optically Excited THz Modulator
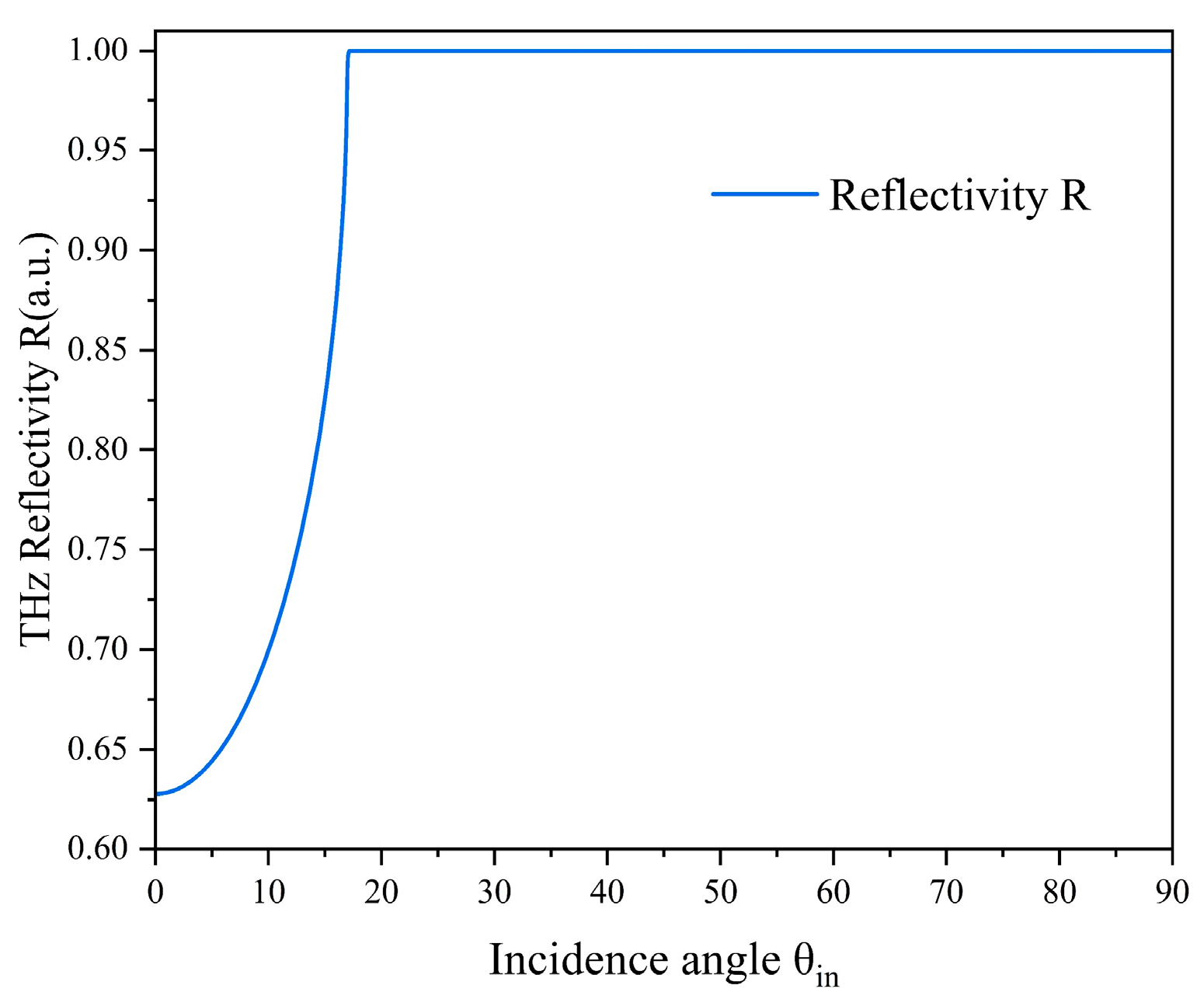
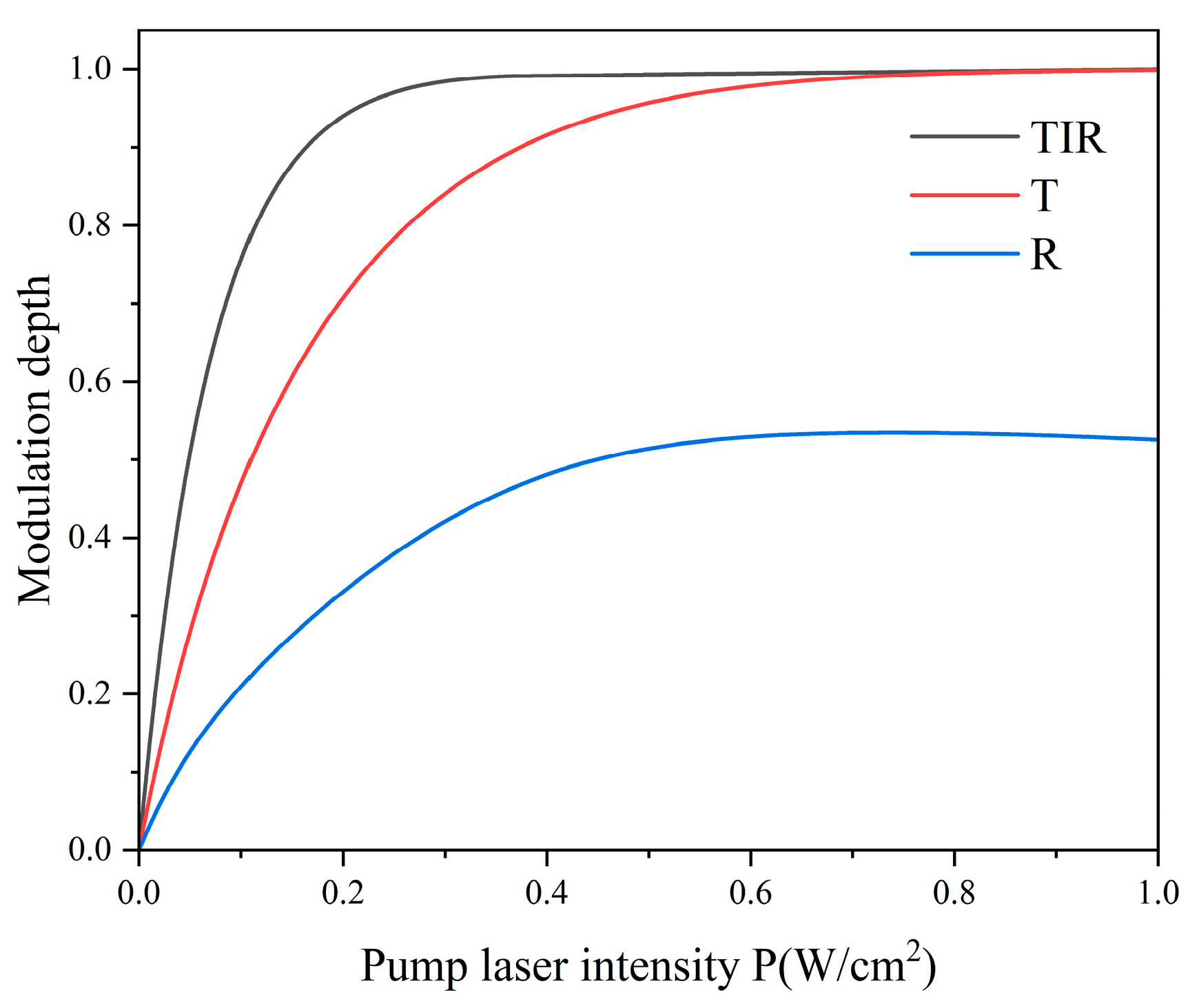
3.1. The Transmittance and Reflectance of THz Waves
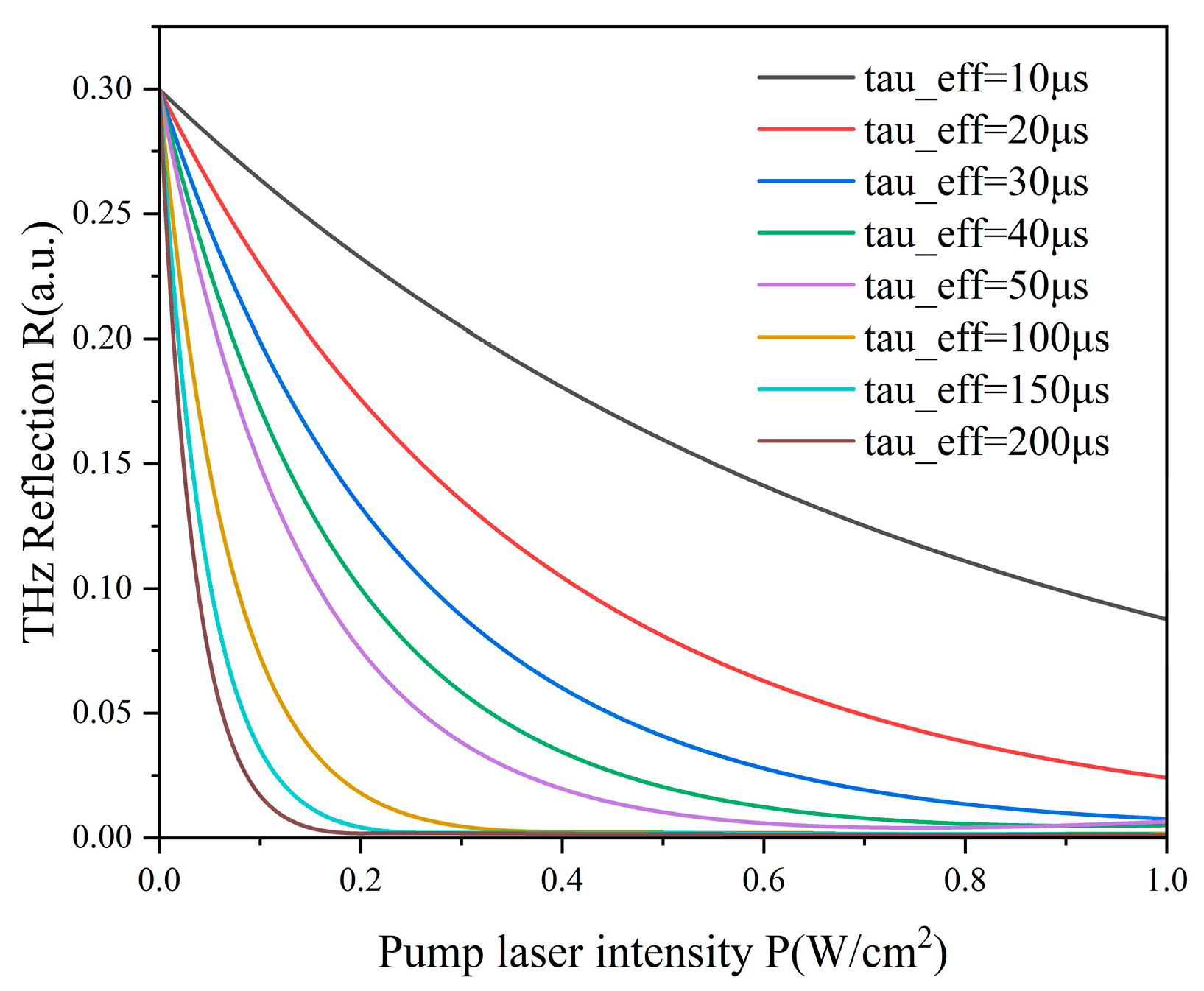
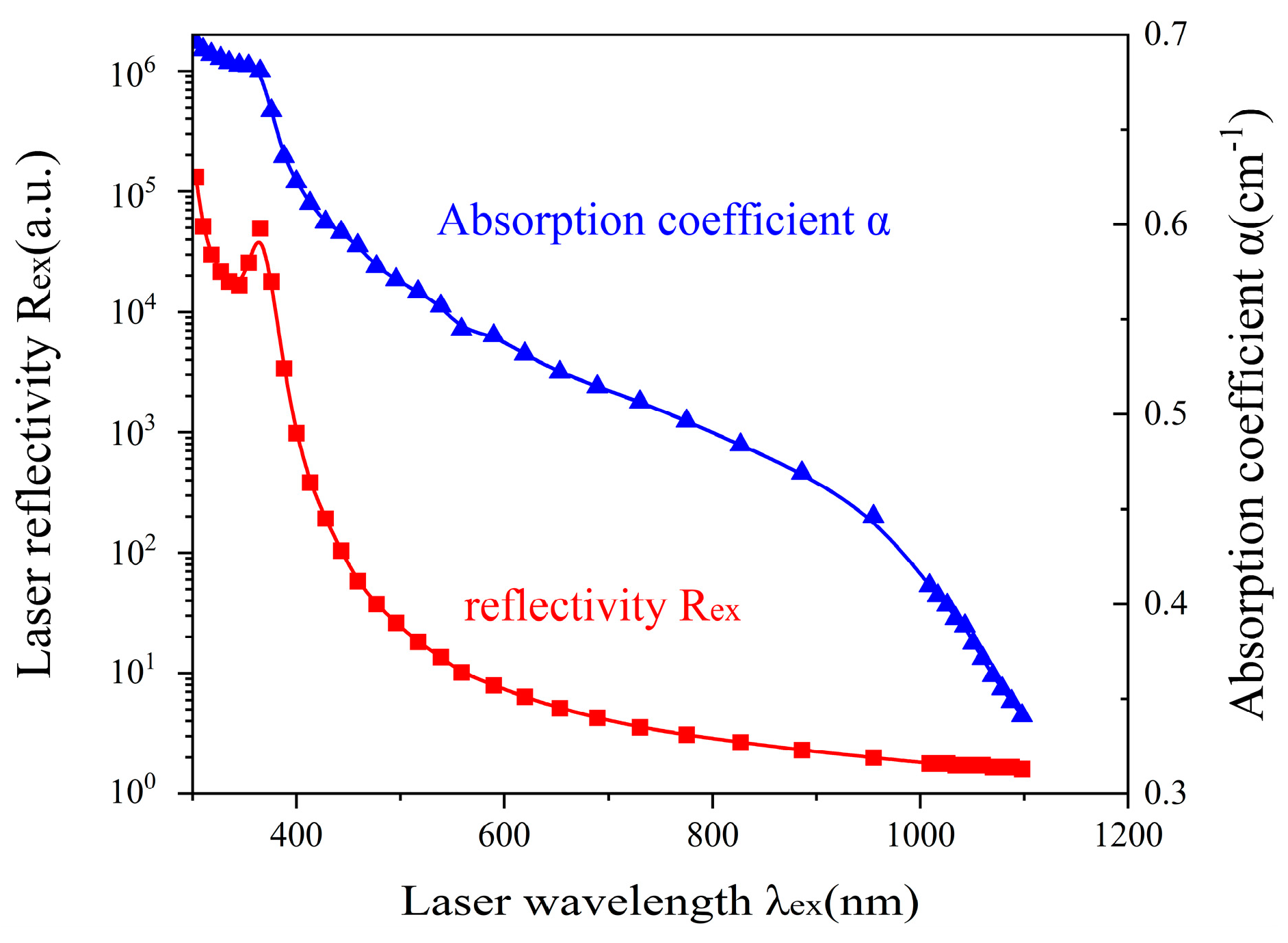
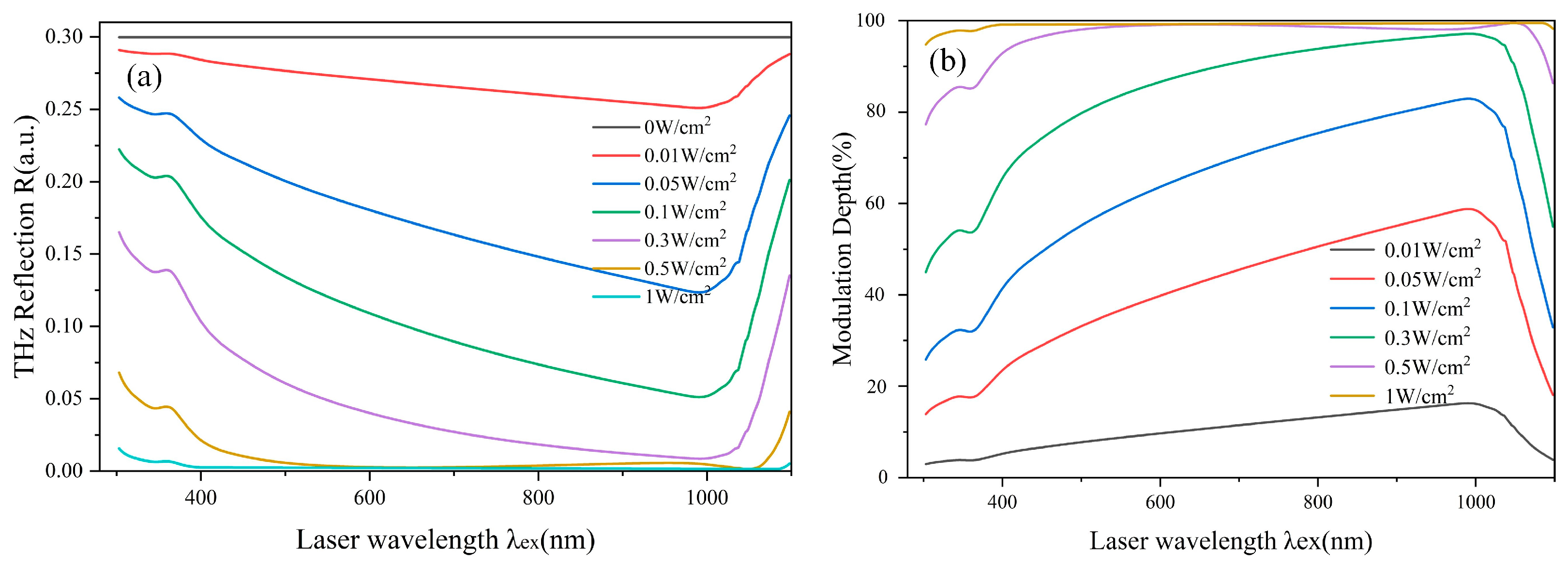
3.2. The Influence of Different Physical Parameters on the Performance of THz Modulator
- Photogenerated carrier lifetime
- 2.
- Excitation light wavelength
- 3.
- Incident THz wave frequency
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, H.; Redo-Sanchez, A.; Zhang, X.-C. Identification and classification of chemicals using terahertz reflective spectroscopic focal-plane imaging system. Opt. Express 2006, 14, 9130–9141. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, M.; Kawase, K.; Otani, C.; Kiwa, T.; Tonouchi, M. Imaging of large-scale integrated circuits using laser terahertz emission microscopy. Opt. Express 2005, 13, 115–120. [Google Scholar] [CrossRef] [PubMed]
- Son, J.H. Principle and applications of terahertz molecular imaging. Nanotechnology 2013, 24, 214001. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.; He, Y.; Ung, B.S.; Pickwell-MacPherson, E. The growth of biomedical terahertz research. J. Phys. D-Appl. Phys. 2014, 47, 374009. [Google Scholar] [CrossRef]
- Vamsi, C.S.; Dwivedi, A.K.; Bharti, G.; Verma, V.R.; Sharma, A. Efficient graphene-based circularly polarized MIMO antenna for THz applications. Appl. Opt. 2022, 61, 8155–8161. [Google Scholar] [CrossRef] [PubMed]
- Kleine-Ostmann, T.; Nagatsuma, T. A review on terahertz communications research. J. Infrared Millim. Terahertz Waves 2011, 32, 143–171. [Google Scholar] [CrossRef]
- Wang, X.; Shen, C.; Jiang, T.; Zhan, Z.; Deng, Q.; Li, W.; Wu, W.; Yang, N.; Chu, W.; Duan, S. High-power terahertz quantum cascade lasers with ~0.23 W in continuous wave mode. AIP Adv. 2016, 6, 075210. [Google Scholar] [CrossRef]
- Mehdi, I.; Siles, J.V.; Lee, C.; Schlecht, E. THz diode technology: Status, prospects, and applications. Proc. IEEE 2017, 105, 990–1007. [Google Scholar] [CrossRef]
- Stantchev, R.I.; Phillips, D.B.; Hobson, P.; Hornett, S.M.; Padgett, M.J.; Hendry, E. Compressed sensing with near-field THz radiation. Optica 2017, 4, 989–992. [Google Scholar] [CrossRef]
- Savo, S.; Shrekenhamer, D.; Padilla, W.J. Liquid crystal metamaterial absorber spatial light modulator for THz applications. Adv. Opt. Mater. 2014, 2, 275–279. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, S.; Sun, L.; Shi, Q.W.; Huang, W.; Li, L.; Yang, Z. Photoinduced active terahertz metamaterials with nanostructured vanadium dioxide film deposited by sol-gel method. Opt. Express 2014, 22, 11070–11078. [Google Scholar] [CrossRef]
- Herrmann, E.; Gao, H.; Huang, Z.; Sitaram, S.R.; Ma, K.; Wang, X. Modulators for mid-infrared and terahertz light. J. Appl. Phys. 2020, 128, 140903. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Jaroszewicz, L. Active control of terahertz radiation using a metamaterial loaded with a nematic liquid crystal. Liq. Cryst. 2016, 43, 1120–1125. [Google Scholar] [CrossRef]
- Ramachandran, T.; Faruque, M.R.I.; Islam, M.T.; Khandaker, M.U.; Alqahtani, A.; Bradley, D.A. Development and Analysis of Coding and Tailored Metamaterial for Terahertz Frequency Applications. Materials 2022, 15, 2777. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.; Maeng, I.; Kang, C.; Oh, M.-K.; Kee, C.-S. Strong polarization-dependent terahertz modulation of aligned Ag nanowires on Si substrate. Opt. Express 2018, 26, 13677–13685. [Google Scholar] [CrossRef] [PubMed]
- She, R.; Liu, W.; Wei, G.; Lu, Y.; Li, G. Terahertz single-pixel imaging improved by using silicon wafer with SiO2 passivation. Appl. Sci. 2020, 10, 2427. [Google Scholar] [CrossRef]
- Wu, X.; Pan, X.; Quan, B.; Wang, L. Optical modulation of terahertz behavior in silicon with structured surfaces. Appl. Phys. Lett. 2013, 103, 121112. [Google Scholar] [CrossRef]
- Kamaraju, N.; Rubano, A.; Jian, L.; Saha, S.; Venkatesan, T.; Nötzold, J. Subcycle control of terahertz waveform polarization using all-optically induced transient metamaterials. Light-Sci. Appl. 2014, 3, e155. [Google Scholar] [CrossRef]
- Guan, S.; Cheng, J.; Chang, S. Recent progress of terahertz spatial light modulators: Materials, principles and applications. Micromachines 2022, 13, 1637. [Google Scholar] [CrossRef]
- He, J.W.; Wang, X.K.; Xie, Z.W.; Xue, Y.Z.; Wang, S.; Zhang, Y. Reconfigurable terahertz grating with enhanced transmission of TE polarized light. APL Photonics 2017, 2, 076102. [Google Scholar] [CrossRef]
- Guo, J.; Wang, T.; Zhao, H.; Wang, X.; Feng, S.; Han, P.; Sun, W.; Ye, J.; Situ, G.; Chen, H.; et al. Reconfigurable terahertz metasurface pure phase holograms. Adv. Opt. Mater. 2019, 7, 1801696. [Google Scholar] [CrossRef]
- Shams, I.B.; Jiang, Z.; Rahman, S.M.; Cheng, L.-J.; Hesler, J.L.; Fay, P.; Liu, L. A 740-GHz dynamic two-dimensional beam-steering and forming antenna based on photo-induced reconfigurable Fresnel zone plates. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 310–319. [Google Scholar] [CrossRef]
- Sun, Q.; Chen, X.; Liu, X.; Stantchev, R.I.; Pickwell-MacPherson, E. Exploiting total internal reflection geometry for terahertz devices and enhanced sample characterization. Adv. Opt. Mater. 2020, 8, 1900535. [Google Scholar] [CrossRef]
- Liu, X.; Parrott, E.P.J.; Ung, B.S.-Y.; Pickwell-MacPherson, E. Exploiting total internal reflection geometry for efficient optical modulation of terahertz light. APL Photonics 2016, 1, 076103. [Google Scholar] [CrossRef]
- Stantchev, R.I.; Yu, X.; Blu, T.; Pickwell-MacPherson, E. Real-time terahertz imaging with a single-pixel detector. Nat. Commun. 2020, 11, 2535. [Google Scholar] [CrossRef] [PubMed]
- Georgiou, G.; Tyagi, H.K.; Mulder, P.; Bauhuis, G.J.; Schermer, J.J.; Rivas, J.G. Photo-generated THz antennas. Sci. Rep. 2014, 4, 3584. [Google Scholar] [CrossRef]
- Vogel, T.; Dodel, G.; Holzhauer, E.; Salzmann, H.; Theurer, A. High-speed switching of far-infrared radiation by photoionization in a semiconductor. Appl. Opt. 1992, 31, 329–337. [Google Scholar] [CrossRef]
- Wilson, T.E. Modeling the high-speed switching of far-infrared radiation by photoionization in a semiconductor. Phys. Rev. B 1999, 59, 12996. [Google Scholar] [CrossRef]
- Kannegulla, A.; Bin Shams, I.; Liu, L.; Cheng, L.-J. Photo-induced spatial modulation of THz waves: Opportunities and limitations. Opt. Express 2015, 23, 32098–32112. [Google Scholar] [CrossRef]
- Ulbricht, R.; Hendry, E.; Shan, J.; Heinz, T.F.; Bonn, M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 2011, 83, 543. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University: Cambridge, UK, 1999. [Google Scholar]
- Liu, L.; Xiao, Q.; Xu, H.; Schultz, J.C.; Lichtenberger, A.W.; Weikle, R.M. Design, Fabrication and Characterization of a Submillimeter-Wave Niobium HEB Mixer Imaging Array Based on the “Reverse-Microscope” Concept. IEEE. Trans. Appl. Supercond. 2007, 17, 407–411. [Google Scholar] [CrossRef]


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Carrier lifetime of silicon | 100 s | Reduced Planck constant | |
| Intrinsic carrier concentration | Excitation optical power density | ||
| Absorption coefficient | Reflectivity | 0.329 | |
| Thermodynamic temperature | 293.15 K | Boltzman constant | |
| Electron mobility | Hole mobility | ||
| Electron effective mass | Hole effective mass | ||
| Dielectric constant | 11.7 | Diffusion coefficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Wang, D.; Lin, S.; Zhao, J.; Wang, Y.; Rong, L. Design Optimization of Silicon-Based Optically Excited Terahertz Wave Modulation. Photonics 2024, 11, 202. https://doi.org/10.3390/photonics11030202
Zhao C, Wang D, Lin S, Zhao J, Wang Y, Rong L. Design Optimization of Silicon-Based Optically Excited Terahertz Wave Modulation. Photonics. 2024; 11(3):202. https://doi.org/10.3390/photonics11030202
Chicago/Turabian StyleZhao, Chenyu, Dayong Wang, Shufeng Lin, Jie Zhao, Yunxin Wang, and Lu Rong. 2024. "Design Optimization of Silicon-Based Optically Excited Terahertz Wave Modulation" Photonics 11, no. 3: 202. https://doi.org/10.3390/photonics11030202
APA StyleZhao, C., Wang, D., Lin, S., Zhao, J., Wang, Y., & Rong, L. (2024). Design Optimization of Silicon-Based Optically Excited Terahertz Wave Modulation. Photonics, 11(3), 202. https://doi.org/10.3390/photonics11030202





