Using Planar Metamaterials to Design a Bidirectional Switching Functionality Absorber—An Ultra-Wideband Optical Absorber and Multi-Wavelength Resonant Absorber

Abstract

This study aimed to investigate a bidirectional switching functionality absorber, which exhibited an ultra-wideband characteristic in one direction, while in the other direction it demonstrated the absorption of three different resonant wavelengths (frequencies). The fully layered planar structure of the absorber consisted of Al₂O₃, Zr, yttria-stabilized zirconia (YSZ), Zr, YSZ, Al, YSZ, and Al. The simulations were conducted using the COMSOL Multiphysics^® simulation software (version 6.1) for analyses, and this study introduced three pivotal innovations. Firstly, there had been scarce exploration of YSZ and Zr as the materials for designing absorbers. The uses of YSZ and Zr in this context were a relatively uncharted territory, and our research endeavored to showcase their distinctive performance as absorber materials. Secondly, the development of a planar absorber with multifunctional characteristics was a rarity in the existing literature. This encompassed the integrations of an ultra-wideband optical absorber and the creation of a multi-wavelength resonant absorber featuring three resonant wavelengths. The design of such a multi-wavelength resonant absorber holds promise for diverse applications in optical detection and communication systems, presenting novel possibilities in related fields. Lastly, a notable discovery was demonstrated: a discernible redshift phenomenon in the wavelengths of the three resonant peaks when the thickness of YSZ, serving as the material of resonant absorber layer, was increased.

1. Introduction

An electromagnetic wave absorber is a device designed to absorb electromagnetic waves within a specific frequency range or within multiple specific frequencies. These absorbers are categorized into different types based on their design and functionality, including ultra-wideband optical [1,2] or electromagnetic-wave absorbers [3,4] and multi-wavelength (frequency) resonant absorbers [5,6,7]. The distinguishing feature of ultra-wideband optical absorbers is their ability to absorb an extremely broad spectrum of light, ranging from ultraviolet to infrared. Applications of ultra-wideband optical absorbers include solar cells, optical sensors, and other devices capable of effectively capturing light energy across multiple wavelengths. Multi-wavelength resonant absorbers focus more on achieving efficient absorption within specific wavelength ranges. These designs often incorporate resonant structures that can be tuned to resonate at different wavelengths. This makes multi-wavelength resonant absorbers particularly useful in applications within specific communication frequency bands or radar wave bands. These absorbers are the subject of extensive research due to their versatile applications, including but not limited to sensors [8], detectors [9], energy harvesting [10], and thermal emitters [11]. Researchers are actively investigating the impacts of dispersion, absorption, and scattering, recognizing their pivotal roles in optimizing the system performance of multifunctional absorbers across different wavelengths or frequencies.

Zhang et al., introduced a bidirectional metamaterial absorber aimed at overcoming limitations associated with conventional designs. This innovative absorber showcased the ability to seamlessly transition between dual-narrowband and ultra-wideband absorption characteristics. Zhang et al.’s absorber structure arranged the specific configuration of four-layer continuous plane films and two-layer square cubes [12]. While the absorber investigated in this study achieved dual functionality, the optimal configuration for achieving the multi-functional absorber, as identified in another study, is a fully planar type [13,14]. Peng et al. further addressed the need for an enhanced design by developing a planar and multilayer metamaterial structure capable of serving multiple functions. This improved design not only functions as a narrowband sensor but also exhibits ultra-broadband and high-efficiency absorption capabilities [15]. However, the shortcoming of this research was that only one narrowband resonant absorption was achieved. In this study, we employed COMSOL Multiphysics^® to meticulously optimize and simulate a recently devised absorber with multi-functionalities [16].

By systematically exploring different materials and their combinations within the eight-layer continuous plane films, we aimed to fine-tune the absorber’s properties in achieving both triple-narrowband and ultra-wideband absorption characteristics. This study encompassed three crucial innovations. Firstly, there had been limited exploration into the utilization of YSZ and Zr metals in the design of absorber materials. The characteristics of YSZ include:

(1)

High refractive index: YSZ typically exhibits a relatively high refractive index, usually ranging from 1.8 to 2.2. This makes it a preferred choice as a high refractive index material for optical thin films.

(2)

Low absorption coefficient: YSZ generally demonstrates extremely low absorption across the near-ultraviolet, visible, and near-infrared spectra, approaching zero. This implies its potential application as a transparent material in optical thin films.

(3)

Chemical and high-temperature stabilities: YSZ possesses chemical stability and can withstand high temperatures. These attributes render it versatile for various optical devices, including serving as an excellent material for optical resonators.

Zr metal’s characteristics in optical thin film applications include:

(1)

Low refractive index: Zr metal typically exhibits a refractive index close to one within the visible spectrum (400 nm to 700 nm), possibly slightly higher.

(2)

High absorption rate: Zr metal tends to have a high absorption rate in the visible spectrum, typically close to one. This indicates its significant ability to absorb visible light rather than transmitting it.

While YSZ and Zr metals are not commonly utilized in optical thin film applications individually, their unique characteristics made them suitable for developing a multifunctional absorber in this study. This pioneering approach opened up new perspectives for the potential uses of YSZ and Zr as the dielectric and metal layers in enhancing absorber performance. Secondly, this study introduced a groundbreaking flat-structured absorber with multifunctional characteristics, incorporating an ultra-wideband optical absorber from visible to near infrared and a multi-wavelength resonant absorber with three resonant waves. This innovative design held promise for applications in various optical detection and communication systems, ushering in new possibilities in related fields.

In the past, most Fabry–Perot cavities typically generated only one or at most two resonance signals within the same cavity. However, with YSZ as the dielectric layer of a Fabry–Perot cavity, we observed different results [17,18]. Lastly, a compelling discovery was present: increasing the thickness of YSZ enabled the formation of a Fabry–Perot cavity with different resonance wavelengths, allowing us to design a planar multi-wavelength resonant absorber. The noteworthy redshift phenomenon in the resonance wavelengths of the three resonant waves became particularly evident with an increase in the thickness of YSZ, serving as the absorber with a tunable wavelength feature. This observed variation not only provides profound insights into material properties but also introduces new avenues for fine-tuning absorber performance and wavelengths.

2. Structure of the Investigated Bidirectional Switching Functionality Absorber

The geometric structure of the investigated absorber under examination is illustrated in Figure 1, which comprises eight layers. The individual layer thicknesses were as follows: t1 (aluminum oxide, Al₂O₃) = 100 nm, t2 (zirconium, Zr) = 5 nm, t3 (YSZ) = 80 nm, t4 (Zr) = 15 nm, t5 (YSZ) = 60 nm, t6 (aluminum, Al) = 100 nm, t7 (YSZ) = 250 nm, and t8 (Al) = 5 nm. In the following sections, we delve into the reasoning behind the selection of these particular thicknesses for each layer. The investigated absorber had the functions of a multi-wavelength resonant absorber and high absorptivity across an ultra-broadband range as being incident from one side. The absorber was designed to selectively target the visible light and NIR (near-infrared) bands, covering the energy spectrum of AM1.5G sunlight. To accomplish this goal, extensive numerical simulations and analyses of the absorber device’s structure were conducted using the commercially available simulation software COMSOL Multiphysics^®. To illustrate the optimized parameters for thickness in our proposed multifunctional absorber, the thickness of each layer was systematically varied individually and the thicknesses of the other seven layers were kept constant. Our objective was to determine the ideal thickness for each layer, aiming for optimal performance.

3. Processes to Find the Optimal Thickness of Each Layer

Figure 2 (for t8 Al layer), Figure 3 (for t7 YSZ layer), Figure 4 (for t5 YSZ layer), Figure 5 (for t4 Zr layer), and Figure 6 (for t2 Zr layer) illustrate the variations in absorptivity for different layers of the investigated absorber as the thickness of each layer is altered. This method formed the basis for determining the optimal parameters of the investigated absorber, demonstrating ultra-broadband absorption and high absorptivity. As illustrated in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, to ascertain the optimal parameters for absorption properties, simulations were processed by systematically varying one parameter at a time while keeping the others constant, as depicted by the eight layers shown in Figure 1. The thickness optimizations were carried out across a wavelength range from 300 nm to 3200 nm. The results, as depicted in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, distinctly illustrate the substantial variations in absorptivity based on the thickness variations of different layers. This underscores the considerable influence of each layer’s thickness on the outcome of absorptivity for the investigated multifunctional absorber. 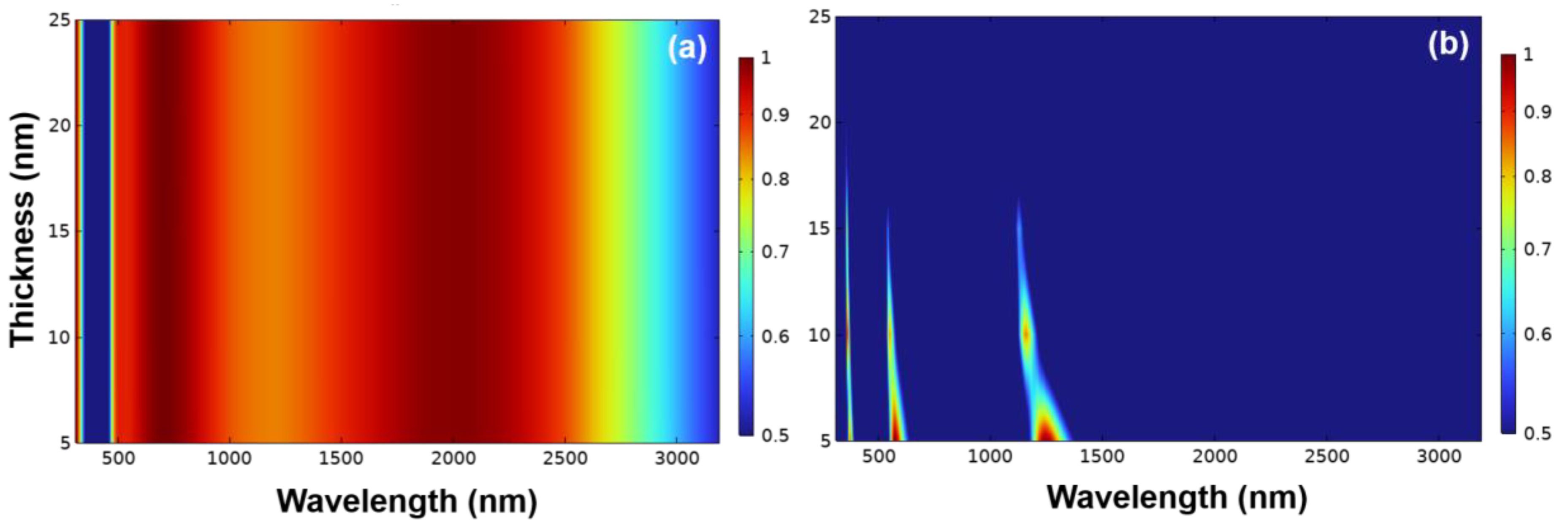Figure 2 illustrates the changes in absorptivity of the designed absorber when only the thickness of the t8 Al layer is adjusted from 5 nm to 25 nm. As shown in Figure 2a, when light is incident on the investigated absorber on the t1 Al₂O₃ layer, increasing the thickness of the t8 Al layer from 5 nm to 25 nm results in a decrease exhibiting absorptivity exceeding 0.900 within the wavelength range of 475–2700 nm.

However, when light was incident on the t8 Al layer, three absorption peaks were observed. According to Figure 2b, three absorption peaks are observed at wavelengths of around 435 nm, 670 nm, and 1425 nm. Notably, the t8 Al layer exhibited higher absorptivity at a thickness of 5 nm, whereas beyond 6 nm, the absorptivity of the three peaks significantly decreased. Therefore, a thickness of 5 nm was chosen for the t8 Al layer, as the thickness analysis for this layer revealed the optimal absorptivity for all three absorption peaks. Resonance absorbers are typically optical materials designed to absorb light at specific wavelengths. These absorbers utilize the phenomenon of surface plasmon resonance, where free electrons on the metal surface resonate when they are excited by light. When the thickness of the metal film is within the range of a few nanometers, these free electrons can move on the metal surface, forming surface plasmons. However, if the metal layer is too thick, the movement of free electrons is restricted, leading to a weakening of the resonance effect and a reduction in absorption efficiency. Additionally, the optical properties of the metal are closely related to the behavior of its electrons, and these behaviors are more easily observed in thinner metal layers. Therefore, to achieve optimal performance of resonance absorbers, the thickness of the metal layer is typically limited to a few nanometers to ensure the effective utilization of the surface plasmon resonance.

When the thickness of the t7 YSZ layer varied from 210 nm to 250 nm, the characteristics of the significantly broadband absorber showed minimal sensitivity to this layer’s thickness when illuminated from the Al₂O₃ layer. There was no apparent change in absorptivity, as is evident from Figure 3a. However, Figure 3b reveals that all three absorption peaks showed a noticeable redshift from around 390 nm, 645 nm, and 1260 nm to around 445 nm, 680 nm, and 1470 nm. When the thickness of the t7 YSZ layer was 250 nm and the light was incident from the Al layer, the absorption peak at the wavelength of 435 nm exhibited a higher absorptivity. Therefore, a thickness of 250 nm was chosen for the t7 YSZ layer, as the thickness analysis for this layer demonstrated the optimal absorption efficiency in this structural configuration. The redshift in the resonance wavelength resulting from an increase in the thickness of the dielectric layer in a resonance absorber is a comprehensive effect, encompassing changes in multiple optical parameters within the structure. When the thickness of the dielectric layer in a resonance absorber increases, a phenomenon known as the redshift of the resonance peak often occurs. As the dielectric layer thickness increases within the resonance absorber, one of the key reasons is the elongation of the resonance path. The thickening of the dielectric layer results in the light waves needing to cover a longer distance within this structure to complete a full oscillation cycle. The elongation of the resonance path can lead to changes in the phase of the light waves, affecting the distribution of peaks and troughs in the wave.

Since the characteristics of resonance are wavelength-dependent, the elongation of the resonance path may induce variations in the overall structure’s resonant wavelength. This type of wavelength variation typically manifests as a redshift, indicating a shift of the resonance wavelength towards longer wavelengths. A typical Fabry–Perot cavity comprises two mirrors with reflective coatings, allowing light waves to undergo numerous reflections between surfaces, resulting in interference phenomena. Resonance occurs when the incident wavelength satisfies specific conditions, leading to pronounced peaks. An increase in cavity thickness causes a decrease in resonant frequency, corresponding to longer wavelengths. This phenomenon is known as the modulation of resonant frequency by cavity thickness. Consequently, augmenting cavity thickness causes a decrease in resonant frequency and a redshift in wavelength. The ability to adjust resonant wavelength by manipulating cavity thickness is a crucial aspect of Fabry–Perot cavity resonance, making it widely applicable in optical sensing and spectroscopy. By manipulating the distance between reflective mirrors, specific wavelengths can be selected for resonance, providing a flexible and controllable tool for tailored optical applications. Hence, the redshift characteristic implies that the t7 YSZ layer plays a significant role in generating Fabry–Perot cavity resonance. This optical phenomenon is based on the multiple reflections and interference of light waves between two parallel reflective surfaces. However, in the following paragraph, we will explain that multiple resonance peaks are generated by the effect of the Fabry–Perot cavity.

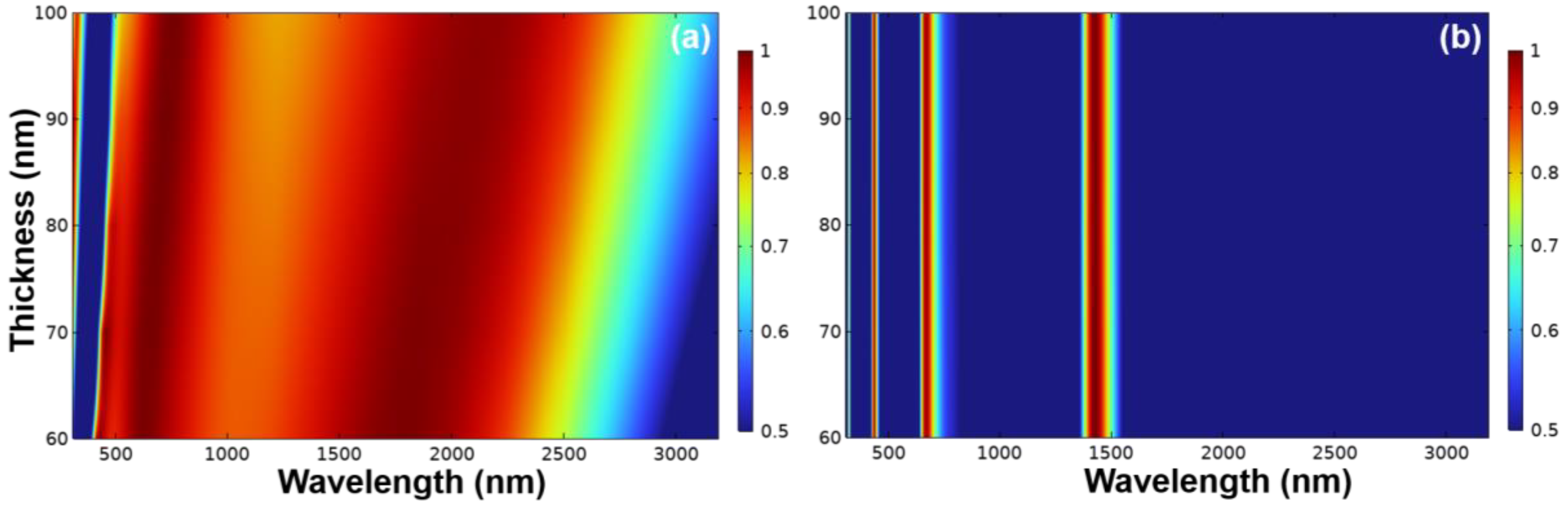
Figure 4 illustrates the impact of increasing the thickness of the t5 YSZ layer from 60 nm to 100 nm on the absorption characteristics. As Figure 4a shows, as the t5 YSZ layer’s thickness increased, although the broadband range expanded, it led to a decrease in the absorptivity. When the thickness was 60 nm, the wavelength increased from 390 nm to 2300 nm exhibited the better absorptivity. When the thickness was 100 nm, the wavelength to reveal the better absorptivity ranged from around 530 nm to 2600 nm. For the absorption spectrum of the ultra-wideband absorber, an overall redshift occurred. In the case of the multi-wavelength resonant absorber, as shown in Figure 4b, there was no apparent influence on the absorption characteristics. This means that changing the thickness of this layer had a weak impact on the overall structure’s absorption characteristics, including no significant changes in absorptivity and absorption peaks’ wavelengths of the three absorption peaks. Therefore, 60 nm was chosen as the t5 YSZ layer because, in the thickness analysis of this layer, it presented the optimal absorption characteristics in the range of visible light.

Figure 5a and Figure 6a depict the influences of the t4 Zr layer and t2 Zr layer thicknesses on the efficiency of the ultra-wideband absorber. In Figure 5a, the impact of varying the thickness of the t4 Zr layer from 5 nm to 25 nm on absorptivity is examined. At a thickness of around 5 nm, an orange-yellow region appeared in the wavelength range of 1500–2000 nm. This result indicates that a thickness of 5 nm is unsuitable for the structure of an ultra-wideband absorber. As the thickness increased, the yellow region diminished, while the deep red region expanded, indicating an increase in absorptivity. A thickness of 15 nm for the t4 Zr layer was chosen based on the analysis, because when combined with different thicknesses of other materials, it demonstrated the optimal absorptivity performance for this structure. In Figure 6a, the impact of t2 Zr layer thickness on the ultra-wideband absorber shows significant variations. Gradually increasing the t2 Zr layer thickness from 5 nm to 25 nm resulted in a red-orange region appearing around a thickness of 5 nm in the wavelength range of approximately 390–2400 nm. Additionally, when the t2 Zr layer was 5 nm thick and the wavelength exceeded 2400 nm, an orange-yellow region emerged.

Alternatively, as the Zr thickness increased, a decrease in the deep red region was observed within the wavelength range of 1500–2000 nm, indicating a decline in absorptivity. For this layer, a thickness of 5 nm for the t2 Zr layer was chosen based on the analysis, because when combined with different thicknesses of other materials, it yielded the optimal absorption performance for the overall structure. Figure 5b and Figure 6b address the efficiency impacts of the t4 Zr layer and t2 Zr layer on the multi-wavelength resonant absorber. As depicted in Figure 5b and Figure 6b, as the thicknesses of the t4 Zr layer and t2 Zr layer gradually increased from 5 nm to 25 nm, no clear influences on absorptivity are evident from the graphs. In other words, the thickness variations of the t4 Zr layer and t2 Zr layer had a minimal effect on the absorptivity of the multi-wavelength resonant absorber. Therefore, thicknesses of 15 nm for the t4 Zr layer and 5 nm for the t2 Zr layer were considered acceptable based on the observed results. However, these simulations demonstrate and optimize the performances of the ultra-wideband optical absorber and multi-wavelength resonant absorber, facilitating the identification of the most effective structural parameters.

4. Ultra-Broadband and Multi-Wavelength Resonant Absorption Characteristics and Discussion

The results in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 specifically present the factors of varying the thicknesses of the t8 Al layer from 5 nm to 25 nm, the t7 YSZ layer from 210 nm to 250 nm, the t5 YSZ layer from 60 nm to 100 nm, the t4 Zr layer from 5 nm to 25 nm, and the t2 Zr layer from 5 nm to 25 nm, respectively. However, the factors of varying the thicknesses of the t6 Al layer from 80 nm to 120 nm, the t3 YSZ layer from 60 nm to 100 nm, and the t1 Al₂O₃ layer from 60 nm to 100 nm were also simulated but not revealed in this study. 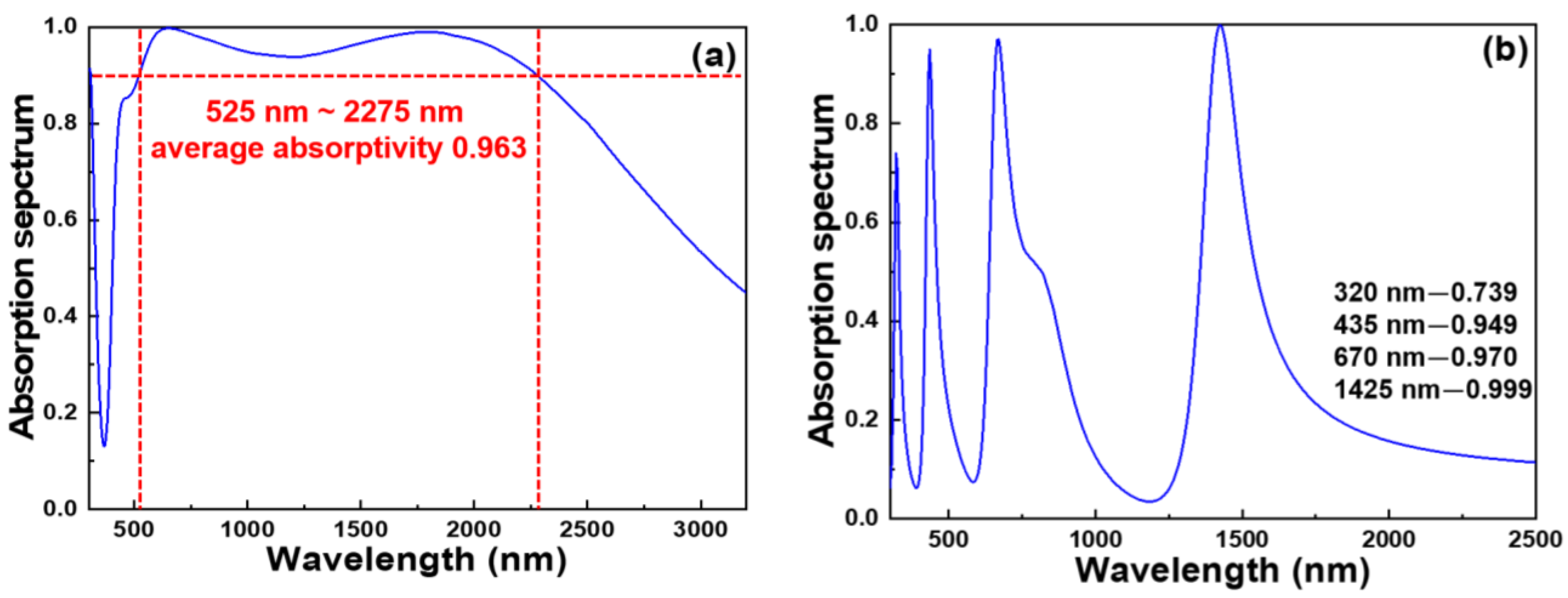Based on the data depicted in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, it was observed that the investigated absorber had an ultra-wideband optical absorption and multi-wavelength resonant characteristics. The multifunctional absorber had absorptivity higher than 0.900 within the range of 525–2275 nm (achieved through the Al₂O₃ layer), as Figure 7a shows, and three narrowband absorption peaks had resonant wavelengths of 435 nm, 670 nm, and 1425 nm (achieved through the Al layer), as Figure 7b shows. Figure 7b further highlights the impact of using Al as the t8 metal layer. It demonstrated an 0.739 absorptivity within the 320 nm band and notable 0.949, 0.970, and 0.999 high absorptivity within the 435 nm, 670 nm, and 1425 nm bands. These results were obtained when the thicknesses of the eight layers were: t8 Al layer—5 nm, t7 YSZ layer—250 nm, t6 Al layer—100 nm, t5 YSZ layer—60 nm, t4 Zr layer—15 nm, t3 YSZ layer—80 nm, t2 Zr layer—5 nm, and t1 Al₂O₃ layer—100 nm. Hence, we selected these thickness values as the optimized thicknesses of the corresponding layers.

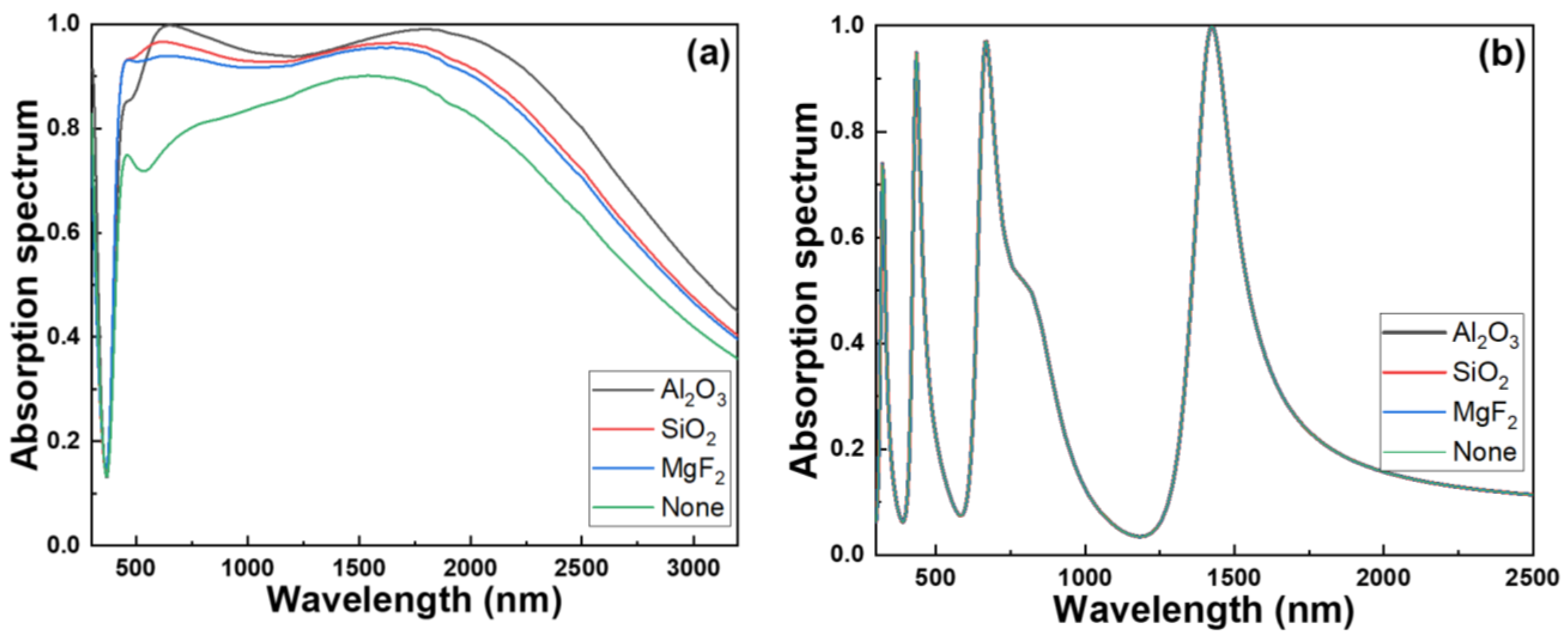
This study also conducted analyses of the impacts of the absence of an anti-reflection Al₂O₃ layer and the uses of different materials on the structural absorption performance. The investigation explored the replacement of the Al₂O₃ anti-reflective layer material to compare the effects of different materials on the absorptivity of the model. As shown in Figure 8a, a comparison was made using SiO₂ or MgF₂ as examples, revealing a significant impact of changing the top anti-reflective layer, resulting in a noticeable difference in the absorption spectra. When SiO₂ or MgF₂ were used as anti-reflective layers, there was no significant variation in the starting wavelength of absorption for the low-wavelength range. However, as compared with that of using Al₂O₃ as an anti-reflective layer, the overall absorption spectrum exhibited a clear decrease and a narrowing of the bandwidth in both overall absorption efficiency and the 0.900 absorption bandwidth when SiO₂ or MgF₂ were used as anti-reflective layers. When using Al₂O₃ as an anti-reflection coating, the absorptivity exceeded 0.900 was ranged from 520 nm to 2275 nm, with the highest absorptivity reaching 0.990. In contrast, when SiO₂ or MgF₂ was employed as the anti-reflective layer, the absorptivity surpassed 0.900 in the ranges of 435 nm to 2065 nm and 2010 nm, with the highest absorptivity being 0.964 and 0.955, respectively.

Moreover, when employing Al₂O₃, SiO₂, or MgF₂ as anti-reflective layers, the average absorptivity values for wavelengths beyond 0.900 were 0.963, 0.944, and 0.933, respectively. Additionally, when no anti-reflection layer was used, the maximum absorptivity was 0.901 and the overall absorptivity exceeded 0.9 only in the range of 1510–1585 nm. This demonstrates that Al₂O₃, SiO₂, and MgF₂ all had anti-reflection effects, with Al₂O₃ providing superior anti-reflection performance compared to SiO₂ and MgF₂. The reasons for these results will be further explained in the following paragraph, which will discuss the impact of varying optical impedance. As illustrated in Figure 8b, since light enters the component through the t8 Al layer, the absorption properties of the multi-wavelength resonant absorber showed almost no change. Significant differences in absorption were observed when using different materials, such as SiO₂ or MgF₂, as top anti-reflective layers or when no material was used as an anti-reflection layer. Therefore, selecting Al₂O₃ as the anti-reflective layer maximized the overall structural absorption efficiency of the investigated ultra-wideband optical absorber, a choice made to enhance the absorption characteristics of the entire structure.

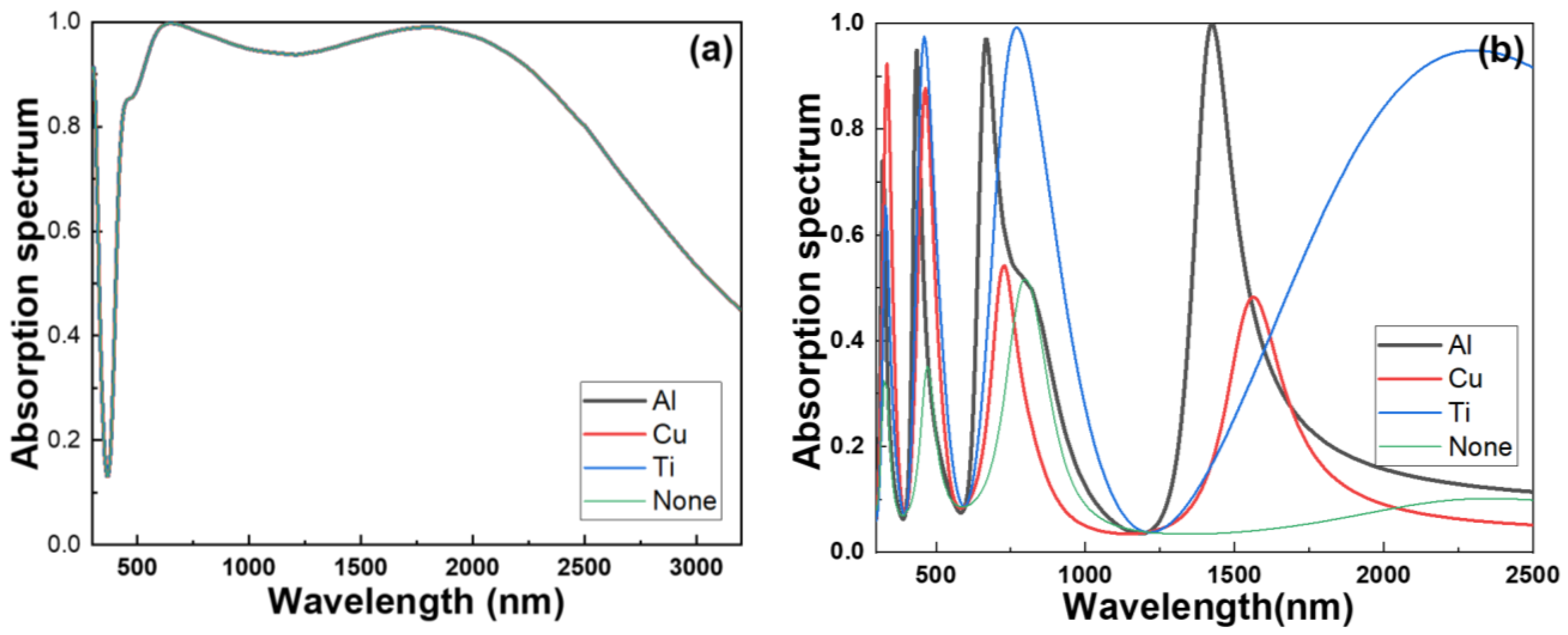
This study also meticulously analyzed the influences of different metals on the structural absorption performance. The impact of altering the t8 metal layer was systematically compared to evaluate its effect on the absorptivity of the model. Significant variations in absorptivity were observed through scenarios with Cu, with Ti, and without metal. The absorption spectra of the specially investigated planar and dual-functional absorber are depicted when illuminated with light from the t1 Al₂O₃ layer direction in Figure 9a, and from the t8 metal layer direction in Figure 9b. The absorption spectra in Figure 9a were obtained with the optimization of parameters for each layer, as mentioned above. However, the only variation made was in the metal of the right t8 Al layer, either replacing it with another metal or omitting the use of metal altogether, while the incident light was directed from the Al₂O₃ side. Clearly, as the incident light direction was through the Al₂O₃ layer, the characteristics of the wideband absorption spectra remained largely unchanged when the metal material of the t8 Al layer was altered.

Distinct absorption curves were evident for different t8 metal materials, with Al displaying three narrow absorption peaks in its spectrum, indicative of higher absorptivity compared to other metals. This suggests a robust localized surface plasmon resonance (LSPR) effect contributing to the high absorptivity in these peaks when Al was employed. These findings underscored the nuanced and material-specific nature of structural absorption performance, offering valuable insights for optimizing absorber designs in various applications. Conversely, when no metal was used, or Cu or Ti were used as the t8 metal layer, the absorption peaks shifted to different wavelengths. Among the four conditions considered, when no metal was used, only three emission peaks were observed at 325 nm, 470 nm, and 795 nm, with maximum absorptivity of 0.324, 0.351, and 0.516, respectively. These results indicated a noticeable decrease in absorptivity. When Cu was introduced, four emission peaks appeared at 335 n, 465 nm, 730 nm, and 1560 nm, with maximum absorptivity of 0.933, 0.877, 0.542, and 0.482, respectively, also indicating a significant decrease in absorptivity. In the case of Ti, three emission peaks were identified at 330 nm, 460 nm, and 765 nm, with maximum absorptivity of 0.655, 0.975, and 0.991, along with a broadened emission peak at 2285 nm with a maximum absorptivity of 0.948.

When Cu was utilized as the t8 metal absorption layer, although the absorption peaks differed from those observed with Al, there was no significant difference in the maximum absorptivity compared to Al. Therefore, Cu could be considered as an alternative choice for a metal absorption layer. These analyses underscored the influence of metal choice on the absorber’s spectral characteristics and absorptivity. The distinctive absorption patterns associated with different metals highlighted the importance of careful material selection to optimize the absorber’s performance for specific wavelengths. Furthermore, these findings provide valuable insights into tailoring the absorber’s properties for diverse applications, emphasizing the significance of understanding the interplay between metal type and absorption characteristics in a multi-wavelength resonant absorber. Notably, the absence of metal and the use of Cu or Ti as the absorption layer resulted in distinct differences in absorptivity. Because of the notable 0.949, 0.970, and 0.999 absorptivity within the 435 nm, 670 nm, and 1425 nm bands, choosing Al as the t8 absorption layer was deemed optimal, leading to the maximization of the overall structural absorptivity of the investigated multi-wavelength resonant absorber.

Optical impedance refers to the resistance or damping effect encountered by light waves during propagation in an optical system. The magnitude and nature of optical impedance depend on the characteristics of the medium, including refractive index, transmittance, and so forth. In optical absorbers, optical impedance can influence their absorptivity. This is mainly because optical impedance affects the speed of light propagation and energy loss in the medium, thereby impacting the absorber’s ability to absorb light. Therefore, optical impedance can be considered a significant parameter of optical absorbers, directly affecting their efficiency in absorbing incident light. Various factors influence the optical impedance value, including the angle of incidence of light waves at the boundary, the wavelength of light, and the characteristics of the medium. Different materials and boundaries exhibit distinct optical impedance values at specific angles and wavelengths, finding applications in optical materials, light sensing, and optical design. Optical impedance elucidates the resistance encountered by light waves as they traverse a medium or a boundary, comprising two components: the phase difference (imaginary part) and the impedance magnitude (real part). Designing an absorber entails striking a balance where the real part approaches one, indicating minimal variation in light speed, and the imaginary part approaches zero, indicating minimal energy loss, thus achieving optimal absorption efficiency. A real part nearing one implies improved impedance matching between the boundary and the light wave, resulting in reduced reflective losses.

An imaginary part close to zero indicates minimal energy dispersion, resulting in lower energy loss on the boundary and enhancing absorption efficiency. Such structures are typically considered effective absorbers in optical applications. Comparing impedance and absorptivity plots offers a more intuitive understanding, ensuring that optical components or films achieve optimal optical performance at specific wavelengths. Additionally, the thickness of the absorber structure’s film also impacts impedance matching. In other words, the film thickness must adhere to specific conditions to achieve impedance matching; otherwise, it may lead to a decrease in absorption efficiency. This highlights the crucial role of film thickness selection in optical design, influencing the impedance of the light absorber. The resistance to light increases with a greater difference in refractive index between media. At the interfaces of different media, changes in refractive index induce both reflection and refraction of light waves.

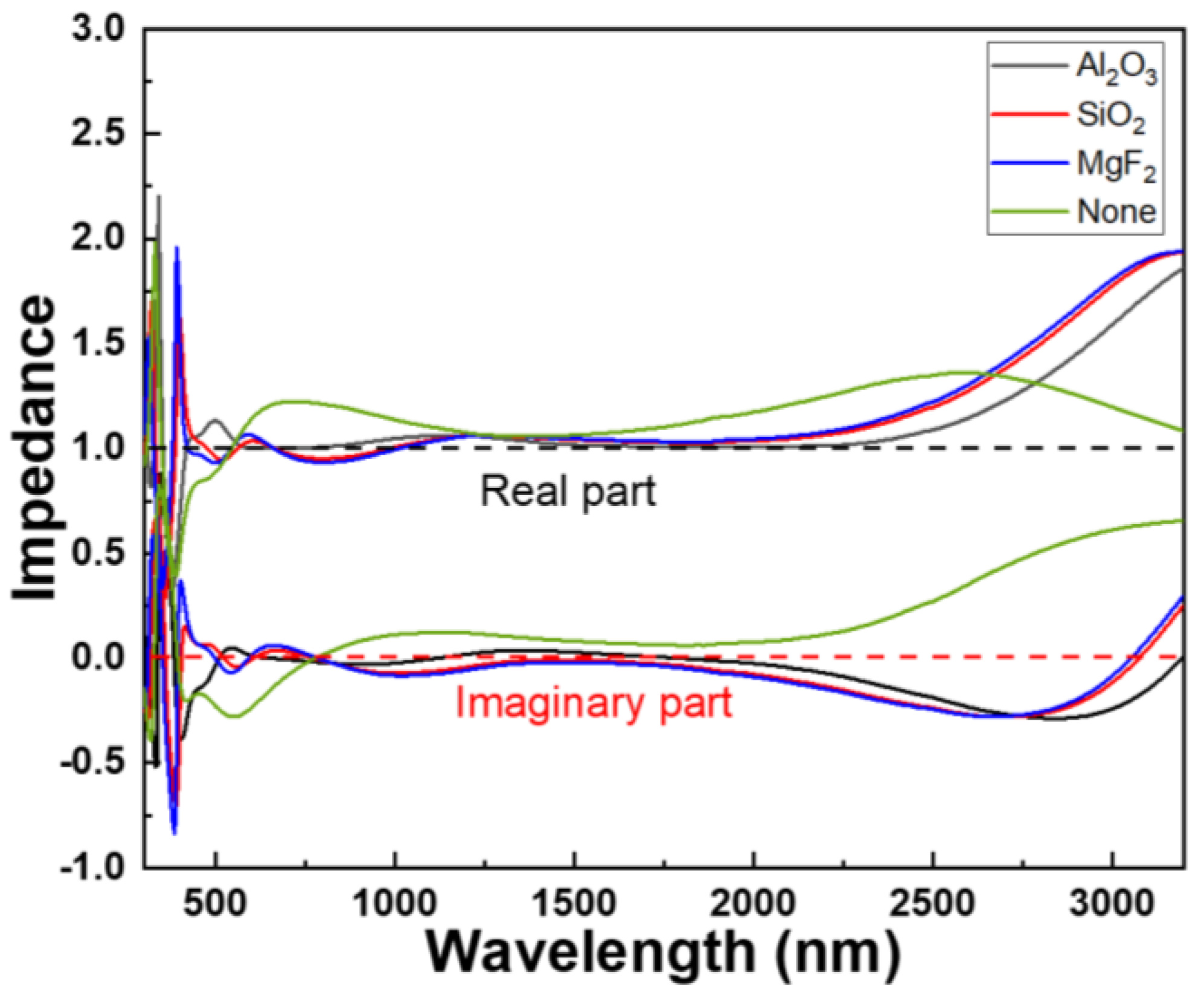
The phase difference of the light wave is reflected by the imaginary part on the boundary, associated with scattering and absorption phenomena, and it approaches zero for the absorber, as depicted in Figure 10, indicating minimal energy loss. Optical impedance, commonly used to describe the propagation of light between different media, serves to characterize the reflection and refraction behaviors of light at interfaces. The optical impedance in Figure 10 primarily calculates the impedance values of light between the top t1 Al₂O₃ layer of a light absorber and air and refers to the resistance encountered by light as it propagates between the two mediums. The variations in the impedance of different materials’ real and imaginary parts with increasing wavelength were then examined. When Al₂O₃ served as an anti-reflection layer, the imaginary part approached zero and the real part of the absorber approached unity within the wavelength range of 525–2275 nm. This trend suggests a minimal impact on the light speed, consistent with the absorption spectra shown in Figure 9a. In contrast, the absence of an anti-reflection layer resulted in deviations from unity in the real part and non-zero values in the imaginary part. Utilizing SiO₂ or MgF₂ as an anti-reflection layer produced deviations from unity before 1500 nm, aligning with the variation of absorption spectra shown in Figure 9a. Remarkably, when Al₂O₃ was employed as the anti-reflection layer, the imaginary part approached zero more closely than when SiO₂ or MgF₂ were used, or when no anti-reflection layer was present. This evidence supports the conclusion that using Al₂O₃ as the anti-reflection layer can reduce loss in the absorber. Additionally, these results demonstrate that the choice of anti-reflection materials does not significantly affect the absorption properties of the multi-wavelength resonant absorber (not shown here).

Optical impedance is a physical quantity that describes the resistance and reflection characteristics of light when propagating through a boundary, typically represented as a complex number with real and imaginary parts. When the real part of a light absorber’s impedance approaches one, it suggests that the boundary poses minimal resistance to light, facilitating easier penetration of light through the boundary. This preference stems from the fact that a real part close to one signifies reduced refraction effects as light traverses the boundary, thereby enhancing the efficiency of light entry and absorption. Simultaneously, when the imaginary part approaches zero, it signifies low absorption of light by the boundary. This property allows light to effectively propagate on the boundary and be absorbed rather than being scattered or reflected. A higher absorptivity implies that light can be more efficiently absorbed by the boundary, minimizing reflection or transmission. This characteristic is crucial in optical applications such as solar cells and optical sensors, where the goal is to maximize the absorption of light energy and convert it into other forms of energy. Therefore, light absorbers exhibit a higher absorptivity when the real part of their impedance approaches one and the imaginary part approaches zero, as these characteristics facilitate the propagation and absorption of light on the boundary. Optical impedance of the investigated metamaterials with imaginary parts close to zero and real parts close to one are more conducive to achieving broadband absorption, as they exhibit better absorption performance across various wavelengths.

The relationship between the free space impedance S and Z parameters can be found from the effective medium theory and expressed as follows [19,20]:

$$S_{11}=S_{22}=\frac{i}{2}\left(\frac{1}{Z}-Z\right)\sin \left(nkd\right)$$

(1)

$$S_{21}=S_{12}=\frac{1}{\cos \left(nkd\right)-\frac{i}{2}\left(Z+\frac{1}{2}\right) \sin \left(nkd\right)}$$

(2)

In these formulas, d, k, and n are the thickness of the proposed absorber, the wave vector, and the refractive index, respectively. S₁₁, S₂₂, S₁₂, and S₂₁ all represent S parameters, and the reflectivity R is defined to be equal to S₁₁. Since our metal substrate exceeds the skin depth of the incident light, T = S₁₂ = 0. The free space impedance of the investigated absorber can be found by:

$$Z=\pm \sqrt{\frac{{\left(1+S_{11}\right)}^2-{S_{21}}^2}{{\left(1-S_{11}\right)}^2-{S_{21}}^2}}$$

(3)

When the impedance of the absorber matches the impedance of free space (Z = Z₀), the absorber can reach its maximum absorptivity. As depicted in Figure 10, when the imaginary part is close to zero and the real part of the impedance is near one, the structure exhibits the highest absorption performance, aligning well with the perfect absorptivity across a wide bandwidth. However, if the thicknesses of the various layers of the investigated absorber are either too thick or too thin, it will fail to match the impedance of free space. Consequently, the strong LSPR essential for the designed structure cannot be effectively excited.

To assess the absorption capacity of the ultra-wideband optical absorber developed in this study for solar energy, Figure 11 illustrates the computed absorption of solar energy across the AM1.5 spectrum (ranging from 280 nm to 4000 nm). Notably, there was an impressive 0.900 absorptivity in the near-infrared range. Additionally, within the absorption bands spanning 280 nm to 400 nm, 400 nm to 700 nm, 700 nm to 1400 nm, and 1400 nm to 4000 nm, the absorber achieved absorptivity of 0.389, 0.909, 0.962, 0.960, and 0.606, respectively, for AM1.5G solar energy. Hence, the investigated absorber showcased impressive absorption capability under the AM1.5 solar spectrum, attaining an overall absorptivity of 0.934 across the entire spectrum spanning from 280 nm to 4000 nm. These findings highlight the effectiveness of the designed absorber in efficiently capturing solar energy across the mid-IR, NIR, and visible spectra. This superior absorption performance holds significant promise for applications in solar conversion and energy harvesting initiatives. The absorber’s nearly ideal wideband absorption across the NIR and visible range is particularly noteworthy, aligning with the high-energy portion of the primary solar radiation. These findings emphasize the potential uses of the investigated ultra-wideband optical absorber for advancing solar-related technologies and establishing it as a valuable component in the pursuit of sustainable energy solutions.

5. Distributions of the Magnetic and the Electric Field Intensities and Discussion

The absorption spectrum of a broadband optical absorber is commonly generated through the mechanism of LSPR (localized surface plasmon resonance). Unlike large-scale surface plasmon resonance, LSPR occurs on small-scale structures or nanomaterials. Broadband optical absorbers typically integrate nanostructures or specially engineered surfaces with dimensions spanning the wavelength range of light. These structures are capable of supporting LSPR at various wavelengths, thereby yielding a broad absorption spectrum. The frequency and intensity of LSPR are often contingent upon the geometric material, size, and shape characteristics of the nanostructures. An optical absorber with broadband absorption spectrum is also influenced by Fabry–Perot cavity resonance, particularly regarding interference phenomena occurring as light reflects back and forth between material layers. This resonance entails multiple reflections of light within the cavity, and that will result in distinctive absorption peaks. However, the frequency and characteristics of this resonance typically differ from those of LSPR. Essentially, while LSPR primarily governs the absorption spectrum of a broadband optical absorber, Fabry–Perot cavity resonance may exert an impact under certain conditions. These combined characteristics empower broadband optical absorbers to efficiently capture light energy across a wider spectrum, thereby showcasing their potential applications in the solar energy conversion.

The resonance peaks observed in a multi-layer planar optical resonant absorber are likely the result of a combination of various resonance phenomena, including LSPR, Fabry–Perot cavity resonance, and PSPR (propagation surface plasmon resonance). The specific contributions of each depend on the material structure and optical properties employed. Fabry–Perot cavity resonance arises from interference effects due to the reflection of light between different layers within the structure. This resonance is intimately linked to the optical path length and the wavelength of light between the layers, potentially giving rise to discernible resonance peaks in multi-layer planar configurations. PSPR, on the other hand, involves the propagation of surface plasmon resonances along a metal surface, often associated with the presence of a metal layer. The resonance is triggered by the interaction of light with the metal interface, with its manifestation being influenced by both the optical properties and geometric shape of the metal layer. Understanding and harnessing these diverse resonance effects enable the engineering of highly efficient optical absorbers with tailored spectral responses, presenting promising avenues for applications in fields such as photonics, sensing, and energy conversion.

LSPR manifests in small-scale structures, such as nano-particles or nano-holes, significantly enhancing the absorption of light at specific wavelengths. Moreover, LSPR can induce an intensified electric field effect, thereby amplifying absorption efficiency. This phenomenon extends its influence to multi-layer planar structures, introducing additional resonance effects within localized regions. In multi-layer planar optical resonant absorbers, the interplay of these resonance phenomena enables the realization of robust optical performance across diverse frequency ranges. The relative significance of each resonance effect is contingent upon factors such as material composition, structural geometry, and the characteristics of incident light. Consequently, these absorbers may exhibit multiple resonance peaks in their absorption spectrum, reflecting the sensitivity of various mechanisms to incident light. By leveraging these intricate resonance effects, multi-layer planar optical resonant absorbers offer versatile solutions for applications spanning from photonics to sensing and beyond. Their ability to tailor absorption characteristics makes them invaluable tools in the pursuit of efficient light manipulation and energy conversion.

For the ultra-wideband optical absorber, TE-polarized light was used at normal incidence on the t1 Al₂O₃ layer to excite the absorber at wavelengths of 650 nm and 1800 nm. These specific wavelengths were selected based on the absorption peaks of the absorption spectra, which are revealed in Figure 9a. As presented in Figure 12a, the distributions of the electric field intensity caused by the normal incident TE-polarized light at different wavelengths showed coupling effects along the edge of the t1 Al₂O₃ layer. PSPR refers to a phenomenon wherein incident light interacts with surface plasmons propagating along the interface of a dielectric medium and a metal film. The intensity of LSPR, on the other hand, generally increased with the thickness of the film up to a certain point. Beyond this threshold, the intensity of LSPR either saturated or began to decrease. This behavior stems from the fact that thicker films can accommodate more plasmon modes, thereby enhancing light scattering or absorption. However, when the film exceeds a critical thickness, destructive interference between multiple plasmon modes may arise, resulting in a reduction in LSPR intensity. This phenomenon underscores the intricate interplay between film thickness, plasmon modes, and the resulting optical properties, offering insights into the design and optimization of plasmonic devices and structures.

Figure 12a shows that the strong electric fields were not only revealed on the t1 Al₂O₃ layer but also present beneath the six continuous layers. Figure 12a further confirms that the electric fields were predominantly distributed across the t1 to t6 layers across incident light wavelengths ranging from 650 nm to 1800 nm. However, Figure 12a also indicates the presence of Fabry–Perot cavity resonance, which was located at the t7 YSZ layer, in the 650 nm absorption characteristic. Additionally, Figure 12b displays the magnetic field distributions corresponding to excitation wavelengths of 650 nm and 1800 nm. The findings illustrated in Figure 12b clearly demonstrate the magnetic field distribution linked to different excitation wavelengths across the layers t1 Al₂O₃, t2 Zr, t3 YSZ, and t4 Zr. When aiming to generate Fabry–Perot cavity resonance in an absorber, two parallel flat semi-transparent metals can be utilized as reflective mirrors. In the examined absorber configuration, the layers t6 Al and t8 Al were delineated by a lossless t7 YSZ dielectric layer. Consequently, the metal layers t8–t6, separated by the YSZ layer, gave rise to distinct Fabry–Perot cavities. When 650 nm and 1800 nm were used as the excitation wavelengths, they also satisfied the Fabry–Perot cavity resonance condition. As depicted in Figure 12b, variations in the intensities of magnetic field distributions originating from Fabry–Perot cavity resonances within the YSZ cavity layer were observed when the excitation wavelengths differed. When the normal incident light was used to interact with the absorber on the t1 Al₂O₃ layer, the reflected light underwent either destructive or constructive interference with the incident light, and the magnetic field distribution showed a condition of distinct patterns. These patterns clear prove that the Fabry–Perot cavity resonance was present within the YSZ dielectric layers.

A multi-wavelength resonant absorber, exhibiting absorption peaks at distinct wavelengths, holds the potential to serve as a sensor for precise measurement and detection of light at those specific wavelengths. The absorption peaks illustrated in Figure 8b clearly depict the strong light absorption characteristics at 435 nm, 670 nm, and 1425 nm. This observation suggests that the investigated multi-wavelength resonant absorber was likely designed with the intention of functioning as a photodetector [21]. Even though the absorptivity at the 320 nm peak did not exceed 0.900, Figure 11 provides insight into the analysis results of electric field (Figure 13a) and magnetic field (Figure 13b) processes at wavelengths of 320 nm, 435 nm, 670 nm, and 1425 nm. The examination of these fields revealed the inconspicuous presence of LSPR on the surface of the Al film. This is attributed to the fact that when light interacted with the Al surface at the mentioned wavelengths, the free electrons within the Al layer did not undergo resonant oscillation, as depicted by the electric and magnetic field analyses. However, Figure 13a,b reveal that strong electric and magnetic fields extended through the six continuous layers, from t1 to t6. In the distribution of electric fields shown in Figure 13a, it was observed that when the absorption peaks were at 320 nm, 435 nm, 670 nm, and 1425 nm, there were 3, 2, 1, and 0 Fabry–Perot cavity resonances appearing sequentially. Similarly, in the magnetic field distribution illustrated in Figure 13b, when the absorption peaks were at 320 nm, 435 nm, 670 nm, and 1425 nm, there were 4, 3, 2, and 1 Fabry–Perot cavity resonances appearing in the same order.

These findings highlight that the multi-wavelength resonance absorption observed can be attributed to both Fabry–Perot cavity resonance and LSPR. The occurrence of multi-wavelength resonance absorption in the optical resonant absorber’s medium was rooted in the potential for multiple Fabry–Perot cavity resonances. This occurrence depends on both the medium’s characteristics and the structural design of the optical resonant absorber. Fabry–Perot cavity resonance arises from the reflection and refraction of light waves within the medium, and different structures or multi-layered media can give rise to multiple resonance peaks. These resonance wavelengths are dictated by the optical path difference of the Fabry–Perot cavity, which encompasses the round-trip optical path of the light wave within the cavity. This optical path is modulated by factors such as the refractive index of the medium and the thickness of the film layers. While the existence of multiple peaks within the same Fabry–Perot cavity can be ascribed to distinct modes or orders of reflection and interference, it is notable that an escalating number of resonances within the same cavity may signify shorter resonance wavelengths.

Figure 14 presents the evolution of absorption performance of the designed ultra-wideband optical absorber concerning changes in incident light angles from 0° to 90°, considering both TE (Figure 14a) and TM (Figure 14b) polarizations. The simulation results in Figure 14 represent a curve showing absorptivity surpassing 0.900 across various incident wavelengths and angles. It is noteworthy that when the absorber was stimulated under TE polarization, as Figure 14a shows, and the wavelength spanned from approximately 420 nm to 2300 nm, absorptivity exceeding 0.900 was observed for incident light with angles between 0° and approximately 48° to 70°. This highlights the exceptional performance of the absorber in achieving high absorptivity within a specific range of incident angles and wavelengths during TE polarization. Conversely, when the absorber was activated under TM polarization, as Figure 14b shows, and the wavelength ranged from 420 nm to 2250 nm, the absorptivity exceeding 0.900 gradually changed in the range of approximately 55° and 65°. As the wavelength extended beyond 2250 nm to 2600 nm, the absorptivity exceeding 0.900 declined from 50° to 0°. These findings suggest that the designed ultra-wideband optical absorber is insensitive to incident angles. Because the investigated absorber has highly symmetrical structure, it presents exceptional absorption performance independent of polarization. This feature contributes to the absorber’s versatility and effectiveness across a broad range of incident angles and polarization states.

The absorptivity caused by the TE-polarized and TM-polarized light was investigated at normal incidence as well as different oblique angles for the achievement of a multi-wavelength resonant absorber, and the results are presented in Figure 15. In both absorption diagrams, spanning angles from 0° to 90°, prominent absorptions were observed at 320 nm, 435 nm, 670 nm, and 1425 nm. When TE-polarized light exceeded 65°, and TM-polarized light surpassed 50°, the width of the absorption peaks gradually decreased. Additionally, the absorption peaks induced by TM-polarized light exhibited a slight blue shift as the excitation angle increased. These results indicate that the angle of incidence light did not significantly affect the absorption characteristics of the investigated device. In other words, regardless of the incident angle, the absorption performance of the multi-wavelength resonant absorber showed little variation. Nevertheless, this study proposes a novel design wherein the planar metamaterial structure not only exhibits ultra-wideband optical absorber characteristics but also possesses multi-wavelength resonant absorber properties. Furthermore, by adjusting the thickness of YSZ, it is possible to shift or tune the wavelength of the resonant waves. This technology offers significant value as a reference for future designs aiming to integrate various functional absorbers within the same optical component. The examined multi-functional absorber has attained ultra-wideband and high absorptivity properties, along with the capability of serving as a multi-wavelength resonant absorber with a tunable wavelength feature.

6. Conclusions

The multifunctional absorber under investigation demonstrated a significant absorptivity exceeding 0.9 across the ultra-wideband spectrum of 525–2275 nm. Moreover, it exhibited high absorptivity in a multi-wavelength resonant pattern, with a weak absorption peak of 0.739 at 320 nm and notable absorptivity values of 0.949, 0.970, and 0.999 at triple wavelengths approximately centered on 435 nm, 670 nm, and 1425 nm, respectively. When the thickness of the t7 YSZ layer varied from 210 nm to 250 nm the light illuminated from the Al₂O₃ layer, three absorption peaks showed a noticeable redshift from around 390 nm, 645 nm, and 1260 nm to around 445 nm, 680 nm, and 1470 nm. When employing Al₂O₃, SiO_2, or MgF₂ as anti-reflection coatings, the absorptivity extended beyond 0.900 in the wavelength ranges of 520 nm to 2275 nm, 435 nm to 2065 nm, and 435 nm to 2010 nm, respectively. The highest absorptivity values were observed to be 0.990, 0.964, and 0.955 for Al₂O₃, SiO₂, or MgF₂, respectively. Additionally, the average absorptivity values for wavelengths exceeding 0.900 were 0.963, 0.944, and 0.933 for the respective coatings. As Al₂O₃ was used as the anti-reflection layer and within the absorption bands for AM1.5G solar energy spanning 280 nm to 400 nm, 400 nm to 700 nm, 700 nm to 1400 nm, and 1400 nm to 3000 nm, the absorber achieved absorptivity of 0.289, 0.909, 0.962, 0.960, and 0.066, respectively, and an overall absorptivity of 0.900 within the entire spectrum from 280 nm to 4000 nm. In this study, an absorber featuring ultra-wideband and high absorptivity properties, as well as a multi-wavelength resonant absorber with a tunable wavelength feature, has been realized.