Abstract
In this paper, we report our recent progress related to advanced digital signal processing (DSP) technologies to address the strong inter-core crosstalk (IC-XT) during multicore fiber (MCF) optical transmissions. MCF transmission technology has significant potential to break through the capacity crunch of single-mode fiber (SMF) transmissions. However, strong coupling among cores, namely, inter-core crosstalk (IC-XT), is unavoidable for high-density space-division multiplexing (SDM) transmissions using MCFs with the standard cladding size. To deal with this issue, we propose some novel DSP structures to eliminate IC-XT with considerable simplicity, based on the neural network equalizer (NNE)-based multiple-input and multiple-output digital signal processing (MIMO-DSP). The traditional NNE-based MIMO-DSP method has the ability to process the coupled SDM tributaries transmitted over MCFs; however, it exhibits complexity limitations for practical implementations. The implementation complexity of the NNE-based method is mainly attributed to the time-consumption of the training process and the large weight (neurons) numbers of the equalizers. Thus, we propose two main approaches to simplify NNE-based MIMO-DSP for the practical implementation of MCF transmissions: (1) To reduce the time-consumption of the training process in NNE-based MIMO-DSP, the idea of transfer learning (TL) is employed for initializing the weights, resulting in the faster convergence of the equalizers. (2) IC-XT cancellation is performed along with MIMO-DSP; thus, the dimensionality of MIMO-DSP could be reduced. To validate the performance improvement of the proposed machine learning DSP methods, both simulations and experiments related to transmissions and reception over MCFs were conducted. The results indicate that the proposed novel DSP structures possess the advantages of reduced complexity and improved robustness to IC-XT, which is beneficial for the next-generation high-density SDM transmissions.
1. Introduction
Driven by the ever-increasing data traffic due to emerging big-data industries such as autonomous driving, high-performance computers, and AR/VR, high-capacity optical fiber transmissions technology is urgently demanded. However, the traditional single-mode fiber (SMF) finds limitations in further increasing the capacity, mainly due to the fiber’s nonlinearity when facing the capacity crunch. Space-division multiplexing (SDM) is a promising approach to scale the capacity with space multiplicity, thus outperforming SMFs whose capacity complies with the logarithmic relationship to the power supply. On the other hand, the cross-sectional power density of fibers during transmission can be significantly reduced by using SDM methods. Optical SDM transmission solutions mainly include multiple-fiber ribbons, multi-core fibers (MCFs), and few-mode fibers (FMFs). In the case of some typical scenarios with restricted physical space for cables, like submarine communications, the MCF solution is advantageous compared to the others, thanks to the balanced performance of spatial density and implementation complexity [1,2,3,4]. Thus, a lot of research has been reported in recent years related to the demonstration of high-capacity optical communications using MCFs [5,6,7,8,9,10]. However, the majority of experiments on MCF transmissions have been conducted using MCFs with nonstandard cladding sizes. When considering practical applications, it is worth noting that MCFs with the standard cladding size are very important to prevent mechanical failures during fiber fabrication and the cabling procedure [11]. For the purpose of fabricating the weakly-coupled MCFs (WC-MCFs) within the C/L-band, the accommodated core count typically hovers around four to maintain low IC-XT. As a consequence, the fabrication of higher-density MCFs containing more cores within the standard cladding size faces the problem of notable IC-XT [1,12]. For realizing higher-density MCF transmissions, one complementary solution is implementing multiple-input multiple-output digital signal processing (MIMO-DSP) at the receiver to mitigate the IC-XT during transmissions.
Nevertheless, the implementation complexity of MIMO-DSP is the key concern when considering the practical deployment of the MCF transmissions [13,14]. The main reasons contributing to MIMO-DSP’s complexity are the larger tap numbers, because a higher dimensionality of MIMO is required to address the IC-XT issue. For instance, a MIMO-DSP configuration is required to address the IC-XT of N-core fibers transmission. To deal with this, several simplified MIMO-DSP methods for MCF transmissions have been proposed. The frequency-domain equalizer (FDE) has been experimentally studied, presenting a lower complexity than the time-domain solution for SDM links [15,16,17]. Another possible approach to reduce complexity is to shorten the MIMO-DSP tap length, which has been investigated for addressing the polarization coupling issue in SMFs [18]. However, it is hard to reduce the dimensionality of MIMO-DSP to mitigate IC-XT due to the presence of IC-XT. Consequently, it is of great significance if the full MIMO-DSP ( MIMO configuration for N-core fibers) scheme can be deconstructed into a partial MIMO-DSP structure.
On the one hand, the employment of machine learning (ML) algorithms in equalizers has shown the improved signaling performance of optical communications [19,20,21]. A common approach for addressing the IC-XT in MCF transmissions involves employing ML to achieve high performance [22]. However, the application potential of ML-based equalizers has always been questioned from the perspective of implementation complexity [23]. For instance, a neural network equalizer (NNE) normally requires a large number of previously known samples to train the network before equalization, which is very time-consuming. Typically, in the case of optical routing, when the optical communication link switches to another link with a different transmission distance, the optimal parameters of the NNE should be reinitialized and trained due to the changes of the noise distribution of the transmission channel [24,25], which introduces a lot of complexity.
As mentioned before, the complexity of NNE-based MIMO-DSP is mainly contributed by the time consumption of training process and the larger number of weights needed to address the IC-XT during MCF transmissions. In this work, we propose two approaches to simplify NNE-based MIMO-DSP for addressing the IC-XT issue in MCF transmissions. The first approach is to use a transfer learning (TL) scheme to initialize the NNE parameters when different optical links are transferred after optical routing, for the purpose of speeding up the training process to accomplish equalizer weight convergence. Here, the channel information state (CIS) difference under investigation for TL is the cut-off frequency in faster-than-Nyquist (FTN) systems. The motivation behind the employment of FTN technology here was to improve the spectral efficiency (SE) in every spatial dimension of MCF transmission systems. Different cut-off frequencies result in a trade-off in performance between SE and Q factors (any other metrics for evaluating the signaling performance). To shorten the training time of NNE-based MIMO-DSP, we utilize TL to expedite convergence, with initialization parameters migrated from the source link. Simulations verify that the convergence speed with assistance by TL is 83.3% faster than that of the classical DFNNE for the transmission of 50-Gbaud DP-16QAM FTN signals over the four-core WC-MCF. As the second approach, we propose an innovative method to reduce MIMO-DSP dimensionality in MCF transmissions by suppressing random IC-XT through orthogonal pulse shaping. Experimental validation is conducted to suppress the IC-XT of a 35 m core pitch four-core MCF link by four independent 2 × 2 MIMO-DSP modules.
2. Principles of NNE-Based MIMO-DSP and Approaches for Its Simplification
2.1. Transfer Learning of NNE-Based MIMO-DSP
In order to improve the SE of SDM transmission systems, FTN technology was adopted to process signals at the transmitter, thereby enabling a reduction in spectral bandwidth without sacrificing information rate. However, the inter-symbol crosstalk (ISI) due to narrow filtering, which interacts with IC-XT in MCF, introduces nonlinear distortions [26], complicating the equalization and decoupling of each SDM channel using traditional MIMO-DSP methods. Since traditional MIMO-DSP approaches based on constant modulus algorithm (CMA) and least mean square (LMS) algorithm are unable to eliminate the nonlinear distortion arising from interaction of ISI and IC-XT, we employed the decision feedback neural network equalizer (DFNNE) to equalize the nonlinearly distorted signals. The input of DFNNE consists of eight components for the feedforward module, corresponding to two polarizations in each core. The presence of the decision feedback module returns the decided symbol information to the equalizer, which aids in mitigating the nonlinear distortion. To address the complexity of SDM systems, we utilize a DFNNE with only one hidden layer in this study, as depicted in Figure 1. D represents the decided symbol and represents the delay symbol. The input of the hidden layer connects eight tributaries of previously known symbols, corresponding to the reception of signal over four-core MCFs, as well as the decided and delayed tributaries through the decision feedback module. Training the weights of the DFNNE using prior-known sequences is expected to mitigate IC-XT, while the ISI resulting from narrow filtering of FTN can be addressed by utilizing the decision feedback structure.
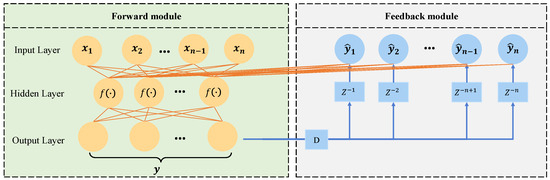
Figure 1.
Structure of the decision feedback neural network equalizer-based MIMO-DSP to equalize the nonlinear distortions.
For N-core MCF transmissions, the input of the feedforward module in DFNNE comprises vectors, represented by . Similarly, the input of the DFNNE from the feedback module also consists of vectors after the decision process, denoted as , where signifies the decision operation applied to samples. Consequently, the outputs of DFNNE, denoted by can be expressed as
where , and , and are the weighted and bias matrices respectively, and the activation function is denoted by . The pseudocode in Algorithm 1 delineates the training process for DFNNE. Initially, the neural networks are initialized, and the training dataset is prepared. The algorithm iterates through a specified number of training epochs, each comprising subsets from the training dataset. During each epoch and for each subset of training data, the weights of each neural network in DFNNE are updated using the backpropagation method. Notably, the algorithm incorporates the feedback module by amalgamating current inputs with previous outputs, thereby facilitating the integration of historical information in the training process. Finally, the algorithm retrieves the current outputs and updates the previous outputs for subsequent iterations.
Since the NNE-based MIMO-DSP needs to be retrained when the CSI of optical transmission links is changed, for the FTN signaling over MCF, the corresponding CSI is dependent on both IC-XT and FTN cut-off frequency. Consequently, the considerable time consumption is expended in reinitializing the parameters of the NNE-based MIMO-DSP for newly switched links with varying CSI. Transfer learning (TL) streamlines the training of the new equalizer implemented in the switched link by leveraging prior knowledge gleaned from the preceding link. This approach not only reduces the training time but also minimizes the volume of data required, owing to the similarity between two links. Thus, employing the TL approach simplifies the training process of the NNE-based MIMO-DSP for MCF transmissions.
| Algorithm 1 DFNNE training process |
|
2.2. Partial MIMO-DSP Enabled by the IC-XT Cancellation via Orthogonal Filtering
To further reduce the complexity of MIMO-DSP, orthogonal pulse shaping for IC-XT cancellation can be used to reduce the dimensionality. Orthogonal filters are constructed by combining the root-raised cosine filter with sine–cosine waveforms. For a four-core MCF with a rectangular core arrangement, in-phase filters can be designated for diagonal cores, while quadrature filters suit neighboring cores. To expand the repertoire of usable orthogonal filters in N-core MCFs, techniques such as frequency resolving, and multidimensional signaling can be employed [27]. At the receiver, matching filters demodulated corresponding tributaries from the coupled sequences. By suppressing the quadrature component of the matching filter, the impact of IC-XT can be mitigated without necessitating a high-dimensional MIMO-DSP. Concerning the proposed simplified MIMO-DSP structure, four lanes of complex sequences require preshaping by finite impulse response (FIR) filters, forming a Hilbert pair: and at the transmitter, where denotes center frequency of sinusoidal waveform and signifies the square-root-raised cosine filter.
2.3. Performance Metrics
To evaluate the performance of our methods for MCF transmissions, both mean square error (MSE) and the Q factor were utilized as metrics. MSE served as a standard metric for assessing the convergence performance of MIMO-DSP during each epoch, while Q factor quantitatively examined the converged performance after a certain number of epochs. This paper presents two distinct DSP methods for MCF transmissions: (1) TL assisted DFNNE (TL-DFNNE); (2) IC-XT cancellation based on orthogonal filtering. For TL-DFNNE, the final evaluation metric, namely, Q factor, was employed to assess the signaling performance. Regarding the evaluation of IC-XT cancellation, MSE was the appropriate metric for investigating MIMO convergence performance.
3. Results and Discussion
In this section, we explore the signaling performance in terms of complexity reduction through the utilization of the two proposed methods in MCF transmissions. Both simulations and experiments were conducted.
3.1. MCF Transmissions Model Based on Coupled Nonlinear Schrödinger Equation
To verify the feasibility of the proposed TL-DFNNE in reducing the complexity of signal reception in MCF transmission, we implemented a concrete MCF transmission model based on the coupled nonlinear Schrödinger equation (CNLSE) [28]. CNLSE effectively models MCF transmissions by comprehensively considering fiber dispersion, nonlinearities, polarization coupling, and IC-XT. Optical field evolution in core A can be described with IC-XT provided by core B using CNSE as follows:
where and are the energies of cores A and B, is the attenuation coefficient, and represents nonlinearity coefficient. is the coupling coefficient between core A and core B, and we utilize the coupling length = as a parameter to investigate IC-XT influence. This assumption is accurate when the step size of split-step Fourier calculation is smaller than or equal to the coupling length . , , and are the Taylor expansion coefficients of at the central angular frequency and can be given by
can be given by the dispersion coefficient :
where and c represent the optical wavelength and the speed of light in vacuum, respectively. can be further given by the dispersion slope :
To ensure the feasibility of the four-core MCF transmission model, we conducted a self-consistency examination to verify both the inter-core crosstalk (IC-XT) and the spatial mode dispersion (SMD). Simulation parameters are presented in Table 1. IC-XT value can be estimated by measuring the power matrices for all cores at the receiver. When an optical pulse with power P was injected into core 1 while the other cores have no pulses, the output power of core i were measured. Subsequently, the actual IC-XT was calculated based on the power ratio.

Table 1.
Parameters in simulations.
Figure 2a depicts the error bars representing the set IC-XT and the estimated IC-XT after 4000 iterations of testing. We simulated IC-XT as a Gaussian distribution with a constant variance. The perfect straight line in Figure 2a indicates the agreement between the set and measured values of IC-XT. To examine spatial mode dispersion (SMD), fiber length was set to 100 km with an SMD of 1 ps/km. During the SMD check, IC-XT should be minimized to observe inter-core skew. Separated pulses become observable when IC-XT can be ignored at a coupling length of 1000 km, as demonstrated in Figure 2b. With the SMD set at 1 ps/km with a transmission length of 100 km, the relative delay between cores was 100 ps. When the coupling length was reduced to 1 km, the received pulses of all cores are plotted in Figure 2c, indicating the advantages of strong-coupled MCF in reducing SMD compared to WC-MCF.
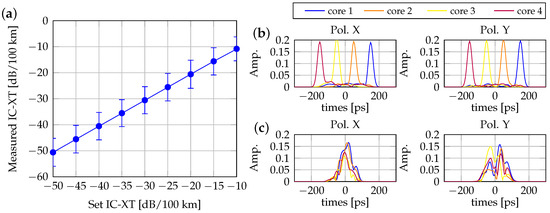
Figure 2.
Self-consistency examinations on the model of 100-km four-core MCF links: (a) Error bar of the estimated IC-XT values. Received pulses in four cores (b) with coupling length at 1000 km and (c) with coupling length at 1 km.
3.2. Simulation Results of the TL-Aided NNE-Based MIMO-DSP
Based on the conducted numerical model of MCF transmission, we further utilized the co-simulation platform of MATLAB and Pytorch to evaluate the performance of the proposed TL-aided NNE-based MIMO-DSP. The simulation setup for the four-core MCF transmission is illustrated in Figure 3. A capacity of 1.6 Tbps was achieved using the DP-16QAM modulation format at a baud rate of 50 Gbaud. The launched optical power was set at 7 dBm. To facilitate the 100 km transmission, an optical amplifier with a noise figure of 5 dB was employed after the fan-out coupler. The fiber attenuation factor, second-order dispersion coefficient, nonlinear coefficients, and SMD were set at 0.16 dB/km, 16 ps/nm/km, 0.81 × W/m, and 27 ps/km, respectively. The coupling length of the MCF was set at 100 m to simulate strong coupling during MCF transmissions.
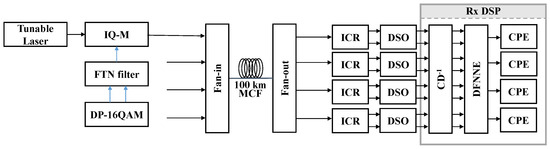
Figure 3.
Simulation setup for evaluating the TL-assisted MIMO-DSP.
For the DFNNE, we utilized the tanh function as the activation function and opted for the stochastic gradient descent (SGD) algorithm as the optimization algorithm. To strike a balance between the signaling performance of DFNNE and the computational complexity of the network, we set the feedforward length of symbol vectors at 15 for every mode and the feedback length at 11. This implies that the number of neurons in the input layer of the DFNNE is 416, calculated as . The number of neurons in the hidden layer was 64, and the number of output neurons was 16. To ensure sufficient convergence, the length of symbols used for DFNNE parameter training was 20,000, and the number of iterations was 50.
To investigate the effect of TL under different cut-off frequencies of FTN filters and coupling lengths , we set the cut-off frequency of the FTN filter (the source link) at 18.75 GHz and the coupling length at 100 m. To examine the similarity between the target link and the source link, we varied the CSI of the target link with cut-off frequencies at 16.25 GHz, 17.5 GHz, 20 GHz, and 21.25 GHz, respectively, and coupling lengths at 50 m and 200 m. Figure 4a indicates that the Q factors of the target link converge faster when cut-off frequencies are set at 17.5 GHz and 20 GHz, compared to 16.25 GHz and 21.25 GHz. This is because the TL-DFNNE performance is enhanced when the similarity between the source link and the target link is greater. Additionally, the initial Q factor of the target link with a cut-off frequency of 17.5 GHz demonstrates approximately a 5 dB improvement compared to the source link, resulting in approximately an 83.3% improvement in convergence speed at a Q factor of 8 dB.
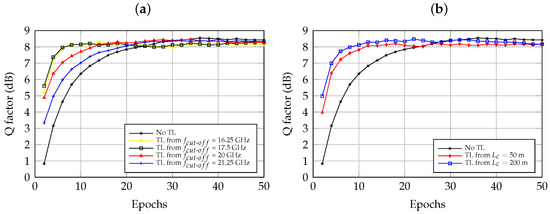
Figure 4.
Q factor vs. epochs for the target link with cut-off frequency at 18.75 GHz and coupling length at 100 m migrated from the source links (a) with cut-off frequency at 16.25 GHz, 17.5 GHz, 20 GHz, and 21.25 GHz; (b) with coupling length at 50 m and 200 m.
In addition, the DFNNE converges faster when transferring from a lower cut-off frequency to a higher cut-off frequency. Figure 4b shows that DFNNE converges better when transferring from a smaller coupling length to a larger coupling length.
3.3. Experimental Setup
The experimental setup for the four-core MCF transmissions is illustrated in Figure 5. The optical transmitter comprised several components, including the generation of digital QPSK symbols with orthogonal pulse shaping, a 40 Gsa/s digital-to-analogue converter (DAC), a tunable laser operating at 1550 nm, and a 20 GHz IQ modulator. To ensure the independence of the four optical signal lanes, three delay fibers corresponding to 2000 relative symbol delays were employed before the fan-in coupler. The four-core MCF under test was designed and fabricated with a 35 m core pitch and standard cladding diameter of 125 m [29]. The randomness of the end-to-end IC-XT of the 10 km MCF link was characterized by measuring the output power of the fan-out coupler while injecting an optical signal (0 dBm) into a single core at the transmitter. The recorded IC-XT values, as displayed in Table 2, show IC-XT levels at −6 dB with a notable power fluctuation exceeding 4 dB during measurements. Typically, addressing IC-XT requires adaptive 8 × 8 MIMO-DSP. To capture the coupled four-core signals, we employed a time-division-multiplexing (TDM) receiver [30], which facilitates the synchronization of eight distinct signal lanes using a four-channel oscilloscope.
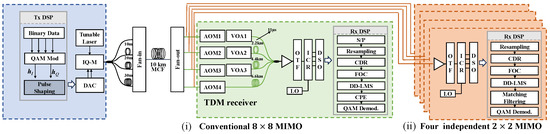
Figure 5.
Experimental validation of the simplified MIMO-DSP in four-core MCF links by orthogonal pulse shaping. Insets: (i) Conventional MIMO-DSP with the assistance of TDM receiver. (ii) Independent MIMO-DSP modules enabled by orthogonal pulse shaping.

Table 2.
Crosstalk matrix of the used MCF (dB).
The TDM receiver, along with the subsequent DSP flowchart including 8 × 8 MIMO-DSP, is depicted in inset (i) in Figure 5. Regarding the proposed simplified MIMO-DSP structure, four lanes of complex sequences need to be preshaped by FIR filters, forming a Hilbert pair and at the transmitter, where represents the square-root-raised cosine shaping filter. The center frequency can be calculated by , where represents the roll-off factor set at 0.1. Upsampling by a factor of 5 was performed during pulse shaping, resulting in a symbol rate of 8 GBaud for shaped QPSK symbols, with the DAC operating at 40 Gsa/s. Considering the rectangular arrangement of the four-core MCF (with stronger crosstalk occurring between adjacent cores), the shaping filters were constructed to be orthogonal exclusively for adjacent cores. It is noteworthy that for MCF signal transmission with orthogonal pulse shaping, there is no need for synchronizing the recording of four-core data at the receiver because it is desired that IC-XT among cores is alleviated. The corresponding receiving DSP flowchart is depicted in inset (ii) in Figure 5. The training sequences are the shaped QPSK symbols, whose constellations are plotted on the left of Figure 5, with a training length of 10,000.
3.4. Experimental Results of Orthogonal Filtering
Symbol rates were set at 8 Gbaud, corresponding received signal power was −20 dBm, and the LO power was 0 dBm. Due to the rotation of state of polarization, the dimensionality of the full MIMO-DSP for four-core MCF link was 8. As indicated in Figure 6a, the full-MIMO structure exhibits the lowest converged values compared to the other two methods. If IC-XT was not well mitigated, MSE of the independent 2 × 2 MIMO-DSP modules was the worst case due to the strong IC-XT. With the assistance of orthogonal pulse shaping, MSE performance was improved with a lower converged value and faster convergence by using the deconstructed 2 × 2 MIMO-DSP modules. Moreover, the difference in the shape of constellations after orthogonal pulse shaping, which is depicted in Figure 5, is beneficial for the MSE convergence. By using the full-MIMO structure and independent 2 × 2 MIMO-DSP modules with IC-XT cancellation, the corresponding 1-sample/symbol taps after 10,000 iterations are shown in Figure 6b,c, respectively. As indicated by the taps of the full-MIMO structure, the pulse spreading due to DGD and IC-XT covers more than 50 symbols. With the IC-XT cancellation, the 2 × 2 MIMO-DSP taps has shorter coverage, which is also beneficial to reduce the MIMO-DSP complexity in addition to the MIMO dimensionality reduction.
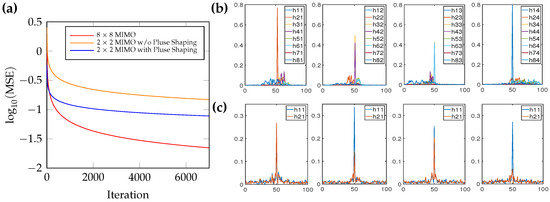
Figure 6.
(a) MSE curves (after fitting) of the full MIMO-DSP (8 × 8), independent 2 × 2 MIMO-DSP modules with and without IC-XT cancellation. Tap coefficients of (b) the full MIMO-DSP, (c) independent 2 × 2 MIMO-DSP modules.
To investigate the performance of the simplified MIMO-DSP structure enabled by IC-XT cancellation, constellations of signals transmitted over 10-km MCF are shown in Figure 7. The full-MIMO structure exhibits the best performance with the clearest constellations. Due to the existence of random IC-XT, the independent 2 × 2 MIMO-DSP struggles to recover the coupled signals along with the inconsistent performance of four cores. Thanks to the IC-XT suppression, clearer constellation can be obtained by orthogonal pulse shaping.
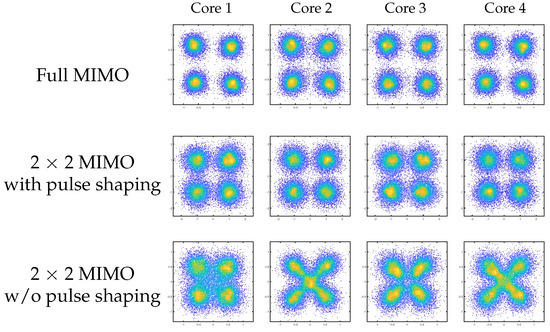
Figure 7.
Comparisons of the constellations of the full 8 × 8 MIMO-DSP, independent 2 × 2 MIMO-DSP with and without IC-XT cancellation for processing the four-core MCF transmitted signals.
As mentioned above, the IC-XT exhibits significant randomness during the crosstalk matrix measurement, which can lead to outage probability in SDM links if not well mitigated. Consequently, we recorded the Q factors through several trials to process the time-variant data sequences. The Q factors of the recorded signals transmitted over MCFs at −20 dBm power are shown in Figure 8 using different MIMO-DSP structures. It indicates that the fluctuation of Q factors is about 7 dB by using 2 × 2 MIMO-DSP without IC-XT cancellation, which is harmful to the outage performance of transmissions. As for the full-MIMO structure and 2 × 2 MIMO modules with orthogonal pulse shaping, Q factor fluctuations are reduced to 1.8 dB and 1.2 dB, respectively. Compared to the full-MIMO structure, a 1.25 dB Q penalty is observed by using the deconstructed 2 × 2 MIMO-DSP modules. Nonetheless, the stable IC-XT cancellation induces an over 4.6 dB Q factor gain by using the simplified 2 × 2 MIMO-DSP modules.
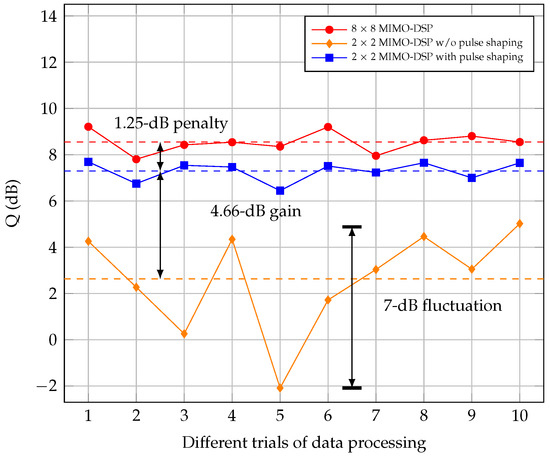
Figure 8.
Comparisons of Q factors of the full 8 × 8 MIMO-DSP, independent 2 × 2 MIMO-DSP with and without IC-XT cancellation for processing the four-core MCF transmitted signals.
4. Conclusions
The complexity of MIMO-DSP is mainly attributed to the time-consuming training process and the dimensionality of the equalizer. To simplify the NNE-based MIMO-DSP in MCF transmission systems, we proposed two novel methods aimed at shortening the training process of the equalizer and reducing the dimensionality of MIMO-DSP. In addressing the time consumption issue during the training process, we utilized the MCF transmission model based on coupled nonlinear Schrödinger equations, employing the transfer learning (TL) concept to apply the weights of the source link to the newly-switched link. Simulation results demonstrated that TL-DFNNE performs better when the similarity between the source link and the target link is higher, achieving up to an 83.3On the other hand, we employed the time-division multiplexing (TDM) receiver to capture the four-core signals, and the dimensionality of MIMO-DSP can be further reduced by using the proposed IC-XT cancellation method. This approach helps process the coupled signals by utilizing four independent MIMO modules. The novel use of orthogonal pulse shaping in MCF transmission systems enables MIMO-DSP dimensionality reduction and stable IC-XT cancellation, resulting in a Q-factor gain of 4.6 dB over standalone MIMO-DSP, which is beneficial for high-density SDM transmission. The main results of the two methods for simplifying the complexity of MIMO-DSP are summarized in Table 3.

Table 3.
Benchmarks of the simplified MIMO-DSP performance.
Author Contributions
Conceptualization, D.H., J.C., J.X. and L.S.; methodology, D.H., J.C., J.X. and L.S.; software, D.H., J.C., J.X. and L.S.; validation, D.H., J.C., J.X. and L.S.; formal analysis, D.H., J.C., J.X. and L.S.; investigation, D.H., J.C., J.X. and L.S.; resources, D.H., J.C., J.X. and L.S.; data curation, D.H., J.C., J.X. and L.S.; writing—original draft preparation, D.H., J.C., J.X. and L.S.; writing—review and editing, D.H., J.C., J.X. and L.S.; visualization, D.H., J.C., J.X. and L.S.; supervision, L.S., L.M., B.C., Y.C. and G.N.L.; project administration, L.S., L.M., B.C., Y.C. and G.N.L.; funding acquisition, L.S., L.M., B.C., Y.C. and G.N.L. All authors have read and agreed to the published version of the manuscript.
Funding
National Key R&D Program of China grant number 2022YFB2903000.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rademacher, G.; van den Hout, M.; Luís, R.S.; Puttnam, B.J.; Sciullo, G.D.; Hayashi, T.; Inoue, A.; Nagashima, T.; Gross, S.; Ross-Adams, A.; et al. Randomly Coupled 19-Core Multi-Core Fiber with Standard Cladding Diameter. In Proceedings of the 2023 Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 5–9 March 2023; p. Th4A.4. [Google Scholar]
- Downie, J.D.; Liang, X.; Makovejs, S. Assessing Capacity and Cost/Capacity of 4-Core Multicore Fibers against Single Core Fibers in Submarine Cable Systems. J. Light. Technol. 2020, 38, 3015–3022. [Google Scholar] [CrossRef]
- Tateno, S.; Takeshita, H.; Hosokawa, K.; de Gabory, E.L.T. Capacity Expansion in Submarine Cable Systems with Bidirectional Transmission Using 4-Core-or-More MCF and MC-EDFA. J. Light. Technol. 2023, 41, 3943–3949. [Google Scholar] [CrossRef]
- Takeshita, H.; Nakamura, K.; Matsuo, Y.; Inoue, T.; Masuda, D.; Hiwatashi, T.; Hosokawa, K.; Inada, Y.; de Gabory, E.L.T. Demonstration of Uncoupled 4-Core Multicore Fiber in Submarine Cable Prototype With Integrated Multicore EDFA. J. Light. Technol. 2023, 41, 980–988. [Google Scholar] [CrossRef]
- Luís, R.S.; Rademacher, G.; Puttnam, B.J.; Eriksson, T.A.; Furukawa, H.; Ross-Adams, A.; Gross, S.; Withford, M.; Riesen, N.; Sasaki, Y.; et al. 1.2 Pb/s Throughput Transmission Using a 160 μm Cladding, 4-Core, 3-Mode Fiber. J. Light. Technol. 2019, 37, 1798–1804. [Google Scholar] [CrossRef]
- Soma, D.; Wakayama, Y.; Beppu, S.; Sumita, S.; Tsuritani, T.; Hayashi, T.; Nagashima, T.; Suzuki, M.; Yoshida, M.; Kasai, K.; et al. 10.16-Peta-B/s Dense SDM/WDM Transmission Over 6-Mode 19-Core Fiber Across the C+L Band. J. Light. Technol. 2018, 36, 1362–1368. [Google Scholar] [CrossRef]
- Fresi, F.; Imran, M.; Malacarne, A.; Meloni, G.; Sorianello, V.; Forestieri, E.; Potì, L. Advances in optical technologies and techniques for high capacity communications. J. Opt. Commun. Netw. 2017, 9, C54–C64. [Google Scholar] [CrossRef]
- Ma, M.; Chang, H.; Gao, R.; Guo, D.; Liu, X.; Yuan, M. Modeling of Multi-Core Fiber Channel Based on M-CGAN for High Capacity Fiber Optical Communication. In Proceedings of the 2023 Asia Communications and Photonics Conference/2023 International Photonics and Optoelectronics Meetings (ACP/POEM), Wuhan, China, 4–7 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Kingsta, R.M.; Selvakumari, R.S. A review on coupled and uncoupled multicore fibers for future ultra-high capacity optical communication. Optik 2019, 199, 163341. [Google Scholar] [CrossRef]
- Awaji, Y.; Sakaguchi, J.; Puttnam, B.J.; Luis, R.S.; Mendinueta, J.M.D.; Klaus, W.; Wada, N. High-capacity transmission over multi-core fibers. Opt. Fiber Technol. 2017, 35, 100–107. [Google Scholar] [CrossRef]
- Matsui, T.; Yamada, Y.; Sagae, Y.; Nakajima, K. Standard cladding diameter multi-core fiber technology. In Proceedings of the 2021 Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 6–10 June 2021; p. Tu6B.4. [Google Scholar]
- Ryf, R.; Alvarado-Zacarias, J.C.; Wittek, S.; Fontaine, N.K.; Essiambre, R.J.; Chen, H.; Amezcua-Correa, R.; Sakuma, H.; Hayashi, T.; Hasegawa, T. Coupled-Core Transmission over 7-Core Fiber. In Proceedings of the 2019 Optical Fiber Communication Conference Postdeadline Papers, San Diego, CA, USA, 3–7 March 2019; p. Th4B.3. [Google Scholar]
- Sakamoto, T.; Mori, T.; Wada, M.; Yamamoto, T.; Yamamoto, F.; Nakajima, K. Strongly-coupled multi-core fiber and its optical characteristics for MIMO transmission systems. Opt. Fiber Technol. 2017, 35, 8–18. [Google Scholar] [CrossRef]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Shibahara, K.; Lee, D.; Kobayashi, T.; Mizuno, T.; Takara, H.; Sano, A.; Kawakami, H.; Miyamoto, Y.; Ono, H.; Oguma, M.; et al. Dense SDM (12-Core × 3-Mode) Transmission over 527 km with 33.2-ns Mode-Dispersion Employing Low-Complexity Parallel MIMO Frequency-Domain Equalization. J. Light. Technol. 2016, 34, 196–204. [Google Scholar] [CrossRef]
- Inan, B.; Spinnler, B.; Ferreira, F.; van den Borne, D.; Lobato, A.; Adhikari, S.; Sleiffer, V.A.J.M.; Kuschnerov, M.; Hanik, N.; Jansen, S.L. DSP complexity of mode-division multiplexed receivers. Opt. Express 2012, 20, 10859–10869. [Google Scholar] [CrossRef] [PubMed]
- Faruk, M.S.; Kikuchi, K. Adaptive frequency-domain equalization in digital coherent optical receivers. Opt. Express 2011, 19, 12789–12798. [Google Scholar] [CrossRef] [PubMed]
- Lavery, D.; Thomsen, B.C.; Bayvel, P.; Savory, S.J. Reduced Complexity Equalization for Coherent Long-Reach Passive Optical Networks. J. Opt. Commun. Netw. 2015, 7, A16–A27. [Google Scholar] [CrossRef]
- Pan, X.; Wang, X.; Tian, B.; Wang, C.; Zhang, H.; Guizani, M. Machine-Learning-Aided Optical Fiber Communication System. IEEE Netw. 2021, 35, 136–142. [Google Scholar] [CrossRef]
- Chen, G.; Du, J.; Sun, L.; Zheng, L.; Xu, K.; Tsang, H.K.; Chen, X.; Reed, G.T.; He, Z. Machine Learning Adaptive Receiver for PAM-4 Modulated Optical Interconnection Based on Silicon Microring Modulator. J. Light. Technol. 2018, 36, 4106–4113. [Google Scholar] [CrossRef]
- Sun, L.; Du, J.; Xu, K.; Liu, B.; He, Z. K-Means Assisted Soft Decision of PAM4 to Mitigate Level Nonlinearity and Level-Dependent Noise for VCSEL-Based 100-Gbps 100-m MMF Optical Interconnection. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; p. M1F.5. [Google Scholar]
- Xiong, Y.; Yang, Y.; Ye, Y.; Rouskas, G.N. A machine learning approach to mitigating fragmentation and crosstalk in space division multiplexing elastic optical networks. Opt. Fiber Technol. 2019, 50, 99–107. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Bülow, H.; Leven, A. Applying Neural Networks in Optical Communication Systems: Possible Pitfalls. IEEE Photonics Technol. Lett. 2017, 29, 2091–2094. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Ji, T.; Ji, H.; Shieh, W. Transfer Learning Aided Neural Networks for Nonlinear Equalization in Short-Reach Direct Detection Systems. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; p. T4D.4. [Google Scholar]
- Zhang, J.; Xia, L.; Zhu, M.; Hu, S.; Xu, B.; Qiu, K. Fast remodeling for nonlinear distortion mitigation based on transfer learning. Opt. Lett. 2019, 44, 4243–4246. [Google Scholar] [CrossRef]
- Ye, C.; Zhang, D.; Hu, X.; Huang, X.; Feng, H.; Zhang, K. Recurrent Neural Network (RNN) Based End-to-End Nonlinear Management for Symmetrical 50 Gbps NRZ PON with 29 dB+ Loss Budget. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Sun, L.; Du, J.; He, Z. Multiband Three-Dimensional Carrierless Amplitude Phase Modulation for Short Reach Optical Communications. J. Light. Technol. 2016, 34, 3103–3109. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, J.; Zhou, G.; Chen, B.; Liu, G.N.; Cai, Y.; Li, Z.; Lu, C.; Shen, G. Theoretical investigations of weakly- and strongly-coupled multi-core fibers for the applications of optical submarine communications under power and fiber count limits. Opt. Express 2023, 31, 4615–4629. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Ma, L.; Shi, Y.; Bai, L.; He, Z. Low Loss Ultra-Small Core Pitch All-Fiber Fan-In/Fan-Out Device For Coupled-Core Multicore Fibers. IEEE Photonics J. 2022, 14, 7146805. [Google Scholar] [CrossRef]
- Van Uden, R.G.; Okonkwo, C.M.; Chen, H.; de Waardt, H.; Koonen, A.M. Time domain multiplexed spatial division multiplexing receiver. Opt. Express 2014, 22, 12668–12677. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).