Engineering Orbital Angular Momentum in Structured Beams in General Astigmatic Systems via Symplectic Matrix Approach

Abstract

We studied theoretically and experimentally the propagation of structured Laguerre–Gaussian (sLG) beams through an optical system with general astigmatism based on symplectic ABCD transforms involving geometry of the second-order intensity moments symplectic matrices. The evolution of the coordinate submatrix ellipses accompanying the transformation of intensity patterns at different orientations of the cylindrical lens was studied. It was found that the coordinate submatrix W and the twistedness submatrix M of the symplectic matrix P degenerate in the astigmatic $\mathrm{sLG}$ beam with simple astigmatism, which sharply reduces the number of degrees of freedom, while general astigmatism removes the degeneracy. Nevertheless, degeneracy entails a simple relationship between the coordinate element $W_{xy}$ and the twistedness elements $M_{xy}$ and $M_{yx}$ of the submatrix M, which greatly simplifies the measurement of the total orbital angular momentum (OAM), reducing the full cycle of measurements of the Hermite–Gaussian (HG) mode spectrum (amplitudes and phases) of the structured beam to the only measurement of the intensity moment. Moreover, we have shown that Fourier transform by a spherical lens enables us to suppress the astigmatic OAM component and restore the original free-astigmatic $\mathrm{sLG}$ beam structure. However, with further propagation, the $\mathrm{sLG}$ beam restores its astigmatic structure while maintaining the maximum OAM.

1. Introduction

The uniqueness of structured vortex beams [1] lies not only in their ability to possess multiple degrees of freedom, but also in the possibility to control their internal mode composition to solve current engineering problems [2,3]. It is a striking variety of fundamental geometric approaches for constructing structured beams in Cartesian [4], parabolic [5], or elliptical [6,7,8] geometry. There are numerous ways to control the properties of scalar and vector-structured beams, which are mostly aimed at shaping a corresponding intensity or polarization patterns, as well as at controlling the spin (SAM) and orbital angular momenta (OAM) [9], which is performed via spatial light modulators, digital micromirror devices [10], metasurfaces, Q-plates [11,12], etc. However, such engineering of structured beams often results in violating initial symmetry without loss of their structural stability, which inevitably leads to manifesting new unusual effects and processes. In this stream, the method of obtaining super-high OAM bursts by controlling the mode radial number in the structured beams, when propagating through astigmatic elements, looks quite usual but informative. One such large family of beams with broken symmetry is two-parametric structured Laguerre–Gaussian (sLG) beams [13] with a complex amplitude in the form

$${\mathrm{sLG}}_{n,\pm \ell }\left(\mathbf{r}\right)=\frac{{(-1)}^n}{2^{2n+3\ell /2}n!}\sum _{j=0}^{2n+\ell }{(\pm \mathrm{i})}^j(1+\epsilon {\mathrm{e}}^{\mathrm{i}j\theta })P_j^{(n+\ell -j,n-j)}\left(0\right){\mathrm{HG}}_{2n+\ell -j,j}\left(\mathbf{r}\right),$$

(1)

where $\mathbf{r}=(x,y)$ is a 2D vector, and $P_j^{(n+\ell -j,n-j)}(·)$ is a Jacobi polynomial. The symmetry breaking down is caused by two control parameters: the amplitude $\epsilon$ and phase $\theta$ parameters, which evoke the appearance of the $N=2n+\ell$ number of Hermite–Gaussian (HG) modes [2]

$${\mathrm{HG}}_{N-j,j}\left(\mathbf{r}\right)=exp\left(-\frac{x^2+y^2}{w_0^2}\right)H_{N-j}\left(\frac{\sqrt{2}x}{w_0}\right)H_j\left(\frac{\sqrt{2}y}{w_0}\right),$$

(2)

which are the main degrees of freedom of the sLG beam and destructing degenerate n ring dislocations in the ${\mathrm{LG}}_{n,\ell }$ mode (ℓ is the azimuthal number). The symmetry destruction is manifested in appearing topological dipoles with opposite signs of the vortex topological charges (TCs), but with the same weights [14]. The control $\epsilon$ and $\theta$ parameters of the sLG beam can be treated as additional independent degrees of freedom. Weak changing of the phase parameter $\theta$ leads to fast OAM oscillations [13], the frequency of which is controlled by the radial number n, whereas the beam OAM cannot exceed the TC of the beam $\mathrm{OAM}\le \ell$. At the same time, at large amplitude parameters, $\epsilon \gg 1$, the astigmatic sLG beam turns into a hybrid Hermite–Laguerre–Gaussian (HLG) beam with symmetry but rotated by $-\pi /4$ relative to the standard HLG beam [4,15]. The equilibrium between the TCs and weights of positively and negatively charged vortices is broken down when the light beam propagates through an astigmatic element (e.g., a cylindrical lens). As a result, the OAM can be controlled by rotating the astigmatic element axes, while the sLG beam control parameters are transformed in such a way that the OAM can exceed the sum of the radial and azimuthal numbers ${\ell }_z>n+\ell$ [16,17,18]. As a rule, the description of sLG beam reconstruction and its OAM calculation in optical systems with general astigmatism assumes employing non-traditional integral procedures identical to mapping onto the 2D sphere [19], which turns out to be cumbersome and unwarrantable for even simple engineering developments. In our opinion, the matrix approach for describing such complex optical systems can turn out to be relatively simple and clear. To achieve this, we use the formalism of symplectic transformations [20,21], which are associated with the formalism of Hamiltonian mechanics, i.e., $SU\left(2\right)$ and $SU\left(3\right)$ symmetry groups. Such a symplectic matrix approach is now widely used in optical signal processing [22], for mapping a structured beam onto the orbital Poincare sphere [23], and for analyzing the wavefront structure of the complex singular beams [24], and it was the basis for standards for measuring the parameters of complex laser beams [25].

Arnaud [26] took the first steps in the $4\times 4$ matrix representation of fundamental Gaussian beams in an optical system with a simple astigmatism. The authors of [27] extended their approach to the transformation of Gaussian beams in systems with general astigmatism at the same time, a technique of symmetrizing astigmatic Gaussian beams in an optical system of five cylindrical lenses was proposed by Nemes and Siegman in [28]. Their description was based on the properties of symplectic ray tracing and intensity moment transforms [20,21] generalizing the standard approaches of the ABCD matrices [29]. Alieva and Bastiaans [23,30] highlighted the basic principles of symplectic transformations in standard laser beams of higher orders. Indeed, the optical system even with a simple astigmatism, destroys the vortex beams’ symmetry [15]. Therefore, detecting the description in frameworks of the ray-tracing ABCD matrices turns out to be insufficient, so it also has to be enriched with symplectic $4\times 4$ block intensity moment matrices [31] that “sense” even the slightest symmetry violation. It is interesting to note that in the simplest of cases, e.g., for a simple astigmatism, the $4\times 4$ matrices may be reduced to $2\times 2$ matrices, as described by Anan’ev and Bekshaev in Ref. [32] and later by Bekshaev et al. [33,34], for breaking down the vortex beam symmetry. At the same time, all sub-blocks of symplectic matrices are used for the laser beam classification by Nemes and Siegman in Ref. [28] and for the beam characterization in Refs. [35,36]. Recently, we also used such a stripped-down approach to describe the transformation of structured beams with a simple astigmatism [37].

In our article, we consider sLG beam transformations in an optical system of the first order with general astigmatism in terms of ray-tracing matrices enriched by a formalism of the second-order intensity moment matrices. Moreover, we touch upon symmetrizing the general astigmatic beam due to the Fourier transform in which the astigmatic OAM is suppressed, but when further propagating, the astigmatic sLG beam becomes a structurally stable one, while the OAM super-burst is maintained.

2. A Ray-Tracing Matrix Approach to a General Astigmatism

2.1. The Beam Structure

According to Arnaud and Kogelnik [38], an optical system with general astigmatism should contain a sequence of astigmatic lenses with oblique axes orientations. Such an optical system does not possess meridional planes of symmetry, and it came to be called a nonorthogonal one, whereas the beam becomes nonorthogonal with general astigmatism at the observation plane [28] (see Figure 1). As a rule, to describe such a system, the integral astigmatic transforms of stigmatic beams are used, as discussed in our recent article [37]. But here, we have chosen a simpler approach, acceptable for engineering calculations. Let the stigmatic HG beam (2) fall onto the input of a cylindrical lens, the axis of which is rotated by the angle $\varphi$ relative to the laboratory coordinate system. It is known [39] that HG beams are eigenmodes of the astigmatic lens if their axes are aligned along the lens astigmatic axes so that the HG mode complex amplitude can be represented in terms of the lens eigenmodes [39] (see also Equation (3.8) in Ref. [40]):

$$\begin{array}{cc}\hfill {\mathrm{HG}}_{n,m}(x^{\prime },y^{\prime })& ={\mathrm{HG}}_{n,m}(xcos\varphi -ysin\varphi ,xsin\varphi +ycos\varphi )\hfill \\ \hfill & =\sum _{k=0}^{n+m}{(-1)}^k{c}_k^{(n,m)}\left(\varphi \right){\mathrm{HG}}_{n+m-k,k}(x,y),\hfill \\ \hfill c_k^{(n,m)}\left(\varphi \right)& ={(cos\varphi )}^{n-k}{(sin\varphi )}^{m-k}{P}_k^{(n-k,m-k)}(-cos2\varphi ).\hfill \end{array}$$

(3)

For simplicity, we assume that the astigmatic element is made in the form of a cylindrical lens with a focal length $f_x$ ($f_y\to \infty$). In essence, this means that the HG modes in Equation (4) along the x and y axes are scaled in different ways. But the transformations along the x and y axes are not coupled to each other. In this case, we still remain within the framework of a simple astigmatism. If the beam then passes through the next astigmatic element with a different axes orientation, or observations are carried out in laboratory coordinates, then we are faced with general astigmatism [28,36]. Obviously, such a situation can no longer be represented in the form of a standard ABCD matrix approach, and the representation of symplectic transforms [23] should be used.

$$\mathbf{S}=\left(\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right),$$

(4)

and $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$, and $\mathbf{D}$ are $2\times 2$ submatrices. Note that the matrices $\mathbf{A}$ and $\mathbf{D}$ are responsible for the independent scaling of the beam along the x and y axes, whereas the submatrices $\mathbf{B}$ and $\mathbf{C}$ carry out coupling the x and y axes. Since the spherical lens in Figure 1 performs the same scaling along the x and y directions, and we remain in the coordinate system $(x,y)$ of the cylindrical lens up to the observation plane, we can independently use matrices $\mathbf{A}$ and $\mathbf{D}$ to transform the beam [37]. However, at the observation plane, we have to switch back to the laboratory coordinates $(x^{\prime },y^{\prime })$:

$$x=x^{\prime }cos\varphi +y^{\prime }sin\varphi ,y=-x^{\prime }sin\varphi +y^{\prime }cos\varphi ,$$

(5)

which leads to coupling x and y directions. Thus, we observe the beam subject to a general astigmatism.

Astigmatic beam transformations are tracked with two complex ray-tracing parameters

$$q_{x,y}=\frac{A_{x,y}{q}_0+B_{x,y}}{C_{x,y}{q}_0+D_{x,y}},$$

(6)

where $q_0=-\mathrm{i}{z}_0$ stands for the initial q-parameter at the $z=0$ plane, and $A_{x,y}\left(z\right)$, $B_{x,y}\left(z\right)$, $C_{x,y}\left(z\right)$, $D_{x,y}\left(z\right)$ are elements of the unitary $2\times 2$ ABCD-matrices with the property $A_{x,y}{D}_{x,y}-B_{x,y}{C}_{x,y}=1$. After passing through an astigmatic system, the complex amplitude of the $\mathrm{sLG}$ beam takes the dimensionless form with $x\to x/w_0$, $y\to y/w_0$, $z\to z/z_0$, $q_{x,y}\to {\overline{q}}_{x,y}$:

$$\begin{array}{c}{\mathrm{asLG}}_{n,\ell }(x^{\prime },y^{\prime },z|\epsilon ,\theta ,\varphi )=\frac{{(-1)}^n}{2^{n+\ell }n!}\sum _{j=0}^N{C}_j{\mathrm{HG}}_{N-j,j}(x^{\prime },y^{\prime }|{\overline{q}}_{x,y}),\end{array}$$

(7)

$$\begin{array}{c}{C}_j={(-1)}^j{\mathrm{e}}^{\mathrm{i}j{\Gamma }_{xy}}\sum _{k=0}^N{(-\mathrm{i})}^k{c}_k^{(n,n+\ell )}(\pi /4){\epsilon }_k{c}_j^{(N-k,k)}(-cos\varphi ),\end{array}$$

(8)

where $N=2n+\ell$, ${\epsilon }_k=(1+\epsilon {\mathrm{e}}^{\mathrm{i}k\theta })$. The scaling of the $(x,y)$ directions and the HG beam phase transformations are carried out in accordance with the ABCD matrix procedure in a system with a simple astigmatism [37] with the complex parameters

$$q_x\left(Z_1\right)=z_0\frac{\left[Z_1({\kappa }_x^2+1)-{\kappa }_x\right]-\mathrm{i}}{{\kappa }_x^2+1}=z_0{\overline{q}}_x\left(Z_1\right),$$

(9)

where ${\kappa }_x=\frac{z_0}{f_x}$, $q_y\left(z_1\right)=z_1-\mathrm{i}{z}_0=z_0{\overline{q}}_y$, and $Z_1=z_1/z_0$, the beam radii $w_{x,y}\left(z\right)$ with a wavenumber $k^{\prime }$:

$$\begin{array}{c}{w}_x^2=w_0^2\left[{(1-Z_1{\kappa }_x)}^2+Z_1^2\right]=w_0^2{\overline{w}}_x^2\left(Z_1\right),\end{array}$$

(10)

$$\begin{array}{c}{w}_y^2=w_0^2(1+Z_1^2)=w_0^2{\overline{w}}_y^2\left(Z_1\right),w_0^2=2z_0/k^{\prime },\end{array}$$

(11)

while the Gouy phases are specified as

$$\begin{array}{c}{\Gamma }_x=\frac{1}{2}arg\frac{q_x}{A_x{q}_x+B_x}=\frac{1}{2}arg(1-{\kappa }_x{Z}_1+\mathrm{i}{Z}_1),\end{array}$$

(12)

$$\begin{array}{c}{\Gamma }_y=\frac{1}{2}arg(1+\mathrm{i}{Z}_1),\end{array}$$

(13)

$$\begin{array}{c}{\Gamma }_{xy}={\Gamma }_x-{\Gamma }_y.\end{array}$$

(14)

The theoretical and experimental intensity patterns of the $\mathrm{asLG}$ beams with typical quantum numbers ($n=\ell =12$) depicted in Figure 2 illustrate the evolution of their states along the z-propagation axis. The initial beam states in front of the astigmatic element are featured by a control parameter $\theta$ corresponding to the first main OAM burst (see Section 2.2). Against the background of each intensity pattern, an ellipse of the $\mathrm{sLG}$ beam astigmatism is displayed, calculated via second-order intensity moments (see Section 3). The ellipticity degree and the angle of the ellipse inclination indicate the astigmatism of the beam structure is affected. The bottom line of Figure 2b represents the experimental results (see Section 5). It is sufficient to visually compare theoretical and experimental intensity patterns to understand that the ABCD matrix technique fairly accurately maps the real processes of the structured beam transformations. After the astigmatic element ($Z_1=0.1$), a structured beam pattern with slightly broken axial symmetry of the generatrix LG mode is reproduced, featuring small values of the phase parameter $\theta$. At the plane of the double focus $(Z_1=1)$ of the cylindrical lens, we observe typical mode conversion $\mathrm{LG}\to \mathrm{HG}$, which enables us to measure the topological charges of vortex beams [41,42] with either n and ℓ numbers. Further, the beam propagation only slightly distorts a rectangular symmetry. It is worth noting that the intensity moment ellipses follow the shape of the intensity pattern and are not tied to the axis ($\varphi =\pi /4$) of the cylindrical lens astigmatism.

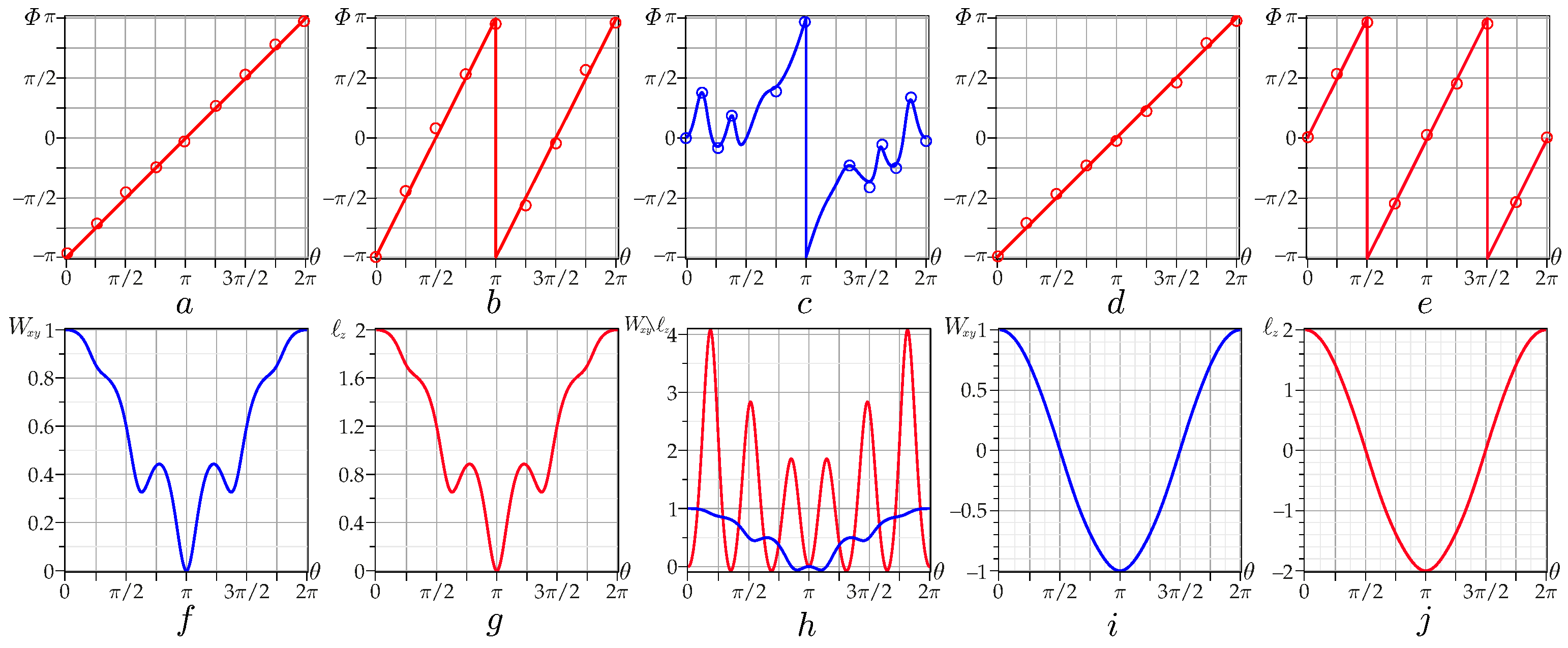
2.2. The OAM Transforms

The specific OAM ${\ell }_z$ of stable structured beams in the non-vortex mode basis can be written for the triple-parametrized OAM as [37] (see also Equation (90) in Ref. [43])

$${\ell }_z\left(Z_1\right|\epsilon ,\theta ,\varphi )=2\sum _{j=0}^{N-1}(N-j)!(j+1)!\mathrm{Im}\left(C_j^{*}{C}_{j+1}\right)/J_{00},$$

(15)

with a total intensity

$$J_{00}=\sum _{j=0}^N(N-j)!j!{\left|C_j\right|}^2.$$

(16)

In order to highlight the featured OAM domains in a multiparametric asLG beam, we have plotted the 3D OAM representation on the $(\theta -\varphi )$ parameters shown in Figure 3. The key properties of the OAM, as we see, are best of all manifested for the ${\mathrm{asLG}}_{n,\ell }$ beams with the same radial and azimuthal numbers $n=\ell$. The pattern in Figure 3 indicates that the OAM maxima for any numbers $(n,\ell )$ and parameters $\theta$ fall on the $\varphi =\pi /4$ angle. Moreover, the main OAM burst is located in the region of small phase $\theta$-parameters (close to zero), while the most pronounced OAM burst is observed at the focal area of a cylindrical lens and, not as previously thought, in the double focus area.

More detailed OAM features are illustrated in Figure 4. Figure 4a illustrates the position of the OAM bursts depending on the parameter $\theta$ and indicates the main OAM burst near the zero $\theta$-parameter. So, for relatively small $n=\ell =5$ quantum numbers, the phase parameter is $\theta =0.236$ (about ${13}^{\circ }$), whereas for $n=\ell =12$, its value becomes $\theta =0.062$ (about ${3.5}^{\circ }$). This means that even a slight violation of the axial symmetry of the generatrix LG mode, i.e., the destruction of its degenerate ring dislocations and appearance of pairs of topological vortex dipoles, leads to a violation of the balance between positive and negative vortex topological charges in dipoles due to general astigmatism, and as a result, the OAM increases sharply, exceeding the sum of the radial and azimuthal numbers ${\ell }_z>n+\ell$. Once we have rotated the astigmatic element axes by $\Delta \varphi =\pi /2$, the OAM sign converts to the opposite ${\ell }_z<-(n+\ell )$ (see Figure 4c). The curves in Figure 4b indicate in which plane it is worth observing the beam with a maximum possible OAM. It turns out that the observation plane should be located at the focal plane of the cylindrical lens $Z_1=0.5$, where displacement from this plane leads to sharply decreasing the OAM; what is more, this optimal position does not depend on the numbers n and ℓ. Further displacement of the observation plane does not significantly change the OAM so that, at large $Z_1\gg 1$, we have $\ell \to n+\ell$, despite a vivid structured transforming of the intensity pattern (see Figure 2). One cannot help but notice one remarkable approximation of the cumbersome expression Equation (15) for the OAM. Analyzing Equation (15), we have obtained numerically an approximate relation for large numbers nℓ

$${\ell }_z^{\left(appr\right)}\left(Z_1\right|\epsilon ,\theta ,\varphi )={\ell }_z\left(Z_1\right|\epsilon ,\theta ,\varphi =\pi /4)sin2\varphi .$$

(17)

A comparison of these expressions is illustrated in Figure 5 for two asLG beam states: (a) $n=\ell =2$ and (b) $n=\ell =10$. The blue curve 1 is plotted by the exact expression (15), while the red curve 2 is displayed by the approximate Equation (17). If for small numbers $n=\ell =2$, the colors of the curves can be distinguished, then for large numbers $n=\ell =10$, the colors merge to the nearest thousandths. This indicates a good approximation accuracy, which significantly reduces the time of computer simulation of complex structured beams.

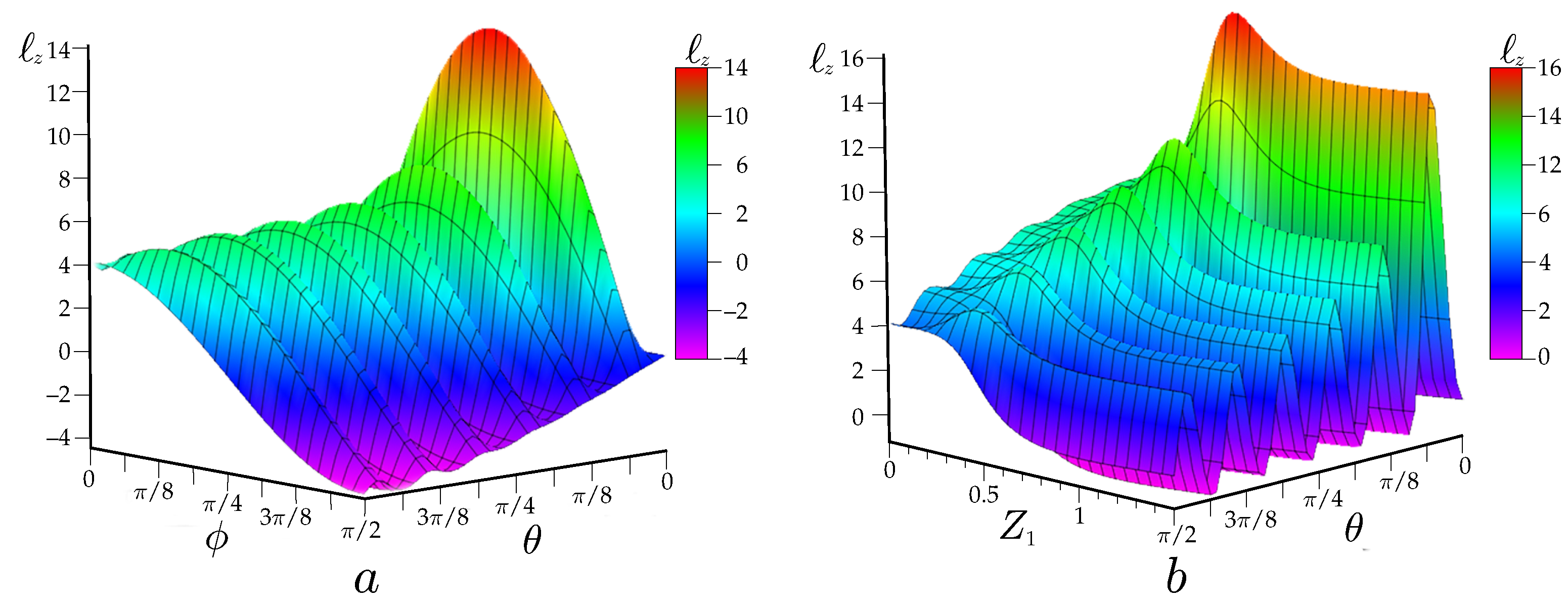
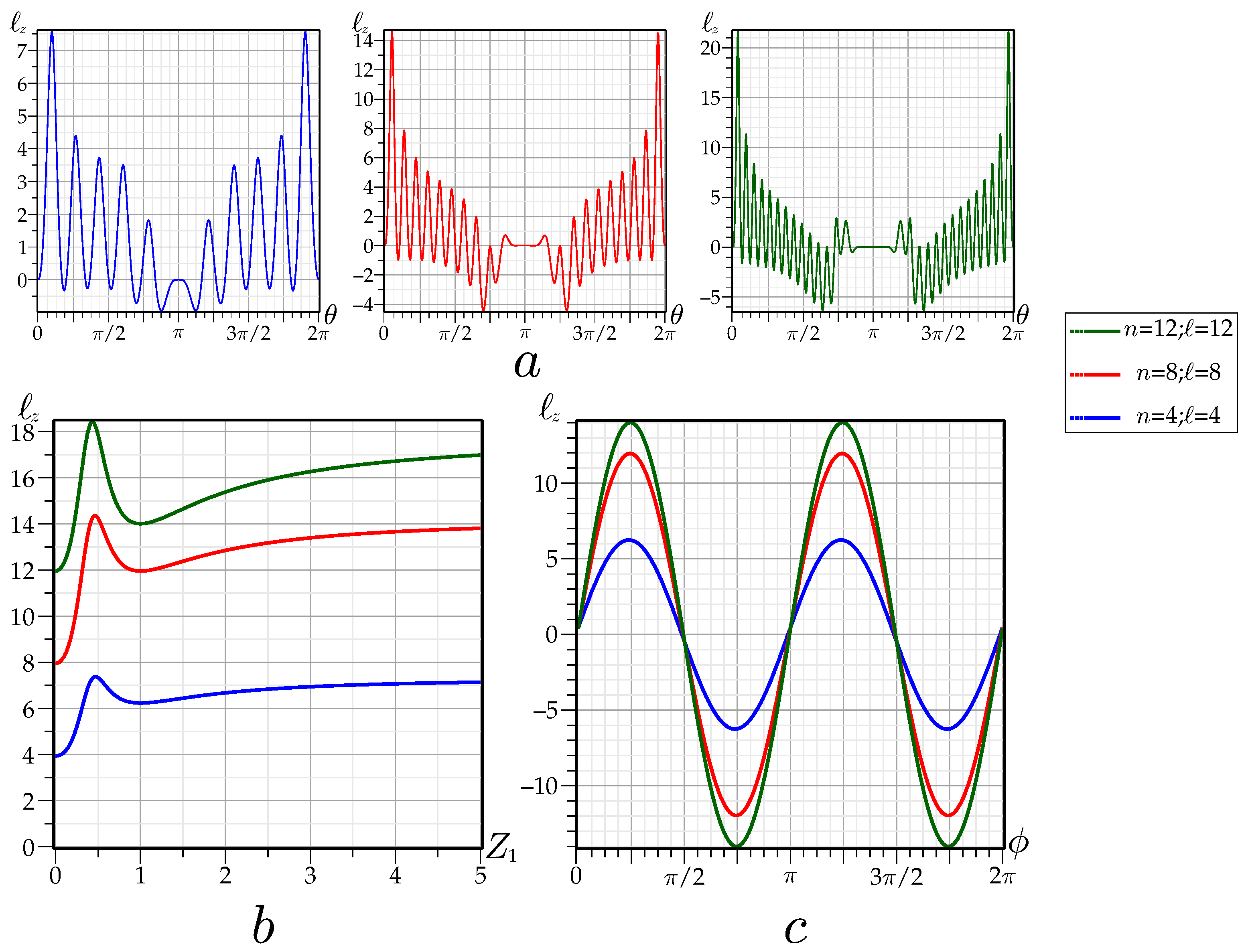
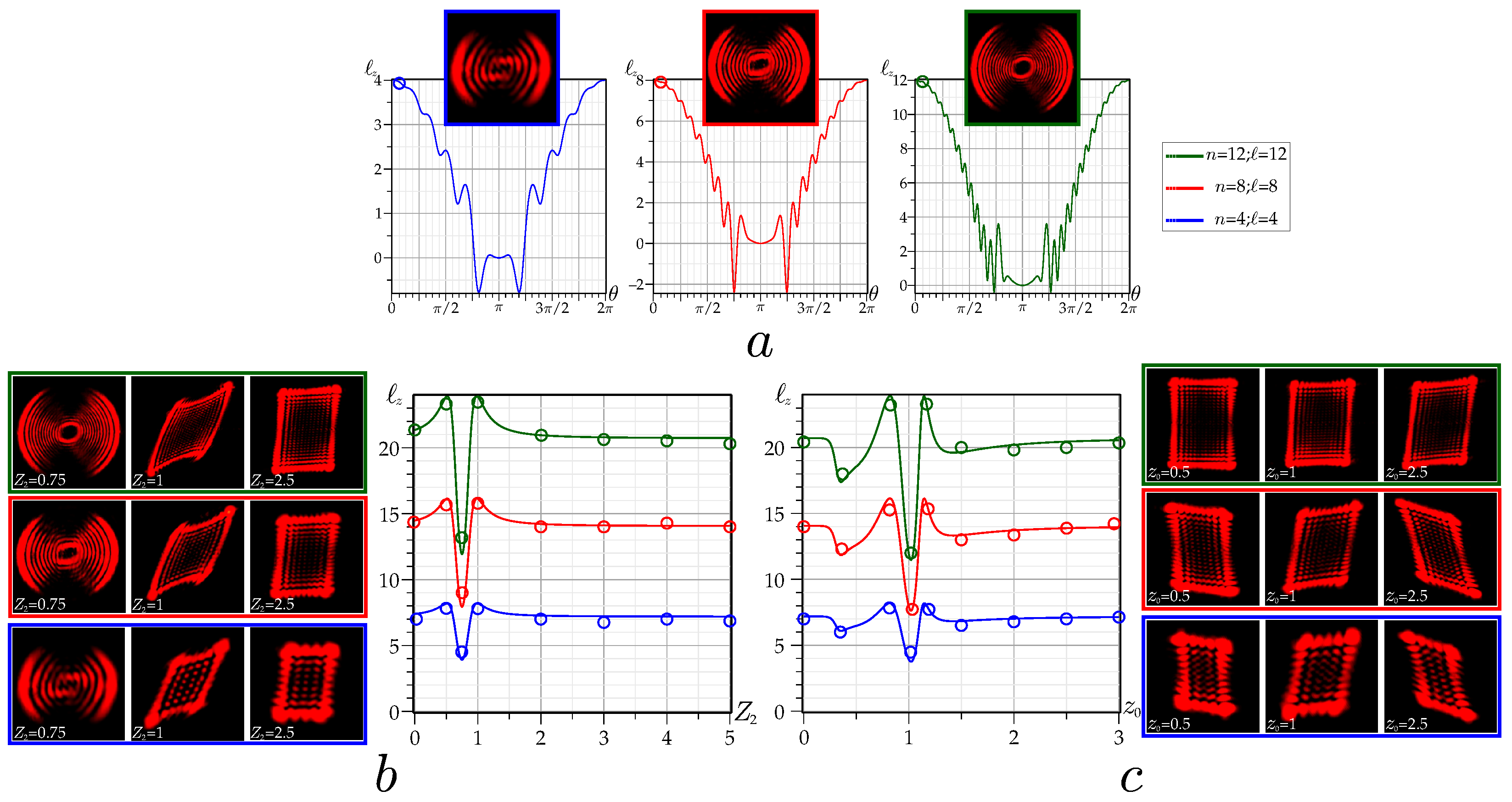
3. Symplectic Intensity Moments Transforms

The astigmatic transforms are described in a unified way within the framework of symplectic $4\times 4$ matrices. The concept of symplectic transforms in optics was first introduced by Hamilton, treating the propagation of light rays based on Lagrange formalism [20,21]. Generally speaking, symplectic geometry studies mappings that preserve the symplectic structure, keeping area measurements constant. The word “symplectic” derives from the Greek word “sumplektikós” ($\sigma \nu \mu \pi \lambda \epsilon \kappa \tau \iota \kappa ó\varsigma$), which means “braided together”, evoking the way the symplectic structure and the complex numbers are intertwined. The symplectic intensity moments block matrix of the second-order in optics can be rewritten as [31]

$$\mathbf{P}=\left(\begin{array}{cc}\mathbf{W}& \mathbf{M}\\ {\mathbf{M}}^T& \mathbf{U}\end{array}\right)=\frac{1}{J_{00}}\int \left(\begin{array}{cccc}{x}^2& xy& x{p}_x& x{p}_y\\ yx& y^2& y{p}_x& y{p}_y\\ p_{x}x& p_{x}y& p_x^2& p_x{p}_y\\ p_{y}x& p_{y}y& p_y{p}_x& p_y^2\end{array}\right)I(\mathbf{r},\mathbf{p}){\mathrm{d}}^2\mathbf{r}{\mathrm{d}}^2\mathbf{p},$$

(18)

where T indicates transposition, $\mathbf{p}={(p_x,p_y)}^T=-\mathrm{i}{\nabla }_{\perp }$, $I(\mathbf{r},\mathbf{p})$ is the Wigner distribution function [36], and $J_{00}$ stands for a total beam intensity. The evolution of the intensity matrix along the optical system is conveniently described by the ratio ${\mathbf{P}}_{out}=\mathbf{S}·{\mathbf{P}}_{in}·{\mathbf{S}}^T$.

Our main interest in this section is focused on the coordinate submatrix $\mathbf{W}$ and the twistedness submatrix $\mathbf{M}$ to describe their degeneracy that promotes simplify significantly measuring a total OAM technique but that dramatically reduces the number of degrees of freedom. The diagonal elements $W_{xx}$ and $W_{yy}$ of the summatrix $\mathbf{W}$ characterize the square beam radii $w_x$ and $w_y$, while the off-diagonal element $W_{xy}=W_{yx}$ points out the beam asymmetry. The off-diagonal elements $M_{12}=〈x{p}_y〉$ and $M_{21}=〈y{p}_x〉$ of the submatrix $\mathbf{M}$ specify the beam twistedness, while ${\ell }_z=M_{12}-M_{21}$ is responsible for the specific OAM [28]. The problem of the intensity moment matrix invariants is considered in detail in Refs. [28,31]. And, here, the main invariant of the astigmatic beams is the normalized parameter

$$a=2k^2\left[Sp(\mathbf{WU}-{\mathbf{M}}^2)-2\sqrt{det\mathbf{P}}\right],$$

(19)

with the symmetric part, ${\mathbf{W}}^{-1}\mathbf{M}$ specifies the beam curvature, whereas the antisymmetric part is the submatrix $\mathbf{M}$. In this case, the physical interpretation of the invariant a is that it enables us to distinguish two non-intercrossed manifold of laser beams: $a=0$ points out the intrinsic stigmatic beams; $a>0$ specifies intrinsic astigmatic beams [36].

In order to explain the unusual behavior of the $\mathrm{sLG}$ beams with broken symmetry in the astigmatic system, let us peer into the geometry of these beams hidden in the symplectic matrix transforms. To achieve this, one makes use of geometry of the submatrix $\mathbf{W}$, namely, its associated ellipse [31], written in the form

$$(\mathbf{r}·{\mathbf{W}}^{-1}·\mathbf{r})=\frac{1}{det\mathbf{W}}(W_{yy}{x}^2+W_{xx}{y}^2-2W_{xy}xy)=1.$$

(20)

The ratio of the ellipse axes is given as

$$\chi =\sqrt{\frac{W_{xx}+W_{yy}+\sqrt{{(W_{xx}-W_{yy})}^2+4W_{xy}}}{W_{xx}+W_{yy}-\sqrt{{(W_{xx}-W_{yy})}^2+4W_{xy}}}},$$

(21)

while the slope of its major axis can be found as

$$\psi =\mathrm{arccot}((W_{xx}-W_{yy})/2W_{xy})/2.$$

(22)

Using Equation (7) in Equation (18), we come to the submatrix-$\mathbf{W}$ elements

$$W_{xy}=({\overline{w}}_x\left(z\right){\overline{w}}_y\left(z\right)/2J_{00})\sum _{j=0}^{N-1}(N-j)!(j+1)!\mathrm{Re}\left(C_j{C}_{j+1}^{*}\right),$$

(23)

$$W_{xx}=({\overline{w}}_x^2\left(z\right)/4J_{00})\sum _{j=0}^N(2N-2j+1)(N-j)!j!{\left|C_j\right|}^2,$$

(24)

$$W_{yy}=({\overline{w}}_y^2\left(z\right)/4J_{00})\sum _{j=0}^N(2j+1)(N-j)!j!{\left|C_j\right|}^2,$$

(25)

The associated ellipses in Figure 2, obtained from Equation (20), track the intensity pattern deformations with a variation of the distance $Z_1$. In Figure 6, we have depicted the evolution of associated ellipses with variations of the $\theta$-phase parameter for two groups of beams: standard $\mathrm{sLG}$ beams with $\epsilon =1$ (Figure 6a) and hybrid $\mathrm{HLG}$ (Figure 6b) beams [4] rotated by $\pi /4$ (i.e., the $\mathrm{sLG}$ beams with $\epsilon \gg 1$ [13]). Both in free space (Figure 6a,b) and the astigmatic system (Figure 6c,d), the directions of the ellipse axes strictly follow the shape of the intensity pattern only for the $\mathrm{HLG}$ beam (i.e., asLG beam with $\epsilon \gg 1$), although astigmatism tries to hold the axes of the ellipse and the intensity pattern (Figure 6c) for the standard $\mathrm{asLG}$ beam. It should be noted that at the end of the XX century, the authors of the articles [28,36] based the laser beam classification on the correspondence between the direction of the associated ellipse axes for submatrices $\mathbf{W}$, $\mathbf{M}$, and $\mathbf{U}$. Here, we will not delve into the cobweb of the beam classification, but peer into the issue of losing degrees of freedom in structured beams when matching the axes of submatrices $\mathbf{W}$ and $\mathbf{M}$. Indeed, the stigmatic beam has only three independent parameters, while their number in the beam with general astigmatism increases to ten [28]. How will the number of independent parameters change when matching the ellipse axes of the $\mathbf{W}$ and $\mathbf{M}$ submatrices?

Let us pay attention to the fact that the OAM in Equation (15) is described through the imaginary part of the mode amplitudes product, while the cross-intensity moments in Equation (23) are given by the real part of these mode amplitudes products. In fact, this indicates an implicit relationship between the $\mathbf{W}$ and $\mathbf{M}$ matrices. If we follow the recommendation of the authors in Ref. [29] , then this relationship should be sought in the orientation of the corresponding ellipses of these matrices. But to simplify the mathematical calculations, let us recall that the difference of the non-diagonal elements of the matrix $\mathbf{M}$ sets the specific OAM ${\ell }_z=M_{xy}-M_{yx}$. Therefore, it is more appropriate to consider the relation ${\ell }_z\left(\theta \right)/4W_{xy}\left(\theta \right)$ and write

$$\mathsf{\Phi }\left(\theta \right)=arctan({\ell }_z\left(\theta \right)/4W_{xy}\left(\theta \right)).$$

(26)

Since $\mathsf{\Phi }\left(\theta \right)/\theta =1$ (see Figure 7a), we can rewrite Equation (26) as

$${\ell }_z\left(\theta \right)=W_{xy}\left(\theta \right)(4tan\theta ).$$

(27)

Figure 7a–e shows the dependencies of two different groups of beams: sLG beams with $\epsilon =1$ and sLG beam with $\epsilon \gg 1$ (the hybrid HLG beams rotated by the $\pi /4$ angle). The straight lines in Figure 7a,b for the beams in free space indicate upon a simple link (Equation (27)) between the matrices $\mathbf{W}$ and $\mathbf{M}$. Moreover, Figure 7f,g show the dependencies of $W_{xy}\left(\theta \right)$ and ${\ell }_z\left(\theta \right)$, respectively, which are identical. This indicates the degeneracy of $\mathbf{W}$ and $\mathbf{M}$ matrices for sLG beams in free space. In an optical system with a simple astigmatism $(\varphi =0)$, the amplitudes of the HG modes are described by Equation (18) in our article [18], which differs from Equation (6) by a multiplier $exp(\mathrm{i}\pi /2)$ in the observation plane $z=2f_x$. This means that the real and imaginary parts in the product $C_j{C}_{j+1}^{*}$ in Equations (8) and (15) are reversed. For the observed values $W_{xy}\left(\theta \right)$ and ${\ell }_z\left(\theta \right)$, this means a shift of $\pi /2$ along the $\theta$-axis, which is observed in Figure 7d,e for both $\epsilon =1$ and $\epsilon \gg 1$ (see Figure 7i,j). Thus, the matrices $\mathbf{W}$ and $\mathbf{M}$ remain degenerate in the case of a simple astigmatism. But, on the other hand, it also means the loss of three degrees of freedom, both for the sLG in free space and for the asLG beam in a system with a simple astigmatism. But as can be seen from Figure 7c,h, the simple dependence between $W_{xy}\left(\theta \right)$ and ${\ell }_z\left(\theta \right)$ in a system with general astigmatism disappears, and, consequently, the degeneration of the symplectic matrix $\mathbf{P}$ is removed. Degeneracy is also removed when the amplitude parameter is not equal to one $\epsilon \ne 1$ except for very large $\epsilon \gg 1$ amplitude parameters. To determine the relationship $W_{xy}\left(\theta \right)$ and ${\ell }_z\left(\theta \right)$, it is necessary to solve a system of 10 equations [28]. In the case $\epsilon \gg 1$, the sLG beam turns into the HLG beam rotated by $3\pi /4$ relative to the standard state of the hybrid mode [4], and Equation (27) turns into

$${\ell }_z\left(\theta \right)=W_{xy}\left(\theta \right)(4tan2\theta ).$$

(28)

Thus, for finding a total OAM of a complex structured beam, only one measurement of the intensity moment $W_{xy}$ is required instead of measuring the entire mode spectrum $C_j$ (see Section 5). It is worth noting that unlike the measurement technique based on the $W_{xy}$ element proposed in Ref. [44], where the main restriction is the availability of a reflective symmetry of the intensity pattern relative to the main diagonals of a cylindrical lens, our technique lacks such a constraint and is applicable to $\mathrm{sLG}$ beams with arbitrary symmetry.

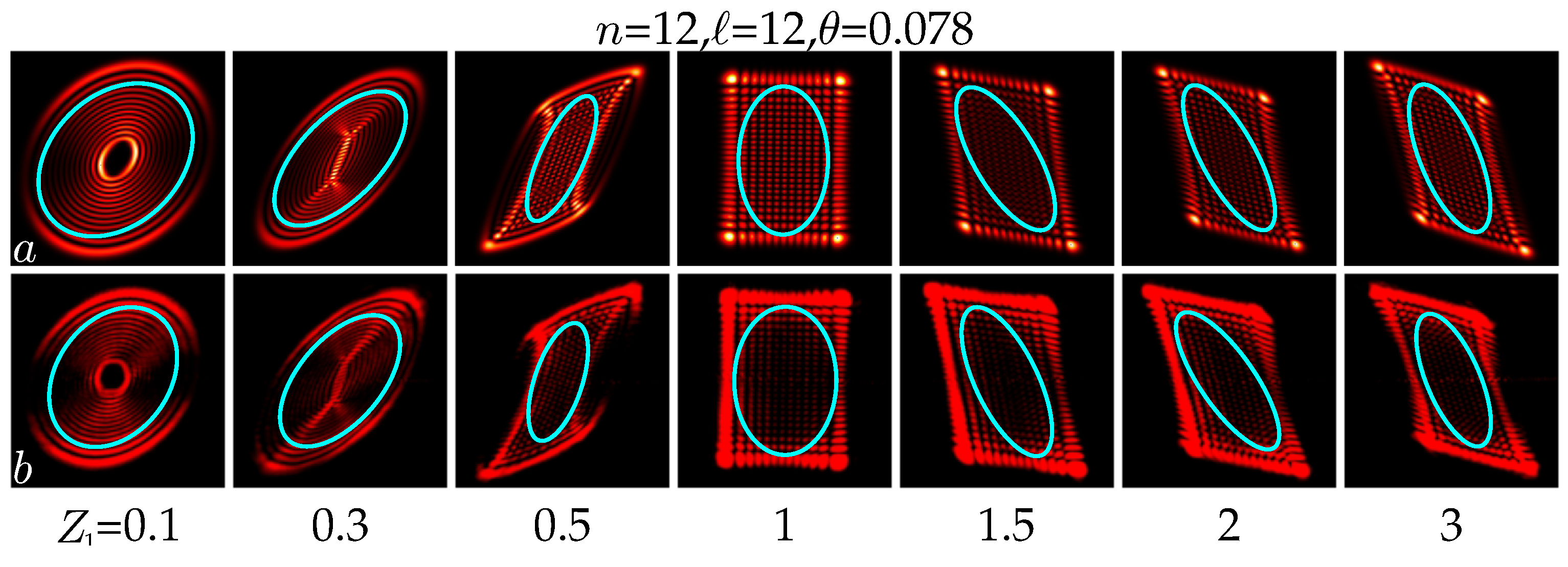
4. Suppression of the Astigmatic OAM with a Spherical Lens

Considering laser beams in optical systems with astigmatic elements, one always wonders what contribution general astigmatism makes to the OAM compared to the optical vortices? The problem of separating vortex and astigmatic constituents in the beam OAM is inextricably linked to the issue of converting astigmatic beams in a first-order optical system. Standard beam transformations with suppression of one of the constituents of astigmatic beams are based on the classification of astigmatic beams according to the ratio between the invariants of the symplectic matrix of second-order intensity moments and their symmetry [25,36]. For example, the correction problem was reduced to the transformation of an astigmatic Gaussian beam into a cylindrically symmetrical form, either with the help of a single cylindrical lens [24,45] or by means of a combination of four cylindrical lenses [35] which has nothing to do with the OAM correction. Nevertheless, we have not found any recommendations on standard transformations or original research on this issue for structured astigmatic vortex beams in the literature. Therefore, we followed the recommendations of the authors in Ref. [23] on using quadratic phase elements for this purpose and our simple consideration that a spherical lens forms a beam in the focus vicinity with the same waist radii along the x and y directions. Moreover, in order to compensate for the additional Gouy phase difference between the x and y beam directions, we proposed employing the Fourier transform. A sketch of such astigmatic transform and phase correction is depicted in Figure 1. As we have said above, the ABCD matrix formalism for a simple astigmatic system can be employed until we remain in the rotated $(x,y)$ coordinates. But once at the observation plane, we have to proceed to the laboratory $(x^{\prime },y^{\prime })$ coordinates to deal with general astigmatism. Thus, as well as before, we find the complex parameters $q_{x2}$ and $q_{y2}$ through the complex parameters of a single cylindrical lens ${\overline{q}}_x$ and ${\overline{q}}_y$ in Equation (6) in the form

$${\overline{q}}_{x2}=\frac{{\overline{q}}_x+Z_2(-{\kappa }_{sph}{\overline{q}}_x+1)}{1-{\kappa }_{sph}{\overline{q}}_x},{\overline{q}}_{y2}=\frac{(1-Z_2{\kappa }_{sph})(Z_1-i)+Z_2}{1+i{\kappa }_{sph}(i{Z}_1+1)},$$

(29)

where ${\kappa }_{sph}=z_0/f_{sph}$, $Z_2=z_2/z_0$.

$${\Gamma }_{x2,y2}=\frac{1}{2}arg\frac{q_{xy2}}{A_{xy}{q}_{xy2}+B_{xy}},$$

(30)

As a result, we reveal that sharp narrow OAM dips of the ${\ell }_z\left(Z_2\right)$ curve surrounded by two small bursts in Figure 8b denote correction of the OAM after a spherical lens with the $f=0.5$ m focal length. The depth of the OAM dip is restricted by the magnitude of the $\mathrm{sLG}$ beam OAM before the astigmatic transform, while the intensity pattern coincides with that of the $\mathrm{sLG}$ beam with non-orthogonal summitry before the transformation that indicates the suppression of the astigmatic OAM component so the main contribution to the OAM is made by optical vortices. As predicted in Ref. [31], the OAM correction occurs when the beam radii $w_x=w_y$ are equal. However, we found a number of additions to this effect inherent in structured beams. First of all, the lens must perform a Fourier transform of the $\mathrm{asLG}$ beam at a given observation plane after a cylindrical lens, while the narrow OAM dip appears in the vicinity of the Fourier plane of a spherical lens, the width of which reduces, rapidly with growing quantum numbers n and ℓ. We selected the beams with the first maximal OAM burst at the angle $\varphi =\pi /4$ of the cylindrical lens, depicted at the callouts in Figure 8a. Moving along the $Z_2$ axis after the spherical lens, sharp OAM dips were detected, while the OAM sharply decreased from ${\ell }_z>n+\ell$ to ${\ell }_z=\ell$ (see Figure 8b,c), that is, the OAM decreased to that in the non-astigmatic $\mathrm{sLG}$ beam in front of the cylindrical lens. Moreover, computer-simulated intensity patterns at these planes practically coincide. (A comparison of the theory and experiment is discussed in the next Section 5). Thus, the OAM suppression in the astigmatic beam leads to the restoration of the initial state of the $\mathrm{sLG}$ beam at the cylindrical lens input with the OAM ${\ell }_{\mathrm{sLG}}$ so that the total OAM is ${\ell }_z={\ell }_{\mathrm{asLG}}={\ell }_{\mathrm{sLG}}+{\ell }_{astigm}$ as was predicted in Ref. [31]. It is also worth noting that the condition $w_x=w_y$ is also fulfilled at the double focus plane after the cylindrical lens. Therefore, an additional condition of phase correction for Gouy phase equality ${\Gamma }_x={\Gamma }_y+2\pi n$ should be taken into account.

The corrected $\mathrm{asLG}$ beam has a number of unique properties. First of all, the corrected $\mathrm{asLG}$ beam becomes invariant to any angular position of the cylindrical lens, i.e., its shape and OAM do not change when the cylindrical lens rotates at any angle $\varphi$. The $\mathrm{asLG}$ beam after a spherical lens in Figure 8b,c becomes a space-invariant one in a far diffraction domain, i.e., its structure does not change up to scale along the beam at $Z_2>2$ whereas the OAM maximum is kept.

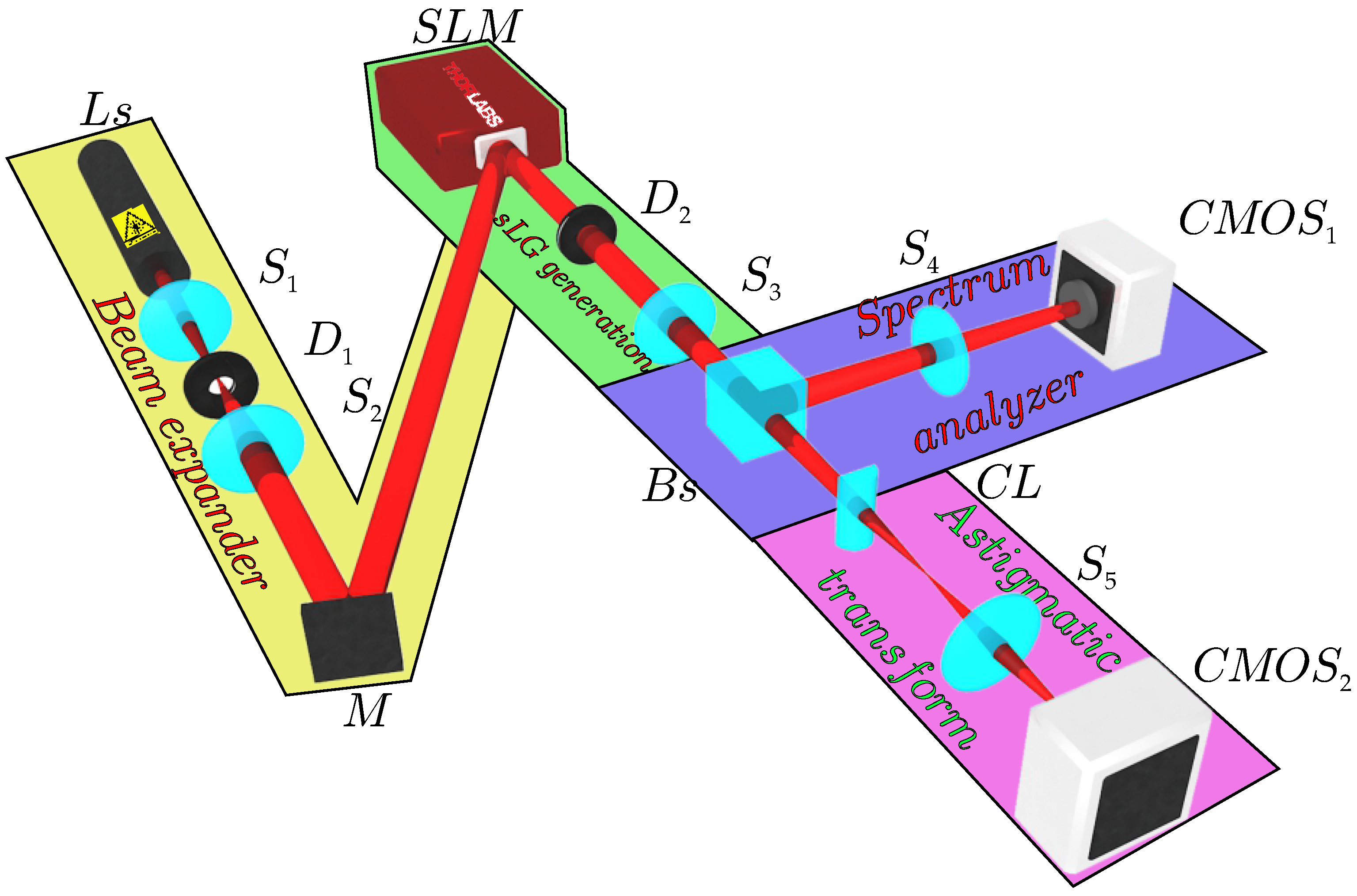
5. The Experiment

Our experiment is aimed at the exposure characteristic features in the $\mathrm{asLG}$ beam mode spectra (squared amplitudes and phases) accompanying the degeneration of submatrices $\mathbf{W}$ and $\mathbf{M}$ in the symplectic $\mathbf{P}$ matrix, as well as suppressing the astigmatic OAM component by a spherical lens. The experiment is based on both the techniques of measuring second-order intensity moments of the $\mathbf{W}$ submatrix and higher-order intensity moments on the basis of HG modes [42,46]. An important feature of these techniques asserts that for measuring the intensity moments, only a single shot of the intensity pattern is required at the observation plane. For measuring the intensity moments of the second order, it was sufficient to restrict ourselves to computer processing of the intensity patterns employing Expressions (7), (29), and (30) for calculating the matrix elements $W_{ij}$, $i,j=1,2$ in Equations (23)–(25). Previously in Refs. [42,46,47], we developed techniques based on standard LG and HG mode bases. But in our case, the optical system contains an astigmatic element that does not allow employing standard $\mathrm{LG}$ modes to find the OAM in an optimal way, while computer processing based on elliptical $\mathrm{LG}$ mode basis [48] optimal for representing astigmatic beams has not yet been developed by us. Therefore, we chose the basis of the standard HG modes, a computer processing technique, which is discussed in detail in Ref. [42] where it is required to measure not only the squared amplitudes, but also the initial mode phases.

A sketch of the experimental setup is illustrated in Figure 9. The critical requirements for elements of the experimental setup are a high resolving power of the structured beam shaping and detection system, which affects the measurement error. Qualitative restoration of structured beams was achieved by using an SLM modulator Thorlabs EXULUS-4K1/M, Thorlabs, USA which allows shaping beams containing more than 150 modes and two complementary metal–oxide–semiconductor detectors CMOS1,2 (Michrome 20). Moreover, a high adjustment accuracy of photodetector and lenses required more precise movements, which were achieved using 6D optical stages with 3D displacements and 3D rotations (Thorlabs, USA “MAX603D”). The accuracy of the longitudinal displacements reached 50 $\mathsf{\mu }$m, and the angular rotations were up to ${50}^{\circ }$.

To measure the matrix elements $W_{ij}$ and the HG mode spectra, it is sufficient to computer-process the intensity pattern located either in the double focus of the cylindrical lens in Figure 9 (when studying the degeneracy of the $\mathbf{W}$ and $\mathbf{M}$ submatrices) or for studying the astigmatic OAM suppression with a spherical lens. The measured values of the matrix elements $M_{ij}$ were directly used in Equation (20) for plotting ellipses of the intensity moments in Figure 2 and Figure 6. A more complex measurement procedure had to be used in plotting linear dependencies between the intensity moment $M_{xy}$ and a total OAM ${\ell }_z$ in Figure 7a,b,d,e. If matrix elements $M_{xy}$ for various phase parameters $\theta$ can be found by only one measurement of the intensity pattern, then to determine the total OAM it was necessary to measure the entire mode spectrum (amplitudes and phases) for each $\theta$ and then calculate the OAM with Equation (15). The measurement results are shown in Figure 7 in the form of experimental points. The mean squared deviation from straight lines does not exceed 5%, which indicates a good agreement between theory and experiment. In addition, the result obtained allows us to use simple relations ${\ell }_z=4M_{xy}$ for $\epsilon =1$ and ${\ell }_z=2M_{xy}$ for $\epsilon \gg 1$ to find a total OAM in the next series of measurements.

To study the astigmatic OAM suppression after a spherical lens, it was necessary to compare the mode spectra at the correction plane with those of the sLG beam before the cylindrical lens, as well as to compare the theory and experiment for the OAM ${\ell }_z\left(Z_2\right)$ after a spherical lens. Typical mode spectra for the $\mathrm{asLG}$ beam with $n=\ell =5$ are shown in Figure 10. The upper line in the figure shows that the squared amplitude spectrum does not change along the beam length, whereas the phase spectrum (the bottom line) undergoes significant transformations in the vicinity of the beam correction plane caused by fast changes of the Gouy phase for x and y directions. At the Fourier plane, the Gouy phases are consistent, suppression of astigmatic OAM occurs, and the phase spectra for these planes (see callout at $Z_2=0.75$) become identical. It is important to note that the intensity patterns of the sLG beam before the astigmatic transform and at the plane of beam correction coincide with the correlation degree equal to 0.96 that (along with the coincidence of the phase spectra) experimentally confirms the suppression of astigmatic OAM by a spherical lens.

6. Discussion and Conclusions

The degenerate ring dislocations inherent in standard LG beams are destroyed in structured sLG beams, begetting a pair of topological vortex dipoles and causing fast OAM oscillations when the sLG beam phase parameter $\theta$ is varied, while the OAM does not exceed the azimuth number ℓ of the initial LG beam. The beam structure becomes more complicated when light passes through astigmatic elements, creating intricate traceries in the beam intensity patterns, and, in such a way, stimulating sharp OAM bursts, which may exceed the sum $\ell +n$ of the azimuthal and radial numbers. In order to analyze such a fine deep structure of such multi-parametric vortex beams, we proposed to employ a combination of techniques of symplectic ABCD matrices and symplectic intensity moment matrices appropriate for optical engineering. We have shown that the astigmatic structured beam model obtained by the ABCD matrix technique turns out to be simpler and more demonstrable compared to one via integral transformations [15] and takes significantly less time when computer simulating the asLG beams evolution with large quantum numbers. We have studied in detail the physical mechanisms of shaping the OAM super-bursts after a cylindrical lens at general astigmatic transforms and suppressing the astigmatic OAM constituted after a spherical lens. Thus, the measurement and analysis of the beam mode spectra showed that both amplitudes and phases of HG modes take part in shaping the OAM super-bursts after a cylindrical lens, whereas suppressing the OAM of the astigmatic constitute occurs only due to the phase redistribution, while the mode amplitudes remain unchanged.

On the other hand, employing the intensity moment techniques makes it possible to measure a diversity of the asLG beam optical features at different lengths of the beam passing through optical elements. We have combined techniques of the second-order and higher-order intensity moments. Symplectic transforms of the second-order moments make it possible to measure both the beam radii along the main directions of astigmatism, but also to reveal the geometric properties of the associated ellipses of intensity moments, while the higher-order intensity moments are key in the measuring technique of the mode spectra (amplitudes and phases) in complex structured beams. The combination of these techniques revealed a deep connection between the geometric properties of astigmatic structured beams and their OAM. We also revealed that with simple astigmatism, degeneration of the $\mathbf{W}$ and $\mathbf{M}$ submatrices of the symplectic matrix $\mathbf{P}$ occurs, which leads to a decrease in the number of degrees of freedom of the structured beam. But, on the other hand, degeneracy entails a directly proportional relationship between the coordinate element $W_{xy}$ and the twistedness elements $M_{xy}$ and $M_{yx}$ of the submatrix $\mathbf{M}$, which greatly simplifies the measurement of the total OAM, reducing the full cycle of measurements of the HG mode spectrum (amplitudes and phases) of the structured beam to the only measurement of the intensity moment. Moreover, we have shown that the Fourier transform by a spherical lens enables us to suppress the astigmatic OAM component and restore the original free-astigmatic sLG beam structure. However, with further propagation, the sLG beam restores its astigmatic structure while maintaining the maximum OAM. The simplified version of symplectic transformations considered by us can be widely used for engineering complex optical systems of the first order in devices and systems of modern photonics. In particular, it can be extended for analyzing structured Ince-Gaussian beams [19], for mapping various types of structured beams onto the orbital Poincare sphere, etc. In addition, a detailed study has not yet been carried out to classify stable structured vortex beams [36]. This can be achieved relatively simply by defining the main invariants of symplectic matrices of the second-order intensity moments and comparing the trajectory shapes on the orbital Poincare sphere. Moreover, the symplectic transform approach makes it possible to generalize the classical properties of structured beams for the purposes of quantum optics [22].