Abstract
The range accuracy of single-photon-array three-dimensional (3D) imaging systems is limited by the time resolution of the array detectors. We introduce a method for achieving super-resolution in 3D imaging through sub-bin delayed scanning acquisition and fusion. Its central concept involves the generation of multiple sub-bin difference histograms through sub-bin shifting. Then, these coarse time-resolution histograms are fused with multiplied averages to produce finely time-resolved detailed histograms. Finally, the arrival times of the reflected photons with sub-bin resolution are extracted from the resulting fused high-time-resolution count distribution. Compared with the sub-delayed with the fusion method added, the proposed method performs better in reducing the broadening error caused by coarsened discrete sampling and background noise error. The effectiveness of the proposed method is examined at different target distances, pulse widths, and sub-bin scales. The simulation analytical results indicate that small-scale sub-bin delays contribute to superior reconstruction outcomes for the proposed method. Specifically, implementing a sub-bin temporal resolution delay of a factor of 0.1 for a 100 ps echo pulse width substantially reduces the system ranging error by three orders of magnitude. Furthermore, Monte Carlo simulations allow to describe a low signal-to-background noise ratio (0.05) characterised by sparsely reflected photons. The proposed method demonstrates a commendable capability to simultaneously achieve wide-ranging super-resolution and denoising. This is evidenced by the detailed depth distribution information and substantial reduction of 95.60% in the mean absolute error of the reconstruction results, confirming the effectiveness of the proposed method in noisy scenarios.
1. Introduction
Three-dimensional (3D) single-photon imaging has made great progress in the past few decades, achieving high-precision imaging using a few reflected photons through a series of laser pulses with a high repetition frequency and narrow pulse width. It has great potential for applications such as long-range [1,2,3,4,5], high-speed [6,7,8], underwater [9,10,11,12,13], and high-precision depth imaging [14,15,16] with the continuous development of sparse-photon processing methods [17,18,19,20]. However, most current single-photon imaging systems are mainly based on single-pixel single-photon detectors or small-scale array detectors. These systems have the corresponding structure to achieve single-photon 3D imaging through scanning, which is often time-consuming and inefficient for imaging [21,22]. The advantage of a large-array single-photon detector is that it allows capturing without scanning. However, an array with multiple parallel detections has a trade-off between the single-pixel size and timing resolution. The time resolution of existing single-pixel single-photon detectors can reach tens of picoseconds [23]. However, for an array of single-photon detectors, adding pixels limits the size of the single-pixel readout circuit. Currently, common arrays of single-photon detectors often have an effective area of less than 10% and time resolution often exceeding several hundred of picoseconds [7,24,25,26]. Each pixel of the array single-photon detector must be equipped with a readout-integrated circuit to detect and extract avalanche signals; however, high-precision detection and extraction circuits often require a large area and high power consumption. Under this situation, the limited pixel size of the array single-photon detector causes great challenges and relatively high costs for highly integrated and high-precision array readout circuits; therefore, computational imaging methods to improve the ranging accuracy are being developed. Jitter information, which refers to added known noise, has been applied to improve the spatial resolution. In this study, we defined jitter information as the sub-bin delay scale between different sub-frame acquisitions and discrete quantitative resolution of the TDC as the time bin. For depth imaging, jitter provides a priori information to improve the ranging accuracy [27]. Chen et al. [28] proposed a three-laser-beam lidar system that sets the third optical path as a half-bin difference from the main path and used the additive average of the results of two measurements to correct the time-to-digital conversion (TDC) discrete sampling error. The optical delay can also achieve sub-bin delayed sampling by adding additional reference optical paths. However, this approach increases the optical system complexity linearly with the delay times increasing, especially under the multi-scale sub-bin delayed situation. In addition, changing the sub-bin delayed scales requires the optical system to also be redesigned. Therefore, this approach is not applicable in practical applications. The electronic delay is more flexible, facilitating a wider range of delay times. Rapp et al. [29] demonstrated the effectiveness of a subtractive-dithered time-correlated single-photon-counting ranging system for improving the depth resolution. Next, the dithered imaging generalised Gaussian instrument response function (IRF) approximation and exponentially modified Gaussian IRF model provided accurate ranging results from sub-bin delayed imaging [30,31,32]. Chang et al. [33] achieved kilometre-scale dither super-resolution depth imaging. These results demonstrate the effectiveness of additional sub-bin delays in improving the ranging resolution. However, for a narrow pulse-width echo with a coarse time-bin quantised single-photon detector, the echoes tend to be distributed between one or two time bins, and the IRF of such a system is difficult to obtain. If we use only multiple sub-delayed results with the subtractive dither, the reconstruction algorithm should be implemented multiple times, and the detailed sub-bin difference distribution caused by the sub-bin delay is not utilised.
Different from other sub-bin delay processing methods, which only use the known sub-bin delayed scale as a priori of photon flight time., in this paper, we pay more attention to the change in photon count histogram distribution caused by sub-bin delays, which is more suitable for photon counting imaging data. We found that the broadening of signal caused by coarsening time bin discrete sampling is related to the starting acquisition time. In addition, there is a signal distribution consistency prior to sub-bin delayed acquisition within a single frame. So, sub-bin delayed acquisition times are used as known prior to registration and multiplication as fusion processing in our method. It is possible to achieve the auto correlation of multiple sub-frame signals while increasing sampling, thereby effectively enhancing and refining the theoretical distribution of effective signal photon numbers and reducing broadening caused by coarse sampling for the photon count histogram. Specifically, we first analysed the relationship between the gate start time of TDC, quantisation error, and count distribution. Refined histograms with time-resolved differences were obtained by multiplying the fused multiple subframe coarsened histograms based on the a priori known sub-bin delays while assuming echo consistency. Finally, the arrival times of the echo photons were obtained from a sub-bin photon-counting histogram. By establishing a theoretical target model and using Monte Carlo simulations, we verified the applicability of the developed method under noisy conditions.
The remainder of this article is organised as follows. Section 2 introduces the observation model of the photon-counting imaging system. Section 3 introduces and analyses the quantisation error. Section 4 details the imaging principle of the sub-bin shift scanning acquisition and fusion method, and Section 5 presents the experimental results. Section 6 presents our discussion, which includes suggestions for future work.
2. Observation Model
The schematic diagram of a typical photon-counting 3D imaging system is depicted in Figure 1a. Laser pulses emitted from a high-frequency pulse laser illuminate the target scene, and the reflected photons from the target are detected by a single-photon detector for photon counting. An external trigger signal serves as the start signal for both the laser and the TDC module. When a photon is detected by the single-photon detector, TDC will receive a stop signal generated by the single-photon detector. The TDC then converts the time interval between the start and stop signals into a digital signal, recording as the photon arrival time to the single photon detector. Single-photon detectors do not allow distinction in the detection of the number of photons and only detect a photon or the absence of a photon; therefore, multiple pulses are continuously emitted and accumulated to achieve 3D imaging, utilizing time-correlated single-photon counting (TCSPC) techniques [34], as shown in Figure 1b, to obtain the photon-counting histograms and retrieval of the target distance.
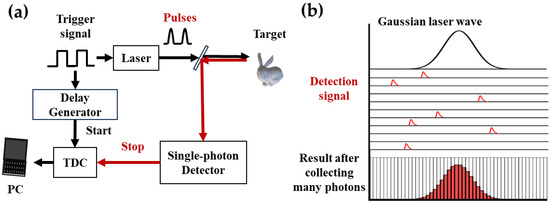
Figure 1.
(a) Diagram of single-photon 3D imaging system (PC, personal computer; TDC, time-to-digital conversion); (b) the principle of time-correlated single-photon counting.
Suppose that the distribution of laser pulses, , in a time series is an approximately Gaussian distribution given by
where is the maximum number of photons contained in a single pulse and τp is the laser pulse width. According to the linear transmission theory, the echo signal can be expressed as
where η is the detector quantum efficiency, is the intensity at pixel (i, j), is a constant denoting the background noise rate, is the dark count rate, , is the target distance, c is the speed of light, IRF is the per-pixel instrument response function, and ∗ represents the convolution operation. Under a low light intensity, the detector captures photon events as a random process obeying a Poisson distribution according to the probability theory of photon detection. The average number of echo photons in time bin at pixel (i, j) is given by
where represents a discrete sampling-time binary scale. For a general multipixel parallel readout detector, the detection probability of a single pixel is not affected by the photon distribution of other pixels. Let Y represent the data cube of Nr × Nc pixels and T histogram bins and be the observed photon count at pixel (i, j) and time bin , which obeys Poisson distribution . The probability of in the timeslot is expressed as
The likelihood function for the distribution of reflected photons is expressed as
Target distance R can be estimated by maximising the likelihood in Equation (5). This is equivalent to minimising the negative log-likelihood by removing irrelevant constants as follows:
3. Quantisation Error
The ranging error mainly considers the deviation between the system measurement and actual arrival time of the flying photons, which is caused by the limited time-resolved scale during discrete sampling of the single-photon detector. For the real distance of the target, R0, is the flight time of the laser pulse from the target emission to reflection. However, because of the TDC discrete sampling, the recorded photon arrival time, U, is a coarse time bin containing given by
where represents the quantisation. If the centre of the time bin is measured, time of flight can be included in the following expression:
When the system implements a delay-gating acquisition to reduce background noise, the gate start time is given by Ts, and Equation (9) can be rewritten as
The quantitative error is calculated as
Consider a target distance of 5.7 m, tbin = 1 ns, and Ts = 30–32 ns in intervals of 0.1 ns. The quantisation error distributions of the measurements at different gate start times are shown as black lines in Figure 1. When the start time of the time gate is set to 30 ns, the reflected echo is approximately at the junction of the eighth and nineth timeslots, while the quantisation error is negative, and the absolute error reaches the maximum in the entire period, . With the delay in the gate start time, the reflected echo gradually approaches the middle position of the eighth timeslot, and the quantisation error is still negative. However, the absolute error gradually decreases until the echo is approximately in the middle of the eighth timeslot, and the quantisation error is 0. As the delay gradually increases, the quantisation error becomes positive until it approaches the edge of the seventh timeslots, and the quantisation error reaches its maximum.
In practice, the reflected echo must have pulse width . Even for , if the reflected echo position is close to the boundary of the timeslot, the echo is distributed between the two timeslots. In this case, a more accurate reflected photon arrival time can be calculated by comparing the centroid with the weighted average of the distribution over one timeslot. Let Yn represent the number of photon-count distributions accumulated several times, obtaining an N × 1 vector that gathers the elements of the observation photon-count distribution over time, where N is the number of time bins in the acquisition gate. The centroid error can be calculated using Equation (12) as follows:
Consider an echo characterised by a Gaussian distribution with a pulse width of 200 ps and other fixed acquisition parameters. In Figure 2, the red curve indicates the distribution of the quantised centroid errors with respect to the gate start time. Weighted averaging across multiple timeslots reduces the absolute ranging error at the boundaries of the timeslots. In addition, when the reflected signal centroid is aligned with the midpoint between the two slots, the quantised centroid error is minimised to 0. Although the centroid contributes to error reduction, as , most collected results for the gate start times are still located within one timeslot. Therefore, the predominant source of error is the quantisation error arising from coarse discrete sampling.
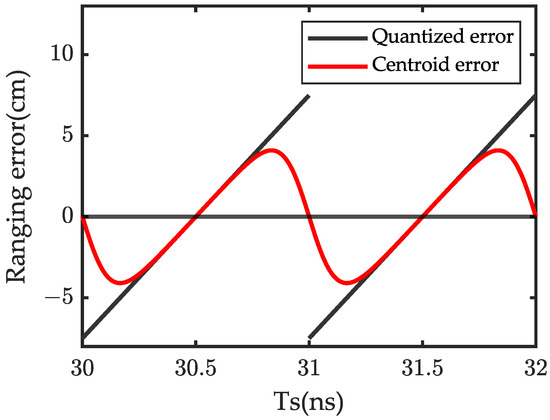
Figure 2.
Distribution of quantisation error and quantisation centroid error with difference gate start time at 5.7 m target distance.
4. Sub-Bin Delayed Acquisition Imaging and Fusion Method
Single photon detection often requires accumulating multiple pulses to obtain a single frame result. Therefore, the implementation of the sub-bin delayed scanning acquisition requires the acquisition and fusion of multiple sub-frames to obtain one frame. If the number of accumulated pulses per frame is Np and the sub-bin delays are implemented a K number of times, we define the accumulated Np/K pulses as subframe acquisition in this paper. For single-frame acquisition, we assume consistent reflected signals are unchanged target information. The theoretical signal remains consistent despite the addition of an acquisition start-time delay in the subframe. Thus, the recorded photon arrival time measurements contain sub-bin differences. By accumulating within multiple subframes, multiple coarse-resolution photon-count histograms with sub-bin differences can be obtained. We introduce a delay module to preselect the time gate before the trigger signal reaches the time to digital convert as shown in Figure 1. This is because the delay accuracy of the existing delayer is often very high. For example, the DG535 digital delay generator [35] can achieve a 5 ps digital delay control. Thus, the system achieves a sub-bin-resolved delay by precisely controlling the module parameters. After obtaining K coarse photon-counting histograms with sub-bin differences, we resolve the arrival time from each coarse photon-counting histogram by subtracting the known delays and averaging the results. As discussed in [28,31], where only sub-bin differences are used after solving for the statistical results, the sub-bin difference in each slot is not fully used. Hence, we apply multiplication or addition to a sub-bin delayed acquisition histogram fusion method to obtain an approximate sub-bin photon-counting histogram and improve the ranging accuracy. The method steps are detailed as follows:
- 1.
- Perform sub-bin alignment on coarse photon-count histograms obtained from multiple sub-bin delayed acquisitions.
- 2.
- Refine the coarse photon-counting histogram and equally divide the photon counts of each bin into sub-bin counts.
- 3.
- Multiply or add the refined histograms according to Equations (13) and (14).
- 4.
- Solve the photon-arrival time based on the results of step 3.
A schematic of the process of double delaying is depicted in Figure 3.
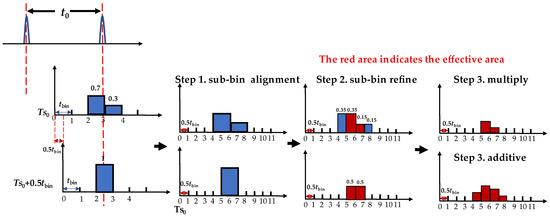
Figure 3.
Example of proposed method for double delaying.
We assume that the sub-bin delay scale is . The times of implemented sub-bin delays can be calculated as . If the first acquisition gate start time is set to , Ts is given by . The photon-counting histograms obtained from the subframes are represented as and gather the elements of the K observed sub-bin delayed photon-count distributions over time. contains K vectors of dimension N × 1. We assume that the target does not change in a single frame and only the sampling location changes. Therefore, the theoretical signal distribution remains consistent within a subframe. Multiple sub-bin-resolved acquisition histograms represent discrete samples of the same signal with a different sub-bin acquisition position. All the histogram values are non-negative. Along with the assumption of single-pixel signal consistency within a frame, multiple histograms of the sub-bin distribution theoretically continue to represent the signal after averaging through multiplication or summation. The specific formulation is expressed as
This is similar to the concept of multi-frame image spatial super-resolution, which leverages complementary information across various sequences. The sub-bin delay information is also mixed into the photon-counting histogram by processing the additive averaging or multiplying the averaging in each timeslot. Thus, multiplication can be used to fuse the coarse histograms of multiple sub-temporal-resolution delay differences, and the sub-temporal resolution differences can be introduced into each fine timeslot.
Consider a target distance of 6 m, , , , and . The photon-count histograms of coarse discrete sampling with sub-bin delay are shown in Figure 4.
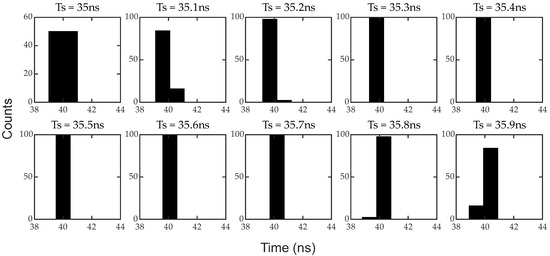
Figure 4.
Delay of 0.1 ns for acquisition coarse histograms at 6 m target distance.
The results of histogram fusion using different methods are shown in Figure 5. It can be seen that the photon-count distribution of direct measurement as shown in Figure 5b widened compared to Figure 5a and with any distribution information, which is mainly caused by coarsening the quantisation. Both the additive and multiplicative fusion methods can obtain photon-count distributions information as shown in Figure 5c,d, but Figure 5d seems more closer to Figure 5a. Different from the additive method, which retained all distributions by directly adding all the sub-bin counts, the signal consistency was checked while implementing the multiply fusing method. The value of any time bin including the reflected signal is not zero for any delayed acquisition, which means that any sub-bin that has one zero value is not an effective signal sub-bin. Multiplication can eliminate this area; if any sub-bin in every subframe has a zero value, multiplication results in zero. Therefore, multiplication can reduce the width of the edge regions caused by coarse discrete sampling during fusion. Similarly, the proposed multiplication fusion method can mitigate background noise with large variance.
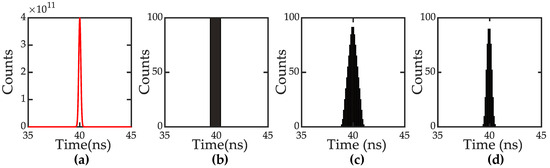
Figure 5.
Counts over time using different fusion methods. (a) Theoretical photon-count distribution. (b) Direct measurement histogram distribution. (c) Additive fusion-count distribution. (d) Multiplicative fusion-count distribution.
5. Simulations and Results
First, we analyse the proposed method under different sub-bin delay effects. Consider a Gaussian distribution for echo pulse width . The maximum target distance is set to 5.78 m, and the closest distance is set to 5.48 m for , , and a time gate range of 20 ns. The results of the ranging error distribution for different sub-bin delay scales and methods are shown in Figure 6. The range error can be reduced using both subtractive dither and the proposed method by implementing a certain sub-bin delay. However, at a given sub-bin delay scale, the proposed method always has a smaller ranging error than subtractive dither, demonstrating its effectiveness under different sub-bin delay scales. With a delay of 1/2 ns, the period over which the ranging error varies with the theoretical distance is reduced to half the initial period, as illustrated in Figure 6a. This phenomenon is further exemplified in Figure 6b–d, where delays of 1/4 ns, 1/5 ns, and 1/10 ns also exhibit similar effects. As the sub-bin delay scale decreases, the error period is correspondingly shortened to 1/4 ns, 1/5 ns, 1/10 ns. In Section 3, we dis-cussed the relationship between the quantisation error period and the quantization error and found that the period corresponding to the quantization error corresponds exactly to one quantisation time slot; theoretically speaking, implementing the sub-bin delay K times with a 1/K ns scale can reduce the quantization resolution of the system to 1/K ns. Therefore, the improvement of the proposed method depends on the delay accuracy of the delay module. The highest delay accuracy of the DG535 delayer system can reach 5 ps.
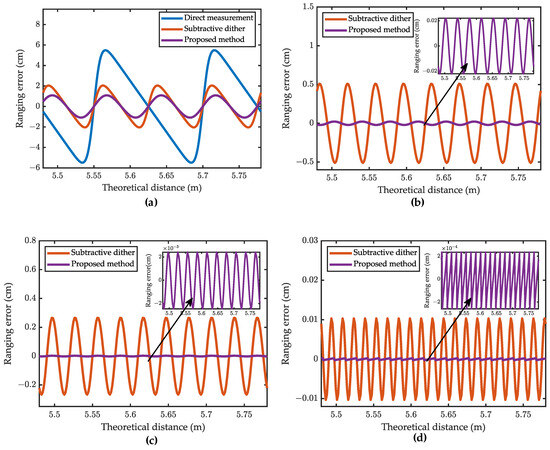
Figure 6.
Distribution of ranging error with theoretical distance for (a) , (b) , (c) , and (d) .
We also constructed an inclined flat target to simulate a distance range from 5.48 m to 5.78 m. Consider of 1/5 ns as an example to evaluate the proposed method for reducing the ranging error with the theoretical distance for different reflected echo pulse widths. The distributions of the calculated and theoretical distances for different pulse widths are shown in Figure 7 and Figure 8. The mean absolute error (MAE) is computed for each reconstructed depth image to evaluate the efficacy of different methods in estimating depth images.
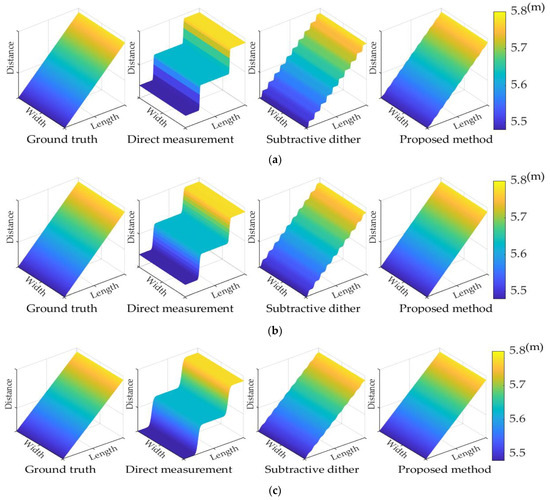
Figure 7.
Reconstructed target distances at reflected echo pulse width τ of (a) 20 ps, (b) 50 ps, and (c) 100 ps.
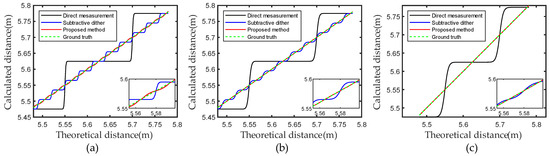
Figure 8.
Distribution of calculated and theoretical distances for pulse width τ of (a) 20 ps, (b) 50 ps, and (c) 100 ps.
As shown in Figure 7 and Figure 8, for any pulse width, the reconstruction results of the proposed method are consistently closer to the real image. When the pulse width is very small, the details of the sub-bin-resolved delay distribution at a delay scale of 0.2 ns are limited. Therefore, the proposed method slightly outperforms subtractive dither reconstruction. For τ = 20 ps and tsub = 1/5 ns, the subtractive dither reduces the MAE by 82.55%, whereas the proposed method reduces it by 96.40% for a pulse width of 100 ps. The sub-bin delay scale provides more details about the sub-bin count histogram distribution. The proposed method yields good reconstruction results, as shown in Figure 7c and Figure 8c. The abstractive dither reduces the MAE by nearly one order of magnitude, whereas the proposed method reduces it by approximately three orders of magnitude, as shown in Table 1. Hence, the sub-bin differential distribution information obtained using the proposed method contributes to the reconstruction accuracy.

Table 1.
MAE for different echo pulse widths and methods.
However, with an increase in pulse width, the reconstruction results tend to be closer to the ground truth when the sub-bin delay processing is employed which conflicts with our general understanding that a larger pulse width results in a low measurement accuracy. From the perspective of reconstruction, when the pulses are distributed over one time bin, a more accurate centroid position can be obtained by weighing the distribution of multiple time bins. The impact of pulse width on measurement error was discussed in Section 3. In this study, although pulse widths were set to be shorter than the time bin width, under the sub-bin delay acquisition, a longer pulse width results in the photon counts, distributed in the two bins, to be collected more times. As a result, our simulation results have higher measurement accuracy when the echo pulse width is larger. In this paper, we set all pulse widths to be smaller than the time bin width; however, the larger the pulse width, the more times the photon counts distributed in the two bins are collected during sub-bin delay shifting acquisition. So, the simulation results have higher measurement accuracy when the echo pulse width is larger. In order to analyse the performance of the proposed method under noise conditions, we built a tank model to simulate a distance ranging from 5.5 m to 5.8 m for , , , and 0.1 photons per pulse for a single pixel. The signal-to-background noise ratio (SBR) was set to 2 to establish a high-SBR scenario and to 0.05 to establish a low-SBR scenario. The number of simulation acquisitions per frame was set to 1000, corresponding to 100 acquisitions per subframe. A Monte Carlo simulation was used to describe the reflected photons along with Equations (1)–(4). The simulation reconstruction results are shown in Figure 9. Table 2 lists the MAE under different noise conditions.
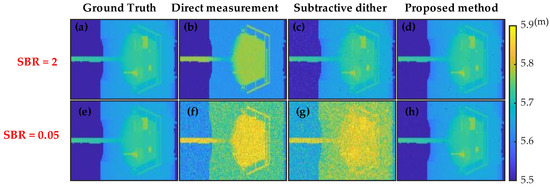
Figure 9.
(a,e) Ground truth. (b,f) Direct measurement reconstruction results for different SBR levels. (c,g) Subtractive dither reconstruction results for different SBR levels. (d,h) Proposed method reconstruction results for different SBR levels.

Table 2.
MAE of different reconstruction methods.
As shown in Figure 9a–d, both subtractive dither and the proposed method can improve the range resolution in the high-SBR scenario. Subtractive dither and the proposed method reduce the MAE by 71.37% and 87.68%, respectively. Figure 9e–h shows that the proposed method has a better performance in the low-SBR scenario because it achieves consistency across multiple subframes for multiplication fusion, thereby filtering background noise by exploiting its large variance characteristics. Therefore, the influence of background noise on the range resolution and error can be mitigated, achieving an MAE reduction of 95.60% at an SBR of 0.05.
The increase in acquisition time caused by additional delayed scanning is also a concern. A longer time can improve the signal-to-noise ratio by accumulating multiple pulses. Therefore, we mainly simulated under a low-SBR scenario, where SBR = 0.05, and collected the reconstruction results with different acquisition times set to , , , and 0.1 photons per pulse for a single pixel. The pulses contained in each frame of direct measurement are 200 pulses, 500 pulses, 1000 pulses and 2000 pulses; the number of pulses per sub-frame were set to 20, 50, 100 and 200, respectively, which can ensure that direct measurement and sub-bin delayed measurement set the same acquisition time per frame. The simulation reconstruction result is shown in Figure 10.
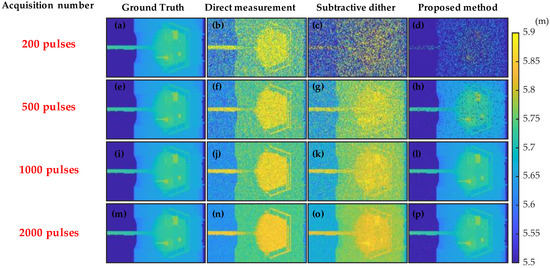
Figure 10.
(a,e,i,m) Ground truth. (b,f,j,n) Direct measurement reconstruction results for different acquisition pulse numbers. (c,g,k,o) Subtractive dither reconstruction results for different acquisition pulse number. (d,h,l,p) Proposed method reconstruction results for different acquisition pulse numbers.
Figure 10d–h reveals that, under the condition of accumulating two hundred pulses per frame, the average number of collected signal photons per frame is approximately 20. The theoretical average number of photons in an individual sub-frame is merely 2. At this point, several effective signal regions have not captured any photons, leading to partial signal loss during the multiplicative fusion process. Therefore, when applying the proposed method, the theoretical number of photons accumulated in each sub-frame should exceed 10 photons, as illustrated in Figure 10l.
We note that, if direct measurement and subtractive dither measurement are employed, a higher acquisition pulse number is required to achieve better reconstructed images, as shown in Figure 10b,f,j,n and Figure 10c,g,k,o. Due to the denoising capability of the proposed method in this study, the acquisition time for a single frame is reduced, and this method is even able to obtain reconstructed images that are superior to the direct measurement method with less acquisition pulses as shown in Figure 10l,n,o. Therefore, we can consider that the additional scanning time introduced by sub-bin delay in our proposed method does not significantly extend the imaging time.
Furthermore, with a long accumulation time, the consistency of noise will be enhanced, thereby reducing the denoising effectiveness of direct multiplicative fusion, as depicted in Figure 10o. In such cases, the impact of noise can be mitigated through preprocessing with a threshold setting followed by fusion processing.
6. Discussion
We established a mathematical model to investigate the influence of the gate start time on the quantisation error of photon-counting 3D imaging. Our analysis revealed the periodic nature of the quantisation error with respect to the gate start time. Subsequently, a novel sub-bin delay scanning acquisition and fusion method was developed to mitigate the quantisation error, enhance the range resolution of the system, and improve the ranging accuracy. Subsequently, a distance target model was built to assess the influence of the delay scale and reflected echo width on distance reconstruction. The results show that by shortening the delay, the system improves the depth resolution and ranging accuracy. Furthermore, because the proposed method employs correlation fusion across multiple subframes, it systematically assesses the signal consistency during sub-bin gap determination. Because the variance of the background noise is much larger than that of the signal, we mitigate the noise to improve the results even under a low SBR. To ensure correlation among multiple subframes, more than 10 photons should be preferably collected in a single subframe. When few photons are collected, which leads to high randomness in the subframe distribution and reduced consistency, it is recommended to employ additive fusion and denoising during reconstruction. Additionally, to ensure the integrity of delayed sampling, we conducted a performance analysis under known equal-interval delays, leaving the investigation of data processing under random sub-bin delays for future work. Relevant articles have been explored on the acquisition of experimental data for sub-bin delays. We will continue to study the reliability of the proposed method under experimental data in the future. In addition, we will explore other spatial super-resolution methods for application to photon-counting imaging systems and possibly extend them to other super-resolution applications.
Author Contributions
Conceptualisation, H.-M.Y.; methodology, H.-M.Y. and H.Z.; writing—original draft preparation, H.-M.Y.; investigation, H.-M.Y. and M.-Y.Y.; supervision, H.Z. and X.-W.F.; validation. Y.-A.L. and L.-Z.S.: writing—review and editing, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by a grant from State Key Laboratory of Transient Optics and Photonics, Chinese Academy of Sciences (SKLST202219).
Data Availability Statement
The data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, Z.-P.; Huang, X.; Cao, Y.; Wang, B.; Li, Y.-H.; Jin, W.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z. Single-photon computational 3D imaging at 45 km. Photonics Res. 2020, 8, 1532–1540. [Google Scholar] [CrossRef]
- Li, Z.-P.; Ye, J.-T.; Huang, X.; Jiang, P.-Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z.; et al. Single-photon imaging over 200 km. Optica 2021, 8, 344–349. [Google Scholar] [CrossRef]
- Krichel, N.J.; McCarthy, A.; Buller, G.S. Resolving range ambiguity in a photon counting depth imager operating at kilometer distances. Opt. Express 2010, 18, 9192–9206. [Google Scholar] [CrossRef]
- Chan, S.; Halimi, A.; Zhu, F.; Gyongy, I.; Henderson, R.K.; Bowman, R.; McLaughlin, S.; Buller, G.S.; Leach, J. Long-range depth imaging using a single-photon detector array and non-local data fusion. Sci. Rep. 2019, 9, 8075. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, B.; Wang, R.; Li, Z.; Chen, Z.; Zhao, B.; Guo, G.; Fan, W.; Huang, F.; Yang, Y. Photon counting lidar working in daylight. Opt. Laser Technol. 2023, 163, 109374. [Google Scholar] [CrossRef]
- Tachella, J.; Altmann, Y.; McLaughlin, S.; Tourneret, J.-Y. On fast object detection using single-photon lidar data. In Proceedings of the Wavelets and Sparsity XVIII, San Diego, CA, USA, 13–15 August 2019; Volume 11138, pp. 252–261. [Google Scholar] [CrossRef]
- Gyongy, I.; Hutchings, S.W.; Halimi, A.; Tyler, M.; Chan, S.; Zhu, F.; McLaughlin, S.; Henderson, R.K.; Leach, J. High-speed 3D sensing via hybrid-mode imaging and guided upsampling. Optica 2020, 7, 1253–1260. [Google Scholar] [CrossRef]
- Altmann, Y.; McLaughlin, S.; Davies, M.E. Fast online 3D reconstruction of dynamic scenes from individual single-photon detection events. IEEE Trans. Image Process. 2019, 29, 2666–2675. [Google Scholar] [CrossRef] [PubMed]
- Maccarone, A.; McCarthy, A.; Tachella, J.; Garcia, D.A.; Della Rocca, F.M.; Altmann, Y.; McLaughlin, S.; Henderson, R.; Buller, G.S. Underwater depth imaging using time-correlated single-photon counting at video frame rates. In Proceedings of the Electro-Optical Remote Sensing XIII, Strasbourg, France, 9–10 September 2019; pp. 125–133. [Google Scholar] [CrossRef]
- Shi, H.; Qi, H.; Shen, G.; Li, Z.; Wu, G. High-resolution underwater single-photon imaging with Bessel beam illumination. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 8300106. [Google Scholar] [CrossRef]
- Halimi, A.; Maccarone, A.; McCarthy, A.; McLaughlin, S.; Buller, G.S. Object depth profile and reflectivity restoration from sparse single-photon data acquired in underwater environments. IEEE Trans. Comput. Imaging 2017, 3, 472–484. [Google Scholar] [CrossRef]
- Altmann, Y.; Ren, X.; McCarthy, A.; Buller, G.S.; McLaughlin, S. Robust Bayesian target detection algorithm for depth imaging from sparse single-photon data. IEEE Trans. Comput. Imaging 2016, 2, 456–467. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, S.; Wang, J.; Ma, C.; Su, X. Precision improvement of underwater single photon imaging based on model matching. IEEE Photonics Technol. Lett. 2023, 35, 253–256. [Google Scholar] [CrossRef]
- Heide, F.; Diamond, S.; Lindell, D.B.; Wetzstein, G. Sub-picosecond photon-efficient 3D imaging using single-photon sensors. Sci. Rep. 2018, 8, 17726. [Google Scholar] [CrossRef]
- Ren, X.; Connolly, P.W.; Halimi, A.; Altmann, Y.; McLaughlin, S.; Gyongy, I.; Henderson, R.K.; Buller, G.S. High-resolution depth profiling using a range-gated CMOS SPAD quanta image sensor. Opt. Express 2018, 26, 5541–5557. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Yin, Y.; Sun, B. High precision 3D imaging with timing corrected single photon LiDAR. Opt. Express 2023, 31, 24481–24491. [Google Scholar] [CrossRef]
- Harmany, Z.T.; Marcia, R.F.; Willett, R.M. This is SPIRAL-TAP: Sparse Poisson intensity reconstruction algorithms—Theory and practice. IEEE Trans. Image Process. 2011, 21, 1084–1096. [Google Scholar] [CrossRef]
- Tachella, J.; Altmann, Y.; Ren, X.; McCarthy, A.; Buller, G.S.; Mclaughlin, S.; Tourneret, J.-Y. Bayesian 3D reconstruction of complex scenes from single-photon lidar data. SIAM J. Imaging Sci. 2019, 12, 521–550. [Google Scholar] [CrossRef]
- Rapp, J.; Goyal, V.K. A few photons among many: Unmixing signal and noise for photon-efficient active imaging. IEEE Trans. Comput. Imaging 2017, 3, 445–459. [Google Scholar] [CrossRef]
- Lussana, R.; Villa, F.; Dalla Mora, A.; Contini, D.; Tosi, A.; Zappa, F. Enhanced single-photon time-of-flight 3D ranging. Opt. Express 2015, 23, 24962–24973. [Google Scholar] [CrossRef] [PubMed]
- Kirmani, A.; Venkatraman, D.; Shin, D.; Colaço, A.; Wong, F.N.; Shapiro, J.H.; Goyal, V.K. First-photon imaging. Science 2014, 343, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.; Xu, F.; Wong, F.N.; Shapiro, J.H.; Goyal, V.K. Computational multi-depth single-photon imaging. Opt. Express 2016, 24, 1873–1888. [Google Scholar] [CrossRef] [PubMed]
- Cova, S.; Lacaita, A.; Ghioni, M.; Ripamonti, G.; Louis, T.A. 20-ps timing resolution with single-photon avalanche diodes. Rev. Sci. Instrum. 1989, 60, 1104–1110. [Google Scholar] [CrossRef]
- Henderson, R.K.; Johnston, N.; Hutchings, S.W.; Gyongy, I.; Abbas, T.A.; Dutton, N.; Tyler, M.; Chan, S.; Leach, J. 5.7 A 256 × 256 40 nm/90 nm CMOS 3D-stacked 120 dB dynamic-range reconfigurable time-resolved SPAD imager. In Proceedings of the 2019 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 106–108. [Google Scholar] [CrossRef]
- Della Rocca, F.M.; Mai, H.; Hutchings, S.W.; Al Abbas, T.; Buckbee, K.; Tsiamis, A.; Lomax, P.; Gyongy, I.; Dutton, N.A.; Henderson, R.K. A 128 × 128 SPAD motion-triggered time-of-flight image sensor with in-pixel histogram and column-parallel vision processor. IEEE J. Solid-State Circuits 2020, 55, 1762–1775. [Google Scholar] [CrossRef]
- Villa, F.; Lussana, R.; Bronzi, D.; Tisa, S.; Tosi, A.; Zappa, F.; Dalla Mora, A.; Contini, D.; Durini, D.; Weyers, S.; et al. CMOS imager with 1024 SPADs and TDCs for single-photon timing and 3-D time-of-flight. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 364–373. [Google Scholar] [CrossRef]
- Raghuram, A.; Pediredla, A.; Narasimhan, S.G.; Gkioulekas, I.; Veeraraghavan, A. Storm: Super-resolving transients by oversampled measurements. In Proceedings of the 2019 IEEE International Conference on Computational Photography (ICCP), Tokyo, Japan, 15–17 May 2019; pp. 1–11. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, R.; Li, X.; Dong, Z.; Zhou, Z.; Ye, G.; Chen, D. Accuracy improvement of imaging lidar based on time-correlated single-photon counting using three laser beams. Opt. Commun. 2018, 429, 175–179. [Google Scholar] [CrossRef]
- Rapp, J.; Dawson, R.M.; Goyal, V.K. Dither-enhanced lidar. In Applications of Lasers for Sensing and Free Space Communications; JW4A-38; Optica Publishing Group: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Rapp, J.; Dawson, R.M.; Goyal, V.K. Improving lidar depth resolution with dither. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1553–1557. [Google Scholar] [CrossRef]
- Rapp, J.; Dawson, R.M.; Goyal, V.K. Dithered depth imaging. Opt. Express 2020, 28, 35143–35157. [Google Scholar] [CrossRef] [PubMed]
- Rapp, J.; Dawson, R.M.; Goyal, V.K. Estimation from quantized Gaussian measurements: When and how to use dither. IEEE Trans. Signal Process. 2019, 67, 3424–3438. [Google Scholar] [CrossRef]
- Chang, J.; Li, J.; Chen, K.; Liu, S.; Wang, Y.; Zhong, K.; Xu, D.; Yao, J. Dithered depth imaging for single-photon lidar at kilometer distances. Remote Sens. 2022, 14, 5304. [Google Scholar] [CrossRef]
- Buller, G.; Wallace, A. Ranging and three-dimensional imaging using time-correlated single-photon counting and point-by-point acquisition. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 1006–1015. [Google Scholar] [CrossRef]
- Digital Delay Generator. Available online: https://thinksrs.com/products/dg535.html (accessed on 1 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).